Open Access Article
Open Access ArticleConnecting the complex microstructure of LDPE to its rheology and processing properties via a combined fractionation and modelling approach
Kristina Maria Zentel ac,
Paul Severin Eselem Bungu
ac,
Paul Severin Eselem Bungu b,
Jonas Degenkolbc,
Harald Pasch
b,
Jonas Degenkolbc,
Harald Pasch *b and
Markus Busch
*b and
Markus Busch *c
*c
aUniversität Hamburg, Institute for Technical and Macromolecular Chemistry, Bundesstr. 45, 20146 Hamburg, Germany
bUniversity of Stellenbosch, Department of Chemistry and Polymer Science, PO Box X1, 7602 Matieland, South Africa. E-mail: hpasch@sun.ac.za
cTechnical University of Darmstadt, Institute for Technical and Macromolecular Chemistry, Alarich-Weiß-Straße 8, 64287 Darmstadt, Germany. E-mail: markus.busch@pre.tu-darmstadt.de
First published on 7th October 2021
Abstract
Well-defined mini-plant low density polyethylene samples were fractionated preparatively according to their crystallizability via preparative temperature rising elution fractionation and according to molecular weight via preparative solvent gradient fractionation (pSGF). Rheology of the fractions was measured in both the small amplitude oscillatory shear (SAOS) and the non-linear extension regimes. The linear and non-linear rheology of the pTREF fractions were dominated by molecular weight effects, while the impact of the higher degree of long chain branching for the pSGF fractions with higher molecular weights was observed in van Gurp–Palmen plots and in strain hardening behavior in the extensional rheology measurements. Additionally, the experimental fractionation process was mimicked via modelling. The branching topologies of the bulk samples were obtained by coupled kinetic and Monte Carlo calculations. These topologies were fractionated computationally and the result were used to predict the rheological behavior of the individual fractions by applying the BoB algorithm with no parameter adjustment. The experimental observed trends were predicted by the model and the overall agreement was acceptable. This study demonstrates, that polymer fractionation is possible on a preparative scale and allows for the polymer flow properties characterization of the individual fractions, a method that is highly relevant during processing. Moreover, the fractionation process is followed and understood from the modelling point of view.
Introduction
Polyethylene (PE) is a polymeric material of high industrial relevance mainly due to its extremely broad field of applications.1 Although PE is chemically simple, its microstructure is very complex, especially with respect to short- and long-chain branching (SCB and LCB, respectively).2 While HDPE (high density PE) consists of mainly linear macromolecules, LLDPE (linear low density PE) exhibits SCB and LDPE (low density PE) shows the most extraordinary structure with both SCB and LCB. SCB in LLDPE stems from the copolymerization of ethylene with higher α-olefins while branches in LDPE are formed during the free radical polymerization process via intra- and intermolecular transfer to polymer backbone chains and subsequent chain growth. Thus, these branches are produced randomly and vary strongly in number and length. The different microstructural diverse products define the final product properties, such as density, crystallinity, solubility and viscosity.3 Analytical methods such as size exclusion chromatography (SEC), nuclear magnetic resonance (NMR) or crystallization-based methods facilitate the detailed characterization of these materials, especially the quantification of molecular weight and SCB density.4–8In addition, LCB in LDPE influences the processing behavior significantly, especially the extensional behavior, and are thus investigated by rheology.8–14 For instance, the hydrodynamic radius of a LCB polymer is significantly smaller compared to its linear counterpart of the same molecular weight.7 On the other hand, linear macromolecules can rearrange and relax stress via reptation, whereas branched molecules relax hierarchically from the outside segments inwards via different relaxation mechanisms.15–17 The linear viscoelastic regime of polymers is usually characterized by frequency sweeps in small amplitude oscillatory shear (SAOS) measurements, and is strongly dominated by molecular weight and polydispersity. However, a van Gurp–Palmen plot, which gives the phase angle versus the absolute value of the complex modulus |G*|, can be used to characterize both LCB and the effect of polydispersity from SAOS measurements.18–20
When looking at the non-linear regime in rheology, LCB show a more significant impact on flow behavior.12–14,20,21 It could be demonstrated, that large amplitude oscillatory shear (LAOS) measurements in combination with Fourier transform rheology is sensitive to long-chain branching in polyolefins.11–14 In addition, LCB increases the network connectivity in polymer melts and thus reduces the rate of disentanglement when external stress is applied. In this case, the so-called strain hardening is observed: a strong increase in elongation viscosity with time.10 This effect can be measured via extensional rheology22 and is more pronounced for polymers with a higher degree of branching and longer branch length.23 With regard to processing, strain hardening is regarded as beneficial in the context of film blowing, blow molding, foaming or fiber spinning.24
In addition to sensitive measurements, polymer properties and rheological responses can be predicted theoretically by various models.25 Non-linear responses can be simulated using nonlinear constitutive equations such as the Giesekus model,26 the Pom–Pom model23,27 or the molecular stress function theory.28 However, rheological parameters used for modelling often have to be determined by fitting to experimental data.
Typically, a LDPE sample that exhibits a broad molecular weight distribution and displays a high degree of LCB can be regarded as a blend of molecules that strongly vary in length, number of branches and consequently would exhibit a very broad distribution of relaxation times. This makes it very challenging to understand the direct effect of all the microstructural parameters affecting the melt flow behavior. In order to enhance this understanding, models that combine the polymeric architecture and rheological behavior, such as the Pom–Pom model,27 have been proven to be very beneficial. Most recently it was shown that coupling kinetic, stochastic and rheological modelling is an approach capable of predicting LDPE flow behavior based on the reaction conditions applied during polymerization.29,44 This approach was validated on a set of mini-plant LDPE samples, of which two samples were fractionated preparatively in a previous study.30 The advantage of this preparative fractionation approach is that a highly heterogeneous and complex material can be separated into fractions with narrow molecular properties such as molecular weight and branching/crystallinity.4,6,31
For the purpose of this study, well-defined LDPE samples from a high-pressure mini-plant set-up are investigated, which were specifically fractionated and subsequently characterized comprehensively. Two preparative fractionation techniques were applied: temperature rising elution fractionation (pTREF) and preparative solvent gradient fractionation (pSGF). pTREF fractionates macromolecules predominately according to their crystallizability on nucleating supports, which is defined mainly by branches. On the other hand, pSGF provides fractions with similar SCB density but varying molecular weight.30 Those techniques were developed and widely used, when the determination of the molecular weight distribution via size exclusion chromatography was not yet established as the standard method.32,33 To the knowledge of the authors such fractions have rarely been subject to rheological investigations34,35 and were never coupled to a corresponding modelling approach, although their careful investigation in the linear and non-linear flow should provide interesting insights into the flow behavior of complex LDPEs.
Moreover, the three-step modelling approach used with the bulk samples provides an ensemble of detailed polymeric microstructures. This includes exact chain lengths and branching distributions (frequency and length). The structures or topologies are produced stochastically and are based on the kinetic network of the LDPE polymerization. These microstructural parameters were used to follow the fractionation process computationally, to check the robustness and validity of the method. This is interesting from an academic point of view as the contribution of the individual fractions to the bulk flow behavior are determined. At the same time it is industrially relevant as it enhances the understanding of how branched LDPE materials are formed in the reactor during the polymerization process and how this affects processing and product properties. This finally enables simulation-based product design, which is highly time- and cost-efficient compared to trial-and-error approaches on an experimental basis.
Materials and analytical methods
In order to understand the complex interplay of LDPE microstructure and flow properties of long-chain branched materials, two LDPE samples (code 04-2 and 03-4) and their respective fractions were chosen for a detailed examination. The bulk samples were produced in a continuously operated mini-plant scaled 100 mL autoclave reactor under well-defined steady-state conditions at 2000 bar and 250 °C. The detailed experimental conditions can be found in literature.29 The samples were characterized with respect to their molecular weight distributions, branching densities and crystallizabilities, which was described in a previous study.30 In order to gain detailed insight into the complex microstructure, the samples were fractionated preparatively. One sample (04-2) was fractionated via pTREF, and the other sample (03-4) was fractionated by means of pSGF. The fractionation processes were repeated in order to gain sufficient material (2.5 g) for rheological investigations of the individual fractions.Rheological characterization
The PE samples were stabilized with 500 ppm Irganox 1010 and 1000 ppm Irgafos 168 and then hot-pressed at 200 °C and 200 bar into discs (for frequency sweeps) or strips of 1 mm thickness (for extension rheology). The rheological measurements were performed on Physica MCR 300 Anton Paar rheometers under a nitrogen atmosphere and repetitive measurements gave identical results. Oscillatory frequency sweeps were made using a 25 mm parallel plate geometry with a sample thickness of 1 mm in the linear range of deformation (5% strain). Measurements were performed at 150 °C, 170 °C and 190 °C and a master curve was obtained via time–temperature superposition at 150 °C. Extensional rheology was measured with the stretching device SER (Sentmanat Elongational Rheology). After clamping the sample onto the cylinders, they were tempered at 150 °C. Elongational rheology was measured at Hencky strain rates![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) from 0.05 s−1 to 10 s−1.
from 0.05 s−1 to 10 s−1.
Modelling strategy
In order to predict the flow behavior of the LDPE samples and their fractions, the modelling strategy depicted in Fig. 1 was used. The rheology of long-chain branched materials such as LDPE is determined by both its molecular weight distribution (MWD) and the branching. The effect of branching is particularly complex, as the number of branches, the branch length and the branch type (between the two extremes of star and comb) have an effect on stress relaxation and thus flow behavior. For this reason, it is essential to know the MWD and the detailed branching structure of the material in question.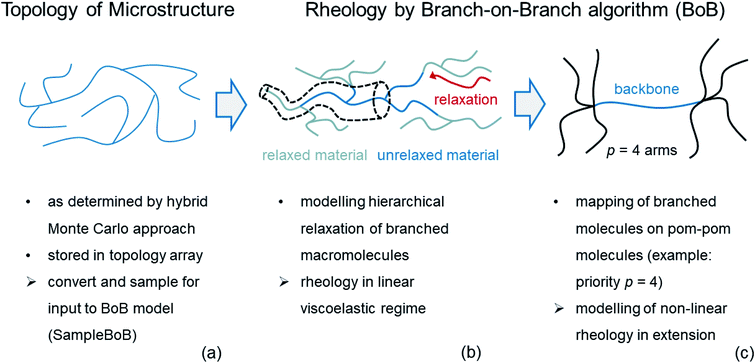 | ||
| Fig. 1 Schematic depiction of the modelling strategy: branching structures are taken from Monte Carlo models and used to perform linear and non-linear rheology simulations via the BoB algorithm.36 | ||
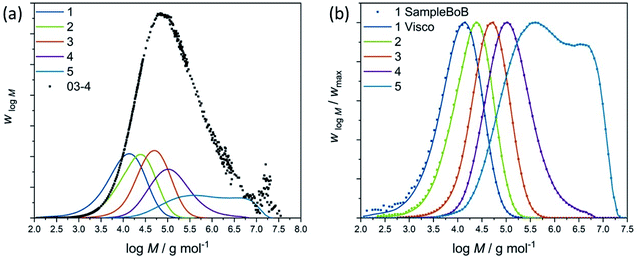
The biggest advantage of this study and approach is that a representative set of topologies of individual microstructures is available for the bulk samples. It was determined by a hybrid stochastic Monte Carlo approach in a previous study29 and consists of five million molecules. The ensemble was modelled by a method,37 which is only based on process conditions and the kinetics of the systems so that no assumptions about structure, branching density, distribution or length etc. were made. Moreover, the agreement between model and experiment was checked extensively by means of comprehensive analytics,29,30 which indicated the modelling approach used to model the individual branching structures are valid and gave representative topologies. These structures are stored in topology arrays. Due to the flexible data structure of the BoB algorithm, the individual microstructures generated by the Monte Carlo algorithm can be used as the basis to calculate the full rheological response of randomly branched LDPE. However, they have to be converted with respect to topology structure and sample (reduced in number) to serve as an input for the BoB algorithm in the first step.36 Therefore, the algorithm SampleBoB29 restructures the topology arrays and reduces the number of molecules per bin on a logarithmic molar mass axis to a maximum per bin and then weights them with respect to their contribution to the MWD. For the bulk samples, the original MWD from the Monte Carlo simulation is used for rescaling, while for the fractions the experimental determined MWDs via SEC (size exclusion chromatography) are used. This procedure is demonstrated for the pSGF fractions in Fig. 2(a). The MWD of the Monte Carlo ensemble from the bulk material is shown (black dots) together with the MWD of the fractions (lines 1–5), which were measured by SEC with an online viscometer (SEC-Visco). The topologies of the Monte Carlo ensemble were then sampled following these experimentally determined MWDs by SampleBoB so that five separate ensembles were obtained. The good agreement between the sampled MWDs (dots) and the experimental ones (lines) is demonstrated in Fig. 2(b).
With this approach, SampleBoB was developed as an effective interface between the Monte Carlo simulation and the BoB algorithm: the topology ensemble is reduced to a manageable and suitable size for the BoB algorithm (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 100
000 to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 macromolecules), while the highest possible amount of branching and topology information is maintained, especially in the high molecular weight area.
000 macromolecules), while the highest possible amount of branching and topology information is maintained, especially in the high molecular weight area.
The actual rheology is modelled in the next step by the BoB algorithm of Das et al..17,38 This algorithm is capable of modelling the flow behavior of branched polymers in the linear viscoelastic regime as well as in non-linear shear and extension if detailed information about the branching structure of the macromolecules to be modelled is available. The rheology modelling itself is also divided into two steps: firstly, the relaxation of branched molecules in the linear viscoelastic regime is followed. From a theoretical point of view branched polymers are assumed to relax from the outside inwards, which is known as hierarchical relaxation and is schematically depicted in Fig. 1(b). While the terminal arms relax first via contour-length fluctuation, the branch points can only relax by so-called branch point hopping along the backbone path, when the corresponding arms have relaxed. As soon as only a linear segment is left, it can relax via reptation and finally, the central segment escapes its confining tube (reptation theory). After successful modelling of the linear viscoelastic regime, the non-linear flow is modelled. In this work, the Pom–Pom model developed by McLeish and Larson27 will be applied, which is based on an idealized Pom–Pom molecule as depicted in Fig. 1(c). The backbone segment indicated in blue has two branch points with p arms on each side. In non-linear flow, the polymer chains and their respective tubes experience a strong orientation as well as a stretch in the direction of flow, which leads to extension hardening (extensional stress exceeds value predicted by linear rheology). Each chain has a maximum stretch, which is reached when the chain tension along the backbone is balanced by the summed chain tensions within the available arms. At this point, the number of arms p gets important again: p is also known as the so-called priority and marks the maximum stretch the backbone can endure before the branch points are pulled inside the backbone tube (branch point withdrawal). This sets the limit of extension hardening in branched polymer melts, a significant value when evaluating extensional rheology measurements. More details about the numerical prediction of branched polymer rheology and the BoB algorithm can be found in literature.15,17,36,38
The only input the BoB algorithm requires besides the topology are four parameters, which describe the chemical nature of the modelled polymer. Those are; the monomer molecular weight (MM), the polymer density (ρ), the entanglement time (τe) as well as the number of monomer per entanglement (Ne). The latter two values were taken from a publication by Read et al.16 and were successfully used to model a series of industrial LDPE samples. The summarized input parameters are given in Table 1.
| Monomer molar mass MM/g mol−1 | 28 |
| Density ρ/g cm−3 | 0.93 |
| Entanglement time τe/s | 5.8 × 10−8 |
| Monomers per entanglement Ne | 57 |
Results and discussion
As follows, the experimental and modelling results regarding the linear and non-linear rheology of the LDPE preparative fractions are presented and discussed. Table 2 summarizes the physical properties of the bulk sample and its TREF fractions. The yield in g of each fraction shown in Table 2 is sufficiently high to enable frequency sweeps and some extensional rheology measurements. Back in the 1960s, when SEC was not yet established as a standard technique for the determination of molecular weight distributions, preparative fractionation techniques were used more frequently.32,33 In this context successful attempts were made to fractionate several hundred grams of polymer at once.34,35,39 However, the set-ups and procedures used within this work were designed to give sufficient material for analytical characterization without excessive solvent or support use.4,30,31 In order to maintain those validated and reliable conditions, repetition was preferred over scale-up for the present study.| Material | Bulk | 70 | 75 | 80 | 85 |
|---|---|---|---|---|---|
| Yield/% | — | 24.5 | 33.3 | 32.7 | 8.0 |
| Yield/g | — | 5.95 | 8.06 | 7.93 | 1.93 |
| Mn/kg mol−1 | 18.5 | 7.2 | 33.6 | 32.1 | 29.9 |
| Mw/kg mol−1 | 113.5 | 50.7 | 147.1 | 124.7 | 125.5 |
| Đ | 6.1 | 7.1 | 4.4 | 3.9 | 4.2 |
| SCB/1000C | 19.4 | 19.7 | 16.6 | 14.4 | 14.8 |
In a similar way, the yield by mass and the molecular properties of the pSGF fractions are given in Table 3. Quantitatively, each fraction was sufficient to enable all the rheology measurements. As mentioned earlier, fractionation by TREF yields narrowly branched fractions with varying crystallizability, which is synonymous with a varying degree of branching. On the other hand, fractionation by SGF provides fractions with systematically different molecular weights and relatively narrow polydispersities. More details on the analytics and interpretation of the individual fractions are given in a previous study.30
| Material | Bulk | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Yield/% | — | 12.9 | 8.5 | 8.7 | 24.8 | 37.9 |
| Yield/g | — | 3.50 | 2.33 | 2.36 | 6.76 | 10.31 |
| Mn/kg mol−1 | 27.2 | 5.2 | 9.6 | 29.0 | 61.3 | 153.9 |
| Mw/kg mol−1 | 318.2 | 12.8 | 22.2 | 49.1 | 143.8 | 649.0 |
| Đ | 11.7 | 2.5 | 2.3 | 1.7 | 2.4 | 4.2 |
| SCB/1000C | 18.4 | 15.8 | 14.6 | 14.3 | 14.8 | 16.8 |
In order to model the rheology of the fractions, it was paramount to understand which of the three detectors connected to SEC is most capable of mimicking the fractionation process computationally. In our case, the three detectors used to measure the MWDs include IR, Visco and MALLS.
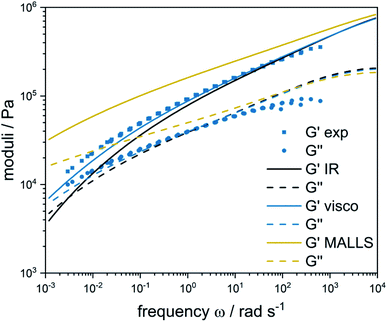
In principle, all three detectors could act as comparative to sample the Monte Carlo ensembles of microstructures via SampleBoB. This was done for a representative sample and the respective results of the linear rheology modelling (lines) are given along with the experimental results (dots) in Fig. 3. From a theoretical point of view, the Visco detector works via flow behavior and is best for the complete MW range. To proof this, rheology modelling as described in section Modelling strategy was performed with SEC results from the three detectors. It can be seen that the predicted storage modulus G′ and loss modulus G′′ (yellow) are significantly overestimated for the MALLS-MWD. The highest sensitivity of static light scattering is obtained with large molecules, which scatter light strongly and thus lie in the high MW area of a polymer. Consequently, MALLS results tend to overestimate the high molecular weight fractions and the predicted rheology shows a more solid-like behavior. The IR detector, on the contrary, predicts lower storage and loss moduli (black), which are characterized by a more liquid-like behavior. This can be explained by the fact that the IR detector is concentration-sensitive and thus the high concentration in the low-molecular weight range is emphasized. The Visco detector determines MWD based on the flow behavior of the polymer solution. Thus, it is the measuring principle most closely related to rheology. More precisely, it determines the intrinsic viscosity of the polymer solution using a pressure drop measurement. Thus, it gives the most reliable results for the complete molecular weight range and the experimentally determined storage and loss moduli (blue) are in good agreement with the modelling results. Consequently, the molecular weight distributions as determined by the Visco detector were used to fractionate all the microstructure ensembles and model the rheology.
Linear rheology measurements of the four TREF fractions are given in Fig. 4 (dots). The flow behaviors of the 75, 80 and 85 °C fractions are very similar, while the storage and loss moduli of the 70 °C fraction are distinctly reduced. This indicates lower viscosity and a more liquid-like behavior. These observations can be understood when the separation principle of TREF is taken into account.
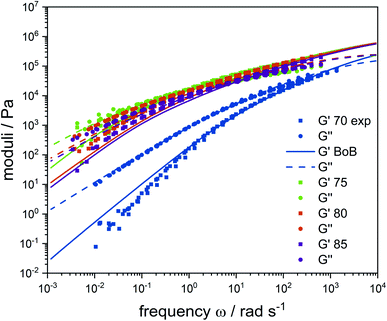 | ||
| Fig. 4 Experimental (dots) and simulated (lines) storage and loss moduli of TREF fractions. Excellent agreement between experiments and simulations is found for all fractions. | ||
Crystallinity correlates well with the irregularity in the microstructure, such as short-chain branching, but also the number of chain ends (EOC, end of chains) as well as long-chain branching. If Table 2 is considered, the average molecular weights and consequently the EOC of the 75, 80 and 85 °C fractions are very similar and the SCB densities lie in a similar range from 13.6 to 16.6/1000C atoms. However, SCBs are too short to affect flow behavior of polymers as they fall far below the entanglement length of 57 with an average length of two (butyl branches). The flow behavior of the 75, 80 and 85 °C fractions shows that the measured storage and loss moduli are similar. The moduli decrease slightly with increasing fractionation temperature from 75 to 85 °C, which can be nicely correlated to slightly decreasing average molecular weights and molecular weight distributions from fractions 75 to 85 °C. However, fraction 70 has a significantly lower molecular weight, which results in a strongly increased number of EOC. The chains are shorter, relax faster and thus, the measured storage and loss moduli are lower. This is the first time that the rheological behavior of TREF fractions was systematically studied. The results give further proof that the separation principle is predominantly based on crystallinity, as these effects would not strongly affect the melt flow behavior of LDPE. The predicted rheological behavior (lines) follows the same trends as the measured values (dots and squares) of all the fractions and the overall agreement between the data is extremely good. This indicates that the applied modelling approach of fractionating the Monte Carlo ensemble of polymeric microstructures is valid and does indeed give a good representation of the existing microstructures in complex LDPE materials.
Frequency sweeps of the SGF fractions 1 to 5 are given in Fig. 5. The dots and squares represent the experimental results, while the line plots are indicating the modelling results. When comparing the measured moduli, one realizes that the individual fractions are very diverse with respect to flow behavior: storage and loss moduli vary over three orders of magnitude and the crossover point varies over more than five orders of magnitude. This is a powerful representation of the strong diversity and complexity of a highly heterogeneous, randomly branched LDPE material. Fractions 1 and 2 that demonstrated the lowest molecular weight, also exhibit the lowest moduli and the highest crossover point. This is in line with the expectation that low molecular weight polymers behave very liquid-like and have short relaxation times due to short chains and low long-chain branching. Although the experimentally observed trend is also captured by the model, these two fractions are least well described by the model. On the one hand, experimental measurement of the moduli was challenging especially for fraction 1 due to very low sample viscosity. On the other hand from the modelling point of view, the mathematical fractionation process might not reflect the physical one due to non-idealities or synergetic effects, such as a hypothetical co-elution of differently branched big and small molecules during elution.30,40 This would lead to microstructures, which might not have represented the present material sufficiently precisely.
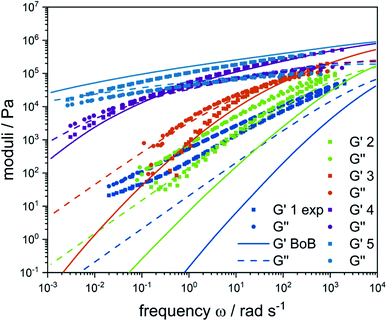 | ||
| Fig. 5 Experimental (dots) and simulated (lines) storage and loss moduli of SGF fractions. The experimentally observed trends are predicted correctly by the model. | ||
With increasing fraction number from 3 to 5, the material (rheological behavior) gets more viscous and solid-like. This can be attributed correctly to the systematic increase of molecular weight. While fractions 3 and 4 are still typical for high molecular weight polymers, fraction 5 does not show a crossover point indicating that a network is developing. The very slow relaxation times observed can be attributed to both the very high molecular weight and strong long-chain branching. For fractions 3 to 5, the model is capable of predicting the experimental results very well, indicating that the used theoretical microstructures adequately represented the material.
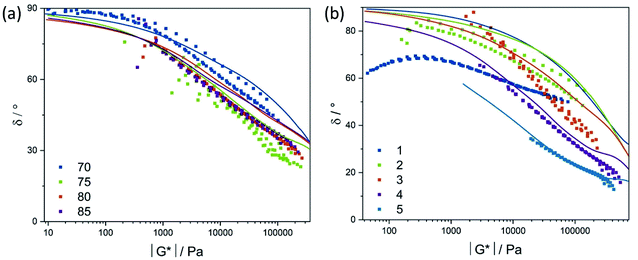
The storage and loss moduli, which were studied as a function of frequency are strongly dominated by the molecular weight of the material. However, LDPE flow behavior also depends strongly on LCB. In order to assess the effect of LCB, the experimental and modelling data in Fig. 4 and 5 were used to construct van Gurp–Palmen plots, which largely exclude molecular weight effects.18,21,41 In a van Gurp–Palmen plot the phase angle is plotted versus the complex modulus |G*|. A decrease of the phase angle can be attributed to an increasing level of LCB, while the shape changes depending on the LCB level.12,20,21,41 The plots which are given in Fig. 6(a) for the TREF fractions and in Fig. 6(b) for the SGF fractions provide information on phase angle versus absolute values of complex shear modulus. The plateau modulus is not reached for the samples due to crystallization.21 van Gurp–Palmen plots of the 75, 80 and 85 °C fractions are very similar and also in very good agreement with modelling results, indicating very similar molecular weight dispersities as well as LCB frequencies and distributions. The 70 °C fraction exhibits increased loss angles, which cannot be explained by a reduced dispersity (Đ = 7.1) and thus corresponds to a reduced long-chain branching frequency typical of the lower molecular weight components.
van Gurp–Palmen plots of the SGF fractions give a more diverse picture: except for fraction 1, the experimental and modelled results are in good agreement and follow a systematic trend. For the reasons discussed above regarding fraction 1, this fraction will not be considered further for evaluation. In the case of fraction 2 to 5, the observed loss angle is significantly reduced with increasing fraction number. Since molecular weight effects are excluded with this plotting technique, the observed shift in loss angle can be attributed to changes from a linear polymeric material to a strongly long-chain branched material. This result is in line with the experimental expectations that an increase in molecular weight corresponds well with an increase in the fractionation number and automatically gives material with a higher LCB frequency. This observation can be ascribed to the nature of the free radical polymerization mechanism. Trinkle et al. observed similar trends, when studying van Gurp–Palmen plots of blends of LCB–metallocene PE and linear PE, with systematically varying LCB to linear contents.19
In our study, it was shown that the strong differences in the rheology behavior are due to differences in the LCB densities and were observed within fractions of a single polymer material. The plots have further demonstrated that an increasing level of LCB observed from fraction 2 to 5 is better observed rheologically as compared to light scattering measurements30 and underline the high sensitivity of rheology towards long-chain branching.
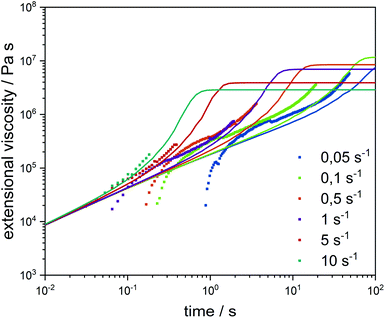
Finally, the fractions were characterized for their rheological behavior in non-linear extensional flow by extensional rheometry. Due to their extremely low molecular weight and consequently very low viscosity, fractions 1 and 2 were excluded from the Physica MCR Anton Paar rheometer measurements. As presented in Fig. 7, the extensional rheology of SGF fraction 4 was measured (dots) at 6 different strain rates (0.05 s−1, 0.1 s−1, 0.5 s−1, 1 s−1, 5 s−1 and 10 s−1). Added to this, the extensional flow was also modelled by the BoB algorithm shown in lines. For all the strain rates applied, strain hardening behavior was observed. The model is capable of describing the level of viscosity and the onset and slope of strain hardening and were predicted satisfactorily, even though the achieved absolute level of strain hardening is overestimated for high strain rates. An adjustment of modelled strain hardening to the experimental results could be done by rheology. However, trends can already be observed with the current model and like any adjustment to measured data the predictive power of the model might be reduced.
In order to quantify the strain hardening of the fractions, time-dependent strain hardening coefficients χ were calculated for both the measured and the modelled extensional viscosities according to eqn (1).10
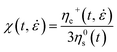 | (1) |
Here ηe+(t, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) is the transient elongation viscosity at time t and strain rate
) is the transient elongation viscosity at time t and strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) and η0s(t) is the shear viscosity in the linear range of deformation. The strain hardening coefficient χ was used in literature to evaluate and compare the elongational behavior of different LDPE samples.10 Experimental (dashed lines) and predicted (lines) strain hardening coefficients of all fractions are given in Fig. 8.
and η0s(t) is the shear viscosity in the linear range of deformation. The strain hardening coefficient χ was used in literature to evaluate and compare the elongational behavior of different LDPE samples.10 Experimental (dashed lines) and predicted (lines) strain hardening coefficients of all fractions are given in Fig. 8.
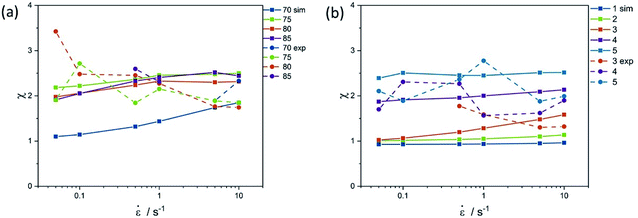
The predicted strain hardening coefficients for the 75, 80 and 85 °C TREF fractions fall close together indicating similarity in the LCB density and topology. The strain hardening coefficients of fraction 70 is lower due to reduced molecular weight and subsequently a reduced level of LCB. Experimental strain hardening coefficients are in the same order of magnitude as the predicted ones, which corresponds to a proof of concept. However, they do scatter strongly, so that a detailed interpretation is not possible.
Strain hardening coefficients of the SGF fractions are presented in Fig. 8(b). The measured data scatter, which might be due to the fractionation process and/or the accuracy of extensional rheology. The strain hardening shows a significant increase with increasing fraction number and thus also with increased long-chain branching. Interestingly, this is seen in both the modelled and the measured results, which indicates that the microstructural prediction via the modelling approach yields LCB frequencies and distributions that are representing the actual material.
Within this exploratory work, the feasibility of connecting preparative fractionation with rheology on both the experimental and modelling side could be demonstrated. The preparative fractionation30 as well as the applied modelling approach29 for predicting polymer rheology of long-chain branched polymers based on polymerization reactions could be expanded to this system and they are valid and robust.
This opens new possibilities for several open questions: (1) by coupling preparative fractionation to a modelling approach for the determination of individual polymer microstructures, the underlying mechanism can now be studied more carefully. The contribution of individual errors to the observed discrepancies can be addressed – both from the modelling and the experimental part. Moreover, non-ideal elution effects, such as co-elution,30,40 could be investigated. (2) As mentioned earlier, scaling up the fractionation process is a challenging task, especially when considering solvent and support amounts. However, scaling up polymer fractionation – especially for the highly industrially relevant polyolefins – is an exciting task in the context of circular economy and polymer fractionation. If polymers, such as PE, are mechanically recycled, various grades from industry are mixed,42 which were originally tailored with respect to molecular, branching and possibly comonomers to reach desired product properties. Fractionation according to molecular weight and/or chemical composition is possible, even it is not always efficient.43 But selective separation of waste fractions with negative properties could potentially help yield recycled material of higher quality and thus improve recycling of PE and advance the circular economy.
Conclusion and summary
In this study, the rheological properties of individual LDPE fractions received from well-defined lab-scale mini-plant samples were investigated from an experimental and a modelling point of view. Fractions of varying crystallizabilities/branching and varying molecular weights were obtained by pTREF and pSGF, respectively. The fractionation scale was high enough to allow rheology measurements of the individual fractions, which is highly relevant for processing.The coupled sampling and rheology modelling approach could mimic TREF as well as SGF processes and predict both the linear and non-linear rheological behavior of the fractions. The beauty of this approach is that the experimentally determined rheology of polymer fractions could be compared to modelling results, which are based on an ensemble of individual polymeric microstructures constructed via a kinetically based Monte Carlo simulation without assumptions regarding branching structure or density or parameter adjustments. All trends were predicted correctly by the model and the overall agreement of simulated and experimental results is good, which validates the applied approach and demonstrates its robustness. The linear and non-linear rheology investigations of the pTREF fractions were dominated by molecular weight effects and revealed a similar LCB topology for all fractions, demonstrating the high selectivity of pTREF towards SCBs. pSGF, on the other hand, provided fractions with strongly increasing molecular weight, which was visible in the frequency sweeps. The effect of molecular weight was suppressed by conducting van Gurp–Palmen plots and non-linear extensional rheology experiments to lay emphasis on the effect of long-chain branching. A strong increase in long-chain branching was observed with increasing fraction number, which is synonymous to increasing molecular weight. This effect is not based on the fractionation technique, but rather a result of the free radical polymerization mechanism: under supercritical conditions, LCBs are formed via the transfer of primary radicals to dead polymer and subsequently monomer addition to the formed secondary radicals site. The probability of a transfer to a polymer reaction hence increases with increasing chain length, so that higher molecular weight materials/fractions are expected to exhibit higher levels of LCB. These observations were made both experimentally and through modelling.
The studies are proof of concept that the applied modular modelling approach to predict polymer rheology based on polymerization kinetics and reaction conditions coupled to hybrid stochastic modelling of the polymeric microstructure is valid in all its three steps. The theoretical results and their experimental validation demonstrated that the structure formation during polymerization and the effect of structure (branching) on flow behavior is correctly described – physically and chemically. So, the fractionation process could be followed from a modelling point of view and the contributions of the individual fractions to the flow behavior of the bulk sample could be determined, which is highly challenging but equally valuable for the highly heterogeneous LDPE material. It helps to understand, how various microstructures shape LDPE flow behavior and thus directly determine processing properties. In the future, this will enable targeted simulation-based product design for enhanced processing properties.
In further investigations, the contribution of individual errors to the observed discrepancies between experiments and model can be addressed, which will further improve the understanding of the underlying physics as well as enable further development of predictive models. Non-ideal behavior observed during fractionation, such as the so-called co-elution effect, could also be tackled with the presented approach.
Author contributions
All authors contributed equally to the work and the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank Dr Iakovos Vittorias and Dr Thomas Herrmann (LyondellBasell Polyolefine GmbH) for fruitful discussions and support regarding the rheology measurements. We acknowledge Fonds der Chemischen Industrie for granting Kristina Maria Zentel a PhD scholarship. We acknowledge support by the Deutsche Forschungsgemeinschaft (DFG – German Research Foundation) and the Open Access Publishing Fund of Technical University of Darmstadt.References
- Plastics, Plastics – the Facts 2016-An analysis of European and plastics and production and demand and waste data, 2016 Search PubMed.
-
(a) J. B. P. Soares and A. E. Hamielec, Macromol. React. Eng., 2007, 1, 53–67 CrossRef CAS
; (b) K. S. Whiteley, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2000 Search PubMed
.
- G. Strobl, Rev. Mod. Phys., 2009, 81, 1287–1300 CrossRef CAS
.
- P. S. Eselem Bungu and H. Pasch, Polym. Chem., 2017, 8, 4565–4575 RSC
.
-
(a) P. S. Eselem Bungu, K. Pflug, M. Busch and H. Pasch, Polym. Chem., 2018, 9, 5051–5065 RSC
; (b) A. Ndiripo, P. S. Eselem Bungu and H. Pasch, Polym. Int., 2019, 68, 206–217 CrossRef CAS
; (c) K. Klimke, M. Parkinson, C. Piel, W. Kaminsky, H. W. Spiess and M. Wilhelm, Macromol. Chem. Phys., 2006, 207, 382–395 CrossRef CAS
; (d) I. Suárez and B. Coto, Eur. Polym. J., 2013, 49, 492–498 CrossRef
; (e) P. S. Eselem Bungu, K. Zentel, S. Hintenlang, M. Busch and H. Pasch, ACS Appl. Polym. Mater., 2020, 2, 5864–5877 CrossRef CAS
.
- P. S. Eselem Bungu, K. Pflug and H. Pasch, Polym. Chem., 2018, 9, 3142–3157 RSC
.
- W.-J. Wang, S. Kharchenko, K. Migler and S. Zhu, Polymer, 2004, 45, 6495–6505 CrossRef CAS
.
- P. M. Wood-Adams and J. M. Dealy, Macromolecules, 2000, 33, 7481–7488 CrossRef CAS
.
-
(a) H. Münstedt, T. Steffl and A. Malmberg, Rheol. Acta, 2005, 45, 14–22 CrossRef
; (b) F. J. Stadler, C. Piel, J. Kaschta, S. Rulhoff, W. Kaminsky and H. Münstedt, Rheol. Acta, 2005, 45, 755–764 CrossRef
; (c) J. F. Vega and J. Martínez-Salazar, Polym. Bull., 2003, 50, 197–204 CrossRef CAS
; (d) J. Vega, M. Aguilar, J. Peón, D. Pastor and J. Martínez-Salazar, e-Polym., 2002, 46, 1–35 Search PubMed
; (e) I. Vittorias, D. Lilge, V. Baroso and M. Wilhelm, Rheol. Acta, 2011, 50, 691–700 CrossRef CAS
.
- F. J. Stadler, J. Kaschta, H. Münstedt, F. Becker and M. Buback, Rheol. Acta, 2008, 48, 479–490 CrossRef
.
- M. Abbasi, N. G. Ebrahimi and M. Wilhelm, J. Rheol., 2013, 57, 1693–1714 CrossRef CAS
.
- D. Ahirwal, S. Filipe, I. Neuhaus, M. Busch, G. Schlatter and M. Wilhelm, J. Rheol., 2014, 58, 635–658 CrossRef CAS
.
- I. Vittorias, M. Parkinson, K. Klimke, B. Debbaut and M. Wilhelm, Rheol. Acta, 2006, 46, 321–340 CrossRef
.
- I. Vittorias and M. Wilhelm, Macromol. Mater. Eng., 2007, 292, 935–948 CrossRef CAS
.
- D. J. Read, J. Polym. Sci., Part B: Polym. Phys., 2014, 53, 123–141 CrossRef
.
- D. J. Read, D. Auhl, C. Das, J. den Doelder, M. Kapnistos, I. Vittorias and R. C. B. McLeish, Science, 2011, 333, 1868–1871 CrossRef PubMed
.
- C. Das, N. J. Inkson, D. J. Read, M. A. Kelmanson and T. C. B. McLeish, J. Rheol., 2006, 50, 207–234 CrossRef CAS
.
- S. Trinkle and C. Friedrich, Rheol. Acta, 2001, 40, 322–328 CrossRef CAS
.
- S. Trinkle, P. Walter and C. Friedrich, Rheol. Acta, 2002, 41, 103–113 CrossRef CAS
.
- G. Fleury, G. Schlatter and R. Muller, Rheol. Acta, 2004, 44, 174–187 CrossRef CAS
.
- G. Schlatter, G. Fleury and R. Muller, Macromolecules, 2005, 38, 6492–6503 CrossRef CAS
.
-
(a) J. Aho, V. H. Rolón-Garrido, S. Syrjälä and M. H. Wagner, Rheol. Acta, 2010, 49, 359–370 CrossRef CAS
; (b) M. Sentmanat, B. N. Wang and G. H. McKinley, J. Rheol., 2005, 49, 585–606 CrossRef CAS
; (c) H. Münstedt, J. Rheol., 1979, 23, 421–436 CrossRef
.
- N. J. Inkson, T. C. B. McLeish, O. G. Harlen and D. J. Groves, J. Rheol., 1999, 43, 873–896 CrossRef CAS
.
- H. Münstedt and D. Auhl, J. Non-Newtonian Fluid Mech., 2005, 128, 62–69 CrossRef
.
-
(a) R. G. Larson, Macromolecules, 2001, 34, 4556–4571 CrossRef CAS
; (b) M. H. Wagner, P. Rubio and H. Bastian, J. Rheol., 2001, 45, 1387–1412 CrossRef CAS
; (c) A. V. Raghu, G. S. Gadaginamath, S. S. Jawalkar, S. B. Halligudi and T. M. Aminabhavi, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 6032–6046 CrossRef CAS
; (d) S. S. Jawalkar, S. K. Nataraj, A. V. Raghu and T. M. Aminabhavi, J. Appl. Polym. Sci., 2008, 108, 3572–3576 CrossRef CAS
; (e) A. F. Behbahani, L. Schneider, A. Rissanou, A. Chazirakis, P. Bačová, P. K. Jana, W. Li, M. Doxastakis, P. Polińska, C. Burkhart, M. Müller and V. A. Harmandaris, Macromolecules, 2021, 54, 2740–2762 CrossRef CAS
; (f) M. H. Nafar Sefiddashti, B. J. Edwards and B. Khomami, Macromolecules, 2019, 52, 8124–8143 CrossRef CAS
.
-
(a) H. Giesekus, J. Non-Newtonian Fluid Mech., 1982, 11, 69–109 CrossRef CAS
; (b) A. Kate Gurnon and N. J. Wagner, J. Rheol., 2012, 56, 333–351 CrossRef
.
- T. C. B. McLeish and R. G. Larson, J. Rheol., 1998, 42, 81–110 CrossRef CAS
.
- M. H. Wagner, M. Yamaguchi and M. Takahashi, J. Rheol., 2003, 47, 779–793 CrossRef CAS
.
- K. M. Zentel, J. Degenkolb and M. Busch, Macromol. Theory Simul., 2021, 30, 2000047 CrossRef CAS
.
- K. M. Zentel, P. S. Eselem Bungu, H. Pasch and M. Busch, Polym. Chem., 2021, 12, 3026–3041 RSC
.
- P. Eselem Bungu, K. Pflug and H. Pasch, Macromol. Chem. Phys., 2020, 221, 2000095 CrossRef CAS
.
- V. Kokle and F. W. Billmeyer, J. Polym. Sci., Part C: Polym. Symp., 1965, 8, 217–232 CrossRef
.
- N. S. Schneider, J. Polym. Sci., Part C: Polym. Symp., 1965, 8, 179–204 CrossRef
.
- A. S. Kenyon, I. O. Salyer, J. E. Kurz and D. R. Brown, J. Polym. Sci., Part
C: Polym. Symp., 1965, 8, 205–216 CrossRef
.
- J. E. Guillet, R. L. Combs, D. F. Slonaker, D. A. Weemes and H. W. Coover, J. Appl. Polym. Sci., 1965, 9, 767–776 CrossRef
.
- C. Das and D. Read, bob-rheology/Wiki/Home, available at: https://sourceforge.net/p/bob-rheology/wiki/Home/, accessed 10 March 2020.
- E. Neuhaus, T. Herrmann, I. Vittorias, D. Lilge, G. Mannebach, A. Gonioukh and M. Busch, Macromol. Theory Simul., 2014, 23, 415–428 CrossRef CAS
.
- C. Das, D. J. Read, D. Auhl, M. Kapnistos, J. den Doelder, I. Vittorias and T. C. B. McLeish, J. Rheol., 2014, 58, 737–757 CrossRef CAS
.
- D. F. Slońaker, R. L. Combs, J. E. Guillet and H. W. Coover, J. Polym. Sci., Part A-2, 1966, 4, 523–526 CrossRef
.
- S. Podzimek, Light Scattering, Size Exclusion Chromatography, and Asymmetric Flow Field Flow Fractionation: Powerful Tools for the Characterization of Polymers, Proteins, and Nanoparticles, Wiley, Hoboken, NJ, 2011 Search PubMed
.
- M. Kempf, D. Ahirwal, M. Cziep and M. Wilhelm, Macromolecules, 2013, 46, 4978–4994 CrossRef CAS
.
-
(a) D. S. Achilias, C. Roupakias, P. Megalokonomos, A. A. Lappas and E. V. Antonakou, J. Hazard. Mater., 2007, 149, 536–542 CrossRef CAS PubMed
; (b) D. S. Achilias, A. Giannoulis and G. Z. Papageorgiou, Polym. Bull., 2009, 63, 449–465 CrossRef CAS
; (c) J. M. Soto, G. Blázquez, M. Calero, L. Quesada, V. Godoy and M. Á. Martín-Lara, J. Cleaner Prod., 2018, 203, 777–787 CrossRef CAS
; (d) G. Pappa, C. Boukouvalas, C. Giannaris, N. Ntaras, V. Zografos, K. Magoulas, A. Lygeros and D. Tassios, Resour., Conserv. Recycl., 2001, 34, 33–44 CrossRef
.
- J. Podešva, J. Stejskal, O. Prochazka, P. Špaček and S. Enders, J. Appl. Polym. Sci., 1993, 48, 1127–1135 CrossRef
.
- K. M. Zentel and M. Busch, Macromol. React. Eng., 2021, 2100027 CrossRef
.
| This journal is © The Royal Society of Chemistry 2021 |