Open Access Article
Open Access ArticleModulation of electrophoresis, electroosmosis and diffusion for electrical transport of proteins through a solid-state nanopore†
Jugal Sahariaa,
Y. M. Nuwan D. Y. Bandara‡
 a,
Buddini I. Karawdeniya§
a,
Buddini I. Karawdeniya§
 a,
Cassandra Hammonda,
George Alexandrakisb and
Min Jun Kim
a,
Cassandra Hammonda,
George Alexandrakisb and
Min Jun Kim *a
*a
aDepartment of Mechanical Engineering, Southern Methodist University, Dallas, TX 75275, USA. E-mail: mjkim@lyle.smu.edu
bDepartment of Bioengineering, University of Texas at Arlington, Arlington, TX 76019, USA
First published on 12th July 2021
Abstract
Nanopore probing of molecular level transport of proteins is strongly influenced by electrolyte type, concentration, and solution pH. As a result, electrolyte chemistry and applied voltage are critical for protein transport and impact, for example, capture rate (CR), transport mechanism (i.e., electrophoresis, electroosmosis or diffusion), and 3D conformation (e.g., chaotropic vs. kosmotropic effects). In this study, we explored these using 0.5–4 M LiCl and KCl electrolytes with holo-human serum transferrin (hSTf) protein as the model protein in both low (±50 mV) and high (±400 mV) electric field regimes. Unlike in KCl, where events were purely electrophoretic, the transport in LiCl transitioned from electrophoretic to electroosmotic with decreasing salt concentration while intermediate concentrations (i.e., 2 M and 2.5 M) were influenced by diffusion. Segregating diffusion-limited capture rate (Rdiff) into electrophoretic (Rdiff,EP) and electroosmotic (Rdiff,EO) components provided an approach to calculate the zeta-potential of hSTf (ζhSTf) with the aid of CR and zeta potential of the nanopore surface (ζpore) with (ζpore–ζhSTf) governing the transport mechanism. Scrutinization of the conventional excluded volume model revealed its shortcomings in capturing surface contributions and a new model was then developed to fit the translocation characteristics of proteins.
Introduction
Nanopores are nanofluidic apertures spanning an impervious membrane that separates two electrolyte reservoirs. When an appropriate voltage bias is applied across the membrane, a molecule translocates from one chamber (cis) to the other (trans), perturbing the open pore current and generating resistive pulses that are characteristic of the molecule under analysis. The applications of nanopores span a wide range of fields such as genomics,1,2 proteomics,3–6 glycomics,7,8 virology,9–11 and lipid nanoparticles.12–14 Analyte transport generally occurs through electrophoresis, electroosmosis, dielectrophoresis or diffusion mechanisms.15–18 Nanopore and analyte surface charges play an integral role in electrophoresis and electroosmosis driven transport.19–22 Depending on the surface charge of the nanopore and the analyte, electrophoretic and electroosmotic forces (FEP and FEO respectively) can be opposing or reinforcing. Electrophoresis is mainly dictated by the analyte charge (pH-dependent) and applied voltage whereas electroosmosis primarily relies on the nanopore surface charge (pH-dependent), electrolyte concentration and applied voltage. The nanopore surface charge is a complex interfacial property due to the nanopore's restricted volume and depends on a host of factors such as pH,23 surface head groups,24,25 and fabrication method.26,27 For charge-neutral molecules, electroosmosis is imperative for translocations to occur.8,28 Moreover, it has been shown that in case of charged particles, electroosmosis can capture particles against electrophoresis, the key factors being the nanopore surface (for electroosmosis) and particle charge (for electrophoresis) which are dependent on the solution pH.16,18 The electrolyte concentration also plays a vital role in the electroosmotic transport mechanism.29,30 For example, at higher electrolyte concentrations, the electrical double layer (EDL) which has been established to come to the fore in the electroosmosis-dominant transport mechanism, would be more compact and vice versa at lower concentrations. The activation of surface charge effects by electrolyte tuning is also evident by the deviation of the expected open-pore conductance from the observed values at low electrolyte concentrations if surface contributions are not accounted for properly.31,32 Thus, by tuning the electrolyte concentration, one can tune the magnitude of the contribution of EO to the overall transport and thereby, the capture rate (CR) and direction/magnitude of molecular transport depending on whether FEO opposes or reinforces the FEP and their relative magnitudes. Electroosmosis can be minimized through nanopore surface modifications where the surface remains charge-neutral over a range of pH values.24 In our previous work, we have shown that a simple change to the electrolyte chemistry during pore fabrication (using controlled dielectric breakdown, CDB) yields nanopores with considerably different surface chemistry compared to the conventional CDB nanopores. The surface charge density of these chemically tuned CDB (CT-CDB) nanopores do not change appreciably up to pH ∼8.27 Since the surface charge of a CT-CDB nanopore at pH ∼8 is (slightly) negative, for a negatively charged analyte, if FEP > FEO, the translocation would occur under positive voltage polarity and at opposite polarity if FEO > FEP.Electrolytes are known to have a complex effect on the 3D structure of proteins through interactions with, for example, unpaired charged side chains (e.g., crosslinking through multivalent ion binding) and the dipole peptide bonds.33 Destabilization of the protein occurs if ions bind preferentially to the non-native state over the native state.34 The electrolyte type, according to the Hofmeister series – originating from the work of Franz Hofmeister nearly 130 years ago – can either have salting-in (chaotropic; destabilizing effects) or salting-out (kosmotropic; stabilizing effects) effects on protein stability.35 The work of Green et al. suggests that the Hofmeister effects are prominent at high salt concentrations (0.5–3 M)36 – the range where a host of nanopore-based protein profiling experiments are done. More recently, Medda et al. showed that these effects are present at physiological concentrations as well.37 Thus, the electrolyte chemistry plays an important role in both intra- and inter-protein interactions and ultimately on the protein 3D structure.
To test the transport mechanism in response to electrolyte type and concentrations, we used the holo form of hSTf as the model protein. The hSTf is a blood glycoprotein comprised of 679 amino acids, with a molecular weight of ∼80 kDa that binds to iron with a high affinity constant (1020 M−1) at physiological pH.38 This protein is critical for iron homeostasis with iron release from hSTf clefts taking place at lower endosomal pH. In a previous study, we observed hSTf to be dominantly translocating via the electrophoretic mechanism at pH ∼6 and ∼8 while diffusion was seen to play a key role at pH ∼4.3 These observations were inextricably linked with the pI of hSTf (∼5.2–5.6), which is also the case with most other nanopore-based protein studies.19,39 However, that study was done at a relatively high salt concentration (2 M KCl), diminishing the possibility of electroosmosis dominating the transport mechanism due to charge screening. In this study, we used 0.5–4 M LiCl and KCl (mostly in 0.5 M steps, buffered at pH ∼ 8) across an appreciably wide voltage range (±50 mV to ±800 mV) to enable the study of CR, transport mechanism and 3D conformation (e.g., chaotropic vs. kosmotropic effects). A shift in responsive voltage polarity correlated to a transition in the transport mechanism from electrophoresis (typically at higher electrolyte concentrations) to electroosmosis through a diffusion phase at intermediate electrolyte concentration levels. Although, in most studies, the applied voltage is chosen arbitrarily to be in high (diffusion-limited) or low (barrier-limited) electric field regime, our results reveal the shortcomings of such choices because CR was observed to have a voltage threshold where the behavior was considerably different on either side of the said threshold. This is thought to be a combination of voltage driven unfolding coupled with chaotropic/kosmotropic effect of ions in the electrolyte and the magnitude and direction of FEP and FEO. To understand the transport direction, the zeta potential of both the nanopore surface (ζpore) and holo-hSTf (ζhSTf) were calculated. Since conventional zeta potential measurements (using a Zetasizer at relatively higher hSTf concentrations) proved to be inadequate, we resorted to measuring the CR of holo-hSTf as a function of ζpore to estimate ζhSTf. Since CR is dependent on the resultant of competing forces generated by electrophoresis and electroosmosis, when the two forces are equal, the capture rate could be anticipated to approach zero, from which ζhSTf was calculated.
Methods section
Nanopore fabrication and size estimation
Nanopores were fabricated on nominally ∼12 nm thick silicon nitride (SixNy) membranes (NBPX5001Z-HR) purchased from Norcada Inc. using the CT-CDB method27 with 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 sodium hypochlorite (425044, Sigma Aldrich): 1 M KCl (P9333, Sigma-Aldrich) buffered at pH ∼7 using 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES, Sigma-Aldrich, H0527). In brief, an electric field of <1 V nm−1 was applied until an abrupt increase in the leakage current was observed which is indicative of a pore formation. After the initial pore-formation, voltage pulses were applied until the pore-size of interest was reached. To measure the final pore size, all content was thoroughly exchanged with 1 M KCl buffered at pH ∼7 and a current–voltage (I–V) curve was obtained. The diameter of the fabricated pores was calculated using the slope of the I–V curve with a formulation that included bulk, surface, and access resistance contributions,
9 sodium hypochlorite (425044, Sigma Aldrich): 1 M KCl (P9333, Sigma-Aldrich) buffered at pH ∼7 using 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES, Sigma-Aldrich, H0527). In brief, an electric field of <1 V nm−1 was applied until an abrupt increase in the leakage current was observed which is indicative of a pore formation. After the initial pore-formation, voltage pulses were applied until the pore-size of interest was reached. To measure the final pore size, all content was thoroughly exchanged with 1 M KCl buffered at pH ∼7 and a current–voltage (I–V) curve was obtained. The diameter of the fabricated pores was calculated using the slope of the I–V curve with a formulation that included bulk, surface, and access resistance contributions,
 | (1) |
Electrolyte preparation
All electrolyte solutions, KCl and LiCl (213233, Sigma Aldrich), were prepared using ultra-pure water (ARS-105 Aries high purity water systems, resistivity of >18 MΩ cm). All LiCl electrolytes were buffered with 10 mM Tris buffer (J61036, Fisher Scientific). The pH was adjusted by adding concentrated HCl (H1758, Sigma-Aldrich) or KOH (306568, Sigma-Aldrich) dropwise and measured with an Orion Star™ pH meter.Electrical measurements
Axopatch 200B (Molecular Devices LLC) was used for electrical measurements. A PCIe-6321 (controlled through a custom LabVIEW script (version 2016, National Instruments)) connected to a BNC 2110 (National Instruments) was used to digitize the output for I–V measurements. Signal digitization was carried out using a Digidata 1440A (Molecular Devices LLC) for translocation experiments. Current traces were acquired at a sampling frequency of 250 kHz and lowpass filtered at 10 kHz using the in-built Bessel filter of the Axopatch 200B.Nanopore-based biomolecule measurements
After nanopore fabrication, baseline profiles (before the addition of hSTf to the cis side) were obtained for each electrolyte concentration of LiCl and KCl across all operational applied voltages (±50 mV to ±800 mV). All baseline profiles were free of any resistive pulse-like perturbations. The hSTf was purchased from Sigma Aldrich (T0665). The hSTf stock solution was stored at ∼5 °C and used within 7 days from preparation. The hSTf was added to the cis side to a final concentration of ∼100 nM. The experiments were carried out using 500 mM (∼4.1 S m−1), 1 M (∼7.4 S m−1), 1.5 M (∼11.1 S m−1), 2 M (∼12.4 S m−1), 2.5 M (∼13.8 S m−1), 3 M (∼15.2 S m−1) and 4 M (∼17.6 S m−1) LiCl or 500 mM (∼5.9 S m−1), 1 M (∼11.1 S m−1), 1.5 M (∼15.9 S m−1), 2 M (∼20.9 S m−1), 2.5 M (∼27.9 S m−1), 3 M (∼32.9 S m−1) and 4 M (∼40.7 S m−1) KCl buffered at pH 8. Single nanopores of ∼14 nm diameter fabricated on ∼12 nm thick silicon nitride membranes were used for translocation experiments. Events were analyzed using a custom script written in MATLAB (version 9.4). Three key parameters were extracted for a given event: baseline current (I0), the magnitude of current perturbation (ΔI) and event duration (Δt). The Δt was calculated using the full width at the half maximum (FWHM) approach as discussed in ESI Section 1.†Zeta potential measurements
Measurements were obtained using a Zetasizer Nano ZS (Malvern Instruments) using the procedure described in our previous work.3 The hSTf was dissolved to a final concentration of ∼25 μM in 50 mM LiCl (0.573 S m−1), 50 mM KCl (0.729 S m−1) and KCl at 0.573 S m−1 (conductivity equivalent of 50 mM LiCl). The refractive index, dielectric constant and viscosity were selected as 1.662, 80.4 and 0.87 cP for LiCl and 1.488, 80.4 and 0.89 cP for KCl, respectively. The data were treated with the Smoluchowski model in the operating software. A total of 10 cycles were performed for each electrolyte type.Results and discussion
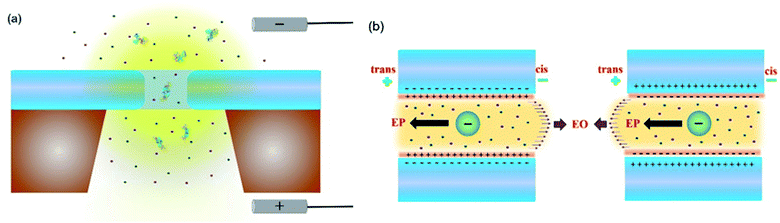
Solid-state nanopore experimental setup and change in conductance
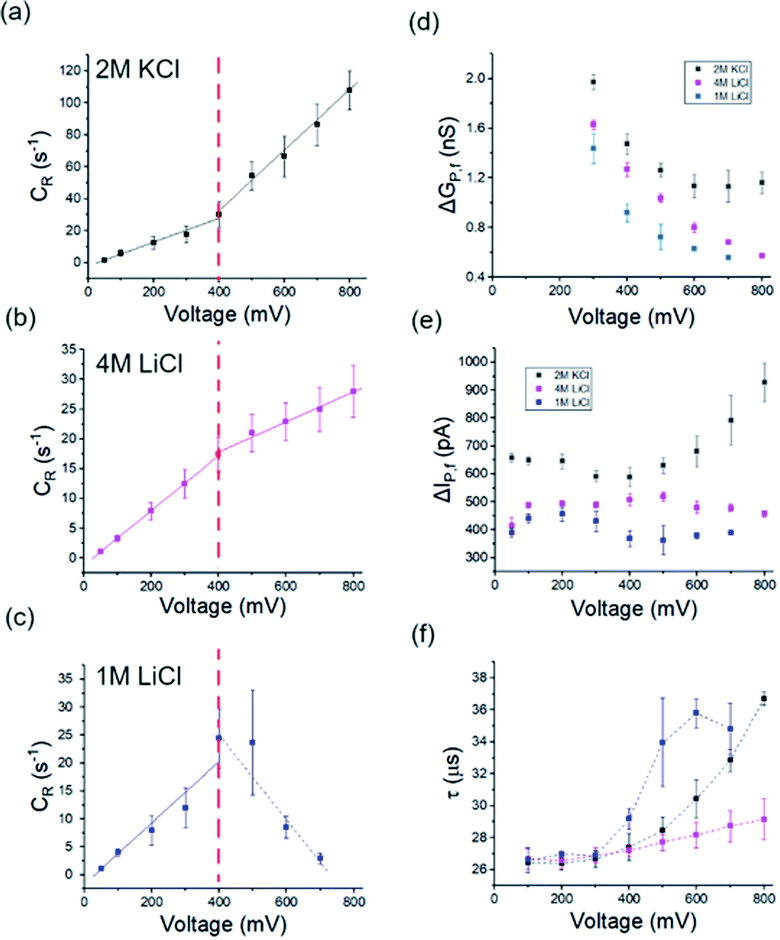
The holo form of hSTf was added to the cis side of the nanopore and driven across the pore in response to a voltage (Vapp) applied to the trans side as seen in Fig. 1a. Fig. 1b shows the directions of electrophoresis and electroosmosis originating from the interplay of the nanopore surface charge and positive Vapp. These directions would be reversed under a negative Vapp. For a molecule to translocate through a nanopore, it should (i) diffuse from the bulk to the capture zone of the nanopore, (ii) funnel (drift dominant) to the pore entrance, and (iii) overcome entropic (in case of long-chain polymeric molecules) and/or electrostatic barriers. If the Vapp is not sufficient to overcome these energetic barriers, the molecule could simply collide with the pore entrance rather than translocating through it. Generally, the transport would either be diffusion-limited or barrier-limited. The diffusion-limited paradigm is typically seen with long-chain molecules under a high electric field whereas the barrier limited paradigm is typically observed with short molecules under a weak electric field. The CR and Vapp would be linearly correlated in the case of diffusion-limited transport (i.e., Smoluchowski's rate equation) whereas the relationship is exponential in the case of barrier limited transport (i.e., van't Hoff–Arrhenius formalism). The Vapp would also dictate the translocation time (τ) and 3D structure (e.g., voltage driven protein unfolding, soft particle electro-deformation) to a large extent. Using hSTf as the model molecule, we first investigated the translocation behavior across an appreciably wide Vapp range (±50 mV to ±800 mV) using the two ubiquitous electrolytes in nanopore technology (LiCl and KCl buffered at pH ∼8) as seen in Fig. 2a–f. The experiments were initially conducted with 4 M and 1 M of LiCl and 2 M of KCl. Experiments with 4 M KCl could not be conducted over the entire Vapp range (overloads the Axopatch 200B system) while 1 M KCl yielded extremely poor CR. At lower electrolyte concentrations, the contributions from electroosmosis and the analyte-counterions to the overall pore conductance during confinement increase. The former (i.e., electroosmosis) opposes the electrophoretic motion in the case of hSTf and CT-CDB fabricated pores, and the latter increases the overall ions available for conductance. These would cause a decrease in CR and the signal-to-noise ratio (SNR) of the resistive pulse, respectively. Lower SNR could also lead resistive pulses to be not detected by the algorithm leading to a decrease in CR. Thus, we chose 2 M KCl, 4 M LiCl and 1 M LiCl for further investigation. A broad range of concentrations were later investigated as seen in Fig. 3 with a single Vapp rather than a range. The initial investigation with 2 M KCl, 4 M LiCl and 1 M LiCl was to find a suitable Vapp for the study depicted in Fig. 3.Events were only observed for positive Vapp for 2 M KCl, and 4 M LiCl whereas in 1 M LiCl it is the opposite polarity that generated events (Fig. S2†). The change in response to the Vapp polarity is attributed to the change in the transport mechanism (i.e., from electrophoresis at high LiCl concentrations to electroosmosis at low LiCl concentrations). In all three electrolyte conditions, the CR with Vapp exhibited two distinct linear regimes (i.e., a breakpoint at ∼400 mV). While 2 M KCl (Fig. 2a) demonstrated a higher sensitivity (i.e., higher slope) after the breakpoint (∼2.5× compared to pre-breakpoint slope), in 4 M LiCl (Fig. 2b), the sensitivity dropped by ∼1.8× after the breakpoint. Interestingly, with 1 M LiCl (Fig. 2c) an inverse relationship between CR and Vapp was observed after the breakpoint. The change in conductance due to hSTf translocation (ΔGp,f) decreased with increasing Vapp and plateaued at ∼400 mV in 2 M KCl while it continued to drop in the other two cases (Fig. 2d). The ΔGp was calculated by fitting a Gaussian mixture model to the histogram distribution of change in open pore current (ΔI) as outlined in ESI Section 3.† The nonlinear behavior of ΔGp,f with Vapp is indicative of voltage-driven unfolding and the plateauing is indicative of maximum possible unfolding under the experimental conditions.3,41 An unfolded protein is typically more surface charged than its folded counterpart due to the exposure of charged moieties that are otherwise hidden due to folding.42 According to the Hofmeister series, Li+ is a chaotropic cation while K+ is a kosmotropic cation.43 It is possible that with voltage-driven unfolding, the ions of the electrolyte would have more access to the otherwise shielded moieties due to the folded structure with chaotropic cations denaturing and destabilizing the protein structure compared to kosmotropic cations. Although, the unfolding plateaus in 2 M KCl (Vapp > 400 mV), the continued unfolding in both 4 M and 1 M LiCl could be due to these chaotropic effects of Li+. Taken together, these could provide explanations to the change in slope after the breakpoint in Fig. 2a–c: (i) exposure of charged moieties through protein unfolding would increase the contribution to electrophoretic movement and thereby increasing the capture probability, (ii) chaotropic destabilization would reduce the number of detectable molecules which would increase with additional unfolding contributions. For example, an extra degree of unfolding component could be introduced due to the opposing electroosmosis (dominant transport mechanism) and electrophoresis mechanisms in the case of 1 M LiCl (Fig. 2c) which would further destabilize the protein structure and by extension the detectable molecules. The increase in the molecular length of hSTf caused by voltage-driven unfolding would also minimize fast translocations that defy the electronic limitations of the Axopatch system (i.e., more molecules are detected) and would also lead to an increase in τ with Vapp as seen in Fig. 2f and has been observed previously as well.3 As expected, the opposing electroosmotic and electrophoretic forces lead to a higher τ in 1 M LiCl as evident by Fig. 2f (blue trace). However, we note that the bandwidth limitations of the Axopatch 200B amplifier may cause ballistic events to be not detected and only those that are delayed through interactions with the pore to be detected as noted by previous work in the literature.44 To affirm the missed events, we first calculated the effective capture radius (reff) using reff = CR/2πDC where D and C are bulk diffusion coefficient (estimated using the Stokes–Einstein equation and was found to be ∼7.6 × 10−7 cm2 s−1 for hSTf) and hSTf concentration (∼100 nM) respectively. The reff at ±400 mV was found to be ∼1 nm, ∼0.6 nm and ∼0.9 nm in 2 M KCl, 4 M LiCl and 1 M LiCl respectively which is at least 14× smaller than the pore radius. While high bandwidth equipment would permit to detect fast moving protein events, as noted by Tabard Cossa et al., we obtained statistically significant data (>1000 events) across all events to draw conclusions based on events slowed down through interactions with the pore.44
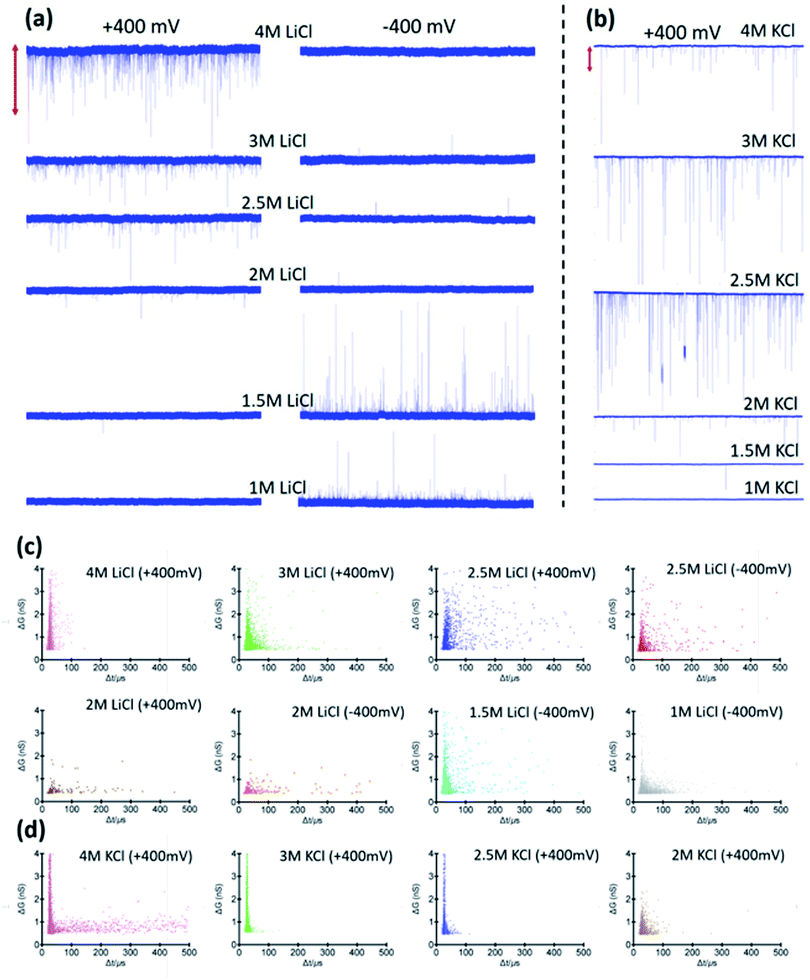
At higher electric fields, experiments with 0.5 M LiCl were not possible for two reasons: persistent clogging and poor CR at high electric fields. Moreover, as mentioned, hSTf continues to unfold beyond 400 mV in 4 M LiCl and 1 M LiCl while ΔGp,f plateaus at ∼400 mV in 2 M KCl. Furthermore, the capture rate in 1 M LiCl drops at voltages higher than 400 mV. Taking the above observations of the voltage-dependent study into account, we decided to conduct further studies at ±400 mV for the electrolyte concentration range from 1–4 M. The resistive pulses (also called events) in response to ±400 mV applied voltages are shown in Fig. 3a and b for 1–4 M LiCl and KCl (buffered at pH ∼8), respectively. The corresponding scatter plots are shown in Fig. 3c (LiCl) and Fig. 3d (KCl). Selected extended current traces are shown in Fig. S3 and S4,† which showcase the stability of CT-CDB nanopores and their resilience to lengthy experiments spanning a considerable number of sensing conditions (Fig. S5† shows the response at ±50 mV for 0.5–4 M LiCl and KCl with selected extended current traces shown in Fig. S6 and S7†). Thus, the concentration analysis was limited to 1–4 M at ±400 mV. Interestingly, as seen in Fig. 3b, KCl showed events only for +400 mV across all concentrations whereas LiCl (Fig. 3a) showed a transition from being solely responsive to +400 mV at higher concentrations (electrophoresis-dominant transport mechanism), to both polarities at intermediate concentrations and solely responsive to −400 mV at lower concentrations (electroosmosis-dominant transport mechanism). The zeta potential of the protein (hSTf in this case) and the nanopore for each electrolyte type and concentration is believed to play a vital role in the transport direction. Considering the zeta potential of hSTf (ζhSTf) and that of the nanopore wall (ζpore), the resultant drift velocity of hSTf can be expressed as 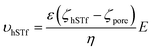 where E, ε and η are average electric field strength, solution permittivity and viscosity of the medium, respectively.45 The quantity ζhSTf − ζpore would to a large extent determine whether the mechanism is electroosmotic (ζhSTf < ζpore) or electrophoretic (ζhSTf > ζpore) dominated and is more broadly discussed below.
where E, ε and η are average electric field strength, solution permittivity and viscosity of the medium, respectively.45 The quantity ζhSTf − ζpore would to a large extent determine whether the mechanism is electroosmotic (ζhSTf < ζpore) or electrophoretic (ζhSTf > ζpore) dominated and is more broadly discussed below.
Transport mechanism and capture based zeta potential measurement
To quantitatively assess the transport mechanism, ζhSTf must be compared against ζpore. At high salt concentrations (smaller Debye length compared to pore radius), ζpore could be calculated using an approximate extension of Grahame equation (see ESI Section 4† for further information),
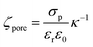 | (2) |
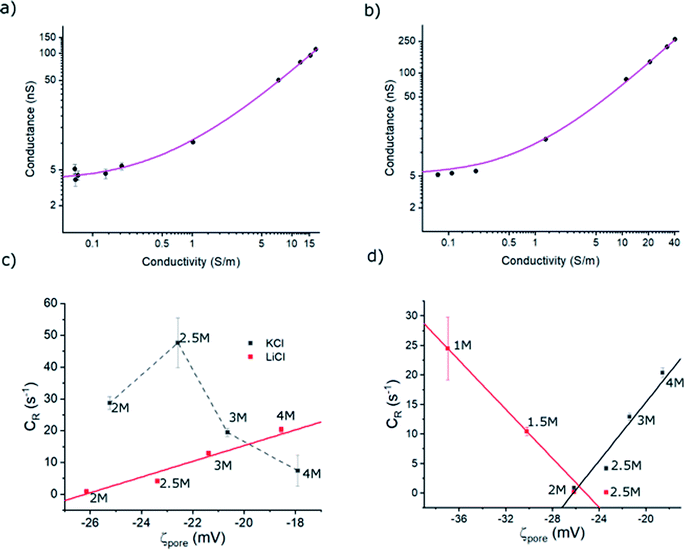 | ||
| Fig. 4 Open-pore conductance (G) as a function of (a) LiCl conductivity and (b) KCl conductivity. The solid line in each is the best fit to the data made using eqn (1) with σp as the sole free parameter. Full length of each error bar corresponds to the standard deviation of the replicated measurements. (c) Event rate of hSTf in KCl (black) and LiCl (red) with the zeta potential of the nanopore surface (ζpore) from 4 M to 2 M electrolyte concentrations at +400 mV applied voltage. (d) Event rate of hSTf in 1 M to 4 M LiCl in response to +400 mV (black) and −400 mV (red). The electrolyte concentrations of (c) and (d) are indicated adjacent to the corresponding data point. | ||
ζhSTf was also estimated using a Zetasizer (see Methods section for more details).46–48 The measured values are shown in Table S2† and support the notion of LiCl shielding the charge of the charged biomolecules compared to KCl.49 Although these values are in agreement with what we have obtained previously,3 it only satisfy the ζhSTf < ζpore condition which suggests that the transport mechanism should be electroosmosis-dominant across all electrolyte concentrations (see Table S1† for tabulated ζpore values). However, as seen in Fig. 3a, this is not the case where a clear shift in the mechanism from electrophoresis to electroosmosis was observed with decreasing LiCl concertation (with KCl been purely electrophoretic). Thus, even when providing the correct sign, the magnitude of zeta-potential measurements may not be accurate to describe the observed results. Although nanopore-based zeta potential calculation is possible,46–48 missed events arising from the bandwidth limitation of the Axopatch 200B impede the proper estimation of electrophoretic mobility essential for such calculations. Our efforts to calculate ζhSTf through the translocation time based nanopore methods outlined in literature corroborated this notion where the calculated values in 2 M KCl and 4 M LiCl were in unrealistic sub-μV regime (calculations not shown). Due to the shortcomings of the ζhSTf estimation through above methods, we present a CR vs. ζpore method to calculate ζhSTf. Interestingly, the CR of hSTf in KCl (unlike LiCl) drops at higher concentrations as seen in Fig. 4c while CR in LiCl showed a linear dependence. This result also supports the notion that electrolyte chemistry and Vapp should be chosen with utmost care since proteins, unlike rigid particles and DNA undergo significant molecular level changes especially with Vapp. Hereafter, we limit the discussion to LiCl. To quantify the observed capture rates, we resorted to the diffusion-limited capture rate (Rdiff) which is given by 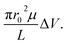 50 The electrophoretic mobility (μ) can be expressed using apparent zeta potential and the dielectric constant of the medium (εd) as
50 The electrophoretic mobility (μ) can be expressed using apparent zeta potential and the dielectric constant of the medium (εd) as 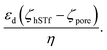 45 Thus, Rdiffcan now be expressed as,
45 Thus, Rdiffcan now be expressed as,
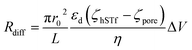 | (3) |
Using each of the linear fit lines shown in Fig. 4d, one can calculate the ζhSTf when Rdiff approaches zero (Rdiff → 0). The zeta potential of hSTf at Rdiff → 0 point (ζhSTfrevents→0) was found to be −26.2 mV (black trace, electrophoresis dominant fit) and −25.2 mV (magenta trace, electroosmosis dominant fit): both yielded appreciably close zeta potential values that are much greater than those obtained from the Zetasizer. A zeta potential <−30 mV generally indicates an unstable solution where analytes tend to aggregate irreversibly51 and given the fact ζhSTfrevents→0 ∼ −30 mV, hSTf may be stable under the experimental conditions of Fig. 4d. Since LiCl produced statistically significant event counts across all electrolyte concentrations, Rdiff → 0 may not be the best way to determine ζhSTf. Eqn (3) can be separated into electrophoretic and electroosmotic components as 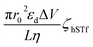 (Rdiff,EP) and
(Rdiff,EP) and 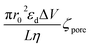 (Rdiff,EO) respectively. Since the transport direction depends on the difference in the zeta potential of the nanopore surface and the analyte (i.e., ζhSTf − ζpore), when the condition ζpore ≈ ζhSTf is satisfied, the event rate is expected to approach zero provided diffusion alone does not lead to an appreciable event rate. To check the validity of this claim, we first calculated the frequency factor (Rf0) from the barrier penetration using, Rf0 = CDA/l where C, D and A are bulk concentration of hSTf, diffusion coefficient of hSTf and the cross-sectional area of the channel.52 For a ∼14 nm diameter pore through a 12 nm thick membrane with 100 nM hSTf, Rf0 was found to be ∼12.4 s−1 (D was estimated using the Stokes–Einstein equation and was found to be ∼7.6 × 10−7 cm2 s−1 for hSTf). Using event rate at the intersection point (∼1.2 s−1) the activation energy (U) was found to be ∼2.4kBT using R0 = k × Rf0
(Rdiff,EO) respectively. Since the transport direction depends on the difference in the zeta potential of the nanopore surface and the analyte (i.e., ζhSTf − ζpore), when the condition ζpore ≈ ζhSTf is satisfied, the event rate is expected to approach zero provided diffusion alone does not lead to an appreciable event rate. To check the validity of this claim, we first calculated the frequency factor (Rf0) from the barrier penetration using, Rf0 = CDA/l where C, D and A are bulk concentration of hSTf, diffusion coefficient of hSTf and the cross-sectional area of the channel.52 For a ∼14 nm diameter pore through a 12 nm thick membrane with 100 nM hSTf, Rf0 was found to be ∼12.4 s−1 (D was estimated using the Stokes–Einstein equation and was found to be ∼7.6 × 10−7 cm2 s−1 for hSTf). Using event rate at the intersection point (∼1.2 s−1) the activation energy (U) was found to be ∼2.4kBT using R0 = k × Rf0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−U/kBT) with R0, k and kB the activation energy (U) governed zero voltage capture rate, probability factor (assumed to be 1) and Boltzmann constant.52–54 Since U > kBT we wouldn't expect diffusion alone to produce an appreciable CR. The intersection point in Fig. 4d (Rdiff,EP = Rdiff,EO) may in fact be a better representation of ζhSTf. The ζpore at this intersection point was found to be ∼ −25.7 mV (ζEP=EOhSTf). The ζhSTf can also be used to estimate the net charge of the protein assuming spherical shape of the protein and uniformly distributed surface charge.55 We used a similar framework at a weaker electric field (Vapp = ±50 mV) from which ζEP=EOhSTf was found to be ∼ −25.9 mV (Fig. S11†). However, one must understand that eqn (3) is not properly applicable to weak electric fields. At lower voltages (i.e., voltage approaching 0 mV), the transport mechanism become barrier limited. In such cases, the Van't Hoff–Arrhenius formalism is more applicable which is given by Rbar = k × Rf0
exp(−U/kBT) with R0, k and kB the activation energy (U) governed zero voltage capture rate, probability factor (assumed to be 1) and Boltzmann constant.52–54 Since U > kBT we wouldn't expect diffusion alone to produce an appreciable CR. The intersection point in Fig. 4d (Rdiff,EP = Rdiff,EO) may in fact be a better representation of ζhSTf. The ζpore at this intersection point was found to be ∼ −25.7 mV (ζEP=EOhSTf). The ζhSTf can also be used to estimate the net charge of the protein assuming spherical shape of the protein and uniformly distributed surface charge.55 We used a similar framework at a weaker electric field (Vapp = ±50 mV) from which ζEP=EOhSTf was found to be ∼ −25.9 mV (Fig. S11†). However, one must understand that eqn (3) is not properly applicable to weak electric fields. At lower voltages (i.e., voltage approaching 0 mV), the transport mechanism become barrier limited. In such cases, the Van't Hoff–Arrhenius formalism is more applicable which is given by Rbar = k × Rf0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(U − ΔU)/kBT), where Rbar and ΔU, are the barrier-limited capture rate and, activation energy, respectively. The ΔU is typically given by qΔV where q and ΔV are the effective charge of the molecule and applied voltage to the electrodes. Thus, with increasing applied voltage, the capture rate would expect to increase exponentially. However, if the limiting case of translocation is diffusion, the eqn (3) is applicable and a linear increase of capture rate with applied voltage is observed.
exp(−(U − ΔU)/kBT), where Rbar and ΔU, are the barrier-limited capture rate and, activation energy, respectively. The ΔU is typically given by qΔV where q and ΔV are the effective charge of the molecule and applied voltage to the electrodes. Thus, with increasing applied voltage, the capture rate would expect to increase exponentially. However, if the limiting case of translocation is diffusion, the eqn (3) is applicable and a linear increase of capture rate with applied voltage is observed.
Modeling of change in conductance
As our previous study with hSTf showed voltage-driven unfolding of protein with increasing applied voltage,3 to minimize such, we now operated at a low Vapp (±50 mV) using 0.5–4 M LiCl.3 The change in conductance because of hSTf translocations exhibited a bimodal distribution (see Fig. S12 and ESI Section 3† for fit details). The lower ΔG (ΔGp,c) did not show a significant dependence on the electrolyte conductivity whereas the higher ΔG (ΔGp,f) showed a proportional relationship with electrolyte conductivity (Fig. S13†). The ΔGp,f, given the low applied voltage, could correlate to globular-like translocations since voltage-driven unfolding would be negligible at weak electric fields (i.e., the protein is closer to its native state). If we disregard surface contributions – both from pore wall and particle – the conductance change of the second population (ΔGp,f) can be expressed as;
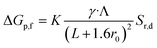 | (4) |
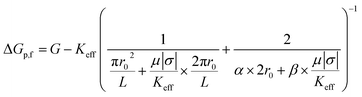 | (5) |
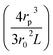 in a solution with conductivity, K can be expressed as
in a solution with conductivity, K can be expressed as 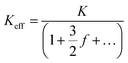 . The raw data (ΔGp,f) was fitted with both eqn (4) (Sr,d set to 1, Fig. 5a) and eqn (5) (Fig. 5b). The resulting rp values were ∼3.84 (eqn (4)) and ∼3.14 (eqn (5)). While both models yielded similar R2 values (∼0.987), the rp value produced by our model (eqn (5)) is in close agreement with the reported value for hSTf based on its molecular volume (∼3.2 nm).3,38 For simplicity, in eqn (5), we have neglected contributions from the protein charge as proteins do not have a uniform charge or shape. Further refinement of eqn (5), we believe, is beyond the scope of this paper, as it would require substantial analytical modelling.
. The raw data (ΔGp,f) was fitted with both eqn (4) (Sr,d set to 1, Fig. 5a) and eqn (5) (Fig. 5b). The resulting rp values were ∼3.84 (eqn (4)) and ∼3.14 (eqn (5)). While both models yielded similar R2 values (∼0.987), the rp value produced by our model (eqn (5)) is in close agreement with the reported value for hSTf based on its molecular volume (∼3.2 nm).3,38 For simplicity, in eqn (5), we have neglected contributions from the protein charge as proteins do not have a uniform charge or shape. Further refinement of eqn (5), we believe, is beyond the scope of this paper, as it would require substantial analytical modelling.
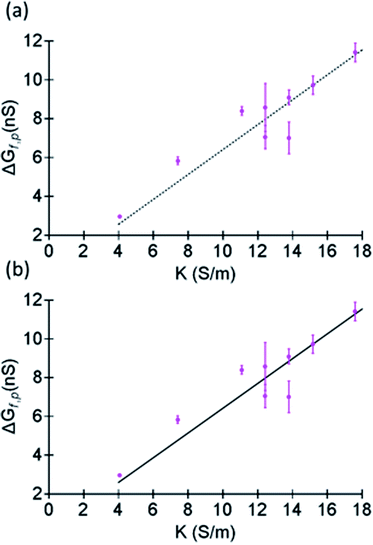 | ||
| Fig. 5 Fits made to ΔGp,f (corresponding to the histograms shown in Fig. S12†) as a function of the conductivity of LiCl at pH ∼8 using (a) eqn (4) and (b) eqn (5) with rp as the free parameter. The fit was done by having rp as the sole free parameter. In the case of eqn (4), Sr,d and γ were set to 1 and 1.5 respectively and Λ was substituted by the volume of a sphere. Full length of each error bar corresponds to the standard deviation of the replicated measurements. | ||
Conclusions
In this study, we have demonstrated the responsiveness of the holo form of hSTf in LiCl and KCl concentrations ranging from 4 M to 0.5 M at pH ∼8, using silicon nitride nanopores fabricated through the CT-CDB process. While the responsiveness was found to be purely electrophoretic for KCl, in LiCl, a transition from electrophoretic to electroosmotic was observed at low electrolyte concentrations (typically <2 M) while at intermediate concentrations (e.g., 2 M and 2.5 M) events were observed for both voltage polarities suggesting diffusion plays a vital role in the translocation mechanism at such concentrations. To further understand this reversal of translocation mechanism with decreasing electrolyte concentration, the zeta potential of both the nanopore surface (ζpore) and holo-hSTf (ζhSTf) were calculated. The ζpore was calculated by surveying the open pore nanopore conductance (G) with electrolyte concentration and by fitting the raw data with eqn (1) to obtain the surface charge density (σp). Then ζpore was calculated for the range of LiCl and KCl concentrations used herein. The ζhSTf was measured (Zetasizer) and subsequently calculated using the correlation between ζpore and the diffusion-limited capture rate (Rdiff). We used the relationship between Rdiff and ζpore as an alternative way to estimate ζhSTf. By extrapolating the Rdiff to zero (point where ζpore ≈ ζhSTf), the ζhSTf found (ζhSTfrevents→0). Although mathematically Rdiff can be extrapolated to zero, for electrolytes such as LiCl, it is not a pragmatic approximation as events are produced for either voltage polarity under the concentration range considered in this study. Therefore, we looked at the event rate components corresponding to electrophoresis (Rdiff,EP) and electroosmosis (Rdiff,EO) and determined the ζpore at which the two contributions become equal (the intersection point of the rate profiles). The ζhSTf at the intersection point (ζEP=EOhSTf) was found to be ∼25.7 mV. We then ventured into modelling the conductance change (ΔG) because of hSTf translocations. The conventionally used eqn (4) was found to have shortcomings for its adaptation to nanopore-based profiling and a new equation was proposed to quantify the conductance change due to protein translocation process (eqn (5)).Conflicts of interest
The authors have declared no conflict of interest.Acknowledgements
This work was supported by the National Science Foundation (CBET #2022398 and #2022374) and National Institutes of Health (R21CA240220).References
- K. J. Freedman, C. W. Ahn and M. J. Kim, Detection of long and short DNA using nanopores with graphitic polyhedral edges, ACS Nano, 2013, 7, 5008–5016 CrossRef CAS PubMed.
- J. Feng, K. Liu, R. D. Bulushev, S. Khlybov, D. Dumcenco, A. Kis and A. Radenovic, Identification of single nucleotides in MoS2 nanopores, Nat. Nanotechnol., 2015, 10, 1070 CrossRef CAS PubMed.
- J. Saharia, Y. N. D. Bandara, G. Goyal, J. S. Lee, B. I. Karawdeniya and M. J. Kim, Molecular-Level Profiling of Human Serum Transferrin Protein through Assessment of Nanopore-Based Electrical and Chemical Responsiveness, ACS Nano, 2019, 13, 4246–4254 CrossRef CAS PubMed.
- J. Saharia, Y. N. D. Bandara, J. S. Lee, Q. Wang, M. J. Kim and M. J. Kim, Fabrication of hexagonal boron nitride based 2D nanopore sensor for the assessment of electro-chemical responsiveness of human serum transferrin protein, Electrophoresis, 2020, 41, 630–637 CrossRef CAS.
- K. J. Freedman, M. Jürgens, A. Prabhu, C. W. Ahn, P. Jemth, J. B. Edel and M. J. Kim, Chemical, thermal, and electric field induced unfolding of single protein molecules studied using nanopores, Anal. Chem., 2011, 83, 5137–5144 CrossRef CAS PubMed.
- Y. M. N. D. Y. Bandara, J. Tang, J. Saharia, L. W. Rogowski, C. W. Ahn and M. J. Kim, Characterization of Flagellar Filaments and Flagellin through Optical Microscopy and Label-Free Nanopore Responsiveness, Anal. Chem., 2019, 91, 13665–13674 CrossRef PubMed.
- B. I. Karawdeniya, Y. N. D. Bandara, J. W. Nichols, R. B. Chevalier, J. T. Hagan and J. R. Dwyer, Testing, Challenging Nanopores with Analyte Scope and Environment, J. Anal. Test., 2019, 3, 61–79 CrossRef.
- B. I. Karawdeniya, Y. N. D. Bandara, J. W. Nichols, R. B. Chevalier and J. R. Dwyer, Surveying silicon nitride nanopores for glycomics and heparin quality assurance, Nat. Commun., 2018, 9, 3278 CrossRef.
- H. Wu, Y. Chen, Q. Zhou, R. Wang, B. Xia, D. Ma, K. Luo and Q. Liu, Translocation of rigid rod-shaped virus through various solid-state nanopores, Anal. Chem., 2016, 88, 2502–2510 CrossRef CAS.
- L. Liu, H. Wu, J. Kong and Q. Liu, Solid-state nanopore for rod-like virus detection, Sci. Adv. Mater., 2013, 5, 2039–2047 CrossRef CAS.
- B. I. Karawdeniya, Y. M. N. D. Y. Bandara, A. I. Khan, W. T. Chen, H.-A. Vu, A. Morshed, J. Suh, P. Dutta and M. J. Kim, Adeno-associated virus characterization for cargo discrimination through nanopore responsiveness, Nanoscale, 2020, 12, 23721–23731 RSC.
- A. Darvish, G. Goyal, R. Aneja, R. V. Sundaram, K. Lee, C. W. Ahn, K.-B. Kim, P. M. Vlahovska and M. J. Kim, Nanoparticle mechanics: deformation detection via nanopore resistive pulse sensing, Nanoscale, 2016, 8, 14420–14431 RSC.
- J. S. Lee, J. Saharia, Y. N. D. Bandara, B. I. Karawdeniya, G. Goyal, A. Darvish, Q. Wang, M. J. Kim and M. J. Kim, Stiffness measurement of nanosized liposomes using solid-state nanopore sensor with automated recapturing platform, Electrophoresis, 2019, 40, 1337–1344 CrossRef CAS.
- G. Goyal, A. Darvish and M. J. Kim, Use of solid-state nanopores for sensing co-translocational deformation of nano-liposomes, Analyst, 2015, 140, 4865–4873 RSC.
- M. Chinappi, M. Yamaji, R. Kawano and F. Cecconi, Analytical model for particle capture in nanopores elucidates competition among electrophoresis, electroosmosis, and dielectrophoresis, ACS Nano, 2020, 14, 15816–15828 CrossRef PubMed.
- A. Asandei, I. Schiopu, M. Chinappi, C. H. Seo, Y. Park and T. Luchian, Electroosmotic trap against the electrophoretic force near a protein nanopore reveals peptide dynamics during capture and translocation, ACS Appl. Mater. Interfaces, 2016, 8, 13166–13179 CrossRef CAS.
- K. Tian, K. Decker, A. Aksimentiev and L.-Q. Gu, Interference-free detection of genetic biomarkers using synthetic dipole-facilitated nanopore dielectrophoresis, ACS Nano, 2017, 11, 1204–1213 CrossRef CAS PubMed.
- G. Huang, K. Willems, M. Soskine, C. Wloka and G. Maglia, Electro-osmotic capture and ionic discrimination of peptide and protein biomarkers with FraC nanopores, Nat. Commun., 2017, 8, 1–11 CrossRef CAS PubMed.
- M. Firnkes, D. Pedone, J. Knezevic, M. Doblinger and U. Rant, Electrically facilitated translocations of proteins through silicon nitride nanopores: conjoint and competitive action of diffusion, electrophoresis, and electroosmosis, Nano Lett., 2010, 10, 2162–2167 CrossRef CAS PubMed.
- A. Squires and A. Meller, DNA Capture and Translocation through Nanoscale Pores—a Fine Balance of Electrophoresis and Electroosmosis, Biophys. J., 2013, 105, 543–544 CrossRef CAS.
- R. Gasparac, D. T. Mitchell and C. R. Martin, Electrokinetic DNA transport in a nanopore membrane, Electrochim. Acta, 2004, 49, 847–850 CrossRef CAS.
- A. Y. Grosberg and Y. Rabin, DNA capture into a nanopore: interplay of diffusion and electrohydrodynamics, J. Chem. Phys., 2010, 133, 165102 CrossRef PubMed.
- D. P. Hoogerheide, S. Garaj and J. A. Golovchenko, Probing surface charge fluctuations with solid-state nanopores, Phys. Rev. Lett., 2009, 102, 256804 CrossRef.
- Y. N. D. Bandara, B. I. Karawdeniya, J. T. Hagan, R. B. Chevalier and J. R. Dwyer, Chemically Functionalizing Controlled Dielectric Breakdown Silicon Nitride Nanopores by Direct Photohydrosilylation, ACS Appl. Mater. Interfaces, 2019, 11, 30411–30420 CrossRef CAS.
- B. N. Anderson, M. Muthukumar and A. Meller, pH tuning of DNA translocation time through organically functionalized nanopores, ACS Nano, 2012, 7, 1408–1414 CrossRef.
- Y. N. D. Bandara, B. I. Karawdeniya and J. R. Dwyer, Push-Button Method To Create Nanopores Using a Tesla-Coil Lighter, ACS Omega, 2019, 4, 226–230 CrossRef CAS.
- Y. M. N. D. Y. Bandara, J. Saharia, B. I. Karawdeniya, J. T. Hagan, J. R. Dwyer and M. J. Kim, Beyond nanopore sizing: improving solid-state single-molecule sensing performance, lifetime, and analyte scope for omics by targeting surface chemistry during fabrication, Nanotechnology, 2020, 31, 335707 CrossRef PubMed.
- J. W. Robertson, C. G. Rodrigues, V. M. Stanford, K. A. Rubinson, O. V. Krasilnikov and J. J. Kasianowicz, Single-molecule mass spectrometry in solution using a solitary nanopore, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8207–8211 CrossRef CAS PubMed.
- R. M. Smeets, U. F. Keyser, D. Krapf, M.-Y. Wu, N. H. Dekker and C. Dekker, Salt dependence of ion transport and DNA translocation through solid-state nanopores, Nano Lett., 2006, 6, 89–95 CrossRef CAS.
- H. Bruus, Theoretical Microfluidics, Oxford University Press, Oxford, 2008; vol. 18 Search PubMed.
- C. M. Frament, N. Bandara and J. R. Dwyer, Nanopore surface coating delivers nanopore size and shape through conductance-based sizing, ACS Appl. Mater. Interfaces, 2013, 5, 9330–9337 CrossRef CAS PubMed.
- J. Dwyer, Y. Bandara, J. Whelan, B. Karawdeniya and J. Nichols, Silicon Nitride Thin Films for Nanofluidic Device Fabrication, Nanofluidics, 2016, 41, 190 Search PubMed.
- E. Y. Chi, S. Krishnan, T. W. Randolph and J. F. Carpenter, Physical stability of proteins in aqueous solution: mechanism and driving forces in nonnative protein aggregation, Pharm. Res., 2003, 20, 1325–1336 CrossRef CAS PubMed.
- D. S. Maclean, Q. Qian and C. R. Middaugh, Stabilization of proteins by low molecular weight multi-ions, J. Pharm. Sci., 2002, 91, 2220–2229 CrossRef CAS PubMed.
- J. M. Broering and A. S. Bommarius, Evaluation of Hofmeister effects on the kinetic stability of proteins, J. Phys. Chem. B, 2005, 109, 20612–20619 CrossRef CAS.
- A. A. Green, Studies in the physical chemistry of the proteins X. The solubility of hemoglobin in solutions of chlorides and sulfates of varying concentration, J. Biol. Chem., 1932, 95, 47–66 CrossRef.
- L. Medda, C. Carucci, D. F. Parsons, B. W. Ninham, M. Monduzzi and A. Salis, Specific cation effects on hemoglobin aggregation below and at physiological salt concentration, Langmuir, 2013, 29, 15350–15358 CrossRef CAS PubMed.
- S. Welch, Transferrin: The Iron Carrier, CRC Press, Boca Raton, 1992, pp. 60–90 Search PubMed.
- I. Nir, D. Huttner and A. Meller, Direct sensing and discrimination among ubiquitin and ubiquitin chains using solid-state nanopores, Biophys. J., 2015, 108, 2340–2349 CrossRef CAS.
- C. Lee, L. Joly, A. Siria, A.-L. Biance, R. m. Fulcrand and L. r. Bocquet, Large apparent electric size of solid-state nanopores due to spatially extended surface conduction, Nano Lett., 2012, 12, 4037–4044 CrossRef CAS PubMed.
- K. J. Freedman, S. R. Haq, J. B. Edel, P. Jemth and M. J. Kim, Single molecule unfolding and stretching of protein domains inside a solid-state nanopore by electric field, Sci. Rep., 2013, 3, 1638 CrossRef PubMed.
- X. Wang, M. D. Wilkinson, X. Lin, R. Ren, K. R. Willison, A. P. Ivanov, J. Baum and J. B. Edel, Single-molecule nanopore sensing of actin dynamics and drug binding, Chem. Sci., 2020, 11, 970–979 RSC.
- B. Kang, H. Tang, Z. Zhao and S. Song, Hofmeister series: Insights of ion specificity from amphiphilic assembly and interface property, ACS Omega, 2020, 5, 6229–6239 CrossRef CAS.
- A. T. Carlsen and V. Tabard-Cossa, Mapping shifts in nanopore signal to changes in protein and protein-DNA conformation, bioRxiv, 2020 DOI:10.1101/2020.04.01.020420.
- D. Y. Ling and X. S. Ling, On the distribution of DNA translocation times in solid-state nanopores: an analysis using Schrödinger’s first-passage-time theory, J. Phys.: Condens. Matter, 2013, 25, 375102 CrossRef PubMed.
- N. Arjmandi, W. Van Roy, L. Lagae and G. Borghs, Measuring the electric charge and zeta potential of nanometer-sized objects using pyramidal-shaped nanopores, Anal. Chem., 2012, 84, 8490–8496 CrossRef CAS PubMed.
- P. Waduge, R. Hu, P. Bandarkar, H. Yamazaki, B. Cressiot, Q. Zhao, P. C. Whitford and M. Wanunu, Nanopore-based measurements of protein size, fluctuations, and conformational changes, ACS Nano, 2017, 11, 5706–5716 CrossRef CAS PubMed.
- H. Wu, H. Liu, S. Tan, J. Yu, W. Zhao, L. Wang and Q. Liu, The estimation of field-dependent conductance change of nanopore by field-induced charge in the translocations of AuNPs-DNA conjugates, J. Phys. Chem. C, 2014, 118, 26825–26835 CrossRef CAS.
- S. W. Kowalczyk, D. B. Wells, A. Aksimentiev and C. Dekker, Slowing down DNA translocation through a nanopore in lithium chloride, Nano Lett., 2012, 12, 1038–1044 CrossRef CAS PubMed.
- M. Wanunu, W. Morrison, Y. Rabin, A. Y. Grosberg and A. Meller, Electrostatic focusing of unlabelled DNA into nanoscale pores using a salt gradient, Nat. Nanotechnol., 2010, 5, 160 CrossRef CAS PubMed.
- P. Sherman, Rheology of disperse systems, Industrial Rheology, Academic Press Inc., London, 1970, pp. 97–183 Search PubMed.
- S. E. Henrickson, M. Misakian, B. Robertson and J. J. Kasianowicz, Driven DNA transport into an asymmetric nanometer-scale pore, Phys. Rev. Lett., 2000, 85, 3057 CrossRef CAS PubMed.
- B. Cressiot, A. Oukhaled, G. Patriarche, M. Pastoriza-Gallego, J.-M. Betton, L. c. Auvray, M. Muthukumar, L. Bacri and J. Pelta, Protein transport through a narrow solid-state nanopore at high voltage: experiments and theory, ACS Nano, 2012, 6, 6236–6243 CrossRef CAS.
- A. Oukhaled, B. Cressiot, L. Bacri, M. Pastoriza-Gallego, J.-M. Betton, E. Bourhis, R. Jede, J. Gierak, L. Auvray and J. Pelta, Dynamics of completely unfolded and native proteins through solid-state nanopores as a function of electric driving force, ACS Nano, 2011, 5, 3628–3638 CrossRef CAS.
- I. Gitlin, J. D. Carbeck and G. M. Whitesides, Why are proteins charged? Networks of charge–charge interactions in proteins measured by charge ladders and capillary electrophoresis, Angew. Chem., Int. Ed., 2006, 45, 3022–3060 CrossRef CAS.
- N. Grover, J. Naaman, S. Ben-Sasson and F. Doljanski, Electrical sizing of particles in suspensions, Biophys. J., 1969, 9, 1398–1414 CrossRef CAS.
- R. DeBlois and C. Bean, Counting and sizing of submicron particles by the resistive pulse technique, Rev. Sci. Instrum., 1970, 41, 909–916 CrossRef.
- G. Di Muccio, A. E. Rossini, D. Di Marino, G. Zollo and M. Chinappi, Insights into protein sequencing with an α-Hemolysin nanopore by atomistic simulations, Sci. Rep., 2019, 9, 1–8 CAS.
- J. Wilson, K. Sarthak, W. Si, L. Gao and A. Aksimentiev, Rapid and accurate determination of nanopore ionic current using a steric exclusion model, ACS Sens., 2019, 4, 634–644 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03903b |
| ‡ Y. M. N. D. Y. B is presently employed at University of California, Riverside. |
| § B. I. K is presently employed at The Australian National University. |
| This journal is © The Royal Society of Chemistry 2021 |