Open Access Article
Open Access ArticleMolecular dynamics simulations of amino acid adsorption and transport at the acetonitrile–water–silica interface: the role of side chains†
Yong-Peng Wang
a,
Fei Lianga and
Shule Liu *ab
*ab
aSchool of Materials Science and Engineering, Sun Yat-sen University, Guangzhou 510275, P. R. China. E-mail: liushle@mail.sysu.edu.cn
bKey Laboratory for Polymeric Composite & Functional Materials of Ministry of Education, Sun Yat-sen University, Guangzhou 510275, P. R. China
First published on 18th June 2021
Abstract
The solvation and transport of amino acid residues at liquid–solid interfaces have great importance for understanding the mechanism of separation of biomolecules in liquid chromatography. This study uses umbrella sampling molecular dynamics simulations to study the adsorption and transport of three amino acid molecules with different side chains (phenylalanine (Phe), leucine (Leu) and glutamine (Gln)) at the silica–water–acetonitrile interface in liquid chromatography. Free energy analysis shows that the Gln molecule has stronger binding affinity than the other two molecules, indicating the side chain polarity may play a primary role in adsorption at the liquid–solid interface. The Phe molecule with a phenyl side chain exhibits stronger adsorption free energy than Leu with a non-polar side chain, which can be ascribed to the better solvated configuration of Phe. Further analysis of molecular orientations found that the amino acid molecules with apolar side chains (Phe and Leu) have ‘standing up’ configurations at their stable adsorption state, where the polar functional groups are close to the interface and the side chain is far from the interface, whereas the amino acid molecule with a polar side chain (Gln) chooses the ‘lying’ configuration, and undergoes a sharp orientation transition when the molecule moves away from the silica surface. Extending our simulation studies to systems with different solute concentrations reveals that there is a decrease in the adsorption free energy as well as surface diffusion as the solute concentration increases, which is related to the crowding in the interfacial layers. This simulation study gives a detailed microscopic description of amino acid molecule solvation and transport at the acetonitrile–water–silica interface in liquid chromatography and will be helpful for understanding the retention mechanism for amino acid separation.
1. Introduction
Liquid chromatography (LC) has become a robust technology in the field of separation and chemical analysis of biomolecules.1–4 LC utilizes its special separation mechanisms that different fluid components in the mobile phase have different adsorption strength on the stationary phase interface, resulting in differences in transport rate, and has become the standard bioanalytical tool of preferred choice in many laboratories. Compared with other separation methods, LC has many advantages, such as high resolving power, reproducibility, the broad selection of types and modes and compatibility with other analysis technologies, which makes it the technique of choice for protein and peptide separation in particular, where high resolution is particularly important for reducing or even eliminating the ion-suppression effects.5–7Proteins are the most abundant biomolecules, existing in all cells. The efficient separation of mixtures of proteins or peptide is important for proteomics,5,6 food science,8 the pharmaceutical industry9,10 and etc. Amino acid molecules are the basic unit of proteins. Therefore, a good understanding of the protein retention and partition mechanism in LC requires a thorough investigation of the interactions between amino acid molecules or residues and the stationary phase. In the past decades, separation methods for amino acids have developed rapidly including liquid chromatography11–15 and capillary electrophoresis,16–18 combined with analysis techniques such as mass spectrometry,12,13,17,19 nuclear magnetic resonance,20 ultraviolet and fluorescence detection,15,18 and amino acid analyzer.21 In particular, as the most commonly used separation method in biochemistry, the hydrophilic interaction liquid chromatography (HILIC), which is comprised of polar stationary phase and aprotic mobile phase, is widely utilized to separate the amino acids samples.22–27
At the microscopic level, the interactions between the stationary phase and amino acids as well as the mobile phase determine the actual separation efficiency. Therefore, controlling the interaction between amino acids and mineral surfaces plays a crucial role in improving the separation, purification, and retention of amino acids in practical application. Understanding how amino acids interact with an inorganic surface at the molecular level could be the significant challenges, and urgently needed.
Molecular dynamics (MD) simulations are powerful tools to study the microscopic interactions between amino acid molecules and solid surfaces. In the past decades, a number of MD simulations are performed to investigate the binding and adsorption of amino acid molecules at inorganic surfaces. Walsh et al. have used MD simulations to quantify the adsorption strength of the amino acid analogues at water–TiO2 (ref. 28 and 29) and water–SiO2 (ref. 30) interfaces interface and revealed the following trends in binding with TiO2 and SiO2 surface: “charged > polar aliphatic > nonpolar aliphatic” and “nonpolar aromatic > negatively charged > nonpolar aliphatic > polar > positively charged”, respectively. Brandt et al. characterized the adsorption free energies of amino acid side chain analogs to be used for qualitative estimation of binding affinities and binding modes of proteins at water–TiO2 interface, and found the strongest binders are the polar and aromatic side chain analogs.31 Shchelokov et al. reported that thermodynamic features of the amino acid adsorption on nanocrystalline TiO2 with experiment and molecular dynamics calculations based on density functional theory (DFT-MD), and showed that the ammonium group plays an important role in this process.32 Drobny et al. studied the interaction between the amino acids and water–TiO2 interface with both experiments and MD simulations, and their data indicated basic amino acids were adsorbed onto rutile TiO2 surfaces in multiple forms that depends on the surface hydroxyl group density.33 In spite of recent progress on simulations of amino acid adsorption at water–solid interfaces as well as the retention and transport of small organic molecules on interfaces in LC,34–39 the microscopic simulation studies of amino acid solvation and transport at the liquid–solid (LS) interfaces in LC are still lacking.
In this study, we used MD simulations with umbrella sampling technique to study the solvation and transport of three amino acid molecules (phenylalanine (Phe), leucine (Leu), glutamine (Gln)) at the acetonitrile (ACN)–water–silica interface. The three amino acid molecules have different types of side chains: polar (Gln), non-polar (Leu) and phenyl (Phe), while the ACN–water solution and silica are frequently used as the mobile phase and stationary phase in HILIC in many separation practice of amino acid molecules, respectively. The MD simulations performed in this study are trying to illustrate the free energy landscape of amino acid solvation at ACN–water–silica surface as well as its dependence on the side chain of amino acid molecules. The structure of this paper is organized as follows. The first part gives the introduction. The second part gives a brief introduction to the model system and MD simulation details. In the third part, the free energy profile, structure and dynamics of amino acid molecules are analyzed and discussed. The conclusion is given in the fourth part.
2. Simulation details
Umbrella sampling (US) simulations40,41 for the three types of amino acids solvation at the water–ACN–silica interface in the NVT ensemble at T = 298 K were performed. The simulation box contains a slab of silica in contact with water–ACN binary mixture composed of 1314 ACN molecules and 438 water molecules. This composition corresponds to the ACN–water volume ratio of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is the composition of mobile phase frequently used in the separation of amino acids and peptides with HILIC.23–25,27 The silica slab was set up by taking the top four layers of the (111) surface in the idealized β-cristobalite crystal and the force field parameters of the silica slab were taken from previous work by Rossky and coworkers.42 The β-cristobalite silica surface has been used in previous simulations of LS interface in LC extensively.34,37–39,43,44 The silica surface is fully terminated with hydroxyl groups, which are in contact with water and ACN molecules. The size of the simulation box is 50.67 Å × 43.88 Å × 150.00 Å in the x, y and z directions. The system is periodic in both x and y directions and non-periodic in the z direction due to the slab geometry. Fig. 1b gives a snapshot of the simulated system.
1, which is the composition of mobile phase frequently used in the separation of amino acids and peptides with HILIC.23–25,27 The silica slab was set up by taking the top four layers of the (111) surface in the idealized β-cristobalite crystal and the force field parameters of the silica slab were taken from previous work by Rossky and coworkers.42 The β-cristobalite silica surface has been used in previous simulations of LS interface in LC extensively.34,37–39,43,44 The silica surface is fully terminated with hydroxyl groups, which are in contact with water and ACN molecules. The size of the simulation box is 50.67 Å × 43.88 Å × 150.00 Å in the x, y and z directions. The system is periodic in both x and y directions and non-periodic in the z direction due to the slab geometry. Fig. 1b gives a snapshot of the simulated system.
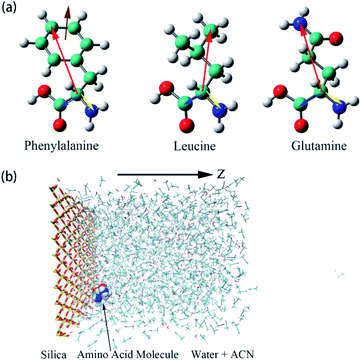 | ||
| Fig. 1 (a) Illustrations of the three amino acids, phenylalanine (Phe), leucine (Leu), glutamine (Gln). The specific notations for each atom are given in Fig. S1 of the ESI.† Moreover, schematic representations of colored arrows show defined vectors for the corresponding amino acid molecules to describe their orientation and rotational dynamics. (b) Overall view of the simulation box of water–acetonitrile binary mixture containing a single amino acid next to the silica slab. Hydrogen, oxygen, silicon, nitrogen, and carbon atoms are shown in white, red, yellow, blue, and cyan coloring, respectively. For the silica surface, the reference position for z = 0 is the top layer of silicon atom in the silica slab and the z-axis is normal to the silica surface. | ||
The six-site model of Nikitin and Lyubartsev45 for ACN and the TIP3P46 model for water were used to describe their intra- and inter-molecular interactions. As shown by Tobias and coworkers,47 the densities of ACN–water mixture at different concentrations predicted by this choice of force field parameters are in good agreement with experimental values. The force field parameters of the amino acid molecules are from the Generalized Amber Force Field (GAFF)48 generated by the Antechamber49 module. The charges of amino acid molecule are obtained with the AM1-BCC method.50,51 The non-bonding force field parameters of amino acid molecules, water, ACN and the silica surface are given in Tables S1–S4 of the ESI.† For inter-molecular van der Waals interactions, parameters were calculated by applying the Lorentz–Berthelot combination rule, as they are employed for all pairwise Lennard-Jones (LJ) potentials in the AMBER force field: σij = (σi + σj)/2 and 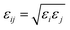 . The long-range coulombic interactions were calculated by the particle–particle–particle–mesh (PPPM) solver.52,53 Since the system in non-periodic along the z direction, the slab correction to 3D PPPM by Berkowitz et al.54 was also applied to the calculation of electrostatic interactions.
. The long-range coulombic interactions were calculated by the particle–particle–particle–mesh (PPPM) solver.52,53 Since the system in non-periodic along the z direction, the slab correction to 3D PPPM by Berkowitz et al.54 was also applied to the calculation of electrostatic interactions.
The reaction coordinate (RC) in umbrella sampling is defined as the z-direction distance between silica surface and center-of-mass (COM) of the amino acid molecule, which is biased at various points (windows) with a harmonic potential.55 The simulations of 19 umbrella sampling windows that were set every 0.5 Å along the RC and covered the range of RC from ξ = 3.0 Å to ξ = 12.0 Å were used. The spring constant for the harmonic restraint in the US simulation is 30 kcal mol−1 Å−2. The initial configuration for each window was built with the amino acid molecule placed at the equilibrium position of the harmonic potential. Each window was equilibrated at 298 K for 4.0 ns by the Nosé–Hoover thermostat56,57 after minimization of the initial configurations, 18.0 ns simulation was performed afterward to collect the data of trajectory. The time step for US simulations was 1.0 fs and the cutoff distance was set at 14.0 Å. All the simulations were performed using the large-scale Atomic/Molecular Massively Parallel Simulator58 (LAMMPS). The weighted histogram analysis method (WHAM)40,59 was used to construct the potential of mean force (PMF) from US simulation data.
3. Results and discussion
3.1 Solvent density profiles
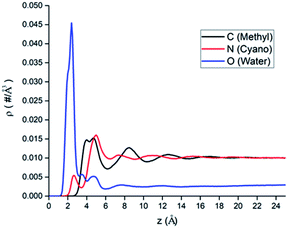
The atomic number density profiles of water–ACN solvent near the hydrophilic silica surface are shown in Fig. 2, including the methyl carbon atom (black line), the nitrogen atom (red line), and the oxygen atom of water (blue line) density profiles. Compared to the atoms of ACN, density profile of the oxygen atom of water exhibits a peak near the silica surface that is about 18 times of its bulk value, indicating strong adsorption of water molecules at the hydrophilic silica surface due to the hydrogen bonding with silanol groups.60 However, the highest peaks of the two atomic density profiles of ACN are only 1.5 times of its bulk value. Moreover, the major peaks of the atoms in ACN (z = 4.0–5.0 Å) are also farther away from the interface than that of the water oxygen (z = 2.5 Å) in the atomic density profiles. The above all shows that because water is more polar than ACN, water molecules are more easily adsorbed at the hydrophilic silica surface than ACN molecules.All atomic density profiles have 2 or 3 peaks. For the density profile of the ACN nitrogen atom, the first peak could be spotted at z = 2.5 Å, which is close to the interface and its position is similar to that of the first peak of the oxygen atom, and its value is just half of bulk value. This indicates that the attractive interaction between the polar cyano groups with the hydrophilic silica interface facilitate the adsorption of ACN molecules and they can penetrate the adsorbed water layer. Since the polarity of cyano groups is much weaker than hydroxyl groups of water, so the first peak of the nitrogen's density profile is much smaller than the second peak (z = 5.0 Å), and it is also noticeable that at the position of ACN nitrogen's second peak the density of water molecules is low. Compared with the oxygen and the nitrogen density profiles, the position of the first (z = 4.5 Å) and second peaks (z = 8.5 Å) of the methyl carbon atom density is more distant from the LS interface obviously. This again shows that cyano groups, which are more polar than methyl groups, tend to be distributed closer to the hydrophilic silica interface. Water oxygen density also has a two consecutive shoulder peaks z = 3.5 Å and z = 4.5 Å, which can be viewed as two sublayers.
The inhomogeneity of solvent density profiles can propagate for more than 12 Å into the bulk, and our following analysis will primarily focus on the solvation of amino acid molecules in this inhomogeneous environment.
3.2 Solvation of solute molecules
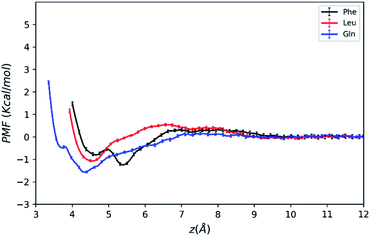 | ||
| Fig. 3 PMFs of amino acid molecules on silica surface solvated by water–acetonitrile binary mixture as a function of the COM distance from the surface. | ||
As mentioned above, the positions of the minima are at least 4 Å away from the silica surface for the three amino acids. This indicates that at the most stable adsorption state amino acid molecules are not in direct contact with the silica surface since the surface is already densely covered with water molecules (blue line in Fig. 2). The global minimum of the Phe molecule's PMF is at z = 5.5 Å, which is greater than that of Leu and Gln molecules at z = 4.3–4.5 Å, and this suggests that both Leu and Gln molecules are closer to the ACN–water–silica interface when adsorbed to the surface, due to less steric hindrance from their smaller side chains than the Phe molecule.
As illustrated in Fig. 3, the PMF of the polar Gln molecule shows the deepest minimum at z = 4.35 Å with depth of the minimum of −1.58 kcal mol−1. Meanwhile, it is noticeable that the Gln molecule has a local minimum about −0.49 kcal mol−1 at z = 3.7 Å in the PMF dramatically, and such metastable state doesn't appear in PMFs of the Phe and Leu molecules. All of the analysis above shows that the Gln molecule with polar side chain has a stronger tendency to be adsorbed to the silica surface at shorter distance from the surface, and its adsorption is the strongest at the global minimum of its PMF. This also shares some similarities with previous simulation studies that found amino acids with polar side chains have stronger binding affinity at the water–TiO2 interface.28,29
The PMFs also show that the Phe molecule is more stabilized at the global minimum of its PMF with the free energy value of −1.25 kcal mol−1 than that of −1.08 kcal mol−1 for Leu. This indicates that although the Phe molecule experienced more steric hindrance when adsorbed to the LS interface, it still takes more work to transfer the Phe molecule from the LS interface to the bulk than the Leu molecule. In the previous studies, amino acids with larger non-polar side chains are more stabilized than those with smaller side chains at high ACN concentration61 in bulk solutions, and amino acids with non-polar side chains are more exposed to the ACN solvent compared to the polar ones,62 while the underlying microscopic picture is not quite clear. Therefore, the free energy of transferring an amino acid molecule from the interface to the bulk may not solely depend on polarity of amino acid, and it should be interpreted with the collective effect of the LS interface, the solvent and the solute. The following sections will focus on revealing the microscopic origin for the free energy landscape described above with solvation structure and molecular orientation analysis.
| Amino acid | CN (ACN) | CN (OH) |
|---|---|---|
| Phe | 4.33 | 4.63 |
| Leu | 4.11 | 3.86 |
| Gln | 3.42 | 3.79 |
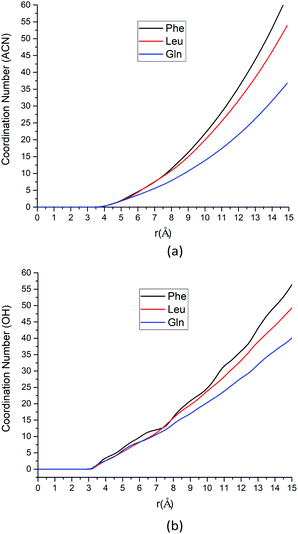
As the solute–solvent distance increases, the coordination number increases. Especially, the Phe molecule always has larger CNs of both water and ACN solvent molecules than Gln and Leu molecules. There are more solvent molecules (water, silanol groups and ACN) in the solvation shell near the Phe molecule than Gln and Leu molecules, as Fig. 4 suggested. Our analysis of CNs in the first solvation shell as well as those further away indicates that the Phe molecule is better solvated in both water and ACN the interfacial layers. Therefore, the Phe molecule can still get stabilized at the interface without a polar side chain, unlike the case of Gln. That can answer the question left over in the previous section where the PMF of the Phe molecule has deeper minimum near the silica surface than the Leu molecule. The solvent molecules play collective roles in the stable adsorption states of amino acids at the interface.
Our solvation structure analysis above shows that the Phe molecule is better solvated at the interface than Leu. To get solvated, the Phe molecule is expected to place its polar groups in the water phase while its less polar side chains are in the ACN phase. This suggests that the Phe molecule will choose an orientation where its polar groups are closer to the silica surface while its side chain is pointing toward the bulk. We will show this in the next section in our orientation distribution analysis.
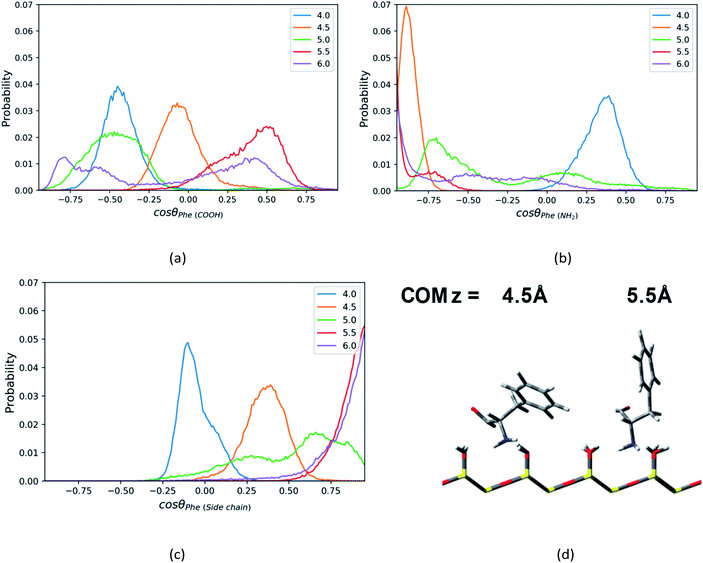
For the Phe molecule, its amino group points toward the silica surface, and its benzene ring inserts into the ACN phase at the minimum of the PMF (z = 5.5 Å) as illustrated in Fig. 5d. This ‘standing up’ orientation is also indicated by the peak of C1–C3 vector's profiles at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 1.00 in Fig. 5c. The Phe molecule choose this orientation such that the benzene ring can get solvated by ACN better. This preferential orientation at the LS interface agrees with our conjecture in the solvation structure analysis in previous sections, in which its polar groups and side chain point toward the surface and bulk, respectively. When the Phe molecule is closer to the silica surface, at z = 4.0 Å, Fig. 5a and c have shown peaks for cos
θ = 1.00 in Fig. 5c. The Phe molecule choose this orientation such that the benzene ring can get solvated by ACN better. This preferential orientation at the LS interface agrees with our conjecture in the solvation structure analysis in previous sections, in which its polar groups and side chain point toward the surface and bulk, respectively. When the Phe molecule is closer to the silica surface, at z = 4.0 Å, Fig. 5a and c have shown peaks for cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0, which suggests the C1–C2 and C1–C3 vectors of the Phe molecule are pointing toward the silica surface. The schematic diagram of the representative configurations is shown in Fig. S6 of the ESI.† At z = 4.5 Å, the Phe molecule points its C1–N1 vector toward the silica surface, as indicated by the peak at cos
θ < 0, which suggests the C1–C2 and C1–C3 vectors of the Phe molecule are pointing toward the silica surface. The schematic diagram of the representative configurations is shown in Fig. S6 of the ESI.† At z = 4.5 Å, the Phe molecule points its C1–N1 vector toward the silica surface, as indicated by the peak at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = −0.88 in Fig. 5b as well as the snapshot in Fig. 5d. This is probably due to the hydrogen bonding between amino group and the silanol groups. As the Phe molecule moves further away from its most stable state, at z = 6 Å, its configuration keeps ‘standing up’, in which the amino group and the benzene ring are close to the surface and bulk respectively. The peak that appears in the region with cos
θ = −0.88 in Fig. 5b as well as the snapshot in Fig. 5d. This is probably due to the hydrogen bonding between amino group and the silanol groups. As the Phe molecule moves further away from its most stable state, at z = 6 Å, its configuration keeps ‘standing up’, in which the amino group and the benzene ring are close to the surface and bulk respectively. The peak that appears in the region with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0 in Fig. 5b corresponds to the C1–N1 vector, while the peak of the C1–C3 vector's profiles appears in the region with cos
θ < 0 in Fig. 5b corresponds to the C1–N1 vector, while the peak of the C1–C3 vector's profiles appears in the region with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ > 0 in Fig. 5c.
θ > 0 in Fig. 5c.
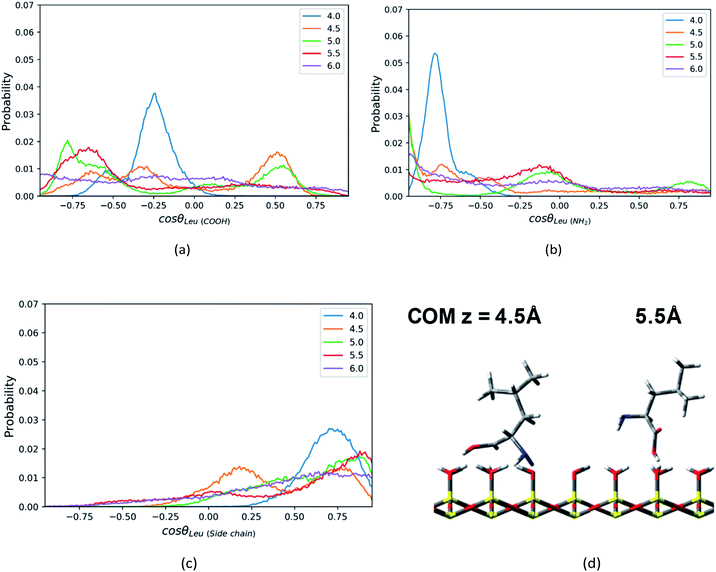
In addition, the Leu molecule with non-polar isobutyl side chain shows similar orientation distributions to that of the Phe molecule, which are illustrated in Fig. S4a–S4c in the ESI.† At its minimum of the PMF (z = 4.5 Å), the polar groups (amino group and carboxyl group) are adjacent to the silica surface due to the hydrogen bonding between them, and the non-polar side chain is solvated in the ACN phase, as shown in Fig. 6d. The Leu molecule has both polar and non-polar functional groups. According to the “like dissolves like” rule, the polar end is easier to get solvated in the water phase adsorbed on the surface than the ACN phase. When the Leu molecule is further away from the silica surface, due to the decay of the surface adsorption strength and the repulsion from adsorbed water against the side chain, its side chain keeps pointing toward the bulk phase dominantly, whose peaks of orientation distribution (C1–C4 vector) always appear in the region with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ > 0 in Fig. 6c. Besides, to be solvated by the interfacial water molecules and adsorbed on the silica surface in terms of hydrophilic interactions, the carboxyl and amino groups also always have a tendency to point toward the surface, as confirmed by the peaks of C1–C2 and C1–N1 vector's orientation distribution profiles in regions with cos
θ > 0 in Fig. 6c. Besides, to be solvated by the interfacial water molecules and adsorbed on the silica surface in terms of hydrophilic interactions, the carboxyl and amino groups also always have a tendency to point toward the surface, as confirmed by the peaks of C1–C2 and C1–N1 vector's orientation distribution profiles in regions with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0 in Fig. 6a and b. Therefore, the stable configuration of the Leu molecule at the LS interface shows the “standing” orientation predominantly, which shares some similarities with the orientation of the Phe molecule at the LS interface. However, compared to the non-polar phenyl side chain in the Phe molecule, the orientation of the non-polar isobutyl side chain in Leu near surface moves somewhat further away from the silica surface. This is due to the fact that the adsorption of the non-polar isobutyl side chain on the silica surface is weaker, and the benzene ring of the Phe molecule is relatively constrained at the silica surface due to the Coulomb interaction with the partial charges of the silica polar surface.64 As illustrated in Fig. S6 in the ESI,† the behavior of the benzene ring adsorbed in the vicinity (z < 5 Å) of the silica surface shows that it tends to orientate itself non-perpendicularly to the silica surface, as observed in the previous computational study.65
θ < 0 in Fig. 6a and b. Therefore, the stable configuration of the Leu molecule at the LS interface shows the “standing” orientation predominantly, which shares some similarities with the orientation of the Phe molecule at the LS interface. However, compared to the non-polar phenyl side chain in the Phe molecule, the orientation of the non-polar isobutyl side chain in Leu near surface moves somewhat further away from the silica surface. This is due to the fact that the adsorption of the non-polar isobutyl side chain on the silica surface is weaker, and the benzene ring of the Phe molecule is relatively constrained at the silica surface due to the Coulomb interaction with the partial charges of the silica polar surface.64 As illustrated in Fig. S6 in the ESI,† the behavior of the benzene ring adsorbed in the vicinity (z < 5 Å) of the silica surface shows that it tends to orientate itself non-perpendicularly to the silica surface, as observed in the previous computational study.65
When moving away from the silica surface, the change of the orientation of Leu's non-polar side chain is similar to that of the Phe molecule. As illustrated in Fig. S6 and S7 of the ESI,† away from the silica surface, the configurations for the corresponding amino acids have converted from “lying” to “standing up”.
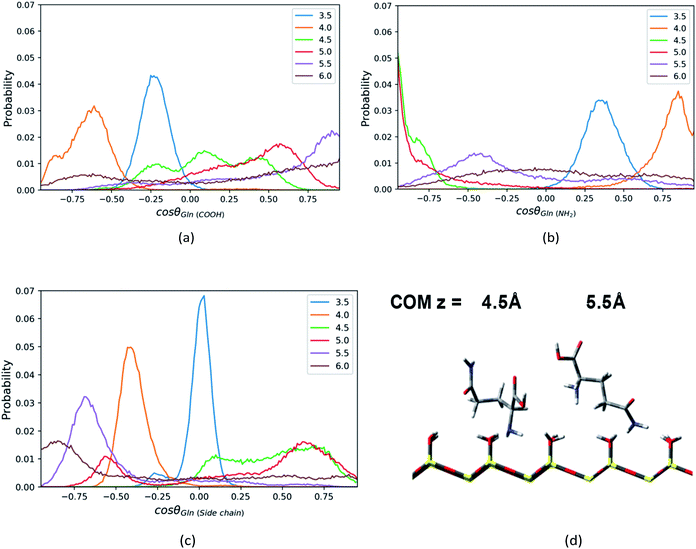
Similar to the Phe and Leu molecules, the polar functional group (amino group) of the Gln molecule points to the silica surface, and the polar side chain (amide group) tends to point toward the opposite direction when the Gln molecule reaches to the minimum of PMF (z = 4.5 Å). That is because the amino group has stronger interaction with the silica surface and less steric hindrance than other functional groups. According the PMF of the Gln molecule shown above, the Gln molecule also has a metastable state at z = 3.5 Å, where both amide group and carboxyl group is closer to surface in the Gln molecule as indicated in Fig. S8 of the ESI.†
Compared to the orientation distributions of Phe and Leu molecules shown above, the Gln molecule reorients itself several times as it moves away from the silica surface. The carboxyl group of the Gln molecule near the silica surface region (z < 4.5 Å) tends to point toward the silica surface and then reorients toward the bulk away from the silica surface (z > 4.5 Å), as suggested by Fig. 7a (C1–C2 vector), where the position of the orientation distribution peak moves from the region with negative cosine to that with positive values as z increases. The amino group of Gln points toward the bulk near the surface region (z < 4.0 Å) and then turns toward the silica surface within a few angstroms as the distance between the Gln molecule and the surface increases. As shown in Fig. 7b, the peak of the orientation distribution profile for C1–N1 vector is located where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is close to 1.0 when z = 4.0 Å, but when z = 4.5 Å the position of the peak suddenly changes to cos
θ is close to 1.0 when z = 4.0 Å, but when z = 4.5 Å the position of the peak suddenly changes to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = −1. Moreover, the Gln molecule rearranges its orientation again remarkably at z = 5.5 Å, and the amino group begins to keep away from the interfacial region like the carboxyl group, as suggested by the snapshot in Fig. 7d. At the same time, in the preferred orientation the polar side chain points toward the polar silica surface rather than the bulk away from the silica surface, and this suggests the side chain of the Gln molecule interacts more strongly with the silica surface. This can be inferred from the C1–N2 vector orientation distribution peak mainly show up in the region with cos
θ = −1. Moreover, the Gln molecule rearranges its orientation again remarkably at z = 5.5 Å, and the amino group begins to keep away from the interfacial region like the carboxyl group, as suggested by the snapshot in Fig. 7d. At the same time, in the preferred orientation the polar side chain points toward the polar silica surface rather than the bulk away from the silica surface, and this suggests the side chain of the Gln molecule interacts more strongly with the silica surface. This can be inferred from the C1–N2 vector orientation distribution peak mainly show up in the region with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0 when z > 5.5 Å (Fig. 7c). As illustrated in Fig. S8,† the configuration of the Gln molecule changing from the “lying” to the “standing up” is similar to that of the Phe and the Leu molecules, but the polar side chain closer to the silica surface shows a different configuration for the Gln molecule and this suggests that the molecule is experiencing a reorientation. The interpretation for this will be later discussed in the section of rotation dynamics.
θ < 0 when z > 5.5 Å (Fig. 7c). As illustrated in Fig. S8,† the configuration of the Gln molecule changing from the “lying” to the “standing up” is similar to that of the Phe and the Leu molecules, but the polar side chain closer to the silica surface shows a different configuration for the Gln molecule and this suggests that the molecule is experiencing a reorientation. The interpretation for this will be later discussed in the section of rotation dynamics.
3.3 Dynamics of solute molecules
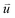 at time 0 and time t according to the following formula:
at time 0 and time t according to the following formula:
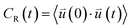 | (1) |
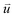 is the intra-molecular vector for characterizing molecular orientations, as illustrated in Fig. 1a. With the calculated rotational TCFs, the rotational relaxation time τ (τ = Aτ1 + (1 − A)τ2) can be obtained by fitting the rotational TCF to the bi-exponential function CR(t) = A
is the intra-molecular vector for characterizing molecular orientations, as illustrated in Fig. 1a. With the calculated rotational TCFs, the rotational relaxation time τ (τ = Aτ1 + (1 − A)τ2) can be obtained by fitting the rotational TCF to the bi-exponential function CR(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + (1 − A)exp(−t/τ2),66–68 consisting of amplitude A and exponential decay terms with correlation times τ1 and τ2.
exp(−t/τ1) + (1 − A)exp(−t/τ2),66–68 consisting of amplitude A and exponential decay terms with correlation times τ1 and τ2.The rotational relaxation time τ for the intramolecular vectors of each amino acid at different distances away from the silica surface is shown in Fig. 8. In general, as the distance from the surface increases, the rotational relaxation time τ for all vectors is relatively smaller, which is due to the fact that the strength of adsorption with the silica surface is weaker. At the z = 5.5 Å and 4.5 Å where the minimum of PMF is located for Phe and Leu molecules respectively, the vectors pointing to non-polar side chain (C1–C3 vector and C1–C4 vector) have smaller value of τ compared to Phe and Leu molecules own C1–C2 vector or C1–N1 vector in Fig. 8a and b. That is because adsorption with the silica surface hinders the rotation of the polar functional groups, as indicated by the configurations in Fig. 5d and 6d. Therefore, compared with the amino group and carboxyl groups, the non-polar side chains are able to rotate faster.
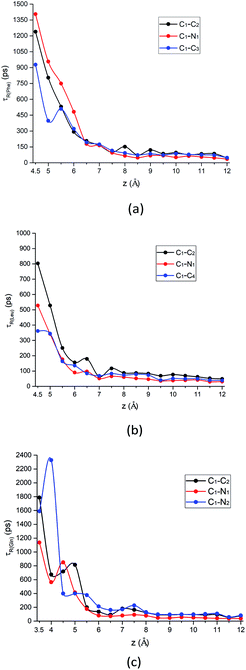 | ||
| Fig. 8 The rotational relaxation time τ for intramolecular vectors of each amino acid molecule defined in Fig. 1a as a function of the COM z distance from the surface. Black curve: alpha-carbon pointing to the carboxyl group (C1–C2 vector); red curve: alpha-carbon pointing to amino group (C1–N1 vector); blue curve: alpha-carbon pointing to the above-mentioned atom for the side chain of each amino acid (C1–C3 vector, C1–C4 vector, and C1–N2 vector, respectively) for (a) Phe, (b) Leu and (c) Gln molecules. | ||
What is more special is the change of the rotational relaxation time τ of the Gln molecule's polar chains at different distance from the silica surface. The polar side chain is adsorbed to the LS interface when the Gln molecule is in the metastable state at z = 3.5 Å, as indicated by that the τ of the C1–N2 vector is larger than that of the C1–C2 and the C1–N1 vector in Fig. 8c. Although the amino and carboxyl groups rotate faster at the metastable state than the side chain, the rotation relaxation times of their corresponding vectors increase and are greater than that of the side chain at the minimum of the PMF with z = 4.5 Å. This rotational dynamics at the stable state is consistent with the molecular orientation shown in Fig. 7d, where the polar functional groups of the Gln molecule are easier to be adsorbed to the silica surface. However, starting from z = 5 Å, the τ values of the Gln side chain and the polar chain show a crossover as distance from the surface increases (Fig. 8c). This is because the polar chains lose their dominance in the competition with the side chain for adsorption with interface, which is also consistent with the orientation change shown in Fig. 7d.
In addition, the relaxation times for C1–C3 vector, C1–C4 vector, and C1–N2 vector in Fig. 8 are also consistent with their orientation distribution in the previous section: the adsorption strength increases with increasing side-chain polarity to adsorb on the silica surface, but the aromatic side chain to bind to the silica surface are stronger compared to the others. Fig. S9 in the ESI† also shows that the stronger adsorption strength of the aromatic benzene ring near the silica surface would give rise to the larger rotational relaxation time of the benzene ring normal vector. Further away from the hydrophilic silica surface, the decay of Phe's non-polar side chain (C1–C3 vector) relaxation time is faster than the others (C1–C2 vector and C1–N1 vector), as shown in Fig. 8a.
| MSDx–y(t) = 〈(x(t) − x(0))2 + (y(t) − y(0))2〉 | (2) |
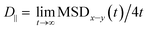 .69,70
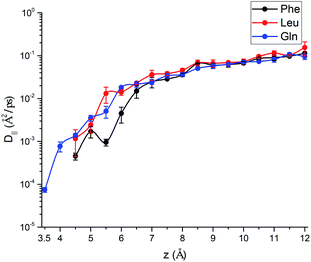
.69,70The parallel diffusion coefficients D∥ for all three amino acids in different umbrella windows are shown in Fig. 9. With increasing the distance from the silica surface, the parallel diffusion coefficient D∥ of each amino acid follows a very similar trend, which gradually increases to the same order of magnitude in the bulk region. Near the silica surface, each amino acid has a lower parallel diffusion, meaning the adsorption strength between each amino acid and surface is relatively stronger. It can be found here that the diffusion of the Phe molecule is the slowest, which corresponds to the observation that the Phe molecule has the largest solvation shell in Fig. 4. For Phe and Leu molecules, the diffusion coefficients have local minima at their respective minima of the free energy (z = 5.5 Å and 4.5 Å respectively). Although the diffusion coefficient of the Gln molecule doesn't have a local minimum at the lowest point of PMF, the local minimum appears at z = 3.7 Å, where the local minimum of the PMF occurs. These all illustrate that adsorption of amino acids inhibits their transport parallel to the surface.
3.4 Collective effects of multiple solute molecules
The free energy landscape and translational dynamics above are helpful for understanding the solvation structure and dynamics of a single molecule standalone. However, multiple solute molecules are present at the interface between the liquid and the solid phase in the practical separation process of the LC. Therefore, we have added more amino acid molecules to the system tentatively to study the collective effects of multiple solute molecules. The number of solute molecules starts from 10 and gradually increases to 50 with an increment of 10 molecules. The protocols of the simulations are the same as above US simulations except no biasing potential is applied.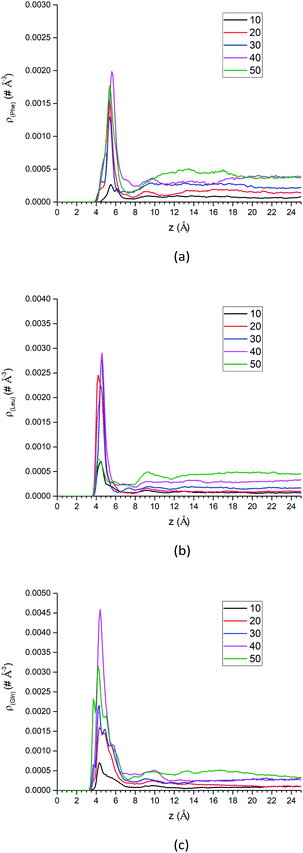 | ||
| Fig. 10 The center-of-mass density profiles of (a) Phe, (b) Leu and (c) Gln molecules with different number of solute molecules. | ||
Additional analysis can be performed on the density profiles of amino acid molecules. First, we have scaled all the density profiles by the number of amino acid molecules in the system, and this gives us the spatial probability distribution of amino acid molecules along the z-axis, shown in Fig. S13 of the ESI.† The spatial probability distributions at the silica surface reached maximum at 20 amino acid molecules for Phe and Leu (Fig. S13a and b†), while that of Gln reached maximum at 40 molecules. Once again this shows that the polar side chain of the Gln molecule could enhance the adsorption of more Gln molecules on the silica surface.
It is more instructive to explore the difference of solute molecule distribution at the interface and in the bulk. Therefore, the PMFs for multiple solute molecules are calculated via taking the logarithm of the ratio between the singlet density and the bulk density.72
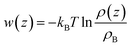 | (3) |
The details of PMF profiles for amino acids at different concentration are displayed in Fig. S14 of the ESI.† What's the most important is the values of PMF profiles' minima, and the trend graphs of those with the number of amino acid molecules are plotted in Fig. S15 of the ESI.† In general, as the number of the solute molecules increases, the values of the free energy minima gradually increase for the Phe and the Leu molecules. This indicates that the interface area becomes more crowded and the repulsion between solute molecules becomes stronger, so less work is required to transfer molecules from the surface to the bulk. In contrast to the Gln molecule, the values of PMF profiles' lowest points don't change much with concentration (1 to 40 Gln molecules in the simulated system), which may be related to the fact that Gln molecules have polar groups at both ends and can be adsorbed more stably with the silica surface.
In summary, as more amino acid molecules are added to the LS interface, the adsorption of amino acids still exists at silica surface, even though the repulsion between solute molecules becomes larger within the crowded interfacial adsorption layer. That can be reflected by the density peaks at interface region in Fig. 10 and decreased parallel diffusion coefficients in Fig. S16.† However, as shown in the density profiles of Fig. 10, as the number of amino acid molecules increases, the surface adsorption will become saturated, which implies that there is an upper limit for increasing the injection rate of the mixed amino acid reagent in order to improve the separation efficiency of LC. Otherwise, if the stationary phase of LC reaches saturation for adsorption of amino acid molecules, the separation efficiency may start to change.
4. Conclusions
In this work, using umbrella sampling molecular dynamics simulations, we have characterized structures, dynamics, binding affinities of neutral-form amino acids classified according to their side chains (aromatic: Phe, non-polar: Leu, polar: Gln) at the acetonitrile–water–silica interface. The interaction between amino acids and the silica surface is strongly affected by the polarity and size of side chains. Our free energy calculations indicated that the binding affinity of three amino acids is ranked as: Gln > Phe > Leu. The Gln molecule with polar side chain is closer to the silica surface than Phe and Leu molecules, and this indicates that side chain polarity still plays an important role in the interfacial adsorption. Further solvation structure analysis suggest that the Phe molecule is better solvated by ACN and hydroxyl groups at the LS interface, which explains why the Phe molecule is the easier to be adsorbed on the silica surface than the Leu molecule. Orientation analysis suggests that “lying” to “standing up” transition occurred when the solute molecule moves away from the silica surface, and this rearrangement of orientation is determined by the interplay of steric hindrance, side chain polarity and size, as well as the solvation of side chains. In addition, the Gln molecule has an interesting reorientation pattern as the molecule moves away from the silica surface, which is consistent with rotation dynamics analysis that polar functional groups lose their dominance in the competition with the side chain for adsorption with interface.Moreover, we have explored the collect effect of solute concentration on the interfacial structure and dynamics with unbiased simulations. As the number of amino acid molecules increases, the density distribution at the interface increases, and the values of the free energy minima generally increases. This suggests multiple solute molecules are still adsorbed on the interface, but the less work is needed to transfer solute molecules from the interface to the bulk. Due to the repulsion with other molecules except for adsorption, the parallel diffusion coefficients of amino acids decrease in interface region. From the density profiles, it can be seen that the saturated adsorption would appear on the surface as the concentration of amino acid increases. Our simulations provide useful tools to explore the effect of side chains on microscopic interfacial solvation, transport and adsorption of amino acids in HILIC. It is also possible to extend such simulation methodology further to explore the separation mechanisms of small peptide in liquid chromatography, with more complicated collective variables such as molecular orientation74 or conformation75 taken into consideration.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported in part by NSFC (11804400) and by the Fundamental Research Funds for the Central Universities (No. 19lgpy19). We also thank the computer time from Tianhe-2 system at National Supercomputer Center in Guangzhou.References
- S. R. Needham, Bioanalysis, 2017, 9, 1935–1937 CrossRef CAS PubMed.
- Q. Wu, H. Yuan, L. Zhang and Y. Zhang, Anal. Chim. Acta, 2012, 731, 1–10 CrossRef CAS PubMed.
- N. Afeyan, N. Gordon, I. Mazsaroff, L. Varady, S. Fulton, Y. Yang and F. Regnier, J. Chromatogr. A, 1990, 519, 1–29 CrossRef CAS PubMed.
- J. Bellot and J. Condoret, Process Biochem., 1993, 28, 365–376 CrossRef CAS.
- Y. Shi, R. Xiang, C. Horváth and J. A. Wilkins, J. Chromatogr. A, 2004, 1053, 27–36 CrossRef CAS.
- P. J. Boersema, S. Mohammed and A. J. R. Heck, Anal. Bioanal. Chem., 2008, 391, 151–159 CrossRef CAS PubMed.
- X. Zhang, A. Fang, C. P. Riley, M. Wang, F. E. Regnier and C. Buck, Anal. Chim. Acta, 2010, 664, 101–113 CrossRef CAS PubMed.
- L. Ponce-Robles, G. Rivas, B. Esteban, I. Oller, S. Malato and A. Agüera, Anal. Bioanal. Chem., 2017, 409, 6181–6193 CrossRef CAS PubMed.
- H. John, M. Walden, S. Schäfer, S. Genz and W.-G. Forssmann, Anal. Bioanal. Chem., 2004, 378, 883–897 CrossRef CAS PubMed.
- C. T. Mant and R. S. Hodges, High-performance liquid chromatography of peptides and proteins: separation, analysis, and conformation, CRC Press, 2017 Search PubMed.
- M.-L. Oldekop, K. Herodes and R. Rebane, Int. J. Mass Spectrom., 2017, 421, 189–195 CrossRef CAS.
- M. L. Oldekop, R. Rebane and K. Herodes, Eur. J. Mass Spectrom., 2017, 23, 245–253 CrossRef CAS PubMed.
- S. Kowalski, M. Kopuncova, Z. Ciesarova and K. Kukurova, J. Food Sci. Technol., 2017, 54, 3716–3723 CrossRef CAS PubMed.
- L. Gwatidzo, B. M. Botha and R. I. McCrindle, Food Chem., 2013, 141, 2163–2169 CrossRef CAS PubMed.
- H. Wang, Y. R. McNeil, T. W. Yeo and N. M. Anstey, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2013, 940, 53–58 CrossRef CAS PubMed.
- S. Chalavi, A. R. Fakhari, S. Nojavan and P. Mirzaei, Electrophoresis, 2018, 39, 2202–2209 CrossRef CAS PubMed.
- N. M. Schiavone, S. A. Sarver, L. Sun, R. Wojcik and N. J. Dovichi, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2015, 991, 53–58 CrossRef CAS PubMed.
- J. Qiu, J. Wang, Z. Xu, H. Liu and J. Ren, PLoS One, 2017, 12, e0179892 CrossRef PubMed.
- B. S. Reddy, V. N. Chary, P. Pavankumar and S. Prabhakar, J. Mass Spectrom., 2016, 51, 638–650 CrossRef CAS PubMed.
- X. Shi, G. P. Holland and J. L. Yarger, Anal. Biochem., 2013, 440, 150–157 CrossRef CAS PubMed.
- Q. Zhao, Y. Cao, Y. Wang, C. Hu, A. Hu, L. Ruan, Q. Bo, Q. Liu, W. Chen, F. Tao, M. Ren, Y. Ge, A. Chen and L. Li, Asia Pac. J. Clin. Nutr., 2014, 23, 429–436 CAS.
- D. Moravcová and J. Planeta, Separations, 2018, 5, 48 CrossRef.
- P. Hemström and K. Irgum, J. Sep. Sci., 2006, 29, 1784–1821 CrossRef PubMed.
- Y. Konya, M. Taniguchi, M. Furuno, Y. Nakano, N. Tanaka and E. Fukusaki, J. Chromatogr. A, 2018, 1578, 35–44 CrossRef CAS PubMed.
- V. Spicer and O. V. Krokhin, J. Chromatogr. A, 2018, 1534, 75–84 CrossRef CAS PubMed.
- Y. Wen, X. Yuan, F. Qin, L. Zhao and Z. Xiong, Biomed. Chromatogr., 2019, 33, e4387 CrossRef PubMed.
- A. J. Alpert, J. Chromatogr., 1990, 499, 177–196 CrossRef CAS PubMed.
- S. Monti and T. R. Walsh, J. Phys. Chem. C, 2010, 114, 22197–22206 CrossRef CAS.
- A. M. Sultan, Z. E. Hughes and T. R. Walsh, Langmuir, 2014, 30, 13321–13329 CrossRef CAS PubMed.
- L. B. Wright and T. R. Walsh, J. Phys. Chem. C, 2012, 116, 2933–2945 CrossRef CAS.
- E. G. Brandt and A. P. Lyubartsev, J. Phys. Chem. C, 2015, 119, 18126–18139 CrossRef CAS.
- A. Shchelokov, N. Palko, V. Potemkin, M. Grishina, R. Morozov, E. Korina, D. Uchaev, I. Krivtsov and O. Bol'shakov, Langmuir, 2019, 35, 538–550 CrossRef CAS PubMed.
- M. Xue, J. Sampath, R. N. Gebhart, H. J. Haugen, S. P. Lyngstadaas, J. Pfaendtner and G. Drobny, Langmuir, 2020, 36, 10341–10350 CrossRef CAS PubMed.
- J. Rybka, A. Höltzel and U. Tallarek, J. Phys. Chem. C, 2017, 121, 17907–17920 CrossRef CAS.
- J. L. Rafferty, L. Zhang, J. I. Siepmann and M. R. Schure, Anal. Chem., 2007, 79, 6551–6558 CrossRef CAS PubMed.
- J. L. Rafferty, J. I. Siepmann and M. R. Schure, J. Chromatogr. A, 2012, 1223, 24–34 CrossRef CAS PubMed.
- J. L. Rafferty, J. I. Siepmann and M. R. Schure, J. Chromatogr. A, 2011, 1218, 9183–9193 CrossRef CAS PubMed.
- R. K. Lindsey, J. L. Rafferty, B. L. Eggimann, J. I. Siepmann and M. R. Schure, J. Chromatogr. A, 2013, 1287, 60–82 CrossRef CAS PubMed.
- K. Ren, Y.-P. Wang and S. Liu, Phys. Chem. Chem. Phys., 2021, 23, 1092–1102 RSC.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- S. H. Lee and P. J. Rossky, J. Chem. Phys., 1994, 100, 3334–3345 CrossRef CAS.
- J. Rybka, A. Höltzel, S. M. Melnikov, A. Seidel-Morgenstern and U. Tallarek, Fluid Phase Equilib., 2016, 407, 177–187 CrossRef CAS.
- F. Liang, J. Ding and S. Liu, Langmuir, 2021, 37, 2091–2103 CrossRef CAS PubMed.
- A. M. Nikitin and A. P. Lyubartsev, J. Comput. Chem., 2007, 28, 2020–2026 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- M. J. Makowski, A. C. Stern, J. C. Hemminger and D. J. Tobias, J. Phys. Chem. C, 2016, 120, 17555–17563 CrossRef CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- D. A. Case, T. E. Cheatham 3rd, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2000, 21, 132–146 CrossRef CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer simulation using particles, Adam Hilger, 1988 Search PubMed.
- I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- S. Nose, Mol. Phys., 1984, 52, 255–268 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- Y.-P. Wang, K. Ren and S. Liu, Phys. Chem. Chem. Phys., 2020, 22, 10322–10334 RSC.
- K. Mahali, S. Roy and B. Dolui, J. Solution Chem., 2013, 42, 1096–1110 CrossRef CAS.
- L. Zhu, W. Yang, Y. Y. Meng, X. Xiao, Y. Guo, X. Pu and M. Li, J. Phys. Chem. B, 2012, 116, 3292–3304 CrossRef CAS PubMed.
- M. Tuckerman, Statistical mechanics: theory and molecular simulation, Oxford University Press, 2010 Search PubMed.
- B. Coasne, C. Alba-Simionesco, F. Audonnet, G. Dosseh and K. E. Gubbins, Langmuir, 2009, 25, 10648–10659 CrossRef CAS PubMed.
- B. Coasne and J. T. Fourkas, J. Phys. Chem. C, 2011, 115, 15471–15479 CrossRef CAS.
- B. J. Loughnane, R. A. Farrer, A. Scodinu and J. T. Fourkas, J. Chem. Phys., 1999, 111, 5116–5123 CrossRef CAS.
- B. J. Loughnane, R. A. Farrer and J. T. Fourkas, J. Phys. Chem. B, 1998, 102, 5409–5412 CrossRef CAS.
- C. M. Morales and W. H. Thompson, J. Phys. Chem. A, 2009, 113, 1922–1933 CrossRef CAS PubMed.
- P. Liu, E. Harder and B. J. Berne, J. Phys. Chem. B, 2004, 108, 6595–6602 CrossRef CAS.
- Y. von Hansen, S. Gekle and R. R. Netz, Phys. Rev. Lett., 2013, 111, 118103 CrossRef PubMed.
- K. Miyabe and G. Guiochon, J. Chromatogr. A, 2010, 1217, 1713–1734 CrossRef CAS PubMed.
- D. Chandler, Introduction to modern statistical mechanics, Oxford University Press, 1987 Search PubMed.
- K. Ren and S. Liu, Phys. Chem. Chem. Phys., 2020, 22, 1204–1213 RSC.
- J. Zhou, J. Zheng and S. Jiang, J. Phys. Chem. B, 2004, 108, 17418–17424 CrossRef CAS.
- M. Deighan and J. Pfaendtner, Langmuir, 2013, 29, 7999–8009 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03982b |
| ‡ Y.-P. Wang and F. Liang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |