Open Access Article
Open Access ArticleHelium-induced damage in U3Si5 by first-principles studies†
Yibo Wanga,
Zhenbo Pengb,
Nianxiang Qiu*a,
Heming Hec,
Rongjian Pan d,
Lu Wud,
Qing Huang
d,
Lu Wud,
Qing Huang a and
Shiyu Du
a and
Shiyu Du *a
*a
aEngineering Laboratory of Nuclear Energy Materials, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, Zhejiang 315201, P. R. China. E-mail: qiunianxiang@nimte.ac.cn; dushiyu@nimte.ac.cn
bInstitute of Energy Storage & Conversion Technology, Ningbo Polytechnic, China
cSchool of Mechanical and Electrical Engineering, Guangzhou University, Guangzhou 510006, China
dThe First Sub-Institute, Nuclear Power Institute of China, Chengdu, Sichuan 610005, China
First published on 5th August 2021
Abstract
Uranium silicide U3Si5 has been explored as an advanced nuclear fuel component for light water reactor to enhance the accident tolerance. In this paper, in order to understand the fuel performance of U3Si5, the primary point defects, secondary point defects, and the dissolution of He gas were studied by first-principles methods. Compared with U atoms and another type of Si2 atoms, Si1 atoms far from intrinsic Si vacancies are more likely to form point defects, implying that Si vacancies are prone to form separate single vacancies rather than vacancy clusters in the initial stage. From the calculated anti-site defect energies, it can be predicted that non-stoichiometric U-rich phase of U3Si5 are more likely to be formed than Si-rich phase, which are consistent with the chemical analysis of experimentally sintered Si-lean U3Si5 sample. It can be found that a single He atom favors residence in the interstitial site in the U layer directly above/below the intrinsic vacancy. It can also be seen that Vac-U, Vac-Si1, and Vac-Si2 vacancies can energetically accommodate up to 4, 0, and 3 He atoms, respectively. The formation of secondary vacancy defects is strongly dependent on the helium concentration. The current results show that the He-filled vacancy can promote the formation of adjacent secondary vacancy, leading to the formation of gas bubbles. This work may provide theoretical insights into the He irradiation-induced damage in U3Si5 as well as provide valuable clues for improving the design of the UN–U3Si5 composite fuel.
Introduction
After the Fukushima Daiichi accident, the concept of accident tolerant fuels (ATFs) has been proposed in order to provide reliable operational safety.1 Uranium silicides such as U3Si2 and U3Si5 compounds are being explored as advanced nuclear fuels with higher thermal conductivity and increased fission density, both as stand-alone fuels2 and as a second phase in composite fuels, compared to the conventional uranium dioxide (UO2) fuel used in the commercial light water reactor (LWR).3,4 The mechanical, thermo-physical, and thermochemical properties of U–Si compounds such as elastic moduli, heat expansion, heat capacity, thermal conductivity, phase stability, and oxidation reaction are reported experimentally and theoretically.5–12 Under LWR conditions, point defects, fission products, and the gas species will inevitably continuously change in the fuel materials, which results in the swelling of the fuel and a reduction in the thermal conductivity and mechanical properties.6 A number of theoretical studies on the behavior of fission products in U–Si compounds has been reported, including H, H2, Xe, Zr, Sr, Ba, Nd, and Ce.6–15 Helium, one of the main gases in LWR, has a low diffusion barrier within materials, such as metals and even the MAX phase Ti3AlC2;16 thus, it tends to aggregate and form bubbles within these materials. However, the He gas behavior in U3Si5, which has one of the very important fuel performance behaviors in U3Si5, are not yet understood.U3Si5, though having a uranium density (7.5 g U cm−3) lower than both traditional UO2 (9.7 g U cm−3) and U3Si2 (11.3 g U cm−3),17 and presenting a high melting point (2043 K) compared with those of UO2 (3130 K) and U3Si2 (1983 K),18 possesses a higher thermal conductivity than UO2 in a broad temperature range from ∼573 K to at least 1773 K.17 In addition, it may have better resistance toward oxidation than U3Si2 by both experimental and theoretical studies.19,20 Moreover, the UN–U3Si5 composite fuel using U3Si5 as the second phase has received much attention as a potential nuclear fuel material for ATF4,21 due to its neutronic similarity to UO2 and improved oxidation resistance compared to U3Si2. In our previous theoretical studies,22 the silicon vacancies of β-USi2 are determined to be more prone to form among the different types of point defects studied and U3Si5 can be treated as a structural derivation of hexagonal β-USi2 with silicon vacancy defects. Furthermore, in contrast to the susceptibility of U3Si2 to ion irradiation-induced amorphization, U3Si5 remains crystalline up to 8 dpa at room temperature and up to ∼50 dpa by 1 MeV Ar2+ or 150 keV Kr+ at 623 K,23 probably due to its more simple and isotropic crystal structure.
In this study, in order to gain a deep insight into the irradiation-induced damage and swelling of the fission gas produced in the fuel, which are valuable for the evaluation of the fuel performance of U3Si5, the behaviors of the fission gas He in U3Si5 are studied by the first-principles method. The primary point defects, secondary vacancies, trapping of He in U3Si5, as well as the volume change associated with He accommodation are discussed. Our results may provide theoretical insights into the solution of He in U3Si5 and provide a valuable clue for improving the design of the UN–U3Si5 composite fuel.
Calculation methods and models
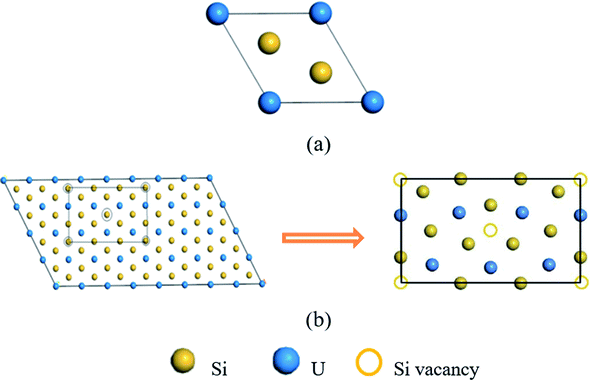
The electronic structure calculations of helium irradiation-induced damage in U3Si5 are performed using projector augmented-wave (PAW) method and Perdew–Burke–Ernzerhof (PBE) functional24 for exchange-correlation potential implemented in Vienna Ab initio Simulation Package (VASP) codes.25–27 The Hubbard U (PBE + U) method is applied to describe the strong correlation effect of localized uranium 5f orbitals.28U3Si5 has a P6/mmm AlB2-type structure, derived from β-USi2 (Fig. 1(a)) by removing one sixth of silicon atoms.29 Sasa et al.30 suggested that U3Si5 be represented in the form of U6Si10 (Fig. 1(b)), as obtained by removing two silicon atoms of the U6Si12 supercell based on β-USi2. Different U values ranging from 0 to 3.5 are tested to obtain a suitable configuration that balances the lattice parameters and stability of U3Si5. The lattice constants of U3Si5 calculations predicted by the PBE + U method agree well with the experiments when U = 2.5.21,31 It is worth noting that the calculated formation energy (−0.462 eV per atom) of U3Si5 also agrees well with the experimental one (−0.45 eV per atom).20 Moreover, it is experimentally found that U3Si5 is a Curie–Weiss paramagnet above 4.2 K (ref. 32) but becomes non-magnetic below 0.6 K.33 Also, non-magnetic U3Si5 is theoretically determined to be dynamically stable from the phonon spectrum.22 Therefore, the non-spin polarized calculation and Hubbard U value of 2.5 are adopted in this study.
Defect configurations are calculated in the 2 × 2 × 1 supercell made up of 64 atoms of U6Si10. The plane-wave cutoff energy is set to 500 eV, and 5 × 5 × 5 and 2 × 2 × 3 k-point meshes generated by the Monkhorst–Pack scheme are performed for the U6Si10 cell and the U24Si40 supercell, respectively. The atomic positions, supercell volume, and supercell shape are fully relaxed in all the calculations to obtain the minimum energy structure. The convergence criteria of energy and atomic force are 10−6 eV and 0.01 eV Å−1, respectively.
Results and discussion
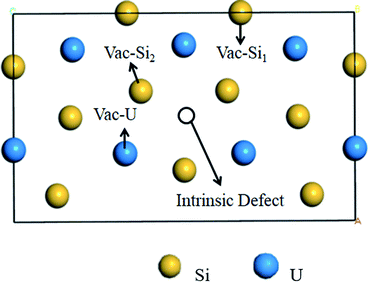
Point defects and fission products can inevitably be continuously produced in the U3Si5 nuclear fuel under the serving conditions. These defects provide accommodations of fission products and influence the thermo-mechanical properties of the fuel materials. There are two types of Si defects and one type of U defect in U3Si5. The three-point defect types (i.e., Vac-Si1 far from the intrinsic vacancy, Vac-Si2 near intrinsic vacancy, and Vac-U) in Fig. 2 and the three anti-site defect types (Anti-USi1 for substitution of one Si1 with U, Anti-USi2 for the substitution of one Si2 with U and Anti-SiU for the substitution of one U with Si) are investigated in this study. In order to determine the accommodations for gas He, the trapping and secondary defect formation of He into the vacancy defects and/or interstitial defects of U3Si5 are also calculated.In order to assess the stability of vacancies and anti-site defects, the point defect energy EVacp and defect formation energy EVacf are calculated, respectively, with respect to isolated U or Si atom and silicon in the diamond structure or α-uranium according to ref. 22.
| EVacp = EVacref − Eref + EX | (1) |
| EVacf = EVacref − Eref + μX | (2) |
| EApB = EArefB + EB − EA − Eref | (3) |
| EAfB = EArefB + μB − μA − Eref | (4) |
The point defect energies and defect formation energies of the vacancies and anti-site defects are summarized in Table 1. Regardless of the defect energies calculated based on the isolated atom as the reference state or the elementary substance as the reference state, Vac-Si1 is determined to be the lowest and Vac-Si2 is the greatest. It can be readily identified that Vac-Si1 is the most readily produced instead of both Vac-Si2 and Vac-U adjacent to the intrinsic Si vacancy, which may be an implication of the formation of separated Si vacancies rather than the vacancy clusters. It can be also seen that Vac-U is slightly more likely to be produced than Vac-Si2, even though the U atomic radius is larger than that of Si. This current result is consistent with the finding of the U3Si2 system.13,34 This observation can be understood in that the intrinsic defect of U3Si5 slightly elongates the Si–Si bond length and weakens the bond strength so that Vac-Si1 is more likely to be formed than Vac-U. However, the removal of the Si2 atom to form the bivacancy defect could locally disturb the U3Si5 structure and increase the energy of the system. As for the anti-site defects, it can be noted that Anti-USi1/Anti-USi2 have lower defect energies than Anti-SiU, which indicates that the non-stoichiometric U-rich phase of U3Si5 is more likely to be sintered than the Si-rich phase, which is consistent with the chemical analysis of the experimentally sintered Si-lean U3Si5 sample.17 In addition, the defect formation energies of Anti-USi1 and Anti-USi2 are similar and both are negative, which may also be a sign of the U-rich phase present in the U3Si5 sample.
| Point defect energy | Defect formation energy | |
|---|---|---|
| Vac-U | 8.85 | 2.10 |
| Vac-Si1 | 5.26 | 0.75 |
| Vac-Si2 | 9.86 | 2.71 |
| Anti-SiU | 2.48 | 9.68 |
| Anti-USi1 | 1.50 | −6.08 |
| Anti-USi2 | 1.51 | −5.91 |
To identify the preferential site for a single He atom residing in perfect or defect U3Si5, the solution energy of He trapped in U3Si5 without and with point defects is calculated by ref. 35 and 36.
| Es(He) = EHeref − Eref − E(He) | (5) |
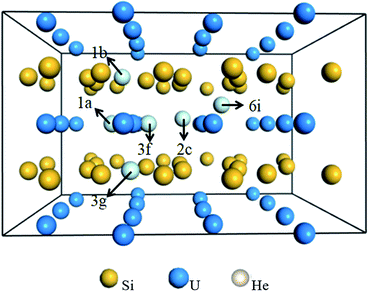
![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m is investigated to determine the preferential interstitial site. There are six types of interstitial sites considered in Fig. 3, i.e., the intrinsic vacancy as an interstitial site 1b (0.0, 0.0, 0.5) in the Si layer, 1a (0.0, 0.0, 0.0) site in the U layer directly below or above the intrinsic vacancy, pentagonal bipyramidal 3g (0.3635, 0.3635, 0.50) site in the Si layer between two U atoms, 3f (0.2486, 0.0, 0.0) site in the U layer between two Si2 atoms, trigonal bipyramidal 2c (2/3, 1/3, 0.0) site in the U layer between two Si1 atoms, and 6i (0.5575, 0.5575, 0.25) site between adjacent U and Si layers. The solution energies of single He incorporation into the interstitial sites are summarized in Table 2. It can be readily identified that the lowest solution energy interstitial site for a single He is to be located in 1a instead of the intrinsic vacancy 1b. It could be interesting to point out that the 1a site in the U layer has a larger free volume for He accommodation as compared to the 1b site due to the longer U–U bond. Moreover, the introduction of the intrinsic Si vacancy eliminates the repulsion of helium atoms residing in the U atomic layer from the nearest Si atoms. By comparing the calculated interstitial site solution energy, it can be concluded that the interstitial site 1a below or above the intrinsic vacancy provides a good sink for He accommodation.
2m is investigated to determine the preferential interstitial site. There are six types of interstitial sites considered in Fig. 3, i.e., the intrinsic vacancy as an interstitial site 1b (0.0, 0.0, 0.5) in the Si layer, 1a (0.0, 0.0, 0.0) site in the U layer directly below or above the intrinsic vacancy, pentagonal bipyramidal 3g (0.3635, 0.3635, 0.50) site in the Si layer between two U atoms, 3f (0.2486, 0.0, 0.0) site in the U layer between two Si2 atoms, trigonal bipyramidal 2c (2/3, 1/3, 0.0) site in the U layer between two Si1 atoms, and 6i (0.5575, 0.5575, 0.25) site between adjacent U and Si layers. The solution energies of single He incorporation into the interstitial sites are summarized in Table 2. It can be readily identified that the lowest solution energy interstitial site for a single He is to be located in 1a instead of the intrinsic vacancy 1b. It could be interesting to point out that the 1a site in the U layer has a larger free volume for He accommodation as compared to the 1b site due to the longer U–U bond. Moreover, the introduction of the intrinsic Si vacancy eliminates the repulsion of helium atoms residing in the U atomic layer from the nearest Si atoms. By comparing the calculated interstitial site solution energy, it can be concluded that the interstitial site 1a below or above the intrinsic vacancy provides a good sink for He accommodation.
| Wyckoff position | Solution energy (eV) | Comment |
|---|---|---|
| 1b | 2.081 | Relaxed to 1a |
| 1a | 2.074 | |
| 3g | 5.085 | A neighboring U atom is relaxed to the adjacent Si atomic layer |
| 3f | 2.086 | Relaxed to 1a |
| 2c | 2.856 | |
| 6i | 2.762 | A neighboring Si2 atom is relaxed to an intrinsic vacancy |
It is well known that the lattice constants and volume will change when a fission gas is accommodated. The changes in the lattice constants and volume for He accommodated in the interstitial sites are listed in Table A1.† Compared to the perfect U3Si5, the volume associated with He residing in the interstitial site anisotropically expands from 0.43% for the 1a site to 1.99% for the 3g site. It can also be seen that the order of volume change is consistent with that of single He interstitial solution energy and the volume expansion associated with He trapped in the 1a site is estimated to be the lowest among the interstitials investigated. This means that the He gas incorporated into the 1a site in the U layer above/below the adjacent intrinsic vacancy causes the lowest strain on the U3Si5 structure, resulting in the smallest solution energy.
The solution energies of a single He incorporated into the three types of vacancies in U3Si5 are also predicted to assess their ability of He accommodation. The calculated helium vacancy solution energies at Vac-Si1, Vac-U, and Vac-Si2 are 2.59, 1.96, and 0.47 eV, respectively, which are in contrast with the defect formation energies of the corresponding vacancies but appear to be inversely proportional to the vacancy volume because Vac-Si2 coupled with the intrinsic vacancy has the largest free volume among the vacancies studied, then Vac-U with a U vacancy, and finally Vac-Si1 with a Si1 vacancy. It is also interesting to point out that the introduction of vacancy reduces the solution energy of He in the adjacent interstitial site closest to the vacancy by increasing the residence volume. For example, the respective solution energies of He residing in the Vac-U and Vac-Si1 are smaller than that of the interstitial sites 1a and 2c, respectively. Therefore, it can be reasonably inferred that the trapping of helium into the vacancy is dominated by entropy. In addition, the filling of the interstitial site 1a directly above the intrinsic vacancy or Vac-Si2 coupled with the intrinsic vacancy with an He atom is found to be the most favorable. This is an indication that the intrinsic vacancies of the U3Si5 structure helps to provide a good sink or become a part of a good sink for the fission gas, which provides an explanation of the exceptional stability of U3Si5 against ion radiation damage made from the experimental work by Y. Sasa et al.30
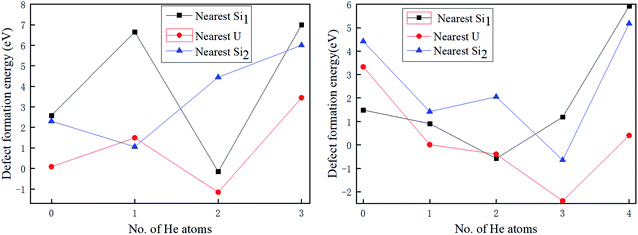
In order to obtain the number of He atoms accommodated in the three types of vacancies investigated, we calculated the trapping energy of an additional He atom residing in the vacancy using eqn (6).35,36
| Etrap = EU3Si5(nHe, V) − EU3Si5((n − 1)He, V) − EU3Si5(He, 1a) + EU3Si5 | (6) |
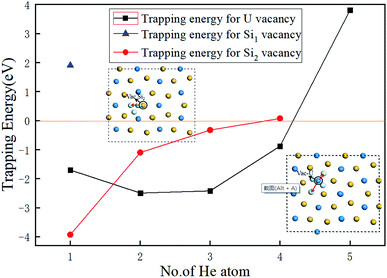 | ||
| Fig. 4 The dependence of the trapping energy on the number of He atoms trapped in Vac-U, Vac-Si1, and Vac-Si2 vacancies of U3Si5. | ||
In order to more deeply understand the influence of the crystal structure of U3Si5 on the number of implanted He atoms, the lattice constants and volume as increasing number of He atoms are summarized in Table 3. When a U or Si vacancy is introduced, the volume and lattice parameters a and c exhibit a weak contraction while the lattice parameter b expands. This can be explained by the fact that when a U or Si atom is removed, the adjacent U or Si atoms in the U or Si layer on the a/c plane move closer to the vacancy, causing the lattice constants a and c to shrink, while the loss of U–Si bonds along the b-axis makes the structure expand along the b-axis direction. It is interesting to point out that when one He atom is implanted into a U vacancy, the volume continues to shrink anisotropically by −2.37%, which may cause the compression of the structure, resulting in a small trapping energy in Fig. 4, and the change of the b value increases from 1.69% to 3.14%. However, when there are more than one He atoms implanted, although the parameters a and c still shorten relative to U3Si5, the volume expands instead from 0.063% for two He atoms to 2.58% for 4He atoms. This means that the tensile strength of U3Si5 along the b-axis becomes the dominant factor as the implanted He atoms increase, thereby increasing the system energy and reducing the trapping energy, as depicted in Fig. 4. From Table 3, the structural variant of U3Si5 with Vac-Si2 and implanted He atoms is slightly different from that of Vac-U. It can be clearly seen that when He atoms are trapped in Vac-Si2, the lattice constants all show an expansion except for the lattice constant b associated with two implanted He atoms. Thus, the corresponding crystal volume enlarges by 0.45%, associated with one trapped He to 1.21% associated with three trapped He. It can be found carefully that as the implanted He increases, the rapid expansion along the c-axis may destroy the strong silicon–silicon covalent bonds and uranium–uranium metallic bonds, thereby increasing the instability of the system, resulting in the He trapping ability of the Vac-Si2 vacancy being weaker than that of the Vac-U vacancy. Therefore, it provides a structural understanding of the evolution of the He trapping ability in different types of vacancies by varying the number of He atoms implanted.
| Structures | a (Å) | b (Å) | c (Å) | V (Å3) | Δa/a (%) | Δb/b (%) | Δc/c (%) | ΔV/V (%) |
|---|---|---|---|---|---|---|---|---|
| U3Si5 | 13.231 | 8.048 | 11.397 | 1213.64 | 0 | 0 | 0 | 0 |
| Vac-U | 13.032 | 8.184 | 11.265 | 1201.54 | −1.505 | 1.690 | −1.161 | −0.997 |
| Vac-U + 1He | 12.810 | 8.301 | 11.142 | 1184.90 | −3.181 | 3.144 | −2.237 | −2.368 |
| Vac-U + 2He | 13.025 | 8.293 | 11.243 | 1214.41 | −1.557 | 3.040 | −1.351 | 0.063 |
| Vac-U + 3He | 13.122 | 8.309 | 11.326 | 1234.92 | −0.824 | 3.243 | −0.824 | 1.753 |
| Vac-U + 4He | 13.055 | 8.439 | 11.299 | 1244.97 | −1.330 | 4.858 | −1.330 | 2.581 |
| Vac-Si2 | 12.869 | 8.288 | 11.144 | 1188.57 | −2.736 | 2.982 | −2.220 | −0.207 |
| Vac-Si2 + 1He | 13.255 | 8.086 | 11.399 | 1219.06 | 0.181 | 0.472 | 0.0175 | 0.447 |
| Vac-Si2 + 2He | 13.201 | 8.071 | 11.447 | 1219.66 | −0.227 | 0.286 | 0.439 | 0.496 |
| Vac-Si2 + 3He | 13.270 | 8.050 | 11.498 | 1228.27 | 0.295 | 0.025 | 0.886 | 1.205 |
To further study the evolution of helium bubble-induced defect structure of U3Si5, the secondary point defects (nearest U, nearest Si1, and nearest Si2) nearest to the primary vacancies with the trapped He atoms discussed above are investigated and the corresponding secondary defect formation energies are provided in Fig. 5 according to ref. 35 and 36.
| Ef2(VA) = E(VA+B) − E(VB) + μA | (7) |
Here, E(VA+B) is the total energy of the system with one primary vacancy B and one secondary vacancy A, E(VB) is the energy of the system that contains one vacancy of type B, and μA is the elemental chemical potential of species A.
One can see from Fig. 5 that the formation of secondary defects is strongly dependent on the helium concentration. When there is no He atom residing in the primary Vac-Si2, the respective secondary defect formation energies of the nearest U, nearest Si1, and nearest Si2 are 0.087, 2.57, and 2.30 eV, respectively, which is an implication that the nearest U vacancy induced by primary Vac-Si2 is much more likely to be produced than nearest Si1 and nearest Si2. With the increase in the He atoms trapped, the secondary defect formation energy of the nearest Si2 almost continues to increase to 6.00 eV with three He atoms, which is the maximum number of He atoms residing in Vac-Si2 because the He atoms implanted near Vac-Si2 have a strong interaction with the nearest Si2 so that the removal of the nearest Si2 is prevented in Fig. A1b.† However, there is an obvious exception for nearest U and nearest Si1, where the respective defect formation energy drops dramatically to −1.16 and −0.16 eV when the two He atoms are accommodated. This means that 2He-filled Vac-Si2 can promote the spontaneous formation of nearest U and nearest Si1. By contrast, it would be interesting to note that the fully filled Vac-Si2 can significantly raise the secondary defect formation energy to at least 3.44 eV (for nearest U). From the above analysis, once the Vac-Si2 vacancy of U3Si5 is formed under the serving conditions; the U vacancy nearest to the Vac-Si2 is prone to be produced in terms of the secondary defect formation energy. When the He-filled Vac-Si2 has secondary defects, the chain-like bubbles containing volume of interstitial site 1a and Vac-Si2 are formed, while the secondary U of the adjacent U layer and Si1 of the same Si layer nearest to the 2He-filled Vac-Si2 could be formed spontaneously, resulting in a three-dimensional (spherical) defect structure, which will also lead to the formation of spherical bubbles.
As shown in Fig. 5(b), when no He atom enters the primary Vac-U vacancy, the secondary defect formation energy of the nearest Si1 is positive and the smallest among the secondary vacancies is studied, indicating that it prefers to form U–Si1 bivacancy. With the increase in the helium atoms implanted, all the secondary defect formation energies of the nearest Si1, nearest U, and nearest Si2 roughly decrease first and then increase. As in the case of Vac-Si2, fully 4He-filled Vac-U shown in Fig. A2† will significantly enhance the stability of the structure and prevent the generation of nearby defects. However, the secondary defect formation energy of the nearest Si1 becomes negative and reaches a minimum of −0.58 eV when two He atoms exist, while those of the nearest U and Si2 reach the minimum values (−2.39 eV for nearest U and −0.65 eV for nearest Si2) when the third He atom is placed at these vacancies, which can be explained by the fact that the Vac-U and Vac-Si2 vacancies have much smaller He solution energies than Vac-Si1 and thus provide a better sink for the third He atom. In other words, the partially filled Vac-U can also promote the spontaneous formation of the secondary defects Si1 and Si2 of the adjacent Si layer as well as U of the same U layer, and thus generate both three- and two-dimensional vacancy structures, i.e., plate-like and spherical bubbles. For the fully He-filled Vac-U, the development of the secondary defects is prevented and the plate-like bubbles will be formed with high probability, which is similar to the gas bubble structure of an irradiated U3Si2 dispersion fuel made from the experimental work.10
Conclusions
In this paper, the behaviors of the fission gas He in U3Si5 are studied by the first-principles method. The primary point defects, secondary point defects, and the dissolution of fission gas He are studied. The results show that the defect formation energies of the point defects investigated follow the order Si2 > U > Si1, indicating that Vac-Si1 is more likely to form, and Si vacancies are prone to form separate single vacancies rather than vacancy clusters. It can be found that the non-stoichiometric U-rich phase of U3Si5 is more likely to be formed than the Si-rich phase, which is consistent with the chemical analysis of the experimentally sintered Si-lean U3Si5 sample. By comparing the calculated interstitial site solution energy, it can be concluded that the interstitial site 1a below or above the intrinsic vacancy provides a good sink for He accommodation. It can be also seen that Vac-U, Vac-Si1, and Vac-Si2 vacancies can energetically accommodate up to 4, 0, and 3 He atoms relative to the interstitial site 1a, respectively. In addition, although the fully He-filled primary vacancy can prevent the growth of the secondary defects, partially He-filled vacancy can promote the formation of an adjacent secondary vacancy, leading to the formation of three-dimensional spherical gas bubbles. This work may provide a theoretical insight into the He irradiation-induced damage in U3Si5 as well as provide valuable clues for improving the design of the UN–U3Si5 composite fuel.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge the financial support of the National Key Research and Development Program of China (No. 2016YFB0700100), National Natural Science Foundation of China (Grants No. 21707147, 11604346, 21671195, 21875271, 51872302), K. C. Wong Education Foundation (rczx0800), the Foundation of State Key Laboratory of Coal Conversion (Grant J18-19-301) and the Defense Industrial Technology Development Program JCKY 2017201C016. We also acknowledge One Thousand Youth Talents Program of China, Hundred-Talent Program of Chinese Academy of Sciences.References
- S. J. Zinkle and G. S. Was, Materials challenges in nuclear energy, Acta Mater., 2013, 61(3), 735–758, DOI:10.1016/j.actamat.2012.11.004.
- S. J. Zinkle, K. A. Terrani, J. C. Gehin, L. J. Ott and L. L. Snead, Accident tolerant fuels for LWRs: A perspective, J. Nucl. Mater., 2014, 448(1–3), 374–379, DOI:10.1016/j.jnucmat.2013.12.005.
- K. D. Johnson, A. M. Raftery, D. A. Lopes and J. Wallenius, Fabrication and microstructural analysis of UN-U3Si2 composites for accident tolerant fuel applications, J. Nucl. Mater., 2016, 477, 18–23, DOI:10.1016/j.jnucmat.2016.05.004.
- N. R. Brown, M. Todosow and A. Cuadra, Screening of advanced cladding materials and UN–U3Si5 fuel, J. Nucl. Mater., 2015, 462, 26–42, DOI:10.1016/j.jnucmat.2015.03.016.
- Y. Zhang and A. D. R. Andersson, A Thermal Conductivity Model for U-Si Compounds, LA-UR-16-27736, 2017, vol. 02, pp. 1–9, DOI:10.2172/1342838.
- Y. Miao, et al., “Gaseous swelling of U3Si2 during steady-state LWR operation: A rate theory investigation”, Nucl. Eng. Des., 2017, 322, 336–344, DOI:10.1016/j.nucengdes.2017.07.008.
- Y. Miao, K. A. Gamble, D. Andersson, Z. G. Mei and A. M. Yacout, Rate theory scenarios study on fission gas behavior of U3Si2 under LOCA conditions in LWRs, Nucl. Eng. Des., 2018, 326, 371–382, DOI:10.1016/j.nucengdes.2017.11.034.
- S. C. Middleburgh, P. A. Burr, D. J. M. King, L. Edwards, G. R. Lumpkin and R. W. Grimes, Structural stability and fission product behaviour in U3Si, J. Nucl. Mater., 2015, 466, 739–744, DOI:10.1016/j.jnucmat.2015.04.052.
- Y. Miao, et al., “Bubble morphology in U3Si2 implanted by high-energy Xe ions at 300 °C”, J. Nucl. Mater., 2017, 495, 146–153, DOI:10.1016/j.jnucmat.2017.07.066.
- Y. S. Kim, G. L. Hofman, J. Rest and A. B. Robinson, Temperature and dose dependence of fission-gas-bubble swelling in U3Si2, J. Nucl. Mater., 2009, 389(3), 443–449, DOI:10.1016/j.jnucmat.2009.02.037.
- T. Barani, et al., “Multiscale modeling of fission gas behavior in U3Si2 under LWR conditions”, J. Nucl. Mater., 2019, 522, 97–110, DOI:10.1016/j.jnucmat.2019.04.037.
- T. Winter and C. Deo, Comparison of fission gas swelling models for amorphous U3Si2 and crystalline UO2, Ann. Nucl. Energy, 2017, 100, 31–41, DOI:10.1016/j.anucene.2016.08.008.
- A. D. Andersson, “Density Functional Theory Calculations of Defect and Fission Gas Properties in U–Si Fuels”, 2016, vol. 03, doi: DOI:10.2172/1237246.
- T. Yao, B. Gong, L. He, J. Harp, M. Tonks and J. Lian, Radiation-induced grain subdivision and bubble formation in U3Si2 at LWR temperature, J. Nucl. Mater., 2018, 498, 169–175, DOI:10.1016/j.jnucmat.2017.10.027.
- D. A. Andersson, X. Y. Liu, B. Beeler, S. C. Middleburgh, A. Claisse and C. R. Stanek, Density functional theory calculations of self- and Xe diffusion in U3Si2, J. Nucl. Mater., 2019, 515, 312–325, DOI:10.1016/j.jnucmat.2018.12.021.
- Y. Xu, et al., “New insight into the helium-induced damage in MAX phase Ti3AlC2 by first-principles studies”, J. Chem. Phys., 2015, 143(11) DOI:10.1063/1.4931398.
- J. T. White, A. T. Nelson, D. D. Byler, D. J. Safarik, J. T. Dunwoody and K. J. McClellan, Thermophysical properties of U3Si5 to 1773 K, J. Nucl. Mater., 2015, 456, 442–448, DOI:10.1016/j.jnucmat.2014.10.021.
- V. S. Yemel'Yanov and A. L. Yevstyukhin, Metall. Nucl. Fuel., 1969 Search PubMed.
- A. T. Nelson, J. T. White, D. D. Byler, J. T. Dunwoody, J. A. Valdez and K. J. McClellan, Overview of properties and performance of uranium-silicide compounds for light water reactor applications, Trans. Am. Nucl. Soc., 2014, 110, 987–989 Search PubMed.
- C. K. Chung, et al., “Enthalpies of formation and phase stability relations of USi, U3Si5 and U3Si2”, J. Nucl. Mater., 2019, 523, 101–110, DOI:10.1016/j.jnucmat.2019.05.052.
- K. James, FY2016 Ceramic Fuels Development Annual Highlights, 2016, vol. 05 Search PubMed.
- X. Zhang, et al., “Electronic structures, mechanical properties and defect formation energies of U3Si5 from density functional theory calculations”, Prog. Nucl. Energy, 2019, 116, 87–94, DOI:10.1016/j.pnucene.2019.03.045.
- T. Yao, et al., “In situ TEM study of the ion irradiation behavior of U3Si2 and U3Si5”, J. Nucl. Mater., 2018, 511, 56–63, DOI:10.1016/j.jnucmat.2018.08.058.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561, DOI:10.1103/PhysRevB.47.558.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- S. Dudarev and G. Botton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505–1509, DOI:10.1103/PhysRevB.57.1505.
- A. Brown and J. J. Norreys, “Uranium Disilicide”, Nature, 1961, 191, 61–62, DOI:10.1038/191061a0.
- Y. Sasa and M. Uda, Structure of stoichiometric USi2, J. Solid State Chem., 1976, 18(1), 63–68, DOI:10.1016/0022-4596(76)90079-7.
- S. Auffret, J. Pierre, B. Lambert, J. L. Soubeyroux and J. A. Chroboczek, Crystallographic and magnetic structures of Er3Si5, Phys. B, 1990, 162(3), 271–280, DOI:10.1016/0921-4526(90)90022-m.
- T. Miyadai, et al., “Magnetic and electrical properties of the U-Si system (part II)”, J. Magn. Magn. Mater., 1992, 104–107(1), 47–48, DOI:10.1016/0304-8853(92)90697-M.
- N. Sato, M. Kagawa, K. Tanaka, N. Takeda, T. Satoh and T. Komatsubara, Magnetic properties of a mass-enhanced ferromagnet U2PtSi3, J. Magn. Magn. Mater., 1992, 108, 115–116, DOI:10.1016/0304-8853(92)91373-2.
- T. Wang, et al., “First-principles investigations on the electronic structures of U3Si2”, J. Nucl. Mater., 2016, 469, 194–199, DOI:10.1016/j.jnucmat.2015.11.060.
- C. Duan, et al., “First-principles study on dissolution and diffusion properties of hydrogen in molybdenum”, J. Nucl. Mater., 2010, 404(2), 109–115, DOI:10.1016/j.jnucmat.2010.06.029.
- Y. L. Liu, Y. Zhang, H. B. Zhou, G. H. Lu, F. Liu and G. N. Luo, Vacancy trapping mechanism for hydrogen bubble formation in metal, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(17), 1–4, DOI:10.1103/PhysRevB.79.172103.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra04031f |
| This journal is © The Royal Society of Chemistry 2021 |