Microscopic mechanism of light-induced tetrazole-quinone 1,3-dipolar cycloaddition: a MS-CASPT2 theoretical investigation

Abstract

Recently, experimentalists have developed a green and efficient method to synthesize pyrazole-fused quinones through light-induced tetrazole-quinone 1,3-dipole cycloadditions. However, the underlying microscopic mechanisms remain to be clarified. In this work, we have employed several electronic structure calculation methods (MS-CASPT2, CASSCF, DFT) to systematically explore the microscopic mechanism of related light-induced reactions and deactivation pathways. Upon excitation with ultraviolet light, one of the original reactants 2-(4-fluorophenyl)-5-phenyl-2H-tetrazole (FPT) reaches its S₁ excited state. After that, due to the ultrahigh energy and the small energy barrier, the FPT molecule breaks the N2–N3 and N4–C5 bonds sequentially, removing the nitrogen atom finally in the S₁ state. Combined with the cleavage of the second N4–C5 bond, the system reaches its conical intersection region and deactivates ultrafast to the ground state, generating the active intermediate ((4-fluorophenyl)diazen-1-ium-1-ylidene) (phenyl)methanide (FPNI). Subsequently, the active intermediate FPIN can react with naphthoquinone in the ground state by overcoming an energy barrier of about 5.7 kcal mol⁻¹, after which the 1-(4-fluorophenyl)-3-phenyl-1H-benzo[f]indazole-4,9(3aH, 9aH)-dione (FP2HQ) is formed. The FP2HQ can be oxidized to obtain the 1-(4-fluorophenyl)-3-phenyl-1H-benzo[f]indazole-4,9-dione (PFQ). Due to the high energy and small barrier, the entire reaction process can easily take place, which ultimately leads to the efficient reaction. Our present work not only explains the experimental mechanism in detail but can also be helpful for the future design of related photoinduced reactions with the aid of theoretical calculations.

---

Introduction

Pyrazolquinones, as a derivative of nitrogen-containing heterocyclic quinones, are widely used in daily life.^1–4 It is reported that some of these derivatives, such as aziridinyl-substituted 1(2)H-indazole-4,7-diones, can significantly inhibit the growth activity of P-388 lymphoid leukemia cells in male BDF1 mice.⁵ The pyrazole-fused quinones of tricyclic scaffolds can be used to resist glioblastoma cancer cells.⁶ They can also be made into carbonyl reductase inhibitors, such as 3-(methyl-N-ethylcarbamate)-6-(NO-ethylphenylamino) indazol-4,7-dione, to reduce the risk of cardiotoxicity and improve the efficiency of anticancer agents,⁷ 2-position ester substituted indazole-4,7-dione can be applied to treat acute infections of Trypanosoma cruzis,⁸ and benzimidazolone is adopted for weeding.⁹ At the same time, some can also be employed as organic photocatalysts, such as 1,3-bis(4-methoxyphenyl)-1H-benzo[f]indazole-4,9-dione, to participate in the photooxidation process.¹⁰ In addition, they may have a potential fluorescence¹⁰ and are used for optical attachment and light labeling of biomolecules.^11–13 Currently, the commonly used methods for synthesizing such pyrazoquinones are: (1) under a certain condition, 1,3-dipolar cycloaddition between diazomethane and benzoquinone; (2) the intermediate of diazopropane and appropriate benzoquinone or naphthoquinone derivatives by 1,3-dipolar cycloaddition in the mixture of THF/Et₂O at room temperature;¹⁴ (3) the benzoquinone analogues and N,N-disubstituted hydrazone undergo a similar Michael addition first, and then get through the closing loop after peroxidation or high heat;¹⁵ (4) at room temperature and alkaline conditions, the corresponding arylhydrazone acyl chlorides or their nitrile imine reacts with the benzoquinone derivatives to obtain monocyclic or bicyclic adducts.¹⁶ Among these, method (1) is particularly suitable for asymmetric 2,3-disubstituted p-benzoquinones, which can avoid the mixing of isomerized 5- and 6-substituted p-benzoquinones, but the yield is usually low, and the reactants in equimolar amounts often lead to difficulties in purifying the cycloadducts due to the lack of regioselectivity of isomers; the 1,3-dipolar cycloaddition reaction of the diazopropane intermediate with almost all quinones has regioselectivity in method (2), but the overall yield is not high, which is 26–49%; method (3) usually has a high yield (27–90%), but the reaction conditions are harsh; the molar ratio of reactants will also affect the relative number of adducts that form monocyclic or bicyclic (derived from two 1,3-dipolar cycloadditions) in method (4), but the reaction has significant regioselectivity, which makes compounds easier to separate, and the yield is still low (less than 30%). In general, because most of the above traditional organic synthetic methods of pyrazoquinone are not environmentally friendly, energy-consuming, and low-profit, the development of a green and efficient method for synthesizing pyrazoquinone is an urgent problem to be solved.

In order to improve the problems of low yield and poor regioselectivity, new synthetic methods for tricyclic pyrazoquinones have gradually emerged. Bakare et al. relied on the [2 + 4] cycloaddition of 1-diazo-4-aminopropane and suitable benzoquinones to construct a tricyclic pyrazoquinone system, and the yield was greater than 45%;¹⁷ Bertuzzi et al. used C-heteroaryl-N-arylnitrile imines and substituted isoquinoline-5,8-diones to synthesize a variety of tricyclic pyrazoquinones through 1,3-dipolar cycloaddition, with a yield of 45–80%.⁶ Although these methods have improved the yield, the control of conditions during synthesis is also stricter with more wastage of materials. It is also imperative to find a better way to synthesize pyrazoquinones. Since the light-induced 1,3-dipolar cycloaddition of tetrazole-alkene is an effective synthesis route for the preparation of pyrazoline adducts,¹⁸ the nitrile imine produced by the photolysis of tetrazole is of great value for most alkenes and alkynes.^19–22 However, in the photochemical process, quinones (with potential C=C) as dipolar nucleophiles remain rarely explored. Recently, Ortiz-Rojano et al. have proposed a method that uses light as the only reagent to induce the light-licking reaction of tetrazole-quinone to synthesize a series of potential pharmacological pyrazoquinones, which arouses great interest.¹⁰ At room temperature in the open air, ethyl acetate as the solvent, high-pressure ultraviolet lamp as the radiation source, and equimolar mixing of the reactants as the optimum reaction conditions, the experiment uses different photoactivatable 2,5-disubstituted tetrazoles (synthesized from different arylsulfonyl hydrazides and diazonium salts, and is the main light absorber) to react with 1,4-naphthoquinone to obtain a higher yield (50–95%) of various types of monoadditive pyrazoquinones. The formation of pyrazoquinone involves the photogeneration of nitrile imine dipole, followed by 1,3-dipolar cycloaddition with 1,4-naphthoquinone and enolization, and finally maybe oxidized by naphthoquinone and air in the last step (the structure of hydronaphthoquinone reduction of the product has not been observed throughout). The reaction in argon gas proceeds more slowly than in air. In addition, it is also proved that the electronic properties of the aryl group in the tetrazole have no impact and the electron-donating group on N-2 facilitates the reaction in the whole process. Another thing worth mentioning is that it can take place effectively regardless of the electronic properties of tetrazole. The literature also further reports that the reaction of benzoquinones and tetrazoles under the same conditions as above will also be affected by the molar ratio between the reactants to form monocyclic or bicyclic adducts. In short, compared with other synthetic methods of pyrazoquinone, the main advantages of this method are the clean reaction conditions that only require light radiation, and all the differently substituted tetrazoles are easy to prepare and are also stable raw materials, and it usually does not require excessive dipolar nucleophiles.

Based on the above experimental research, although the potential value of the product, optimal reaction conditions, reaction process, the influence of the electronic properties of the substituents on the tetrazole in this reaction, and unique advantages have been clarified, there still exists some mechanistic pathways in the system to be explored. For example, does the light-induced bond breakage of tetrazole and the cycloaddition reaction with quinones occur in the ground state or in the excited state? Is the cleavage of tetrazole a coordinated or stepwise process? What are the energy barriers and time scales related to the reaction? The clarification of these key issues is possible with the help of computational chemistry. Therefore, in this case, we decided to use the experimentally reported 3i (for convenience, hereafter referred to as PFQ) with good yield (50%) and potential medicinal values as an example. Several static electronic structure calculation methods (MS-CASPT2, CASSCF, DFT) are used to systematically study the microscopic mechanism of the light-induced reaction and the decay pathways occurring during its formation.

Computational details

All the excited state related structures and minimum energy paths are then optimized using the SA-CASSCF method. Since the reaction coordinates for the removal of nitrogen is clear, i.e., along the bond cleavage of C–N and N–N bonds, the minimum energy paths are therefore obtained using the relax-scan method with constrained optimization along the bond cleavage coordinates. In order to obtain more accurate potential energy profiles, the MS-CASPT2 method is employed to refine the single-point energies of all optimized structures.^23,24 As shown in Table S1† and Fig. S2–S4,† the CASSCF obtained PES are overall similar to the MS-CASPT2 refined ones, and the absorption spectrum agrees with the experimental result, confirming the reliability of our computational strategy. In CASSCF calculations, 12π and 2σ electrons are placed in the active space that comprised 6π, 1σ, and 3π* orbitals and two roots with equal weights are included in the relevant SA-CASSCF calculations. In MS-CASPT2 computations, an additional σ* is added in the calculations. The Cholesky decomposition technique with unbiased auxiliary basis sets is used for accurate two-electron integral evaluation;²⁵ the ionization potential-electron affinity (IPEA) shift is not applied,²⁶ whereas the imaginary shift technique of 0.2 a. u. is employed to avoid intruder-state issues.²⁷ Due to their large sizes, the structures relevant to the ground state [3 + 2] cycloaddition are optimized using the density functional theory (DFT) method with M06-2X functional.^28,29 Finally, the 6-31G* basis set is used in all the involved calculations.^30,31 Additionally, all DFT calculations are performed using the GAUSSIAN09 package,³² while all SA-CASSCF and MS-CASPT2 calculations are conducted using the OpenMolcas package.^33,34

Results and discussion

In order to explore the entire light-induced chemical reaction process, we first need to clarify the ground state structure of 2-(4-fluorophenyl)-5-phenyl-2H-tetrazole (denoted as FPT afterwards for simplicity) and the nature of the absorption spectrum to determine the initially populated excited states upon excitation. Therefore, we first optimized the ground state structure of FPT using the CASSCF method, as shown in the left panel of Fig. 1. Due to the conjugated structure of the system, all the atoms are located on the same plane, and the system, therefore, belongs to the Cs point group. Moreover, according to previous experimental works, the system could undergo a cleavage reaction and remove the nitrogen molecule upon irradiation. Therefore, the relevant bond lengths of the fiver-membered tetrazole ring are also labeled in Fig. 1. As can be seen, the bond lengths of the tetrazole ring in the middle have nearly averaged bond lengths, i.e., all the five bond lengths are close to 1.300 Å. Among these bonds, the N3–N4 bond length is the shortest, with a value of 1.284 Å, and the N4–C5 bond is the longest, with a value of 1.355 Å. The remaining three bonds are all approximately 1.310 Å, i.e., 1.311 Å for N2–N3, 1.314 Å for N1–N2, and 1.316 Å for C1–N5. At the same time, we also find that the N2–C6 bond connected to the p-fluorophenyl group and the C5–C7 bond connected to the phenyl group are slightly longer than the bonds of the tetrazole ring, ca. 1.419 Å and 1.478 Å, respectively. The N2–C6 bond is about 0.060 Å shorter than the C5–C7 bond. On the basis of the optimized ground state structure S0-MIN, we have further calculated its vertical excitation energy. As depicted in Fig. 2, the optimal excited electronic state S₁ of the system corresponds to the ¹π → ¹π* transition of the fluorophenyl ring and the tetrazole ring. The excitation energy is refined to be 4.98 eV (249 nm) at the MS-CASPT2 level, which is in the range of the ultraviolet light, and the oscillator strength is 0.396. Based on these results, we can conclude that the S₁ singlet excited state is a spectroscopically bright state, i.e., upon irradiation with a suitable wavelength of ultraviolet light, the FPT molecule can be effectively populated on this excited state, from which subsequent photoreaction processes take place.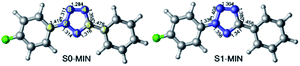

Fig. 1 CASSCF optimized minimum energy structures in S₀ (left, S0-MIN) and S₁ (right, S1-MIN) states, respectively. Also shown are the relevant bond lengths in angstrom.

Fig. 2 Molecular orbitals that are involved in the vertical excitation of the ground state minimum energy structure S0-MIN to the S₁ excited state. Also shown are the electronic state characters and the vertical excitation energy.

As stated above, the system can be promoted to the Franck–Condon region of the S₁ state upon irradiation. The molecule in the Franck–Condon region usually has much higher energy, which would relax to its corresponding minimum-energy structure of the S₁ state ultrafast. Therefore, we further optimized the minimum energy structure of the S₁ state of FPT, which is shown in the right panel of Fig. 1. In comparison with S0-MIN, the S1-MIN structure maintains the original nearly planar structure. However, the bond lengths of the tetrazole ring in the middle increase more or less compared to their ground state counterparts. Specifically, the N2–N3 bond has the most significant elongation, i.e., from 1.311 Å to 1.408 Å, while the smallest change is in the N3–N4 bond, which increases by less than 0.020 Å. The remaining three bonds, such as N1–N2, N1–C5, and N4–C5, increase from 1.314 Å, 1.316 Å, and 1.355 Å to 1.356 Å, 1.341 Å, and 1.380 Å, respectively, and the extent of these changes is in the range from 0.030 Å to 0.040 Å. These results indicate that the S₁ state of the system can significantly weaken the N2–N3 bond, but have nearly no effect on the N3–N4 bond, which is understandable considering the related ¹π → ¹π* transition of the S₁ state of the tetrazole ring. At the same time, the N2–C6 and C5–C7 bonds connected to the p-fluorophenyl and phenyl are shortened by 0.060 Å and 0.020 Å, respectively, indicating that these two bonds are strengthened in this S₁ state.

The above results are consistent with the previous experimentally observed photoinduced denitrification reaction, i.e., after the FPT molecule is excited, the N2–N3 and N4–C5 bonds are likely to break since these bonds are weakened in the S₁ excited state. Finally, we need to point out that in S1-MIN, the energy difference between the S₁ and S₀ states is 89.9 kcal mol⁻¹. Even though this energy difference is greatly reduced in comparison with the 114.7 kcal mol⁻¹ difference in the Franck–Condon region, such a large value is insufficient for the molecule to deactivate to the ground state via ultrafast non-adiabatic transitions, which seems contrary to the efficient photochemical reactions observed in experiments.

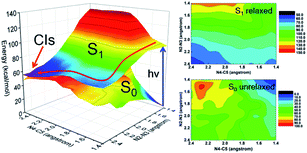
Despite the valuable information on mechanisms these minima and vertical excitations provide, the details of bond breaking processes are still unclear and need to be further explored. For example, whether the nitrogen removal process is concerted or stepwise? If it is a concerted process, whether it is concerted-synchronous or concerted-asynchronous? Motivated by these questions and considering the fact that the two coordinates, namely N2–N3 and N4–C5 bonds, are directly involved in the denitrification reaction, we decided to perform a relaxed scan along these two coordinates spanning the potential energy surface of the S₁ state. As shown in Fig. 3, we depict the obtained 2D reaction coordinate spanned potential energy surface (left) and the corresponding color-filled contour surface of S₀ and S₁ states (right). The constrained optimizations in the S₁ state are conducted using the CASSCF methods, and all the energies are then refined using the MS-CASPT2 method. Since only the N2–N3 and N4–C5 bonds are broken during the reaction process of photolysis, we have only performed a relaxed scan by constraining only the distances of N2–N3 and N4–C5 with different values given in this article, while other molecular coordinates are relaxed without any constraints. The S₀ energies are obtained using the same structure as obtained by the S₁ state without further optimizations. We can see from the potential energy surface that upon relaxation from the Franck–Condon region, the FPT molecule tends to remove the nitrogen molecule in a stepwise way, i.e., the breaking of the N2–N3 bond takes place first and the N4–C5 bond cleavage occurs subsequently.

Fig. 3 MS-CASPT2/CASSCF computed two-dimensional S₁ and S₀ potential energy surfaces spanned by the N2–N3 and N4–C5 bond cleavage coordinates (left). Also shown are the estimated minimum-energy reaction paths (red arrows) and the color filled contour maps of S₁ and S₀ states (right).

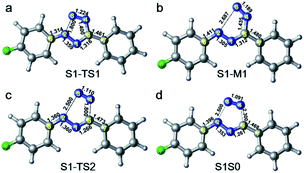
In order to further clarify the corresponding processes, we have selected two important reaction paths from the 2D potential energy surface, i.e., the minimum-energy path along the breaking of N2–N3 bonds from S1-MIN, and the following N4–C5 breaking reaction path, as depicted in Fig. 4. It can be seen that the system only needs to overcome a very small energy barrier of about 2.1 kcal mol⁻¹ from the S₁ minimum energy structure to reach the intermediate structure. For the convenience of subsequent discussions, we use the highest point on the reaction path to approximate the transition state structure of the relevant processes, which is denoted as TS, and the intermediate is marked as M. We depict the structure of S1-TS1 and S1-M1 in the panels a and b of Fig. 5. It is necessary to emphasize that S1-M1 is further optimized in the S₁ state based on the constrained optimized structure in Fig. 4. As can be seen, the excited FPT molecule still maintains its planar configuration during the bond breaking process. Compared to S1-MIN, the N2–N3 in S1-TS1 has the largest change, increasing from 1.408 Å to 1.800 Å. At the same time, N3–N4 is further shortened to 1.224 Å. The changes in N4–C5, N1–N2, and N1–C5 bond lengths are less than 0.040 Å. In the S1-M1 structure, the N2–N3 bond further increases to 2.687 Å, while N3–N4 is shortened to 1.189 Å. At this time, the N4–C5 bond length increases to 1.435 Å. Therefore, the N4–C5 bond turns out to be the weakest bond in the tetrazole ring. For the S1-M1 structure, the energy difference between S₁ and S₀ is much reduced (ca. 20.5 kcal mol⁻¹) compared to S1-MIN, which might facilitate the non-adiabatic transitions from S₁ to S₀ state. From the structure close to S1-M1, we then perform a relaxed scan along the cleavage path of the N4–C5 bond. As shown on the right panel of Fig. 4, starting from M1, the molecule only needs to overcome a smaller S1-TS2 energy barrier while N4–C5 equals 1.800 Å, ca. 5.2 kcal mol⁻¹, reaching the nearly degenerate conical intersection region of S₁ and S₀ states. The crucial structures along this reaction coordinate are depicted in panels c and d in Fig. 5. The length of the N2–C3 bond in S1-TS2 is 2.500 Å, and the bond length of N3–N4 decreases further to 1.110 Å, which is close to the bond length of 1.095 Å of the nitrogen molecule, indicating the formation of nitrogen in the excited S₁ state. At the same time, the other bonds, such as N2–C6, N1–N2, N1–C5, and C5–C7 form a new conjugated structure with the removal of a nitrogen molecule. When the bond length of N4–C5 is further above 2.100 Å, the system reaches the conical intersection region, where the energy difference between S₁ and S₀ is less than 3.0 kcal mol⁻¹. It is worth noting that the conical intersections in this work are obtained by minimum energy path relaxed scans rather than direct optimization. Therefore, they do not correspond to the minimum energy conical intersections (MECIs), which are local minima in the 3N-8 dimensional conical intersection subspace. Due to their degenerate energies, these conical intersections beyond the MECIs are also crucial for the non-adiabatic transitions due to strong couplings between the electronic and nuclear motions. Once at the conical intersection region, the system can then relax to the ground state via ultrafast non-adiabatic transitions accompanying the removal of nitrogen, from which the subsequent 1,3-dipolar cycloaddition might happen.

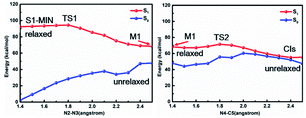Fig. 4 MS-CASPT2/CASSCF computed minimum energy paths in the S₁ state along the cleavage of N2–N3 bond and N4–C5 bond, respectively, based on the stepwise mechanism.

Fig. 5 The relevant structures along the cleavage of N2–N3 and N4–C5 bonds.

In order to confirm that the stepwise denitrification mechanism is more preferred than the concerted one, we depict the potential energy profiles where the N2–N3 equals N4–C5 in Fig. 6. As expected, the molecule needs to overcome a much larger barrier of about 18.8 kcal mol⁻¹ to remove the nitrogen molecule, indicating that the concerted mechanism is unlikely to take place in comparison with the stepwise mechanism.

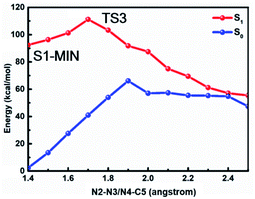Fig. 6 MS-CASPT2/CASSCF computed minimum energy paths in the S₁ state along the cleavage of N2–N3 and N4–C5 bonds based on the concerted mechanism, where N2–N3 bond equals N4–C5 bond all the time.

Based on the above results of the S₁ excited state, we can thus summarize the photoinduced chemical reaction and deactivation paths of the FPT molecule, as shown in Fig. 7. Upon excitation with ultraviolet light, the FPT molecule can be promoted to the spectroscopically bright state S₁ with a ¹ππ* character. Then, the excited molecule relaxes from the Franck–Condon region to its corresponding minimum energy structure of S₁, S1-MIN. However, due to the small barrier for the elongation of the N2–N3 bond in the S₁ state (2.1 kcal mol⁻¹), the FPT molecule can break the N2–N3 bond easily, reaching the intermediate S1-M1 structure. Similar to the S1-MIN, S1-M1 also cannot exist stably since breaking the N4–C5 bond only needs to overcome a small energy barrier of 5.2 kcal mol⁻¹. Therefore, the cleavages of both N2–N3 and N4–C5 bonds are accompanied by the formation of the nitrogen molecule. In comparison with the formidable high energy barrier of about 18.8 kcal mol⁻¹ for the concerted reaction coordinates, we conclude that the stepwise denitrification mechanism would be more preferred than the concerted one. The removal of the nitrogen molecule is completed in the excited S₁ state rather than the ground state. With the breaking of the second N4–C5 bond, the system reaches the conical intersection region where the energies of S₁ and S₀ states are nearly the same. Due to the strong non-adiabatic coupling in this region, the denitrified system can finally deactivate to the ground state in an ultrafast way, resulting in the intermediate product ((4-fluorophenyl)diazen-1-ium-1-ylidene)(phenyl)methanide (FPNI) and nitrogen molecule. Considering the high energy of the molecule obtained upon excitation, the whole process is expected to be completed easily and ultrafast. The timescale of the entire excited state dynamics might be completed within a few picoseconds based on previous dynamics investigations. After the deactivation, the intermediate FPNI can then react with the 1,4-naphthoquinone (NPQ) to generate 1-(4-fluorophenyl)-3-phenyl-1H-benzo[f]indazole-4,9(3aH,9aH)-dione (FP2HQ), which can be oxidized to the final product PFQ.

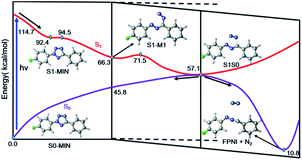Fig. 7 Proposed excited state reaction and deactivation mechanisms of FPT upon excitation based on our static electronic structure calculations. All the relevant energies are in kcal mol⁻¹.

In order to investigate the 1,3-dipolar cycloaddition reaction of the ground state using FPNI and NPQ as reactants, we employ the DFT method with the M06-2X functional to optimize the relevant reactants, products, and transition states of the related [3 + 2] reactions. As shown in Fig. 8, the system only needs to overcome a small energy barrier of about 5.7 kcal mol⁻¹ to generate the precursor FP2HQ. Through the frequency analysis of the transition state structure, we can further conclude that the ground state [3 + 2] cycloaddition reaction is a concerted synchronous process, i.e., the N2–C8 and C5–C9 bonds are formed at the same time. Considering the high energy of FPNI obtained by the deactivation of the excited states, the cycloaddition reaction can easily occur and finally generate the FP2HQ structure. Through further oxidation, the final product PFQ is acquired.

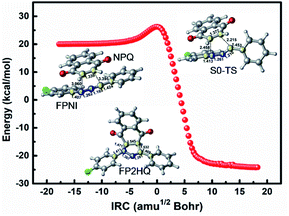Fig. 8 The IRC path for the [3 + 2] cycloaddition of FPNI and NPQ in the ground state to generate the precursor of PFQ.

The process from the generated FP2HQ to the final product PFQ corresponds to an oxidation process, which removes two hydrogen atoms attached to C8 and C9 atoms of FP2HQ, after which a C=C double bond is formed, and the final PFQ is generated. Since our present theoretical work is based on the experimental work of Ortiz-Rojano et al.,¹⁰ which fails to mention the oxidation details of FP2HQ, we, therefore, presume that this process is a mature method experimentally and need not be explored anymore. Moreover, the highlight of this work is the photoinduced reactions between FPT and NPQ rather than the oxidation of FP2HQ to PFQ. Therefore, the details of the oxidation of FP2HQ depicted in Fig. 9 is neglected in this work as well.

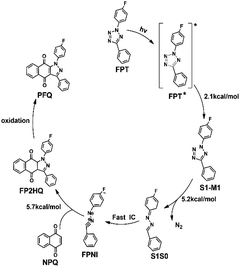Fig. 9 The proposed overall light-induced tetrazole-quinone 1,3-dipolar cycloaddition mechanism based on our calculated results.

Conclusions

In summary, we have employed static electronic structure calculations in this work to explore the light-induced tetrazole-quinone 1,3-dipolar cycloaddition mechanism at the atomic level, which can be summarized as shown in Fig. 9. Upon excitation with the ultraviolet light, one of the original reactant FPT reaches its S₁ excited state. Subsequently, due to the ultrahigh energy and the small energy barrier, the FPT molecule breaks the N2–N3 and N4–C5 bonds sequentially, removing the nitrogen atom finally in the S₁ state. With the cleavage of the second N4–C5 bond, the system reaches its conical intersection region and deactivates to the ground state ultrafast, thereby generating the active intermediate FPIN. Subsequently, the active intermediate FPIN can react with naphthoquinone in the ground state by overcoming an energy barrier of about 5.7 kcal mol⁻¹, after which the FP2HQ is formed. The FP2HQ can be oxidized to produce the PFQ finally. Due to the high energy and small barrier, the entire reaction process can easily occur, which ultimately leads to an efficient synthetic reaction. Our present work not only explains the experimental mechanism in detail, but also provides a theoretical basis for the rational design of related photoinduced reactions in the future.

Author contributions

Yang He: data curation; formal analysis; writing-original draft. Dong-Hui Xu: data curation; writing-review. Yan-Jun Zhang: data curation. Chun Zhang: data curation. Jian-Min Guo: supervision. Laicai Li: supervision; editing. Xiao-Qin Liang: supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research was supported by the Science and Technology Support Program Project of the Sichuan Provincial Health Commission (19PJ287), the joint project of Southwest Medical University of Luzhou, Sichuan (2018LZXNYD-ZK07), the Supported Program Project of the Science and Technology Bureau of Luzhou, Sichuan Province [2017-S-39 (4/5)] and the High Performance Computing Center Sichuan Normal University, China.

References

1. L. Garuti, M. Roberti and D. Pizzirani, Mini-Rev. Med. Chem., 2007, 7, 481–489.
2. J. M. Holstein, D. Stummer and A. Rentmeister, Chem. Sci., 2015, 6, 1362–1369.
3. Z. Li, L. Qian, L. Li, J. C. Bernhammer, H. V. Huynh, J.-S. Lee and S. Q. Yao, Angew. Chem., Int. Ed., 2015, 55, 2002–2006.
4. T. Fryatt, H. I. Pettersson, W. T. Gardipee, K. C. Bray, S. J. Green, A. M. Z. Slawin, H. D. Beall and C. J. Moody, Bioorg. Med. Chem., 2004, 12, 1667–1687.
5. G. A. Conway, L. J. Loeffler and I. H. Hall, J. Med. Chem., 1983, 26, 876–884.
6. G. Bertuzzi, S. Crotti, P. Calandro, B. F. Bonini, I. Monaco, E. Locatelli, M. Fochi, P. Zani, E. Strocchi, A. Mazzanti, M. Chiariello and M. C. Franchini, ChemMedChem, 2018, 13, 1744–1750.
7. A. Thangadurai, M. Minu, S. Wakode, S. Agrawal and B. Narasimhan, Med. Chem. Res., 2011, 21, 1509–1523.
8. R. A. Tapia, C. Carrasco, S. Ojeda, C. Salas, J. A. Valderrama, A. Morello and Y. Repetto, J. Heterocycl. Chem., 2002, 39, 1093–1096.
9. R. W. Hoffmann and K. Ditrich, Liebigs Ann. Chem., 1990, 1990, 23–29.
10. L. Ortiz-Rojano, J. Rojas-Martín, C. Rodríguez-Diaz, M. C. Carreño and M. Ribagorda, Chem.–Eur. J., 2019, 25, 15050–15054.
11. C. P. Ramil and Q. Lin, Curr. Opin. Chem. Biol., 2014, 21, 89–95.
12. Z. Yu, L. Y. Ho and Q. Lin, J. Am. Chem. Soc., 2011, 133, 11912–11915.
13. P. An, T. M. Lewandowski, T. G. Erbay, P. Liu and Q. Lin, J. Am. Chem. Soc., 2018, 140, 4860–4868.
14. S. Berhe, A. Slupe, C. Luster, H. A. Charlier Jr, D. L. Warner, L. H. Zalkow, E. M. Burgess, N. M. Enwerem and O. Bakare, Bioorg. Med. Chem., 2010, 18, 134–141.
15. H. Buff and U. Kuckländer, Tetrahedron, 2000, 56, 5137–5145.
16. N. G. Argyropoulos, D. Mentzafos and A. Terzis, J. Heterocycl. Chem., 1990, 27, 1983–1988.
17. O. Bakare, L. H. Zalkow and E. M. Burgess, Synth. Commun., 1997, 27, 1569–1576.
18. E. Blasco, Y. Sugawara, P. Lederhose, J. P. Blinco, A.-M. Kelterer and C. Barner-Kowollik, ChemPhotoChem, 2017, 1, 159–163.
19. P. An and Q. Lin, Org. Biomol. Chem., 2018, 16, 5241–5244.
20. X. Shang, R. Lai, X. Song, H. Li, W. Niu and J. Guo, Bioconjugate Chem., 2017, 28, 2859–2864.
21. P. Lederhose, D. Abt, A. Welle, R. Müller, C. Barner-Kowollik and J. P. Blinco, Chem.–Eur. J., 2017, 24, 576–580.
22. J. P. Menzel, F. Feist, B. Tuten, T. Weil, J. P. Blinco and C. Barner-Kowollik, Angew. Chem., Int. Ed., 2019, 58, 7470–7474.
23. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
24. K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
25. F. Aquilante, R. Lindh and T. Bondo Pedersen, J. Chem. Phys., 2007, 127, 114107.
26. G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
27. N. Forsberg and P.-Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204.
28. R. G. Parr and W. T. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, USA 1994.
29. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
30. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
31. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven and J. A. Montgomery Jr, et al., Gaussian 09, revision A.02, Gaussian, J. Mater. Chem. C, page 18 of 20, J. Mater. Chem. C, accepted manuscript 19 Inc., Wallingford, CT 2009.
33. F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117.
34. I. Galván, M. Vacher, A. Alavi, C. Angeli and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.

---

Footnote

† Electronic supplementary information (ESI) available: All CASSCF active orbitals and Cartesian coordinates of all optimized structures. See DOI: 10.1039/d1ra04636e

---