DOI:
10.1039/D1RA04886D
(Paper)
RSC Adv., 2021,
11, 24456-24465
Study of anisotropic thermal conductivity in textured thermoelectric alloys by Raman spectroscopy†
Received
23rd June 2021
, Accepted 2nd July 2021
First published on 13th July 2021
Abstract
Polycrystalline p-type Sb1.5Bi0.5Te3 (SBT) and n-type Bi2Te2.7Se0.3 (BTS) compounds possessing layered crystal structure show anisotropic electronic and thermal transport properties. This research is in pursuit of better understanding the anisotropic thermal properties using Raman spectroscopy. A systematic Raman spectroscopic study of the hot-pressed pellet of the textured p-type SBT and n-type BTS is reported in both directions: parallel (‖) and perpendicular (⊥) to the pressing axis as a function of temperature and laser power. The first-order temperature coefficient, optical thermal conductivity, and phonon lifetime are qualitatively determined from the temperature and laser power-dependent frequency and full-width half maximum (FWHM) of Raman peaks (A11g, E2g & A21g). Anisotropy in experimental phonon thermal conductivity in both directions is correlated with the approximated optical thermal conductivity, phonon lifetime and phonon anharmonicity. The anisotropy in phonon anharmonicity in both directions is explained by the modified Klemens–Hart–Aggarwal–Lax phonon decay model. In this study, the symmetric three-phonon scattering process is considered responsible for thermal transport in the temperature range of 300 to 473 K.
1. Introduction
Polycrystalline p-type BixSb2−xTe3 and n-type Bi2Te3−xSex thermoelectric (TE) bulk materials are frequently used at near room temperature (<100 °C) heat-harvesting applications.1–5 In a broader context, the Seebeck coefficient (S), electrical conductivity (σ), and total thermal conductivity (κ) are temperature-dependent materials properties, and can be used to measure the TE performance of various materials by a given relation, known as a dimensionless figure of merit zT = S2σTκ−1, where T is the absolute temperature. κ is the combination of carrier contributed thermal conductivity (κc) and phonon contributed thermal conductivity (κp). Therefore, high S & σ and low κ are essential to attain a high TE performance. These chalcogen based thermoelectric materials are also besides being used in infrared (IR) detectors and phase-change memory materials for information storage.6,7 These alloys possess a rhombohedral crystal structure with the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m h and these are constructed of anisotropic layers, in which a five mono-atomic layer sequence along the c-axis, the –A(1)–B–A(2)–B–A(1)– is a known quintuple (Fig. S1(a)†).8 In this instance, A could be either Te or Se and B could be either Bi or Sb. The lamellar structure and the weak van der Waal attractions between quintuple layers are caused for the anisotropy and hence, anisotropic properties along and across the layers. As reported, the σ and κ show a high anisotropy, while the S is almost isotropic, resulting in anisotropic power factor (defined by PF = S2σ) and zT.4
m h and these are constructed of anisotropic layers, in which a five mono-atomic layer sequence along the c-axis, the –A(1)–B–A(2)–B–A(1)– is a known quintuple (Fig. S1(a)†).8 In this instance, A could be either Te or Se and B could be either Bi or Sb. The lamellar structure and the weak van der Waal attractions between quintuple layers are caused for the anisotropy and hence, anisotropic properties along and across the layers. As reported, the σ and κ show a high anisotropy, while the S is almost isotropic, resulting in anisotropic power factor (defined by PF = S2σ) and zT.4
The Raman technique is powerful and non-destructive, allowing researchers to look into the internal structures, like whether different phases, composition, and defects are present. It also provides insight into the strain and compression that is present in thin films and nanostructured materials.9 It is also a very useful tool to study phonon dispersions in thermoelectric materials.10–15 From Raman spectra, one can study the phonon–phonon, electron–phonon, and plasmon–phonon interactions. Furthermore, as the temperature changes, the interatomic spacing and overlap between neighboring electronic orbitals will change, making temperature-dependent Raman spectra useful for determining optical thermal conductivity and relative phonon lifetimes.11 The phonon anharmonicity can be understood through the frequency and FWHM variations of Raman modes with temperature, while phonon interactions can be understood by variation in the intensity of Raman peaks. The broadening of Raman peaks can also be used to understand the decrease in thermal conductivity with temperature caused by phonon softening. Raman spectra have been used in recent times as a non-contact approach to determine an approximate thermal conductivity of thin films.16 Basically, this non-contact approach is depending on the laser power and temperature. Several reports are available on Raman spectra of p-type SBT and n-type BTS thin films.17,18 However, only a few reports are available for bulk materials to date. Most of the published studies are related to the investigation of uni-directional data, i.e., measurements on a surface perpendicular to the pressing direction.19 The anisotropic structure of these alloys causes the difference in frequency values of in- and out-of-plane Raman modes with respect to temperature.20 Thus, it is necessary to investigate the directional Raman studies and understanding of phonon scattering mechanisms to realize the anisotropy in thermal properties to improve the TE efficiency.
We report here a directional Raman spectroscopy study of the textured p-type SBT and n-type BTS thermoelectric alloys produced by melt-quenching-hot press processing. Temperature and laser power dependent Raman spectra are taken in both parallel and perpendicular directions. These measurements are the first of their kind and provide insights into the non-destructive way of estimating the optical thermal conductivity and phonon lifetime. The determined optical thermal conductivity and phonon lifetime in both directions are correlated with the temperature-dependent phonon thermal conductivity. Further, the anisotropic thermal conductivity in both directions resulted from the anisotropy in phonon anharmonicity, which is explained by the modified Klemens–Hart–Aggarwal–Lax phonon decay model.
2. Experimental details
Polycrystalline nanostructured p-type SBT and n-type BTS textured pellets were prepared by melt-quenching-hot press process. The steps involved in the preparation methods were given elsewhere in our previous reports.4,5 First, the phase pure bulk samples were prepared by melt-rotation-quenching process. The bulk samples were powdered and these powders were used to prepare pellet by hot-press sintering. This pellet was sawn in the appropriate directions: parallel and perpendicular to the pressing axis to study anisotropic properties, shown in Fig. 1. Rigaku Smart Lab X-ray diffractometer was used to take the X-Ray Diffraction (XRD) patterns of p-type SBT and n-type BTS hot-pressed pellets in the 2θ range of 25–60°. Carl Zeiss Ultra 55 field emission scanning electron microscopy (FESEM) and JEOL 2000 FX-II transmission electron microscopy (TEM) were used to capture the micrographs. Kratos Axis Ultra DLD X-ray photoelectron spectroscopy was used to investigate the elemental composition and oxidation states. The thermal diffusivity (α) of 10 mm square and 1 mm thick pellet is measured by LINSEIS LFA 1000 in Ar atmosphere. The specific heat capacity (Cp) is measured in N2 atmosphere by TA SDT650 DSC in the temperature range between 300 and 473 K. The κ values were calculated from a relation, given as κ = αCpd, where d is the density of hot-pressed pellets, measured by Archimedes principle. The obtained relative densities were 95% and 97% for p-type SBT and n-type BTS, respectively. Raman spectra as a function of temperature and laser power were recorded from polished pellets of 10 mm square and 2 mm thickness in a vacuum (10−3 mbar) by HORIBA JOBIN YVON, HR 800 with laser light wavelength of 532 nm and laser power of 5 × 10−2 W. To avoid thermal effect on the sample, the laser beam was kept focused on the top surface of the pellet for 1 s. The penetration depth of the laser was calculated by the relation, given as 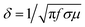 , where f is the laser light frequency (Hz), σ is the electrical conductivity (S m−1), and μ is the magnetic permeability. The estimated penetration depths were ∼75 nm and ∼80 nm for p-type SBT and n-type BTS, respectively. The peaks obtained in Raman spectra were fitted with the Lorentzian function to extract the frequency, FWHM and Intensity. Hereafter, the XRD, Raman and thermal conductivity characterizations on pellet perpendicular and parallel to the pressing axis (PA) were labelled by symbols of ⊥ and ‖, respectively.
, where f is the laser light frequency (Hz), σ is the electrical conductivity (S m−1), and μ is the magnetic permeability. The estimated penetration depths were ∼75 nm and ∼80 nm for p-type SBT and n-type BTS, respectively. The peaks obtained in Raman spectra were fitted with the Lorentzian function to extract the frequency, FWHM and Intensity. Hereafter, the XRD, Raman and thermal conductivity characterizations on pellet perpendicular and parallel to the pressing axis (PA) were labelled by symbols of ⊥ and ‖, respectively.
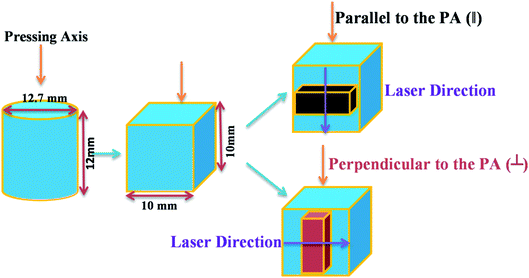 |
| | Fig. 1 Schematic representation of hot-pressed pellet sawed in appropriate directions to investigate the directional XRD, thermal conductivity and Raman spectra. | |
3. Results and discussion
3.1. Directional microstructure characterizations
Fig. 2(a) and (b) show the XRD patterns of p-type SBT and n-type BTS hot-pressed pellets (‖ to PA & ⊥ to PA), respectively. In both cases, the XRD peaks are indexed with rhombohedral crystal structure with space group: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m h.4,5 Impurity peaks with very low intensity (>2%) are found in both XRDs, might be due to the surface oxidation. These peaks are assigned to Sb2O3 in p-type SBT and Bi2O3 in n-type BTS. Both ‖ to PA & ⊥ to PA have similar XRD patterns. However, the intensity of (0015) peak differs, indicating that the hot-press sintering exhibit a significant anisotropy of grain orientation without altering the crystal structure. Lotgering factor (F) is determined to confirm the anisotropic orientation from XRD patterns of both ‖ to PA and ⊥ to PA.4 The higher F values (0.4 for p-type SBT and 0.2 for n-type BTS) are observed in case of parallel direction while lower F values (0.06 for both p-type SBT and n-type BTS) in the perpendicular direction. The high intensity of the (00l) peaks in the ‖ to PA, reveals that the compound's ab-orientation is in the perpendicular direction to the pressing axis. Therefore, the p-type SBT and n-type BTS may have the anisotropic physical transport properties. This prompted us to use Raman spectra to investigate anisotropic thermal properties.
m h.4,5 Impurity peaks with very low intensity (>2%) are found in both XRDs, might be due to the surface oxidation. These peaks are assigned to Sb2O3 in p-type SBT and Bi2O3 in n-type BTS. Both ‖ to PA & ⊥ to PA have similar XRD patterns. However, the intensity of (0015) peak differs, indicating that the hot-press sintering exhibit a significant anisotropy of grain orientation without altering the crystal structure. Lotgering factor (F) is determined to confirm the anisotropic orientation from XRD patterns of both ‖ to PA and ⊥ to PA.4 The higher F values (0.4 for p-type SBT and 0.2 for n-type BTS) are observed in case of parallel direction while lower F values (0.06 for both p-type SBT and n-type BTS) in the perpendicular direction. The high intensity of the (00l) peaks in the ‖ to PA, reveals that the compound's ab-orientation is in the perpendicular direction to the pressing axis. Therefore, the p-type SBT and n-type BTS may have the anisotropic physical transport properties. This prompted us to use Raman spectra to investigate anisotropic thermal properties.
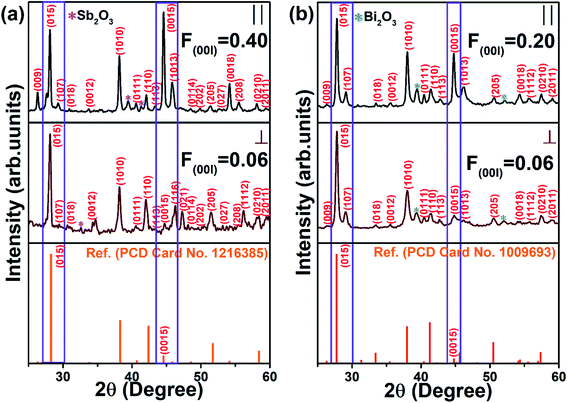 |
| | Fig. 2 XRD patterns of (a) p-type SBT (‖ to the PA, ⊥ to the PA & Ref.), and (b) n-type BTS (‖ to the PA, ⊥ to the PA & Ref.) hot-pressed pellets. | |
The SEM images of the cross-sectional surface of the hot-pressed pellet of both p-type SBT and n-type BTS are shown in Fig. 3(a) and (b). The layers are densely grown in ab-plane and oriented perpendicularly to the pressing axis, as seen in these figures, which is consistent with XRD results. High-resolution TEM images taken on hot-pressed pellets are shown in Fig. 3(c) and (d). As seen from these figures, the layers are oriented perpendicular to the pressing axis, and each layer is made up of nanograins. The SAED images show a ring pattern, indicating that the material is polycrystalline.
 |
| | Fig. 3 SEM image of the cross-sectional surface of the hot-pressed pellet of (a) p-type SBT, (b) n-type BTS, and High-resolution TEM (HRTEM) image (inset is SAED) of (c) p-type SBT, (d) n-type BTS. | |
Fig. S2† shows the XPS spectra of p-type SBT and n-type BTS hot-pressed pellets. The chemical states of Sb 3d, Bi 4f, and Te 3d in the p-type SBT and Bi 4f, Te 3d, and Se 3d in the n-type BTS are consistent with the previous reports.21,22 The obtained XPS peaks are deconvoluted by XPSPEAK41 program with Gaussian–Lorentzian (GL) function. The surface compositions of constituted elements are determined from the integrated area ratio of the spectra after normalization by equation 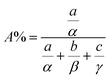 with corresponding atomic sensitivity factors (α, β and γ); where A% is the atomic percentage, a, b and c are the area under the ground state peaks of each element.23,24 The Sb
with corresponding atomic sensitivity factors (α, β and γ); where A% is the atomic percentage, a, b and c are the area under the ground state peaks of each element.23,24 The Sb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi
Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te atomic ratio in p-type SBT is obtained as 1.49
Te atomic ratio in p-type SBT is obtained as 1.49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50
0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.01 while the Bi
3.01 while the Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te
Te![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Se atomic ration in n-type BTS is 2.02
Se atomic ration in n-type BTS is 2.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.70
2.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.28. The obtained shoulder peaks at higher binding energy may indicate the surface oxidation, consistent with the XRD analysis.
0.28. The obtained shoulder peaks at higher binding energy may indicate the surface oxidation, consistent with the XRD analysis.
3.2. Directional thermal conductivity
Fig. 4 depict the temperature dependent total thermal conductivity (κ), carrier thermal conductivity (κc) and phonon thermal conductivity (κp) of both p-type SBT and n-type BTS. These properties are measured parallel (‖ to PA) and perpendicular (⊥ to PA) to the pressing axis at a temperature ranging from 300 K to 473 K. The κ is the sum of κc, κp, it can be expressed as κ = κc + κp. The κc is estimated from Wiedemann–Franz relation, κc = LσT, where L is the Lorenz number. The L values are calculated from S values using the single parabola band (SPB)-acoustic phonon scattering (APS) approximation (Fig. S3†).5 The κp values are calculated by the formula κp = κ − κc. The obtained κp values increase with increasing temperature. In addition, the κp along the perpendicular direction to the pressing axis is higher than that of parallel direction as the mean free path of phonon is higher along ab-plane than in the c-axis.4,5 It is clarified by the fact that the high density of layer interfaces and high density of grain boundaries may produce thermal barriers along the parallel direction to the pressing axis. Directional Raman spectra were taken with respect to laser power and temperature to study the anisotropy in thermal conductivity.
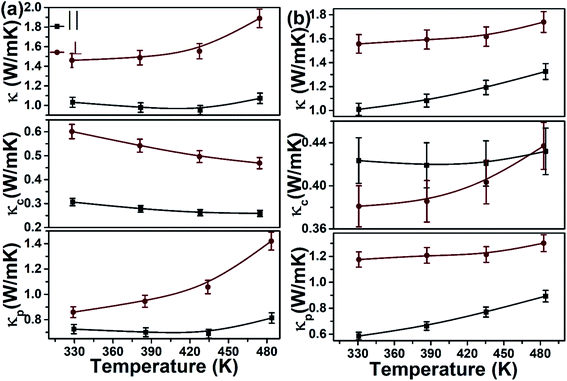 |
| | Fig. 4 Temperature dependent total thermal conductivity, carrier thermal conductivity and phonon thermal conductivity of (a) p-type SBT and (b) n-type BTS. | |
3.3. Directional Raman spectra
The bulk p-type SBT and n-type BTS crystals show 15 lattice vibrational modes, anticipated according to the group theory. Among these, 12 are optical modes (2A1g + 2Eg + 2A1u + 2Eu) and 3 are acoustic modes. Fig. 5(a) and (d) show Raman spectra of p-type SBT and n-type BTS taken in both directions. As can be seen from these figures, three Raman peaks A11g, E2g, and A21g, are observed out of four in both the compounds.19 Aside from these Raman-active vibrational modes, an infrared (IR) active vibrational mode is also observed, known as A21u. In general, the presence of IR modes is associated with the breaking of symmetry, likely resulting from the abundant dislocations. This finding is matched with the recent computational study.13 The schematic representation of these modes, is shown in Fig. S1(b).† In the A1g and A1u modes, the oscillation usually occurs along the c-axis, meaning that the atoms oscillate out-of-plane. In the Eg mode, on the other hand, the atoms oscillate along the basal plane, i.e., oscillate in-plane. The frequency values of all modes are listed in Table S1† indicates that the observed peak frequencies are very close to the reported peaks of the p-type SBT and n-type BTS bulk samples. The Raman modes are observed in the higher frequency range for p-type SBT, while for n-type BTS, the Raman modes appear in the lower frequency range. This may be due to the higher bonding forces in p-type SBT compared to n-type BTS.13 The E2g mode is the most pronounced Raman mode due to its highest intensity than other modes. Fig. 5(b), (c) & (e), (f) show the variation of frequency of E2g mode with temperature and laser power, respectively. These figures clearly show frequency shift, the difference in FWHM, and intensity differences in different directions. Raman spectra with all modes of p-type SBT and n-type BTS in both directions as a function of temperature and laser power are shown in Fig. S4.† Raman spectra are recorded at four distinct temperatures (323 K, 373 K, 423 K & 473 K) and at four different laser powers (5 mW, 12.5 mW, 25 mW, & 50 mW) in both directions for both compounds.
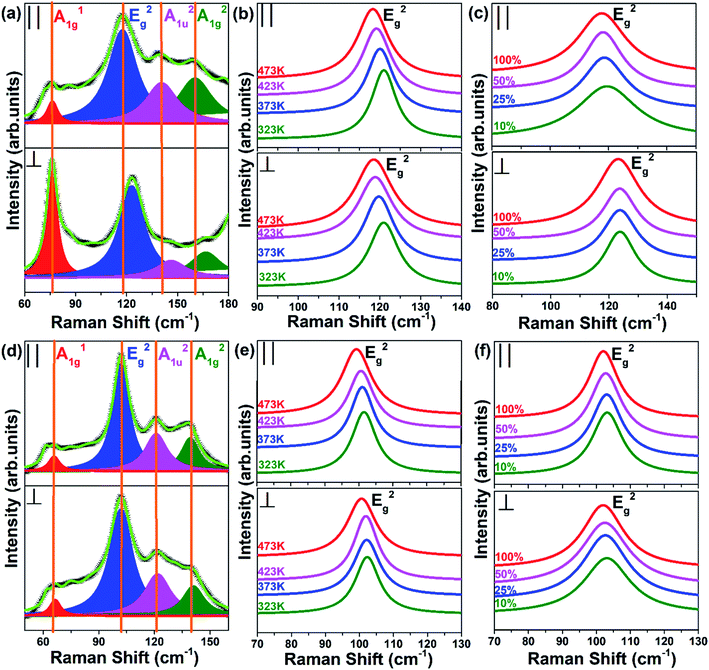 |
| | Fig. 5 (a) Directional Raman spectra, (b) variation in frequency of E2g mode with temperature, & (c) variation in frequency of E2g mode with laser power of p-type SBT; and (d) directional Raman spectra, (e) variation in frequency of E2g mode with temperature, & (f) variation in frequency of E2g mode with laser power of n-type BTS. | |
3.4. Estimation of optical thermal conductivity (κop)
The phonon thermal conductivity (κp) is the combination of optical contribution (κop) and acoustic contribution (κac), κp = κop + κac.25 The optical thermal conductivity (κop) values are estimated from the three Raman active vibrational modes A11g, E2g and A21g in both compounds in both directions by the following eqn (1)26| |
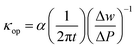 | (1) |
where α is the first-order temperature coefficient, t is the pellet thickness, 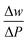 is the variation in the frequency of phonon with laser power, w is the frequency of Raman mode, and P is the laser power. α is the slope of the linear plot of Raman shifts and temperature (Fig. 6(a) and (e)) while
is the variation in the frequency of phonon with laser power, w is the frequency of Raman mode, and P is the laser power. α is the slope of the linear plot of Raman shifts and temperature (Fig. 6(a) and (e)) while 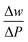 is the slope of the linear plot of Raman shifts and laser power (Fig. 6(b) and (f)). The frequency of all three Raman active modes shows systematic redshifts with increasing temperature and laser power. In general, the temperature-dependent frequency is mainly dependent on two factors: (1) quasiharmonic lattice thermal expansion (Δwthermal) and (2) anharmonic contribution (three-phonon and four-phonon scattering processes) (Δwan), w(T) = Δwthermal + Δwan.27 It can be found that the |α| value in parallel direction is larger than that of perpendicular direction, indicates that stronger anharmonicity in the parallel direction. The α is directly proportional to the volume thermal coefficient (γ = (dln
is the slope of the linear plot of Raman shifts and laser power (Fig. 6(b) and (f)). The frequency of all three Raman active modes shows systematic redshifts with increasing temperature and laser power. In general, the temperature-dependent frequency is mainly dependent on two factors: (1) quasiharmonic lattice thermal expansion (Δwthermal) and (2) anharmonic contribution (three-phonon and four-phonon scattering processes) (Δwan), w(T) = Δwthermal + Δwan.27 It can be found that the |α| value in parallel direction is larger than that of perpendicular direction, indicates that stronger anharmonicity in the parallel direction. The α is directly proportional to the volume thermal coefficient (γ = (dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V/dT)p) and Gruneisen parameter (β = −(dln
V/dT)p) and Gruneisen parameter (β = −(dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w/dln
w/dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V)T), α = γ × β.20 Generally, the larger the α, the larger the β, leading to a stronger anharmonic effect. It is reported that 40% of the temperature-dependent total phonon frequency change occurs through the thermal expansion contribution in p-type SBT and n-type BTS.13 This indicates that the observed temperature-dependent frequency can be well modelled by incorporating anharmonic components. Thus, comparing with the in-plane modes, the out-of-plane modes show larger α in both directions, reveals their important role in directional thermal transport.
V)T), α = γ × β.20 Generally, the larger the α, the larger the β, leading to a stronger anharmonic effect. It is reported that 40% of the temperature-dependent total phonon frequency change occurs through the thermal expansion contribution in p-type SBT and n-type BTS.13 This indicates that the observed temperature-dependent frequency can be well modelled by incorporating anharmonic components. Thus, comparing with the in-plane modes, the out-of-plane modes show larger α in both directions, reveals their important role in directional thermal transport.
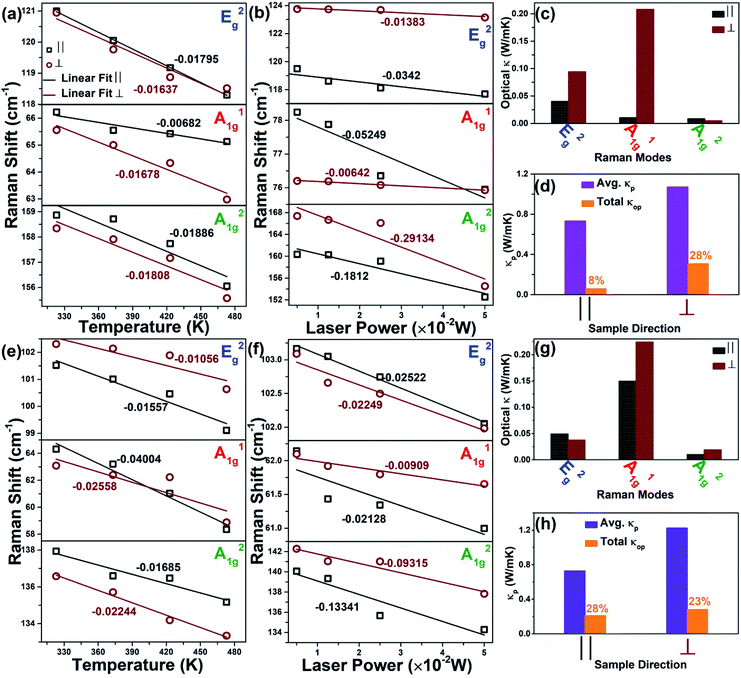 |
| | Fig. 6 (a) Variation in frequencies with temperature, (b) variation in frequencies with laser power, (c) mode wise optical thermal conductivity, & (d) correlation between experimental and optical thermal conductivity of p-type SBT; and (e) variation in frequencies with temperature, (f) variation in frequencies with laser power, (g) mode wise optical thermal conductivity, & (h) correlation between experimental and optical thermal conductivity of n-type BTS. | |
The estimated mode wise optical thermal conductivity values are shown in Fig. 6(c) and (g) and Table 1, indicate variation in values in both directions. Fig. 6(d) and (h) show the relation between experimental κp and total κop, indicating the optical contribution in phonon thermal conductivity is different in different directions.25 In general, the acoustic phonon modes contribute most of the phonon thermal conductivity, as they have a long life and high group velocities. In SnSe, the lattice thermal conductivity of the optical contribution is more than 60% based on theoretical studies by Guo et al.28 It is said that optical phonons with a w of about 100 cm−1 contribute about 18% to a and b axes, and 35% to c axis in SnSe.29 As can be seen that the total κop values are different in different directions and higher values are observed in the perpendicular to the pressing axis in both compounds (p-type SBT & n-type BTS), as like κp in different directions. This might be due to the variation in phonon lifetime (τ) in both directions, which will be discussed further. The direct correlation between κp and τ is given by the following eqn (2)30
| |
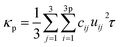 | (2) |
where
cij is the Einstein heat capacity per volume of the
ith vibrational mode, and
uij is the group velocity.
Table 1 Experimental phonon thermal conductivity, estimated optical thermal conductivity and phonon lifetime values of p-type SBT and n-type BTS in both directions
| |
p-Type SBT |
n-Type BTS |
| Parallel (‖) |
Perpendicular (⊥) |
Parallel (‖) |
Perpendicular (⊥) |
| Avg κp (W mK−1) |
0.732 |
1.070 |
0.728 |
1.224 |
| κp (⊥/‖) |
1.46 |
1.68 |
| Total κop (W mK−1) |
0.058 (8%) |
0.307 (28%) |
0.208 (28%) |
0.280 (23%) |
| Total τ (cm) |
23.223 |
25.731 |
23.914 |
30.083 |
| τ (⊥/‖) |
1.11 |
1.26 |
3.5. Estimation of phonon lifetime (τ)
Raman mode wise τ values qualitatively estimated from the following eqn (3), is the reciprocal of FWHM.31| |
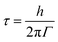 | (3) |
where Γ is the FWHM of Raman peaks, shown in Fig. 7(a) and (e). In general, the temperature-dependent variation in FWHM is mainly dependent on both contributions: (1) phonon–phonon interaction because of anharmonicity in the lattice (Γan) and (2) electron–phonon coupling (ΓEPC).27 However, in the case of p-type SBT and n-type BTS, the variation in FWHM is significantly dependent on the term Γan because ΓEPC is present in a system with EF = 0. The linear plots in Fig. S5† represent that the electrical conductivity is decreasing with increasing temperature. This indicates that the EPC is increasing with increasing temperature and at low temperatures, the contribution of ΓEPC to FWHM can be ignored. The FWHM of all three Raman modes demonstrates the manifestation of downshifts and upshifts with rising temperature is only attributed to the alteration of the anharmonic potential constants. This is to say that FWHM measurements are more accurate to calculate the anharmonic constants because of the greater variation between temperature-dependent values.
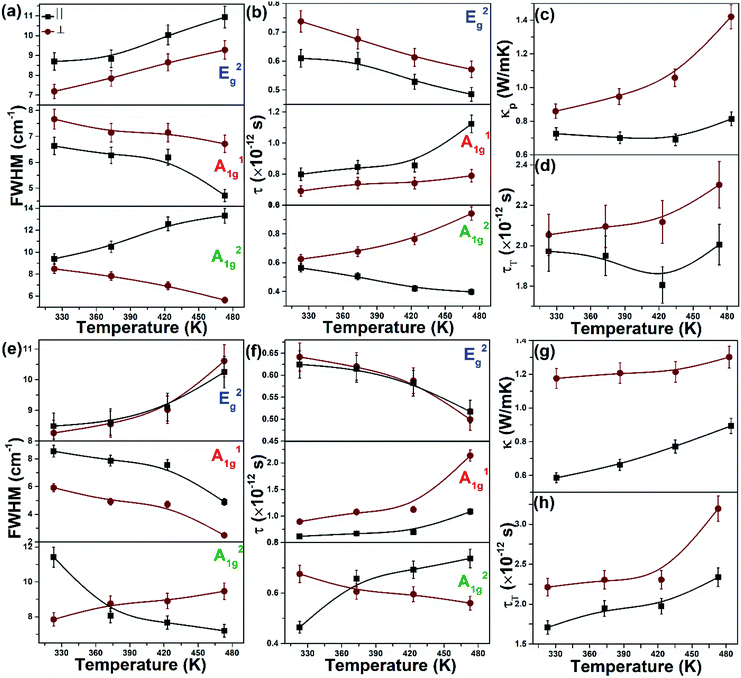 |
| | Fig. 7 Temperature dependent (a) mode wise FWHM (b) mode wise phonon lifetime, (c) experimental thermal conductivity, and (d) total phonon lifetime of p-type SBT; temperature dependent (e) mode wise FWHM, (f) mode wise phonon lifetime, (g) experimental thermal conductivity, and (h) total phonon lifetime of n-type BTS. | |
The estimated mode wise phonon lifetime values are shown in Fig. 7(b) and (f), and Table 1, provide an additional understanding of anisotropy in thermal conductivity in distinct angles. Total phonic lifetime (τT) increases with increasing temperature is shown in Fig. 7(d) and (h). The temperature-dependent τT in distinct directions is validated with the trend of temperature-dependent phonon thermal conductivity (Fig. 7(c) and (g)), i.e., the greater τT shows the higher κp. The τT values in the perpendicular direction to the pressing axis are larger than that of parallel direction in both compounds. This can be directly related to the relatively larger mean free path of the phonons in the perpendicular direction. This prediction well supported by anisotropic phonon anharmonicity in different directions will be discussed through the modified Klemens–Hart–Aggarwal–Lax three-phonon decay model. The variation in frequencies and FWHMs is a manifestation of optical phonon anharmonicity, which also indicates that they have a significant influence on the anisotropic thermal properties in both directions.
3.6. Anharmonic three phonon decay model
As a result of the anharmonic process, zone-center optical phonon decay can yield either two or more acoustic phonons.32 The modified Klemens–Hart–Aggarwal–Lax phonon decay model is the simplest approach to describing anharmonic decay, in which two (three phonon process) and/or three (four phonon process) acoustic phonons are generated as the result of the optical phonon decay (Fig. S1(c)†).12 During the symmetrical three phonon decay, an optical phonon decay into two phonons with equal energies and opposite moments, whereas an optical phonon decay into three phonons with uneven energies with the same moments in the asymmetric three phonon decay process.33 According to the modified Klemens–Hart–Aggarwal–Lax phonon decay model, the frequency and FWHM can be fitted by the following eqn (4) & (5), as shown in Fig. S6.†| |
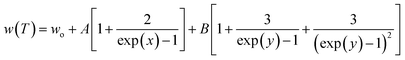 | (4) |
| |
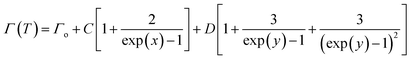 | (5) |
where x = hwo/4πkBT, and y = hwo/6πkBT; wo, and Γo, are the bare harmonic frequency, and bare harmonic FWHM at T = 0 K, respectively, and the coefficients A, B, C, and D are anharmonic constants. In the above equations, the first, second and third terms represent the bare harmonic contribution, three-phonon anharmonic contribution and four-phonon anharmonic contribution, respectively. The fitting indicates that the symmetrical three-phonon scattering process dominates the temperature-dependent frequency and FWHM in both directions. The symmetrical three-phonon process is most effective below 620 K, and contributions from the four-phonon scattering process become more prominent as the temperature increases.12 Table 2 presents the fit parameters. The parallel direction shows larger values of the phonon anharmonic constants A and C, whereas the perpendicular direction shows smaller values. These findings show that phonon anisotropy causes the directional variation in thermal conductivity. This conclusion is supported by the results regarding the phonon lifetimes as well. The aforementioned results provide even more evidence that the three-phonon process is at the core of the anharmonicity of phonon in p-type SBT and n-type BTS compounds. The temperature-dependent Raman peak intensities must be considered along with peak positions and peak FWHMs to understand the phonon anharmonicity (Fig. S7†).20 It can be seen from this figure that the higher intensity values in the perpendicular direction lead to stronger lattice vibrations. The variation in the intensity as a function of temperature indicates the anharmonic phonon–phonon interactions.
Table 2 List of the calculated phonon anharmonic parameters of p-type SBT and n-type BTS from the fits by using eqn (4) and (5)
| |
Parallel (‖) |
Perpendicular (⊥) |
| E2g |
A11g |
A21g |
E2g |
A11g |
A21g |
| p-Type SBT |
| wo (cm−1) |
126.77 |
68.29 |
165.34 |
126.03 |
71.14 |
164.44 |
| Γo (cm−1) |
3.32 |
10.57 |
0.42 |
2.59 |
9.44 |
14.72 |
| A (cm−1) |
4.32 |
0.88 |
5.92 |
3.91 |
2.26 |
5.64 |
| C (cm−1) |
3.81 |
1.50 |
8.70 |
3.39 |
0.77 |
5.88 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| n-Type BTS |
| wo (cm−1) |
106.72 |
77.66 |
143.25 |
105.94 |
71.88 |
143.88 |
| Γo (cm−1) |
4.51 |
16.20 |
18.98 |
3.12 |
12.87 |
4.75 |
| A (cm−1) |
3.15 |
5.91 |
4.58 |
2.12 |
3.51 |
6.13 |
| C (cm−1) |
2.34 |
3.32 |
7.11 |
3.02 |
2.87 |
2.74 |
4. Conclusions
In conclusion, the Raman spectroscopy as a function of temperature and laser power is applied for the estimation of optical thermal conductivity and the phonon lifetime of both p-type Sb1.5Bi0.5Te3 (SBT) and n-type Bi2Te2.7Se0.3 (BTS) bulk materials prepared by the melting-quenching-hot press process. Raman spectra are taken in both directions: parallel and perpendicular to the pressing axis. The anisotropy in experimental phonon thermal conductivity is correlated with estimated optical thermal conductivity and phonon lifetime. The temperature-dependent frequencies and FWHMs are fitted with a symmetric three-phonon scattering model. It is found that the anharmonic constants values vary for different phonon modes. The study found that in strong anharmonicity, the contribution of the higher energy phonon modes E2g and A21g is significant. These findings have provided a better understanding of the anisotropy in thermal properties. This study, in addition to providing more clarity on the phonon anharmonicity in both directions, showed a correlation between the anisotropic thermal conductivity and the phonon anharmonicity.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are grateful for the funding from CSIR India, which received grant no: SP/CSIR-19-0004. Also, we recognize the University Grants Commission, Ministry of Human Resource Development (Ref: F.530/26/CAS-VI/2018(SAP-I)), India, for measuring thermal conductivity.
References
- M. Zebarjadi, Appl. Phys. Lett., 2015, 106, 203506 CrossRef.
- T. Caillat, J.-P. Fleurial and A. Borshchevsky, AIP Conf. Proc., 1998, 140, 1647 CrossRef.
- Z. Chan and J. H. Lim, AIP Conf. Proc., 2020, 2233, 020003 CrossRef.
- R. S. C. Bose, V. Sheoran, P. S. H. Vaishnavi, D. S. Prem, S. Chakravarty, R. Raman, D. A. Babu, P. Saharan, S. Nair and J. Ram, J. Alloys Compd., 2021, 859, 157828 CrossRef CAS.
- R. S. C. Bose, K. M. Dilip, P. Mele and K. Ramesh, J. Phys. D: Appl. Phys., 2021, 54, 235503 CrossRef CAS.
- S. K. Mishra, S. Satpathy and O. Jepsen, J. Phys.: Condens. Matter, 1997, 9, 461 CrossRef CAS.
- M. Wuttig and N. Yamada, Nat. Mater., 2007, 6, 824 CrossRef CAS PubMed.
- R. R. Urkude and U. A. Palikundwar, AIP Conf. Proc., 2016, 1728, 1 CrossRef.
- Z. Dong, H. Xu, F. Liang, C. Luo, C. Wang, Z. Y. Cao, X. J. Chen, J. Zhang and X. Wu, Molecules, 2019, 24, 88 CrossRef PubMed.
- Y. Kim, X. Chen, Z. Wang, J. Shi, I. Miotkowski, Y. P. Chen, P. A. Sharma, A. L. Lima Sharma, M. A. Hekmaty, Z. Jiang and D. Smirnov, Appl. Phys. Lett., 2012, 100, 071907 CrossRef.
- F. Zhou, Y. Zhao, W. Zhou and D. Tang, AIP Adv., 2018, 8, 125330 CrossRef.
- L. C. Chen, Z. Y. Cao, H. Yu, B. Bin Jiang, L. Su, X. Shi, L. D. Chen and X. J. Chen, Appl. Phys. Lett., 2018, 113, 022105 CrossRef.
- K. M. F. Shahil, M. Z. Hossain, V. Goyal and A. A. Balandin, J. Appl. Phys., 2012, 111, 054305 CrossRef.
- P. Wu, F. R. Fan, M. Hagihala, M. Kofu, K. Peng, Y. Ishikawa, S. Lee, T. Honda, M. Yonemura, K. Ikeda, T. Otomo, G. Wang, K. Nakajima, Z. Sun and T. Kamiyama, New J. Phys., 2020, 22, 083083 CrossRef CAS.
- I. Efthimiopoulos, M. Berg, A. Bande, L. Puskar, E. Ritter, W. Xu, A. Marcelli, M. Ortolani, M. Harms, J. Müller, S. Speziale, M. Koch-Müller, Y. Liu, L. D. Zhao and U. Schade, Phys. Chem. Chem. Phys., 2019, 21, 8663 RSC.
- D. Li, L. Li, D. W. Liu and J. F. Li, Phys. Status Solidi RRL, 2012, 6, 268 CrossRef CAS.
- Y. S. Wudil, M. A. Gondal, S. G. Rao and S. Kunwar, Ceram. Int., 2020, 46, 7253 CrossRef CAS.
- Y. S. Wudil, M. A. Gondal, S. G. Rao, S. Kunwar and A. Q. Alsayoud, Ceram. Int., 2020, 46, 24162 CrossRef CAS.
- W. Richter, H. Kohler and C. R. Becker, Phys. Status Solidi, 1977, 84, 619 CrossRef CAS.
- X. Gong, H. Wu, D. Yang, B. Zhang, K. Peng, H. Zou, L. Guo, X. Lu, Y. Chai, G. Wang and X. Zhou, Vib. Spectrosc., 2020, 107, 103034 CrossRef CAS.
- S. Aminorroaya-Yamini, C. Zhang, X. Wang and I. Nevirkovets, J. Phys. D: Appl. Phys., 2012, 45, 125301 CrossRef.
- H. Wang, C. Gao and X. Yan, IEEE Electron Device Lett., 2020, 41, 1504 CAS.
- F. J. Ochoa-Estrella, A. Vera-Marquina, I. Mejia, A. L. Leal-Cruz, M. I. Pintor-Monroy and M. Quevedo-López, J. Mater. Sci.: Mater. Electron., 2018, 29, 20623 CrossRef CAS.
- C. D. Wagner, J. Electron Spectrosc. Relat. Phenom., 1983, 32, 99 CrossRef CAS.
- Z. Tian, K. Esfarjani, J. Shiomi, A. S. Henry and G. Chen, Appl. Phys. Lett., 2011, 99, 1 Search PubMed.
- S. Sahoo, A. P. S. Gaur, M. Ahmadi, M. J. F. Guinel and R. S. Katiyar, J. Phys. Chem. C, 2013, 117, 9042 CrossRef CAS.
- H. N. Liu, X. Cong, M. L. Lin and P. H. Tan, Carbon, 2019, 152, 451 CrossRef CAS.
- R. Guo, X. Wang, Y. Kuang and B. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1 Search PubMed.
- R. L. González-Romero, A. Antonelli and J. J. Meléndez, Phys. Chem. Chem. Phys., 2017, 19, 12804 RSC.
- A. M. Hofmeister, Science, 1999, 283, 1699 CrossRef CAS PubMed.
- J. Pandey, S. Mukherjee, D. Rawat, S. Athar, K. S. Rana, R. C. Mallik and A. Soni, ACS Appl. Energy Mater., 2020, 3, 2175 CrossRef CAS.
- T. Tadano and S. Tsuneyuki, AIP Conf. Proc., 2015, 1702, 090063 CrossRef.
- A. Cammarata, RSC Adv., 2019, 9, 37491 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra04886d |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
K. Ramesh
and
K. Ramesh *
*
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m h and these are constructed of anisotropic layers, in which a five mono-atomic layer sequence along the c-axis, the –A(1)–B–A(2)–B–A(1)– is a known quintuple (Fig. S1(a)†).8 In this instance, A could be either Te or Se and B could be either Bi or Sb. The lamellar structure and the weak van der Waal attractions between quintuple layers are caused for the anisotropy and hence, anisotropic properties along and across the layers. As reported, the σ and κ show a high anisotropy, while the S is almost isotropic, resulting in anisotropic power factor (defined by PF = S2σ) and zT.4
m h and these are constructed of anisotropic layers, in which a five mono-atomic layer sequence along the c-axis, the –A(1)–B–A(2)–B–A(1)– is a known quintuple (Fig. S1(a)†).8 In this instance, A could be either Te or Se and B could be either Bi or Sb. The lamellar structure and the weak van der Waal attractions between quintuple layers are caused for the anisotropy and hence, anisotropic properties along and across the layers. As reported, the σ and κ show a high anisotropy, while the S is almost isotropic, resulting in anisotropic power factor (defined by PF = S2σ) and zT.4
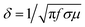 , where f is the laser light frequency (Hz), σ is the electrical conductivity (S m−1), and μ is the magnetic permeability. The estimated penetration depths were ∼75 nm and ∼80 nm for p-type SBT and n-type BTS, respectively. The peaks obtained in Raman spectra were fitted with the Lorentzian function to extract the frequency, FWHM and Intensity. Hereafter, the XRD, Raman and thermal conductivity characterizations on pellet perpendicular and parallel to the pressing axis (PA) were labelled by symbols of ⊥ and ‖, respectively.
, where f is the laser light frequency (Hz), σ is the electrical conductivity (S m−1), and μ is the magnetic permeability. The estimated penetration depths were ∼75 nm and ∼80 nm for p-type SBT and n-type BTS, respectively. The peaks obtained in Raman spectra were fitted with the Lorentzian function to extract the frequency, FWHM and Intensity. Hereafter, the XRD, Raman and thermal conductivity characterizations on pellet perpendicular and parallel to the pressing axis (PA) were labelled by symbols of ⊥ and ‖, respectively.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m h.4,5 Impurity peaks with very low intensity (>2%) are found in both XRDs, might be due to the surface oxidation. These peaks are assigned to Sb2O3 in p-type SBT and Bi2O3 in n-type BTS. Both ‖ to PA & ⊥ to PA have similar XRD patterns. However, the intensity of (0015) peak differs, indicating that the hot-press sintering exhibit a significant anisotropy of grain orientation without altering the crystal structure. Lotgering factor (F) is determined to confirm the anisotropic orientation from XRD patterns of both ‖ to PA and ⊥ to PA.4 The higher F values (0.4 for p-type SBT and 0.2 for n-type BTS) are observed in case of parallel direction while lower F values (0.06 for both p-type SBT and n-type BTS) in the perpendicular direction. The high intensity of the (00l) peaks in the ‖ to PA, reveals that the compound's ab-orientation is in the perpendicular direction to the pressing axis. Therefore, the p-type SBT and n-type BTS may have the anisotropic physical transport properties. This prompted us to use Raman spectra to investigate anisotropic thermal properties.
m h.4,5 Impurity peaks with very low intensity (>2%) are found in both XRDs, might be due to the surface oxidation. These peaks are assigned to Sb2O3 in p-type SBT and Bi2O3 in n-type BTS. Both ‖ to PA & ⊥ to PA have similar XRD patterns. However, the intensity of (0015) peak differs, indicating that the hot-press sintering exhibit a significant anisotropy of grain orientation without altering the crystal structure. Lotgering factor (F) is determined to confirm the anisotropic orientation from XRD patterns of both ‖ to PA and ⊥ to PA.4 The higher F values (0.4 for p-type SBT and 0.2 for n-type BTS) are observed in case of parallel direction while lower F values (0.06 for both p-type SBT and n-type BTS) in the perpendicular direction. The high intensity of the (00l) peaks in the ‖ to PA, reveals that the compound's ab-orientation is in the perpendicular direction to the pressing axis. Therefore, the p-type SBT and n-type BTS may have the anisotropic physical transport properties. This prompted us to use Raman spectra to investigate anisotropic thermal properties.


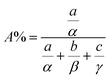 with corresponding atomic sensitivity factors (α, β and γ); where A% is the atomic percentage, a, b and c are the area under the ground state peaks of each element.23,24 The Sb
with corresponding atomic sensitivity factors (α, β and γ); where A% is the atomic percentage, a, b and c are the area under the ground state peaks of each element.23,24 The Sb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi
Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te atomic ratio in p-type SBT is obtained as 1.49
Te atomic ratio in p-type SBT is obtained as 1.49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50
0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.01 while the Bi
3.01 while the Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te
Te![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Se atomic ration in n-type BTS is 2.02
Se atomic ration in n-type BTS is 2.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.70
2.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.28. The obtained shoulder peaks at higher binding energy may indicate the surface oxidation, consistent with the XRD analysis.
0.28. The obtained shoulder peaks at higher binding energy may indicate the surface oxidation, consistent with the XRD analysis.
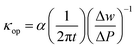
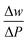 is the variation in the frequency of phonon with laser power, w is the frequency of Raman mode, and P is the laser power. α is the slope of the linear plot of Raman shifts and temperature (Fig. 6(a) and (e)) while
is the variation in the frequency of phonon with laser power, w is the frequency of Raman mode, and P is the laser power. α is the slope of the linear plot of Raman shifts and temperature (Fig. 6(a) and (e)) while 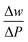 is the slope of the linear plot of Raman shifts and laser power (Fig. 6(b) and (f)). The frequency of all three Raman active modes shows systematic redshifts with increasing temperature and laser power. In general, the temperature-dependent frequency is mainly dependent on two factors: (1) quasiharmonic lattice thermal expansion (Δwthermal) and (2) anharmonic contribution (three-phonon and four-phonon scattering processes) (Δwan), w(T) = Δwthermal + Δwan.27 It can be found that the |α| value in parallel direction is larger than that of perpendicular direction, indicates that stronger anharmonicity in the parallel direction. The α is directly proportional to the volume thermal coefficient (γ = (dln
is the slope of the linear plot of Raman shifts and laser power (Fig. 6(b) and (f)). The frequency of all three Raman active modes shows systematic redshifts with increasing temperature and laser power. In general, the temperature-dependent frequency is mainly dependent on two factors: (1) quasiharmonic lattice thermal expansion (Δwthermal) and (2) anharmonic contribution (three-phonon and four-phonon scattering processes) (Δwan), w(T) = Δwthermal + Δwan.27 It can be found that the |α| value in parallel direction is larger than that of perpendicular direction, indicates that stronger anharmonicity in the parallel direction. The α is directly proportional to the volume thermal coefficient (γ = (dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V/dT)p) and Gruneisen parameter (β = −(dln
V/dT)p) and Gruneisen parameter (β = −(dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w/dln
w/dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V)T), α = γ × β.20 Generally, the larger the α, the larger the β, leading to a stronger anharmonic effect. It is reported that 40% of the temperature-dependent total phonon frequency change occurs through the thermal expansion contribution in p-type SBT and n-type BTS.13 This indicates that the observed temperature-dependent frequency can be well modelled by incorporating anharmonic components. Thus, comparing with the in-plane modes, the out-of-plane modes show larger α in both directions, reveals their important role in directional thermal transport.
V)T), α = γ × β.20 Generally, the larger the α, the larger the β, leading to a stronger anharmonic effect. It is reported that 40% of the temperature-dependent total phonon frequency change occurs through the thermal expansion contribution in p-type SBT and n-type BTS.13 This indicates that the observed temperature-dependent frequency can be well modelled by incorporating anharmonic components. Thus, comparing with the in-plane modes, the out-of-plane modes show larger α in both directions, reveals their important role in directional thermal transport.
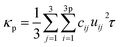
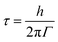
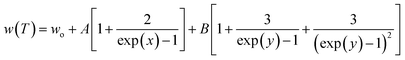
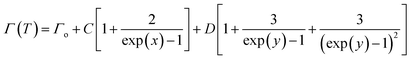
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)



