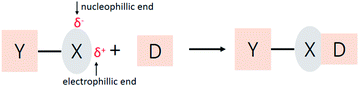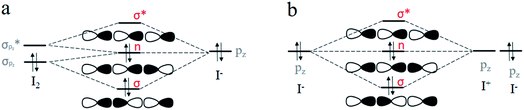Open Access Article
Open Access ArticleRevisiting the covalent nature of halogen bonding: a polarized three-center four-electron bond†
Dan Lia,
Tao Xiaa,
Wanwan Fenga and
Longjiu Cheng *ab
*ab
aDepartment of Chemistry, Anhui University, Hefei, 230601, PR China. E-mail: clj@ustc.edu
bKey Laboratory of Structure and Functional Regulation of Hybrid Materials (Anhui University), Ministry of Education, Hefei, 230601, PR China
First published on 6th October 2021
Abstract
As an important intermolecular interaction, halogen bonding has been studied extensively, but its nature still suffers from controversy without one uniform essence. Electrostatics, charge transfer, polarization and dispersion are emphasized, but the covalent nature is usually overlooked except for the strong halogen bonding species I3−, which is widely accepted as a result of a three-center four-electron (3c-4e) interaction. In our study, the potential energy surface of I3− has been evaluated to explore the dissociation from I3− to I2⋯I−. We found that different from an equivalent 3c-4e bond in I3−, I2⋯I− can be rationalized by a polarized one. In addition, when the orbitals are polarized, it is exactly what traditional charge transfer or the popular σ-hole picture describes. I3− can be described by the Lewis theory model with the middle I+ cation serving as the Lewis acid and two terminal I− anions acting as Lewis base. Therefore, we further extended this model to a series of I-containing species with chemical composition of L–I+–L, F−–I+–L and H3P–I+–L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) to explore the nature of halogen bonding. When the forces of two bases around I+ are the same, it corresponds to an equivalent 3c-4e bond, such as I3−. Otherwise, it is a polarized multicenter bond, such as I2⋯I−. This work gives a new insight into the nature of halogen bonding compounds: besides the well-known I3−, the nature of the other species is also a multicenter bond, existing as equivalent and polarized 3c-4e bonds, respectively.
1. Introduction
Halogen atoms are usually considered as species of high electron density owing to their high electronegativity and interaction with electron-deficient groups. In addition, halogen-containing compounds can also interact with electron-rich species, which is known as halogen bonding.1–6 The ability of halogen atoms to attractively interact with electron donors was recognized as early as 1814, when the adduct reaction between iodine and ammonia was observed.7 Decades later in 1863, the complex was first purified and identified as a NH3⋯I2 adduct by Guthrie.8 Similar adducts involving bromine and chlorine were obtainedshortly after.9 Until now, halogen bonding has been under active investigation.10–21 It plays an essential role in controlling the construction of supramolecular complexes in solid,2,3,22,23 liquid,24–27 and gas phases.28 Besides, halogen bonding has led to a range of applications in the biological field,3,29 such as drug design30 and protein–ligand complexation.31Halogen bonding has a general form of Y–X⋯D5,32 (Scheme 1), where X is a halogen atom, and it functions as the electrophilic species (halogen bond donor), and D is a donor of electron density (halogen bond acceptor). The distance of X⋯D is shorter than the sum of their van der Waals radii, and the YX bond length is slightly elongated than the YX monomer, and the Y–X⋯D angle is approximately linear.2–4
Though studied extensively, the exact nature of halogen bonding is still disputed. Classically, the chemical nature of the interaction was explained as charge transfer by Mulliken in 1950.33 More precisely, in a charge transfer picture, halogen bonding is described as a donation from the donor lone pair into the σ* antibonding orbital.34–40 Some computational studies have found a good correlation between the degree of charge transfer and the halogen bonding strength.40,41 Besides, a more widespread model of this kind of interaction is based on the electrostatic effect. The electron density in a halogen atom is anisotropically distributed when the atom is covalently bonded to other atoms, resulting in regions with positive potential at the terminus of the YX bond (δ+ in Scheme 1), which is introduced as a “σ-hole” in 2007 based on computational studies.42,43 The σ-hole perspective states that halogen bonding is an electrostatic attraction between the σ-hole and the negative potential of a Lewis base.2–4 This concept is frequently used, but pure electrostatic interactions have been questioned.44,45 Huber et al. have found that in case of CX3I (X = F, Cl, Br and I), the σ-hole trend is exactly opposite to the trend in binding energy.46 Furthermore, polarization and dispersion contributions cannot be overlooked.2,3,47,48 Energy decomposition analysis is widely used by theoretical methods to analyze the components of different interactions.32,41,49 Overall, the nature depends upon the individual interacting species,3 and no model can explain all observed features.
Halogen bonding is comparable in interaction energy (from 5 to 200 kJ mol−1) to the well-known hydrogen bonding,50–54 and I3− is the strongest.4,5,55 It is widely accepted that I3− can be considered as the result of a three-center four-electron (3c-4e) interaction.56–61 The 3c-4e bonding pattern for I3− can be rationalized by an MO picture in Fig. 1a. Three MOs are bonding (σ), non-bonding (n) and antibonding (σ*) orbitals formed primarily by σpz and 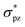 orbitals of I2 and pz orbital of I−. I− lone pair contributes two electrons, and I–I bonding pair contributes another two, for a total of 4e. These two pairs of electrons occupy σ and n orbitals, leaving the σ* orbital vacant. A similar case is the short strong hydrogen bond, represented by [F–H–F]−, which can also be considered as an equivalent multicenter interaction, and was recently verified experimentally by Tokmakoff et al.62
orbitals of I2 and pz orbital of I−. I− lone pair contributes two electrons, and I–I bonding pair contributes another two, for a total of 4e. These two pairs of electrons occupy σ and n orbitals, leaving the σ* orbital vacant. A similar case is the short strong hydrogen bond, represented by [F–H–F]−, which can also be considered as an equivalent multicenter interaction, and was recently verified experimentally by Tokmakoff et al.62
In our opinion, as shown in Fig. 1b, I3− can be described by the Lewis theory model with the middle I+ cation serving as the Lewis acid and two terminal I− anions acting as the Lewis base, each ion providing one pz orbital to form bonding (σ), non-bonding (n) and antibonding (σ*) orbitals. Similarly, 4e occupy σ and n orbitals. We speculate that its nature of an equivalent 3c-4e bond is ascribed to the same forces coming from two terminal I−. Inspired by this, in this study, we performed theoretical studies on species composed of I+ and two bases (L–I+–L, F−–I+–L and H3P–I+–L, where L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) to explore the nature of the halogen bonding. We found that besides I3−, other halogen bond compounds can also be well explained by multicenter bonds by analyzing their structural and electronic properties. Thus, we propose a new perspective on halogen bonding: its nature should be a multicenter bond, corresponding to equivalent and polarized 3c-4e bonds, respectively.
2. Computational methods
To confirm the computational method for our system, we performed calculations under several density functional theory (DFT) and the CCSD(T) theoretical levels to compare the values of the bond length, frequency and interaction energy with the corresponding experimental results for I2. As depicted in Table 1, the I–I bond length at the M06-2X63/def2tzvpp level (2.652 Å) was close to that at the CCSD(T)/dhf-QZVP level (2.659 Å), and they were slightly shorter than the experimental value (2.666 Å).64 Compared with other methods, M06-2X/def2-TZVPP was considered to be appropriate, and our calculations on halogen bonding in this study were all given at the M06-2X/def2tzvpp level.| Theoretical level | RI–I (Å) | FreqI–I (cm−1) | Eba (kcal mol−1) |
|---|---|---|---|
| a Binding energy of I2 is defined based on the calculation of Eb = E(I2) − 2E(I), where E(I2) or E(I) suggests the corresponding single point energies.b Refer to the ref. 64. | |||
| Experimentb | 2.666 | 215.5 | −35.9 |
| CCSD(T)/dhf-QZVP | 2.659 | 224.4 | −44.9 |
| B3LYP-D3(BJ)/dhf-QZVP | 2.694 | 213.5 | −46.3 |
| B3LYP-D3(BJ)/def2-TZVPP | 2.688 | 214.1 | −46.5 |
| M06-2X/dhf-QZVP | 2.651 | 233.3 | −33.7 |
| M06-2X/def2-TZVPP | 2.652 | 232.5 | −33.8 |
All the geometric structures were fully relaxed at the M06-2X/def2tzvpp level of theory. Frequencies of all the halogen bonding compounds were all checked to ensure that they were true local minimums. All bonding energies were calculated including basis set superposition error (BSSE) corrections65 and were referenced to the optimized geometries of the fragments that compose the molecule.
Noncovalent interactions (NCI)66 indexes, which is an approach to detect the strength of the weak interactions based on the electron density and its derivatives was selected. The results are shown in the scatter plots of the reduced density gradient (RDG) versus the electron density (ρ) multiplied by the sign of λ2 (sign(λ2)ρ). The low-density regime represents non-covalent/weak interactions. Negative values (sign(λ2)ρ < 0) indicate an attractive interaction, while positive values (sign(λ2)ρ > 0) are indicative of a steric repulsion. Spike mentioned in this study corresponds to the value of sign(λ2)ρ of interaction. In general, more negative values of NCI spikes indicate a stronger interaction between the fragments.
Chemical bonding analysis was carried out using the adaptive natural density partitioning (AdNDP)67 method. It is a tool that provides the partitioning of electron density. It allows an electron pair to be delocalized over n atoms with n ranging from one to the total number of atoms in the whole molecule. This method accepts only those bonding elements whose occupation numbers (ON) exceed the specified threshold values, which are usually chosen to be close to 2.00|e|.
All DFT calculations and natural bond orbital (NBO)68,69 analysis were performed on the Gaussian 16 package.70 Wiberg bond index (WBI)71 and NCI analysis were performed by the Multiwfn 3.4 program.72 Molecular visualization was performed using the MOLEKEL 5.4 software.73
3. Results and discussion
3.1 Structural and electronic properties of I3−
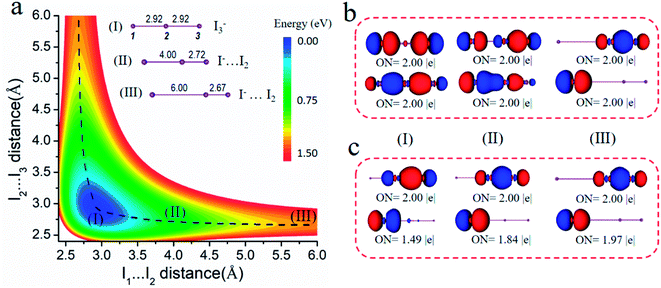
It is well known that I2 can react with I− easily in a solution, forming the strong halogen bonding complex I3−. As shown in Fig. 2a, we scanned the energy of I3− by changing the distance of I(1)⋯I(2) and I(2)⋯I(3) from 2.4 Å to 6.0 Å. It is clear that the most stable structure is a linear molecule with two equal I⋯I length of 2.92 Å (structure I). The black dash line can be seen as the dissociation pathway of I3− to I2⋯I−, and we chose structures II and III with the distance of I(1)⋯I(2) of 4.00 and 6.00 Å, respectively, to investigate the changes in the chemical bonding. Fig. 2b gives the 3c-4e chemical bonding patterns of structures I, II and III by the AdNDP method.For structure I, there are two symmetric 3c-2e bonds with idealized occupation numbers 2.00|e|, corresponding to bonding and non-bonding bonds composed of three 5p orbitals of I atoms. When the length of I(1)⋯I(2) is fixed at 4.00 Å, the I(2)⋯I(3) distance is shortened to 2.73 Å (structure II). Different from the symmetric 3c-2e bonds for structure I, more electrons concentrate on I(1) and I(2) in the bonding orbital, while more electrons focus on I(2) and I(3) in the non-bonding orbital. Therefore, I2⋯I− can also be explained by the 3c-4e bond model, just like I3−, and the difference is that the 3c-4e bond is polarized. Furthermore, when the I(1)⋯I(2) distance is further elongated to 6.00 Å (structure III), the 3c-4e bonds is totally polarized, corresponding to one lone pair on I(1) and one 2c-2e σ orbital between I(2) and I(3). Taken together, we can obtain that during dissociation, electrons of the 3c-2e bonding orbital in I3− undergoes a shift to I(1)⋯I(2) and finally focus on I(1), while that of 3c-2e non-bonding orbitals finally concentrate on the σ bond between I(2) and I(3). Therefore, we can conclude that besides I3−, interactions in other products during dissociation should also be ascribed to multicenter bonds.
Traditionally, halogen bonding complexes should be explained as a charge transfer from the donor lone pair of I− to the σ* orbital of I2 or electrostatic attraction between I− and σ-hole of I2. For comparison, Fig. 2c gives the AdNDP bonding orbitals of structures I, II and III based on the I2 + I− model (2c-2e/1c-2e). In structure III, I− is far enough with I2 molecule, so it is a typical compound with a weak halogen bond. In this situation, the 3c-4e model is very similar to the 2c-2e/1c-2e model in the bonding picture. In structure II, the halogen bond [I(1)⋯I(2)] is strengthened, and the non-Lewis component of the bonding orbitals according to the I2 + I− model increases, where the ON value of 1c-2e orbital decreases to 1.84|e|. The lower ON value suggests that electron transfer from I− to I2 should be considered. This phenomenon becomes more obvious for the equilibrium structure (I), the ON value of non-bonding orbital being quite small (1.49|e|). Therefore, the polarized 3c-4e bond model is consistent with the traditional 2c-2e/1c-2e model for the cases with a weak halogen bond (structure III), whereas it is more reasonable to describe the cases with a strong halogen bond (structures I and II).
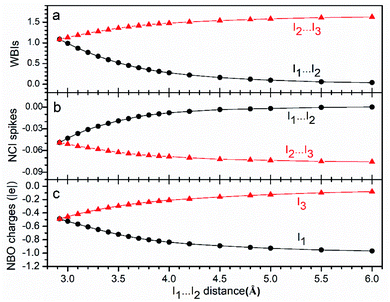
To further confirm the essence of the multicenter bond discussed above, other properties corresponding to products obtained from the dissociation of I3− were studied, as shown in Fig. 3. The bond order (Fig. 3a) of I(1)⋯I(2) decreases with the increase in the I(1)⋯I(2) distance, and gradually approaches to zero. Moreover, those of I(2)⋯I(3) increase gradually and finally reach 1.5. Besides, the spike values of the NCI analysis (Fig. 3b) indicate that the interaction between I(2) and I(3) becomes stronger during dissociations with more negative values, and NBO charges (Fig. 3c) show that most charges finally concentrate on I(1). All the results are in good accordance with the AdNDP results discussed above, and suggest the same conclusion: interaction between I(1) and I(2) being weakened, whereas that between I(2) and I(3) being strengthened during dissociation, corresponding to the symmetric 3c-4e bond changing to a polarized 3c-4e one.
3.2 Structural and electronic properties of L–I+–L
I3− can be described by the Lewis theory model with the middle I+ cation serving as the Lewis acid and two terminal I− anions acting as the Lewis base. Inspired by this, a series of electron donors L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) were chosen to interact with I+ to explore whether multicenter bonding can also be applied to other equivalent halogen bonding compounds (L–I+–L). Binding energies of I+ with different bases were calculated (Table 2, Eb = E(I+–L) − E(I+) − E(L)), spanning over a wide range, from −16.25 to −252.40 kcal mol−1. Based on the binding energy, it is clear that the strength of the Lewis base decreases in the order: OH− > F− > Cl− > Br− > I− > PH3 > NH3 > H2S > HI > H2O > HBr > HCl.| Bases | OH− | F− | Cl− | Br− | I− | PH3 |
| Eb (kcal mol−1) | −252.40 | −227.47 | −206.16 | −201.61 | −201.29 | −89.88 |
| Bases | NH3 | H2S | HI | H2O | HBr | HCl |
| Eb (kcal mol−1) | −64.66 | −52.12 | −40.10 | −29.15 | −25.74 | −16.25 |
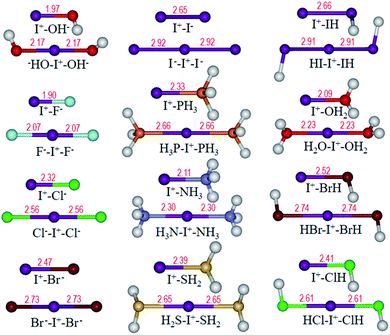
Optimized structures of I+–L and L–I+–L are shown in Fig. 4. It can be observed that all the L–I+–L angles are nearly linear with two equal I+⋯L distances, which are obviously longer than those in L–I+ monomers, similar to that in I3−. Besides, WBIs in Fig. 5 suggest that the values of bond order between I+ and L in L–I+–L complexes are less than those in the corresponding I+–L monomers, which is in accordance with the changes in the bond lengths.
 | ||
| Fig. 4 Optimized structures of L–I+ and L–I+–L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) complexes. Bond length (Å) is labelled in red. | ||
 | ||
| Fig. 5 Values of WBIs of L–I+–L and I+–L complexes with different bases (OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) as the electron donors. | ||
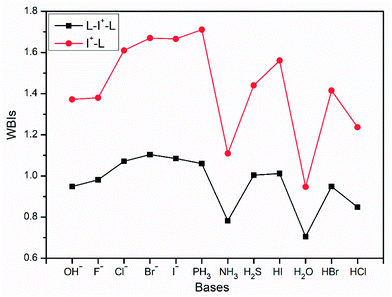
Furthermore, it can be easily observed from the AdNDP analysis (Fig. 6) that all complexes can be well described by two symmetric bonding and non-bonding orbitals with reliable occupation numbers (1.93–2.00|e|), just like I3−. Therefore, as long as two forces around the central I+ are the same, it corresponds to an equivalent 3c-4e bond interaction.
 | ||
| Fig. 6 Bonding (right) and non-bonding (left) 3c-2e orbitals of L–I+–L complexes by the AdNDP analysis. | ||
3.3 Structural and electronic properties of F−–I+–L
Frequently, halogen bonding compounds do not own a perfect structural symmetry. Thus, we further extended our study to more general species. Electron donors on one side of I+ was fixed to F−, and the other side was different bases, as shown in Table 2, forming halogen boding complexes of F−–I+–L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl). The optimized structures (Fig. 7) show that the angles of F⋯I⋯L approach to 180°, and F⋯I distances are all longer than that in the FI monomer of 1.90 Å (Fig. 7) at the same theoretical level.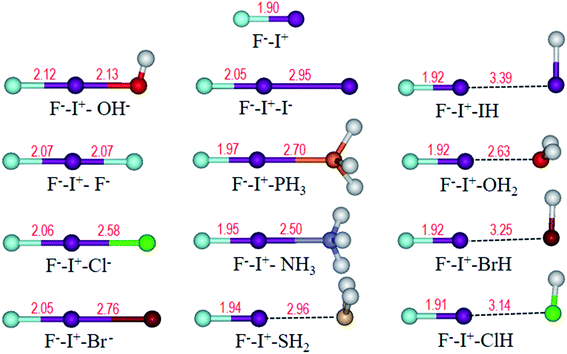 | ||
| Fig. 7 Optimized structures of F−–I+ and F−–I+–L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) complexes. Bond length (Å) is labelled in red. | ||
As expected, the chemical bonding analysis (Fig. 8) indicated that there are two 3c-2e orbitals for each species with idealized occupation numbers (1.95–2.00|e|). In case of OH−, F−, Cl− and Br− as electron donors, all bonding and non-bonding orbitals are evident and in good symmetry. When the electron donors change to I−, PH3 and NH3, it is clear that 3c-4e orbitals are polarized, just like those in I2⋯I−, bonding orbitals being mainly focused on the I+–L segment, while non-bonding orbitals concentrating on the other terminals. In terms of the rest of the complexes, owing to their weak binding ability with I+, the polarization becomes clearer. Two 3c-2e orbitals of each are totally polarized to one σ bond between F and I and one lone pair electrons at the other end. In addition, NCI spikes (Fig. 9a) are in good agreement with the AdNDP results. As the bases change from OH− to HCl, interaction between F and I become stronger with more negative values, while those between I and L become weaker. WBIs in Fig. 9b further support the conclusion; when the binding ability of bases is strong enough (OH−, F−, Cl−, Br−, I−), values of the bond order of F−–I+ are close to those of I+–L. However, there are big gaps for weak bases, and electrons mainly concentrate on F−–I+. Therefore, we can infer that the multicenter bond can be extended to rationalize more general halogen bonding compounds.
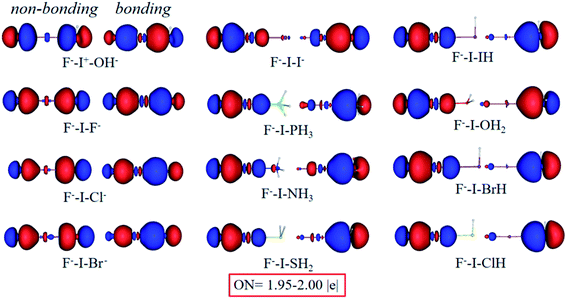 | ||
| Fig. 8 Bonding (right) and non-bonding (left) 3c-2e orbitals of F−–I+–L complexes by the AdNDP analysis. | ||
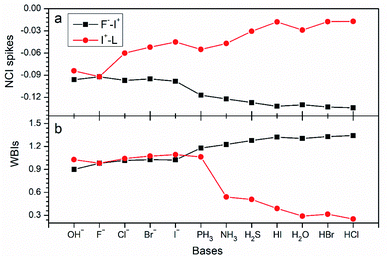 | ||
| Fig. 9 Values of (a) NCI spikes and (b) WBIs of F−–I+ and I+–L in F−–I+–L complexes with different bases (OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) as the electron donors. | ||
3.4 Structural and electronic properties of H3P–I+–L
Finally, we fixed the medium base PH3 to investigate the halogen bonding property with various bases: H3P–I+–L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl). Similarly, the optimized structures (Fig. 10) show that two bases interact with I+ at 180° angles. Compared with the P–I bond length of 2.33 Å in the H3P–I+ monomer (Fig. 10), P⋯I distances are elongated when bonding to other electron donors and vary within a wide range from 2.35 to 3.20 Å.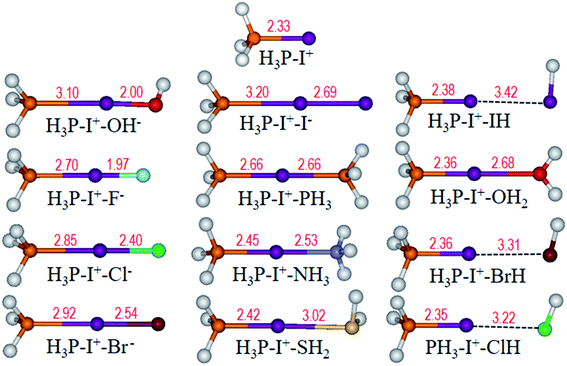 | ||
| Fig. 10 Optimized structures of H3P–I+ and H3P–I+–L (L = OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) complexes. Bond length (Å) is labelled in red. | ||
Chemical bonding analysis with two 3c-2e orbitals for each are depicted in Fig. 11. Differently from the F−–I+–L complexes in Fig. 8, because OH−, F−, Cl− and I− are stronger bases than PH3, orbitals of these species are directly polarized, and more σ character focus on the I+–L segments in the bonding orbitals, whereas the non-bonding orbitals serve as the lone pair electrons. Symmetric bonding and non-bonding orbitals emerge when I+ interacts with two equal PH3 groups. When the bases are further weakened (NH3, SH2, HI, H2O, HBr and HCl), the orbitals are polarized again. Differently from the first four strong groups (OH−, F−, Cl− and I−) as bases, more electrons concentrating on the H3P–I+ segments and finally act as 2c-2e σ bonds in the 3c-2e non-bonding orbitals. Moreover, in the 3c-2e bonding orbitals, more electrons focus on the I+–L parts and finally serve as the lone pair electrons. NCI and bond order analysis in Fig. 12 show that stronger interactions (more negative values in spikes and more positive values in WBIs) located on the I+–L segments in case of OH–, F–, Cl– and I–, but when it comes to NH3, SH2, HI, H2O, HBr and HCl, stronger interactions transfer to the P–I+ segments, following the same trend with the AdNDP methods. Therefore, the multicenter bond is further illustrated to be capable to be applied to more halogen bonding compounds.
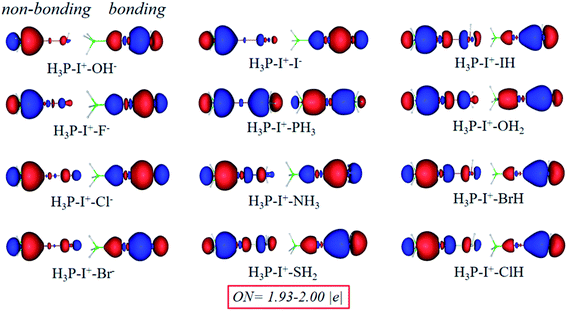 | ||
| Fig. 11 Bonding (right) and non-bonding (left) 3c-2e orbitals of PH3–I+–L complexes by the AdNDP analysis. | ||
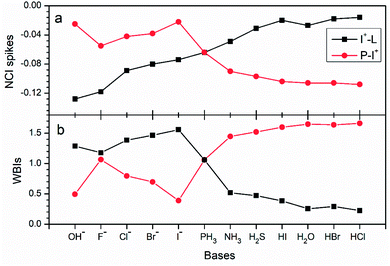 | ||
| Fig. 12 Values of (a) NCI spikes and (b) WBIs of I+–L and P–I+ in H3P–I+–L complexes with different bases (OH−, F−, Cl−, Br−, I−, PH3, NH3, H2S, HI, H2O, HBr and HCl) as the electron donors. | ||
4. Conclusions
A series of complexes formed by I+ and representative electron donors as well as I3− have been examined theoretically to gain a deeper insight into the nature of halogen bonding. It can be easily observed that during the dissociation of I3−, equivalent 3c-4e bonds gradually changed to polarized orbitals, and finally served as one 2c-2e σ bond and one lone pair of electrons. We concluded that both I3− and I2⋯I− can be described by a multicenter bond, and the traditional charge transfer or σ-hole model should be incorporated into a polarized 3c-4e bond. In addition, the other I-containing complexes can also be explained by the 3c-4e bond, all of them having two 3c-2e orbitals with reliable ON values. When the forces of two bases around I+ are the same, it possesses clear bonding and non-bonding orbitals, corresponding to the equivalent 3c-4e bond. When the forces are different, it is a polarized 3c-4e bond. Thus, our study revisits the covalent nature of halogen bonding and comes to the conclusion that not only the well-known I3−, but also all halogen bonding compounds are dominant by a multicenter bond, existing equivalent and polarized 3c-4e bonds, respectively. We hope that it can be applied to explain more halogen bonding complexes.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21873001) and by the Foundation of Distinguished Young Scientists of Anhui Province.References
- C. B. Aakeroy, M. Fasulo, N. Schultheiss, J. Desper and C. Moore, J. Am. Chem. Soc., 2007, 129, 13772 CrossRef PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 CrossRef CAS PubMed.
- P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395 CrossRef CAS PubMed.
- P. Von R. Schleyer and R. West, J. Am. Chem. Soc., 1959, 81, 3164–3165 CrossRef CAS.
- M. Colin, Ann. Chim., 1814, 91, 252–272 Search PubMed.
- F. Guthrie, J. Chem. Soc., 1863, 16, 239–244 RSC.
- I. Remsen and J. Norris, Am. Chem. J., 1896, 18, 90–95 CAS.
- J. M. Guevara Vela, D. Ochoa Resendiz, M. A. Costales Castro, R. Hernández Lamoneda and Á. Martín Pendás, ChemPhysChem, 2018, 19, 2512–2517 CrossRef CAS PubMed.
- D. M. Ivanov, A. S. Novikov, I. V. Ananyev, Y. V. Kirina and V. Y. Kukushkin, Chem. Commun., 2016, 52, 5565–5568 RSC.
- A. C. Legon, Phys. Chem. Chem. Phys., 2010, 12, 7736–7747 RSC.
- C. Z. Liu, S. Koppireddi, H. Wang, D. W. Zhang and Z. T. Li, Angew. Chem., Int. Ed., 2019, 58, 226–230 CrossRef CAS PubMed.
- M. Niyas, R. Ramakrishnan, V. Vijay, E. Sebastian and M. Hariharan, J. Am. Chem. Soc., 2019, 141, 4536–4540 CrossRef CAS PubMed.
- P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- S. Scheiner, CrystEngComm, 2013, 15, 3119–3124 RSC.
- S. Scheiner, CrystEngComm, 2019, 21, 2875–2883 RSC.
- A. Vanderkooy, A. K. Gupta, T. Földes, S. Lindblad, A. Orthaber, I. Pápai and M. Erdélyi, Angew. Chem., Int. Ed. Engl., 2019, 131, 9110–9114 CrossRef.
- A. R. Voth, P. Khuu, K. Oishi and P. S. Ho, Nat. Chem., 2009, 1, 74 CrossRef CAS PubMed.
- L. Meazza, J. A. Foster, K. Fucke, P. Metrangolo, G. Resnati and J. W. Steed, Nat. Chem., 2013, 5, 42–47 CrossRef CAS PubMed.
- T. Caronna, R. Liantonio, T. A. Logothetis, P. Metrangolo, T. Pilati and G. Resnati, J. Am. Chem. Soc., 2004, 126, 4500–4501 CrossRef CAS PubMed.
- A. Farina, S. V. Meille, M. T. Messina, P. Metrangolo, G. Resnati and G. Vecchio, Angew. Chem., Int. Ed., 1999, 38, 2433–2436 CrossRef CAS PubMed.
- G. Bergamaschi, L. Lascialfari, A. Pizzi, M. I. M. Espinoza, N. Demitri, A. Milani, A. Gori and P. Metrangolo, Chem. Commun., 2018, 54, 10718–10721 RSC.
- B. Hawthorne, H. Fan-Hagenstein, E. Wood, J. Smith and T. Hanks, Int. J. Spectrosc., 2013, 2013, 216518–216527 Search PubMed.
- J. Xu, X. Liu, T. Lin, J. Huang and C. He, Macromolecules, 2005, 38, 3554–3557 CrossRef CAS.
- T. M. Beale, M. G. Chudzinski, M. G. Sarwar and M. S. Taylor, Chem. Soc. Rev., 2013, 42, 1667–1680 RSC.
- N. Cheetham and A. Pullin, Chem. Commun., 1967, 233–234 RSC.
- R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388 CrossRef CAS PubMed.
- Y. Lu, Y. Wang and W. Zhu, Phys. Chem. Chem. Phys., 2010, 12, 4543–4551 RSC.
- H. Matter, M. Nazaré, S. Güssregen, D. W. Will, H. Schreuder, A. Bauer, M. Urmann, K. Ritter, M. Wagner and V. Wehner, Angew. Chem., Int. Ed., 2009, 48, 2911–2916 CrossRef CAS PubMed.
- T. Xia, D. Li and L. Cheng, Chem. Phys., 2020, 539, 110978 CrossRef CAS.
- R. S. Mulliken, J. Am. Chem. Soc., 1950, 72, 600–608 CrossRef CAS.
- H. A. Bent, Chem. Rev., 1968, 68, 587–648 CrossRef CAS.
- D. Bulfield and S. M. Huber, Chem.–Eur. J., 2016, 22, 14434–14450 CrossRef CAS PubMed.
- O. Hassel, Science, 1970, 170, 497–502 CrossRef CAS PubMed.
- S. M. Huber, J. D. Scanlon, E. Jimenez-Izal, J. M. Ugalde and I. Infante, Phys. Chem. Chem. Phys., 2013, 15, 10350–10357 RSC.
- A. E. Reed, F. Weinhold, R. Weiss and J. Macheleid, J. Phys. Chem., 1985, 89, 2688–2694 CrossRef CAS.
- S. W. Robinson, C. L. Mustoe, N. G. White, A. Brown, A. L. Thompson, P. Kennepohl and P. D. Beer, J. Am. Chem. Soc., 2015, 137, 499–507 CrossRef CAS PubMed.
- C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput., 2014, 10, 3726–3737 CrossRef CAS PubMed.
- L. P. Wolters and F. M. Bickelhaupt, ChemistryOpen, 2012, 1, 96–105 CrossRef CAS PubMed.
- P. Politzer, P. Lane, M. C. Concha, Y. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643–650 CrossRef CAS PubMed.
- Y.-X. Lu, J.-W. Zou, Y.-H. Wang, Y.-J. Jiang and Q.-S. Yu, J. Phys. Chem. A, 2007, 111, 10781–10788 CrossRef CAS PubMed.
- K. E. Riley, J. S. Murray, P. Politzer, M. C. Concha and P. Hobza, J. Chem. Theory Comput., 2009, 5, 155–163 CrossRef CAS PubMed.
- S. M. Huber, E. Jimenez-Izal, J. M. Ugalde and I. Infante, Chem. Commun., 2012, 48, 7708–7710 RSC.
- K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2013, 15, 17742–17751 RSC.
- J. Thirman, E. Engelage, S. M. Huber and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 905–915 RSC.
- B. Pinter, N. Nagels, W. A. Herrebout and F. De Proft, Chem.–Eur. J., 2013, 19, 519–530 CrossRef CAS PubMed.
- L. J. Prins, D. N. Reinhoudt and P. Timmerman, Angew. Chem., Int. Ed., 2001, 40, 2382–2426 CrossRef CAS PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- B. Chen, I. Ivanov, M. L. Klein and M. Parrinello, Phys. Rev. Lett., 2003, 91, 215503 CrossRef PubMed.
- C. Laurence and M. Berthelot, Perspect. Drug Discov. Des., 2000, 18, 39–60 CrossRef CAS.
- C. F. Matta, J. Hernández-Trujillo, T. H. Tang and R. F. Bader, Chem.–Eur. J., 2003, 9, 1940–1951 CrossRef CAS PubMed.
- E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Angew. Chem., Int. Ed., 2000, 39, 1782–1786 CrossRef CAS.
- G. A. Landrum, N. Goldberg and R. Hoffmann, J. Chem. Soc., Dalton Trans., 1997, 3605–3613 RSC.
- M. L. Green and G. Parkin, Dalton Trans., 2016, 45, 18784–18795 RSC.
- G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448 CrossRef CAS.
- K. Sonnenberg, L. Mann, F. A. Redeker, B. Schmidt and S. Riedel, Angew. Chem., Int. Ed., 2020, 59, 5464–5493 CrossRef CAS PubMed.
- A. Y. Rogachev and R. Hoffmann, Inorg. Chem., 2013, 52, 7161–7171 CrossRef CAS PubMed.
- S. Shaik, New J. Chem., 2007, 31, 2015–2028 RSC.
- B. Dereka, Q. Yu, N. H. C. Lewis, W. B. Carpenter, J. M. Bowman and A. Tokmakoff, Science, 2021, 371, 160–164 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- K. P. Huber and G. Herzberg, Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- A. Rosa, A. W. Ehlers, E. J. Baerends, J. G. Snijders and G. t. Velde, J. Phys. Chem., 1996, 100, 5690–5696 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian, Inc., Wallingford CT: 2016.
- L. K. Harper, A. L. Shoaf and C. A. Bayse, ChemPhysChem, 2015, 16, 3886–3892 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- U. Varetto, MOLEKEL 5.4, Swiss National Supercomputing Centre, Manno, Switzerland, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra05695f |
| This journal is © The Royal Society of Chemistry 2021 |