Structural investigation of three distinct amorphous forms of Ar hydrate

Abstract

Three amorphous forms of Ar hydrate were produced using the crystalline clathrate hydrate Ar·6.5H₂O (structure II, Fd3̄m, a ≈ 17.1 Å) as a precursor and structurally characterized by a combination of isotope substitution (³⁶Ar) neutron diffraction and molecular dynamics (MD) simulations. The first form followed from the pressure-induced amorphization of the precursor at 1.5 GPa at 95 K and the second from isobaric annealing at 2 GPa and subsequent cooling back to 95 K. In analogy to amorphous ice, these amorphs are termed high-density amorphous (HDA) and very-high-density amorphous (VHDA), respectively. The third amorph (recovered amorphous, RA) was obtained when recovering VHDA to ambient pressure (at 95 K). The three amorphs have distinctly different structures. In HDA the distinction of the original two crystallographically different Ar guests is maintained as differently dense Ar–water hydration structures, which expresses itself in a split first diffraction peak in the neutron structure factor function. Relaxation of the local water structure during annealing produces a homogeneous hydration environment around Ar, which is accompanied with a densification by about 3%. Upon pressure release the homogeneous amorphous structure undergoes expansion by about 21%. Both VHDA and RA can be considered frozen solutions of immiscible Ar and water in which in average 15 and 11 water molecules, respectively, coordinate Ar out to 4 Å. The local water structures of HDA and VHDA Ar hydrates show some analogy to those of the corresponding amorphous ices, featuring H₂O molecules in 5- and 6-fold coordination with neighboring molecules. However, they are considerably less dense. Most similarity is seen between RA and low density amorphous ice (LDA), which both feature strictly 4-coordinated H₂O networks. It is inferred that, depending on the kind of clathrate structure and occupancy of cages, amorphous states produced from clathrate hydrates display variable local water structures.

---

1. Introduction

Water forms three distinct amorphous ices, which are called low- (LDA), high- (HDA), and very-high-density amorphous ice (VHDA).¹ The longest known has been LDA which can be prepared by vapor deposition or hyper-quenching liquid water below 100 K.² HDA is obtained from pressure-induced amorphization (PIA) of hexagonal ice I_h at about 1 GPa and temperatures below 140 K.³ HDA can be converted to VHDA when heating isobarically above 1 GPa (ref. 4) to about 160 K.⁵ Both HDA and VHDA are recoverable and can be studied, like LDA, at ambient pressure at low temperatures (<100 K). That the three amorphs represent distinct states is reflected in their drastically different density, which is 0.94, 1.17,³ and 1.26 g cm⁻³ for LDA, HDA, and VHDA, respectively, at ambient pressure.^5,6 Underlying the different densities is an increase in the coordination of water molecules in the amorphous hydrogen-bond networks from 4- to 5- to 6-fold. The polyamorphism of water ice, or, generally, the phase diagram of the metastable non-crystalline states of ice, has been intensively investigated as it is thought to provide a link to the numerous anomalies of liquid water.^7–9

To understand better the versatility of water's hydrogen-bond structures, interest in glassy states has been extended to those of water-rich compounds, such as clathrate hydrates, which, as ice I_h, show the PIA phenomenon at low temperatures. The presence of apolar solute implies disruption of the hydrogen-bond network through volume exclusion. The connectivity of the water network is reestablished around the solute species and for clathrate hydrates local restructuring leads to polyhedral cages, which host guest species. These can range from larger molecules (e.g. tetrahydrofuran (THF), SF₆) to single (noble gas) atoms.¹⁰ Weak van der Waals interactions between guest and water molecules are essential to maintain clathrate hydrate structures.^11,12 There are two major structures, called cubic structure I (CS-I) with space group Pm3̄n and composition (2D + 6T)·46H₂O, and cubic structure II (CS-II) with space group Fd3̄m and composition (16D + 8H)·136H₂O, respectively. D stands for dodecahedral cage (5¹²), T for tetrakaidecahedral cage (5¹²6²) and H for hexakaidecahedral cage (5¹²6⁴). Accounting for the van der Waals radius of water, the internal free diameter of D, T, and H cages are 5.0, 5.9, and 6.7 Å, respectively.¹³ There is a natural relation between the size of the guest species and the kind of realized structure. Large organic molecules (such as THF) fit only in H cages and thus would adopt the CS-II.¹⁴ When both cages are occupied in simple clathrate hydrates (i.e. containing only one kind of guest) their occupancy is oftentimes at a 80 to 90% level at atmospheric pressure.

PIA of clathrate hydrates was first recognized with THF and SF₆ hydrates^15,16 and later especially studied with other CS-II systems containing large molecules (e.g. acetone, cyclobutanone).^17–19 Due to exclusively filled H cages, these systems realize the most water-rich composition for clathrate hydrates, 1 : 17, which at the same time is well-defined. Their PIA behavior is strikingly similar to ice I_h, occurring at around 1.3 GPa below 130 K.¹⁹ However, there is a decisive difference in that the obtained “HDA” form is not recoverable, but “springs back” to the clathrate CS-II upon pressure release.^15,17,19 The amorphous state however can be stabilized and made recoverable when heating at pressures >1 GPa to 160–170 K.^16,20 This annealing leads to densification, which again is similar to the creation of VHDA ice from the HDA form. Also, upon warming a glass transition at ∼140 K is seen in both amorphized clathrate hydrate and HDA, which is attributed to kinetic unfreezing of H₂O molecules.^18,19,21

The PIA behavior of clathrate hydrates containing guest species in higher concentrations is less well investigated. Methane hydrate, CH₄·6.26H₂O, which adopts the CS-I,^22,23 was shown to undergo pressure-induced collapse at a significantly higher pressure, 3.2 GPa at 100 K.²³ On the other hand, Ar·6.5H₂O with the CS-II amorphizes around 1.5 GPa (95 K), which again is close to the amorphization pressure of ice I_h.³ Both amorphized hydrates showed densification upon annealing, but recoverability has only been demonstrated for the Ar hydrate. Brant Carvalho et al. attempted to provide a more unified picture on clathrate hydrate amorphization by studying the noble gas series Ne–Xe for which both types of clathrate structures are realized and the size effect of the guest can be studied without a significant change of the host–guest interaction.²⁴ Major findings include that PIA of clathrate hydrates can be expected in the pressure range 1.3 to 2.5 GPa, and that resistance toward PIA increases when both types of cages are occupied and with increasing size of the guest species.

Clearly, the differences and similarities between glassy forms of ice and hydrates originate in the diversity of the latter with respect to solute/guest : water ratio, nature and size of the guest, and possibly also the kind of structure of the crystalline precursor. Crucial is a fundamental understanding of (interrelated) hydration structure of the guest species and hydrogen-bond structure of the surrounding H₂O network in the amorphs. Structural investigations require the measurement and analysis of X-ray and/or neutron structure factors functions S(Q). Hitherto this has been only reported for amorphous CH₄ and THF hydrate.^17,25 In this work we extend such a study to amorphous Ar hydrate, for which there are several unique aspects. First, since the composition of the CS-II crystalline precursor is well characterized, the composition of the amorphous Ar hydrate is also known. Second, with amorphous Ar hydrate a “triangle” – consisting of initial PIA, densification upon annealing, and subsequent recovery – can be performed, which rises expectations into distinct amorphous forms, similar to ice. Finally, with Ar hydrate isotope substitution can be exploited in neutron scattering experiments. The isotopic contrast between ^NatAr and the ³⁶Ar isotope allows elegant separation of information on local Ar hydration structure from the scattering data. For our structural investigation, neutron total scattering measurements were performed for amorphous ^NatAr hydrate and the isotope-substituted ³⁶Ar hydrate, in situ at high pressures for the PIA produced and the annealed form, and at ambient pressure for the recovered one. Subsequent analysis of neutron structure factors by pair distribution functions (PDF) analysis was guided by molecular dynamics (MD) simulations of the amorphous states.

2. Experiments

2.1. In situ neutron powder diffraction

Fully deuterated CS-II ^NatAr hydrate and ³⁶Ar hydrate with a composition Ar·6.5H₂O were synthesized at the SNAP beamline at the Spallation Neutron Source (SNS), Oak Ridge National Laboratory (ONRL), USA, as described by Brant Carvalho et al.²⁴ The samples were virtually free from unreacted ice I_h. Pressurization and heating experiments were performed using a standard VX Paris–Edinburgh (PE) pressure cell with liquid nitrogen (LN₂)-cooled stainless steel anvils and monitored in situ by time-of-flight neutron powder diffraction (NPD). The set-up can achieve pressures up to 10 GPa and can be cooled down to LN₂ temperature at a precision of ∼1 K and ∼0.1 GPa.

Samples were handled at LN₂ temperature, loaded into a null-scattering Ti–Zr alloy encapsulated gasket and subsequently set into the pre-cooled stainless steel anvils. Lead powder was added to each sample as pressure marker. The gaskets were pressurized to ∼0.1 GPa upon loading for sealing and stabilizing the samples, which warmed up to about 170 K during transferring the pressure cell to the closed-cycle refrigerator cryostat where they were cooled to 95 K. Pressurization was done in steps of 0.1–0.2 GPa, followed by data collection during 15 min to up to several hours. Samples were compressed until their full amorphization. Neutron scattering data were collected for the initial HDA state for ∼10 hours. Subsequently, to produce VHDA, samples were warmed to 170 K, annealed for 30 min and cooled back to 95 K. Back at 95 K, total scattering data were collected for ∼10 hours. Lastly, samples were decompressed in small pressure steps. Because the gasket could keep the sample under pressure (∼0.4 GPa) even without load applied, the PE press was opened and unscrewed to completely release the pressure on the samples. At this stage, with the samples at 95 K and atmospheric pressure, total scattering data for RA were collected for ∼10 hours. In addition, vanadium and silicon powder as well as an empty gasket were measured at different pressure conditions for background treatment and normalization of the total scattering data. Masking of the detector banks was done on the highest pressures due to partial shading of the detectors by the anvil and press materials. Details on data reduction have been discussed in the supplemental material of an earlier publication.²⁴

The steps for extracting neutron structure factor functions S(Q) from the original diffraction data were performed with the Mantid package (MantidPlot and Workbench).²⁶ Diffraction patterns of crystalline samples were subjected to Rietveld refinement, performed with GSAS-II.²⁷ For pressure determination, the equation of state of Pb according to Strässle et al. was employed.²⁸ Refined parameters included background and peak profile terms, and lattice parameters. Diffraction patterns of amorphous samples were treated for Bragg diffraction peaks arising from lead (pressure marker) and steel and cubic boron nitride (c-BN) (from the anvil materials) by Rietveld refinement, followed by the subtraction of the modeled peaks. No background treatment was done to keep diffuse scattering intact. The total scattering data were smoothed and Fourier transformed using Workbench.

2.2. Molecular dynamics simulations

MD simulations were performed using GROMACS.²⁹ Periodic boundary conditions were used in all simulations. NPT simulations were carried out using velocity-rescaling thermostat³⁰ and Parrinello–Rahman barostat.³¹ The time step was 1 fs. Coulomb interactions were treated according to the SPME (Smooth Particle-Mesh Ewald)³² technique. A cutoff of 12 Å was used for the Lennard-Jones interactions. A 2 × 2 × 2 supercell of the CS-II Ar clathrate hydrate, containing 1088 water molecules and 192 Ar atoms was constructed with the GenIce software.³³ GenIce sets the oxygen atoms at their crystallographic sites, randomizes the distribution of the hydrogen atoms considering the Bernal–Fowler³⁴ ice rules and chooses the configuration with zero net polarization. Note that, for simplicity, both types of polyhedral cages H and D were assumed to be fully occupied (which gives an overall composition Ar·5.67H₂O). To describe the interatomic interactions in the course of the MD simulations the TIP4P/ice³⁵ and the Universal force field (UFF)³⁶ were used for the ice and Ar atoms, respectively. The Lorentz–Berthelot mixing rules were applied. Simulations started at 95 K, 1 bar, and the pressure was increased by 0.05 GPa steps until reaching 2 GPa. The structure in each step started from the last snapshot of the previous one. At each pressure increment, the simulation box was equilibrated for 0.5 ns, followed by 2 ns production until 1.7 GPa and 20 ns for completeness of the amorphization process. After amorphization, each pressure increment was simulated for 10 ns.

Post amorphization heat cycling was carried out starting from the stabilized structure at 2 GPa, by heating in 15 K steps from 95 to 230 K. At each annealing step, the system was equilibrated for 0.5 ns followed by a further 10 ns production simulation. The structures obtained at 170, 200, 215 and 230 K were cooled in 15 K steps until 95 K using the same protocol. These structures were then recovered to 1 bar pressure at 95 K using 1 ns simulations for equilibration, followed by 50 ns production. The PDFs were calculated using the Visual Molecular Dynamics (VMD)³⁷ software. Snapshots of the simulation boxes were produced with VMD and Diamond.³⁸ Total neutron scattering patterns for ³⁶Ar/²H isotope substituted amorphs were simulated from single frame atomic coordinates using the XaNSoNS code.³⁹ Densities were extracted from time-averaged data of portions of the trajectories in which volume was already converged.

3. Results and discussion

3.1. Three amorphous forms of Ar hydrates

Deuterated ³⁶Ar and ^NatAr clathrate hydrates with the CS-II were pressurized at 95 K in a PE press. The composition Ar·6.5H₂O was determined from Rietveld refinement, showing an occupancy of the H and D cages of 83 and 89%, respectively. PIA, as indicated by the disappearance of all Bragg diffraction peaks, occurred at 1.45(2) and 1.47(4) GPa for the ^NatAr hydrate and ³⁶Ar hydrate sample, respectively. Subsequently a few extra compression steps were taken, which resulted in a final pressure 1.9(1) GPa and 2.0(1) GPa for amorphous ^NatAr and ³⁶Ar hydrate, respectively. This form obtained from initial PIA is termed HDA, in analogy to ice I_h and according to the terminology used in previous works.^17,24 To prepare the VHDA state, the HDA samples were warmed to 170 K at 2 GPa and kept at the target temperature for 1 hour before cooling back to 95 K. Subsequently the VHDA samples were depressurized at 95 K. The amorphous state was retained at ambient pressure. The recovered amorphs of Ar and ³⁶Ar hydrates, which are crystallization-resistant up to ∼120 K, will be called RA.

In MD simulations PIA was observed at 1.7 GPa which is in good agreement with the experiment, considering that the simulations referred to the idealized composition Ar·5.67H₂O with fully occupied H- and D-type cages. The density vs. pressure curve is provided as ESI, Fig. S1.† The compressibility of the crystalline form corresponded well with the experiment. The density increase in the pressure interval 1.7–2.0 GPa, accounting for full densification, is from 1.26 g cm⁻³ to 1.48 g cm⁻³, about 15%. Warming at 2 GPa to 170 K resulted in further densification of just 1–2%, which was deemed insufficient to reproduce the experimental transition into VHDA. In order to compensate for the time restrictions of the MD simulations when compared to 1 hour annealing in the experiment, warming to higher temperatures was applied. At 215–230 K the occurrence of Ar dimers (Ar atoms separated by a distance 3.3 Å) was observed, which was interpreted as instability toward crystallization. At the same time, significant increase in diffusion of H₂O molecules was noticed at 230 K (which is shown in the ESI, Fig. S2†). Experimentally above 1 GPa at ambient temperature, Ar and H₂O would form a tetragonal-structured (TS) clathrate hydrate, in which two Ar atoms occupy a single cage of a very large, ellipsoid-shaped (4²5⁸6⁴).⁴⁰ In MD, the timescale does not permit crystallization of the system (which could transform to any crystalline clathrate hydrate). We considered the simulations after annealing to 215 K most representative to the experimental annealing process producing VHDA. In analogy to experiment, MD annealing led to a crystallization-resistant phase at ambient pressure, whereas the decompression of the HDA state showed reformation of the polyhedral cages of crystalline CS-II. The MD density change between HDA and VHDA from annealing at 215 K was about 3%, from 1.48 to 1.52 g cm⁻³, at 2 GPa and 95 K. Upon recovery to ambient pressure the material expanded considerably, by about 21%. The MD density of RA at 95 K was 1.26 g cm⁻³.

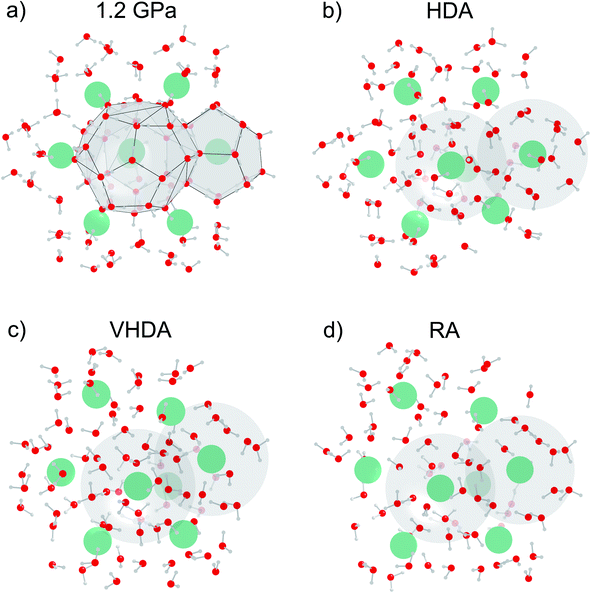
Fig. 1a presents an MD snapshot showing the cage structure of CS-II Ar hydrate at 1.2 GPa, i.e. slightly below the transition pressure to HDA. As initially mentioned, CS-II is built up from two types of polyhedral cages, D and H, which are defined by 20 and 26 molecules, respectively. PIA is initiated by the deformation of the 6-membered rings of the large H cages.^17,24,25 When approaching PIA, the translational motion of Ar atoms inside the cages decreased drastically. A similar hindrance of rotational motion of molecular guests was found in MD simulations of PIA of CS-II THF hydrate¹⁷ and CS-I CH₄ hydrate.²⁵ Actual PIA implies the “collapse” of D cages.²⁴ Fig. 1b–d show a section of the amorphous structures of HDA, VHDA, and RA, respectively, matching with that of the crystalline section (Fig. 1a) which is a projection along [111]. We summarize some key findings here. These will then be made clear from the results of the neutron diffraction experiments and MD simulations, as discussed in the forthcoming sections.

Fig. 1 MD snapshots for Ar clathrate hydrate at 95 K. (a) Crystalline CS-II at 1.2 GPa; (b) HDA at 2.0 GPa; (c) VHDA at 2.0 GPa after temperature cycling to 215 K; and (d) RA at atmospheric pressure. Atoms are shown as spheres (red: oxygen, light-gray: hydrogen, green: argon). Gray areas emphasize Ar–water coordinations, H and D cages in crystalline CS-II and spheres at a 4 Å radius for the amorphous forms.

During PIA to HDA (Fig. 1b) some water molecules undergo translational motion toward equalizing the hydration shells for the originally different Ar atoms in the H and D cages. Yet the orientations of water molecules from the crystalline state appear partially maintained and there are differences in the hydration structure of the Ar atoms. When defining the hydration shell out to 4 Å, which exceeds the sum of van der Waals radii of Ar and O (3.3 Å)^35,36 by about 17%, one finds in average 15 and 13 water molecules around Ar originating from D and H cages, respectively. The figure also visualizes that the Ar hydration environments overlap to a large extent, i.e. that water is confined to a “porous” space with a wall thickness ∼2 molecules. Turning to VHDA (Fig. 1c) the local water structure appears relaxed and hydration shells (and thus the two kinds of Ar guests) seem indistinguishable. Ar atoms are moved significantly and irregularly from their crystalline equilibrium positions and have in average 15 molecules within the 4 Å sphere. This picture is maintained for RA, which however is considerably expanded compared to VHDA. In average there are 11 H₂O molecules in a 4 Å sphere around Ar atoms.

3.2. Structure of amorphous Ar hydrates – Ar hydration structure

The isotopic contrast between ³⁶Ar and ^NatAr provides an excellent opportunity to obtain more detailed structural information from isotope substitution NPD experiments. ³⁶Ar scatters neutrons over ten times more efficiently than ^NatAr, and its normalized neutron-weighed total structure factor functions S(Q) displays enhanced Ar correlations (Ar–Ar, Ar–O and Ar–D). The total structure factor measured by neutron diffraction is given by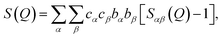 with S_αβ(Q) the partial structure factor for species α, β and Q the magnitude of the scattering vector, while c are the atomic fractions and b are the coherent neutron scattering lengths of each species. If structurally identical samples contain each Ar·6.5²H₂O or 13.3 mol% of ^NatAr [b_coherent(^NatAr) = 1.909 fm]⁴¹ and ³⁶Ar [b_coherent(³⁶Ar) = 24.90 fm = ∼13 × b_coherent(^NatAr)], Ar correlations give rise to different S(Q) functions which affect all individual atoms due to the cross-terms. Nevertheless, S_αβ(Q) with {α, β} ≠ Ar will be identically weighted and can be eliminated by a first-order isotope difference, 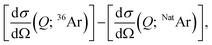with dσ/dΩ the observed and normalized scattering cross-section. In this treatment the OO, OD and DD terms (all pure water correlations) are removed. The usefulness of the ^NatAr/³⁶Ar isotopic difference method has been demonstrated earlier for the structural investigation of vapor co-deposited samples of amorphous ice with Ar.⁴² The S(Q) for the various amorphous ³⁶Ar hydrates are compiled in Fig. 2 and compared to MD modeled ones. Note that results for HDA and VHDA refer to 2 GPa, whereas those for RA refer to ambient pressure. In the ESI, Fig. S3† shows a comparison between ³⁶Ar and ^NatAr S(Q).

Fig. 2 Experimental and MD simulated neutron structure factors, S(Q), for amorphous Ar clathrate hydrate samples with ³⁶Ar and ²H isotope substitution at 95 K. (a) HDA at 2 GPa; (b) VHDA at 2 GPa; and (c) RA at atmospheric pressure. In (c) MD simulations are shown from systems after temperature cycling to 215 K (red line) and 230 K (blue line). Insets emphasize the region of the first diffraction peak, 1.5–3.0 Å⁻¹.

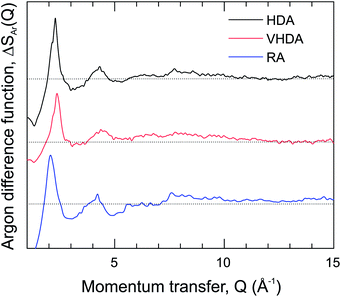
The S(Q) are dominated by the first diffraction peak (FDP), which correlates with intermediate range (3–6 Å) structural organization in liquids and glasses.⁴³ The FDP is located between 2.0 and 2.5 Å⁻¹, and it can be suspected that it accounts for Ar–water correlations. The peak is clearly split for HDA, with contributions at 2.12 and 2.30 Å⁻¹. It represents a single peak for VHDA and RA with the maximum at 2.40 Å⁻¹ and 2.08 Å⁻¹, respectively. The shifts of the FDP with respect to HDA express the higher and lower density of VHDA and RA. Generally there is a good agreement between measured and MD simulated S(Q). The MD modeled ones for VHDA and RA indicate a somewhat lower and higher density, respectively, compared to the experiment. This discrepancy is probably connected and reflects the shortcoming of MD to achieve completely relaxed VHDA within the simulation time scale. Fig. 3 shows the isotopic difference function according to the treatment described above.

Fig. 3 Isotopic difference neutron structure functions for amorphous Ar clathrate hydrates. HDA (black line), VHDA (red line) and RA (blue line). The dotted horizontal lines show the structure factor functions asymptotically converging to 1 at high Q.

The difference function (which is void of water–water correlations) makes clear that the FDP indeed reflects the nearest neighbor Ar–water correlations. Importantly, the split feature for HDA is maintained, which implies that there are two length scales for the Ar–water correlations. Note that a split FDP is a recurring, and possibly characteristic, feature for HDA obtained from PIA of clathrate hydrates. It has been observed first for CH₄ and later also for THF hydrate and, thus, appears independent of the kind of clathrate structure and cage occupancy.^17,23 Yet its origin has to be different. For HDA Ar hydrate, through the isotope substitution neutron diffraction experiment, it can be unambiguously attributed to two different length scales for Ar–water correlations. For CH₄ and THF hydrate it was suggested that the split FDP reflects different length scale for CH₄–water and water–water correlations, with the latter expressing a denser local structure.^17,23 For THF hydrate this is certainly reasonable because of its water rich composition (1 : 17) and THF occupying only one type of cage (H) in the crystalline CS-II. Lastly, we remark on the S(Q) of RA which shows resemblance to that of amorphous Ar hydrates obtained from vapor co-deposition.^42,44 However, the latter forms seem more expanded with FDP maxima located at 1.9 and 2.0 Å⁻¹ for samples with 8 and 13 at% Ar, respectively.

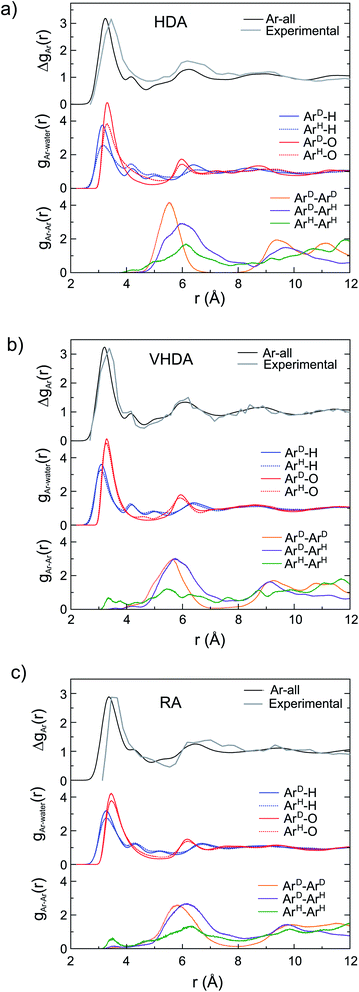
Via Fourier transform of the first-order isotope difference ΔS_Ar(Q), the real-space correlation function Δg_Ar(r) was obtained which represents the collective PDFs for the various correlations involving Ar. Δg_Ar(r) allows the detailed analysis of the local structure of Ar in the amorphs when relating to PDFs (g(r)) from MD simulations. This is shown in Fig. 4. The peak in Δg_Ar(r) around 3.5 Å is clearly assigned to the Ar–O and Ar–H correlations defining the hydration structure. Peaks at higher r (around 6 and 9 Å) are due to Ar–Ar correlations. For HDA (Fig. 4a) the distinction of the originally different Ar atoms in the crystalline structure is maintained since g_Ar–O(r) and g_Ar–H(r) look rather different for Ar originating from H and D cages. The peak maxima are roughly at the same distance (3.3 Å and 3.1 Å for g_Ar–O(r) and g_Ar–H(r), respectively) but the different peak heights for Ar^H and Ar^D indicate a lower coordination (less dense hydration structure) for Ar originating from H cages. The distinction of the two types of Ar is also visible in g_Ar–Ar(r). After annealing (Fig. 4b), g_Ar–O(r) and g_Ar–H(r) of both types of Ar superimpose which implies that Ar atoms attained like hydration structures. At the same time, the differences in the g_Ar–Ar(r) are essentially removed. Thus, VHDA has a homogenous amorphous structure with Ar atoms in average 5.6 Å apart. The picture is maintained for RA (Fig. 4c). The less dense hydration structure of Ar with respect to VHDA is expressed in the significantly reduced height of the first peak in the g_Ar–O(r) and g_Ar–H(r) and the slightly shifted position of the maxima (Ar–O 3.4 Å, Ar–H 3.3 Å). The average nearest neighbor Ar–Ar distance is increased to 6.1 Å.

Fig. 4 Experimental and MD simulated partial Ar correlation functions (Ar–Ar, Ar–H and Ar–O). Functions are deconvoluted in individual pair contributions for each amorphous system. (a) HDA; (b) VHDA; and (c) RA.

The distinctly different Ar hydration structures in the three amorphs can be summarized when plotting the Ar–O integrated coordination numbers, n_Ar–O(r), as shown in Fig. 5. For VHDA and RA the n_Ar–O(r) for the two types of Ar look essentially the same. At r = 4 Å the coordination numbers are ∼15 and ∼11, respectively (cf. Fig. 1c and d). The n_Ar^D–O(r) is very similar for HDA and VHDA whereas the n_Ar^H–O(r) for HDA shows significantly lower values up to r = 4.5 Å. Using r = 4 Å as a cut-off, the coordination number for Ar^H is ∼13, cf. Fig. 1b. The equalization of the Ar hydration structure in VHDA (via annealing) is a prerequisite to form the thermodynamically metastable but crystallization-resistant RA upon pressure release. By contrast, HDA springs back to the CS-II as still distinguishable Ar guests serve as nucleating sites for crystallization. The situation for amorphized THF clathrate hydrate is most likely very similar. As initially described, amorphous THF hydrate from PIA can also be densified and subsequently recovered to ambient pressure. However, the CS-II precursor hosts THF exclusively in H cages. We conjecture that in the HDA form, THF molecules attain a low density hydration structure, following from the collapsed H cages (like Ar^H), which upon annealing (and going through a glass transition)¹⁸ relaxes into the VHDA form with a densified hydration structure. Like amorphous Ar hydrate, the VHDA form can then be recovered as an expanded RA form. The detailed structure of amorphous THF hydrate's VHDA and RA forms is yet unresolved.

Fig. 5 Running coordination numbers of Ar–O pairs for HDA at 2 GPa, 95 K; VHDA at 2 GPa, 95 K; and RA at atmospheric pressure, 95 K. Ar coordinations are discriminated as Ar^H and Ar^D, corresponding to their original location in the crystalline CS-II.

3.3. Structure of amorphous Ar hydrates – local water structure

How is water arranged in amorphous hydrates and how does the local structure compare to those in amorphous ices? As pointed out earlier, the presence of apolar guest confines water to a “thin-walled” porous space where the hydrogen-bond network accommodates simultaneously the guest's hydration structure. Thus, the local water structure in amorphous hydrates is expected to vary with the concentration and size of the guest species. The local and intermediate range structures of the amorphous ices have been determined from both neutron and X-ray scattering investigations and can be considered as well-established.^6,7,45–47

Fig. 6a shows the O–O PDF, g_O–O(r), for HDA, VHDA and RA respectively. (The g_O–H(r) and g_H–H(r) are provided as ESI, Fig. S4a and b,† respectively.) For amorphous ices, the first coordination shell is usually defined out to r = 3.3 Å.⁴⁸ For crystalline ice I_h, values of g_O–O(r) are zero between the sharp shells defined by the translational periodicity. Maxima corresponding to the first, second, and third shell are at ∼2.8, ∼4.5, and ∼5.3 Å, respectively.⁶ The g_O–O(r) for VHDA and HDA Ar hydrate are very similar and the small maximum at 3.2 Å indicates that molecules are (at least partly) coordinated by more than four molecules in the nearest neighbor environment. This maximum is characteristic for VHDA ice, but appears much more prominent there. The integrated water coordination number, n_O–O(r), highlights clearly the disparity of the water structures of HDA and VHDA Ar hydrates and ices (Fig. 6b). The n_O–O(r) are very similar for the hydrates, parallel the similar g_O–O(r), but radically different for ices. At r = 3.3 Å average coordination numbers are 4.7 and 5 for the hydrates (referring to 2 GPa) whereas they are 5 and 6 for the ices (referring to zero pressure). Thus densification to the VHDA form has little impact on the local water structure in amorphous Ar hydrate but changes drastically the local structure in amorphous ice.

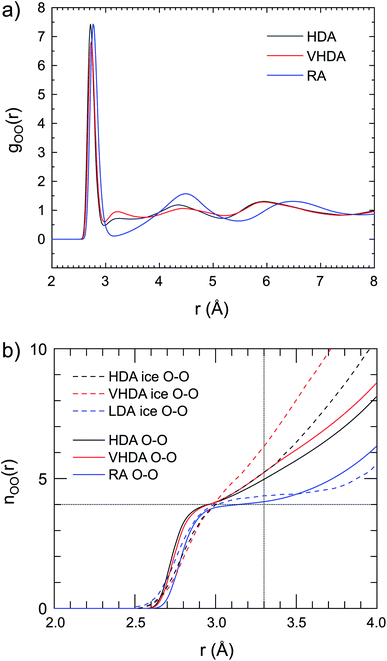Fig. 6 (a) Partial correlation functions for oxygen–oxygen interactions for HDA at 2 GPa, 95 K (gray line); VHDA at 2 GPa, 95 K (red line); and RA at atmospheric pressure, 95 K (blue line). (b) Running O–O coordination number of the amorphous Ar hydrates, compared to amorphous ice data (at ambient pressure) according to D. Mariedahl et al.⁶

The water structure of RA is clearly distinguished from those of HDA and VHDA. The almost zero value of g_O–O(r) around r = 3.2 Å and the rather pronounced oscillations at higher r indicate a high degree of tetrahedrality of the hydrogen-bond network. Indeed the n_O–O(r) for RA shows a plateau around four molecules. It is interesting to note that both g_O–O(r) and n_O–O(r) for RA bear great resemblance to the LDA form of ice which also represents a tetrahedral network, albeit with lower density. Fig. 7 summarizes these findings with MD snapshots. In contrast with Fig. 1, we emphasize now the local water structures. Fig. 7a shows the open tetrahedral network of the CS-II at 1.2 GPa. The network of the HDA form (at 2 GPa, Fig. 7b) constitutes 4- and 5- coordinated water molecules whereas the network of the VHDA form (also at 2 GPa. Fig. 7c) constitutes 4-, 5- and 6-coordinated water molecules. By contrast, the RA form (at zero pressure, Fig. 7d) possesses a strictly 4-connected network based on distorted tetrahedra. The large high-symmetry cages of the open network of the CS-II, which is built from regular tetrahedra, are exchanged for smaller and irregularly shaped hydration shells. The density of stable crystalline Ar clathrate is slightly lower than that of metastable RA, 1.140(7)/1.13 g cm⁻³ (experimental/MD) and 1.26 g cm⁻³ (MD), respectively, which – because of the absence of large cages in RA – implies a more dense water structure in the latter.

Fig. 7 MD snapshots for Ar clathrate hydrate at 95 K emphasizing the local water structure (cf. Fig. 1). (a) Crystalline CS-II at 1.2 GPa; (b) HDA at 2.0 GPa; (c) VHDA at 2.0 GPa after temperature cycling to 215 K; and (d) RA at atmospheric pressure. Water molecules are depicted as “sticks” (red and white) and Ar atoms as faded-green spheres. Dashed lines show O–O distances up to 3.1 Å. 5- and 6-coordinated water molecules are highlighted as gray and red polyhedra, respectively. The latter are only present in VHDA.

The local water structure in amorphous hydrates is expected to be quite variable and because of the yet limited number of studies it is not clear how the situation for Ar hydrates will apply to other systems. Also the comparison of HDA and VHDA forms of different systems is impeded by different pressures of PIA and annealing. According to MD studies, n_O–O(r) at 3.3 Å is 5.76 for HDA CH₄ hydrate at 3.3 GPa, 6.02 for VHDA CH₄ hydrate at 5.5 GPa,²³ and 5.75 for HDA THF hydrate at 2 GPa.¹⁷ These are substantially larger values compared to Ar hydrate and may indicate that the local water structures in CH₄ and THF hydrates are more similar to HDA/VHDA ices. Likewise variable could be the local water structure of RA forms which have been least investigated. Here recovered amorphous THF hydrate represents an interesting case. Because of the more water rich (1 : 17) composition one could envision a denser local water structure in comparison to amorphous Ar hydrate, perhaps more relating to that of HDA ice.

4. Conclusions

PIA of clathrate hydrates allows fabrication of amorphous water-rich hydrates in which an apolar solute (i.e. the guest species in the crystalline clathrate hydrate) may be considered as modifier, disrupting the H-bond network of glassy ice. In this work crystalline Ar clathrate hydrate with the CS-II was subjected to PIA at 95 K and the resulting amorphous form (HDA) further transformed into a densified state (VHDA) by annealing to 170 K, which was recoverable to ambient pressures (RA) at 95 K. The structures of the three amorphs were found to be distinctly different. In HDA, although fully amorphous, intermediate range order is maintained in that the originally different Ar atoms of the crystalline precursor attain differently dense hydration structures. The different hydration structures are evened out in VHDA upon thermal activation of re-orientational motion of the water molecules. At 2 GPa, the local water structure in HDA constitutes 4- and 5-coordinated molecules, whereas the hydrogen-bond network of VHDA contains in addition 6-coordinated H₂O molecules. Upon recovery of VHDA at ambient pressure the hydrogen-bond network changes into a strictly tetrahedral one in the RA form.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been funded by the Swedish Foundation for Strategic Research (SSF) within the Swedish National Graduate School in neutron scattering (SwedNess). A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The simulations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC), partially funded by the Swedish Research Council through grant agreement no. 2018-05973. The authors thank also the financial support from the Swedish Foundation for International Cooperation in Research and Higher Education (STINT) and the Brazilian agency CAPES (project CAPES/STINT No. 88887.304724/2018).

References

1. T. Loerting, K. Winkel, M. Seidl, M. Bauer, C. Mitterdorfer, P. H. Handle, C. G. Salzmann, E. Mayer, J. L. Finney and D. T. Bowron, How many amorphous ices are there?, Phys. Chem. Chem. Phys., 2011, 13, 8783–8794.
2. K. Winkel, M. Bauer, E. Mayer, M. Seidl, M. S. Elsaesser and T. Loerting, Structural transitions in amorphous H₂O and D₂O: the effect of temperature, J. Phys.: Condens. Matter, 2008, 20, 494212.
3. O. Mishima, L. D. Calvert and E. Whalley, ‘Melting ice’ I at 77 K and 10 kbar: A new method of making amorphous solids, Nature, 1984, 310, 393–395.
4. O. Andersson and A. Inaba, Dielectric properties of high-density amorphous ice under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 184201.
5. T. Loerting, C. Salzmann, I. Kohl, E. Mayer and A. Hallbrucker, A second distinct structural ‘state’ of high-density amorphous ice at 77 K and 1 bar, Phys. Chem. Chem. Phys., 2001, 3, 5355–5357.
6. D. Mariedahl, F. Perakis, A. Späh, H. Pathak, K. H. Kim, G. Camisasca, D. Schlesinger, C. Benmore, L. G. M. Pettersson, A. Nilsson and K. Amann-Winkel, X-ray Scattering and O–O Pair-Distribution Functions of Amorphous Ices, J. Phys. Chem. B, 2018, 122(30), 7616–7624.
7. K. Amann-Winkel, D. T. Bowron and T. Loerting, Structural differences between unannealed and expanded high-density amorphous ice based on isotope substitution neutron diffraction, Mol. Phys., 2019, 117(22), 3207–3216.
8. K. Winkel, E. Mayer and T. Loerting, Equilibrated High-Density Amorphous Ice and Its First-Order Transition to the Low-Density Form, J. Phys. Chem. B, 2011, 115(48), 14141–14148.
9. K. Amann-Winkel, R. Böhmer, F. Fujara, C. Gainaru, B. Geil and T. Loerting, Colloquium: Water's controversial glass transitions, Rev. Mod. Phys., 2016, 88, 011002.
10. J. S. Loveday and R. J. Nelmes, High-pressure gas hydrates, Phys. Chem. Chem. Phys., 2008, 10, 937–950.
11. Q. Shi, P. Cao, Z. Han, F. Ning, H. Gong, Y. Xin, Z. Zhang and J. Wu, Role of Guest Molecules in the Mechanical Properties of Clathrate Hydrates, Cryst. Growth Des., 2018, 18(11), 6729–6741.
12. D. W. Davidson, Y. P. Handa, C. I. Ratcliffe, J. S. Tse and B. M. Powell, The ability of small molecules to form clathrate hydrates of structure II, Nature, 1984, 311, 142–143.
13. D. W. Davidson in Water: A Comprehensive Treatise: Volume 5: Water in Disperse Systems, ed. F. Franks, Plenum Press, New York, NY, 1973.
14. J. A. Ripmeester, C. I. Ratcliffe, D. D. Klug and J. S. Tse, Molecular Perspectives on Structure and Dynamics in Clathrate Hydrates, Ann. N. Y. Acad. Sci., 1994, 715, 161–176.
15. Y. P. Handa, J. S. Tse, D. D. Klug and E. Whalley, Pressure-induced phase transitions in clathrate hydrates, J. Chem. Phys., 1991, 94, 623–627.
16. Y. Suzuki, Evidence of pressure-induced amorphization of tetrahydrofuran clathrate hydrate, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 172108.
17. P. H. B. Brant Carvalho, A. Mace, C. L. Bull, N. P. Funnell, C. A. Tulk, O. Andersson and U. Häussermann, Elucidation of the pressure induced amorphization of tetrahydrofuran clathrate hydrate, J. Chem. Phys., 2019, 150, 204506.
18. O. Andersson and Y. Nakazawa, Transitions in pressure collapsed clathrate hydrates, J. Phys. Chem. B, 2015, 119(9), 3846–3853.
19. O. Andersson, P. H. B. Brant Carvalho, Y. J. Hsu and U. Häussermann, Transitions in pressure-amorphized clathrate hydrates akin to those of amorphous ices, J. Chem. Phys., 2019, 151, 014502.
20. M. Bauer, D. M. Többens, E. Mayer and T. Loerting, Pressure-amorphized cubic structure II clathrate hydrate: crystallization in slow motion, Phys. Chem. Chem. Phys., 2011, 13, 2167–2171.
21. O. Andersson and U. Häussermann, A Second Glass Transition in Pressure Collapsed Type II Clathrate Hydrates, J. Phys. Chem. B, 2018, 122(15), 4376–4384.
22. J. S. Loveday, R. J. Nelmes, D. D. Klug, J. S. Tse and S. Desgreniers, Structural systematics in the clathrate hydrates under pressure, Can. J. Phys., 2003, 81, 539–544.
23. C. A. Tulk, D. D. Klug, J. J. Molaison, A. M. dos Santos and N. Pradhan, Structure and stability of an amorphous water-methane mixture produced by cold compression of methane hydrate, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 54110.
24. P. H. B. Brant Carvalho, A. Mace, O. Andersson, C. A. Tulk, J. Molaison, A. P. Lyubartsev, I. M. Nangoi, A. A. Leitão and U. Häussermann, Pressure-induced amorphization of noble gas clathrate hydrates, Phys. Rev. B, 2021, 103, 064205.
25. N. J. English and J. S. Tse, Pressure-induced amorphization of methane hydrate, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 104109.
26. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Mantid - Data analysis and visualization package for neutron scattering and µSR experiments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
27. B. H. Toby and R. B. Von Dreele, GSAS-II: The genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46(2), 544–549.
28. T. Strässle, S. Klotz, K. Kunc, V. Pomjakushin and J. S. White, Equation of state of lead from high-pressure neutron diffraction up to 8.9 GPa and its implication for the NaCl pressure scale, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 014101.
29. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25.
30. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101.
31. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190.
32. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593.
33. M. Matsumoto, T. Yagasaki and H. Tanaka, GenIce: Hydrogen-Disordered Ice Generator, J. Comput. Chem., 2018, 39, 61–64.
34. J. D. Bernal and R. H. Fowler, A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions, J. Chem. Phys., 1933, 1, 515–548.
35. J. L. F. Abascal, E. Sanz, R. G. Fernández and C. Vega, A potential model for the study of ices and amorphous water: TIP4P/Ice, J. Chem. Phys., 2005, 122, 234511.
36. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035.
37. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
38. K. Brandenburg and H. Putz, Diamond: Crystal and Molecular Structure Visualization, version 4.6.5, Crystal Impact GbR, 2005, Bonn, Germany.
39. V. S. Neverov, XaNSoNS: GPU-accelerated simulator of diffraction patterns of nanoparticles, SoftwareX, 2017, 6, 63–68.
40. A. Y. Manakov, V. I. Voronin, A. V. Kurnosov, A. E. Teplykh, V. Y. Komarov and Y. A. Dyadin, Structural investigations of argon hydrates at pressures up to 10 kbar, J. Inclusion Phenom., 2004, 48, 11–18.
41. V. F. Sears, Neutron scattering lengths and cross sections, Neutron News, 1992, 3, 26–37.
42. J. C. Dore, D. M. Blakey, P. Chieux and P. Palleau, Neutron diffraction studies of an argon/amorphous ice co-deposit using isotopic substitution, Phys. Chem. Chem. Phys., 2000, 2, 1603–1606.
43. D. T. Bowron, J. L. Finney, A. Hallbrucker, I. Kohl, T. Loerting, E. Mayer and A. K. Soper, The local and intermediate range structures of the five amorphous ices at 80 K and ambient pressure: A Faber-Ziman and Bhatia-Thornton analysis, J. Chem. Phys., 2006, 125, 194502.
44. T. Kikuchi, Y. Inamura, N. Onoda-Yamamuro and O. Yamamuro, Structures and low-energy excitations of amorphous gas hydrates, J. Phys. Soc. Jpn., 2012, 81, 094604.
45. J. S. Tse and D. D. Klug, Pressure amorphized ices – an atomistic perspective, Phys. Chem. Chem. Phys., 2012, 14, 8255–8263.
46. R. J. Nelmes, J. S. Loveday, T. Strässle, C. L. Bull, M. Guthrie, G. Hamel and S. Klotz, Annealed high-density amorphous ice under pressure, Nat. Phys., 2006, 2, 414–418.
47. K. Amann-Winkel, M. C. Bellissent-Funel, L. E. Bove, T. Loerting, A. Nilsson, A. Paciaroni, D. Schlesinger and L. Skinner, X-ray and Neutron Scattering of Water, Chem. Rev., 2016, 116(13), 7570–7589.
48. G. Malenkov, Liquid water and ices: understanding the structure and physical properties, J. Phys.: Condens. Matter, 2009, 21, 283101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra05697b

---