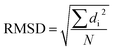Open Access Article
Open Access ArticleMolecular structure recognition by blob detection†
Qing Lu
Beijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: qinglu@iccas.ac.cn
First published on 5th November 2021
Abstract
Molecular structure recognition is fundamental in computational chemistry. The most common approach is to calculate the root mean square deviation (RMSD) between two sets of molecular coordinates. However, this method does not perform well for large molecules. In this work, a new method is proposed for structure comparison. Blob detection is used for recognizing structural features. Fragmentation of molecules is proposed as the pre-treatment. Mapping between blobs and atoms is developed as the post-treatment. A set of key parameters important for blob detections are determined. The dissimilarity is quantified by calculating the Euclidean metric of the blob vectors. The overall algorithm is found to be accurate to distinguish structural dissimilarity. The method has potential to be combined with other pattern recognition techniques for new chemistry discoveries.
Introduction
The identification of molecular structures is important in chemistry and biology. It is almost inevitable in fields such as conformer exploration, molecular assembly, molecular descriptor definition, etc. With the increasing complexity of research problems, it becomes more and more difficult to find a rule governing the multivariate input data and the target output data. Therefore, the design of experiments approach becomes important to narrow down the number of variables.1 Such approach has been used to solve different problems such as solar cell preparation,2–5 nutrients analysis,6 and sparse-sensor-selection problem.7 The chemometrics takes advantages of mathematical, statistical and other methods to explore new chemical insights. In particular, the pattern recognition techniques have been developed to extract features from a large amount of input data.8 The major applications involve discriminant analysis for food quality,9 quality assessment of herbal medicine,10 design of chemical sensor,11 and recognizing ligands,12 etc.Comparing similarities between different chemical structures is one of the most important steps in computational chemistry. It is often the starting point for sophisticated multi-step computational studies,13–15 since a convincing computation relies on a good agreement between optimized structures and crystalized structures. In addition, comparing structures is also important in the prediction of structures of proteins,16 comparing trajectories from molecular dynamic simulations,17 database searching or analysis,18,19 and benchmark studies testing new methods or basis sets.20
Among all approaches to comparing structural similarities, the root-mean-square-deviation (RMSD) is the most widely used one. It calculates the square sum of distances between corresponding atoms (di) in two structures and takes the division by the total number of atoms (N), followed by a square root operation.
Despite its wide use, the RMSD measurement suffers a few limitations such as difficult of interpretation, lack of normalization and diminishing ability to distinguish conformers with increasing system size.17,21,22 To remedy these problems, some improvements upon RMSD have been proposed, such as introducing weighting functions into the calculation of RMSD,17 taking advantage of the graph theory23 or symmetry.24 Other alternatives include configuration fingerprint vector,25 global and local descriptors,26 geometric hashing algorithm27 and several different score functions.21,28–33
On another aspect, the pattern recognition has received considerate success in recent years. It is the frontier in the field of deep learning, and it is fast, accurate and visually straightforward. In biology or chemistry, the applications taking advantages of pattern recognition techniques dominantly rely on principle component analysis, cluster analysis, classification methods and regression methods.8 In term of image processing techniques, the blob analysis has been used to identify ligands in electron density maps,12 identify cells,34 analyze the Leukemic blood image,35 or detect trees from satellite images.36
There is a great advance in the image understanding, which could be used in the analysis for molecular structures. However, molecules are much more complicated in shape and it is therefore not trivial to transplant pattern recognition and machine learning technique to recognize molecules. Besides, molecules usually have tertiary structures (like proteins). As a result, even if outlook or profile of molecules are recognized identical, the core structures may still vary. Lastly the structural difference could be small, so recognition technique should be sensitive and accurate to avoid over-detection or under-detection.
Although it is challenging, it is attractive to apply pattern recognition techniques to recognize molecules. Such an approach is potential to benefit database analysis, molecule docking analysis or quantitative structure–activity relationship analysis. It is even potential to be extended to combine with other machine learning techniques. Accordingly, one can better understand molecular structures, intra- or inter-molecular interactions. Expecting on these, we initiate this project to explore pattern recognition techniques for the structure recognition. The outcome of this work borrows the advantages of the pattern recognition technique and avoids the problems met by the RMSD calculations. In addition, I further propose a pre-treatment and a post-treatment for recognizing structural dissimilarities. The outcome shows that the proposed method is accurate, intuitive and visually straightforward in structure recognition.
Methods
As discussed above, it does not work to directly borrow facial recognition techniques to recognize molecules, unless the molecular structure is very simple. Yet as a starting point, we initiate the study by recognizing simple molecular systems. For recognizing molecules, one may consider to compare the molecular shape, for example the convex hull for molecule recognition. However, this method cannot be extended to complicated structures and it cannot recognize the concave part of the molecule, thus leading to an under-detection problem. Another widely used method in the field of pattern recognition is to compare the histogram of color distribution of the molecular image. This method, however, is not appropriate since it cannot correctly differentiate conformational structure differences. The most brute-force method is to directly compare the image matrices of two structures. However, this method does not work well either, as it suffers numerical noise when converting 3D molecular structure to images, thus leading to over-detection problem.To circumvent this first problem, we remove the chemical bonds from images, as the molecular structures are determined by the atom positions. Therefore, the problem of recognizing molecules is converted to recognize a set of scattered atoms/dots. The blob detection can be used to recognize these atoms. For complicated molecules, however, there will be blob overlap during the detection. Therefore, before the blob detection, I propose a pre-treatment for molecules as well as images to help the successful detection. Also, it is often of interest to tell which atoms cause the dissimilarity. Therefore, a post-treatment is also proposed to fulfill this goal.
(1) Pre-treatment of images and parameter determination
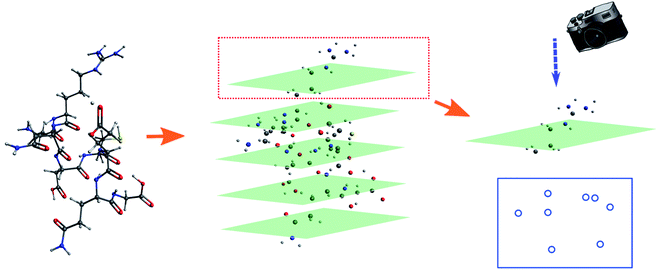
The molecular image is the basis for the following analysis. Providing the atoms have been well aligned,37 the molecular 3D image is generated from its XYZ coordinates (Fig. 1a). Since the atoms are those that determine the molecular structure, we eliminate the chemical bonds from the 3D image (Fig. 1b). Benefiting from this, the molecule is now represented by a set of dots or blobs, and therefore the blob detection is used to recognize molecules. For easier visualization and easier treatment in the latter stage, the azimuthal angle and the elevation angle was set as 90° for exhibiting the image (Fig. 1c) (the projection angle is along the Z-axis). Unless explicitly stated, the following discussion is based on this projection angle.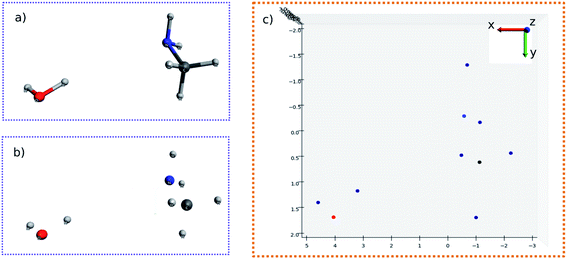 | ||
| Fig. 1 (a) 3D structure of H2O–MeNH2 system. (b) 3D structure of H2O–MeNH2 system eliminating chemical bonds. (c) Projected view of H2O–MeNH2 along Z direction. | ||
As any other pattern recognition application, the quality of the picture is important. After a modest number of tests, I set the picture height and width of 100 × 100 inches with 80 dots per inch (dpi). Accordingly, the final resolution of the figure is 800 × 800 pixel. The resolution of an image is mathematically represented as the matrix size. An image of resolution being 800 × 800 indicates that the matrix size is 800 × 800. Setting the resolution too high would lead to a slowdown of the image processing, while setting the resolution to low would lead to an incapability of distinguishing different blobs. The size of the blobs is also important. If the radius is too large, there will be overlaps of blobs, so that it will not detect the correct number of blobs. On the other hand, if the blob radius is too small, it would likely fail to detect all the blobs. As it will be shown later, the Gaussian kernel is used in the blob detection. The Gaussian kernel is a scalar function with a shape of a Gaussian normal distribution curve. It is used to enhance the contrast between blobs and backgrounds. Since the numerical difference is used, theoretically, the blob size should be at least of 3 pixel. In practice, it is found that the radius of blobs to be 35 pixel is optimal in detecting the correct number of blobs with the given image resolution.
(2) Pre-treatment of molecules
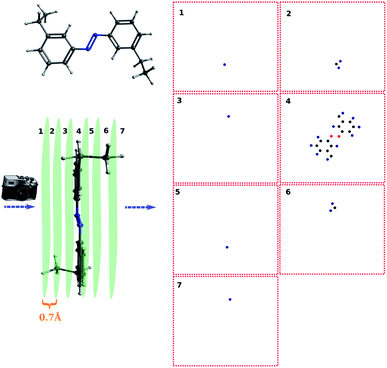
In this work, I chose five different molecular systems to examine the capability of pattern recognition upon distinguishing molecular structures. Although the selected systems are relatively simple, they are representative in terms of molecular complexity, planarity, and symmetry. The complex 3D molecules obtained from X-ray cryptograph could also be used as an examination, but for easier visualization only the chosen molecules are discussed.The H2O–MeNH2 system (Fig. 2a) serves as an introduction system due to its simple composition. The trans-4,4-diethyl-azobenzene and C60 systems (Fig. 2b and c) serve to illustrate how the blob detection was carried out. The 18-crown-6 ether and the virtual peptide of α-helix composed of Ala–Arg–Asn–Asp–Cys–Glu–Gln–Gly, generated by Avogadro38 (Fig. 2d and e), serve to exhibit the results of blob detection upon complex systems, as well as quantifying the dissimilarity between different structures.
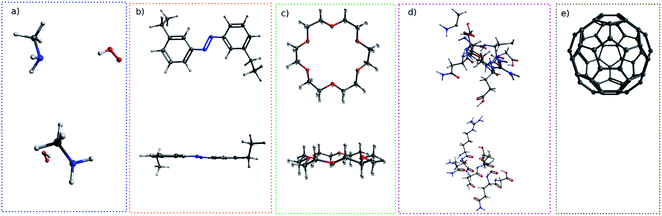
For simple molecules, like H2O–MeNH2 in Fig. 2a, it is possible to find out a projection angle so that all atoms can be projected on one plane without overlaps. For complicated molecules, however, this becomes increasingly impossible. The molecular structure is 3-dimensional, while the image is 2-dimensional. This is equivalent to ask the question how to convert a 3D problem to a 2D problem without losing information. To solve this problem, I slice the whole molecule into layers, and take the snapshot for each layer to run the blob detection (Fig. 3). However, it is not trivial of slicing the molecule, as the double counting of atoms may take place. Eventually, I slice the molecule along the projection angle, and set the distance between layers to be 0.7 Å. This value is close to a H–H bond distance. For any reasonably determined structure, it is not possible to have two atoms with a distance smaller than 0.7 Å. Therefore, the layers separated by 0.7 Å can well slice the whole molecule into different fragments, and it is accordingly guaranteed that the layer-based blob detection can detect all atoms/blobs.
(3) Feature extraction
To detect the blobs on each layer projected by atoms, the determinant of Gaussian algorithm by Bay et al.39,40 is adopted. There are other two widely-used detection algorithms, namely the Laplacian of Gaussian algorithm and the difference of Gaussian algorithm. In the current case, the Bay's determinant of Hessian algorithm outperforms the other two (see ESI† for details). After fragmenting the molecule, the blob figure of each layer was first converted to gray-scale. As a result, only one matrix (I(x,y)) was enough to represent the image, instead of three matrices (the three matrices represent red, blue, and green colors, respectively). Such a grey image matrix was then converted to the integral image (f(x,y)) to denoise:41
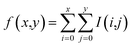 | (1) |
For the integral image matrix f(x,y), a convolution product is defined by multiplying a Gaussian kernel (g(x,y;σ)) with the integral image matrix:
| L(x,y;σ) = g(x,y;σ) × f(x,y) | (2) |
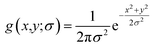 | (3) |
The Hessian determinant H(x,y;σ) is defined as:24
| H(x,y;σ) = Lxx(x,y;σ)Lyy(x,y;σ) − 0.81Lxy(x,y;σ)Lxy(x,y;σ) | (4) |
The blobs (B(x,y;σ)) are finally detected by locating the local maxima of the H(x,y;σ), depending on whether the background color is black or white:
| B(x,y;σ) = argmaxlocal(x,y;σ)(H(x,y;σ)) | (5) |
(4) Pattern recognition
After detecting the blobs, the arrays containing each blob position (Bi(x,y)) and blob radius are obtained. The Euclidean norm between corresponding blobs of two structures are compared. The Euclidean norm between two blobs is calculated as square sum of dx and dy, where dx and dy are the difference in terms of blob coordinate (Bi(x,y)). If the norm differs by more than 7.5 pixels, then the corresponding atoms are identified as having different location. It is also possible to quantify the difference (d) between the two structures by summing up all of the blob norms:
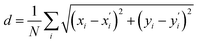 | (6) |
(5) Post-treatment
In addition to recognize the dissimilarity between the two structures, it is often of interest to tell which part of the molecule leads the difference. To fulfill this purpose, the molecule is first projected along the Z direction:
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ZG(x,y,z) = g(x,y) ZG(x,y,z) = g(x,y)
| (7) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Z is the projection operator along the Z direction, G(x,y,z) is the molecular coordinate and g(x,y) is the image matrix element of the projected atoms.
Z is the projection operator along the Z direction, G(x,y,z) is the molecular coordinate and g(x,y) is the image matrix element of the projected atoms.
The image matrices for each layer are then converted to gray-scale as above mentioned. Next, the local maxima or minima were obtained for each gray-scale image matrix, depending whether the background color is white or black:
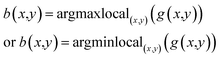 | (8) |
Such local maxima or minima usually have a good overlap with the detected blobs (the pixel difference is lower than 3). Accordingly, the correlation between atom and blobs can be established by any sorting algorithm. However, such a method is not satisfactory if the two blobs are spatially close. In that case, for each atom, a blob detection is performed. The problem can be circumvented at the expense of slower processing speed.
Results and discussion
To start with, the H2O–MeNH2 system was first studied as the testing case. Fig. 4a shows the 3D structure for H2O–MeNH2 system. Fig. 4b shows the projection view along the Z axis for only atoms. Since all the atoms can be projected on the same plane without overlaps, so the fragmentation of the molecule is not necessary. Fig. 4c shows the detected blobs marked with red circles. It is evident that all atoms are properly detected.To test the sensitivity of the method to distinguish the dissimilarity, the X or Y coordinate of one of the CH3 hydrogen is gradually displaced by 0.1 Å from its equilibrium position. For the H2O–MeNH2 case, a difference of 0.1 Å is sensitive enough for the blob detection, as shown in Fig. 4d, where the original and displaced hydrogen are marked with red and blue color, respectively. However, for complicated systems like the peptide system, such a difference cannot guarantee a successful detection for the displaced atom. Eventually, it is found that 0.3 Å is a good threshold for the detection of displaced atoms. To further test the reliability of this threshold, a random displacement (dx and dy) between −0.3 and 0.3 Å was added on the X and Y coordinates of the first 10 atoms of the peptide. A constraint was introduced to the displacements that dx2 + dy2 is no lower than 0.09. The displaced atoms can be correctly detected. Therefore, 0.3 Å is chosen as the sensitivity threshold for the blob detection. As a further examination, the random displacement was generated 100 times, and the successful detection was achieved 100 times.
For complicated molecules, it is often necessary to fragment the molecule into several layers to avoid blob overlaps. Fig. 5a and b show the top view and side view of the trans-4,4-diethyl-azobenzene, respectively. Especially, in Fig. 5b the molecule was fragmented into 7 layers. The projection angle is perpendicular to the planes. The blob detection is performed for each layer picture and each layer is shown in Fig. 5c. It can be seen that layer 1 contains 1 blob, which is identified as the methyl proton after the post-treatment of mapping atoms and blobs. The layer 2 contains 3 blobs, which correspond to the CH2 atoms of that methyl group. Layer 3 contains 1 blob corresponding to the methylene proton on the other ring side. Layer 4 contains the azobenzene skeleton. Layer 5, 6, 7 are “mirror” layers to the layer 3, 2, 1, respectively.
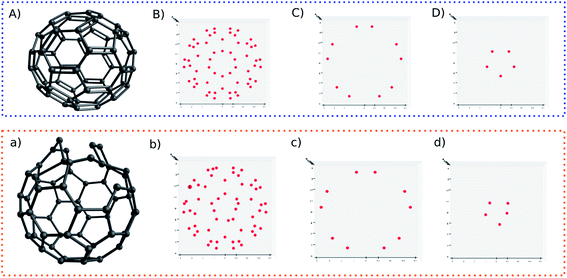
For another showcase, the upper panel of Fig. 6 shows the C60 molecule and its detected blobs, while the lower panel shows the counterpart of the distorted C60 molecule. The distorted C60 molecule was obtained by adding a random number between −0.3 and 0.3 on the X,Y,Z coordinates of the first 10 atoms. As before, the dx and dy is constrained by dx2 + dy2 ≥ 0.09. For the normal C60 molecule, it is visually convenient to find out that the detected blobs show an expected circular distribution (Fig. 6B). What is not expected (to some degree), on the other hand, it is that it is not necessary to slice the C60 molecule into layers. All 60 carbons can be projected on one plane without overlap. The radial spacing for each lap of blobs is not evenly distributed. Thus, the pattern recognition technique could provide a new perspective to understand molecular structures.
Nonetheless, I still slice the C60 molecule into layers. For normal C60 molecule, different layers show an expected symmetric blob pattern (Fig. 6C and D). As a comparison, Fig. 6d shows an asymmetric blob distribution, since those atoms are displaced. On the other hand, Fig. 6c shows a blob pattern identical to its counterpart of the original C60 molecule (Fig. 6C), since the atoms corresponding to these blobs belong to the remaining unperturbed 50 atoms.
Lastly, one may quantify the dissimilarity between two images. In this work, the quantification of the dissimilarity is expressed by the Euclidean norm between two blob vectors. The calculation of the Euclidean norm is similar to the RMSD calculation. The variable is the blob position, instead of the atom coordinate.
Table 1 shows the Euclidean norm between blob vectors of unperturbed systems and perturbed systems. For the perturbed systems, the first 10 atoms are randomly displaced (dR) at X,Y,Z direction by 0.3, 0.5 and 1 Å, respectively, with the constraint that dx2 + dy2 ≥ 0.09. It can be seen that the Euclidean norm increases as the displacement becomes larger. Therefore, the dissimilarity between two structures can be quantified.
| dR = ±0.3 Å | dR = ±0.5 Å | dR = ±1 Å | |
|---|---|---|---|
| H2O–MeNH2 | 31.6 | 62.2 | 82.6 |
| 18-Crown-6-ether | 24.1 | 32.3 | 62.2 |
| Peptide | 10.6 | 12.6 | 21.4 |
Conclusions
In this work, the pattern recognition technique is developed for molecular structure recognition. This method provides a new approach to distinguish the similarity of two structures, and it is potential to be further developed with other machine learning techniques in understanding molecular structures, inter- or intra-molecular interactions. The blob detection is used to recognize molecules and the determinant of Hessian algorithm is found performing well for the blob detection. For complicated molecules, it is necessary to fragment molecules in different layers. Thus, a pre-treatment of molecules and images is proposed. Five different systems were examined for the reliability of the proposed method. It is found that the new method can accurately detect the atomic geometry difference as small as 0.3 Å. A post-treatment is proposed to map the blobs and atoms. The new method is visually straightforward to compare structural differences and can provide a new perspective to understand molecular structures. The dissimilarity can be quantified by calculating the Euclidean norm of blob vectors. Overall, the proposed method provides a new approach to recognize molecules and it is potential to be further developed with other machine learning techniques to study molecular interaction. The relevant study is undergoing in this lab.Funding sources
The author gratefully acknowledges the support from the National Natural Science Foundation of China (No. 22003068), the Beijing Municipal Natural Science Foundation (No. 2214065) and the Beijing National Laboratory for Molecular Sciences and Chinese Academy of Sciences.Data and software availability
The scripts used for this work were written by Python 3.6.9. All images were generated by the associated Matplotlib 3.3.4 module. The Numpy version is 1.19.5 and the Skimage module is 0.17.2. The molecular 3D visualization is carried out by Avogadro 1.2.0. All data and source code are freely available by the request from the author.Conflicts of interest
There are no confilcts to declare.References
- A. R. Gottu Mukkula, M. Mateáš, M. Fikar and R. Paulen, Robust multi-stage model-based design of optimal experiments for nonlinear estimation, Comput. Chem. Eng., 2021, 155, 107499 CrossRef CAS.
- S. Galliano, F. Bella, M. Bonomo, G. Viscardi, C. Gerbaldi, G. Boschloo and C. Barolo, Hydrogel Electrolytes Based on Xanthan Gum: Green Route towards Stable Dye-Sensitized Solar Cells, Nanomaterials, 2020, 10, 1585 CrossRef CAS PubMed.
- S. Galliano, F. Bella, M. Bonomo, F. Giordano, M. Grätzel, G. Viscardi, A. Hagfeldt, C. Gerbaldi and C. Barolo, Xanthan-Based Hydrogel for Stable and Efficient Quasi-Solid Truly Aqueous Dye-Sensitized Solar Cell with Cobalt Mediator, Sol. RRL, 2021, 5, 2000823 CrossRef CAS.
- D. Pugliese, F. Bella, V. Cauda, A. Lamberti, A. Sacco, E. Tresso and S. Bianco, A Chemometric Approach for the Sensitization Procedure of ZnO Flowerlike Microstructures for Dye-Sensitized Solar Cells, ACS Appl. Mater. Interfaces, 2013, 5, 11288–11295 CrossRef CAS PubMed.
- F. Bella, D. Pugliese, J. R. Nair, A. Sacco, S. Bianco, C. Gerbaldi, C. Barolo and R. Bongiovanni, A UV-crosslinked polymer electrolyte membrane for quasi-solid dye-sensitized solar cells with excellent efficiency and durability, Phys. Chem. Chem. Phys., 2013, 15, 3706–3711 RSC.
- M. Arvapally, A. Asati, N. K. Nagendla and M. K. R. Mudiam, Development of an analytical method for the quantitative determination of multi-class nutrients in different food matrices by solid-phase extraction and liquid chromatography-tandem mass spectrometry using design of experiments, Food Chem., 2021, 341, 128173 CrossRef CAS PubMed.
- T. Nagata, T. Nonomura, K. Nakai, K. Yamada, Y. Saito and S. Ono, Data-Driven Sparse Sensor Selection Based on A-Optimal Design of Experiment With ADMM, IEEE Sens. J., 2021, 21, 15248–15257 Search PubMed.
- P. Oliveri, C. Malegori, E. Mustorgi and M. Casale, Qualitative pattern recognition in chemistry: Theoretical background and practical guidelines, Microchem. J., 2021, 162, 105725 CrossRef CAS.
- J. Zeng, Y. Guo, Y. Han, Z. Li, Z. Yang, Q. Chai, W. Wang, Y. Zhang and C. Fu, A Review of the Discriminant Analysis Methods for Food Quality Based on Near-Infrared Spectroscopy and Pattern Recognition, Molecules, 2021, 26, 749 CrossRef CAS PubMed.
- Y. Wang, Z.-T. Zuo and Y.-Z. Wang, Pattern recognition: An effective tool for quality assessment of herbal medicine based on chemical information, J. Chemom., 2021, 35, e3305 CrossRef CAS.
- Z.-H. Chen, Q.-X. Fan, X.-Y. Han, G. Shi and M. Zhang, Design of smart chemical ‘tongue’ sensor arrays for pattern-recognition-based biochemical sensing applications, TrAC, Trends Anal. Chem., 2020, 124, 115794 CrossRef CAS.
- M. Kowiel, D. Brzezinski, P. J. Porebski, I. G. Shabalin, M. Jaskolski and W. Minor, Automatic recognition of ligands in electron density by machine learning, Bioinformatics, 2019, 35, 452–461 CrossRef CAS PubMed.
- M. Zhang, H. Wu, J. Yang and G. Huang, A Computational Mechanistic Analysis of Iridium-Catalyzed C(sp3)–H Borylation Reveals a One-Stone–Two-Birds Strategy to Enhance Catalytic Activity, ACS Catal., 2021, 11, 4833–4847 CrossRef CAS.
- Q. Lu, F. Neese and G. Bistoni, London dispersion effects in the coordination and activation of alkanes in sigma-complexes: a local energy decomposition study, Phys. Chem. Chem. Phys., 2019, 21, 11569–11577 RSC.
- Q. Lu, F. Neese and G. Bistoni, Formation of Agostic Structures Driven by London Dispersion, Angew. Chem., Int. Ed. Engl., 2018, 57, 4760–4764 CrossRef CAS PubMed.
- J. Yang, I. Anishchenko, H. Park, Z. Peng, S. Ovchinnikov and D. Baker, Improved protein structure prediction using predicted interresidue orientations, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 1496–1503 CrossRef CAS PubMed.
- A. Wagner and H.-J. Himmel, aRMSD: A Comprehensive Tool for Structural Analysis, J. Chem. Inf. Model., 2017, 57, 428–438 CrossRef CAS PubMed.
- G. J. Kleywegt, Recognition of spatial motifs in protein structures 11 Edited by J. Thornton, J. Mol. Biol., 1999, 285, 1887–1897 CrossRef CAS PubMed.
- J. A. Barker and J. M. Thornton, An algorithm for constraint-based structural template matching: application to 3D templates with statistical analysis, Bioinformatics, 2003, 19, 1644–1649 CrossRef CAS PubMed.
- N. Sylvetsky, M. K. Kesharwani and J. M. L. Martin, MP2-F12 basis set convergence for the S66 noncovalent interactions benchmark: Transferability of the complementary auxiliary basis set (CABS), AIP Conf. Proc., 2017, 1906, 030006 CrossRef.
- J. C. Baber, D. C. Thompson, J. B. Cross and C. Humblet, GARD: A Generally Applicable Replacement for RMSD, J. Chem. Inf. Model., 2009, 49, 1889–1900 CrossRef CAS PubMed.
- P. C. D. Hawkins, Conformation Generation: The State of the Art, J. Chem. Inf. Model., 2017, 57, 1747–1756 CrossRef CAS PubMed.
- B. Helmich and M. Sierka, Similarity recognition of molecular structures by optimal atomic matching and rotational superposition, J. Comput. Chem., 2012, 33, 134–140 CrossRef CAS PubMed.
- W. J. Allen and R. C. Rizzo, Implementation of the Hungarian Algorithm to Account for Ligand Symmetry and Similarity in Structure-Based Design, J. Chem. Inf. Model., 2014, 54, 518–529 CrossRef CAS PubMed.
- A. Sadeghi, S. A. Ghasemi, B. Schaefer, S. Mohr, M. A. Lill and S. Goedecker, Metrics for measuring distances in configuration spaces, J. Chem. Phys., 2013, 139, 184118 CrossRef PubMed.
- A. Ramirez-Manzanares, J. Peña, J. M. Azpiroz and G. Merino, A hierarchical algorithm for molecular similarity (H-FORMS), J. Comput. Chem., 2015, 36, 1456–1466 CrossRef CAS PubMed.
- A. C. Wallace, N. Borkakoti and J. M. Thornton, Tess: A geometric hashing algorithm for deriving 3D coordinate templates for searching structural databases. Application to enzyme active sites, Protein Sci., 1997, 6, 2308–2323 CrossRef CAS PubMed.
- Y. Zhang and J. Skolnick, Scoring function for automated assessment of protein structure template quality, Proteins: Struct., Funct., Bioinf., 2004, 57, 702–710 CrossRef CAS PubMed.
- A. Zemla, LGA: a method for finding 3D similarities in protein structures, Nucleic Acids Res., 2003, 31, 3370–3374 CrossRef CAS PubMed.
- S. Cristobal, A. Zemla, D. Fischer, L. Rychlewski and A. Elofsson, A study of quality measures for protein threading models, BMC Bioinf., 2001, 2, 5 CrossRef CAS PubMed.
- L. Rychlewski, D. Fischer and A. Elofsson, LiveBench-6: Large-scale automated evaluation of protein structure prediction servers, Proteins: Struct., Funct., Bioinf., 2003, 53, 542–547 CrossRef CAS PubMed.
- A. Zemla, Č. Venclovas, J. Moult and K. Fidelis, Processing and analysis of CASP3 protein structure predictions, Proteins: Struct., Funct., Bioinf., 1999, 37, 22–29 CrossRef.
- N. Siew, A. Elofsson, L. Rychlewski and D. Fischer, MaxSub: an automated measure for the assessment of protein structure prediction quality, Bioinformatics, 2000, 16, 776–785 CrossRef CAS PubMed.
- M. Gupta, Cell Identification by Blob Detection, 2012 Search PubMed.
- C. Di Ruberto, A. Loddo and G. Puglisi, Blob Detection and Deep Learning for Leukemic Blood Image Analysis, Appl. Sci., 2020, 10, 1176 CrossRef.
- M. Mahour, V. Tolpekin and A. Stein, Automatic Detection of Individual Trees from VHR Satellite Images Using Scale-Space Methods, Sensors, 2020, 20, 7194 CrossRef PubMed.
- B. Temelso, J. M. Mabey, T. Kubota, N. Appiah-Padi and G. C. Shields, ArbAlign: A Tool for Optimal Alignment of Arbitrarily Ordered Isomers Using the Kuhn–Munkres Algorithm, J. Chem. Inf. Model., 2017, 57, 1045–1054 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 17 CAS.
- H. Bay, A. Ess, T. Tuytelaars and L. Van Gool, Speeded-Up Robust Features (SURF), Comput. Vis. Image Underst., 2008, 110, 346–359 CrossRef.
- X. Xu, ed. S. Li, C. Liu and Y. s. Wang, Blob Detection with the Determinant of the Hessian, Pattern recognition, Pattern recognition, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014 Search PubMed.
- P. Viola and M. Jones, Rapid Object Detection Using a Boosted Cascade of Simple Features, Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, 2001, DOI:10.1109/CVPR.2001.990517.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra05752a |
| This journal is © The Royal Society of Chemistry 2021 |