Open Access Article
Open Access ArticleMapping the effect of geometry on the radiative rate in core/shell QDs: core size dictates the conduction band offset†
Maxwell P. Hoffman‡
a,
Autumn Y. Lee‡a,
Nejc Nagelja,
Youjin V. Leeb and
Jacob H. Olshansky *a
*a
aDepartment of Chemistry, Amherst College, Amherst, MA 01002, USA. E-mail: jolshansky@amherst.edu
bDepartment of Chemistry, University of California, Berkeley, Berkeley, CA, USA
First published on 4th November 2021
Abstract
Computational models have been developed that can accurately predict the electronic structure and thus optical properties of a variety of quantum dot (QD) materials. However, the application of these models to core/shell and other heterostructured QDs has received less experimental corroboration owing to the difficulty in systematically synthesizing and characterizing large ranges of geometries. In the current work, we synthesized a library of core/shell CdSe/CdS QDs with varying core sizes and shell thicknesses, and have characterized their radiative recombination rates. We find that the core size has only a modest effect on the radiative recombination rates, far less than is predicted by conventional effective mass models. In order to theoretically describe the experimental data, we performed an empirical modification of an effective mass model. We find that the conduction band offset between CdSe and CdS must be empirically altered based on QD core size in order to match our experimental data. This is hypothesized to be a result of reduced interfacial strain in core/shell QDs with smaller cores. The resultant relationship between conduction band offset and core size is used to create a predictive map of radiative lifetime as a function of core size and shell thickness. This map will be useful to researchers implementing CdSe/CdS core/shell QDs for a variety of applications since it can provide geometry specific excited state lifetimes.
Introduction
A defining characteristic of semiconducting nanocrystals, or quantum dots (QDs), is that their size dictates their emission energy in a predictable way since a photoexcited charge in a QD behaves like a quantum particle-in-a-box.1 Advances in synthetic techniques have allowed for the generation of QDs with tunable size,2 shape,3 and composition,4,5 as well as heterostructured materials.6–9 Concomitantly, design rules and theories have been developed that relate these architectures to the material optical properties. Understanding of these properties has, in turn, been harnessed to advance technological applications in photovoltaics,10,11 photocatalysis,7,12 lasers,13,14 displays,15 bio-imaging,16 and quantum information science.17–19 Further advances in these fields will surely be aided by elaboration of the design rules that help researchers select specific QD geometries for their application needs. In this paper, we demonstrate this type of elaboration by mapping the effect of geometry on the radiative recombination rate in core/shell QDs. We employ an effective mass model with core-size-dependent corrections that can serve as a guide for predicting the radiative recombination rate based on core size and shell thickness. We further hypothesize that these corrections are necessitated by core-size-dependent lattice strain.The current work focuses on CdSe/CdS spherical core/shell QDs since these materials have shown promise in a variety of light-emitting applications including luminescent solar concentrators,20,21 low-threshold lasers,14,22 light-emitting diodes (LEDs),23,24 and bio-imaging.25,26 Growth of the larger bandgap semiconductor, CdS, on the CdSe core serves to insulate the photoexcited charges from surface states, thereby increasing photoluminescence quantum yields (PLQY).25,27–29 Growth of the CdS shell is always accompanied with an elongation of photoluminescence (PL) lifetimes that is particularly pronounced in very thick-shelled QDs.27,28,30–38 This observation is well understood within the context of an effective mass particle-in-a-spherical-box model.14,33–35,39–42 In such models, the relatively small effective mass of the electron in CdSe and CdS as well as the small difference in energy between the conduction bands of CdSe and CdS result in an electron wavefunction that can delocalize into the CdS shell. The hole wavefunction, however, is typically confined to the core. This quasi-type II electronic structure results in a progressively decreased electron–hole overlap with increasing shell thickness (Fig. 1). A decreased electron–hole overlap results in longer radiative recombination times.
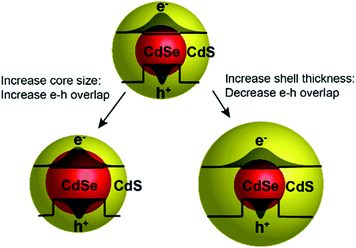 | ||
| Fig. 1 Cartoon showing the effect of increasing core size (left) and shell thickness (right) on the electron and hole wavefunctions in CdSe/CdS core/shell QDs. | ||
Quantifying the relationship between geometry, electronic structure, and the associated PL properties of CdSe/CdS core/shell QDs has suffered from an inconsistency in reported values for the conduction band offset. The conduction band energies of CdSe and CdS are quite close, such that small changes in this value can significantly alter expected electron localization. Most reported values are theoretically derived since direct measurements of the conduction band offset are difficult.43 The reported values for the conduction band offset, CBCdS − CBCdSe = ΔEc, range from −0.25 to 0.32 eV.35,43,44 Studies on CdSe/CdS spherical core/shell QDs have employed values of ΔEc = 0.32,14,33,39 0.30,31 0.27,35 0.1,40 and 0.0 eV (ref. 41) in models that match experimental findings. Importantly, a theoretical treatment of CdSe/CdS nanorods that takes into account interfacial strain, shows that including the effects of this strain alters ΔEc from 0.3 to 0 eV.45 The authors also suggest that varying the core size will result in different degrees of strain, and therefore a core-size-dependent conduction band offset.
A range of theoretical models have been employed that use these conduction band offsets to predict radiative rates in CdSe/CdS core/shell QDs, sometimes with contradictory results. In non-interacting effective mass models14 and in a theoretical model that takes into account fine structure, Coulomb attraction, and exchange interactions,46 the core size of CdSe/CdS QDs is predicted to have a large role in determining electron–hole overlap, and thus recombination lifetime (see Fig. 1). For example, in thick-shelled CdSe/CdS QDs, a change in core radius from 1.5 to 2.5 nm is predicted by both models to decrease the radiative rate by at least a factor of two.14,46 In contrast, multiband k·p calculations that incorporate strain-induced piezoelectricity predict a weak dependence of core size on electron–hole overlap.38 This model further predicts that giant core/shell CdSe/CdS QDS with 2.0 nm cores will exhibit faster radiative rates than 2.5 nm cores (opposite of the trend predicted by effective mass models).38
Experimental verification of these theoretical predictions is lacking, since systematic studies of CdSe/CdS QD geometries often focus on either varying the core size or shell thickness, but rarely both values. In one report that explores both core size and shell thickness effects on optical properties, the photoluminescence lifetimes for only one shell thickness is reported.37 To build a wholistic picture of the dependence of radiative rate on both core size and shell thickness, we have prepared a library of CdSe/CdS core/shell QDs with varying core sizes and shell thicknesses.
In the current work, we characterize the optical properties of this library of CdSe/CdS spherical core/shell QDs. The effect of core radius and shell thickness on both emission energy and PL lifetime are analysed. In agreement with prior reports, we find that the PL lifetimes increase with increasing shell thickness. We also find that for a given QD diameter, smaller cores result in longer lifetimes. However, the effect of changing the core size is subtler than what is predicted by models that employ constant values of ΔEc. We hypothesize that the conduction band offset is dependent on core size, possibly because of changing interfacial strain. An effective mass model is then implemented with empirically adjusted, core-size specific values of ΔEc, that can accurately simulate the PL lifetime data for all geometries. The empirically derived relationship between ΔEc and core size is used to create a predictive map of PL lifetime as a function of core size and shell thickness.
Methods
Experimental methods
CdSe core QDs were synthesized and purified in accordance with previously published methods.47 CdS shells were grown using a slow injection of octanethiol and cadmium-oleate solutions, as reported previously.25,48 During the course of the injection, aliquots were removed from the reaction mixture, diluted in hexanes, and filtered prior to characterization with electron microscopy and optical spectroscopy. Photoluminescence lifetime measurements were acquired using a Picoquant Fluotime 300 spectrometer and an LDH-P-C-405 diode laser with a 407 nm excitation wavelength. Consistent with prior work using the same instrumentation and materials, the average number of excitons per QD per pulse is ≪1, thus precluding any multiexcitonic effects.31 Further evidence for the lack of multi-excitons is the absence of ∼100–300 ps decay features expected from bi-excitons of CdSe/CdS core/shell QDs.49 Full experimental details are available in the ESI.†Computational methods
Analytical solutions can be obtained for the same core/shell/shell spherical geometries that we investigate, and are described elsewhere.50–52 We chose to solve the Schrödinger equation numerically, employing the finite difference method. Details are available in the ESI.† This approach is chosen since it can easily be adapted to continuously changing potential energy surfaces (rather than discrete steps from core to shell to shell), although this is not explored in the current work. The parameters used in our model included the electron effective masses of 0.13, 0.19, and 1.0 and hole effective masses of 0.45, 0.8, and 1.0 for CdSe, CdS, and the ligand shell respectively. The electron and hole potentials (vs. vacuum) were −4.04 and −5.74 for CdSe, and −1.0 and −8.4 eV for the ligand shell. The CdS hole potential was −6.34 eV and the electron potential varied from −4.04 to −3.84 eV depending on the conduction band offset. Electron and hole wavefunctions were solved independently to produce results with no Coulomb interaction (this data is presented in the ESI†). The potentials were then adjusted to account for Coulombic forces and the wavefunctions were solved again. This process was repeated iteratively until the wavefunctions no longer changed. Typically, convergence occurred after three iterations, consistent with prior work employing the same technique.53 The wavefunctions that include Coulombic interactions are presented in the main text.Results and discussion
To build a wholistic picture of the dependence of radiative rates on both core size and shell thickness, and to ultimately test the hypothesis of a core-size-dependent conduction band offset, we prepared a library of CdSe/CdS core/shell QDs with varying core sizes and shell thicknesses. The three different batches of CdSe core QDs are referred to as the “small core” (1.3 nm radius), “medium core” (2.0 nm radius), and “large core” (2.6 nm radius). Three CdS shelling reactions were performed on each batch of cores (denoted as “run 1”, “run 2”, and “run 3”) to give a total of nine shell-growth reactions. During the course of each CdS shelling reaction, 5–8 aliquots were removed and analysed by electron microscopy (Fig. 2).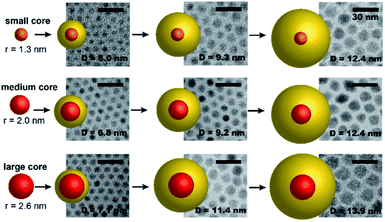 | ||
| Fig. 2 Representative micrographs of the CdSe/CdS core/shell QDs. All scale bars are 30 nm. Cartoons with CdSe cores (red/orange) and CdS shells (yellow) are shown at relative scale for comparison. | ||
Optical measurements were performed on each aliquot to determine excited state energies and dynamics. The time-resolved photoluminescence (TRPL) data (Fig. 3a–c) demonstrates a clear trend in that radiative lifetime increases with increasing shell thickness, as has previously been observed.27,30–35 The TRPL data is used to extract excited state lifetimes, τ, and excited state recombination rates, τ−1 (Fig. 3d–f). Values were determined by fitting the first decade of the lifetime data to either mono or bi-exponential decays (see ESI† for the fits) to extract intensity weighted average lifetimes (τ). Core size clearly impacts the observed rates, with the smallest cores exhibiting recombination rates that are smaller than those for the largest cores. However, fitting this data to various effective mass models (as described below) was not possible with a single value for the conduction band offset. Any such model predicted a larger effect of core size on the radiative rate.
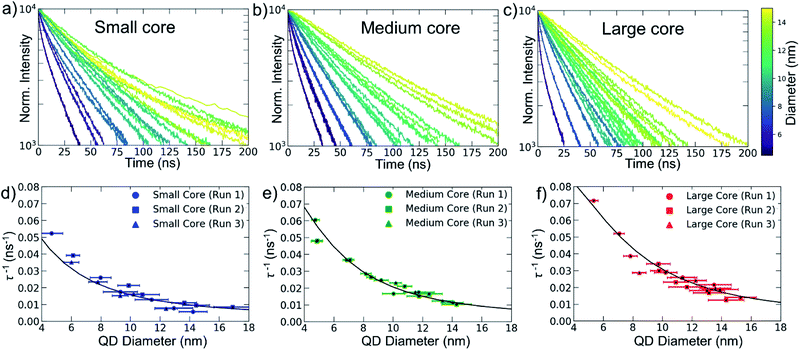 | ||
| Fig. 3 TRPL decays for the (a) small, (b) medium, and (c) large core CdSe/CdS core/shell QDs with different total diameters. Comparisons between theoretical electron–hole overlap (black lines) and experimentally determined excited state recombination rates for (d) small, (e) medium, and (f) large cores. Error bars are based on the standard deviation in QD diameters given by electron microscopy analysis (see ESI†). | ||
Before describing the computational model employed, it is worth elaborating on why the rate extracted from the first decade of the TRPL data is a good estimate for the radiative recombination rate. For materials that possess uniform (across the sample) and constant (in time) non-radiative and radiative recombination channels, with rates of knr and kr, respectively, the PLQY can be expressed as:
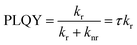 | (1) |
Computationally solving the Schrödinger equation for photoexcited electrons and holes in QDs by employing the effective mass approximation is a useful way to understand radiative recombination in QDs. Specifically, the square of the electron–hole overlap is proportional to the radiative rate as given by the Fermi's “golden rule” derived expression:54,56
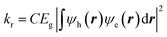 | (2) |
In this equation, Eg is the band gap of the material (and a proxy for emission frequency), ψe(r) and ψh(r) are the electron and hole wavefunctions, respectively, and C is a material dependent pre-factor. Note that C includes the optical density of states or local field factor, which has been shown to be constant for different geometries of core/shell CdSe/CdS QDs.55 Wavefunctions were obtained both with and without explicit Coulomb interactions between the electron and hole. The main text shows predictions from wavefunctions obtained with Coulomb interactions, but the non-interacting model yields qualitatively similar results (see ESI†).
As mentioned above, constant values of the conduction band offset for all core sizes resulted in a poor correspondence between electron–hole overlap and radiative rate (using eqn (2), see ESI† for plots). For each core size, the conduction band offset was adjusted until an adequate match was obtained between the experimental radiative rate data and the theoretically derived wavefunction overlap. It is conceivable that a shell-thickness-dependent conduction band offset would achieve similar results, but this would not be consistent with results of lattice strain modelling as described below. Comparisons between the theoretical (black lines) and experimental radiative rates are shown in Fig. 3d–f. Conduction band offsets of ΔEc = 0.18, 0.04, and 0.0 eV were employed for the small, medium, and large cores respectively.
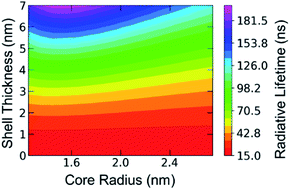
The agreement between the empirically adjusted theoretical model and experimental data across a variety of geometries motivated us to extend our predictions to other core sizes and shell thicknesses with similar geometries to those studied (core radii of 1.2–2.8 nm, and shell thicknesses up to 7 nm). The three core sizes and associated conduction band offsets presented above were used to create an empirical relationship for the conduction band offset for any core radius in the 1.2–2.8 nm range (see ESI, Table S1†). This allowed for the construction of a contour plot (Fig. 4) that can predict radiative lifetime based on the core size and shell thickness. This empirically adjusted theoretical model may be of use to researchers optimizing the geometry of CdSe/CdS core/shell QDs for specific applications.
A striking feature of Fig. 4 and the experimental data on which it is based is that the radiative rate does not show a significant dependence on core size. This is in contrast with behaviour predicted by consistent conduction band offsets (see ESI† for examples). Importantly, the empirically adjusted contour plot (with the weak dependence of core size on radiative rate) is built from experimental data. We chose to employ an adjustable core-size-dependent conduction band offset to enable the effective mass model to adequately fit the data. We believe this adjustment is justified (see below), however other empirical adjustments to the effective mass model designed to fit the experimental data would result in qualitatively similar versions of Fig. 4. For example, more advanced theories such as the multiband k·p calculations that incorporate strain-induced piezoelectricity can account for experimental observations.38 Moreover, the reliance on experimental data in producing the contour plot makes it a reliable predictor no matter the underlying theoretical model.
We hypothesize that the observed weak dependence of core size on radiative rate can be explained by a core-size-dependent change in the conduction band offset. This metric is the source of empirical adjustments to the model (as described above), and can be justified by literature precedent. Luo et al. performed electronic structure calculations on CdSe/CdS core/shell nanorods and found that including the effects of lattice strain reduced the conduction band offset from 0.3 eV to nearly 0 eV.45 The authors suggest that different core and shell geometries would affect the amount of lattice strain, and therefore the value of ΔEc. Similar results were found for CdSe/ZnSe core/shell QDs.57 Gong et al. calculated the strain energy density of CdSe/CdS core/shell QDs and found that this value increases with increasing core size, but is relatively independent of shell thickness (past 1.0 nm).58 If increased strain energy reduces the conduction band offset, then this trend is consistent with the findings of our current work. Core/shell QDs with larger cores (and greater lattice strain) appear to have values of ΔEc near zero, while core/shell QDs with smaller cores (and less strain) appear to have values of ΔEc that are closer to the value of ΔEc = 0.3 eV, determined in the absence of strain. As mentioned before, this analysis, albeit promising, represents just one of many possible ways to interpret the empirical adjustments required to match the theoretical work to the experimental observations. Going forward, we hope that the experimental data can be used as a benchmark for testing more complex electronic structure theories that explicitly incorporate interfacial strain.
Conclusions
In conclusion, we have compiled experimentally determined radiative rates from a variety of CdSe/CdS core/shell QDs that cover three distinct core sizes and shell thicknesses up to 7 nm. These data were compared to theoretical calculations of electron–hole overlap for the same QD geometries. The proportionality between electron–hole overlap and radiative recombination rate allows for this comparison, however we found that no single value of conduction band offset, ΔEc, could describe the data from all three core sizes. In particular, using a consistent conduction band offset predicts that the core size will play a larger role in dictating radiative recombination rate than what is observed experimentally. We therefore empirically adjusted ΔEc for each core size to produce adequate correspondence between theory and experiment. The values of ΔEc that gave the best correspondence were 0.18, 0.04, and 0.0 eV for 1.3, 2.0, and 2.6 nm radius cores, respectively. We can qualitatively justify the decreased conduction band offset for larger cores as a result of increased lattice strain in these QDs. The empirically adjusted theoretical model can be used as a predictor of radiative rates for other CdSe/CdS geometries, as well as a testing ground for more sophisticated electronic structure calculations.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Alivisatos Lab at UC Berkeley for experimental support and the Amherst College SURF program for funding. We also thank Prof. Joshua Schrier and Prof. Ren Wiscons for fruitful discussions and feedback.Notes and references
- L. E. Brus, J. Chem. Phys., 1984, 80, 4403–4409 CrossRef CAS.
- C. B. Murray, D. J. Norris and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706–8715 CrossRef CAS.
- L. Manna, E. C. Scher and A. P. Alivisatos, J. Am. Chem. Soc., 2000, 122, 12700–12706 CrossRef CAS.
- L. De Trizio and L. Manna, Chem. Rev., 2016, 116, 10852–10887 CrossRef CAS PubMed.
- B. J. Beberwyck, Y. Surendranath and A. P. Alivisatos, J. Phys. Chem. C, 2013, 117, 19759–19770 CrossRef CAS.
- R. S. Selinsky, Q. Ding, M. S. Faber, J. C. Wright and S. Jin, Chem. Soc. Rev., 2013, 42, 2963–2985 RSC.
- K. Wu and T. Lian, Chem. Soc. Rev., 2016, 45, 3781–3810 RSC.
- D. V. Talapin, J. H. Nelson, E. V. Shevchenko, S. Aloni, B. Sadtler and A. P. Alivisatos, Nano Lett., 2007, 7, 2951–2959 CrossRef CAS PubMed.
- A. M. Smith and S. Nie, Acc. Chem. Res., 2010, 43, 190–200 CrossRef CAS PubMed.
- G. H. Carey, A. L. Abdelhady, Z. Ning, S. M. Thon, O. M. Bakr and E. H. Sargent, Chem. Rev., 2015, 115, 12732–12763 CrossRef CAS PubMed.
- G. S. Selopal, H. Zhao, Z. M. Wang and F. Rosei, Adv. Funct. Mater., 2020, 30, 1908762 CrossRef CAS.
- M. S. Kodaimati, K. P. McClelland, C. He, S. Lian, Y. Jiang, Z. Zhang and E. A. Weiss, Inorg. Chem., 2018, 57, 3659–3670 CrossRef CAS PubMed.
- S. Bisschop, P. Geiregat, T. Aubert and Z. Hens, ACS Nano, 2018, 12, 9011–9021 CrossRef CAS PubMed.
- F. García-Santamaría, Y. Chen, J. Vela, R. D. Schaller, J. A. Hollingsworth and V. I. Klimov, Nano Lett., 2009, 9, 3482–3488 CrossRef PubMed.
- Y. E. Panfil, M. Oded and U. Banin, Angew. Chem., Int. Ed., 2018, 57, 4274–4295 CrossRef CAS PubMed.
- E. Petryayeva, W. R. Algar and I. L. Medintz, Appl. Spectrosc., 2013, 67, 215–252 CrossRef CAS PubMed.
- J. H. Olshansky, S. M. Harvey, M. L. Pennel, M. D. Krzyaniak, R. D. Schaller and M. R. Wasielewski, J. Am. Chem. Soc., 2020, 142, 13590–13597 CrossRef CAS PubMed.
- J. A. Gupta, D. D. Awschalom, X. Peng and A. P. Alivisatos, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, R10421–R10424 CrossRef CAS.
- C. R. Kagan, L. C. Bassett, C. B. Murray and S. M. Thompson, Chem. Rev., 2020, 121, 3186–3233 CrossRef PubMed.
- N. D. Bronstein, Y. Yao, L. Xu, E. O'Brien, A. S. Powers, V. E. Ferry, A. P. Alivisatos and R. G. Nuzzo, ACS Photonics, 2015, 2, 1576–1583 CrossRef CAS.
- F. Meinardi, A. Colombo, K. A. Velizhanin, R. Simonutti, M. Lorenzon, L. Beverina, R. Viswanatha, V. I. Klimov and S. Brovelli, Nat. Photonics, 2014, 8, 392–399 CrossRef CAS.
- B. Guzelturk, Y. Kelestemur, K. Gungor, A. Yeltik, M. Z. Akgul, Y. Wang, R. Chen, C. Dang, H. Sun and H. V. Demir, Adv. Mater., 2015, 27, 2741–2746 CrossRef CAS PubMed.
- B. N. Pal, Y. Ghosh, S. Brovelli, R. Laocharoensuk, V. I. Klimov, J. A. Hollingsworth and H. Htoon, Nano Lett., 2012, 12, 331–336 CrossRef CAS PubMed.
- F. Todescato, I. Fortunati, A. Minotto, R. Signorini, J. J. Jasieniak and R. Bozio, Materials, 2016, 9, 672 CrossRef PubMed.
- O. Chen, J. Zhao, V. P. Chauhan, J. Cui, C. Wong, D. K. Harris, H. Wei, H.-S. Han, D. Fukumura, R. K. Jain and M. G. Bawendi, Nat. Mater., 2013, 12, 445–451 CrossRef CAS PubMed.
- M. Chern, T. T. Nguyen, A. H. Mahler and A. M. Dennis, Nanoscale, 2017, 9, 16446–16458 RSC.
- D. A. Hanifi, N. D. Bronstein, B. A. Koscher, Z. Nett, J. K. Swabeck, K. Takano, A. M. Schwartzberg, L. Maserati, K. Vandewal, Y. van de Burgt, A. Salleo and A. P. Alivisatos, Science, 2019, 363, 1199–1202 CrossRef CAS PubMed.
- C. Pu and X. Peng, J. Am. Chem. Soc., 2016, 138, 8134–8142 CrossRef CAS PubMed.
- A. B. Greytak, P. M. Allen, W. Liu, J. Zhao, E. R. Young, Z. Popović, B. J. Walker, D. G. Nocera and M. G. Bawendi, Chem. Sci., 2012, 3, 2028 RSC.
- S. Christodoulou, G. Vaccaro, V. Pinchetti, F. D. Donato, J. Q. Grim, A. Casu, A. Genovese, G. Vicidomini, A. Diaspro, S. Brovelli, L. Manna and I. Moreels, J. Mater. Chem. C, 2014, 2, 3439–3447 RSC.
- A. D. Balan, H. Eshet, J. H. Olshansky, Y. V. Lee, E. Rabani and A. P. Alivisatos, Nano Lett., 2017, 17, 1629–1636 CrossRef CAS PubMed.
- W. K. Bae, L. A. Padilha, Y.-S. Park, H. McDaniel, I. Robel, J. M. Pietryga and V. I. Klimov, ACS Nano, 2013, 7, 3411–3419 CrossRef CAS PubMed.
- S. Brovelli, R. D. Schaller, S. A. Crooker, F. García-Santamaría, Y. Chen, R. Viswanatha, J. A. Hollingsworth, H. Htoon and V. I. Klimov, Nat. Commun., 2011, 2, 280 CrossRef CAS PubMed.
- G. S. Selopal, H. Zhao, X. Tong, D. Benetti, F. Navarro-Pardo, Y. Zhou, D. Barba, F. Vidal, Z. M. Wang and F. Rosei, Adv. Funct. Mater., 2017, 27, 1701468 CrossRef.
- X. Peng, M. C. Schlamp, A. V. Kadavanich and A. P. Alivisatos, J. Am. Chem. Soc., 1997, 119, 7019–7029 CrossRef CAS.
- K. Gong, J. E. Martin, L. E. Shea-Rohwer, P. Lu and D. F. Kelley, J. Phys. Chem. C, 2015, 119, 2231–2238 CrossRef CAS.
- J. van Embden, J. Jasieniak and P. Mulvaney, J. Am. Chem. Soc., 2009, 131, 14299–14309 CrossRef CAS PubMed.
- C. Segarra, J. I. Climente, A. Polovitsyn, F. Rajadell, I. Moreels and J. Planelles, J. Phys. Chem. Lett., 2016, 7, 2182–2188 CrossRef CAS PubMed.
- Y. Nandan and M. S. Mehata, Sci. Rep., 2019, 9, 2 CrossRef PubMed.
- F. García-Santamaría, S. Brovelli, R. Viswanatha, J. A. Hollingsworth, H. Htoon, S. A. Crooker and V. I. Klimov, Nano Lett., 2011, 11, 687–693 CrossRef PubMed.
- H. Zhu, N. Song, W. Rodríguez-Córdoba and T. Lian, J. Am. Chem. Soc., 2012, 134, 4250–4257 CrossRef CAS PubMed.
- J. van Embden, J. Jasieniak, D. E. Gómez, P. Mulvaney and M. Giersig, Aust. J. Chem., 2007, 60, 457 CrossRef CAS.
- D. Steiner, D. Dorfs, U. Banin, F. Della Sala, L. Manna and O. Millo, Nano Lett., 2008, 8, 2954–2958 CrossRef CAS PubMed.
- C. Trager-Cowan, P. J. Parbrook, B. Henderson and K. P. O'Donnell, Semicond. Sci. Technol., 1992, 7, 536–541 CrossRef CAS.
- Y. Luo and L.-W. Wang, ACS Nano, 2010, 4, 91–98 CrossRef CAS PubMed.
- A. Shabaev, A. V. Rodina and Al. L. Efros, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205311 CrossRef.
- L. Carbone, C. Nobile, M. De Giorgi, F. D. Sala, G. Morello, P. Pompa, M. Hytch, E. Snoeck, A. Fiore, I. R. Franchini, M. Nadasan, A. F. Silvestre, L. Chiodo, S. Kudera, R. Cingolani, R. Krahne and L. Manna, Nano Lett., 2007, 7, 2942–2950 CrossRef CAS PubMed.
- J. H. Olshansky, A. D. Balan, T. X. Ding, X. Fu, Y. V. Lee and A. P. Alivisatos, ACS Nano, 2017, 11, 8346–8355 CrossRef CAS PubMed.
- D. Kong, Y. Jia, Y. Ren, Z. Xie, K. Wu and T. Lian, J. Phys. Chem. C, 2018, 122, 14091–14098 CrossRef CAS.
- A. Piryatinski, S. A. Ivanov, S. Tretiak and V. I. Klimov, Nano Lett., 2007, 7, 108–115 CrossRef CAS PubMed.
- D. Schooss, A. Mews, A. Eychmüller and H. Weller, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 17072–17078 CrossRef CAS PubMed.
- J. W. Haus, H. S. Zhou, I. Honma and H. Komiyama, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1359–1365 CrossRef CAS PubMed.
- J. Cui, Y. E. Panfil, S. Koley, D. Shamalia, N. Waiskopf, S. Remennik, I. Popov, M. Oded and U. Banin, Nat. Commun., 2019, 10, 5401 CrossRef CAS PubMed.
- F. T. Rabouw and C. de Mello Donega, Top. Curr. Chem., 2016, 374, 58 CrossRef PubMed.
- F. T. Rabouw, M. Kamp, R. J. A. van Dijk-Moes, D. R. Gamelin, A. F. Koenderink, A. Meijerink and D. Vanmaekelbergh, Nano Lett., 2015, 15, 7718–7725 CrossRef CAS PubMed.
- A. F. van Driel, G. Allan, C. Delerue, P. Lodahl, W. L. Vos and D. Vanmaekelbergh, Phys. Rev. Lett., 2005, 95, 236804 CrossRef CAS PubMed.
- D. Jang, Y. Han, S. Baek and J. Kim, Opt. Mater. Express, 2019, 9, 1257 CrossRef CAS.
- K. Gong and D. F. Kelley, J. Chem. Phys., 2014, 141, 194704 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic methods; characterization methods; computational methods; full PL lifetime decays and fits; radiative rates and lifetimes that incorporate PLQY data; wavefunction plots for a variety of geometries with and without Coulomb interactions; comparison of radiative rate data and theoretical electron–hole overlaps for different conduction band offsets; comparison between experimental and theoretical bandgaps. See DOI: 10.1039/d1ra07556j |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2021 |