Open Access Article
Open Access ArticleComparative study of photoinduced surface-relief-gratings on azo polymer and azo molecular glass films†
Xu Li ,
Hao Huang
,
Hao Huang ,
Bing Wu,
Chuyi Liao and
Xiaogong Wang
,
Bing Wu,
Chuyi Liao and
Xiaogong Wang *
*
Department of Chemical Engineering, Laboratory of Advanced Materials (MOE), Tsinghua University, Beijing 100084, P. R. China. E-mail: wxg-dce@mail.tsinghua.edu.cn
First published on 28th October 2021
Abstract
Photoinduced surface-relief-gratings (SRGs) on azo polymer and azo molecular glass films, caused by trans–cis isomerization of azo chromophores, have attracted wide interest for their intriguing nature and many possible applications in recent years. Understanding the mechanical properties of SRGs at the nanoscale is critically important for elucidating their formation mechanism and exploring their applications. In this work, a representative azo polymer (BP-AZ-CA) and a typical azo molecular glass (IAC-4) were comparatively studied for the first time concerning their properties related to SRG formation through a variety of methods. The results indicate that when inscribing SRGs on the films, IAC-4 shows a much higher efficiency for forming SRGs relative to that of BP-AZ-CA. The overall average moduli of SRGs measured by nanomechanical mapping techniques are obviously smaller compared with the moduli of the corresponding films of both materials. The moduli at different regions of SRGs are periodically varied along the grating vector direction for both BP-AZ-CA and IAC-4 gratings. The moduli at the trough regions of SRGs are always larger than those of the crests, while the moduli at the hillsides are the smallest. Distinct from BP-AZ-CA, even the moduli at the trough regions of IAC-4 SRG are smaller compared with that of the original film, and the ratio between the trough and crest moduli is significantly larger for IAC-4. These results provide deep understanding of the SRG formation mechanism and reveal the clear distinction between these two types of glassy materials for their SRG-forming behavior, which are important for future applications.
1 Introduction
Polymers and amorphous molecular materials containing azo chromophores, azo polymers and azo molecular glasses for short, have attracted extensive interest for their intriguing photo-responsive properties and many potential applications in the past decades.1–8 Upon irradiation with light in a certain wavelength range, the aromatic azo chromophores can undergo trans–cis photoisomerization,1,4 which triggers the materials to show a series of unique photo-responsive variations.9–15 Surface-relief-grating (SRG) formation on azo polymer and azo molecular glass films is one of the most interesting properties.16,17 When exposed to two interfering laser beams, a sinusoidal surface profile is formed on the films as a consequence of photo-induced mass transfer.2,4 The photoinduced mass transfer typically occurs at a temperature far below the glass transition temperature (Tg) of the materials. SRGs and other surface patterns at the level of hundreds of nanometers or even a few microns can be inscribed on the films to form one-dimensional or multi-dimensional periodic structures, which show potential for applications ranging from optics, photonics, and sensors to cell-guiding substrates.6,9–11,18,19 Several models and theories have been proposed to elucidate the mechanism of the SRG formation.20–27 The mass transfer caused by the light irradiation has been attributed to the free volume expansion,20,21 the electromagnetic gradient force of the light field,22–24 the photoinduced orientation and the transport induced by the anisotropic intermolecular interactions,25 the anisotropic diffusion of azobenzenes in polymer matrices,26 the mechanical stress caused by the photoinduced orientation anisotropy of azobenzene moieties,27 and others. The directional mass transfer has also been observed on other micro/nano structures and microspheres.28–30 Although it is generally agreed that the photoinduced trans–cis isomerization of azo chromophores plays a critically important role in the mass transfer process, the understanding of the mechanism is still a subject under intensive investigations.Azo polymers were first used to demonstrate the SRG formation,16,17 and have been intensively investigated since then for basic understanding and possible applications.2,4,6,9,10 Azo polymers commonly used in the investigations include polyacrylates/methacrylates and epoxy-based polymers bearing push–pull type azo chromophores.2,4–6,16,17 Distinct from azo polymers, azo molecular glasses are amorphous organic materials with a much lower molecular weight.7,31–35 Azo molecular glasses show the glass transition behavior similar to amorphous polymers and exist in a stable amorphous state below the glass transition temperature (Tg). Despite the similar amorphous nature, azo molecular glasses are distinctly different from azo polymers in several aspects, such as the well-defined molecular structures, no chain entanglement, and mono-dispersed molecular weight.7 These advantages make it possible to investigate the SRG formation caused by photoinduced mass transfer in an easily analysable way.31,33–35 Although both polymeric and molecular films have been widely adopted for investigations of SRGs, and it has been observed that SRGs can be more efficiently formed on an azo molecular glass film compared with that of an azo polymer,34 a systematic study of these two types of materials in respect of their SRG formation and other related properties under the comparable conditions has not been reported yet.
The methods commonly used for investigations on SRGs include surface profile characterizations by an atomic force microscope (AFM) and measurements of diffraction efficiency (DE) during SRG formation by optical method.2,4 These methods report the SRG formation behavior through AFM images and diffraction efficiency curves.16,17 Some specific methods have also been used to investigate the SRG formations such as the confocal Raman microspectroscopy,36,37 X-ray scattering measurements,38 scanning near-field optical microscopy,39 neutron reflectometry.40 These methods have shed new light on the fundamental understanding of SRG formation and photo-induced mass transfer behavior. With the rapid recent development, AFM has become a powerful tool for quantitative nanomechanical investigation.41,42 Through mechanical interaction of the AFM tip with the sample surfaces, it provides great potential to characterize nanomechanical properties of materials in various cases.43 Recently developed PeakForce Quantitative Nanomechanical Mapping (PeakForce QNM or PF-QNM) method allows the mapping of the nanomechanical properties of a sample surface together with topography at a high spatial resolution in a speed as fast as conventional tapping AFM imaging.44–48 By this technique, the elastic moduli can be derived from the force–indentation curves by using the different proposed models, which has been applied in many kinds of materials.46–50 Up to now, only few investigations have been reported to characterize the surface nanomechanical properties of SRGs by AFM.51–53 A study with the newly developed AFM techniques is able to provide a significant piece of the puzzle missing in the previous study. Especially, this method together with other analyses can pave a feasible way to compare the SRG formation behavior of azo polymer with that of azo molecular glass.
In this work, an azo polymer (BP-AZ-CA) and an azo molecular glass (IAC-4) were synthesized as the typical representatives of azo polymers and azo molecular glasses. The properties of BP-AZ-CA and IAC-4 related to the SRG formation were systematically investigated by several methods for comparison. Their SRG formation behavior was investigated by inscribing gratings with interfering laser irradiation. The surface modulus distributions in different areas of the SRGs were determined by the AFM PeakForce QNM technique. The corresponding force–indentation curves at different positions of the SRGs were also obtained by the ramp method, enabling the comparison of the mechanical modulus variations in the crest and trough areas for the SRGs formed after the different time of light irradiation. The nanomechanical measurements supply valuable information of the local structures “frozen” in the fixed positions of gratings as consequences of the mass transfer and molecular orientation. For the first time, the distinctive differences between the two types of glasses are revealed by comparing the SRG formation behavior of these two azo amorphous materials. The results can provide a deep insight into the mechanism of SRG formation and solid basis for applications of the materials.
2 Experimental
2.1 Materials
Isosorbide, 4-nitrobenzoyl chloride, aniline, and p-aminobenzoic acid were purchased from Sigma-Aldrich. Cinnamoyl chloride and N,N-di(hydroxyethyl)aniline were purchased from Alfa Aesar. Diglycidyl ether of bisphenol-A (MW = 392) was purchased as a commercial product from Shell Company. Deionized water (resistivity > 18.25 MΩ cm) was obtained from a Millipore water purification system. Glass slides were treated with the H2SO4/30% H2O2 (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) mixture (caution: this solution is extremely corrosive) for 3 h, rinsed with acetone and washed with plenty of deionized water for several times. Unless otherwise stated, all chemicals and solvents were purchased commercially and used directly without further purification. The synthesis and characterization details of BP-AZ-CA and IAC-4 have been reported in the previous articles,34,54 which can also be seen in the ESI.†
3) mixture (caution: this solution is extremely corrosive) for 3 h, rinsed with acetone and washed with plenty of deionized water for several times. Unless otherwise stated, all chemicals and solvents were purchased commercially and used directly without further purification. The synthesis and characterization details of BP-AZ-CA and IAC-4 have been reported in the previous articles,34,54 which can also be seen in the ESI.†
2.2 Characterization
The 1H NMR spectroscopic measurements were performed at 25 °C using a JEOL JNM-ECA600 NMR spectrometer (Japan, 600 MHz for proton) with tetramethylsilane (TMS) as the internal standard in dimethyl sulfoxide-d6 (DMSO-d6) or chloroform-d (CDCl3) solution. The Fourier transform infrared (FT-IR) spectra were obtained on a Nicolet Magna-IR 560 spectrophotometer (Thermo Fisher, USA) at a resolution of 4 cm−1, where the samples were incorporated in KBr powder and then pressed into thin IR-transparent disks. The wavenumber range for the measurement was 400–4000 cm−1. A total of 32 scans were averaged per sample to ensure high signal-to-noise ratios. The ultraviolet-visible (UV-Vis) spectra of the samples were determined by an Agilent Cary 8453 UV-Vis spectrophotometer (USA). The number average molecular weight and poly-dispersity index (PDI) of BP-AZ-CA were determined using a gel permeation chromatograph (GPC, Shimadzu, Japan), which was equipped with a RID-20A refractive index detector, a LC-20AD liquid chromatograph and a CTO-20AC column oven. The measurement was carried out at 25 °C using THF as eluent with a flow rate of 1.0 mL min−1 and the molecular weight was calibrated with polystyrene standards. The differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA) of the samples were performed utilizing TA Instruments DSC Q2000 and TGA Q5000 systems (USA) with a heating rate of 10 °C min−1 under nitrogen atmosphere. The SEM images were acquired in a field emission scanning electron microscope (FE-SEM) with InLens detector from Zeiss Corporation (GeminiSEM 500, Germany). A high-vacuum (3 × 10−6 mbar, approximately) condition was adopted, while the samples were imaged with an electronic high tension (EHT) of 15.0 kV. Nanoindentation tests were performed on a Nano Indenter G200 (Keysight) system using a Berkovich-type diamond indenter tip. The maximum indentation depth was 500 nm with a loading rate of 10 nm s−1. The BP-AZ-CA and IAC-4 films for nanoindentation tests were prepared by dip-coating the N,N-dimethylformamide (DMF) solutions (10 wt%) of the materials onto clean glass slides, evaporating solvents at 60 °C and drying in a vacuum oven for 48 h. The film thickness was larger than 10 times of the maximum indentation depth, which ensured the absence of substrate effect. To determine the photothermal effect of the sample films upon laser irradiation, the surface temperatures of the film areas with different diameters during the irradiation were measured by an infrared thermal imager (Guide Sensmart Tech Co., Ltd, T120).2.3 Photoinduced surface relief gratings
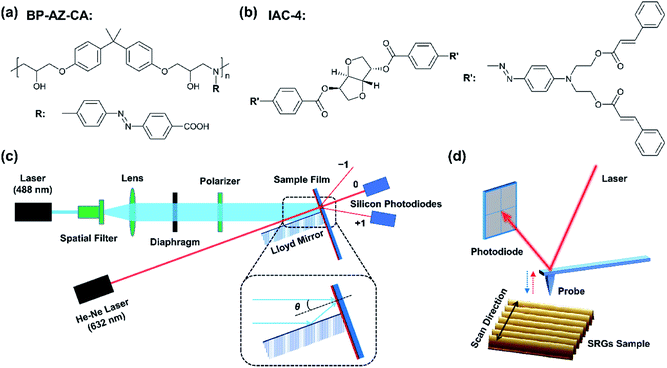
BP-AZ-CA and IAC-4 were dissolved in anhydrous DMF to obtain homogeneous solutions of 10% w/v. The solutions were filtered through 0.45 μm membranes and spin-coated onto the clean glass slides with the spin-coating speed of 800–1000 rpm and the time of 30 s. The spin-coated films were dried under vacuum at 50 °C for 24 h to remove the residual solvent. The experimental setup for inscribing the surface relief gratings is similar to that reported in the previous literatures.16,17 The SRGs were obtained by exposing the solid films to interfering p–p polarized laser beams (λ = 488 nm, 100 mW cm−2). The linearly polarized beam of laser (Genesis CX 488-2000 SLM, Coherent Corporation) was expanded with a spatial filter and collimated by a plano-convex lens to generate a homogeneous beam with the spot size of 6 mm in the diameter. The spatial periods (p) of the gratings were controlled according to the following equation,55
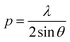 | (1) |
A He–Ne laser beam (λ = 632 nm, JDW-3, Peking University) was incident perpendicularly to the central position of the prepared surface relief gratings. The light intensity exhibited the Gaussian distribution in the beam cross section with a diameter of 2 mm, and the total intensity was measured to be 1.2 mW using a silicon photodiode (Thorlabs, 400–1100 nm). Two silicon photodiodes (Thorlabs, USB Power Meter PM16-120, 400–1100 nm) were adopted to measure the light intensities of the zero-order (I0) beam and first-order (I1) diffraction beam during the SRG inscribing process. The signals were finally transmitted to a computer and processed with Power Meter Driver Switcher software (Thorlabs), through which the light intensities were recorded in a real-time manner. The diffraction efficiency is defined as DE = I1/I0.
2.4 Atomic force microscope (AFM) measurement
The atomic force microscope (AFM) images were acquired by using a scanning probe microscope (Dimension Icon AFM, Bruker, USA) equipped with a Nanoscope V controller and NanoScope 8.15 software in the PeakForce Quantitative Nanomechanical Mapping (PF-QNM) mode. The heating controller and cooling water circulation device were applied to control the temperature of the sample stage. The measurements for the BP-AZ-CA and IAC-4 films at heating condition were performed at the temperature in the range of 30–150 °C in nitrogen atmosphere, while the measurements for the SRGs were carried out at room temperature under ambient condition. According to Bruker's protocol,45,56 the ceramic cantilever holder and the probe RTESP-300 (Bruker) were used for operation under heating condition, while the standard cantilever holder and the probe RTESPA-525 (Bruker) were used for operation at room temperature. The deflection sensitivities of the cantilevers were calibrated using a sapphire standard provided in the PF-QNM kit, and their spring constant k was calculated using the Sader method.57 The tip radius R of the probe was calibrated by the relative method on a polystyrene test sample (Bruker, PS Film, 2.7 GPa). The spring constant k of cantilevers used in this work was 32–40 N m−1 for RTESP-300 probes and 125–160 N m−1 for RTESPA-525 probes. The tip radii R of the RTESP-300 and RTESPA-525 probes were found to be in the range of 8–15 nm and 20–50 nm, respectively. Before the scanning process, the scan size was set to 0 nm and the peak force setpoint was set to 10 nN for the purpose of protecting the probe tip after being engaged to contact the sample surface. The ScanAsyst auto gain was set to on, so that the feedback gain value was dynamically and automatically controlled by the software, resulting in good sample tracking. Another critical parameter to protect the probe tip is that the peak force engage setpoint was set to 0.05 V. Since the RTESP-300 and RTESPA-525 probes both have stiff cantilevers with large spring constants, the relatively small value for the peak force engage setpoint can avoid excessive interaction between the tip and the sample during the engage process, which may cause damage to the probe tip. The peak force setpoints used in PF-QNM measurements at room temperature were 500 nN for BP-AZ-CA and 300 nN for IAC-4, respectively. An appropriate peak force setpoint is important for the AFM measurement in PF-QNM mode. On the one hand, too large peak force setpoint may damage the sample or the tip. On the other hand, if the peak force setpoint is too small, the probe tip may drift out of contact with the sample and will be unable to track the surface. The vertical oscillation frequency of the probe during the measurements was equal to 2 kHz with an amplitude of 50 nm. The lateral scanning rates were 0.5 Hz for images smaller than 5 × 5 μm2 and 0.2 Hz for images larger than 5 × 5 μm2 at a digital resolution of 256 × 256 pixels. As the scan size was gradually increased, the scan rate needed to be reduced to obtain high-quality images. For example, the scan rate was set to 0.2 Hz when the scan size was 10 × 5 μm2 in this study and the tip velocity became 4.0 μm s−1. Under the AFM PeakForce QNM mode, the force spectroscopies at different specific positions of the SRGs were measured by ramping along with the “Point and Shoot” application in the NanoScope software (version 8.15). The trigger mode was set to be relative, and the trig thresholds used for the ramp measurements were 800 nN (for BP-AZ-CA) and 500 nN (for IAC-4), respectively. The ramp rate was 1 Hz (default), and the ramp size was set to be 100 nm.3 Results and discussion
The structures of BP-AZ-CA and IAC-4 are shown in Fig. 1a and b, respectively. BP-AZ-CA is an epoxy-based polymer covalently bearing push–pull type azo chromophores in each repeating unit. IAC-4 is a molecular amorphous material containing a core of isosorbide moiety bearing two push–pull type azo chromophores and peripheral cinnamate groups. BP-AZ-CA and IAC-4 were synthesized according to the previous reports,34,54 and characterized by 1H NMR and FT-IR. The spectra are given in Fig. S1 and S2 (ESI†) together with the related properties listed in Table S1 (ESI†). As reported in the previous articles, both materials show good performance for forming SRGs under the light irradiation.34,54,58 Fig. 1c shows the schematic diagram of the SRG-writing set-up upon exposing the films to the p–p interfering pattern formed by two linearly polarized laser beams. The prepared SRGs were characterized by AFM to map the nanomechanical properties of the surface and give the topographic profiles as well, as shown in Fig. 1d. The spectral and thermal characteristics of the materials are presented in Section 3.1. Although SRGs can be well inscribed on both BP-AZ-CA and IAC-4 films through mass transfer below the glass transition temperature, some important distinctions can be observed for their properties as discussed in the sections below in details.3.1 Spectral and thermal characteristics
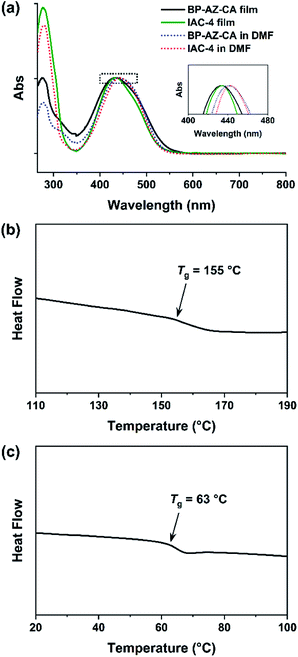
As containing push–pull type azo chromophores, both BP-AZ-CA and IAC-4 show absorption bands in the visible light region, centered at almost the same wavelength (Fig. 2a and S3, ESI†). The maximum absorption wavelengths (λmax) of BP-AZ-CA and IAC-4 in DMF are 440 nm and 443 nm, respectively. Their extinction coefficients (ε) at λ = 488 nm are 22.0 L g−1 cm−1 (BP-AZ-CA) and 29.6 L g−1 cm−1 (IAC-4), which are also in the same order of magnitude. Fig. 2b and c show the DSC heating curves of BP-AZ-CA and IAC-4, which confirm the amorphous nature of the two materials. As shown in the figures, the Tg of BP-AZ-CA is 155 °C, which is markedly higher than that of IAC-4 (63 °C). This difference is attributed to the fact that BP-AZ-CA is a high-molecular-weight polymer with chain entanglement, which largely hinders the movement of chain segments until a high temperature. The number-average molecular weight of BP-AZ-CA was estimated to be 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 with the polydispersity index of 1.8 (Fig. S4, ESI†), while that IAC-4 is a compound with the molecular weight of 1289.4. Nevertheless, the thermal decomposition stability is not directly correlated with the molecular weights. The thermal decomposition temperature (Td, defined as 5% mass loss temperature) of IAC-4 is 335 °C, while that of BP-AZ-CA is 250 °C (Fig. S5, ESI†), which indicates IAC-4 is more stable against thermal degradation at high temperature.
000 with the polydispersity index of 1.8 (Fig. S4, ESI†), while that IAC-4 is a compound with the molecular weight of 1289.4. Nevertheless, the thermal decomposition stability is not directly correlated with the molecular weights. The thermal decomposition temperature (Td, defined as 5% mass loss temperature) of IAC-4 is 335 °C, while that of BP-AZ-CA is 250 °C (Fig. S5, ESI†), which indicates IAC-4 is more stable against thermal degradation at high temperature.
3.2 Surface-relief-grating (SRG) formation behavior
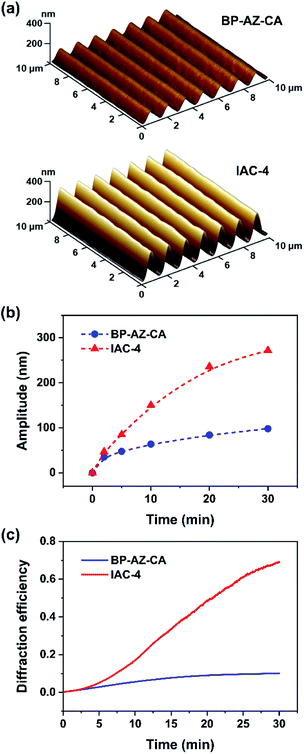
Upon irradiation with interfering laser beams, the film surfaces of azo polymers and azo molecular glasses can undergo mass migration to form SRGs, which is one of the most fascinating characteristics of the materials. Typically, the SRG formation behavior is characterized by observation of the surface profile variations and measurement of diffraction efficiency (DE) of the gratings during SRG formation.2,4 In this work, the BP-AZ-CA and IAC-4 spin-coated films with the thicknesses in the range of 600–750 nm (Fig. S6, ESI†) were prepared and used to inscribe SRGs. The surface profiles of SRGs formed on the films were characterized by AFM, and their DE variations during the SRG formation process were recorded in situ with two optical power meters. Fig. 3a shows the three-dimensional (3D) images of the SRGs on the BP-AZ-CA and IAC-4 films after irradiation with the interfering p–p polarized laser beams (λ = 488 nm, 100 mW cm−2) for 30 min. The SRGs formed on the surfaces show the significantly different amplitudes for the BP-AZ-CA and IAC-4 films, where the value for the IAC-4 grating is much higher. The cross sections of SRGs formed on the BP-AZ-CA and IAC-4 films at different time are given in Fig. S7 and S8 (ESI†). The amplitude variation with the irradiation time is given in Fig. 3b, where the growth rate is much higher for IAC-4. The results all indicate that SRG can be much more efficiently formed on the IAC-4 film than BP-AZ-CA under the same irradiation conditions. Fig. 3c shows the corresponding real-time DE of the SRGs with a spatial period of 1400 nm upon the light irradiation. The DE of SRG of IAC-4 also increases more rapidly than that of BP-AZ-CA. The diffraction efficiency variation of the grating is dependent on the grating amplitude.59,60 The DE has the correlation with the grating amplitude as below,
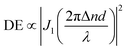 | (2) |
It can be concluded from the above results that IAC-4 demonstrates a significantly higher efficiency for forming SRGs upon the light irradiation as compared to BP-AZ-CA. Although, the Tg of IAC-4 (63 °C) is much lower than that of BP-AZ-CA (155 °C), the temperature increases of the films originated from the photothermal effect by laser irradiation are less than 10 °C at room temperature, proved through simulation and experimental measurement (Table S2, Fig. S9 and S10, ESI†). This limited temperature increase upon the light irradiation is consistent with the previous report.61 It means that the SRGs on the BP-AZ-CA and IAC-4 films are formed below their Tgs. For BP-AZ-CA with the high molecular weight, the ability of segment motion is greatly hindered by the chain entanglement. As a small molecule without such chain interaction, IAC-4 possesses markedly higher molecular mobility upon light irradiation. The light-induced motions of IAC-4 need to overcome a lower energy barrier, while much more energy is demanded to disentangle the chain segments and drive the mass migration of BP-AZ-CA to form SRGs. As a result, SRG formation on BP-AZ-CA film needs a relatively long irradiation time and shows the slower growth rate. The reasons for the two materials to show significantly different SRG-forming characteristics will be further discussed in Section 3.7.
3.3 Analysing moduli via Derjaguin–Muller–Toporov (DMT) model
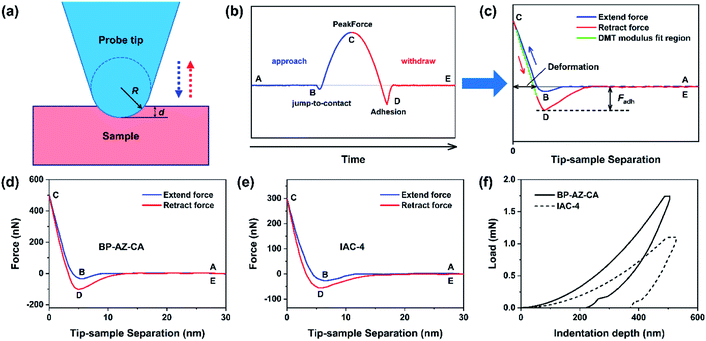
Both the films and SRGs formed on the BP-AZ-CA and IAC-4 films were investigated by the nanomechanical measurements with AFM. Successful measurement of the elastic properties of materials by AFM requires a suitable probe tip/cantilever assembly, since the calculation of elastic modulus has certain requirements for the indentation depth of the sample. Besides that, the cantilever needs a sufficient spring constant to prevent excessive deformation during contact, and the probe tip must be rigid enough to avoid significant deformation of itself.62 The normal working range of the probe RTESPA-525 used in this study is 1 GPa to 20 GPa,45,56 which is compatible with the measured sample moduli at room temperature. Thus, the probe RTESPA-525 was mainly adopted for the current AFM PF-QNM measurement based on the Bruker's protocol, to ensure that the measured moduli are more accurate. The images obtained in AFM experiments were processed through the NanoScope Analysis (Bruker) software. In the AFM PeakForce QNM mode, a series of force–indentation curves were obtained through PeakForce Tapping technology, and then the force curves were fitted and analyzed using the Derjaguin–Muller–Toporov (DMT) model.63 As shown in Fig. 4a, this model assumes a deformation (d) that is much smaller compared to the tip radius, providing spherical contact shape of the tip. In addition, this model considers an adhesion between the tip and the surface.64,65 Consequently, the DMT model is well adapted to the hard material surfaces, which is the case of our samples. Fig. 4b shows a sample of the force curve as a function of time recorded by AFM, including the jump-to-contact point (B), PeakForce point (C), and adhesion point (D). Fig. 4c shows the same data as Fig. 4b but with the force plotted as a function of the tip–sample separation, where the separation is calculated from the Z piezo position and the cantilever deflection after eliminating the time variable.45 The reduced Young's modulus, E*, was thus obtained through fitting the retract curve (green line in Fig. 4c) with the equation,
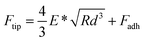 | (3) |
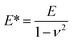 | (4) |
As shown in Fig. 4d and e, there is no force on the tip when the probe is far away from the sample (point A). As the probe tip approaches the BP-AZ-CA or IAC-4 film, the van der Waals attractive force overcomes the cantilever stiffness and the tip is pulled to the sample surface (point B, the so-called jump-to-contact as shown in Fig. 4b). At this time, the force curve is recorded as a negative value. Then the tip stays on the surface of the sample, and the force increases until it reaches the PeakForce (force setpoint), at which the deformation (indentation depth) of the sample reaches its maximum value (point C). To obtain appropriate deformation of the sample, different peak forces were used for BP-AZ-CA (500 nN) and IAC-4 (300 nN), respectively. The deformations of BP-AZ-CA or IAC-4 film in the PF-QNM measurements were controlled in the range of 3–5 nm, which was illustrated in Fig. 4d and e. Then the probe starts to withdraw, and the force decreases until it reaches a minimum at point D. This minimum force is the adhesive force produced by the interaction of the probe tip with BP-AZ-CA and IAC-4 sample. Finally, after the tip comes off the sample surface, the force curve is close to zero again as there is only a weak long-range force (point E). As for the mechanical properties through the AFM PF-QNM measurements and the force–indentation curves analysis, the DMT elastic moduli were obtained to be 6.1 ± 0.4 GPa for BP-AZ-CA films and 4.2 ± 0.3 GPa for IAC-4 films (Fig. 4d, e and S11, ESI†). The mechanical properties of these two azo materials are in the same order of magnitude, but the DMT elastic modulus of BP-AZ-CA is significantly higher than that of IAC-4. This result is also confirmed by the nanoindentation test (Fig. 4f), the Young's moduli obtained by the measurements are 5.6 ± 0.1 GPa for BP-AZ-CA films and 4.0 ± 0.2 GPa for IAC-4 films, respectively. The Young's moduli measured by the two aforementioned methods are very close within the error range, which proves the accuracy and reliability of the AFM PeakForce QNM technology in measuring nanomechanical properties. The significantly higher elastic modulus of the azo polymer can be attributed to the chain entanglement, which needs a higher stress to unjamming the glassy state for deformation.
3.4 Effect of temperature on DMT moduli of BP-AZ-CA and IAC-4
The temperature dependence of the elastic moduli measured by AFM can supply further information of the molecular mobility of the materials. The force spectroscopy curves of BP-AZ-CA and IAC-4 at heating process were measured by ramping the probe onto the sample surface in the AFM PeakForce QNM mode, and their DMT moduli varying with temperature were obtained. To avoid possible by-effect in the heating process, such as causing the metal coating of the probe cantilever to fall off, the probe RTESP-300 without aluminum coating was used under the heating condition and the measurements were carried out at temperature below 150 °C. Due to the drastic variation in mechanical property of the IAC-4 after heating, in order to obtain appropriate deformation of the sample at different temperatures, the trig thresholds in the relative trigger mode (or the peak forces) applied for the ramp measurements of IAC-4 were set to be 3–300 nN. The measurements at each temperature were repeated for at least 5 times, and the fitted modulus value was taken by average. As shown in Fig. 5a, the DMT modulus of BP-AZ-CA reduces gradually during the heating process from 30 to 150 °C, indicating its thermal expansion and density decrease, for which the stress needed to cause the deformation decreases accordingly. For comparison, the DMT modulus of IAC-4 was measured under the same condition in the range of 30–150 °C (Fig. 5b). The DMT modulus of IAC-4 decreases slightly from 4.19 GPa to 3.96 GPa when heating from 30 to 50 °C before the temperature reaches its Tg (63 °C). This effect caused by the volume expansion is similar to that of BP-AZ-CA. However, when the temperature rises above Tg, its modulus drops dramatically. As the temperature of the sample rises to 120 °C, the DMT modulus of IAC-4 decreases to less than 20 MPa.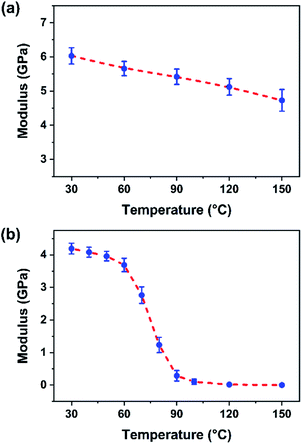 | ||
| Fig. 5 Relationship between the DMT modulus of BP-AZ-CA film (a) and IAC-4 film (b) versus temperature. The error bar is the standard deviation from five measurements. | ||
It is well known that for a polymer, the modulus will enter the rubbery plateau if the temperature is further increased after the glass transition.66 In this temperature range, the polymer chains undergo the short-range diffusional motions of the segments. On the other hand, the long-range cooperative motions of chains are still restricted by the existence of the strong local interactions between the neighboring chains, which is known as the entanglement for a linear polymer.66 However, above nanomechanical investigation indicates that no such rubbery plateau exists for IAC-4 due to the lack of the network formed by the chain entanglement. Therefore, the extremely low modulus is observed after the glass transition, which indicates the high mobility of the molecules. When activated by the light irradiation, the motions only need a much smaller driving force.
3.5 Nanomechanical properties of SRGs
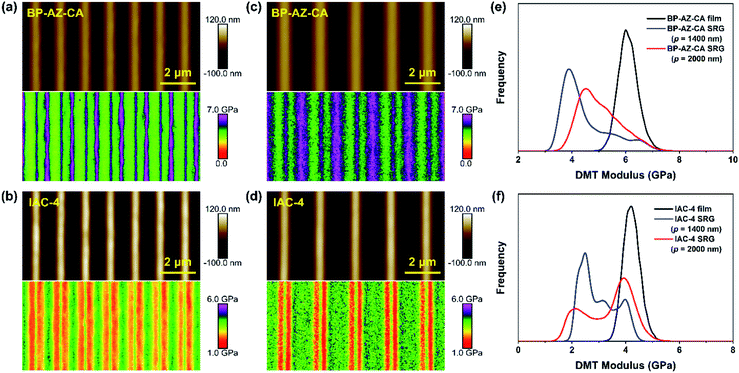
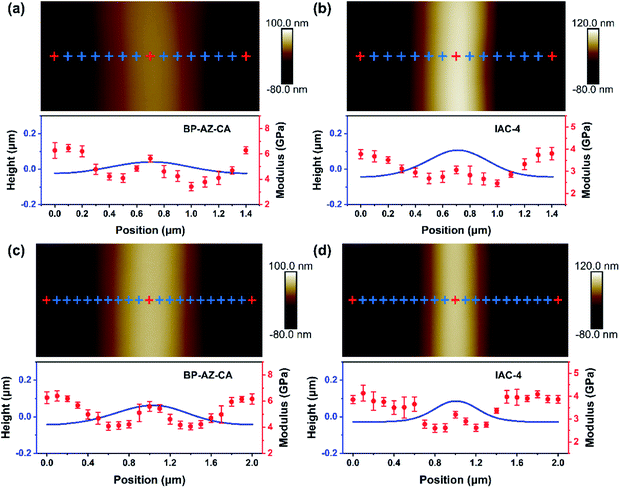
The AFM PeakForce QNM technology enables quantitative measurements of nano-scale material properties involving the morphology and nanomechanical modulus of the sample at the same time. To better understand the similarities and differences between BP-AZ-CA and IAC-4 for their SRG formation behavior, the surface topological structure and nano-scale modulus distribution of SRGs prepared on these two types of films were examined by the AFM PeakForce QNM measurement. It provides us with high-resolution modulus distribution maps of SRGs, so that we can more clearly observe DMT moduli in different regions of SRGs. The probe RTESPA-525 with a nominal tip curvature radius (R) of 8 nm was used in this measurement. The size of the AFM probe tip was much smaller than the periods of SRGs, as confirmed by the SEM images of the probe (Fig. S12, ESI†). The force curves were fitted and analyzed to obtain the elastic moduli of the materials using the DMT model, which required a sufficient sample deformation (usually ≥2 nm). As explained previously, the probe RTESPA-525 is suitable for BP-AZ-CA and IAC-4 with Young's modulus ranges of 1–20 GPa. Fig. 6a–d show the height maps and DMT modulus distribution maps of SRGs with the periods of 1400 nm and 2000 nm formed on BP-AZ-CA and IAC-4 films upon laser irradiation (100 mW cm−2) for 10 min and 30 min, respectively. The periodic variations of the nanomechanical moduli in the grating vector direction of SRGs can be clearly seen from Fig. 6a–d. For both BP-AZ-CA and IAC-4, the moduli of SRGs demonstrate a periodic distribution corresponding to their morphological profiles. The moduli at the trough regions of SRGs are always higher than those of the crests, while the moduli at the areas between the crest and trough regions (hillsides) are the smallest. The trough regions of SRGs correspond to the highest light intensity regions of interference patterns formed by laser beams. Notably, for the SRGs prepared on both BP-AZ-CA and IAC-4 films, the overall averaged moduli are smaller than the corresponding moduli of the initial films as shown in Fig. 6e and f.By the “Point and Shoot” procedure in the NanoScope software, the AFM probe can be precisely moved to the desired positions in a scanning image. This allows us to carry out a single point force spectroscopy measurement at a specific position on the sample surface. To further confirm the above experimental results, the single-point ramp force mode was also used to measure the respective force–indentation curves at the selected positions (the cross mark in Fig. 7) within one period of SRGs, and the corresponding elastic moduli were calculated by DMT model with NanoScope software. Both the DMT modulus distribution map and the single point force spectroscopy measurement reveal the nanomechanical modulus variation along the grating vector direction of SRGs, which are observed for BP-AZ-CA and IAC-4 films and for two different grating periods (1400 nm and 2000 nm). As shown in Fig. 7a–d, the modulus variations of SRGs at different specific positions within one period are highly consistent with the results obtained by the continuous scanning of the PeakForce QNM mode. That is, the moduli at trough regions of SRGs are higher than the crest moduli, and the regions with lowest moduli are located at the hillsides of the SRGs.
3.6 Crest and trough moduli of SRGs varied with irradiation time
As mentioned above, the crest and trough regions are two characteristic positions in the SRGs with the relatively high moduli. To figure out the modulus variations in these two regions with the irradiation time, the nanomechanical moduli at these two regions were measured after the films were exposed to the interfering fringes of the laser beams for different time periods. The SRGs were inscribed on BP-AZ-CA and IAC-4 films under p–p linearly polarized interference laser irradiation (100 mW cm−2). The force spectroscopy curves at the crest and trough positions of SRGs inscribed on BP-AZ-CA and IAC-4 films at different irradiation time were measured using single-point ramp force mode. To ensure the reliability of the results, the force–indentation curves were measured for three times at more than 10 different crest and trough positions for each SRG sample, and the average elastic moduli were fitted and calculated by the DMT model with the NanoScope software.Fig. 8a–d show the DMT modulus variations over the irradiation time at the crests and troughs of SRGs with the periods of 1400 nm and 2000 nm, respectively. Two important observations can be obtained from the results. First, the DMT modulus variations at the crests and troughs of SRGs for the BP-AZ-CA and IAC-4 films are quite different. For BP-AZ-CA, the DMT moduli at the troughs of the prepared SRGs are higher than that of the film and increase gradually, while moduli at the crests are lower than that of the film and decrease with the irradiation time. In contrast, the DMT moduli at the crests and troughs of SRGs on the IAC-4 film are lower than that of the film and decrease with increasing irradiation time. The DMT modulus at the trough is reduced slightly upon irradiation, while that at the crest decreases more obviously as the irradiation time increases. Second, for both BP-AZ-CA and IAC-4, the trough moduli of the SRGs are always higher than the crest moduli and their difference increases with irradiation time. To make a quantitative comparison, the modulus ratio is defined as RE = Et/Ec, where Et and Ec are the average DMT moduli at the troughs and the crests of SRGs, respectively. Fig. 8e and f show the modulus ratio (RE) of BP-AZ-CA and IAC-4 SRGs with different spatial periods (1400 nm and 2000 nm) varying with the irradiation time in the SRG formation. The results show that the RE values increase with the irradiation time for both BP-AZ-CA and IAC-4, but the increase rate is obviously higher for IAC-4. The RE value of SRG of BP-AZ-CA at 30 min is around 1.16, while that of IAC-4 is up to around 1.28 after the light irradiation for the same time.
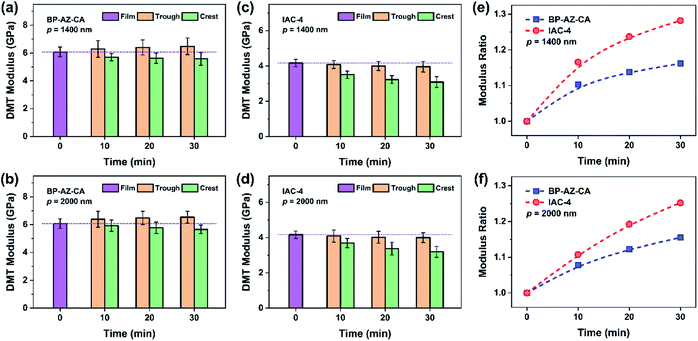 | ||
| Fig. 8 (a–d) DMT modulus variations obtained by the ramp method at the trough and the crest positions (the red cross mark in Fig. 7) of SRGs: (a) BP-AZ-CA, p = 1400 nm; (b) BP-AZ-CA, p = 2000 nm; (c) IAC-4, p = 1400 nm; (d) IAC-4, p = 2000 nm. (e and f) Variations of the modulus ratios of the trough to the crest positions: (e) p = 1400 nm; (f) p = 2000 nm. | ||
3.7 Mechanism and comparison
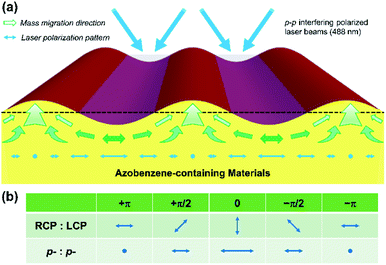
The results reported above can provide new insights into the mechanism of SRG formation and the intrinsic difference between the azo polymer and azo molecular glass for their SRG formation behavior. The formation of SRGs is attributed to the directional mass transfer along the direction of the electric vibration of the polarized light.2,4,6,9 When two p-polarized laser beams are superimposed to form the interference fringe, a periodic distribution of light intensity is achieved with the polarization mode shown in Fig. 9a. The irradiation with the light causes the mass transfer from the high intensity regions to the low intensity regions.22,23 The regions corresponding to the troughs of SRGs are the areas with the high light intensity. Since BP-AZ-CA and IAC-4 contain the similar push–pull type azo chromophores, the driving force to cause SRG formation is comparable for these two materials, but the responses of the materials to light irradiation are quite different. As shown in Fig. 2b and c, BP-AZ-CA has a much higher Tg compared with that of IAC-4. The glass transition occurs at the temperature when the thermal energy is roughly equal to the potential energy barriers to the segment rotation and transition.66 It means that the potential energy barriers for the segment motions are much higher for BP-AZ-CA compared with the molecule motion and transition of IAC-4. The nanomechanical investigation indicates that IAC-4 has the extremely low modulus after the glass transition (Fig. 5), as there is no chain entanglement for the IAC-4 molecules. Therefore, when unjammed by light irradiation, the motions of IAC-4 molecules need a much smaller driving force. These observations can provide rationale for the much high efficiency for IAC-4 to form SRGs as shown in Fig. 3.As the mass transfer and submicron-scale relaxation are relatively slow processes, the local structures are essentially “frozen” in the fixed positions of the formed gratings. The nanomechanical measurements on SRGs can supply the valuable information of the variations caused by the light irradiation. As shown by DMT modulus histogram curves in Fig. 6e and f, SRGs are covered by a large proportion of areas with the lower moduli compared with that of the original film. This observation is consistent with the free volume expansion model.20,21 As the light irradiation causes repeated trans–cis isomerization cycles with the recurrent changes of azo chromophore conjugation length and dipole moment, it shows the effect to increase the free volume and mobility for both IAC-4 and BP-AZ-CA. The significantly lower moduli of IAC-4 compared with those of BP-AZ-CA before and after light irradiation indicate the higher fraction of the free volume existing in the molecular glass, which results in the greater mobility under the light irradiation. As shown in Fig. 8c and d, the DMT moduli at the crests and troughs of SRGs prepared on the IAC-4 film are all lower than that of the film and decreases with increasing irradiation time. These results indicate that the free volume expansion is necessary to accomplish the macroscopic mass transfer, which is also a point to show critical difference between an azo polymer and an azo molecular glass. On the other hand, as the moduli were measured after switching off the irradiation, the modulus decrease could not account for the free volume increase in the dynamic process under the light irradiation. Meanwhile, the free volume expansion caused by the light irradiation is not a process owing to photothermal effect. This point is confirmed by the measured and calculated temperature increases upon the light irradiation, which is less than 10 °C for a macroscopic area (Table S2, Fig. S9 and S10, ESI†).
Comparing the DMT moduli at different regions of SRG can supply further clues to understand the grating formation mechanism. Aforementioned results show that the moduli at trough regions of SRGs are higher than the crest moduli, and the regions with lowest moduli are located at the hillsides of the SRGs (Fig. 6 and 7). The low moduli at the sloping sides of the gratings can be explained by the gradient force theory.22,23 According to the theory, the gradient force is largest in the slopes of the grating. The stress and deformation can increase the mobility in a glass and force them to become more dynamically homogeneous.67,68 The low moduli in the sloping regions evidence the free volume increase caused by the forced motion, where the macroscopic temperature is still much lower than Tg. The crest regions have the higher moduli compared with those of the hillsides are consistent with previous studies.51,52 It has been attributed to the increase in density in the crest regions,51 as the regions correspond to the dark fringes of the interfering light field and are under compression from the sloping sides with the highest gradient force to cause mass transfer. On the other hand, the troughs of SRGs are formed in the areas corresponding to the highest light intensity, the material at these regions migrate along the direction of light polarization to form crests in the regions with the lowest light intensity. Although the most effective trans–cis isomerization of azo chromophores initially occurs in the trough regions due to the high light intensity, the chromophores in the regions will quickly align in the direction perpendicular to the electric vibration direction of the linearly polarized light due to the angular hole burning and redistribution effects.4–6 Therefore, the high moduli in the trough regions are believed to be caused by the chromophore orientation and related intermolecular rearrangement. As p–p polarization mode used in this study is distinct from the orthogonal circular polarization mode (Fig. 9b), the exact regions with the highest moduli are different.52,53 Nevertheless, the highest moduli regions all correspond to the regions with the high molecular orientation. The enhanced orientation will increase van der Waals interaction between neighbored molecules and the local stiffness.52 Results given in Fig. 8 show that the crest moduli decrease but the RE values increase with the irradiation time. This observation can be attributed to the reduced compression pressure from the sloping sides due to the increase of the grating amplitude. Moreover, the increase rate of the RE is obviously higher for IAC-4 compared with that of BP-AZ-CA. Besides the reduced moduli in the crest regions, it could also be related to the higher efficiency of the photo-induced orientation for an azo molecular glass compared with that of an azo polymer.69
Above results indicate that the mass transfer and SRG formation are processes related to the free volume increase, which is a necessary condition for the segment and molecule motions. This trend is similar to the case for an organic material to exhibit the higher mobility at increased temperature. However, a distinct difference is that the free volume increase caused by the light irradiation is not due to a simple thermal effect. In this case, the mass transfer depends on the driving force of light irradiation to cause the mobility increase in the regions with the high stress, which results in the low density and moduli in the regions. Meanwhile, the photo-induced orientation of the azo chromophores and related structure rearrangement also influence the local rigidity. The significantly higher efficiency for IAC-4 to form SRG is attributed to the higher proportion of the free volume and no entanglement of polymer chains. For perspective of application, an azo polymer such as BP-AZ-CA is more suitable for applications to endure the temperature variation. At the temperature above Tg (63 °C), IAC-4 enters the viscous flow state, while BP-AZ-CA is still glassy until 155 °C. On the other hand, the difference between the Tg and the Td of IAC-4 is 272 °C, much larger than that of BP-AZ-CA (less than 100 °C). Therefore, IAC-4 possesses a larger thermoformable temperature range, which endows it with a promising thermal-processing opportunity. As an example, by means of soft-lithographic hot embossing at 110 °C with elastomeric poly(dimethylsiloxane) (PDMS) molds, the periodic sub-micron hexagonal pillar and hole arrays could be fabricated on IAC-4 films, which is described in ESI (Fig. S13†).
4 Conclusions
In this study, for the first time, the surface-relief-grating (SRG) formation behavior of azo polymer and azo molecular glass was studied by a directly comparative manner. The azo polymer (BP-AZ-CA) and azo molecular glass (IAC-4) were synthesized and their properties related to the SRG formation were measured and compared. The investigations showed that IAC-4 forms SRG in a much more efficient manner compared with the capability of BP-AZ-CA. Under the same irradiation condition with p–p interfering laser beams, the SRGs with much higher amplitudes are formed on the IAC-4 films as compared with those on the BP-AZ-CA films. The AFM PeakForce QNM method was used to quantitatively characterize the surface morphology and nanomechanical properties of SRGs. After being irradiated with the interfering laser beams, the overall average moduli of SRGs obviously decrease as compared with the initial moduli of the corresponding films for both BP-AZ-CA and IAC-4. This trend is observed to be more significant for IAC-4 compared with BP-AZ-CA. Distinct from BP-AZ-CA, the moduli in the trough regions of SRG formed on IAC-4 film are lower compared with that of the original film. It evidences the free volume increase is more significant for IAC-4 compared with BP-AZ-CA as no chain entanglement exist in the azo molecular glass. The moduli in different regions of the SRGs are periodically varied along the grating vector direction for both BP-AZ-CA and IAC-4 gratings. The moduli at trough regions of SRGs are higher than the crest moduli, and the regions with lowest moduli are located at the hillsides of the SRGs. The low moduli in the sloping regions are attributed to the free volume increase caused by the larger driving force in the regions, which is consistent with the gradient force model. The moduli at the crest positions of the SRGs are higher than those at the sloping sides, indicating the compression caused by the significant mass transfer in the sloping sides, which result in the higher density in the crest regions. Although the high rate of the trans–cis isomerization initially occurs in trough regions of SRGs with the highest light intensity, the chromophores in the regions quickly align in the direction perpendicular to the electric vibration direction of the polarized light. Therefore, the high moduli in the trough regions correspond to the effect of the high degree of the molecular orientation. The increase of the modulus ratio (Et/Ec) with the irradiation time could be caused by the reduced compression from the sloping sides due to the increase of the grating amplitude and the increased orientation in the trough regions in the process. The more significant increase in the modulus ratio for IAC-4, compared with that of BP-AZ-CA, indicates a higher degree orientation for IAC-4 in the trough regions. Due to the characteristics of the high free volume proportion and no chain entanglement restriction, IAC-4 shows much lower moduli above the glass transition temperature and the good thermal processing performance, which is suitable for hot embossing to prepare micro/nano-scale patterns for further photo-processing applications. Above results clearly indicate that although the free volume increase is a necessary condition for the mass transfer and SRG formation, the free volume increase behavior as a response to light irradiation is obviously different for azo polymer and azo molecular glass. The observations are of benefit to deeply understand the SRG formation mechanism and unjamming transition processes of organic glassy materials with the low and high molecular weight.Author contributions
X. Li: conceptualization, methodology, investigation, writing original draft. H. Huang: resources, investigation, software. B. Wu: formal analysis. C. Y. Liao: review & editing. X. G. Wang: conceptualization, writing, review & editing, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from the National Natural Science Foundation of China (NSFC) under Projects 51773108 and 51233002 is gratefully acknowledged. Also, we wish to thank Professor Ken Nakajima, Dr Xiaobin Liang in Tokyo Institute of Technology and Dr Yang Liu of Bruker (Beijing) Scientific Technology Co., Ltd for their kind helps in the use of AFM.Notes and references
- S. Xie, A. Natansohn and P. Rochon, Chem. Mater., 1993, 5, 403–411 CrossRef CAS.
- N. K. Viswanathan, D. Yu Kim, S. Bian, J. Williams, W. Liu, L. Li, L. Samuelson, J. Kumar and S. K. Tripathy, J. Mater. Chem., 1999, 9, 1941–1955 RSC.
- J. A. Delaire and K. Nakatani, Chem. Rev., 2000, 100, 1817–1846 CrossRef CAS PubMed.
- A. Natansohn and P. Rochon, Chem. Rev., 2002, 102, 4139–4176 CrossRef CAS PubMed.
- Y. Zhao and T. Ikeda, Smart Light-Responsive Materials: Azobenzene-Containing Polymers and Liquid Crystals, Wiley, 2009 Search PubMed.
- X. G. Wang, Azo Polymers: Synthesis, Functions and Applications, Springer, Berlin, 2017 Search PubMed.
- Y. Shirota, J. Mater. Chem., 2005, 15, 75–93 RSC.
- D. Dattler, G. Fuks, J. Heiser, E. Moulin, A. Perrot, X. Yao and N. Giuseppone, Chem. Rev., 2020, 120, 310–433 CrossRef CAS PubMed.
- S. Lee, H. S. Kang and J.-K. Park, Adv. Mater., 2012, 24, 2069–2103 CrossRef CAS PubMed.
- A. Priimagi and A. Shevchenko, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 163–182 CrossRef CAS.
- S. L. Oscurato, M. Salvatore, P. Maddalena and A. Ambrosio, Nanophotonics, 2018, 7, 1387–1422 CAS.
- H. F. Yu and T. Ikeda, Adv. Mater., 2011, 23, 2149–2180 CrossRef CAS PubMed.
- H. Finkelmann, E. Nishikawa, G. G. Pereira and M. Warner, Phys. Rev. Lett., 2001, 87, 015501 CrossRef CAS PubMed.
- M. H. Li, P. Keller, B. Li, X. G. Wang and M. Brunet, Adv. Mater., 2003, 15, 569–572 CrossRef CAS.
- Y. L. Yu, M. Nakano and T. Ikeda, Nature, 2003, 425, 145 CrossRef CAS PubMed.
- P. Rochon, E. Batalla and A. Natansohn, Appl. Phys. Lett., 1995, 66, 136–138 CrossRef CAS.
- D. Y. Kim, S. K. Tripathy, L. Li and J. Kumar, Appl. Phys. Lett., 1995, 66, 1166–1168 CrossRef CAS.
- K. G. Yager and C. J. Barrett, Curr. Opin. Solid State Mater. Sci., 2001, 5, 487–494 CrossRef CAS.
- A. Puliafito, S. Ricciardi, F. Pirani, V. Čermochová, L. Boarino, N. De Leo, L. Primo and E. Descrovi, Adv. Sci., 2019, 6, 1801826 CrossRef PubMed.
- C. J. Barrett, A. L. Natansohn and P. L. Rochon, J. Phys. Chem., 1996, 100, 8836–8842 CrossRef CAS.
- C. J. Barrett, P. L. Rochon and A. L. Natansohn, J. Chem. Phys., 1998, 109, 1505–1516 CrossRef CAS.
- J. Kumar, L. Li, X. L. Jiang, D.-Y. Kim, T. S. Lee and S. Tripathy, Appl. Phys. Lett., 1998, 72, 2096–2098 CrossRef CAS.
- S. Bian, J. M. Williams, D. Y. Kim, L. Li, S. Balasubramanian, J. Kumar and S. Tripathy, J. Appl. Phys., 1999, 86, 4498–4508 CrossRef CAS.
- A. Ambrosio, P. Maddalena and L. Marrucci, Phys. Rev. Lett., 2013, 110, 146102 CrossRef PubMed.
- T. G. Pedersen, P. M. Johansen, N. C. R. Holme, P. S. Ramanujam and S. Hvilsted, Phys. Rev. Lett., 1998, 80, 89–92 CrossRef CAS.
- P. Lefin, C. Fiorini and J.-M. Nunzi, Pure Appl. Opt., 1998, 7, 71–82 CrossRef CAS.
- V. Toshchevikov, J. Ilnytskyi and M. Saphiannikova, J. Phys. Chem. Lett., 2017, 8, 1094–1098 CrossRef CAS PubMed.
- P. Karageorgiev, D. Neher, B. Schulz, B. Stiller, U. Pietsch, M. Giersig and L. Brehmer, Nat. Mater., 2005, 4, 699–703 CrossRef CAS PubMed.
- Y. B. Li, Y. N. He, X. L. Tong and X. G. Wang, J. Am. Chem. Soc., 2005, 127, 2402–2403 CrossRef CAS PubMed.
- Y. B. Li, Y. N. He, X. L. Tong and X. G. Wang, Langmuir, 2006, 22, 2288–2291 CrossRef CAS PubMed.
- H. Nakano, T. Takahashi, T. Kadota and Y. Shirota, Adv. Mater., 2002, 14, 1157–1160 CrossRef CAS.
- E. Ishow, C. Bellaïche, L. Bouteiller, K. Nakatani and J. A. Delaire, J. Am. Chem. Soc., 2003, 125, 15744–15745 CrossRef CAS PubMed.
- M.-J. Kim, E.-M. Seo, D. Vak and D.-Y. Kim, Chem. Mater., 2003, 15, 4021–4027 CrossRef CAS.
- M. C. Guo, Z. D. Xu and X. G. Wang, Langmuir, 2008, 24, 2740–2745 CrossRef CAS PubMed.
- R. Walker, H. Audorff, L. Kador and H.-W. Schmidt, Adv. Funct. Mater., 2009, 19, 2630–2638 CrossRef CAS.
- F. Lagugné Labarthet, T. Buffeteau and C. Sourisseau, J. Phys. Chem. B, 1998, 102, 5754–5765 CrossRef.
- F. Lagugné-Labarthet, J. L. Bruneel, V. Rodriguez and C. Sourisseau, J. Phys. Chem. B, 2004, 108, 1267–1278 CrossRef.
- T. M. Geue, M. G. Saphiannikova, O. Henneberg, U. Pietsch, P. L. Rochon and A. L. Natansohn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 052801 CrossRef CAS PubMed.
- G. di Florio, E. Bründermann, N. S. Yadavalli, S. Santer and M. Havenith, Soft Matter, 2014, 10, 1544–1554 RSC.
- K. G. Yager, O. M. Tanchak, C. Godbout, H. Fritzsche and C. J. Barrett, Macromolecules, 2006, 39, 9311–9319 CrossRef CAS.
- G. Binnig, C. F. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930–933 CrossRef PubMed.
- H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- K. Nakajima, M. Ito, D. Wang, H. Liu, H. K. Nguyen, X. Liang, A. Kumagai and S. Fujinami, Microscopy, 2014, 63, 193–208 CrossRef CAS PubMed.
- O. Sahin, S. Magonov, C. Su, C. F. Quate and O. Solgaard, Nat. Nanotechnol., 2007, 2, 507–514 CrossRef PubMed.
- B. Pittenger, N. Erina and C. Su, Quantitative mechanical property mapping at the nanoscale with PeakForce QNM, 2010 Search PubMed.
- P. Schön, K. Bagdi, K. Molnár, P. Markus, B. Pukánszky and G. Julius Vancso, Eur. Polym. J., 2011, 47, 692–698 CrossRef.
- K. Sweers, K. van der Werf, M. Bennink and V. Subramaniam, Nanoscale Res. Lett., 2011, 6, 270 CrossRef PubMed.
- M. E. Dokukin and I. Sokolov, Langmuir, 2012, 28, 16060–16071 CrossRef CAS PubMed.
- D. Wang, X. Liang, T. P. Russell and K. Nakajima, Macromolecules, 2014, 47, 3761–3765 CrossRef CAS.
- G. Smolyakov, S. Pruvost, L. Cardoso, B. Alonso, E. Belamie and J. Duchet-Rumeau, Carbohydr. Polym., 2017, 166, 139–145 CrossRef CAS PubMed.
- B. Stiller, T. Geue, K. Morawetz and M. Saphiannikova, J. Microsc., 2005, 219, 109–114 CrossRef CAS PubMed.
- P. U. Veer, U. Pietsch and A. D. Mueller, Appl. Phys. Lett., 2009, 94, 231911 CrossRef.
- O. Kulikovska, K. Gharagozloo-Hubmann, J. Stumpe, B. D. Huey and V. N. Bliznyuk, Nanotechnology, 2012, 23, 485309 CrossRef PubMed.
- Y. N. He, X. G. Wang and Q. X. Zhou, Polymer, 2002, 43, 7325–7333 CrossRef CAS.
- J. C. Dainty, Opt. Acta. Int. J. Opt., 1986, 33, 1336–1337 CrossRef.
- B. Pittenger, N. Erina and C. Su, in Nanomechanical Analysis of High Performance Materials, ed. A. Tiwari, Springer, Netherlands, Dordrecht, 2014, pp. 31–51, DOI: DOI:10.1007/978-94-007-6919-9_2.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef CAS.
- B. Liu, M. Q. Wang, Y. N. He and X. G. Wang, Langmuir, 2006, 22, 7405–7410 CrossRef CAS PubMed.
- M. D. Fayer, Annu. Rev. Phys. Chem., 1982, 33, 63–87 CrossRef CAS.
- K. A. Nelson, R. Casalegno, R. J. D. Miller and M. D. Fayer, J. Chem. Phys., 1982, 77, 1144–1152 CrossRef CAS.
- K. G. Yager and C. J. Barrett, J. Chem. Phys., 2004, 120, 1089–1096 CrossRef CAS PubMed.
- S. P. Graham, M. Rouainia, A. C. Aplin, P. Cubillas, T. D. Fender and P. J. Armitage, Rock. Mech. Rock. Eng., 2021, 54, 303–320 CrossRef.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef CAS.
- V. M. Muller, B. V. Derjaguin and Y. P. Toporov, Colloids Surf., 1983, 7, 251–259 CrossRef CAS.
- V. M. Muller, V. S. Yushchenko and B. V. Derjaguin, J. Colloid Interface Sci., 1980, 77, 91–101 CrossRef CAS.
- J. J. Aklonis and W. J. MacKnight, Introduction to Polymer Viscoelasticity, John Wiley & Sons Inc, New York, 2nd edn, 1983 Search PubMed.
- H. N. Lee, R. A. Riggleman, J. J. de Pablo and M. D. Ediger, Macromolecules, 2009, 42, 4328–4336 CrossRef CAS.
- H. N. Lee and M. D. Ediger, Macromolecules, 2010, 43, 5863–5873 CrossRef CAS.
- G. Ye, D. R. Wang, Y. N. He and X. G. Wang, J. Mater. Chem., 2010, 20, 10680–10687 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra06111a |
| This journal is © The Royal Society of Chemistry 2021 |