Open Access Article
Open Access ArticleAnatomies for the thermal decomposition behavior and product rule of 5,5′-dinitro-2H,2H′-3,3′-bi-1,2,4-triazole†
Ruiqi Lyu a,
Zhiyu Huang*b,
Hongbo Dengac,
Yue Weia,
Chuanlin Moua and
Linyuan Wang
a,
Zhiyu Huang*b,
Hongbo Dengac,
Yue Weia,
Chuanlin Moua and
Linyuan Wang *a
*a
aSchool of Chemistry and Chemical Engineering, Southwest Petroleum University, Chengdu, Sichuan 610500, China. E-mail: 13981884015@163.com
bSchool of New Energy and Materials, Southwest Petroleum University, Chengdu, Sichuan 610500, China. E-mail: hzy3019@163.com
cOil & Gas Field Applied Chemistry Key Laboratory of Sichuan Province, Chengdu, Sichuan 610500, China
First published on 17th December 2021
Abstract
High-performance energetic materials are mainly used in the military, aerospace industry and chemical fields. The ordinary technology of producing energetic materials cannot avoid the domination of its unique needs. At present, revealing the underlying mechanism of the formation of high-energy materials is of great significance for improving their quality characteristics. We pay special attention to the decomposition and reactive molecular dynamics (RMD) simulation of 5,5′-dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT). Various forms were captured in the simulation, and the form is determined by the temperature of the initial reactant. By observing the heating pattern and morphological changes under the initial thermal equilibrium, interesting temperature jumps were found in 325 K and 350 K. Observation of continuous heating (simulated temperatures are 2600 K, 2900 K, 3200 K and 3500 K) shows that DNBT has the maximum heating rate at 3500 K. In addition, N2 occupies this dominant position in the product, moreover, N2 and NO2 respectively dominate the gas phase products during the initial heating process. According to the transition state analysis results of the intermediates, we found 4 interesting intermediate products, which were determined by high frequency reaction under the 4 simulated temperatures and performed with transition state calculations. It shows that the selection of reactant temperature and its activity is the key to orderly decomposition of DNBT. It is expected that these findings will be widely used in comprehensive decomposition devices and to improve the concept of learning military and industrial technology.
Energetic materials (EMs), such as TNT, RDX, TATB, nitroguanidine and nitro imidazoles, have risen in the scientific community because of their unique properties.1–4 Findings and discoveries of nitro metal salts and high energy density materials (HEDMs) in the early stage has obviously indicated the beginning of the epoch of EMs. The detonation velocity and pressure depend on the material density, with a high energy density trending to increase the explosive capability. Notably, this dinitrotriazoles are the only ones among these energetic materials whose large-scale industrial production has been an accustomed pursuit.5 Research on triazoles with high thermo stabilities reported by Seth and Matzger in 2016 further highlights the high expectations and applications for triazole materials.6 Dinitrotriazoles have been observed and researched as coordination polymerization, water–salts degradation,7 lighting sensor for fluorescent materials8 and energetic nano microcapsules9 successfully, in contrast with the traditional mechanical,10 electronic11 and optical properties,12 moreover, dinitrotriazoles are applied in various fields of material science and technology such as fuel cells13 and catalysts,14 etc.
5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT) is a potential explosive that can be synthesized in two steps starting from aminoguanidinium carbonate and oxalic acid. The synthesis strategies of DNBT include conventional ways are evaluable, related report mentioned by the crystallization screening experiment that the water solubility is relatively stable for DNBT under the environment of methyl cyanide (MeCN) with a proportion 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.515.15 DNBT prepared via these techniques is always have a diversity sample such as form of crystal, water activity slurry, crystallization of the initial solvates, non-solvates titration (crystal powder used for catalyst), whatsmore, removing these diversity sample is improved to be a changeable task which can turn on the limitation and potential application of DNBT. Despite that, the investigation of thermal decomposition phenomenon16 is still one of the urgent problems to be solved in the current research for EMs, meanwhile, could be a good solution and approaches for DNBT to reveal the insight of the structure from crystal between the inner-molecule and inter-molecules. Nevertheless, the molecule structure analysis and the response character during the decomposition for reaction of DNBT get fail to obtain more effective results from the reactants and products, more than this, existing experimental methods cannot meet the current needs as dealing with these micro-mechanism issues. Unfortunately, these similar issues begin to need a sufficient discussion and the tow mechanism of hot smoking vapored formation which dominated by the polyyne model17 and energetic ion salt research,18–20 are still debating. To learn and comprehensive mechanisms of rules for decomposition reaction under the consideration of choosing starting temperature and setting reactive condition, shall be helpful and advantageous to produce of DNBT controllably and efficiently.
1.515.15 DNBT prepared via these techniques is always have a diversity sample such as form of crystal, water activity slurry, crystallization of the initial solvates, non-solvates titration (crystal powder used for catalyst), whatsmore, removing these diversity sample is improved to be a changeable task which can turn on the limitation and potential application of DNBT. Despite that, the investigation of thermal decomposition phenomenon16 is still one of the urgent problems to be solved in the current research for EMs, meanwhile, could be a good solution and approaches for DNBT to reveal the insight of the structure from crystal between the inner-molecule and inter-molecules. Nevertheless, the molecule structure analysis and the response character during the decomposition for reaction of DNBT get fail to obtain more effective results from the reactants and products, more than this, existing experimental methods cannot meet the current needs as dealing with these micro-mechanism issues. Unfortunately, these similar issues begin to need a sufficient discussion and the tow mechanism of hot smoking vapored formation which dominated by the polyyne model17 and energetic ion salt research,18–20 are still debating. To learn and comprehensive mechanisms of rules for decomposition reaction under the consideration of choosing starting temperature and setting reactive condition, shall be helpful and advantageous to produce of DNBT controllably and efficiently.
In recent years, many kinetic models and dynamic simulations have been developed to describe the chemical process of thermal degradation for nitro-compound and nitro ion salts, though there will be temperature and pressure enhancement in these simulations, it has been proven extensively that the enhancement will not give rise to any artificial feature.21–25 It's a common approach of various molecular dynamics (MD) simulation to increase temperature significantly to overcome the limit for time scale. However, these processes are adopted to both comparing and fitting the elementary reactions with experimental observations to determine dominant reaction in the total conversions, and also cannot provide dynamic details of chemical conversion. Reactive force field with lg potential terms (ReaxFF-lg) become one of the opportunities to solve these problems by simulating chemical reactions via reactive molecular dynamics simulation (RMD), which can parsing more details of complicated chemical procedure under a given specific condition as time and space scale, the energy terms component described as eqn (1)–(3), where Ereax is the energy evaluated from the previous ReaxFF,26 Elg is the long-range correction using the low-gradients method.27
| EReax-lg = EReax + Elg | (1) |
| EReax = Ebond + Elp + Eover + Eunder + Eval + Epen + Ecoa + Etors + Econj + EH-bond + EvdW + ECoulomb | (2) |
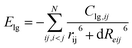 | (3) |
The unknown decomposition and degradation mechanism of different nitro-compound push us to extend the previous studies to more intentional reactive behavior for DNBT during analyses performed by combine the results in the micro scale28–31 that gave us a remarkable understanding of the thermal decomposition behavior of DNBT. Moreover, as a classic secondary explosive32–35 and from the perspective of safety, this makes us need to pay more attention to the performance of heating trend. More interesting information has been found. The initial degradation and decomposition accompany with temperature for DNBT undergoes the following stage, (i) selection of the initial thermal equilibrium temperature, (ii) dynamic changes for the potential and temperature of the system during heating process in the high temperature range, (iii) evaluating the generation of product and statistic the high frequency reaction during the decomposition process. Besides that, the transition state calculation and analysis of the electronic structure for the intermediate product in high-frequency decomposition reactions are also been investigated and discussed.
Results and discussion
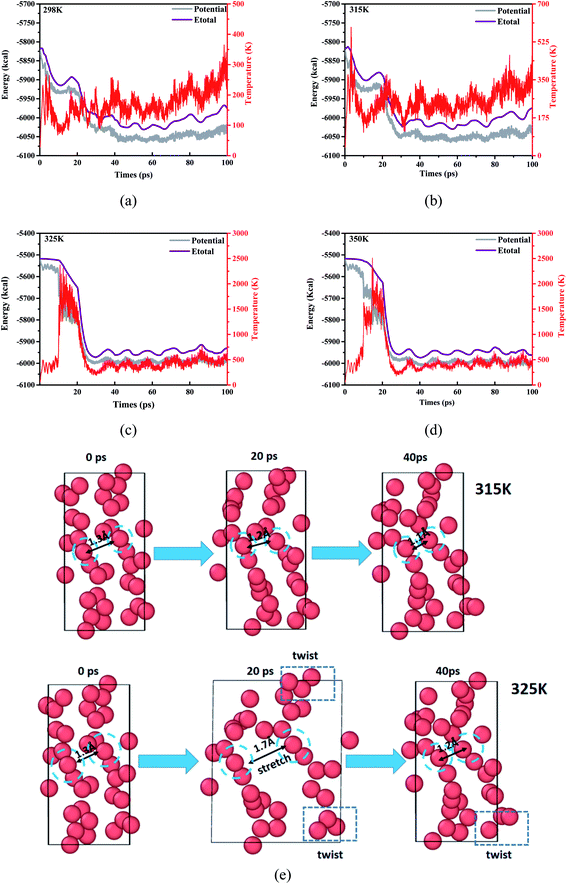
Follow the trajectory of potential energy and temperature of the system during the simulation period cycle, evolution for the process of atomic shift and velocity (temperature) is a simple way to learn the reactive information for DNBT, at the same time, it is particularly necessary to perform a warm-up relaxation with thermal equilibrium before the simulation. Therefore, we establish the relationship between energy and temperature changes with the simulation time, and intend to select the effective range of atomic motion and temperature. Depending on the starting temperature of the reaction and the actual requirement for the storage and transportation of military equipment safety conditions, four initial temperature conditions were considered by statistic the atomic movement position information per time step and calculate the trajectory distribution, meanwhile, the whole balance process maintains 100 ps which demonstrated as time-depended curves in Fig. 1. The range of the initial thermal equilibrium temperature is 298 K, 315 K, 325 K, 350 K. Where the potential energy (pe) and the total energy (Etotal) are the measurement for atomic location layout, all the number of molecules, carbon, nitrogen atoms beside density of the atoms in the whole crystal are counted out in different sizes after homogenization treatment. The initial thermal equilibrium simulation of the unit crystal cell at 100 ps is performed by extracting the standard crystal structure of DNBT from the Cambridge Crystallographic Data Centre (CCDC) and the unit crystal cell structure parameter is monoclinic with space group P21/n, lattice constant a = 5.056 Å, b = 6.308 Å, c = 12.427 Å, α = 90°, β = 95.14°, γ = 90°, and z = 2 molecules.The potential energy of the system for the initial thermal equilibrium decrease with the passage of time and tend towards balance after 100 ps, following as same as Etotal showed from Fig. 1. We found that in the four thermal equilibrium processes with different initial thermal equilibrium temperatures, the potential energy and total energy of the system all began to gradually decrease when they were equilibrated to 20 ps. However, the equilibrium temperature of the system is not the same, reflecting the difference from Fig. 1(a) and (b) is that both Fig. 1(c) and (d) have a temperature jump phenomenon at 20 ps, and the temperature of the system is finally maintained at 500 K. If a new merged atom migrate to another particle groups from the boundary moving to the geometry center, the degradation will turn into thermal decomposition is unavoidable, for the temperature is smooth during the simulation procedure from 298 K, a huge up and downs of a giant line drawing over the temperature at 2000 K broke the stable temperature trend shown in the Fig. 1(c) and (d). The number and the size of initial molecular bonds constructions is one of the information that reflects the analysis which could result in more overview during the reaction. We trace the detail regions and analysis of partially enlarged initial thermal equilibrium processing in order to better observe the DNBT particle from the temperature surface inside, collect the selected illustration frames, and details of the decomposition and degradation of DNBT models are present from radial distribution function and displayed in ESI Fig. S1.†
When the initial thermal equilibrium temperature is 325 K, with the dissociation and recombination of DNBT molecules in the unit cell, the state before 40 ps shows chaotic characteristics including intermolecular collisions and direct atomic motion as is shown in Fig. 1(e). However, when the initial thermal equilibrium temperature is 315 K, the atoms in the unit cell are more moderate. We fixed and marked the two atoms located in the center of the unit cell and found that the average displacement of the two atoms in the DNBT unit cell with an initial thermal equilibrium temperature of 325 K reached 0.45 Å within the entire 40 ps, shows the tendency of the system to undergo a chemical reaction. Thus during the 100 ps before the start of the heating reaction, the first part of the decomposition is the torsion for the nitro group with expansion and contraction of the atoms occurred under the initial thermal equilibrium temperature of 325 K. In addition, there are other small-scale vibrations for the atoms in a molecule. Furthermore, we also found a situation similar to 325 K in the DNBT unit cell with an initial thermal equilibrium temperature of 298 K and 350 K (see ESI Fig. S2†).
In order to select a suitable initial thermal equilibrium temperature for DNBT and avoid the loss of DNBT molecular structure caused by the disordered movement of atoms in the unit cell system, we compared 3 kinds of common energetic materials and used them as a reference training set. These species are three kind of nitro compound [1,3,5-trinitroperhydro-1,3,5-triazine (RDX), 1,3,5,7-tetranitro-1,3,5,7-tetrazacyclooctane (HMX) and 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20)], each compound has demonstrated good mechanical properties and thermal behavior through the combination with the ReaxFF-lg force field.36–42 There have been references that when RDX and HMX changes from β phase to γ phase, the calculation results show that there is a surface effect, and the dipole moment is the main factor that provides the phase change based on the initial thermal equilibrium temperature.43,44 From Fig. 2(a), we can see that among the four initial thermal equilibrium temperatures we have applied, the average potential energy difference of the system is within 50 kcal under the conditions of the initial thermal equilibrium temperature of 298 K and 315 K, while the potential energy of the system at 325 K and 350 K is closer with the average difference value under 60 kcal. The system potential energy of each nitro compound has a large change in the thermal equilibrium temperature of 315 K and 325 K. Among them, in the initial thermal equilibrium temperature of 315 K and 325 K, the average potential energy difference of RDX, DNBT, HMX and CL-20 is 512 kcal, 369 kcal, 450 kcal and 426 kcal, respectively. In particular, from Fig. 2(b), the temperature jump phenomenon of the system temperature also appeared in sequence at the initial thermal equilibrium temperatures of RDX, HMX and CL-20 at 325 K and 350 K, respectively. It can be explained that these temperature jump phenomena obviously act on RDX, HMX and CL-20 is that the floating average of their temperature jump phenomenon exceeds 3000 K. According to the definition of RMD, the potential energy of the system and the temperature of the system are important indicators of the degree of atomic movement and disorder in the feedback system. Therefore, the appearance of this phenomenon will adversely affect the structural changes in the subsequent heating process. Thus the elimination of this unfavorable factor is conducive to the accurate performance of DNBT in the subsequent heating process.
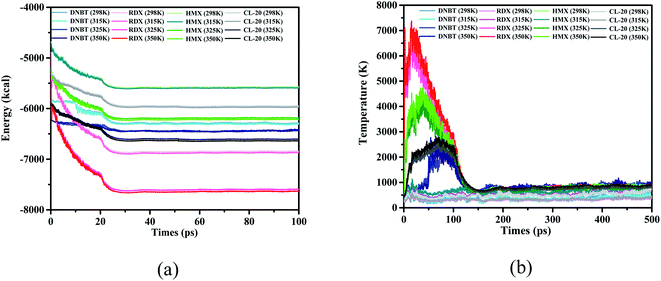 | ||
| Fig. 2 (a and b) The evolution and comparison of DNBT, HMX, RDX, and CL-20 with the initial thermal equilibrium temperature 298 K, 315 K, 325 K and 350 K. | ||
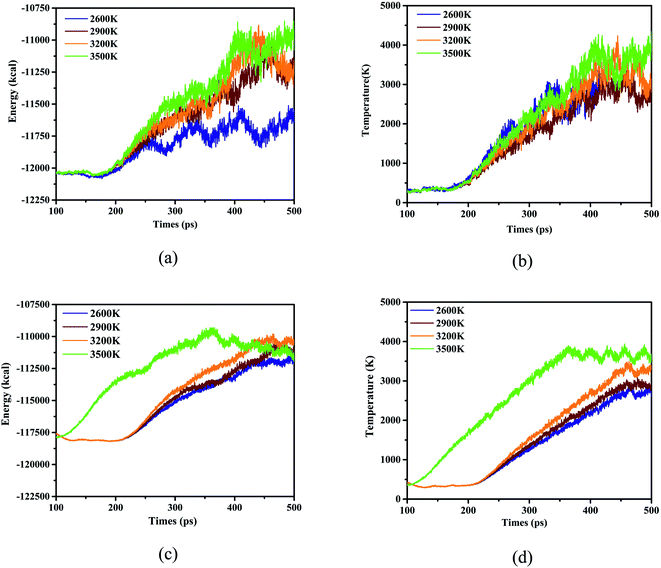
Considering as the mention above, the species for the 4 initial thermal equilibrium temperatures difference between adjacent steps can be calculated and some patterns can be found and studied. Hence further follow-up studies on its behavior and characteristics at high temperatures need to be carried out. Fortunately, ReaxFF-lg has excellent performance in simulating nitro compounds at 2500–3600 K,27,45–48 combined with the structural characteristics of DNBT, which allows us to select a series of temperature for calculation with the form of heating up to explore the decomposition behavior in the high temperature range, and there are 2600 K, 2900 K, 3200 K and 3500 K. We expand side length a, b, and c of the single DNBT unit crystal cell into 2a × 2b × 2c super cells and 4a × 4b × 4c super cells respectively. And select 315 K as the initial thermal equilibrium temperature to simulate the heating process with removing the situation in the room temperature. System energy and temperature for the these 2 kind of super cells were described and shown in Fig. 3.
As been proved by dynamic trajectory, for the thermal decomposition of 2 × 2 × 2 DNBT super crystal cell, a stable thermal equilibrium for system energy of simulated time goes on with the increase in simulate time when the simulated temperature (ST) is 2600 K. It can be figured that the peak energy reached −1.1 × 104 kcal for ST3500 K, meanwhile, ST2600 K exhibited the lowest energy −1.16 × 105 after 100 ps exhibited in Fig. 3(a), furthermore, the system energy has fluctuating states under ST3500 and a peak value appears at 400 ps. Pay attention to the temperature of the system temperature, the thermal decomposition of 2 × 2 × 2 DNBT super crystal cell progresses, the system temperature rises over time and the heating rate during the simulation ordered as ST2600 K > ST3500 K > ST3200 K > ST2900 K before 350 ps, however, the system temperature is always higher than ST2600, ST2900 and ST3200 for the 4 × 4 × 4 super cell of DNBT under ST3500 K, which explain that the heating rate is related to the size of the unit cell in Fig. 3(b). Nevertheless, the system energy of ST3500 K is no longer the maximum after 425 ps in the 4a × 4b × 4c super cell of DNBT, and the system energy for ST3500 K begin to drop after 350 ps from Fig. 3(c). Synchronously, the heating rate after the expansion of the unit cell ordered as ST3500 K > ST3200 K > ST2900 K > ST2600 K mapping from Fig. 3(d).
According to Fig. 4, a large number of product species flow out at the beginning of the reaction. Learning the estimation of these species is helpful to grasp the essential mechanism of decomposition and degradation. Regardless of the atom type and bonding effect, all species with less than 20 atoms, molecules or intermediates will be counted. We follow this rule to match and keep up with the trajectory refresh rate of these decomposition models, and use 500 ps to outline the evolution of the product and the trajectory of the internal atoms. Among these various products, we have identified 4 frequently occurring high-frequency product intermediates, C4N6O4, CNO3H2, C4N5H and C4N8O4 (see ESI Tables S1–S4† for detailed high-frequency reaction). With the appearance of nitrogen, water, nitrogen dioxide, nitric oxide and other products, the quantitative changes of these high-frequency intermediate structures are also recorded and tracked, simultaneously.
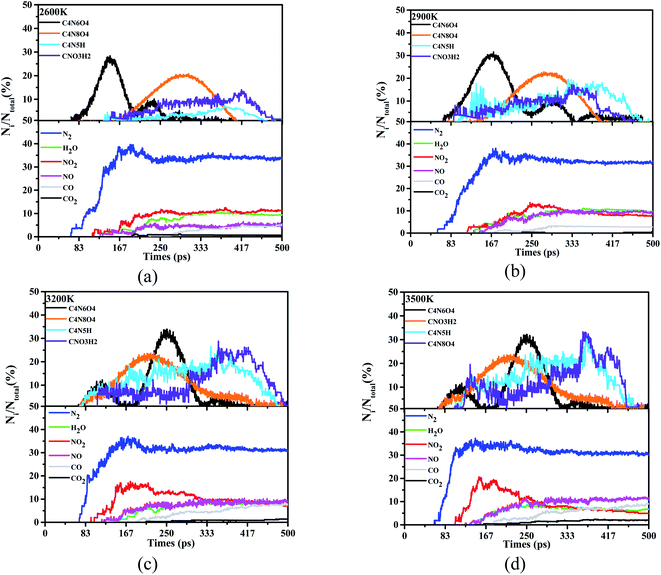 | ||
| Fig. 4 Statistical and evaluation of high-frequency products in the reaction process. Wherein (a) is the case that the ST is 2600 K, (b), (c) and (d) are 2900 K, 3200 K and 3500 K respectively. | ||
According to the analysis of thermal decomposition products, when the ST is 2600 K, the peak N2 yield of DNBT reaches 40%, and decreases with the increase of the simulated temperature until the yield of N2 is gently maintained at about 35%. Similar to this situation, the generation rate of H2O molecules in the system also has this situation, but the difference is that the generation time of H2O molecules is delayed with the increase of ST, which mainly reflected in 3200 K and 3500 K. More interestingly, except the ST 2600 K, the amount of nitrogen dioxide in the system began to shrink. When the simulated temperature is 3200 K and 3500 K, it can be seen that the peak ratio of NO2 is greater than the peak ratio of 2600 K and 2900 K, however, as the reaction time increases, the NO2 yield drops below 10%. The amount of CO and carbon CO2 increases lowly throughout the pyrolysis process. In addition to the above, looking back at the reaction time, both N2 and NO2 appeared in the system before 100 ps, indicating that N2 and NO2 had been produced from the initial stage of the heating reaction.
Among the four high-frequency intermediates, the appearance of C4N8O4 is accompanied by the entire pyrolysis process, with the most frequent occurrences and occupying 30% of the proportion, which is higher than the other three intermediates, while C4N6O4 occupies 20% of the proportion. It is worth noting that we can follow the two intermediates, C4N5H and CNO3H2, account for less than 20% when the ST is 2600 K and 2900 K. On the contrary, when the temperature is lower than 3200 K and 3500 K, their ratio peaks even exceeds 25%. In addition, the existence time of the four intermediates is significantly different between 2900 K and 3200 K. The appearance of C4N8O4 has changed significantly, and the maximum number of C4N8O4 has changed from 167 ps to 250 ps. Furthermore, C4N6O4 no longer appears at 400 ps under ST2600 K and ST2900 K, yet C4N6O4 does not completely disappear until 500 ps under ST3200 K and ST3500 K.
In order to track the above-mentioned interesting product generation results, N2 and NO2 are used as the main labeled products combined with high-frequency product statistics with two paths in the initial heating stage are outlined. We divided the initial decomposition of DNBT under the 4 STs into two modes: (i) initial decomposition and pyrolysis within 100–120 ps to produce N2; (ii) initial decomposition and pyrolysis within 100–120 ps to produce NO2. The circles and their sources in different colors in Fig. 5 have been marked. There have references guiding and believing that the nucleation centers of nitro compounds and high-energy ionic salts come from the dissociation mechanism N–N and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (from–NO2) and the π–π stacking between molecules,49–51 thus the reaction of N2 can be expressed as C4N8O4 → C4N6O4 + N2, NO2 on DNBT can be expressed as C4N8O4 → C4N6O2 + 2NO2, these two 2 reactions can be regarded as the main triggering reactions at this stage. The cleavage reaction of N–C bonds and N
O (from–NO2) and the π–π stacking between molecules,49–51 thus the reaction of N2 can be expressed as C4N8O4 → C4N6O4 + N2, NO2 on DNBT can be expressed as C4N8O4 → C4N6O2 + 2NO2, these two 2 reactions can be regarded as the main triggering reactions at this stage. The cleavage reaction of N–C bonds and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds, meanwhile, the short intermediate reaction C4N8O4 → C4N6O4 + N2, all occur under the 4 STs, and have been found in the high-frequency reaction of the initial decomposition of DNBT, nevertheless, the difference is that the reaction C4N8O4 → C4N6O2 + 2NO2 is rarely occurs at 2600 K and 2900 K during the initial 100–120 ps. Therefore, the increase in the number of NO2 vaguely feedbacks the relationship between temperature and them at ST3200 K and ST3500 K, which is thought-provoking. Therefore, we speculate that the intermediate product C4N6O4 provides the conditions to initiate the bond dissociation sequence.
N bonds, meanwhile, the short intermediate reaction C4N8O4 → C4N6O4 + N2, all occur under the 4 STs, and have been found in the high-frequency reaction of the initial decomposition of DNBT, nevertheless, the difference is that the reaction C4N8O4 → C4N6O2 + 2NO2 is rarely occurs at 2600 K and 2900 K during the initial 100–120 ps. Therefore, the increase in the number of NO2 vaguely feedbacks the relationship between temperature and them at ST3200 K and ST3500 K, which is thought-provoking. Therefore, we speculate that the intermediate product C4N6O4 provides the conditions to initiate the bond dissociation sequence.
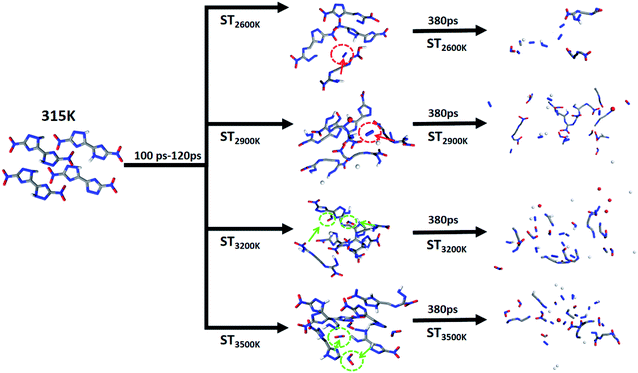 | ||
| Fig. 5 Diagram of the heating reaction path after 100 ps under the initial thermal equilibrium temperature 315 K. | ||
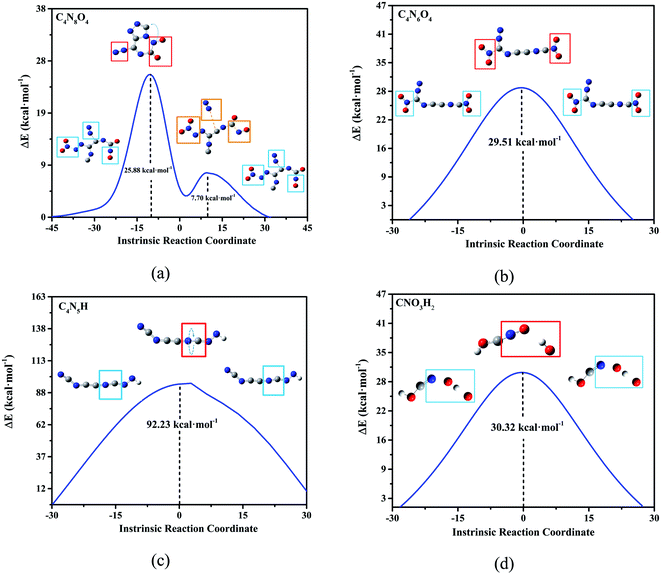
According to the high-frequency intermediate products obtained by four high-temperature annealing simulations of DNBT, transition state (TS) analysis and intrinsic reaction coordinate (IRC) calculation were employed to obtain the reaction pathway information of these intermediate products. As shown in Fig. 6(a), the transition state curve of C4N8O4 goes through two saddle points, the first saddle point energy difference is 25.88 kcal mol−1, and the second saddle point energy difference is only 7.7 kcal mol−1, moreover, the existed distinct for the structure on the two saddle points showed one is that the nitrogen atom and the carbon atom form a ring, while the other is that the two nitrogen atoms are separated from the main structure. The structural changes of C4N6O4 mainly occur on the nitro group and the coordination bond that provides the lone pair of electrons has a potential change, the energy change that occurs in this process needs to provide 29.51 kcal mol−1 of energy. The highest energy barrier is the torsion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond on C4N5H, whose energy barrier value reaches 121.23 kcal mol−1. The O atoms in CNO3H2 are bound to N atoms, and the remaining O atoms and H atoms are bound to dissociate from the ontology. Therefore, from the perspective of overcoming the energy barrier, the difficulty of these reactions with the equilibrium temperature increases is C4N8O4 > C4N6O4 > CNO3H2 > C4N5H. Among these, the vibration of the structure at these saddle points is calculated and put into the supporting Fig. S3.†
N bond on C4N5H, whose energy barrier value reaches 121.23 kcal mol−1. The O atoms in CNO3H2 are bound to N atoms, and the remaining O atoms and H atoms are bound to dissociate from the ontology. Therefore, from the perspective of overcoming the energy barrier, the difficulty of these reactions with the equilibrium temperature increases is C4N8O4 > C4N6O4 > CNO3H2 > C4N5H. Among these, the vibration of the structure at these saddle points is calculated and put into the supporting Fig. S3.†
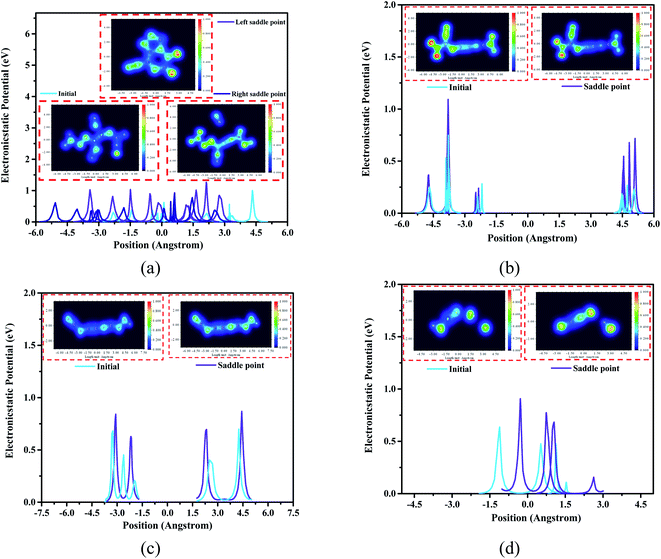
Generally, electrostatic potential (ESP) calculation results show that the ESP value of the saddle point structure is higher than the ESP value of the initial structure. The ESP value of the right saddle point structure at 0.75 Å from the center in Fig. 7(a) is higher than that of the initial structure by 0.93 eV (the part where nitrogen atoms dissociate), while the ESP value of the left saddle point structure in the range of 0.75 Å to 1.5 Å (the C–N binding position), which is 0.52 eV higher than the initial structure. In Fig. 7(c), the ESP value of the saddle point structure is 0.25 eV higher than that of the initial structure at a distance of 1.5 Å to 3 Å from the center position (the C–N torsion position). Meanwhile, the ESP value of the saddle point structure at the position 0–1.5 Å from the center (the part where the oxygen atoms bind) is higher than the initial structure by 0.53 eV demonstrated in Fig. 7(d).
According to the structure of these four high-frequency reaction intermediates, we have adopted electron density distribution statistics and electrostatic potential (ESP) calculations. As shown in Fig. 7(a), the electron density of the structure at the left saddle point of C4N8O4 is significantly greater than that of the initial structure, indicating that more electrons are needed to dominate the entire ring system and the oxygen atoms on the ring become main electrophiles. At the right saddle point, there is a certain electron between the two N atoms that dissociate from the body at this time, and this process produces free N atoms. For the C4N6O4 transition state structure in Fig. 7(b), the electron distribution of the two nitro groups is sparser than that of the transition state structure, moreover, the scattered electron distribution between the carbon atom and the nitrogen atom from the nitro group can potentially promote the dissociation of the nitro group. In Fig. 7(d), we captured the combination of oxygen atoms and hydrogen atoms in CNO3H2 to form a hydroxyl group. It is worth mentioning that for the changed structure, the electrons are mainly concentrated in the nitrogen atoms and oxygen atoms in the structure. Therefore, these atoms serve as potential reaction binding sites during the entire pyrolysis process.
Conclusions
As strict requirements requested by RMD for the accuracy of force field, meanwhile, the force field parameters need to accurately describe the van der Waals interaction between molecules, not only that, being able to effectively overcome the time scale and size effect is also a major challenge for RMD. These have become the main factors affecting and limiting RMD. Fitfully, for the CHON system, the ReaxFF-lg45–48 force field has effectively improved the long-range dispersion correction, which has brought a large number of EMs to RMD simulations, enabled us to continue the research and exploration for the potential excellent EMs such as DNBT.The decomposition and pyrolysis process of DNBT is simulated by reaction molecular dynamics with ReaxFF-lg45–48 force field. Four different initial thermal equilibrium temperature are discussed, temperature jumps at 325 K and 350 K during the initial thermal equilibrium process, the appropriate initial thermal equilibrium temperatures for these thermal equilibrium temperatures is 315 K with the test results given by the training set of RDX, HMX and CL-20. According to the change of the unit cell size, the heating rate is related to the size of the unit cell during the pyrolysis process, the higher the ST is, the faster the heating rate. In addition, based on statistical pyrolysis gas products and high-frequency reaction information, the proportion of N2 in DNBT products reflects the dominant position, followed by NO2 and H2O. NO2 appears more frequently under ST3200 K and ST3500 K, nevertheless, the amount of NO2 in ST2900 K, ST3200 K and ST3500 K showed a downward trend as the temperature increased. In the high-frequency chemical reaction, the reaction is mainly C4N8O4 in ST2600 K and ST2900 K, and the reaction time of C4N6O4 in ST3200 and ST3500 is prolonged. In addition, the amount of C4N5H and CNO3H2 in ST3200 K and ST3500 K is higher than in ST2600 K and ST2900 K. With the calculation of transition state and the potential energy of the electronic structure, the possibility of these high-frequency products in high-temperature environments has been affirmed. Therefore, this work is expected to effectively help deepen the insight mechanism of DNBT and the technical design of military and explosive manufacturing materials.
Methodologies
All the simulations are performed using LAMMPS package with the ReaxFF-lg45 force field which parameterized to reproduce the density function theory (DFT) and take to select system and properties, moreover, the description for ReaxFF-lg45 using low gradient to improve the London dispersion has been a classic DFT method. The temperature and volume ensemble that also referred to as the canonical ensemble (NVT), was employed into RMD calculations with the Nosé–Hoover thermostat method applied to control the thermodynamic temperature. In order to extend and relax the molecule in the crystal unit cell, each cell in thermodynamic progress is under a NVT ensemble simulation with 4 different initial thermal equilibrium temperature set for 100 ps. The timesteps was set 1 fs, time for the process of initial thermal equilibrium is 100 ps, and the time for the process of heating is 400 ps, respectively. The detailing calculation for the TS and IRC calculation of intermediate from the high frequency reactions with a DFT method that implemented with B3LYP/6-311G++** by Gaussian 09 (ref. 52) software package. Each IRC calculation recalculate force constant every 2nd point, and the maxpoint is 60 for C4N5OH, C4N6O4 and CH2O3N. For C4N8O4, the maxpoint is 90. Their calculation stepsize is 1. The value of the ESP and the snapshot drawing of the electron density are used in conjunction with the Multiwfn53 code.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The work was supported by the National Natural Science Foundation of China (No. 51874255) and the Opening Project of Oil & Gas Field Applied Chemistry Laboratory of Sichuan Province (YQKF202102). The refrees who put forward suggestions of considerable values in this work.References
- K. B. Landenberger and A. J. Matzger, Cocrystal Engineering of a Prototype Energetic Material: Supramolecular Chemistry of 2,4,6-Trinitrotoluene, Cryst. Growth Des., 2010, 10, 5341 CrossRef CAS.
- K. B. Landenberger and A. J. Matzger, Cocrystals of 1,3,5,7-Tetranitro-1,3,5,7-tetrazacyclooctane (HMX), Cryst. Growth Des., 2012, 12, 3603 CrossRef CAS.
- M. Riad Manaa and L. E. Fried, Internal Rotation in Energetic Systems:TATB, J. Phys. Chem. A, 2001, 105(27), 6765–6768 CrossRef.
- J. C. Bennion, A. McBain, S. F. Son and A. J. Matzger, Design and Synthesis of a Series of Nitrogen-Rich Energetic Cocrystals of 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT), Cryst. Growth Des., 2015, 15, 2545–2549 CrossRef CAS.
- P. Yin and J. M. Shreeve, From N-Nitro to N-Nitroamino: Preparation of High-Performance Energetic Materials by Introducing Nitrogen-Containing Ions, Angew. Chem., Int. Ed., 2015, 54, 14513–14517 CrossRef CAS PubMed.
- S. Seth and A. J. Matzger, Coordination Polymerization of 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole Leads to a Dense Explosive with High Thermal Stability, Inorg. Chem., 2017, 56, 561–565 CrossRef CAS PubMed.
- J. S. Bangsund, K. W. Hershey and R. J. Holmes, Isolating Degradation Mechanisms in Mixed Emissive Layer Organic Light-Emitting Devices, ACS Appl. Mater. Interfaces, 2018, 10, 5693–5699 CrossRef CAS PubMed.
- Y. X. Tang, G. H. Imler, D. A. Parrish and J. M. Shreeve, Energetic and Fluorescent Azole-Fused 4-Amino-1,2,3-triazine-3-N-oxides, ACS Appl. Energy Mater., 2019, 2, 8871–8877 CrossRef CAS.
- W. Xu, I. Choi, F. A. Plamper, C. V. Synatschke, A. H. E. Müller and V. V. Tsukruk, Nondestructive Light-Initiated Tuning of Layer-by-Layer Microcapsule Permeability, ACS Nano, 2013, 7(1), 598–613 CrossRef CAS PubMed.
- A. Albert, T. Lochner, T. J. Schmidt and L. Gubler, Stability and Degradation Mechanisms of Radiation-Grafted Polymer Electrolyte Membranes for Water Electrolysis, ACS Appl. Mater. Interfaces, 2016, 8, 15297–15306 CrossRef CAS PubMed.
- E. F. C. Byrd and B. M. Rice, Improved Prediction of Heats of Formation of Energetic Materials Using Quantum Mechanical Calculations, J. Phys. Chem. A, 2006, 110(3), 1005–1013 CrossRef CAS PubMed.
- Y. Hu, J. Wang, C. Li, Q. Wang, H. Wang, J. Zhu and Y. Yang, Janus Photonic Crystal Microspheres: Centrifugation-Assisted Generation and Reversible Optical Property, Langmuir, 2013, 29, 15529–15534 CrossRef CAS PubMed.
- Z. M. Bhat and R. Thimmappa, et al., Fuel Exhaling Fuel Cell, J. Phys. Chem. Lett., 2018, 9, 388–392 CrossRef PubMed.
- F. Wang, R. Tsyshevsky, A. Zverev, A. Mitrofanov and M. M. Kuklja, Can a Photosensitive Oxide Catalyze Decomposition of Energetic Materials?, J. Phys. Chem. C, 2017, 121, 1153–1161 CrossRef CAS.
- R. A. Wiscons, M. K. Bellas, J. C. Bennion and A. J. Matzger, Detonation Performance of Ten Forms of 5,5′-Dinitro-2H,2H′-3,3′-bi-1,2,4-triazole (DNBT), Cryst. Growth Des., 2018, 18, 7701–7707 CrossRef CAS.
- F. Wang, G. Wang, H. Du, J. Zhang and X. Gong, Theoretical Studies on the Heats of Formation, Detonation Properties, and Pyrolysis Mechanisms of Energetic Cyclic Nitramines, J. Phys. Chem. A, 2011, 115, 13858–13864 CrossRef CAS PubMed.
- V. D. Ghule, Computational Screening of Nitrogen-Rich Energetic Salts Based on Substituted Triazine, J. Phys. Chem. C, 2013, 117, 16840–16849 CrossRef CAS.
- J. H. Zhang, Q. H. Zhang, T. T. Vo, D. A. Parrish and J. M. Shreeve, Energetic Salts with π-Stacking and Hydrogen-Bonding Interactions Lead the Way to Future Energetic Materials, J. Am. Chem. Soc., 2015, 137, 1697–1704 CrossRef CAS PubMed.
- Y. Liu, Li. Zhang, G. X. Wang, L. J. Wang and X. D. Gong, First-Principle Studies on the Pressure-Induced Structural Changes in Energetic Ionic Salt 3-Azido-1,2,4-triazolium Nitrate Crystal, J. Phys. Chem. C, 2012, 116, 16144–16153 CrossRef CAS.
- H. X. Gao, C. F. Ye, C. M. Piekarski and J. M. Shreeve, Computational Characterization of Energetic Salts, J. Phys. Chem. C, 2007, 111, 10718–10731 CrossRef CAS.
- K. E. Gutowski, J. D. Holbrey, R. D. Rogers and D. A. Dixon, Prediction of the Formation and Stabilities of Energetic Salts and Ionic Liquids Based on ab initio Electronic Structure Calculations, J. Phys. Chem. B, 2005, 109, 23196–23208 CrossRef CAS PubMed.
- C. G. Sun and S. K. Tang, Guanidinium Dicyanamide-Based Nitrogen-Rich Energetic Salts as Additives of Hypergolic Ionic Liquids, Energy Fuels, 2020, 34, 15068–15071 CrossRef CAS.
- I. A. Wojciechowski, S. X. Sun, C. Szakal, N. Winograd and B. J. Garrison, Ion Emission from Water Ice Due to Energetic Particle Bombardment, J. Phys. Chem. A, 2004, 108, 2993–2998 CrossRef CAS.
- V. D. Ghule, S. Deswal, A. Devi and T. R. Kumar, Computer-Aided Design of Energetic Tris (tetrazolyl) amine Derivatives and Salts, Ind. Eng. Chem. Res., 2016, 55, 875–881 CrossRef CAS.
- I. Gospodinov, K. V. Domasevitch, C. C. Unger, T. M. Klapötke and J. Stierstorfer, Midway between Energetic Molecular Crystals and High-Density Energetic Salts: Crystal Engineering with Hydrogen Bonded Chains of Polynitro Bipyrazoles, Cryst. Growth Des., 2020, 20, 755–764 CrossRef CAS.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396 CrossRef CAS.
- L. C. Liu, Y. Liu, S. V. Zybin, H. Sun and W. A. Goddard, ReaxFF-lg: Correction of the ReaxFF Reactive Force Field for London Dispersion, with Applications to the Equations of State for Energetic Materials, J. Phys. Chem. A, 2011, 115, 11016–11022 CrossRef CAS PubMed.
- K. Chenoweth, A. C. T. van Duin and W. A. Goddard, ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation, J. Phys. Chem. A, 2008, 112, 1040 CrossRef CAS PubMed.
- L. X. Hu, K. Tao, Y. D. Lim, J. M. Miao and Y. J. Kim, Self-Steerable Propulsion of Disk-Like Micro-Craft with Dual Off-Center Nanoengines, ACS Appl. Energy Mater., 2019, 2, 1657–1662 CrossRef CAS.
- Y. X. Tang, Z. Y. Yin, A. K. Chinnam, R. J. Staples and J. M. Shreeve, A Duo and a Trio of Triazoles as Very Thermostable and Insensitive Energetic Materials, Inorg. Chem., 2020, 59, 17766–17774 CrossRef CAS PubMed.
- G. X. Zhang, H. Z. Sun, J. M. Abbott and B. L. Weeks, Engineering the Microstructure of Organic Energetic Materials, ACS Appl. Mater. Interfaces, 2009, 1(5), 1086–1089 CrossRef CAS PubMed.
- M. Sorbatovic, N. Filipovic, S. Radakovic, N. Stankovic and Z. Slavkovic, Immune Cytokine Response in Combat Casualties: Blast or Explosive Trauma with or without Secondary Sepsis, Mil. Med., 2007, 2, 190–195 CrossRef PubMed.
- M. N. Borzykh and B. N. Kondrikov, Generalized Dependence of Secondary-Explosive Detonation Rate on Charge Density, Combust., Explos. Shock Waves, 1978, 14, 95–99 CrossRef.
- F. Xiao and W. G. Mcluckie, Laser Ignitibility of Insensitive Secondary Explosive 1,1-Diamino-2 ,2- Dinitroethene (FOX-7), J. Hazard. Mater., 2015, 285, 375–382 CrossRef PubMed.
- A. L. Ramaswamy and J. E. Field, Laser-induced Ignition of Single Crystals of the Secondary Explosive Cyclotrimethylene Trinitramine, J. Appl. Phys., 1996, 79, 3842–3847 CrossRef CAS.
- K. Zhong, J. Liu, L. Y. Wang and C. Y. Zhang, Influence of Atmospheres on the Initial Thermal Decomposition of 1,3,5-Trinitro-1,3,5-triazinane: Reactive Molecular Dynamics Simulation, J. Phys. Chem. C, 2019, 123(2), 1483–1493 CrossRef CAS.
- M. J. Swadley and T. L. Li, Reaction Mechanism of 1,3,5-Trinitro-s-triazine (RDX) Deciphered by Density Functional Theory, J. Chem. Theory Comput., 2007, 3, 505–513 CrossRef CAS PubMed.
- K. B. Landenberger and A. J. Matzger, Cocrystals of 1,3,5,7-Tetranitro-1,3,5,7-tetrazacyclooctane (HMX), Cryst. Growth Des., 2012, 12, 3603 CrossRef CAS.
- O. Sharia, R. Tsyshevsky and M. M. Kuklja, Surface-Accelerated Decomposition of δ-HMX, J. Phys. Chem. Lett., 2013, 4, 730–734 CrossRef CAS PubMed.
- C. M. Lin, C. C. Zeng, Y. S. Wen, F. Y. Gong, G. S. He, Y. B. Li, Z. J. Yang, L. Ding, J. Li and S. Y. Guo, Litchi-like Core−Shell HMX@HPW@PDA Microparticles for Polymer-Bonded Energetic Composites with Low Sensitivity and High Mechanical Properties, ACS Appl. Mater. Interfaces, 2020, 12, 4002–4013 CrossRef CAS PubMed.
- R. W. Molt, R. J. Bartlett, T. Watson and A. P. Bazante, Conformers of CL-20 Explosive and ab initio Refinement Using Perturbation Theory: Implications to Detonation Mechanisms, J. Phys. Chem. A, 2012, 116, 12129–12135 CrossRef CAS PubMed.
- D. I. A. Millar, H. E. Maynard-casely, D. R. Allan, A. S. Cumming, A. R. Lennie, A. J. Mackay, I. D. H. Oswald, C. C. Tang and C. R. Pulham, Crystal engineering of energetic materials: Co-crystals of CL-20, CrystEngComm, 2012, 14, 3742 RSC.
- C. S. Choi and H. P. Boutin, A study of the crystal structure of cyclotetramethylene tetranitramine by neutron diffraction, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1235–1240 CrossRef CAS.
- T. B. Brill and C. O. Reese, Analysis of intra- and intermolecular interactions relating to the thermophysical behavior of alpha-, beta-, and delta-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine, J. Phys. Chem., 1980, 84, 1376–1380 CrossRef CAS.
- Y. W. Xiao, L. Chen, D. S. Geng, K. Yang, J. Y. Lu, J. Y. Wu and B. Y. Yu, Reaction Mechanism of Embedding Oxidizing Small Molecules in Energetic Materials to Improve the Energy by Reactive Molecular Dynamics Simulations, J. Phys. Chem. C, 2019, 123(48), 29144–29154 CrossRef CAS.
- J. P. Larentzos and B. M. Rice, Transferable Reactive Force Fields: Extensions of ReaxFF-lg to Nitromethane, J. Phys. Chem. A, 2017, 121(9), 2001–2013 CrossRef CAS PubMed.
- Y. Zhao, Z. Mei, F. Q. Zhao, S. Y. Xu and X. H. Ju, Thermal Decomposition Mechanism of 1,3,5,7-Tetranitro-1,3,5,7-tetrazocane Accelerated by Nano-Aluminum Hydride (AlH3): ReaxFF-Lg Molecular Dynamics Simulation, ACS Omega, 2020, 5(36), 23193–23200 CrossRef CAS PubMed.
- F. P. Wang, L. Chen, D. S. Geng, J. Y. Lu and J. Y. Wu, Molecular Dynamics Simulations of an Initial Chemical Reaction Mechanism of Shocked CL-20 Crystals Containing Nanovoids, J. Phys. Chem. C, 2019, 123(39), 23845–23852 CrossRef CAS.
- Y. S. Wen, X. G. Xue, X. P. Long and C. Y. Zhang, Cluster Evolution at Early Stages of 1,3,5-Triamino-2,4,6-trinitrobenzene under Various Heating Conditions: A Molecular Reactive Force Field Study, J. Phys. Chem. A, 2016, 120(22), 3929–3937 CrossRef CAS PubMed.
- X. G. Xue, Y. Ma, Q. Zeng and C. Y. Zhang, Initial Decay Mechanism of the Heated CL-20/HMX Cocrystal: A Case of the Cocrystal Mediating the Thermal Stability of the Two Pure Components, J. Phys. Chem. C, 2017, 121(9), 4899–4908 CrossRef CAS.
- Z. P. Lu, X. G. Xue, L. Y. Meng, Q. Zeng, Y. Chi, G. J. Fan, H. Z. Li, Z. M. Zhang, F. D. Nie and C. Y. Zhang, Heat-Induced Solid-Solid Phase Transformation of TKX-50, J. Phys. Chem. C, 2017, 121(15), 8262–8271 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Lu and F. W. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: ESI Fig. S1–S4; ESI Tables S1–S4. See DOI: 10.1039/d1ra06811c |
| This journal is © The Royal Society of Chemistry 2021 |