Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identification of individual conformers in C4H6O isomers using conformer-specific vibrational spectroscopy†
Sung Man Park and
Chan Ho Kwon
and
Chan Ho Kwon *
*
Department of Chemistry, Institute for Molecular Science and Fusion Technology, Kangwon National University, Chuncheon 24341, Korea. E-mail: chkwon@kangwon.ac.kr
First published on 29th November 2021
Abstract
We measured the conformer-specific vibrational spectra of C4H6O isomers in neutral and cationic states using IR resonant vacuum ultraviolet mass-analyzed threshold ionization (VUV-MATI) spectroscopy for the first time. Notably, the measured IR dip and hole-burn VUV-MATI spectra for each isomer represent the identifiable vibrational spectra of individual conformers in both states. Furthermore, we estimated the relative populations of individual conformers in crotonaldehyde (CA) and methyl vinyl ketone (MVK) isomers using the IR dip intensity, the corresponding Franck–Condon factor, and the IR absorption cross section. Our analysis revealed that the compositional ratio of s-trans to s-cis conformers in the CA isomer remained at 95.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.2 even under supersonic expansion, whereas that in the MVK isomer was determined as 90.6
4.2 even under supersonic expansion, whereas that in the MVK isomer was determined as 90.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9.4, which is consistent with previous research. These findings reveal that the conformational stability of each isomer depends on the position of the methyl group relative to the carbonyl group.
9.4, which is consistent with previous research. These findings reveal that the conformational stability of each isomer depends on the position of the methyl group relative to the carbonyl group.
Introduction
The identification of individual conformers is typically performed using unique spectroscopic techniques capable of providing insights into the conformation-dependent reactivity of specific chemical reactions.1–4 Such techniques reduce conformational complexity by utilizing the adiabatic cooling of molecules that results from supersonic expansion in the absence of the non-equilibrium kinetic effect.5,6 Subsequent investigations have revealed that molecules with a sufficiently low conformer interconversion barrier exist in conformational equilibrium even at low temperatures,7–9 whereas conformers with a high interconversion barrier retain their original composition during cooling via supersonic expansion.10–12 For the former case, identifying peaks that correspond to a specific conformer in measured vibrational spectra requires additional exploration of the vibrational temperature-dependent conformational population, which, in turn, depends on the constructed potential energy surfaces associated with conformational interconversion. Nevertheless, deciphering the contribution of each conformer in the congested vibrational spectrum of a polyatomic molecule is still immensely difficult because of the comparable force fields between the atoms in conformers. As such, laser double resonance techniques such as hole-burning and IR depletion spectroscopies13,14 have been suggested as alternative approaches to characterize the structures of individual conformers, although these techniques focus mainly on hydrogen-bonded clusters or van der Waals complexes in chromophore-containing systems, where resonance-enhanced multiphoton ionization (REMPI) is typically adopted.15–18 Meanwhile, for analyzing aliphatic species without an ultraviolet (UV) chromophore group, the IR vacuum ultraviolet (VUV) double resonance techniques that circumvent the limitations of REMPI have been developed, although excess VUV photon energy at 118 nm (the wavelength normally used) may cause uncontrollable fragmentations.19–21α,β-Unsaturated carbonyl compounds that consist of an ethene conjugated to a carbonyl group, providing them with relatively high electrophilicity, have been researched extensively as an important precursor in reactions with nucleophiles as well as in astrochemical-relevant models of the interstellar medium.22–25 Interestingly, even simple precursors such as acrolein exhibit interconversion between s-trans and s-cis conformers, which manifests as rotation along the single bonds between ethene and carbonyl groups in the molecule. In principle, although the stereoselectivities of reactions depend on multiple environmental factors, the reaction pathway is affected primarily by the conformational preference in molecules, as described by the Diels–Alder reaction.23 In addition, it has been reported that compounds with acrolein moiety undergo a variety of photochemical processes when in an excited state, which have prompted attempts to elucidate the photochemistry of conjugated enone molecules.26–28 These subsequent studies indicate that the photoproducts can be governed by the conformational preference of the designated molecule in an electronic state. Therefore, the conformation responsible for photoreaction should be understood in terms of factors such as molecular orbital interactions and stabilization energies, which can be calculated by various theoretical models.29,30
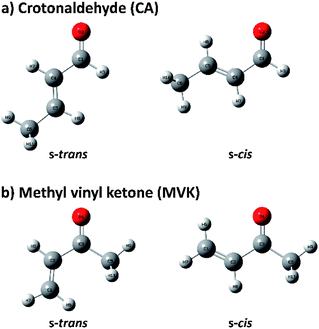
Because of the importance of the methyl-substituted acrolein in both synthetic and atmospheric chemistry, the conformational stabilities and structures of s-trans and s-cis conformers are usually studied by substituting a methyl group in acrolein with crotonaldehyde (CA) and methyl vinyl ketone (MVK), of which conformational geometries are shown in Fig. 1.31–34 Before recent studies using single-photon vacuum ultraviolet mass-analyzed threshold ionization (VUV-MATI) spectroscopy and the Franck–Condon (FC) simulations,9,10 most investigations involving the conformations of these two isomers only examined the temperature-dependence of the peaks corresponding to each neutral conformer in vibrational or rotational spectra. This contributed to the fact that CA and MVK have very short lifetimes, that is, a few hundred femtoseconds, in the excited electronic state owing to the substituent effect of the methyl group on electronic relaxation rates.35 Most spectral analyses are consistent in finding that the s-trans conformer is more stable than the s-cis conformer despite the deviations in their relative stabilities. However, the theoretical predictions regarding the preferential conformation for MVK were inconsistent with the recent experimental results, suggesting that the uncertainty in the calculated energy values can originate from the use of incorrect functions and/or densities.9 Consequently, we were motivated to obtain identifiable vibrational spectra of individual conformers (i.e., s-trans and s-cis) in the two isomers, and thus provide indisputable experimental data regarding the conformational populations while also elucidating how the conformational stabilities in the two isomers change relative to the position of the methyl group.
Experimental
Experiments were performed using a homebuilt VUV-MATI spectrometer, the details of which have been provided in previous studies.36,37 A coherent and tunable VUV laser pulse with a wavelength range of 126.3–128.6 nm was generated by resonant four-wave difference frequency mixing (FWDFM) based on 4p6–5p[1/2]0 or 4p6–5p[5/2]2 transitions in Kr, which were alternated to avoid wavevector mismatches depending on the VUV wavelength. The MATI ion signals were normalized using the power of the tunable visible laser that was used for the FWDM-based VUV generation. For the IR resonant VUV-PI/MATI scheme, high-resolution IR laser light in the range of 2670–3100 cm−1 with an approximate energy of 7 mJ per pulse was generated using a narrowband optical parametric oscillator/amplifier (OPO/OPA) system (LaserVision, ∼0.1 cm−1) pumped by a Nd:YAG laser seeded with a wavelength of 1064 nm. Next, the generated IR laser light was cylindrically focused using a telescope consisting of two CaF2 lenses (f = 75 and −100 mm) and aligned perpendicularly to both the molecular beam and the ion-flight direction into the photoionization chamber. The VUV laser pulse was delayed by approximately 5 ns with respect to the IR laser pulse, which photoexcites the neutral conformers to a vibrational state. The frequencies of all lasers used in the experiments were measured and calibrated using a wavemeter (HighFinesse, Wavelength Meter WS5) with an accuracy of 0.1 cm−1.Results and discussion
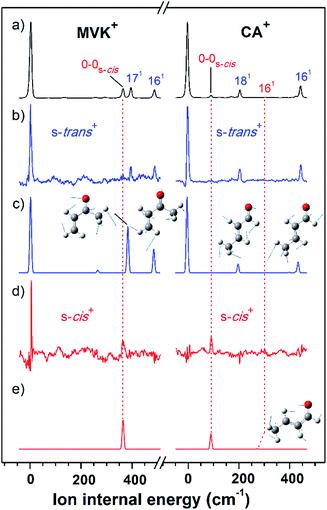
As shown in Fig. 2(a), the VUV-MATI spectra of the MVK and CA isomers, which are essentially the vibrational spectra of the two isomers in the D0 state, were measured as a function of the VUV photon energy. The two most intense peaks, at 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 and 78
861 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 cm−1 correspond to the 0–0 bands of MVK and CA, respectively, which is consistent with the respective adiabatic ionization energy (AIE) values of 77
638 cm−1 correspond to the 0–0 bands of MVK and CA, respectively, which is consistent with the respective adiabatic ionization energy (AIE) values of 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 ± 4 and 78
867 ± 4 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 ± 3 cm−1 determined in previous studies by extrapolating to the zero-field limit of the MVK and CA using VUV-MATI spectroscopy.9,10 At present, other than using FC simulations to determine the ionic transitions of the conformers expected in the S0 state, no method exists for identifying the vibrational peaks corresponding to individual conformers in the MATI spectrum of each isomer. In addition, the IR absorption spectra of the MVK and CA were obtained by utilizing the IR resonant VUV-PI scheme, where the frequency of the IR laser pulse preceding the VUV laser pulse fixed at 77
640 ± 3 cm−1 determined in previous studies by extrapolating to the zero-field limit of the MVK and CA using VUV-MATI spectroscopy.9,10 At present, other than using FC simulations to determine the ionic transitions of the conformers expected in the S0 state, no method exists for identifying the vibrational peaks corresponding to individual conformers in the MATI spectrum of each isomer. In addition, the IR absorption spectra of the MVK and CA were obtained by utilizing the IR resonant VUV-PI scheme, where the frequency of the IR laser pulse preceding the VUV laser pulse fixed at 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762 or 78
762 or 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 cm−1, i.e., below the ionization thresholds of MVK and CA, respectively, was scanned. The IR absorption spectra of the MVK and CA in the S0 state are shown in Fig. 3(a) and 4(a), respectively. The vibrational peaks corresponding to individual conformers in the IR absorption spectrum of each isomer might be identified using the simulated IR spectrum of each conformer in the S0 state, with this process repeated for the MATI spectra. Accordingly, the conformer-specific vibrational spectra of the neutral isomer, that is, the IR dip VUV-MATI spectra of MVK and CA, were recorded by monitoring the 0–0 bands at 77
540 cm−1, i.e., below the ionization thresholds of MVK and CA, respectively, was scanned. The IR absorption spectra of the MVK and CA in the S0 state are shown in Fig. 3(a) and 4(a), respectively. The vibrational peaks corresponding to individual conformers in the IR absorption spectrum of each isomer might be identified using the simulated IR spectrum of each conformer in the S0 state, with this process repeated for the MATI spectra. Accordingly, the conformer-specific vibrational spectra of the neutral isomer, that is, the IR dip VUV-MATI spectra of MVK and CA, were recorded by monitoring the 0–0 bands at 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 and 78
861 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 cm−1 that were observed in the VUV-MATI spectra while scanning the frequency of the IR laser (Fig. 3(b) and 4(b)). The measured IR dip spectra are expected to be a proxy for the vibrational spectra of the stable s-trans conformers for the two isomers in the S0 state. To check this, the IR spectra of the s-trans and the s-cis conformers in each isomer were simulated at various calculation levels using the aug-cc-pVTZ basis set,38 as shown in Fig. S1 and S2.† All simulated vibrational frequencies were scaled to compensate for the uncertainties caused by the vibrational anharmonicity and the incomplete treatment of electron correlation, which are artifacts of using finite basis sets.39,40 Based on the simulated IR spectra (Fig. 3(c) and 4(c)) that agreed most closely with the experimental spectra, peaks observed in the IR dip spectra can be successfully assigned to the fundamental vibrational modes characterizing the C–H stretching vibrations of the s-trans conformer of each isomer (Table 1). As mentioned above, this implies that the measured IR dip spectra correspond to the identifiable vibrational spectra of the s-trans conformers for the two isomers in the S0 state.
638 cm−1 that were observed in the VUV-MATI spectra while scanning the frequency of the IR laser (Fig. 3(b) and 4(b)). The measured IR dip spectra are expected to be a proxy for the vibrational spectra of the stable s-trans conformers for the two isomers in the S0 state. To check this, the IR spectra of the s-trans and the s-cis conformers in each isomer were simulated at various calculation levels using the aug-cc-pVTZ basis set,38 as shown in Fig. S1 and S2.† All simulated vibrational frequencies were scaled to compensate for the uncertainties caused by the vibrational anharmonicity and the incomplete treatment of electron correlation, which are artifacts of using finite basis sets.39,40 Based on the simulated IR spectra (Fig. 3(c) and 4(c)) that agreed most closely with the experimental spectra, peaks observed in the IR dip spectra can be successfully assigned to the fundamental vibrational modes characterizing the C–H stretching vibrations of the s-trans conformer of each isomer (Table 1). As mentioned above, this implies that the measured IR dip spectra correspond to the identifiable vibrational spectra of the s-trans conformers for the two isomers in the S0 state.
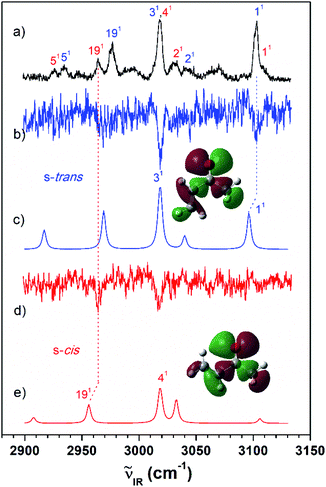 | ||
Fig. 3 (a) IR resonant VUV (77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762 cm−1) photoionization spectra of MVK measured by scanning the IR laser. The IR dip VUV-MATI spectra were measured by monitoring the origin bands expected for (b) s-trans and (d) s-cis conformers (77 762 cm−1) photoionization spectra of MVK measured by scanning the IR laser. The IR dip VUV-MATI spectra were measured by monitoring the origin bands expected for (b) s-trans and (d) s-cis conformers (77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 and 78 861 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 cm−1, respectively). Simulated IR spectra of the (c) s-trans and (e) s-cis conformers calculated at the B3LYP/aug-cc-pVTZ level, which provide the best agreement among the various calculation results, as shown in Fig. S1.† Spectra for the s-trans and s-cis conformers were normalized with respect to the 3-mode and 19-mode intensities, respectively. The highest occupied molecular orbitals of the (c) s-trans and (e) s-cis conformers were inserted in the simulated IR spectra to compare the hyperconjugation-related stabilization between the σ orbitals and the lone-pair p orbital of the oxygen atoms. 216 cm−1, respectively). Simulated IR spectra of the (c) s-trans and (e) s-cis conformers calculated at the B3LYP/aug-cc-pVTZ level, which provide the best agreement among the various calculation results, as shown in Fig. S1.† Spectra for the s-trans and s-cis conformers were normalized with respect to the 3-mode and 19-mode intensities, respectively. The highest occupied molecular orbitals of the (c) s-trans and (e) s-cis conformers were inserted in the simulated IR spectra to compare the hyperconjugation-related stabilization between the σ orbitals and the lone-pair p orbital of the oxygen atoms. | ||
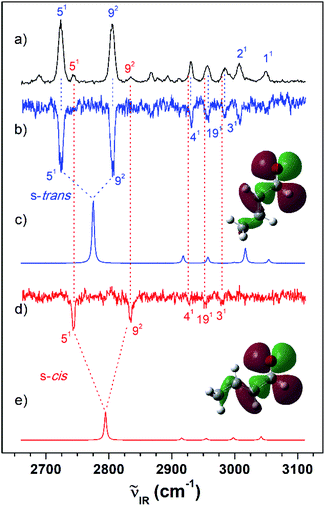 | ||
Fig. 4 (a) IR resonant VUV (78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 cm−1) photoionization spectra of CA measured by scanning the IR laser. IR dip VUV-MATI spectra measured by monitoring the origin bands expected for (b) s-trans and (d) s-cis conformers (78 540 cm−1) photoionization spectra of CA measured by scanning the IR laser. IR dip VUV-MATI spectra measured by monitoring the origin bands expected for (b) s-trans and (d) s-cis conformers (78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 and 78 638 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 cm−1, respectively). Simulated IR spectra of the (c) s-trans and (e) s-cis conformers calculated at the B3LYP/aug-cc-pVTZ level, which provide the best agreement among the various calculation results, as shown in Fig. S2.† Spectra for the s-trans conformer were normalized with respect to the 5-mode intensity, whereas spectra for the s-cis conformer were scaled by a factor of four with respect to the 5-mode intensity for ease of comparison. The highest occupied molecular orbitals of the (c) s-trans and (e) s-cis conformers were inserted in the simulated IR spectra to compare the hyperconjugation-related stabilization between the σ orbitals and the lone-pair p orbital of the oxygen atoms. 734 cm−1, respectively). Simulated IR spectra of the (c) s-trans and (e) s-cis conformers calculated at the B3LYP/aug-cc-pVTZ level, which provide the best agreement among the various calculation results, as shown in Fig. S2.† Spectra for the s-trans conformer were normalized with respect to the 5-mode intensity, whereas spectra for the s-cis conformer were scaled by a factor of four with respect to the 5-mode intensity for ease of comparison. The highest occupied molecular orbitals of the (c) s-trans and (e) s-cis conformers were inserted in the simulated IR spectra to compare the hyperconjugation-related stabilization between the σ orbitals and the lone-pair p orbital of the oxygen atoms. | ||
| Modea | IR + VUV | IR dip | Refb | Calcc | Mode descriptiond |
|---|---|---|---|---|---|
| a Mulliken notation.b Gas-phase IR spectrum from ref. 33.c Harmonic vibrational frequencies calculated from the optimized geometries with Cs symmetry at the B3LYP/aug-cc-pVTZ level.d Vibrational assignment reported in ref. 33.e Peaks split by the Fermi resonance between the carbonyl CH stretching and overtone of carbonyl CH bending. | |||||
| MVK | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| s-trans (Cs) | |||||
| 51 | 2934 | 2949 | 2916 | CH3 sym stretch | |
| 191 | 2977 | 2980 | 2969 | Out-of-plane methyl CH stretch | |
| 31 | 3018 | 3018 | 3018 | 3019 | In-phase terminal CH2 stretch |
| 21 | 3042 | 3072 | 3040 | Central C–H stretch | |
| 11 | 3103 | 3103 | 3104 | 3096 | Out-of-phase terminal CH2 stretch |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| s-cis (Cs) | |||||
| 51 | 2925 | 2935 | 2908 | CH3 sym stretch | |
| 191 | 2964 | 2964 | 2969 | 2956 | Out-of-phase methyl CH stretch |
| 41 | 3018 | 3017 | 3020 | 3018 | Out-of-phase vinyl CH stretch |
| 21 | 3030 | 3061 | 3033 | Vinyl C–H breathing | |
| 11 | 3109 | 3109 | 3106 | Out-of-phase terminal CH2 stretch | |
| CA | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| s-trans (Cs) | |||||
| 51 | 2724 | 2724 | 2722 | 2775e | Carbonyl CH stretch |
| 92 | 2805 | 2805 | 2805 | 2741e | Overtone of carbonyl CH bending |
| 41 | 2931 | 2931 | 2932 | 2918 | CH3 sym stretch |
| 191 | 2957 | 2957 | 2958 | 2957 | Out-of-phase methyl CH stretch |
| 31 | 2986 | 2986 | 2990 | 2999 | In-phase methyl and α-CH stretch |
| 21 | 3007 | 3007 | 3008 | 3017 | Out-of-phase methyl and α-CH stretch |
| 11 | 3048 | 3050 | 3054 | α-C–C(O)–H stretch | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| s-cis (Cs) | |||||
| 51 | 2745 | 2795e | Carbonyl CH stretch | ||
| 92 | 2834 | 2768e | Overtone of carbonyl CH bending | ||
| 41 | 2928 | 2916 | CH3 sym stretch | ||
| 191 | 2953 | 2955 | Out-of-phase methyl CH stretch | ||
| 31 | 2980 | 2998 | In-phase methyl and α-CH stretch | ||
Furthermore, the distinct peaks observed at 3018 and 3103 cm−1 in the IR dip spectrum of the s-trans conformer in MVK (Fig. 3(b)) matched closely with the peaks observed in the IR absorption spectrum of MVK (Fig. 2(a)). The prominent peaks at 2724, 2805, 2931, 2957 and 3007 cm−1 in the IR dip spectrum of the s-trans conformer in CA (Fig. 4(b)) are also observed in Fig. 4(a). Notably, previous research indicates that the splitting of the two intense peaks at 2724 and 2805 cm−1 corresponds to the Fermi resonance between the C(O)–H stretching and the overtone of C(O)–H bending.33,41,42
The characteristic peaks (i.e., the 1(a′) and 5(a′) modes) at 3103 and 2724 cm−1 isolated in the IR dip spectra of the s-trans conformers in MVK and CA were utilized in the IR hole-burn VUV-MATI scheme to acquire the identifiable vibrational spectra of the s-trans conformers for the two isomers in the D0 state. This scheme is based on the fact that when the frequency of the IR laser was fixed at the characteristic peak of the s-trans conformer in the S0 state, the corresponding MATI ion signals decrease owing to the vibrational excitation-induced reduction in the initial population of the s-trans conformer. In reality, the vibrational excitations for the s-trans conformers in the two isomers caused the 0–0 band signals for MVK and CA to be depleted by 5.3% and 8.0%, respectively, which confirms that the two 0–0 bands in the MATI spectra correspond to those of the s-trans conformers in the two isomers. For each isomer, the IR hole-burn spectrum of the s-trans conformer was obtained from the difference in the VUV-MATI spectra of the isomer with and without IR hole-burn laser irradiation, as shown in Fig. 2(b). The FC simulations for the s-trans conformer of each isomer in the D0 state (Fig. 2(c)) confirm that the measured IR hole-burn spectrum of each isomer represents the identifiable vibrational spectrum of each s-trans conformer in the D0 state. Thus, by comparing the IR hole-burn spectra of the s-trans conformers with the VUV-MATI spectra of the two isomers, it was found that the distinct peaks at 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 and 78
217 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 cm−1 in the MATI spectra were absent from the IR hole-burn spectra of the s-trans conformers, indicating that those peaks correspond to the s-cis conformers for the two isomers in the D0 state.
734 cm−1 in the MATI spectra were absent from the IR hole-burn spectra of the s-trans conformers, indicating that those peaks correspond to the s-cis conformers for the two isomers in the D0 state.
To monitor these peaks in the VUV-MATI spectra of MVK and CA, we measured the IR dip spectra while scanning the frequency of the IR laser, as shown in Fig. 3(d) and 4(d), respectively. As expected, the measured IR dip spectra corresponded to the IR spectra of the s-cis conformers in the S0 state for the two isomers, which were supported by the simulated IR spectra of the s-cis conformers in the two isomers shown in Fig. 3(e) and 4(e). The peaks in the measured IR dip spectra were attributed to the CH stretching vibrations of the s-cis conformers of each isomer (Table 1). As for the s-trans conformer, the Fermi resonance-related splitting at two similar frequency vibrations was observed at 2745 and 2834 cm−1. Remarkably, the IR absorption spectra of the MVK and CA (Fig. 3(a) and 4(a)) represent the summed IR dip spectra of the individual conformers, that is, the s-trans and the s-cis conformers for each isomer in the S0 state, which implies that the measured IR dip spectra of the two conformers in each isomer can be determined accurately from the IR absorption spectrum of each isomer.
As for the s-trans conformer, the IR hole-burn spectra of the s-cis conformers in the MVK and CA were acquired by utilizing the characteristic peaks (i.e., the 19(a′) and 5(a′) modes) at 2964 and 2745 cm−1 isolated in the IR dip spectra of the s-cis conformers for the MVK and CA isomers in the S0 state. Despite their low intensity, distinct peaks corresponding to the 0–0 bands of the s-cis conformers were observed in the IR hole-burn spectra of the MVK and CA at 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 and 78
217 and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 cm−1, respectively (Fig. 2(d)). In addition, the 0–0 band positions for the s-cis conformers in the two isomers corroborated the AIE values determined in previous studies.9,10 The assignments of the peaks observed in the IR hole-burn spectra of the individual conformers in the two isomers are listed in Table 2 alongside the calculated results and previously reported values. Owing to the vibrational excitations for the s-cis conformers of MVK and CA in the S0 state, the 0–0 band signals were depleted by 4.3% and 20.9%, respectively.
734 cm−1, respectively (Fig. 2(d)). In addition, the 0–0 band positions for the s-cis conformers in the two isomers corroborated the AIE values determined in previous studies.9,10 The assignments of the peaks observed in the IR hole-burn spectra of the individual conformers in the two isomers are listed in Table 2 alongside the calculated results and previously reported values. Owing to the vibrational excitations for the s-cis conformers of MVK and CA in the S0 state, the 0–0 band signals were depleted by 4.3% and 20.9%, respectively.
| Modea | IR hole-burnb | Refc | Calcd | Mode descriptione |
|---|---|---|---|---|
| a Mulliken notation.b Values in parentheses indicate the ion internal energies of vibrational peaks estimated with respect to the 0–0 band positions of individual conformers.c Ref. 9 and 10 for MVK and CA, respectively.d Harmonic vibrational frequencies calculated from the optimized geometries with Cs symmetry at B3LYP/aug-cc-pVTZ level.e Vibrational assignments for MVK and CA reported in ref. 9 and 10, respectively. | ||||
| MVK | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| s-trans (Cs) | ||||
| 0–0 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 (0) 861 (0) |
77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 ± 4 (0) 867 ± 4 (0) |
0–0 band | |
| 171 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 (385) 246 (385) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 253 (386) 253 (386) |
375 | In plane C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bend O bend |
| 161 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 336 (475) 336 (475) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 (475) 342 (475) |
475 | In plane C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C bend C–C bend |
| s-cis (Cs) | ||||
| 0–0 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 (355) 216 (355) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 ± 4 (355) 222 ± 4 (355) |
0–0 band | |
| CA | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| s-trans (Cs) | ||||
| 0–0 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 (0) 638 (0) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 ± 3 (0) 640 ± 3 (0) |
0–0 band | |
| 181 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 (213) 851 (213) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 (215) 855 (215) |
208 | Out-of-phase C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C bend C–C bend |
| 161 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101 (463) 101 (463) |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103 (463) 103 (463) |
453 | In-phase C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C bend C–C bend |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| s-cis (Cs) | ||||
| 0–0 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 (96) 734 (96) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 ± 3 (96) 736 ± 3 (96) |
0–0 band | |
| 181 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 (315) 953 (315) |
78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984 (344) 984 (344) |
286 | In plane C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C bend C–C bend |
We used the conformer-specific vibrational spectra of the MVK and CA isomers measured via IR dip and hole-burn VUV-MATI spectroscopy to estimate the relative amounts of the s-trans and the s-cis conformers in the S0 state for MVK and CA. When a molecule absorbs the IR photon of high frequency, the intramolecular vibrational relaxation (IVR) from the initially excited vibrational mode can occur to other low-frequency modes. Hence, we utilized the sharp dips in the IR dip VUV-MATI spectra so that the possibility of the IVR process is maximally excluded. Then, assuming that the vibrational excitation-induced conformer population reduction determined via IR absorption reflects the hole-burn in the MATI ion signal produced by the conformer, the relative populations of two conformers can be determined using the dip intensities in their respective IR dip spectra; these intensities should be divided by the FC-factor related to the 0–0 band and the IR absorption probability of vibrational excitation corresponding to the dip frequency. The dip intensities were estimated by fitting the data using the single Gaussian function. To estimate the relative conformer populations in MVK, vibrations 1 and 19 at 3103 and 2964 cm−1 for the s-trans and the s-cis conformers, respectively, were chosen. Then, the dip intensities were divided by FC-factors of 1.56 × 106 (s-trans) and 1.88 × 106 (s-cis) and IR absorption probabilities of 7.2 (s-trans) and 8.0 (s-cis). Thus, the relative populations of two conformers were determined as 90.6% (s-trans) and 9.4% (s-cis), which agree closely with previous values of 88% and 12%, which were determined by one-photon VUV-MATI spectroscopy.9 Similarly, we determined the relative conformer populations in CA by using vibrations 5 and 5 at 2724 (s-trans) and 2735 cm−1 (s-cis), assuming no Fermi resonance-induced changes in intensity. The corresponding FC factors and IR absorption probabilities were 0.38 and 635 (s-trans) and 0.37 and 1052 (s-cis), leading to the relative amounts of the two conformers in CA being calculated as 95.8% (s-trans) and 4.2% (s-cis), which are in excellent agreement with those reported for one-photon VUV-MATI spectroscopy: 96.5% and 3.5%, respectively.10 These results are summarized in Table 3.
| Method | s-trans | s-cis | Stabilityd |
|---|---|---|---|
a Values reported in ref. 9 and 10 for MVK and CA, respectively.b Values reported in ref. 32.c Values reported in ref. 33.d Conformational stabilities between individual conformers determined from the characteristic peaks in the IR dip VUV-MATI spectra of MVK and CA at temperatures of 27 K and 298 K, respectively, utilizing ΔH = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K + TΔS, where K was estimated by the relative populations and ΔS was determined by quantum chemical calculations. K + TΔS, where K was estimated by the relative populations and ΔS was determined by quantum chemical calculations. |
|||
| MVK | |||
| This work | 90.6% | 9.4% | 53 cm−1 |
| VUV-MATIa | 88% | 12% | 48 ± 18 cm−1 |
| IRb | 76% | 24% | 45 cm−1 |
| IR and Ramanc | 69% | 31% | 162 cm−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| CA | |||
| This work | 95.8% | 4.2% | 706 cm−1 |
| VUV-MATIa | 96.5% | 3.5% | 634 cm−1 |
| IR and Ramanc | 97% | 3% | |
The difference in the relative conformational preferences for the MVK and CA isomers can be attributed to the extent to which the highest occupied molecular orbitals, which consist of nonbonding orbitals on the oxygen atom in the carbonyl group interacting with the σ orbitals in the molecular plane, are stabilized. This depends on the position of the methyl group. Stabilization between the σ orbitals and lone-pair p orbital of the oxygen atom occurs through hyperconjugation. Therefore, the stability of the s-cis conformer in MVK is expected to be higher than that in CA because of the interaction between the carbonyl and methyl groups, as shown in Fig. 3 and 4.
Conclusions
Conformers have similar vibrational structures both in the S0 and D0 states due to the comparable force fields between their nuclei. This has led to the continuous development of vibrational spectroscopic techniques to rigorously identify individual conformers of the designated molecule but only in the S0 state. Our results demonstrate that the IR hole-burn VUV-MATI spectra of individual conformers in the D0 state allow the VUV-MATI spectrum of a molecule to be rigorously deciphered, while the IR dip VUV-MATI spectra correspond to identifiable IR absorption spectra of individual conformers in the S0 state. Therefore, we expect that these conformer-specific vibrational spectroscopies will become a highly effective spectroscopic technique to elucidate the conformational structures of a molecule in the S0 and D0 states.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (2020R1A2B5B02001658 and 2021R1I1A1A01047743).Notes and references
- B. C. Dian, A. Longarte and T. S. Zwier, Science, 2002, 296, 2369–2373 CrossRef CAS PubMed.
- S. T. Park, S. K. Kim and M. S. Kim, Nature, 2002, 415, 306–308 CrossRef PubMed.
- B. C. Dian, A. Longarte and T. S. Zwier, Science, 2002, 296, 2369–2373 CrossRef CAS PubMed.
- M. H. Kim, L. Shen, H. Tao, T. J. Martinez and A. G. Suits, Science, 2007, 315, 1561–1565 CrossRef CAS PubMed.
- T. R. Rizzo, Y. D. Park and D. H. Levy, J. Chem. Phys., 1986, 85, 6945–6951 CrossRef CAS.
- G. Scoles, Atomic and Molecular Beam Methods, Oxford University Press, 1988 Search PubMed.
- S. M. Park, H. L. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2018, 20, 27162–27168 RSC.
- Y. R. Lee, M. H. Kim, H. L. Kim and C. H. Kwon, J. Chem. Phys., 2018, 149, 174302 CrossRef PubMed.
- S. M. Park, J. Choi, H. L. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2020, 22, 28383–28392 RSC.
- S. M. Park, H. L. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2018, 20, 27162–27168 RSC.
- S. Y. Eom, Y. R. Lee and C. H. Kwon, Phys. Chem. Chem. Phys., 2020, 22, 22823–22832 RSC.
- S. Y. Eom, D. W. Kang and C. H. Kwon, Phys. Chem. Chem. Phys., 2021, 23, 1414–1423 RSC.
- R. J. Lipert and S. D. Colson, J. Phys. Chem., 1989, 93, 3894–3896 CrossRef CAS.
- C. Riehn, C. Lahmann, B. Wassermann and B. Brutschy, Chem. Phys. Lett., 1992, 197, 443–450 CrossRef CAS.
- T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361 Search PubMed.
- J. M. Bakker, L. Mac Aleese, G. Meijer and G. Helden, Phys. Rev. Lett., 2003, 91, 203003 CrossRef PubMed.
- C. M. Choi, D. H. Choi, J. Heo, N. J. Kim and S. K. Kim, Angew. Chem., Int. Ed., 2012, 51, 7297–7300 CrossRef CAS PubMed.
- A. Min, A. Ahn, C. J. Moon, J. H. Lee, Y. G. Seong, S. K. Kim and M. Y. Choi, Phys. Chem. Chem. Phys., 2017, 19, 4840–4848 RSC.
- H. K. Woo, P. Wang, K.-C. Lau, X. Xing, C. Chang and C. Y. Ng, J. Chem. Phys., 2003, 119, 9333–9336 CrossRef CAS.
- Y. Matsuda, N. Mikami and A. Fujii, Phys. Chem. Chem. Phys., 2009, 11, 1279–1290 RSC.
- H. Han, C. Camacho, H. A. Witek and Y. Lee, J. Chem. Phys., 2011, 134, 144309 CrossRef PubMed.
- A. J. Bowles, W. O. George and W. F. Maddams, J. Chem. Soc. B, 1969, 810–818 RSC.
- R. J. Loncahrich, F. K. Brown and K. N. Houk, J. Org. Chem., 1989, 54, 1129–1134 CrossRef.
- E. Praske, J. D. Crounse, K. H. Bates, T. Kurtén, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. A, 2015, 119, 4562–4572 CrossRef CAS PubMed.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2018, 239, 17 CrossRef CAS.
- K. W. Paulisse, T. O. Friday, M. L. Graske and W. F. Polik, J. Chem. Phys., 2000, 113, 184–191 CrossRef CAS.
- N. R. Pillsobury, J. Choo, J. Laane and S. Drucker, J. Phys. Chem. A, 2003, 107, 10648–10654 CrossRef.
- J. Cao and Z. Xie, Phys. Chem. Chem. Phys., 2016, 18, 6931–6945 RSC.
- M.-C. Kim, E. Sim and K. Burke, Phys. Rev. Lett., 2013, 111, 073003 CrossRef PubMed.
- Y. Kim, S. Song, E. Sim and K. Burke, J. Phys. Chem. Lett., 2019, 10, 295–301 CrossRef CAS PubMed.
- J. R. Durig and T. S. Little, J. Chem. Phys., 1981, 75, 3660–3668 CrossRef CAS.
- K. Sankaran and Y. Lee, J. Phys. Chem. A, 2002, 106, 1190–1195 CrossRef CAS.
- R. Lindenmaier, S. D. Williams, R. L. Sams and T. J. Johnson, J. Phys. Chem. A, 2017, 121, 6420–6428 CrossRef PubMed.
- O. Zakharenko, R. A. Motiyenko, J. R. A. Moreno and T. R. Huet, J. Phys. Chem. A, 2017, 121, 6420–6428 CrossRef CAS PubMed.
- O. Geßner, E. t.-H. Chrysostom, A. M. D. Lee, D. M. Wardlaw, M.-L. Ho, S.-J. Lee, B.-M. Cheng, M. Z. Zgierski, I.-C. Chen, J. P. Shaffer, C. C. Hayden and A. Stolow, Faraday Discuss., 2004, 127, 193–212 RSC.
- Y. R. Lee, D. W. Kang, H. L. Kim and C. H. Kwon, J. Chem. Phys., 2014, 141, 174303 CrossRef PubMed.
- Y. R. Lee, M. H. Kim and C. H. Kwon, J. Chem. Phys., 2019, 151, 164305 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgometry, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- P. Sinha, S. E. Boesch, C. Gu, R. A. Wheeler and A. K. Wilson, J. Phys. Chem. A, 2004, 108, 9213–9217 CrossRef CAS.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed.
- A. Amrein, H. Hollenstein, M. Quack, R. Zenobi, J. Segall and R. N. Zare, J. Chem. Phys., 1989, 90, 3944–3951 CrossRef CAS.
- J. A. Stride, P. H. Dallin and U. A. Jayasooriya, J. Chem. Phys., 2003, 119, 2747–2752 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07397d |
| This journal is © The Royal Society of Chemistry 2021 |