A comparison of hydrogen release kinetics from 5- and 6-membered 1,2-BN-cycloalkanes

Abstract

The reaction order and Arrhenius activation parameters for spontaneous hydrogen release from cyclic amine boranes, i.e., BN-cycloalkanes, were determined for 1,2-BN-cyclohexane (1) and 3-methyl-1,2-BN-cyclopentane (2) in tetraglyme. Computational analysis identified a mechanism involving catalytic substrate activation by a ring-opened form of 1 or 2 as being consistent with experimental observations.

---

Amine boranes have long been targeted as a promising class of potential hydrogen storage materials.¹ The simplest amine borane, ammonia borane (H₃NBH₃), has attracted significant attention by virtue of its particularly high gravimetric hydrogen density (19.6 wt% H₂).² Thermal decomposition of ammonia borane to release H₂, however, frequently generates mixtures of oligomeric and polymeric products, which in turn can complicate efforts to regenerate the fully saturated starting material for reuse.¹ Extensive studies of variously substituted amine boranes have thus been conducted in the interest of identifying a system that releases H₂ more selectively.^3,4

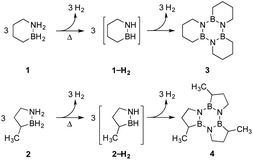
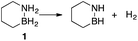
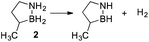
Our approach in this regard has been to incorporate the amine borane H₂NBH₂ unit into carbocyclic structures to form saturated carbon–boron–nitrogen (CBN) heterocycles.⁵ We have previously discovered that two of these compounds, 1,2-BN-cyclohexane (1)⁶ and its constitutional isomer 3-methyl-1,2-BN-cyclopentane (2)⁷ undergo full, thermally-induced BN-dehydrogenation to afford only the trimeric products 3 and 4 through the intermediacy of monomeric BN-“cycloalkene” species 1–H₂ (ref. 8) and 2–H₂, respectively (Scheme 1).

Scheme 1 Selective thermal decomposition of 1 and 2 to trimers 3 and 4, respectively.

While 1 and 2 appeared to exhibit the same general dehydrogenation selectivity, in subsequent experiments using neat material, we observed an intriguing difference in the thermal stability of these compounds. Specifically, thermo-gravimetric analysis-mass spectrometry (TGA-MS) revealed significant loss of H₂ from 2 initiated at ∼50 °C,⁹ but an analogous measure of decomposition of 1 occurred only upon heating to ∼70 °C (Fig. S2; see also Fig. S3† for the temperature-programmed desorption-mass spectrometry (TPD-MS) of 1). Thus, of the two materials, only 1 would meet the minimum requirement for operational stability set by the US Department of Energy's Hydrogen and Fuel Cells Program for on-board vehicular applications.¹⁰

A mechanistic investigation of the origin of this dichotomy of dehydrogenation reactivity would aid in the design of better amine borane-based hydrogen storage materials and add to our fundamental understanding of the reactivity of amine boranes. Herein, we provide a solution-phase kinetic analysis of initial H₂ release from 1 and 2 using ReactIR. The kinetic data establish a second-order decomposition pathway that is in agreement with a computationally-derived mechanistic model. We also provide evidence that the ring strain associated with the 5-membered heterocycle 2 is ultimately responsible for its faster decomposition rates.^11,12

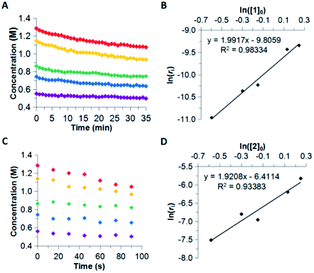
The reaction order for the first step of dehydrogenation of 1 and 2 was determined using the initial rates method. Both 1 and 2 exhibit a characteristic IR frequency at 1600 cm⁻¹ (attributed to an N–H bending mode); the disappearance of starting material can thus be readily monitored in situ by ReactIR.¹³ The initial concentrations ([ ]₀) of either 1 or 2 in a tetraglyme solution at 140 °C were varied between 0.560 M and 1.283 M, and initial rates (r_i) were estimated based on linear regression of the respective portions of the substrate disappearance trends representing up to 20% conversion. As shown in Fig. 1, a linear fit of ln(r_i) vs. ln([ ]₀) yielded a slope of 2 for both 1 and 2, indicating the rate of initial H₂ loss from each follows a second-order concentration dependence.¹⁴

Fig. 1 Abbreviated substrate disappearance trends measured at 140 °C for various initial concentrations of 1 (A) and 2 (C), and reaction order determination by the initial rates method for 1 (B) and 2 (D).

A subsequent Arrhenius analysis was enabled by maintaining a constant initial concentration of 0.742 M, and varying the reaction temperature from 120–160 °C for 1 and from 100–160 °C for 2. As shown in Table 1, the activation energy (E_a) for 2 is lower than that of 1 by 5.0 kcal mol⁻¹. However, the pre-exponential factor (A) of 2 is an order of magnitude smaller than that of 1. Of these two opposing trends, the difference in E_a ultimately dominates within the temperature range studied, and so the reaction rate constants (k) of 2 are more than an order of magnitude greater than those of 1 (Fig. 2). (Extrapolation to lower temperatures, e.g., 50 °C, reveals an even wider gap of approximately three orders of magnitude.) It thus appears that enthalpic factors, as represented by E_a values,¹⁵ are primarily responsible for the faster kinetics of H₂ release from 2 relative to those of 1.

Table 1 Experimentally determined activation energies (E_a) and pre-exponential factors (A) for 1 and 2 based on Arrhenius analyses

Reaction	Ea (kcal mol^−1)	A (M^−1 s^−1)
	23.8	2.25 × 10^8
	18.8	2.02 × 10^7

---

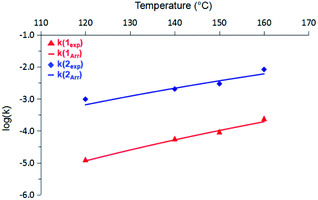Fig. 2 Comparison of rate constants (k) for 1 (red) and 2 (blue) from 120 °C to 160 °C. Solid lines represent predicted values based on the Arrhenius activation terms listed in Table 1.

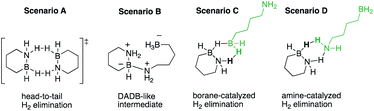
To further refine our understanding of the mechanism of the initial H₂ release from either 1 or 2, we turned to computational modeling. The experimental evidence (vide supra) for a bimolecular process involving two molecules of 1 or 2 in the rate-determining step led us to investigate four distinct possible scenarios (Scheme 2): (A) simultaneous loss of one H₂ equivalent each directly from two substrate molecules interacting in a “head-to-tail” fashion;¹⁶ (B) formation of an intermediate prior to H₂ release analogous to the diammoniate of diborane (DADB) species observed in thermal ammonia borane decomposition;^14a or generation of linear isomers 1′ or 2′ through reversible, heterolytic B–N bond cleavage and subsequent catalysis of H₂ formation by interaction of these isomers' free BH₂ (C) or NH₂ groups (D) with another still cyclized molecule of either 1 or 2.¹⁷ Ultimately, the activation barriers associated with pathways (A), (B), and (D) (Fig. S6–S9†) were calculated to be significantly higher for both 1 and 2 than those predicted for pathway (C), which is shown in detail in Fig. 3 and described in terms of 1 below.

Scheme 2 Proposed bimolecular decomposition scenarios.

Fig. 3 Potential energy surfaces for pathway (C): bimolecular H₂ release from 1 (top) and 2 (bottom) involving catalysis by ring-opened intermediates. Gas-phase enthalpy (black) and free energy [green] values (kcal mol⁻¹) were calculated using DFT (298 K) at the M06/DZVP2 level of theory.

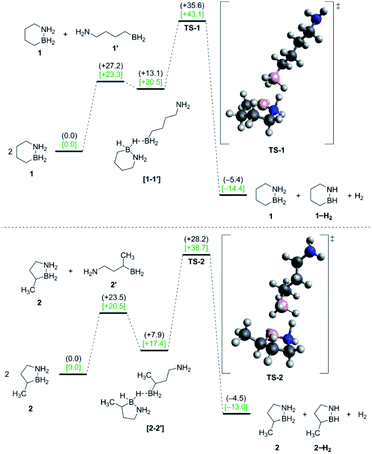
Starting from two ring-closed molecules, B–N bond cleavage first generates one unit of 1′. A bridging hydride interaction between the BH₂ groups of 1 and 1′ results in formation of complex [1–1′], which is lower in energy than the separate mixed species, but still less stable than the ring-closed starting materials. The lowest energy transition state (TS-1) for H₂ release from 1 involves intramolecular transfer of the bridging hydride from 1 completely to 1′, while a proton from the NH₂ group of 1 simultaneously combines with another hydride of the 1′ BH₂ unit to form free H₂.

The above gas-phase model predicts a lower reaction barrier for H₂ release from 2 than from 1 (ΔG₍₂^‡₎ = 38.7 kcal mol⁻¹ vs. ΔG₍₁^‡₎ = 43.1 kcal mol⁻¹), consistent with the trend observed experimentally. (This relative trend was also observed in calculations with an implicit tetraglyme solvent model (Fig. S10†)). Interestingly, the calculated ΔG_{298 K} value for B–N bond dissociation in 2 is also lower than for 1 (ΔΔG_{298 K} = 2.8 kcal mol⁻¹), such that the equilibrium constants for this preliminary step differ by two orders of magnitude at 25 °C (K_eq(2) = 8.15 × 10⁻¹⁶ and K_eq(1) = 7.08 × 10⁻¹⁸). While our model does not predict B–N bond cleavage itself to be rate-limiting, a higher equilibrium concentration of 2′ relative to 1′ would nonetheless influence the observed kinetics of thermal decomposition in favor of faster apparent rates for 2.¹⁸

We propose both the greater facileness of initial B–N bond dissociation and the overall more rapid dehydrogenation of 2 occurs primarily as a result of greater molecular strain energy in 2 as compared to that in 1. Using the homodesmotic reaction scheme devised by Gilbert,¹⁹ we calculated the strain energy of 2 to be 3.1 kcal mol⁻¹ greater than that of 1. Furthermore, experimental evidence in support of this trend arises from a comparison of the length of the B–N bond in five- and six-membered BN-cycloalkanes as determined by single crystal X-ray analysis (see the ESI† for acquisition parameters and detailed structural data). Relative elongation of this bond was presumed to serve as an indicator of greater ring strain, and indeed, the average B–N bond length of a series of BN-cyclopentanes (1.630 Å)²⁰ was found to be longer than that measured for 1 (1.614(1) Å).^21,22 This additional strain destabilizes 2 relative to 1, such that the enthalpic contributions required to reach TS2 are correspondingly diminished compared to those needed to reach TS1 starting from 1. These relationships are reflected in both experimental and computational results, which respectively yield lower E_a and ΔH^‡ values for 2 compared to those for 1.

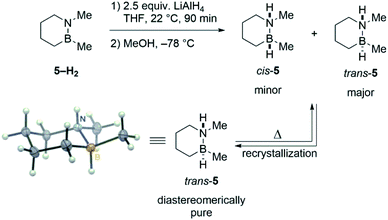
To probe the intermediacy of ring-opened species such as 1′, we prepared a close analogue of 1 that contains a stereochemical label: trans-1,2-dimethyl-1,2-BN-cyclohexane (trans-5).²³ Sequential hydride/proton addition to cyclic aminoborane 5–H₂ (ref. 24) furnishes a mixture of trans- and cis-5 (Scheme 3). The major trans diastereomer could be isolated by recrystallization, and its structure was unambiguously confirmed by single crystal X-ray diffraction analysis.

Scheme 3 Synthesis and structure of trans-5.

Mild heating of pure trans-5 leads to a partial isomerization back to the cis isomer as evidenced by ¹¹B and ¹H NMR (Fig. S1†). Based on previous studies of B–N bond cleavage in related cyclic systems,²⁵ the observed formation of cis-5 is consistent with a mechanism that involves B–N bond dissociation, B–(C3) bond rotation (or nitrogen inversion and N–(C6) rotation), and finally B–N bond re-formation. The studies with 5 thus provide indirect evidence for ring-opened species 1′ and 2′ as viable intermediates in the thermal decomposition of 1 and 2.

In summary, we have experimentally measured the kinetics of the release of the first H₂ equivalent from 1,2-BN-cyclohexane (1) and 3-methyl-1,2-BN-cyclopentane (2) using ReactIR. A second-order concentration dependence was determined for both 1 and 2. Arrhenius analysis revealed a lower reaction barrier for 2 due to a smaller requisite activation energy (E_a). These trends were replicated in a computational model of a bimolecular dehydrogenation mechanism involving substrate activation catalyzed by a ring-opened form of 1 or 2. This mechanistic study sheds light on the origin of the differing thermal stability exhibited by two isomeric cyclic amine boranes and suggests that ring-strain as well as the strength of the B–N bond in cyclic CBN compounds need to be considered in the next generation of materials to provide sufficient thermal stability.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is dedicated to Ms. Grace Ordaz at DOE EERE office, whose support and insightful questions are greatly appreciated. This work was funded by the US Department of Energy (DE-EE0005658 and Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under the Catalysis Center Program). We thank Dr Wei Luo for the preparation of 4- and 5-methyl-1,2-BN-cyclopentane and 1,2-BN-cyclopentane; Dr Lev N. Zakharov for providing single crystal X-ray analyses of these three BN-cyclopentane compounds and Dr Bo Li for the analysis of trans-5; Dr Thomas Gennett for the TPD-MS analysis of 1; and Dr Gabriel Lovinger for helpful discussions related to PES calculations. D. A. Dixon thanks the Robert Ramsay Chair Fund of The University of Alabama for support.

Notes and references

1. For select reviews, see: (a) T. B. Marder, Angew. Chem., Int. Ed., 2007, 46, 8116; (b) C. W. Hamilton, R. T. Baker, A. Staubitz and I. Manners, Chem. Soc. Rev., 2009, 38, 279; (c) A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079; (d) R. Kumar, A. Karkamkar, M. Bowden and T. Autrey, Chem. Soc. Rev., 2019, 48, 5350.
2. For select studies, see: (a) A. Gutowska, L. Li, Y. Shin, C. M. Wang, X. S. Li, J. C. Linehan, R. S. Smith, B. D. Kay, B. Schmid, W. Shaw, M. Gutowski and T. Autrey, Angew. Chem., Int. Ed., 2005, 44, 3578; (b) T. Autrey, M. Bowden and A. Karkamkar, Faraday Discuss., 2011, 151, 157; (c) W. R. H. Wright, E. R. Berkeley, L. R. Alden, R. T. Baker and L. G. Sneddon, Chem. Commun., 2011, 47, 3177; (d) R. J. Keaton, J. M. Bacquiere and R. T. Baker, J. Am. Chem. Soc., 2007, 129, 1844; (e) Z. Tang, X. Chen, H. Chen, L. Wu and X. Yu, Angew. Chem., Int. Ed., 2013, 125, 5944; (f) T. Semelsberger, J. Graetz, A. Sutton and E. C. E. Rönnebro, Molecules, 2021, 26, 1722.
3. For reviews of specifically metal-catalyzed amine-borane dehydrogenation, see: (a) H. C. Johnson, T. N. Hooper and A. S. Weller, in Synthesis and Application of Organoboron Compounds, ed. E. Fernández and A. Whiting, Springer International Publishing, 2015, ch. 6, pp. 153–220; (b) A. Rossin and M. Peruzzini, Chem. Rev., 2016, 116, 8848; (c) X. Zhang, L. Kam, R. Trerise and T. J. Williams, Acc. Chem. Res., 2017, 50, 86; (d) D. Han, F. Anke, M. Trose and T. Beweries, Coord. Chem. Rev., 2019, 380, 260.
4. In addition to the above reviews, summaries of mechanistic studies can also be found in: (a) G. Alcaraz and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2010, 49, 7170; (b) M. Bowden and T. Autrey, Curr. Opin. Solid State Mater. Sci., 2011, 15, 73; (c) P. M. Zimmerman, Z. Zhang and C. B. Musgrave, J. Phys. Chem. Lett., 2011, 2, 276; (d) X. Chen, J.-C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666; (e) A. Al-Kukhun, H. T. Hwang and A. Varma, Int. J. Hydrogen Energy, 2013, 38, 169; (f) S. Bhunya, P. M. Zimmerman and A. Paul, ACS Catal., 2015, 5, 3478; (g) U. B. Demirci, Inorg. Chem. Front., 2021, 8, 1900.
5. (a) M. H. Matus, S.-Y. Liu and D. A. Dixon, J. Phys. Chem. A, 2010, 114, 2644; (b) P. G. Campbell, L. N. Zakharov, D. Grant, D. A. Dixon and S.-Y. Liu, J. Am. Chem. Soc., 2010, 132, 3289; (c) G. Chen, L. N. Zakharov, M. E. Bowden, A. J. Karkamkar, S. E. Whittemore, E. B. Garner III, T. C. Mikulas, D. A. Dixon, T. Autrey and S.-Y. Liu, J. Am. Chem. Soc., 2015, 137, 134.
6. W. Luo, L. N. Zakharov and S.-Y. Liu, J. Am. Chem. Soc., 2011, 133, 13006.
7. W. Luo, P. G. Campbell, L. N. Zakharov and S.-Y. Liu, J. Am. Chem. Soc., 2011, 133, 19326.
8. (a) S. G. Kukolich, M. Sun, A. M. Daly, W. Luo, L. N. Zakharov and S.-Y. Liu, Chem. Phys. Lett., 2015, 639, 88; (b) A. Kumar, J. S. A. Ishibashi, T. N. Hooper, T. C. Mikulas, D. A. Dixon, S.-Y. Liu and A. S. Weller, Chem.–Eur. J., 2016, 22, 310.
9. The temperature at which the release of H₂ is first observed is interpreted as the compound’s decomposition onset temperature; see: W. Luo, D. Neiner, A. Karkamkar, K. Parab, E. B. Garner III, D. A. Dixon, D. Matson, T. Autrey and S.-Y. Liu, Dalton Trans., 2013, 42, 611.
10. Technical System Targets: Onboard Hydrogen Storage for Light-Duty Fuel Cell Vehicles, accessed August 9, 2021, https://www.energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles.
11. For select examples in which ring size has been demonstrated to influence reaction kinetics, see: (a) V. G. Granik, Russ. Chem. Rev., 1982, 51, 119 and references cited therein; (b) E. Masson and F. Leroux, Helv. Chim. Acta, 2005, 88, 1375; (c) J. N. Sanders, H. Jun, R. A. Yu, J. L. Gleason and K. N. Houk, J. Am. Chem. Soc., 2020, 142, 16877.
12. To our knowledge, the effects of varying ring size vis-à-vis amine-borane dehydrogenation have been previously examined only in the context of incorporating the nitrogen atom alone into a cyclic framework; for examples, see A. Staubitz, M. Besora, J. N. Harvey and I. Manners, Inorg. Chem., 2008, 47, 5910 and T. Banu, K. Sen, D. Ghosh, T. Debnath and A. K. Das, RSC Adv., 2014, 4, 1352 . The present analysis fundamentally differs from these earlier works in that in the subject BN-cycloalkanes, i.e., 1 and 2, the nitrogen and boron atoms are both endocyclic..
13. Calculated IR spectra of 1–H₂ and 2–H₂ indicate that no peaks associated with these species overlap with the signature substrate peak at 1600 cm⁻¹ (Fig. S11–S14†).
14. Second-order kinetics have also been reported for the early-phase decomposition of ammonia borane in solution; see: (a) J. W. Shaw, J. C. Linehan, N. K. Szymczak, D. J. Heldebrant, C. Yonker, D. M. Camaioni, R. T. Baker and T. Autrey, Angew. Chem., Int. Ed., 2008, 47, 7493; (b) J. F. Kostka, R. Schellenberg, F. Baitalow, T. Smolinka and F. Merterns, Eur. J. Inorg. Chem., 2012, 2012, 49.
15. We did not conduct a complementary Eyring analysis to also determine ΔH^‡ values because our proposed reaction mechanism involves additional, discrete transformations of 1 and 2 prior to the rate-limiting transition state (vide infra).
16. A transition state for net loss of only one H₂ equivalent from two closed molecules of either 1 or 2 could not be found.
17. For H₃NBH₃, B–N bond dissociation and then substrate activation by the free BH₃ thus generated has been invoked by Nguyen et al. as part of the overall decomposition process. M. T. Nguyen, V. S. Nguyen, M. H. Matus, G. Gopakumar and D. A. Dixon, J. Phys. Chem. A, 2007, 111, 679.
18. Extrapolation to temperatures in the range of experimental study shows that K_eq(2) for B–N bond dissociation remains 1.2–1.5 orders of magnitude greater than K_eq(1).
19. T. M. Gilbert, Tetrahedron Lett., 1998, 39, 9147.
20. An average value was used for comparative purposes due to the observation of disorder with respect to the carbon atoms in the individual crystal structures determined for all extant BN-cyclopentanes, save only 5-methyl-1,2-BN-cyclopentane.
21. The measured average BN-cyclopentane B–N bond length is also notably longer than that determined by Stubbs et al. for a representative acyclic, and therefore completely unstrained, B,N-dialkylated amine-borane (MeH₂NBH₂Me; B–N = 1.605(2) Å). N. E. Stubbs, A. Schäfer, A. P. M. Robertson, E. M. Leitao, T. Jurca, H. A. Sparkes, C. H. Woodall, M. F. Haddow and I. Manners, Inorg. Chem., 2015, 54, 10878.
22. This trend was also reproduced by calculations; see Table S2† for atomic coordinates of the relevant computed structures.
23. When excess tri(n-butyl)phosphine was added as a borane trapping reagent to 1 under the H₂ elimination conditions, no borane-phosphine adduct was observed by NMR.
24. Z. X. Giustra, L.-Y. Chou, C.-K. Tsung and S.-Y. Liu, Organometallics, 2016, 35, 2425.
25. (a) H. Höpfl, N. Farfán, D. Castillo, R. Santillan, R. Contreras, F. J. Martínez-Martínez, M. Galván, R. Alvarez, L. Fernández, S. Halut and J.-C. Daran, J. Organomet. Chem., 1997, 544, 175; (b) S. Toyota, F. Ito, N. Nitta and T. Hakamata, Bull. Chem. Soc. Jpn., 2004, 77, 2081; (c) G. P. Harlow, L. N. Zakharov, G. Wu and S.-Y. Liu, Organometallics, 2013, 32, 6650.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental procedures and analyses, additional computational details, and crystallographic information. CCDC 2103581–2013584. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra07477f

---