Open Access Article
Open Access ArticleA new chemical compound with an unusual ratio of number of carbon and nitrogen atoms – C(N12): quantum-chemical modelling†
Denis V. Chachkovab and
Oleg V. Mikhailov *b
*b
aKazan Department of Joint Supercomputer Center of Russian Academy of Sciences – Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, 420111 Kazan, Russia
bKazan National Research Technological University, K. Marx Street 68, 420015 Kazan, Russia. E-mail: olegmkhlv@gmail.com
First published on 8th November 2021
Abstract
Based on the results of a quantum chemical calculation using the DFT B3PW91/TZVP, MP2/TZVP and MP3/TZVP levels, the possibility of the existence of carbon–nitrogen compounds having the unusual carbon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nitrogen ratio 1
nitrogen ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, which is unknown for these elements at present, was shown. Data on the structural parameters are presented; it was shown that all CN4 groupings are strictly planar. In addition, the bond lengths formed by nitrogen atoms and a C atom are equal to each other, and the bond angles formed by nitrogen atoms and a C atom are equal to 90.0°, or practically do not differ from this value. Thermodynamical parameters, NBO analysis data and HOMO/LUMO images for this compound are presented, too. Good agreement was found between the calculated data obtained using the above three quantum-chemical methods.
12, which is unknown for these elements at present, was shown. Data on the structural parameters are presented; it was shown that all CN4 groupings are strictly planar. In addition, the bond lengths formed by nitrogen atoms and a C atom are equal to each other, and the bond angles formed by nitrogen atoms and a C atom are equal to 90.0°, or practically do not differ from this value. Thermodynamical parameters, NBO analysis data and HOMO/LUMO images for this compound are presented, too. Good agreement was found between the calculated data obtained using the above three quantum-chemical methods.
Introduction
Carbon and nitrogen form among themselves a very significant number of chemical compounds – both neutral and cations and anions.1 Among neutral compounds containing atoms of only these two elements, cyanogens C2N2 (dicyan N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, isocyanogen C
N, isocyanogen C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C
N–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N), diisocyanogen C
N), diisocyanogen C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N
N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), paracyanogen – a cyanogen polymer (NCCN)n, paraisocyanogen – an isocyanogen polymer, (CNCN)n,2–4 percyanoalkynes, -alkenes and -alkanes,5–15 dinitrilopolyynes, perazidoalkynes, -alkenes and -alkanes,16,17 percyanoheterocycles,18 of which in total there are at least several dozen.1 At the end of the 20th – beginning of the 21st centuries, in connection with the discovery of fullerenes, numerous derivatives of them were added to this list, which can be subdivided into two categories – cyanofullerens that are a class of modified fullerenes in which cyano-groups are attached to a fullerene skeleton with the C60(CN)2n formula (n = 1–9), and azafullerenes that are a class of heterofullerenes in which the element substituting for carbon is nitrogen, f.e. bis(aza[60]fullerenyl (C59N)2, diaza[60]fullerene C58N2, triaza[60]fullerene C57N3 and dodecaaza[60]fullerene C48N12.19–24 Tricarbon tetranitride or simply carbon nitride C3N4, first described 100 years ago in ref. 25 and considered in more detail in a number of other works, in particular26–32 and review articles,33–36 stands apart from this background. The carbon
C), paracyanogen – a cyanogen polymer (NCCN)n, paraisocyanogen – an isocyanogen polymer, (CNCN)n,2–4 percyanoalkynes, -alkenes and -alkanes,5–15 dinitrilopolyynes, perazidoalkynes, -alkenes and -alkanes,16,17 percyanoheterocycles,18 of which in total there are at least several dozen.1 At the end of the 20th – beginning of the 21st centuries, in connection with the discovery of fullerenes, numerous derivatives of them were added to this list, which can be subdivided into two categories – cyanofullerens that are a class of modified fullerenes in which cyano-groups are attached to a fullerene skeleton with the C60(CN)2n formula (n = 1–9), and azafullerenes that are a class of heterofullerenes in which the element substituting for carbon is nitrogen, f.e. bis(aza[60]fullerenyl (C59N)2, diaza[60]fullerene C58N2, triaza[60]fullerene C57N3 and dodecaaza[60]fullerene C48N12.19–24 Tricarbon tetranitride or simply carbon nitride C3N4, first described 100 years ago in ref. 25 and considered in more detail in a number of other works, in particular26–32 and review articles,33–36 stands apart from this background. The carbon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nitrogen ratio in these compounds varies from 69
nitrogen ratio in these compounds varies from 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in diheterofullerene (C69N)2 to 1
1 in diheterofullerene (C69N)2 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 in tetraazidomethane C(N3)4.1–36 Since a carbon atom is capable of forming four bonds with a maximum of four neighboring atoms, and a nitrogen atom – with three atoms, then for compounds of the above types, a ratio of 1
12 in tetraazidomethane C(N3)4.1–36 Since a carbon atom is capable of forming four bonds with a maximum of four neighboring atoms, and a nitrogen atom – with three atoms, then for compounds of the above types, a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 seems to be extremely possible. Nevertheless, the indicated ratio C
12 seems to be extremely possible. Nevertheless, the indicated ratio C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N = 1
N = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
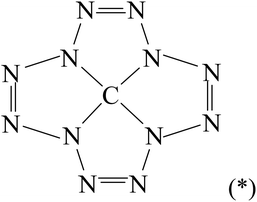
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 can also be realized in another compound, which is an isomer of tetraazidomethane, but which, as far as is known, has not yet been considered in the literature even theoretically, namely in (dodecaazacyclododecantetraene-1,4,7,10)carbon(IV) C(N12) having the structural formula (*)
12 can also be realized in another compound, which is an isomer of tetraazidomethane, but which, as far as is known, has not yet been considered in the literature even theoretically, namely in (dodecaazacyclododecantetraene-1,4,7,10)carbon(IV) C(N12) having the structural formula (*)In this connection, the given communication is devoted to the consideration of the question of the possibility of its existence and, in the case of a positive conclusion, to the determination of the parameters of its molecular structure and thermodynamic characteristics using various modern quantum-chemical methods of calculation, and namely, the density functional theory (DFT), MP2 and MP3 methods.
Method
To carry out the quantum-chemical calculation, in this work we used the density functional theory (DFT), which combines the standard extended split valence basis set TZVP and the hybrid functional B3PW91, described in detail in ref. 37–39 and used by us, in particular, in ref. 40–42. The use of the B3PW91/TZVP method, in this case, is because, according to,37–39 it allows one to obtain, as a rule, the most accurate (i.e., close to experimental) values of the geometric parameters of molecular structures, as well as much more accurate values of thermodynamic and other physical–chemical parameters in comparison with other variants of the DFT method.The calculations were carried out using the Gaussian09 program package.43 As in our previous articles, in which this method of calculation was used,40–42 the correspondence of the found stationary points to the energy minima in all cases was proved by calculating the second derivatives of the energy to the coordinates of the atoms; wherein, all equilibrium structures corresponding to the minimum points on the potential energy surfaces had only real (and, moreover, always positive) frequency values. Of the optimized structures for further consideration, the one with the lowest total energy was selected. Natural Bond Orbital (NBO) analysis was carried out, using NBO version 3.1, integrated with Gaussian09 program package43 according to the methodology described in detail.44 NBO methods are well known for excellent numerical stability and the convergence with respect to basis set expansion, sensibly proportionate to convergence of energy and other calculated wavefunction properties (unlike Mulliken analysis and related overlap-dependent methods in this case). Since the C(N12) structure maybe not trivial, a nontrivial electron density distribution in it is quite possible. As it is well known, the DFT methods when calculating structures with a nontrivial distribution of electron density in some cases can lead to an incorrect order of orbitals and even an incorrect molecular structure. To exclude such a possibility, we decided to carry out the calculation by other ab initio quantum chemical methods, too. However, unfortunately, it was not possible to complete the calculation with such methods with a stricter account of electronic correlation as CCSD and QCISD due to high computational costs. That is why, in addition to the calculation by the DFT B3PW91/TZVP method, as an alternative, we used perturbation theory methods,45 namely MP2 (ref. 46) and MP3 (ref. 47) in the combination with the extended split valence TZVP basis set, the each of which is noticeably less computationally intensive than the CCSD and QCISD methods. At the moment, it was also not possible to complete the calculation using the MP4 method, since in terms of computational complexity it is comparable to the CCSD method. The standard thermodynamic parameters of formation (ΔH0f,298, S0f,298 and ΔG0f,298) for the C(N12) compound under examination were calculated using the G4 method described in ref. 48.
Results and discussion
According to the data of each of the three above-mentioned methods of quantum-chemical calculation, a chemical compound of the composition C(N12) is capable of independent existence. The lengths of chemical bonds between atoms and bond angles for this chemical compound calculated by B3PW91/TZVP, MP2/TZVP and MP3/TZVP methods, were presented in Table 1. As it can be seen from these data, all three methods give very close values of these key parameters of molecular structures, in connection with which it seems appropriate to discuss them together.| Structural parameter | Calculated by | ||
|---|---|---|---|
| DFT B3PW91/TZVP | MP2/TZVP | MP3/TZVP | |
| Carbon–nitrogen bond lengths in the CN4 node, pm | |||
| C1N1 | 149.7 | 151.0 | 148.6 |
| C1N4 | 149.7 | 151.0 | 148.6 |
| C1N7 | 149.7 | 151.0 | 148.6 |
| C1N10 | 149.7 | 151.0 | 148.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Nitrogen–nitrogen bond lengths in macrocycle, pm | |||
| N1N2 | 132.1 | 132.4 | 133.0 |
| N2N3 | 129.1 | 133.0 | 128.6 |
| N3N4 | 132.1 | 132.4 | 133.0 |
| N4N5 | 132.1 | 132.4 | 133.0 |
| N5N6 | 129.1 | 133.0 | 128.6 |
| N6N7 | 132.1 | 132.4 | 133.0 |
| N7N8 | 132.1 | 132.4 | 133.0 |
| N8N9 | 129.1 | 133.0 | 128.6 |
| N9N10 | 132.1 | 132.4 | 133.0 |
| N10N11 | 132.1 | 132.4 | 133.0 |
| N11N12 | 129.1 | 133.0 | 128.6 |
| N12N1 | 132.1 | 132.4 | 133.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bond angles in the CN4 node, deg | |||
| N1C1N4 | 90.0 | 90.2 | 90.3 |
| N4C1N7 | 90.0 | 90.2 | 90.3 |
| N7C1N10 | 90.0 | 90.1 | 90.3 |
| N10C1N1 | 90.0 | 90.1 | 90.3 |
| Bond angles sum (BAS), deg | 360.0 | 360.6 | 361.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Non-bond angles in the CN4 node, deg | |||
| N1N4N7 | 89.9 | 89.7 | 89.5 |
| N4N7N10 | 89.9 | 89.7 | 89.5 |
| N7N10N1 | 89.9 | 89.7 | 89.5 |
| N10N1N4 | 89.9 | 89.7 | 89.5 |
| Non-bond angles sum (NBAS), deg | 359.6 | 358.8 | 358.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bond angles in 5-membered cycles, deg | |||
| C1N1N2 | 116.7 | 117.1 | 116.8 |
| N1N2N3 | 108.3 | 107.8 | 108.0 |
| N2N3N4 | 108.3 | 107.8 | 108.0 |
| N3N4C1 | 116.7 | 117.1 | 116.9 |
| C1N4N5 | 116.7 | 117.1 | 116.8 |
| N4N5N6 | 108.3 | 107.8 | 108.0 |
| N5N6N7 | 108.3 | 107.8 | 108.0 |
| N6N7C1 | 116.7 | 117.1 | 116.9 |
| C1N7N8 | 116.7 | 117.1 | 116.8 |
| N7N8N9 | 108.3 | 107.8 | 108.0 |
| N8N9N10 | 108.3 | 107.8 | 108.0 |
| N9N10C1 | 116.7 | 117.1 | 116.9 |
| C1N10N11 | 116.7 | 117.1 | 116.8 |
| N10N11N12 | 108.3 | 107.8 | 108.0 |
| N11N12N1 | 108.3 | 107.8 | 108.0 |
| N12N1C1 | 116.7 | 117.1 | 116.9 |
It is well known that in all those cases when a carbon atom is bonded to four other atoms through single bonds, a tetrahedral or close to it coordination of these same atoms relative to the carbon atom occurs. Taking this into account, one would expect that in the compound C(N12) with the above structural formula (*), the nitrogen atoms bound to the C atom by single bonds should be located at the vertices of a regular tetrahedron or a polyhedron close to it. However, the calculation of the molecular structure of C(N12), using each of these three quantum chemical methods, indicates that the group of four nitrogen atoms bonded to a carbon atom is practically flat [the sum of angles (N1N4N7), (N4N7N10), (N7N10N1) and (N10N1N4) differ from 360° by no more than 2.0°]. What is even more remarkable, the grouping of CN4 atoms also turns out to be practically flat [the sum of angles (N1C1N4), (N4C1N7), (N7C1N10) and (N10C1N1) also differs from 360° by no more than 1.2°] (Table 1). 5-Membered rings containing four nitrogen atoms and a carbon atom as a kind of “central atom” are also strictly planar since the sum of the internal bond angles in each of them are the same and within the framework of each of the above calculation methods are 540.0°, that coincides with the sum of the interior angles in a flat pentagon (540°). Taking all this into account, it can be argued that the considered compound of carbon with nitrogen, according to the data of each of the quantum-chemical methods used by us, as a whole, has a molecular structure very close to coplanar. Each of the three quantum-chemical calculation methods used by us gives the same lengths of all four carbon–nitrogen bonds taking place in this compound, although, depending on the method, they differ slightly from each other (Table 1). As for the 12 chemical bonds formed by nitrogen atoms, they are subdivided within each of these methods into two groups containing four and eight bonds, respectively, with the same lengths within each of these groups. Wherein, for the molecular structures obtained by the DFT B3PW91/TZVP and MP3/TZVP methods, the bond lengths in the group of four bonds are shorter than the bond lengths in the group of eight bonds, while for the molecular structure obtained by the MP2/TZVP method, the opposite ratio occurs (Table 1). On the whole, the molecular structures of this compound obtained by these three methods show almost complete similarity with each other; an example of such a structure is shown in Fig. 1. The values of the dipole electric moment for this compound calculated using the each of DFT B3PW91/TZVP, MP2/TZVP and MP3/TZVP method, is practically no different from 0.00 Debye units, that, taking into account the practically coplanar structure of C(N12) obtained by each of these methods, seems to be quite expected.
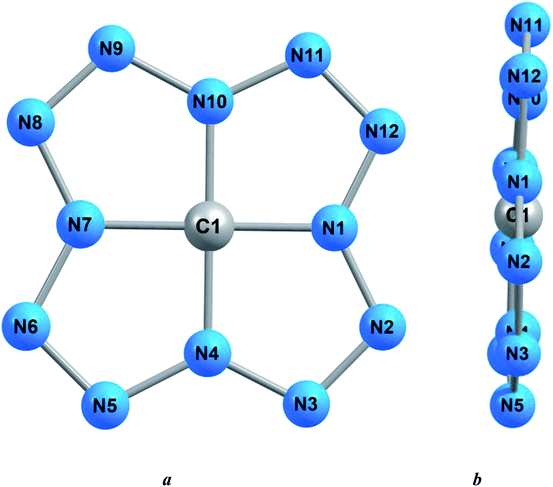 | ||
| Fig. 1 Molecular structures of the C(N12) compound obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation: (a) front view, (b) side view. | ||
Key data of NBO analysis and, namely, the values of effective charges on carbon atom and nitrogen atoms for macrocyclic compound under study obtained by DFT B3PW91/TZVP, MP2/TZVP and MP3/TZVP methods, are presented in Table 2.
| Calculation method | Effective charge on atom, in units of electron charge (ē) | ||||||
|---|---|---|---|---|---|---|---|
| C1 | N1 (N4) | N7 (N10) | N2 (N6) | N3 (N5) | N8 (N12) | N9 (N11) | |
| B3PW91/TZVP | 0.2014 | −0.0680 | −0.0680 | 0.0089 | 0.0088 | 0.0088 | 0.0089 |
| MP2/TZVP | 0.3575 | −0.1366 | −0.1366 | 0.0237 | 0.0236 | 0.0235 | 0.0236 |
| MP3/TZVP | 0.4080 | −0.1607 | −0.1607 | 0.0294 | 0.0293 | 0.0293 | 0.0293 |
As can be seen from these data, the values of the effective charges on individual atoms calculated by the above methods differ quite noticeably from each other, that seems quite natural because these methods take into account electron correlation in different ways. More reliable, in our opinion, are the values obtained using the DFT B3PW91/TZVP method. Howbeit, these values according to their module were considerably lesser than +4.000ē (for C1 atom) and −1.000ē (for N1, N4, N7 and N10 atoms connected with C1 atom by the chemical bonds) which would be in that case if all chemical bonds between C and N atoms would be ionic. This fact indicates that the compound under study has a very high degree of delocalization of the electron density.
The ground state of this compound is a spin singlet (MS = 1), and the values of the operator of the square of the proper angular momentum of the total spin of the system <S**2> in the framework of each of these methods are equal to 0. In addition, according to calculation data, the nearest excited state, which has a different MS value, namely the spin triplet (MS = 3), is 363.7 kJ mol−1 higher than the ground state (according to the G4 method). It should be noted, that testing the wave functions of the ground state for stability using the standard STABLE = OPT procedure showed that the ground state wave function at MS = 1 is stable under the considered perturbations.
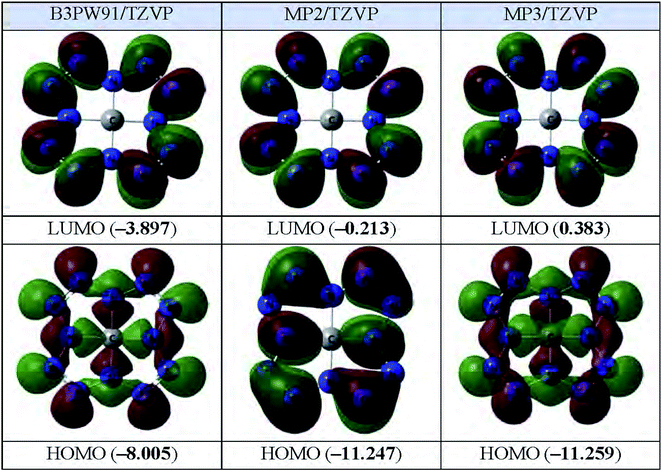
The images of the highest occupied and lowest vacant (unoccupied) molecular orbitals (HOMO and LUMO, respectively) obtained by each of these three calculation methods are presented in Fig. 2. As you can see from it, LUMO forms obtained by each of these three methods, are practically identical to each other; in this case, the electron density in the MO data is concentrated on the peripheral nitrogen atoms, while it is practically absent on the C1 carbon atom. As to HOMO, the above similarities are noted only for orbitals obtained by DFT B3PW91/TZVP and MP3/TZVP methods whereas HOMO obtained by MP2/TZVP method, has another form (Fig. 2). Despite this, the energies of these MOs obtained by the DFT B3PW91/TZVP and MP2/TZVP and MP3/TZVP methods differ quite significantly (Fig. 2).
The standard thermodynamic parameters of formation (ΔH0f,298, S0f,298 and ΔG0f,298) for the chemical compound under examination were given in Table 3. As may be seen from it, all these parameters are positive, and, therefore, this compound, as it should be expected, cannot be obtained from the most thermodynamically stable simple substances formed by carbon and nitrogen (i.e., graphite and molecular nitrogen N2).
| Calculation method | ΔH0f,298, kJ mol−1 | S0f,298, J mol−1 K | ΔG0f,298, kJ mol−1 |
|---|---|---|---|
| B3PW91/TZVP | 1614.8 | 378.1 | 1842.2 |
| G4 | 1581.5 | 374.3 | 1810.1 |
It is of some interest to consider the reaction of the interaction of C(N12) with molecular oxygen, which proceeds in the gas phase according to the eqn (1)
| C(N12) (gas) + O2 (gas) → CO2 (gas) + 6N2 (gas) | (1) |
and the reaction of decomposition of this compound according to the eqn (2)
| C(N12) (gas) → C (diamond) + 6N2 (gas) | (2) |
Standard thermodynamical parameters for these reactions ΔrH0298 and ΔrS0298 are presented in the Table 4. As may be seen from these data, the reaction of the interaction of the C(N12) compound under consideration with molecular oxygen, on the one hand, is strongly exothermic, since the ΔrH0298 values for it are negative, and they themselves are very significant in modulus (∼2000 kJ) within the framework of each of the calculation methods we used. On the other hand, the value of ΔrS0298 is positive for it, and in accordance with the well-known Gibbs – Helmholtz eqn (3)
| ΔrG0(T) = ΔrH0298 − TΔrS0298 | (3) |
| Calculation method | Reaction | |||
|---|---|---|---|---|
| C(N12) (gas) + O2 (gas) → CO2 (gas) + 6N2 (gas) | C(N12) (gas) → C (diamond) + 6N2 (gas) | |||
| ΔrH0298, kJ | ΔrS0298, J K−1 | ΔrH0298, kJ | ΔrS0298, J K−1 | |
| B3PW91/TZVP | −1806.8 | 788.0 | −1613.0 | 823.7 |
| G4 | −1984.8 | 798.2 | −1579.7 | 827.5 |
the ΔrG0(T) value for it will be negative at any temperature, which in turn means that the process described by eqn (1) is irreversible. In this regard, it is interesting to note that a similar situation takes place for reaction (2) (Table 4), which, in principle, can be used to obtain an allotropic modification of carbon – a diamond in the framework of the isobaric process. And since the reaction (2) indicated in the article proceeds in the gas phase [in any case, the initial substance in it is C(N12) (gas)], then we can assume with sufficient confidence that the energy barrier to the activation of this reaction will not be too big and it will not be kinetically inhibited, which means that it can be realized within a reasonable time.
A priori, one would expect that the C(N12) compound considered in our article would be more stable than its isomeric compound, tetraazidomethane C(N3)4, described in ref. 16, since, as is known from organic and coordination chemistry, with the same composition of substances, as a rule, those that have a cyclic structure are more stable. Our calculation of the above parameters using the DFT B3PW91/TZVP method gave the values ΔH0f,298 = 1350.5 and ΔG0f,298 = 1550.3 kJ mol−1, using the G4 method, the values ΔH0f,298 = 1293.0 and ΔG0f,298 = 1490.6 kJ mol−1. Comparing this data with the data in Table 3, it can be found that, in the case of the first of these methods, the difference in the values of ΔH0f,298 is 265.3 kJ mol−1, in the case of the second one, 288.5 kJ mol−1, i.e. tetraazidomethane C(N3)4 turns out to be a somewhat more stable compound than (dodecaazacyclododecantetraene-1,4,7,10)carbon(IV) C(N12). These differences, in our opinion, are not very significant, so this circumstance in no way disproves the possibility of obtaining C(N12) as a result of any chemical reaction (and, possibly, even as a result of isomerization of tetraazidomethane).
Conclusion
So, the data obtained using three different methods of quantum-chemical calculation, namely DFT B3PW91/TZVP, MP2/TZVP and MP3/TZVP methods, presented above, unambiguously predict the possibility of the existence of a new, so far unknown in chemical science, MACROTHETRACYCLIC compound of carbon with nitrogen composition C(N12). Which, on the one hand, is characterized by an unusual (and so far the highest) ratio between the number of nitrogen atoms and the number of carbon atoms (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), on the other hand, it has an almost planar molecular structure. Wherein, the latter circumstance is also unusual, since it has long been well known that in those compounds where a carbon atom is bonded to four other atoms through single chemical bonds, tetrahedral or close coordination of these atoms with respect to the carbon atom takes place. The noted results of quantum-chemical calculations, in our opinion, give all the grounds for a more careful study of such an unusual macrocyclic compound, and now it should confirm its existence experimentally since its synthesis can be important for the further development of physical chemistry and chemical technology of both these chemical elements. Playing a very important role in nature. Predicting the possibility of the existence of such an exotic chemical substance and modelling its molecular and electronic structures using modern quantum-chemical calculations, as it seems to us, can serve as a very useful tool in the decision of the problems associated with this synthesis.
1), on the other hand, it has an almost planar molecular structure. Wherein, the latter circumstance is also unusual, since it has long been well known that in those compounds where a carbon atom is bonded to four other atoms through single chemical bonds, tetrahedral or close coordination of these atoms with respect to the carbon atom takes place. The noted results of quantum-chemical calculations, in our opinion, give all the grounds for a more careful study of such an unusual macrocyclic compound, and now it should confirm its existence experimentally since its synthesis can be important for the further development of physical chemistry and chemical technology of both these chemical elements. Playing a very important role in nature. Predicting the possibility of the existence of such an exotic chemical substance and modelling its molecular and electronic structures using modern quantum-chemical calculations, as it seems to us, can serve as a very useful tool in the decision of the problems associated with this synthesis.
Author contributions
Conceptualization, O. V. Mikhailov; methodology, O. V. Mikhailov and D. V. Chachkov; software, D. V. Chachkov; validation, O. V. Mikhailov and D. V. Chachkov; formal analysis, O. V. Mikhailov and D. V. Chachkov; investigation, O. V. Mikhailov and D. V. Chachkov; resources, D. V. Chachkov; data curation, D. V. Chachkov; writing – original draft preparation, O. V. Mikhailov and D. V. Chachkov; writing – review & editing, O. V. Mikhailov; visualization, O. V. Mikhailov and D. V. Chachkov; supervision, O. V. Mikhailov; project administration, O. V. Mikhailov; funding acquisition, D. V. Chachkov.Conflicts of interest
The authors declare that they have no conflict of interest, financial or otherwise.Acknowledgements
All quantum-chemical calculations were performed at the Joint Supercomputer Center of Russian Academy of Sciences – Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” that is acknowledgement for technical support. Contribution of author Denis V. Chachkov was funded by the state assignment to the Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” for scientific research. Also, this study was carried using the equipment of the Center of Collective Use “Nanomaterials and Nanotechnology” of the Kazan National Research Technological University.References
- Carbon nitride, web-site: https://en.wikipedia.org/wiki/Carbon_nitride Search PubMed.
- A. L. Ringer, C. D. Sherrill, R. A. King and T. D. Crawford, Low-lying singlet excited states of isocyanogen, Int. J. Quantum Chem., 2008, 106, 1137–1140, DOI:10.1002/qua.21586.
- T. K. Brotherton and J. W. Lynn, The Synthesis and Chemistry of Cyanogen, Chem. Rev., 1959, 59, 841–883, DOI:10.1021/cr50029a003.
- L. L. Bircumshaw, F. M. Tayler and D. H. Whiffen, Paracyanogen: its formation and properties. Part I, J. Chem. Soc., 1954, 931–935, 10.1039/jr9540000931.
- A. D. Kirshenbaum and A. V. Grosse, The Combustion of Carbon Subnitride, C4N2, and a Chemical Method for the Production of Continuous Temperatures in the Range of 5000–6000 °K, J. Am. Chem. Soc., 1956, 78, 2020–2021, DOI:10.1021/ja01590a075.
- E. Ciganek and C. G. Krespan, Syntheses of Dicyanoacetylene, J. Org. Chem., 1968, 33, 541–544, DOI:10.1021/jo01266a014.
- C. D. Weis, Reactions of Dicyanoacetylene, J. Org. Chem., 1963, 28, 74–78, DOI:10.1021/jo01036a015.
- R. A. Carboni, Tetracyanoethylene, Org. Synth., 1963, 4, 877 Search PubMed.
- W. J. Linn, Tetracyanoethylene, Org. Synth., 1973, 5, 1007 Search PubMed.
- D. S. Barnes, C. T. Mortimer and E. Mayer, The enthalpy of formation of tetracyanomethane, J. Chem. Thermodyn., 1973, 5, 481–483, DOI:10.1016/s0021-9614(73)80095-3.
- E. Mayer, Darstellung und Eigenschaften von Tetracyanmethan, Monatsh. Chem., 1969, 100, 462–468, DOI:10.1007/bf00904089.s2cid92450428.
- D. Britton, The crystal structure of tetracyanomethane, C(CN)4, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1818–1821, DOI:10.1107/s0567740874005863.
- R. E. Hester, K. M. Lee and E. Mayer, Tetracyanomethane as a pseudo-(carbon tetrahalide), J. Phys. Chem., 1970, 74, 3373–3376, DOI:10.1021/j100712a011.
- D. W. Keefer, H. Gou, Q. Wang, A. Purdy, A. Epshteyn, S. J. Juhl, G. D. Cody, J. Badding and T. A. Strobel, Tetracyanomethane under Pressure: Extended CN Polymers from Precursors with Built-in sp3 Centers, J. Phys. Chem. A, 2018, 122, 2858–2863, DOI:10.1021/acs.jpca.7b10729.
- O. W. Webster, Hexacyanobutadiene, J. Am. Chem. Soc., 1964, 86, 2898–2902, DOI:10.1021/ja01068a026.
- K. Banert, Y.-H. Joo, T. Ruffer, B. Walfort and H. Lang, The Exciting Chemistry of Tetraazidomethane, Angew. Chem., Int. Ed., 2007, 46, 1168–1171, DOI:10.1002/anie.200603960.
- C. I. Schilling and S. Bräse, Stable organic azides based on rigid tetrahedral methane and adamantane structures as high energetic materials, Org. Biomol. Chem., 2007, 5, 3586–3588, 10.1039/b713792c.
- R. F. Del Sesto, A. M. Arif, J. J. Novoa, I. Anusiewicz, P. Skurski, J. Simons, B. C. Dunn, E. M. Eyring and J. S. Miller, Chemical Reduction of 2,4,6-Tricyano-1,3,5-triazine and 1,3,5-Tricyanobenzene. Formation of Novel 4,4',6,6'-Tetracyano-2,2'-bitriazine and Its Radical Anion, J. Org. Chem., 2003, 68, 3367–3379, DOI:10.1021/jo025833h.
- D. J. Harris, Discovery of Nitroballs: Research in Fullerene Chemistry, California State Science Fair, 1993, http://www.usc.edu/CSSF/History/1993/S05.html Search PubMed.
- J. C. Hummelen, B. Knight, J. Pavlovich, R. González and F. Wudl, Isolation of the Heterofullerene C59N as Its Dimer (C59N)2, Science, 1995, 269, 1554–1556, DOI:10.1126/science.269.5230.1554.
- O. Vostrowsky and A. Hirsch, Heterofullerenes, Chem. Rev., 2006, 106, 5191–5207, DOI:10.1021/cr050561e.
- J. C. Hummelen, C. Bellavia-Lund and F. Wudl, Heterofullerenes. Fullerenes and Related Structures, Top. Curr. Chem., 1999, 199, 93–134, DOI:10.1007/3-540-68117-5_3.
- J. Averdung, H. Luftmann, I. Schlachter and J. Mattay, Aza-dihydro[60]fullerene in the gas phase. A mass-spectrometric and quantum-chemical study, Tetrahedron, 1995, 51, 6977–6982, DOI:10.1016/0040-4020(95)00361-b.
- B. Nuber and A. Hirsch, A new route to nitrogen heterofullerenes and the first synthesis of (C69N)2, Chem. Commun., 1996, 1421–1422, 10.1039/cc9960001421.
- E. C. Franklin, The Ammono Carbonic Acids, J. Am. Chem. Soc., 1922, 44, 486–509, DOI:10.1021/ja01424a007.
- A. Liu and M. L. Cohen, Prediction of new low compressibility solids, Science, 1989, 245(4920), 841–843, DOI:10.1126/science.245.4920.841.
- O. F. Pozdnyakov, L. N. Blinov, M. Arif, A. O. Pozdnyakov, S. N. Filippov and A. V. Semencha, Mass spectrometry of carbon nitride C3N4, Tech. Phys. Lett., 2005, 31, 1001–1003, DOI:10.1134/1.2150880.
- M. Arif, L. N. Blinov, R. Lappalainen and S. N. Filippov, Preparation of powdered carbon nitride C3N4, Glass Phys. Chem., 2004, 30, 573–575, DOI:10.1007/s10720-005-0018-8.
- C.-B. Cao, L. Qiang and H.-S. Zhu, Carbon nitride prepared by solvothermal method, Diamond Relat. Mater., 2003, 12, 1070–1074, DOI:10.1016/s0925-9635(02)00309-6.
- J. R. Holst and E. G. Gillan, From Triazines to Heptazines: Deciphering the Local Structure of Amorphous Nitrogen-Rich Carbon Nitride Materials, J. Am. Chem. Soc., 2008, 130, 7373–7379, DOI:10.1021/ja709992s.
- N. Mansor, A. Belen Jorge, F. Corà, C. Gibbs, R. Jervis, P. F. McMillan, X. Wang and D. J. L. Brett, Graphitic Carbon Nitride Supported Catalysts for Polymer Electrolyte Fuel Cells, J. Phys. Chem. C, 2014, 118, 6831–6838, DOI:10.1021/jp412501j.
- F. Fina, S. K. Callear, G. M. Carins and J. T. S. Irvine, Structural Investigation of Graphitic Carbon Nitride via XRD and Neutron Diffraction, Chem. Mater., 2015, 27, 2612–2618, DOI:10.1021/acs.chemmater.5b00411.
- B. L. Korsunskii and V. I. Pepekin, On the way to carbon nitride, Russ. Chem. Rev., 1997, 66, 901–912, DOI:10.1070/rc1997v066n11abeh000378.
- A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J.-O. Müller, R. Schlögl and J. M. Carlsson, Graphitic carbon nitride materials: variation of structure and morphology and their use as metal-free catalysts, J. Mater. Chem., 2008, 18, 4893–4908, 10.1039/b800274f.
- W.-J. Ong, L.-L. Tan, Y. H. Ng, Y. Siek-Ting and S.-P. Chai, Graphitic Carbon Nitride (g-C3N4)-Based Photocatalysts for Artificial Photosynthesis and Environmental Remediation: Are We a Step Closer To Achieving Sustainability?, Chem. Rev., 2016, 116, 7159–7329, DOI:10.1021/acs.chemrev.6b00075.
- S. Wang, J. Zhang, B. Li, H. Sun and S. Wang, Engineered Graphitic Carbon Nitride-Based Photocatalysts for Visible-Light-Driven Water Splitting: A Review, Energy Fuels, 2021, 35, 6504–6526, DOI:10.1021/acs.energyfuels.1c00503.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100, DOI:10.1103/physreva.38.3098.
- J. P. Perdew, K. Burke and Y. Wang, Generalized gradient approximation for the exchange-correlation hole of a many-electron system, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539, DOI:10.1103/physrevb.54.16533.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Density functional theory is straying from the path toward the exact functional, Science, 2017, 355(6320), 49–52, DOI:10.1126/science.aah5975.
- O. V. Mikhailov and D. V. Chachkov, Novel oxidation state—zinc(III) in chelate with 3,7,11,15-tetraazaporphine and one fluorine ligand: quantum-chemical modeling, J. Porphyrins Phthalocyanines, 2019, 23, 685–689, DOI:10.1142/s1088424619500470.
- O. V. Mikhailov and D. V. Chachkov, About possibility of stabilization of unusual copper(IV) oxidation state in complexes with porphyrazine and two fluorine ligands: quantum-chemical design, Inorg. Chem. Commun., 2019, 106, 224–227, DOI:10.1016/j.inoche.2019.05.025.
- O. V. Mikhailov and D. V. Chachkov, DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands, Int. J. Mol. Sci., 2020, 21, 9085, DOI:10.3390/ijms21239085.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. Weinhold, C. R. Landis and E. D. Glendening, What is NBO analysis and how is it useful?, Int. Rev. Phys. Chem., 2016, 35, 399–440, DOI:10.1080/0144235x.2016.1192262.
- C. Møller and M. S. Plesset, Note on an approximation treatment for many-electron systems, Phys. Rev., 1934, 46, 618–622, DOI:10.1103/physrev.46.618.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506, DOI:10.1016/0009-2614(88)85250-3.
- J. A. Pople, R. Seeger and R. Krishnan, Variational Configuration Interaction Methods and Comparison with Perturbation Theory, Int. J. Quantum Chem., 1977, 11, 149–163, DOI:10.1002/qua.560120820.
- J. W. Ochterski, Thermochemistry in Gaussian, Gaussian, Inc., Wallingford CT, 2000 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07549g |
| This journal is © The Royal Society of Chemistry 2021 |