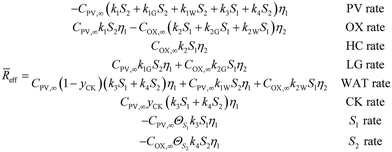Ex situ upgrading of pyrolysis vapors over PtTiO2: extraction of apparent kinetics via hierarchical transport modeling†
Received
20th August 2020
, Accepted 15th October 2020
First published on 15th October 2020
Abstract
Chemical reaction kinetics enable predictive scaling studies and process sensitivity analyses that can substantially accelerate commercial deployment of new catalytic transformation technologies. The absence of suitable kinetic parameters for catalytic fast pyrolysis (CFP) of biomass feedstocks has precluded such de-risking simulation activities. In this work we consider ex situ CFP using a Pt/TiO2 catalyst in a packed bed vapor phase upgrading reactor (VPU) with co-fed H2. We develop a multiscale simulation framework to de-couple apparent kinetics from both intraparticle and reactor-scale transport phenomena. The transport model is integrated with a kinetic scheme that predicts (1) lumped yields of product partially deoxygenated compounds, hydrocarbons, light gases, water, and coke, as well as (2) active site concentration and deactivation of the catalyst. We employ recent advancements in mathematical treatments of cascading reaction systems in the context of an axial-dispersion packed bed reactor model to achieve a rapidly-solving simulation framework that is amenable to iterative regression for kinetic parameter extraction. Results demonstrate accurate predictions of CFP yields within 5% for a variety of conditions, including different reaction times, Pt loadings, and variations in feedstock attributes.
Introduction
Catalytic fast pyrolysis (CFP) in an ex situ configuration is a technology wherein lignocellulosic feedstocks like wood undergo fast pyrolysis and then the vapors are deoxygenated/upgraded to an oil product over a heterogeneous catalyst in a second reactor. Compared to non-catalytic fast pyrolysis, CFP produces a stabilized oil with reduced oxygen content. The CFP oil could then be hydroprocessed to a finished fuel blendstock,1,2 co-processed with refinery intermediates in an oil refinery,3 utilized as a heating fuel, or further transformed into bio-based chemicals or materials.4,5 Co-fed H2 can be also introduced to promote hydrodeoxygenation (HDO) and direct deoxygenation (DDO)6 over a bifunctional metal-acid catalyst such as Pt/TiO2 (ref. 1) or Mo/Al2O3.7 HDO and DDO remove oxygen as water and can improve carbon yields in the CFP oil product by reducing light gas formation and coke deposition on the catalyst.1,4,5,7–12 Recent microreactor6 and bench-scale work1,13 have shown particularly promising CFP oil yields where pine was pyrolyzed in a fluidized bed reactor and the vapors were upgraded over a packed bed of a bifunctional metal–acid Pt/TiO2 catalyst with co-fed H2 at near atmospheric pressure. The PtTiO2 catalyst is considered a class 1 bifunctional catalyst with a noble metal (Pt) dispersed on an acidic reducible/amphoteric oxide (e.g. TiO2) that has demonstrated activity for direct deoxygenation of lignin-derived aromatic oxygenates like phenol in the literature.14–16 The high activity of this catalyst has been attributed to synergistic effects between the metallic phase and the reducible/amphoteric TiO2 support, which promote C–O bond scission at or near the interface.6 Given the encouraging results of these bench-scale experiments, there is considerable interest in further technological development and process scale-up.13
As with any catalytic transformation process, an understanding of the chemical and physical mechanisms that govern the process performance is critical to developing predictive models that will guide and de-risk scale-up. Reasonably advanced predictive models exist for the fast pyrolysis step17–19 but robust predictive models do not exist for the upgrading step using the bifunctional metal–acid Pt/TiO2 catalyst. Developing a predictive model of the upgrading step in ex situ CFP using a Pt/TiO2 catalyst is the focus of this work. Obtaining kinetic rate parameters is essential to predictive model development. Apparent rate constants in this work are not collated with intraparticle diffusion or bulk transport effects and thus allow for parametric studies across different particle sizes, and support porosities, as well as reactor-scale dimensions and operating conditions. Previously, our group employed a protocol based on back-calculation of kinetic rate constants by iterative regression of a multi-scale model to experimental data.20 Here we extend this methodology to obtain apparent kinetic rates for the ex situ CFP Pt/TiO2 process. These are apparent rate constants rather than intrinsic because they combine adsorption, reaction, and desorption at an active site, an exercise approached with microkinetic modelling.21
Modeling packed bed reactors was one of the first tasks taken on by chemical reaction engineers, and differential equation models have been developed that can quickly describe 1-D, idealized plug-flow reactor systems.22–24 Several groups have used 2-D and 3-D computational fluid dynamics (CFD) modeling techniques to model realistic packings and geometries in packed-bed catalytic reactors, as reviewed by Jurtz et al.25 It is evident that these more physically realistic techniques are critical for accurately representing the behaviour for reactors with small tube-to-particle diameter ratios, irregularly shaped particles, non-ideal packing, etc. While these models can indeed add a great deal of accuracy to simulations of packed bed reactors, their use is more computationally demanding and should be balanced with less computationally expensive alternatives such as plug-flow “axial dispersion” models.
In porous catalyst supports with dispersed active sites, surface reaction equations do not accurately describe the effective rate of reaction for reactants and products diffusing into and out of these porous particles. Intraparticle diffusion–reaction behavior has a major impact on the observed reaction rate. Jurtz et al.25 surveyed a variety of tools for modeling intraparticle physics, but the fastest by far is the Thiele effectiveness factor, which is an analytical solution for spherical reaction–diffusion with homogeneous porosity and active site dispersion.26 One of the limitations of the classic Thiele effectiveness factor is that it is only valid for single-step reactions. However, HDO processes using bi-functional metal–acid catalysts involve many reactions, occurring in parallel and in series, and are not accurately represented by single-step reaction approximations. In this work the upgrading process is referred to as the HDO step for simplicity because hydrogen is fed and we are deoxygenating the vapors, but it does not mean that the only reaction pathway occurring is formally hydrodeoxygenation. To expand the range of validity for the effectiveness factor approach, our group recently developed an analytical approach to deal with reactions in series called the multistep effectiveness vector (MEV).27 In this present work, we aim to use an axial dispersion model with an MEV subgrid catalyst model to extract lumped apparent reaction rate constants and explore different experimental conditions that may be used to optimize the HDO step in ex situ catalytic fast pyrolysis using a Pt/TiO2 catalyst (Fig. 1).
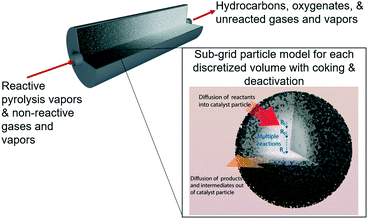 |
| | Fig. 1 Illustration of the packed bed model with discretized volumes for tracking sites and coke formation and the subgrid multistep effectiveness vector (MEV) model describing reaction–diffusion within catalyst particles.‡ | |
Experimental methods
Ex situ catalytic fast pyrolysis experiments
The experiments were performed in a bench scale ex situ catalytic fast pyrolysis reactor comprised of a 2′′ inner diameter fluidized bed fast pyrolysis reactor fed with mixtures of clean pine and forest residue (milled to 2 mm) coupled to a packed bed reactor loaded with Pt/TiO2 catalyst. A detailed description of this system was provided in a previous report1 and illustrated in Fig. 2 and feedstock characterization can be found in Klinger et al.44 Briefly, the pyrolysis reactor was supplied with 85% H2/15% N2 at near atmospheric pressure. The fast pyrolysis vapors together with the gases leave the fluidized bed reactor and flow through a cyclone and then pleated stainless steel hot gas filter with nominal 2 μm openings. These vapors were piped through heat-traced lines into the packed bed VPU reactor, 3.18 cm i.d. by 14 cm long, containing ∼100 g Pt/TiO2 catalyst. The collected liquids spontaneously separate into an oil and aqueous phase and the top aqueous phase is removed by pipetting.
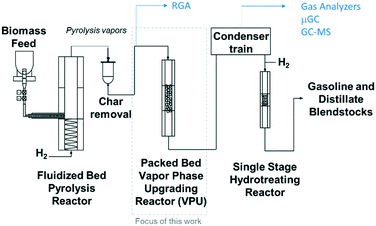 |
| | Fig. 2 Schematic of the bench scale ex situ catalytic fast pyrolysis system utilized in this work with a packed bed (fixed bed) of catalyst. | |
The composition of the vapor leaving the VPU was monitored with a mass spectrometer (residual gas analyzer, RGA). After the RGA, the vapors were condensed, and the liquids collected. The non-condensable gases were analyzed with a micro GC for light gases (LG, consisting of CO, CO2, and C1–4 hydrocarbons) and an online GC-MS-FID for gases and vapors not detected by the micro GC (light condensables, consisting of light oxygenates and some C5+ hydrocarbons). The collected liquids were separated into an oil and aqueous phase, and the oil was analyzed for composition by a GC × GC-TOFMS. After each CFP experiment, the catalyst is regenerated by oxidation of coke and subsequent catalyst reduction. The ESI† contains a more detailed description of the reactor dimensions, flowrates, and analytical procedures.
The experimental data used for fitting the rate constants was based on four replicate experimental runs, each with a cumulative biomass to catalyst mass ratio (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C) of 12, a 7.1 h run time, with 0.5 wt% Pt/TiO2 catalyst, a weight hourly space velocity of 1.5 g biomass per g catalyst h−1, and a 50%/50% clean pine (CP)/forest residue (FR) wood blend as the biomass feed. The pyrolysis temperature was 500 °C and the average internal temperature of the VPU was 450 °C. The biomass ultimate analysis and further analytical details are included in the ESI.† Yields from the pyrolysis + HDO reactor were compared to results from pyrolysis alone. Further experimental data collected for the same catalytic conditions with B
C) of 12, a 7.1 h run time, with 0.5 wt% Pt/TiO2 catalyst, a weight hourly space velocity of 1.5 g biomass per g catalyst h−1, and a 50%/50% clean pine (CP)/forest residue (FR) wood blend as the biomass feed. The pyrolysis temperature was 500 °C and the average internal temperature of the VPU was 450 °C. The biomass ultimate analysis and further analytical details are included in the ESI.† Yields from the pyrolysis + HDO reactor were compared to results from pyrolysis alone. Further experimental data collected for the same catalytic conditions with B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 6 and 21 as well as a data set for a 1 wt% Pt on the same TiO2 support and 100% clean pine as feed at B
C of 6 and 21 as well as a data set for a 1 wt% Pt on the same TiO2 support and 100% clean pine as feed at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3 were used to verify the model. The equations used to calculate lumped product yields across the VPU are detailed in the ESI.†
C 3 were used to verify the model. The equations used to calculate lumped product yields across the VPU are detailed in the ESI.†
Catalyst preparation and characterization
The catalyst had been prepared by a strong electrostatic adsorption (SEA) method on a spherical TiO2 support with an average particle diameter of 0.5 mm provided by Johnson Matthey. A detailed description of the catalyst preparation method can be found in Griffin et al.1 In short, Pt was added to TiO2 particles at pH 11.5 using 1.98 g Pt(NH3)4(NO3)3 and soaked for >24 h in aqueous solution then dried >24 h at 60 °C. This catalyst was reduced in 5% H2/N2 at 450 °C and passivated under 1% O2/N2 at room temperature before loading into the packed bed. Pt particles had an average diameter of 2.7 nm. BET surface area was 44 m2 g−1. For the 0.5% Pt catalyst, Pt CO chemisorption suggested Pt dispersion of 33%. TPD acid site density was 220 μmol g−1 and acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal site ratio is 4.9.
metal site ratio is 4.9.
The catalyst was characterized in part with imaging by scanning electron microscopy (SEM) and transmission electron microscopy (TEM). For scanning electron microscopy, the whole catalyst particles were mounted on aluminum stubs with conductive carbon adhesive. Samples were imaged without coating using a FEI Quanta 400 FEG using an accelerating voltage of 25 kV. For transmission electron microscopy and tomography, catalyst particles were gently crushed and the powder was suspended in ethanol at ∼0.5% wt/vol. A volume of 5 μl of the suspension was placed on carbon-coated copper TEM grids with a grid sized of 200 mesh (SPI Supplies, West Chester, PA). Samples were allowed to air dry prior to imaging. A FEI Tecnai G2 20 Twin 200 kV LaB6 TEM (FEI, Hilsboro, OR) instrument was used at an accelerating voltage of 200 kV; images were collected with a Gatan UltraScan 1000 camera (Gatan, Pleasanton, CA). Tomography was performed by first obtaining dual-axis ±60° tilt series of the region of interest at a pixel size of ∼0.5 nm. Single axis tomograms were constructed from the tilt series using the R-weighted back projection algorithm and then combined to yield the final reconstruction using the IMOD software package.28 Tomographic slices were visualized with IMOD and the volume reconstruction was visualized with PyMOL.29 Particle porosity of 0.592 and an average pore diameter of 28 nm were measured by N2 adsorption with BJH calculations.30
The multiscale nature of this material is shown through light microscopy which shows the spherical shape (Fig. 3a) and scanning electron microscopy which shows the porous support structure formed by the agglomeration of TiO2 nanoparticles (Fig. 3b). Transmission electron tomography was performed to investigate the three-dimensional morphology of intraparticle porosity to inform parameterization of the intraparticle transport model, as shown in Fig. 3c. This technique involves acquiring a series of TEM images at different angles with respect to the electron beam which enables the reconstruction of the 3D sample volume via computational image processing. Slices through the 3D volume obtained using this method are shown at two different magnifications in Fig. 4a and b. Due to the large number of images (∼160) that are averaged to produce the 3D density field, the contrast between the TiO2 support and Pt nanoparticles is enhanced with respect to that observed in 2D TEM images. A 3D visualization of the reconstructed volume is shown in Fig. 4. This analysis reveals that Pt clusters with diameters of roughly 5 nm are well-dispersed on the surface of the support material.
 |
| | Fig. 3 Multiscale imaging of the Pt/TiO2 catalyst particles. (a) Light microscopy of catalyst particles showing the spherical bulk geometry with narrow size distribution. (b) Scanning electron microscopy (SEM) of the particle surface reveals a porous support structure formed by the agglomeration of TiO2 nanoparticles. (c) Transmission electron microscopy shows the presence of ∼5 nm Pt particles visualized as dark spots on the surface of the larger TiO2 support structure. | |
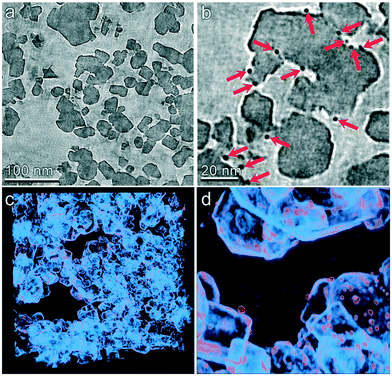 |
| | Fig. 4 TEM tomography of the TiO2 catalyst particle mesostructure. (a and b) Slices through the tomographic volume are shown at two different magnifications. Pt particles are clearly identified by their higher electron density (indicated by red arrows in panel b). (c and d) 3D visualizations of the reconstructed volume are shown at two different magnifications. Density primarily corresponding to the TiO2 support is shown as light blue and that roughly corresponding to the Pt particles is shown as orange. | |
The tomographic reconstruction facilities direct quantification of mesoporous dimensions including void space and distribution of pore dimensions. The void volume was determined by first calculating the average and standard deviation of the tomographic density of a clearly indefinable void region within the reconstructed volume. The void fraction of the entire volume was then determined by the number of voxels within the volume that displayed a density greater than two standard deviations above the mean density of the void volume. The entire reconstruction was divided into 64 sub-volumes and this calculation was performed within each to determine variability of the void space. By this method the average void fraction was determined to be 57% with a standard deviation of 6.8%. The pore size distribution was calculated using a combination of automated computational image transformations. The average pore radius was computed to be 7.82 nm with a standard deviation of 7.84 nm based on microscopy. However 28 nm is used as the pore diameter in the model because the adsorption experiments are more representative of the entire catalyst particle. The SEM and TEM analysis described in further detail in the ESI.†
Experimental results
Catalytic fast pyrolysis yields
A series of catalytic fast pyrolysis experiments were performed in the ex situ pyrolyzer followed by the hydrodeoxygenation (HDO) vapor phase upgrading (VPU) packed bed of porous Pt/TiO2 catalysts. Table 1 shows the mass yields on a dry biomass basis for the datasets used in this work. Table 2 shows the GC × GC composition summary of the collected liquids with lumped species assignments that are used in this model. For the base case experiments used for kinetic parameter extraction (0.5% Pt, B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12), the pyrolysis reactor converted 89% of 50/50 CP/FR wood into volatile and gaseous species that pass into the HDO reactor (Table 1), with the remainder being char. However, not all of the vapors are expected to participate in the catalytic upgrading reactions in the subsequent VPU reactor. Here, light gases (LG), light condensables (LC), and water vapor from pyrolysis were considered to pass through the VPU without being majorly transformed, as the yields of these families increase after the HDO. They may couple but appear to remain in the same category.
C 12), the pyrolysis reactor converted 89% of 50/50 CP/FR wood into volatile and gaseous species that pass into the HDO reactor (Table 1), with the remainder being char. However, not all of the vapors are expected to participate in the catalytic upgrading reactions in the subsequent VPU reactor. Here, light gases (LG), light condensables (LC), and water vapor from pyrolysis were considered to pass through the VPU without being majorly transformed, as the yields of these families increase after the HDO. They may couple but appear to remain in the same category.
Table 1 Mass yields from pyrolysis and CFP, wt% dry biomass basis, normalized to 100% (mass closure >98%)
| Description |
Pyrolysis only |
Pyrolysis only |
Base case |
Test case |
Test case |
Test case |
| 0.5% Pt |
1% Pt |
0.5% Pt |
0.5% Pt |
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, kg/kg C, kg/kg |
— |
— |
12 |
3 |
6 |
21 |
| Feed |
CP/FR |
CP |
CP/FR |
CP |
CP/FR |
CP/FR |
| # of runs |
3 |
3 |
4 |
3 |
1 |
1 |
| Organics in oil |
58.5 ± 0.5 |
56.3 ± 0.1 |
24.7 ± 0.1 |
20.9 ± 0.1 |
23 |
26.6 |
| Organics in aqueous phase |
0.0 ± 0.0 |
0.0 ± 0.0 |
3.8 ± 0.3 |
2.3 ± 0.0 |
3.5 |
4.0 |
| Water |
13.3 ± 0.2 |
17.5 ± 0.4 |
21.7 ± 0.0 |
22.9 ± 0.3 |
21.9 |
20.1 |
| Light condensables |
2.3 ± 0.1 |
0.5 ± 0.2 |
10.0 ± 0.2 |
8.0 ± 0.1 |
8.6 |
9.9 |
| Light gases |
15.2 ± 0.3 |
13.9 ± 0.8 |
28.2 ± 0.5 |
31.6 ± 0.3 |
29.2 |
27.4 |
|
CH
4
|
1.3 ± 0.0
|
0.5 ± 0.1 |
3.2 ± 0.1
|
3.2 ± 0.0
|
3.2
|
3.0
|
|
CO
|
7.5 ± 0.2
|
6.1 ± 0.4 |
14.5 ± 0.6
|
15.7 ± 0.2
|
15.0
|
14.6
|
|
CO
2
|
5.6 ± 0.1
|
6.0 ± 0.3 |
7.6 ± 0.1
|
8.1 ± 0.1
|
8.0
|
7.3
|
|
C
2
–C
4
|
0.9 ± 0.0
|
0.7 ± 0.0 |
2.8 ± 0.1
|
4.0 ± 0.0
|
3.0
|
2.5
|
| Char |
10.7 ± 0.0 |
11.8 ± 0.6 |
10.3 ± 0.0 |
11.8 ± 0.3 |
12.3 |
10.9 |
| Coke |
— |
— |
1.4 ± 0.0 |
2.5 ± 0.1 |
1.8 |
1.1 |
Table 2 GC × GC oil composition summary, wt% wet oil
| Description |
Run |
Pyrolysis only |
0.5% Pt |
1% Pt |
0.5% Pt |
0.5% Pt |
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, kg/kg C, kg/kg |
— |
12 |
3 |
6 |
21 |
| Feed |
CP |
CP/FR |
CP |
CP/FR |
CP/FR |
| HC |
Aromatic hydrocarbons
|
0.02 |
1.3 ± 0.2 |
2.8 ± 0.8 |
1.6 |
0.8 |
| HC |
Alkanes + alkenes
|
0.02 |
0.5 ± 0.1 |
0.6 ± 0.3 |
1.0 |
1.3 |
| OX |
Cyclopente/anones
|
0.99 |
8.0 ± 0.2 |
9.2 ± 0.5 |
7.8 |
8.3 |
| PV |
Other ketones/aldehydes
|
4.15 |
5.4 ± 0.1 |
4.2 ± 0.1 |
6.6 |
3.4 |
| OX |
Phenol
|
0.19 |
4.6 ± 0.2 |
7.0 ± 0.7 |
5.2 |
4.6 |
| OX |
Methylphenols
|
0.18 |
1.7 ± 0.1 |
2.9 ± 0.2 |
2.0 |
1.6 |
| OX |
Other phenols
|
0.36 |
6.1 ± 0.6 |
11.5 ± 2.2 |
7.4 |
6.2 |
| OX |
Furanics
|
2.29 |
4.1 ± 0.1 |
1.9 ± 0.1 |
2.6 |
7.2 |
| PV |
Acids
|
1.42 |
0.9 ± 0.1 |
1.3 ± 0.3 |
1.3 |
2.6 |
| PV |
Methoxyphenols
|
0.92 |
0.6 ± 0.1 |
1.2 ± 0.4 |
0.4 |
1.7 |
| PV |
Sugars
|
0.57 |
0.0 ± 0.0 |
0.0 ± 0.0 |
0.0 |
0.2 |
| PV |
Other oxygenates
|
2.54 |
1.4 ± 0.2 |
1.9 ± 0.4 |
0.7 |
1.9 |
|
Total, wt% in oil
|
13.66 |
34.7 |
44.4 |
36.5 |
39.8 |
LC compounds consist of primarily acetaldehyde, acetone, misc. C5+, butanone, furan, and 2-methyl furan so additional LC is considered to be in the intermediate OX family. In addition, the fraction of CFP oil that was not identifiable by GC × GC-TOFMS (Table 2), which consisted of high molecular weight pyrolsysi vapor (HMW PV) that do not volatilize below the injector temperature of 300 °C and oven temperature of 255 °C. GC × GC methods can be seen in the ESI.† The HMW PV component corresponded to 15% of the biomass. Previous research with similar fluidized beds and pine wood have shown that it is typical to have 15% high molecular weight “pyrolytic lignin”.31–33 For this work, HMW PV is considered generally unreactive, as there is a similar amount of unidentified high MW liquid in all catalytic experiments (∼15%). With these assumptions, only 46 wt% of the biomass is considered “reactive pyrolysis vapors” and included in the kinetic HDO model. This consolidated mass balance is graphically illustrated for clarification in Fig. 5 for the four experimental conditions used in this work. Further oil characterization data can be found in the ESI.†
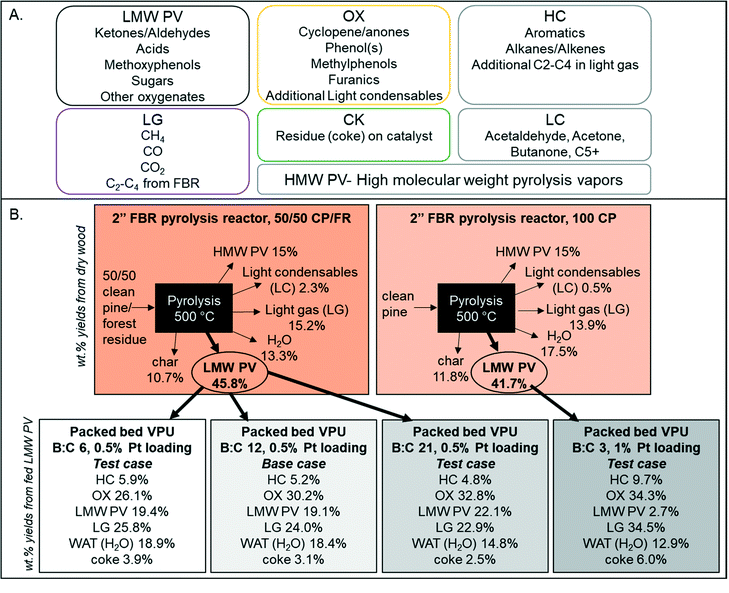 |
| | Fig. 5 (A) Lumped species definitions based on GC/MS quantification and (B) illustrative mass balances of the model development and three test cases with weight percent yields from dry wood for the pyrolysis reactor and weight percent yields from LMW PV for the vapor phase upgrading reactor. | |
Real-time tracking of the vapor products leaving the reactor was accomplished through the RGA. However, due to the response factor variation and sensitivity, not all species were detected. Thus “ambassador compounds” were chosen to represent the chemical families of low molecular weight pyrolysis vapors (LMW PV), partially deoxygenated compounds (OX), and hydrocarbons (HC). For LMW PV, acetic acid/hydroxyacetaldehyde (m/z 60) was chosen; for OX, phenol (m/z 94), furans (m/z 68) and cyclopentenone/methyl furan (m/z 82); for HC, toluene (m/z 91). The lumping procedure is shown in Fig. 5. Data from 0.5% Pt B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 experiments were summed together, and for OX all tracked species were also summed together (Fig. 6). The component groups analyzed by GC × GC were also divided into the same families (LMW PV, OX, HC), (Table 2), and the final yields for each family were calculated. The RGA data provides transient intensities representing these three primary vapor chemical families whose integrals are normalized to equal the yield of each lumped product. The light gases and light condensables were also monitored throughout the experimental runs; the additional light gases formed during VPU were tracked as a separate product family (LG); the additional condensables formed were divided into OX or HC depending on the compound. Thus the data was transformed to represent cumulative yield of products as a function of time based on total LMW PV fed during the experiment for the base case of biomass to catalyst (B
C 12 experiments were summed together, and for OX all tracked species were also summed together (Fig. 6). The component groups analyzed by GC × GC were also divided into the same families (LMW PV, OX, HC), (Table 2), and the final yields for each family were calculated. The RGA data provides transient intensities representing these three primary vapor chemical families whose integrals are normalized to equal the yield of each lumped product. The light gases and light condensables were also monitored throughout the experimental runs; the additional light gases formed during VPU were tracked as a separate product family (LG); the additional condensables formed were divided into OX or HC depending on the compound. Thus the data was transformed to represent cumulative yield of products as a function of time based on total LMW PV fed during the experiment for the base case of biomass to catalyst (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C) ratio of 12 with a 0.5 wt% Pt/TiO2. In addition, the final yield of coke (CK) and additional water formed (WAT) was available. The final yields of each compound family based on the LMW PV from non-catalytic pyrolysis are shown in Fig. 5. The equations for determining the lumped yields are listed in the ESI.†
C) ratio of 12 with a 0.5 wt% Pt/TiO2. In addition, the final yield of coke (CK) and additional water formed (WAT) was available. The final yields of each compound family based on the LMW PV from non-catalytic pyrolysis are shown in Fig. 5. The equations for determining the lumped yields are listed in the ESI.†
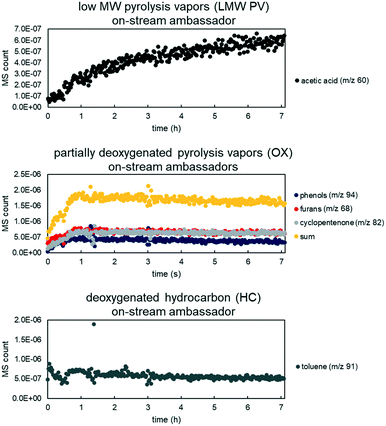 |
| | Fig. 6 MS counts vs. time for three experiments (overlayed) for ambassador compounds with high signal to noise ratio for LMW PV (top), OX (middle), and HC (bottom). Each data set was fit to a regression for model rate fitting. Data from 50/50 CP/FR, B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12, 0.5% Pt loading. C 12, 0.5% Pt loading. | |
Model description
Packed bed model
The reaction scheme for this catalyst was developed based on prior experimental insights into the proposed mechanisms that this Pt/TiO2 catalyst follows for conversion of pyrolysis vapors into partially oxygenated compounds (OX), hydrocarbons (HC), light gas (LG), water (WAT), and coke (CK). Pt/TiO2 is a bifunctional metal–acid catalyst, and HDO is generally considered to progress in two stages: partial deoxygenation of pyrolysis vapors and nearly complete deoxygenation of pyrolysis vapors through a variety of mechanisms including decarbonylation, ketonization, aldol condensation, direct deoxygenation, and hydrogenation.1 In general, we could consider these as two sequential reaction families where LMW PV → OX + LG + WAT → HC + LG + WAT where the first reaction is over catalytic active site S2 and the second is over S1, as shown in Fig. 5. It could be that S2 is an acid site and S1 is a metal site, but the aim of this work was not to prove this hypothesis. There are also simultaneous, competitive coke formation and deactivation reactions for these two catalytic sites. The simplified mechanism used here is shown in Fig. 7. The following equations describe the rates for each species represented in this model. It should be noted that these reaction rates are attenuated by diffusion within the porous catalyst particles, as described later.
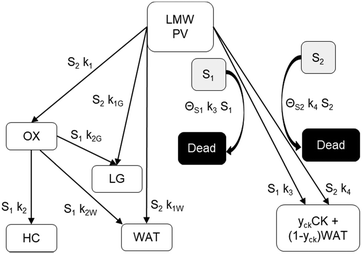 |
| | Fig. 7 Simplified reaction scheme for reactive pyrolysis vapors converting to partially deoxygenated compounds (OX), hydrocarbons (HC), light gas (LG), coke (CK), and water (WAT) over two different reactive catalyst sites (S1 and S2) that can deactivate to fully a dead site. yck is 0.67, representing a mass loss of 33% to remove oxygen in the form of H2O from pyrolysis vapor to leave a nearly graphitic coke. | |
In the packed bed reactor, the vapor reactants and products experience advection, diffusion, and chemical reactions. The following equations describe change in concentration of the reacting species in the void fraction of the packed bed.
| | 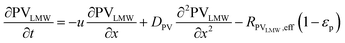 | (1) |
| | 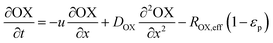 | (2) |
| | 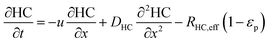 | (3) |
| | 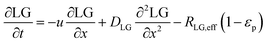 | (4) |
| | 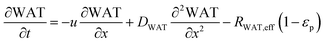 | (5) |
| | 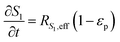 | (6) |
| | 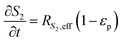 | (7) |
| | 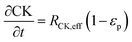 | (8) |
| | | PVLMW = PVLMW,0, x = 0 | (9) |
| | | HC = OX = LG = WAT = 0, x = 0 | (10) |
| | 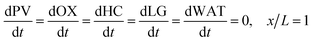 | (11) |
where
Di is the effective Fick's diffusion coefficient,
x is axial length of the reactor bed,
εp is void fraction of the reactor bed,
t is time,
u is nominal gas velocity, eff indicates effective reaction rates attenuated by intraparticle diffusion, and
Ri,eff indicates reaction rate for the solid domain as calculated by the MEV approximation (
a la a Thiele effective reaction rate) which is detailed thoroughly elsewhere.
27 Relevant parameters for the model were taken from the full reactor description shown in the ESI
† or calculated with basic mass balance equations and a summary of model-relevant parameters is shown in
Table 3. These effective reaction rates are a function of each reactions respective local active site concentration, reactant concentration, and rate constant, as illustrated in
Fig. 5. The eight individual apparent reaction rate equations are shown below:
As shown in
Fig. 5, the relative mass yield of coke to water + coke,
yck, is 0.67, representing a mass loss of 33% to remove oxygen in the form of H
2O from pyrolysis vapor to leave a nearly graphitic coke. The purpose of these ratios is to reduce the number of fitted parameters. Parameters
ΘS1 and
ΘS2 are fitted deactivation ratios that relate how quickly sites 1 and 2 deactivate relative to coke formation and are connected to rate constants 3 and 4, respectively.
Table 3 Key parameters used in the packed bed reactor model
| Parameter |
Value |
Description |
|
L
|
0.14 m |
Length of reactor bed |
|
P
tot
|
1 × 105 Pa |
Pressure in reactor, inlet |
|
u
inf
|
0.947 m s−1 |
Nominal gas velocity |
|
U
|
2.167 m s−1 |
Void fraction-corrected gas velocity |
|
T
in
|
450 C |
Temperature reactor |
|
ρ
g
|
0.2247 kg m−3 |
Density gas ([85% H2 + 15% N2] + PV + LG + H2O), inlet |
|
μ
vap
|
1.97 × 10−5 kg m−1 s−1 |
Estimated viscosity of gas + PV |
| AFR |
7.5 × 10−4 m3 s−1 |
Actual volumetric flowrate gas |
| mfPVin50/50 CP/FR |
0.458 |
Mass fraction LMW PV in for 50/50 CP/FR |
| mfPVinCP |
0.417 |
Mass fraction LMW PV in for CP |
|
D
i
|
4 × 10−5 m2 s−1 |
Bulk diffusion coefficient for all species |
|
D
i,eff
|
D
i
ε
ps
|
Effective bulk diffusion coefficient |
|
ε
ps
|
0.437 |
Void fraction reactor bed |
|
ε
pp
|
0.592 |
Void fraction catalyst particle |
|
D
p
|
0.5 × 10−3 m |
Diameter catalyst particle |
|
D
pore
|
2.8 × 10−8 m |
Pore diameter of catalyst particles |
| Re |
12.4 |
Reynolds number with respect to particle |
|
T
|
7 |
Tortuosity within catalyst particle |
|
K
D
|
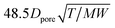
|
Knudsen diffusion coefficient calculation |
| Re |
28 |
Reynolds number with respect to a single catalyst particle with inlet fluid properties |
| Sc |
5 |
Schmidt number |
| Pe |
141 |
Peclet number |
| Sh |
152 |
Sherwood number for creeping flow around sphere39 |
Pressure drop is accounted for via the Ergun equation:34
| | 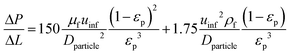 | (20) |
such that the fluid density and fluid velocity can be determined using the ideal gas law based on inlet boundary conditions, which is generally considered to be valid at near-atmospheric pressure.
Deactivation is modeled by calculating the dynamic population of active sites (S1 and S2) and coke formation. These quantities are immobile which requires that the packed bed model be modeled with discretized volume fractions in the axial direction. Plug flow reactor assumptions are made to simplify the reactor model into a 1D simulation. The method of lines numerical approach was used to solve the system of partial differential equations that describe the reactor. A Matlab® script called MatMOL was used, which has been successfully demonstrated for similar problems.35–38
Intraparticle model to decouple porous transport from chemical reactions
To represent intraparticle diffusion–reaction, the multistep effectiveness vector (MEV) approach was implemented. This MEV solution represents a pseudo-steady state analytical solution for diffusion and reaction of multistep reactions within catalyst particles, and is an extension of the Thiele modulus solution.27 The solution represents a single catalyst particle, so it was multiplied by the total number of catalyst particle in each discrete axial subvolume to calculate the total rate of reaction in that subvolume. This approach is illustrated as shown in Fig. 1. The full derivation of the method for using a Thiele modulus with multiple reactions in series can be found in Lattanzi et al.27 (a la the MEV). In short, the unsteady advection–diffusion model is used to describe a spherical porous catalyst particle,| | 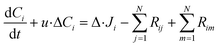 | (21) |
where Ci is the molar concentration of vapor species i, u is velocity of gas, 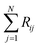 is the sum of reactions consuming i, and
is the sum of reactions consuming i, and 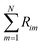 is the sum of reactions forming i, and Ji is the flux of species i. Assuming no advection and using spherical coordinates the equation becomes
is the sum of reactions forming i, and Ji is the flux of species i. Assuming no advection and using spherical coordinates the equation becomes| | 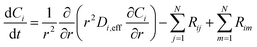 | (22) |
where r is the radial coordinate and Di,eff is the intraparticle diffusion coefficient. Next to non-dimensionalize the problem,| | 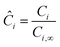 | (23) |
where Ci,∞ is the concentration of reactant i outside the particle,| | 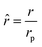 | (24) |
where rp is the particle radius, and| | 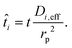 | (25) |
The Thiele modulus for consumption reactions must include all the reactions which consume i, and thus| |  | (26) |
where k is the rate constant for reaction j and Sl is the normalized active site concentration of site l remaining, from 1 to 0. Thus the remaining sites function as a deactivation factor. Similarly, for reactions that produce i from species m,| | 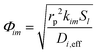 | (27) |
If we then assume quasi steady state and apply boundary conditions we arrive at a dimensionless boundary value problem| | 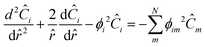 | (28) |
where at the center| | 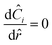 | (29) |
and at the surface| | 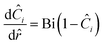 | (30) |
where Bi is the Biot number. Using matrix–vector form with the matrix of Thiele moduli for consumption and production, the whole system of reaction–diffusion can be described as:| | 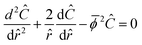 | (31) |
When the eigenvalues (λ) are real, the solution is a hyperbolic function:| | 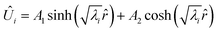 | (32) |
Converting back to concentration and applying the boundary conditions, where P is the eigenvector and D is the determinant, we find the concentration for all species at a given timestep| | 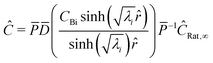 | (33) |
Thus the concentration for each species as a function of radius can be applied to the reaction rate and integrated over the whole particle:| | 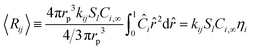 | (34) |
where η is the multistep effectiveness factor for that reaction| | 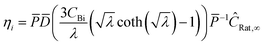 | (35) |
and thus the effective rate for each species becomes| | 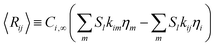 | (36) |
In this particular reaction scheme, the effective reaction rate vector is the following:
The combined packed bed with sub-grid intraparticle MEV model was validated for simple reaction–diffusion following an example presented by Rawlings23 as described in detail in the ESI.†
Constant yck is 0.67, representing a mass loss of 33% to remove oxygen in the form of H2O from pyrolysis vapor to leave a nearly graphitic coke. Initial values of S1 and S2 are 1 within the catalyst, and initial concentration of LMW PV is set to a smooth function along the length of the reactor for stability.
Other key model assumptions include:
1) Uniform coking and deactivation throughout the particle
2) Plug flow model with axial dispersion is valid for this packed bed reactor
3) Void fraction is homogeneous
4) The particles are spherical, particle size is uniform, and interparticle mass transfer is negligible
5) HMW PV, light gas, water, and light condensables are non-reactive
6) H2 is present in excess.
After the model was parameterized and validated, it was used to fit apparent rate constants for the reactions that were decoupled from the mass transport between the particles and within the particles. The simplex method40 was used for numerical optimization of rate constants k1, k2, k3, k4, k1G, k1W, k2G, k2W, Θ1, and Θ2 with the residual function representing the sum of the sum of least squares for the yield curves LMW PV, HC, and OX, and final yields of CK and LG, weighted by the inverse of each respective yield. Initial rate constant guesses were determined manually, and then refined by the simplex method using Matlab's fminsearch function. Optimization was run for 100 iterations with negative values prohibited. Then a mesh refinement study was performed to determine that ∼100 nodes are required for accurate modeling, and the optimization was repeated, or until convergence tolerance <2 × 104 was reached for sum of R2. The fitting was restarted with random numbers if convergence was not reached in 100 iterations.
Simulation results
The packed bed vapor phase upgrading (VPU) reactor model was used to iteratively fit apparent rate constants for our reaction scheme for catalytic upgrading of pyrolysis vapors over the deactivating Pt/TiO2 catalyst up to biomass![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catalyst ratio of 12. Note that these rate constants are for 450 °C and are independent of the catalyst porosity and particle size. Results from this optimization are shown in Table 4. A comparison of model predictions of lumped yields vs. experimental lumped yields vs. time is shown in Fig. 8, wherein the model and experiment match well and trend towards deactivation together.
catalyst ratio of 12. Note that these rate constants are for 450 °C and are independent of the catalyst porosity and particle size. Results from this optimization are shown in Table 4. A comparison of model predictions of lumped yields vs. experimental lumped yields vs. time is shown in Fig. 8, wherein the model and experiment match well and trend towards deactivation together.
Table 4 Reaction rate parameters fit by the optimizer coupled to the packed bed reactor
| Rate constant |
Fitted value |
|
k
1 [s−1] |
76 |
|
k
1G [s−1] |
50.5 |
|
k
1W [s−1] |
39 |
|
k
2 [s−1] |
5.4 |
|
k
2G [s−1] |
0.7 |
|
k
2W [s−1] |
7.9 × 10−10 |
|
k
3 [s−1] |
7 × 10−14 |
|
k
4 [s−1] |
3.7 × 10−4 |
|
Θ
S
1
|
1.2 × 10−3 |
|
Θ
S
2
|
15.2 |
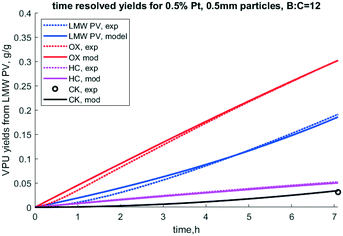 |
| | Fig. 8 Time resolved yields for 0.5% Pt, 0.5 mm particles, B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = 12, 50/50 clean pine/forest residue. N.b. notation hydrocarbon HC, partially deoxygenated hydrocarbon (OX), coke (CK), and reactant low MW pyrolysis vapor (LMW PV), and experimental (exp). C = 12, 50/50 clean pine/forest residue. N.b. notation hydrocarbon HC, partially deoxygenated hydrocarbon (OX), coke (CK), and reactant low MW pyrolysis vapor (LMW PV), and experimental (exp). | |
It is notable that the model predicts that S2 deactivates much faster than S1, as k4 is much larger than k3. Under this model formulation S2 deactivates faster than S1 as indicated by k4 and ΘS2, parameters which are intrinsically coupled with respect to deactivation. If indeed this site does represent acid sites, which this paper does not prove per se, it is consistent with how quickly acid-dominant HZSM-5 deactivates in catalytic fast pyrolysis.41 Since the S1 site corresponds to conversion of OX to HC, the first reaction step, PV to OX, occurs over the rapidly deactivating site. This matches the observation that OX does not dramatically dominate the product profile while the catalyst is deactivating. Deactivation factor ΘS2 is essentially irrelevant because k3, to which it is intrinsically coupled, is so small. Further, k1 is much larger than k2, which indicates higher reactivity of the S2 site. Formation of light gas (LG) and water (WAT) are predicted to form at similar rates from PV, but the model fit seems to predict slower formation of these chemical families for the second stage of the reaction cascade.
To evaluate the accuracy of this model, cumulative yields from three other test case experiments were used: the same catalyst and biomass with B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 6 and 21 and an experiment with a catalyst with twice the platinum loading (1%), a different feed (100% clean pine vs. a 50/50 blend of forest residues and pine), and B
C of 6 and 21 and an experiment with a catalyst with twice the platinum loading (1%), a different feed (100% clean pine vs. a 50/50 blend of forest residues and pine), and B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3. Changing the feedstock was accounted for by reviewing product characterization of the raw pyrolysis vapors. Doubling of the active sites was accounted for in the model by doubling S1 and S2 concentrations. In other tested simulations not presented here, doubling of a single catalytic site only resulted in behavior that did not match the experiments. This does not prove there are exactly two sites, but it does hint that that is the general physical phenomenon here.
C 3. Changing the feedstock was accounted for by reviewing product characterization of the raw pyrolysis vapors. Doubling of the active sites was accounted for in the model by doubling S1 and S2 concentrations. In other tested simulations not presented here, doubling of a single catalytic site only resulted in behavior that did not match the experiments. This does not prove there are exactly two sites, but it does hint that that is the general physical phenomenon here.
Results shown in Fig. 9 show cumulative yields with the mass balance across VPU alone, based on LMW PV. For the base case at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 the model matches with experiments within the error, as expected. At B
C 12 the model matches with experiments within the error, as expected. At B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 6 and 21, which had no replicates, the model predicts yields with an accuracy of 5% with the largest error being in the most abundant product OX. At a B
C of 6 and 21, which had no replicates, the model predicts yields with an accuracy of 5% with the largest error being in the most abundant product OX. At a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 21, the model predicts lower values for HC, OX and LG, but over predicts CK and PV. This could be because the experiment was done in two cycles. Cycle 1 was run until a B
C of 21, the model predicts lower values for HC, OX and LG, but over predicts CK and PV. This could be because the experiment was done in two cycles. Cycle 1 was run until a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 12 and cycle 2 was done the following day from B
C of 12 and cycle 2 was done the following day from B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 to 21. The catalyst was left in N2 flow overnight and was reduced in H2 prior to running cycle 2, which reactivated some active sites. This may explain the discrepancies in the coke yields and shows the need for a thorough examination of coke formation and degradation over these catalysts.
C 12 to 21. The catalyst was left in N2 flow overnight and was reduced in H2 prior to running cycle 2, which reactivated some active sites. This may explain the discrepancies in the coke yields and shows the need for a thorough examination of coke formation and degradation over these catalysts.
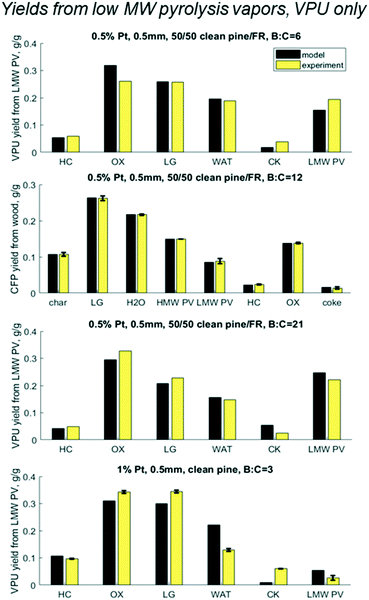 |
| | Fig. 9 Predicted vs. experimental yields of the six lumped species for the mass balance across the vapor phase upgrader (VPU) for three B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios with 50/50 clean pine/forest residue and 0.5% Pt as well as one case with clean pine and 1% Pt. N.b. notation hydrocarbon HC, partially deoxygenated hydrocarbon OX, light gas (LG), reaction water (WAT), coke (CK), and reactant low MW pyrolysis vapor (LMW PV). C ratios with 50/50 clean pine/forest residue and 0.5% Pt as well as one case with clean pine and 1% Pt. N.b. notation hydrocarbon HC, partially deoxygenated hydrocarbon OX, light gas (LG), reaction water (WAT), coke (CK), and reactant low MW pyrolysis vapor (LMW PV). | |
However, most interesting is the case with twice the Pt, a quarter time on stream, and a slightly different biomass feed. Even with all those changes, all yields over the HDO reactor were within 5% with the exception of coke for which the model underpredicted 1% yield vs. experimental 6% from LMW PV. It is possible that the different pine blend resulted in larger changes in the pyrolysis vapors that could not be accounted for in this lumped model, or the coke changes and degrades over time. Future work should explore these hypotheses around coking behavior and mechanisms.
When the cumulative yields are calculated over the mass balance of the whole system – wood to upgraded vapors – the relative variance decreases (Fig. 10). Again, the 0.5% Pt B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 experiment with 50/50 CP/FR matches within the experimental error. More interestingly, the variance between experiment and model is reduced for the 1% Pt B
C 12 experiment with 50/50 CP/FR matches within the experimental error. More interestingly, the variance between experiment and model is reduced for the 1% Pt B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3 with clean pine. For light gas the model predicts 26% vs. experimental 28%; for water the model predicts 27% vs. experimental 23%; for breakthrough of reactant LMW PV the model predicts 2% vs. experimental 1%; for HC the model predicts 4.4% vs. experimental 4%; for OX the model predicts 13% vs. experimental 14%; and for coke the model predicts 0.4% vs. experimental 2.5%. For such a different experimental condition, these predictions exceeded expectations and show that while there is room for improvement, the existing model has valuable predictive capabilities. One of the limitations of this modeling approach is that the coke formation reaction rates were fit to final yields, not time-resolved yields. This could explain why the coke yields are not as accurate across different operating conditions than the other lumped chemical groups. Future modeling work exploring time-resolved coke yields and axial profiles would greatly improve the validity of this modeling approach. However, in general it is logical that if coke is formed from reactive pyrolysis vapors, then it is likely to accumulate near the entrance where there is a higher concentration of these compounds.
C 3 with clean pine. For light gas the model predicts 26% vs. experimental 28%; for water the model predicts 27% vs. experimental 23%; for breakthrough of reactant LMW PV the model predicts 2% vs. experimental 1%; for HC the model predicts 4.4% vs. experimental 4%; for OX the model predicts 13% vs. experimental 14%; and for coke the model predicts 0.4% vs. experimental 2.5%. For such a different experimental condition, these predictions exceeded expectations and show that while there is room for improvement, the existing model has valuable predictive capabilities. One of the limitations of this modeling approach is that the coke formation reaction rates were fit to final yields, not time-resolved yields. This could explain why the coke yields are not as accurate across different operating conditions than the other lumped chemical groups. Future modeling work exploring time-resolved coke yields and axial profiles would greatly improve the validity of this modeling approach. However, in general it is logical that if coke is formed from reactive pyrolysis vapors, then it is likely to accumulate near the entrance where there is a higher concentration of these compounds.
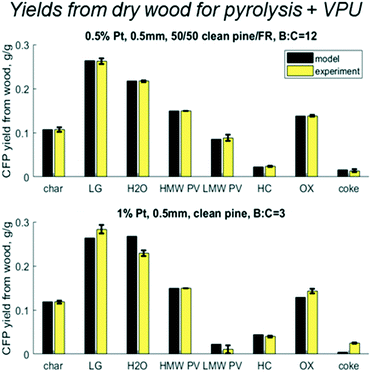 |
| | Fig. 10 Predicted vs. experimental yields of the six lumped species for the mass balance across the pyrolysis reactor and vapor phase upgrader (VPU) for 50/50 clean pine/forest residue, 0.5% Pt, B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 as well as one case with clean pine, 1% Pt, B C 12 as well as one case with clean pine, 1% Pt, B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3. C 3. | |
Nevertheless, this model can be used to perform sensitivity analysis to predict trends over a variety of operating conditions. An important output from the model is the prediction of accumulation of coke. The mass of coke, especially carbon content, directly impacts carbon yield in CFP oil as well as coke oxidation during catalyst regeneration. As shown in Fig. 11, more coke is predicted to accumulate near the entrance of the reactor as the reactive pyrolysis vapors are present in higher abundance there. As time progresses, more coke accumulates down the length of the reactor near the outlet, but the inlet has nearly twice the concentration compared to exit of the reactor.
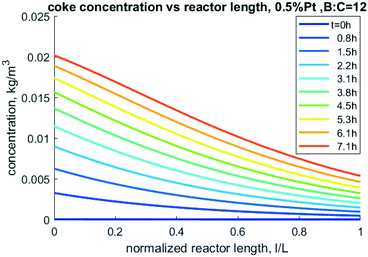 |
| | Fig. 11 Model-predicted coke density profiles through the reactor at different times for 0.5% Pt, 50/50 CP/FR example. | |
Accurately predicting coke formation and localization is critical to de-risk this technology. If coke accumulates at the entrance, regeneration might be more effectively accomplished by feeding the oxidant through the outlet to reduce the risk of overheating the higher-coked inlet region. Over-heating through oxidative regeneration can induce sintering and even particle fragmentation. Further work should be done to validate these predictions and use results to de-risk scaleup of the sensitive regeneration process. Similarly, incorporation of second order reactions with respect to consumption of hydrogen would also be relevant in future work, as the complex dynamics of consumption and generation of this gas has the potential to influence the rates of reaction.
To inform future experimental design, parametric sweeps were performed considering spherical particles from 0.25 mm to 5 mm catalyst diameters. This parameter is important because while it could be intuited that smaller particles will allow for full access to distributed active sites, it also increases the pressure drop in the bed which has an energy cost. Pressure drop from smaller particle sizes can be balanced by increasing the reactor size, to a degree. In these simulations all other parameters remained the same (bed void fraction, inlet conditions, particle porosity, etc.). The fluid density and velocity were back-calculated from the Ergun equation for each unique particle size simulation. Fig. 12 illustrates that reducing the particle diameter below 0.35 mm dramatically increases the pressure drop, and this should likely be avoided unless the reactor diameter is increased to 3.2 cm or larger for this size of catalyst bed (100 g). Going to larger D/L ratios requires expensive mixing distributors, so this may not be feasible. Interestingly, simulations to predict PV conversion over these particle sizes identified a notable regime for optimal performance. Nearly 100% conversion of reactive LMW PV to products is predicted at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 with 0.5% Pt on TiO2 when the reactor diameter is less than 3.2 cm with particle sizes up to 5 mm, also shown in Fig. 10. This “sweet spot” would allow for longer operation before regeneration, less catalyst, and /or lower catalyst loading.
C 12 with 0.5% Pt on TiO2 when the reactor diameter is less than 3.2 cm with particle sizes up to 5 mm, also shown in Fig. 10. This “sweet spot” would allow for longer operation before regeneration, less catalyst, and /or lower catalyst loading.
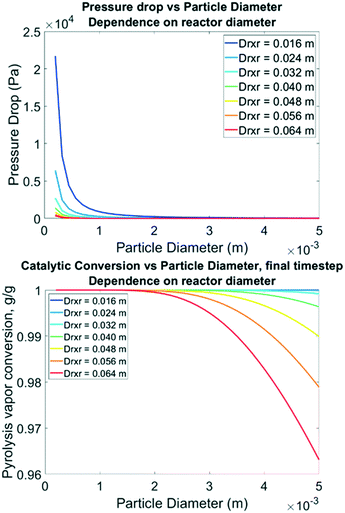 |
| | Fig. 12 Top: Model-predicted pressure drop from inlet to outlet vs. catalyst particle diameter following the Ergun equation with fixed inlet pressure & velocity. Bottom: Model-predicted LMW PV conversion vs. particle diameter for B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12, 0.5% Pt, 50/50 CP/FR. C 12, 0.5% Pt, 50/50 CP/FR. | |
While the model development described in this work does warrant further examination and refinement, it does manage to achieve predictive capacity for lumped yields of products from catalytic fast pyrolysis. It is very rare to find any reports of rate constants for a lumped reaction scheme for the pyrolysis vapor phase HDO,42,43 let alone reaction kinetics that are decoupled from porous diffusion limitations. Lumped kinetics may be more applicable to this process than rate constants for individual reactions when they are extracted from operational data because synergistic or competitive reactions may exist that are not observed in model compound studies. Further, this lumped reaction scheme approach allows for chemical engineers to design reactor systems and predict yields of products with this catalyst and vapor feed with some level of confidence, effectively reducing the risk of scaling up this technology for producing gasoline, diesel, and chemical precursors from renewable resources.
Conclusions
A simulation framework consisting of intraparticle diffusion–reaction for a cascading multistep reaction scheme coupled to an axial-dispersion packed bed reactor model was used to extract apparent reaction rate constants for a lumped catalytic fast pyrolysis scheme. The extracted rate constants were employed to simulate additional conditions beyond those from which they were obtained. The results provided reasonably accurate predictions of yields from a variety of different conditions in the same basic packed bed reactor system which was highly instrumented for near-100% mass closure. The model could be further improved by additional speciation of the pyrolysis vapor composition, as the current version is only valid for pine and some pine blends at 450 °C. Further development should also be done to expand the mathematical underpinnings of the subgrid particle model to account for different particle shapes like cylinders. Nevertheless, this fast-solving fully-integrated multiscale modeling approach can be applied to a variety of catalytic chemical reaction processes with cascading reactions to de-risk critical emergent technologies in fuels and chemical production.
Abbreviations
| Notation | Definition |
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C | Fed biomass to catalyst ratio, g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g g |
| CFP | Catalytic fast pyrolysis |
| CK | Coke deposited on catalysts |
| CP | Clean pine |
| CP/FR | Clean pine/forest residue, 50/50 |
| HC | Deoxygenated hydrocarbons, derived from OX |
| HDO | Hydrodeoxygenation; upgrading reactor |
| HMW PV | High molecular weight, assumed non-reactive pyrolysis vapors |
| LMW PV | Low molecular weight, reactive pyrolysis vapors |
| LG | Light gas |
| MEV | Multistep effectiveness vector (Thiele modulus-style intraparticle reaction–diffusion approximation) |
| OX | Partially deoxygenated hydrocarbons, precursor to HC |
| RGA | Residual gas analyzer |
|
S
1
| Catalytic reaction site 1 |
|
S
2
| Catalytic reaction site 2 |
| VPU | Packed (fixed) bed catalytic vapor phase upgrading reactor after the pyrolysis reactor |
| WAT | HDO reaction water |
Conflicts of interest
There are no conflicts to declare. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Acknowledgements
This work was authored by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding provided by U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Solar Energy Technologies Office and in collaboration with the Chemical Catalysis for Bioenergy Consortium (ChemCatBio), a member of the Energy Materials Network (EMN). The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes. Scott Palmer, Kellene Orton, Chris Golubieski, Rebecca Jackson, Kathleen Brown, and Earl Christensen are acknowledged for their contributions in performing the experiments and analyzing the data. Aaron Lattanzi is acknowledged for his helpful discussions regarding the packed bed reactor model with MEV. The authors would also like to thank Michael Watson and Luke Tuxworth of Johnson Matthey for their important contributions to this work.
References
- M. B. Griffin, K. Iisa, H. Wang, A. Dutta, K. A. Orton, R. J. French, D. M. Santosa, N. Wilson, E. Christensen, C. Nash, K. M. Van Allsburg, F. G. Baddour, D. A. Ruddy, E. C. D. Tan, H. Cai, C. Mukarakate and J. A. Schaidle, Energy Environ. Sci., 2018, 11, 2904–2918 RSC.
- K. Iisa, R. J. French, K. A. Orton, A. Dutta and J. A. Schaidle, Fuel, 2017, 207, 413–422 CrossRef CAS.
- S. D. Stefanidis, K. G. Kalogiannis and A. A. Lappas, Wiley Interdiscip. Rev. Energy Environ., 2018, 7, e281 Search PubMed.
- A. N. Wilson, M. J. Price, C. Mukarakate, R. Katahira, M. B. Griffin, J. R. Dorgan, J. Olstad, K. A. Magrini and M. R. Nimlos, ACS Sustainable Chem. Eng., 2017, 5, 6615–6625 CrossRef CAS.
- A. N. Wilson, A. Dutta, B. A. Black, C. Mukarakate, K. Magrini, J. A. Schaidle, W. E. Michener, G. T. Beckham and M. R. Nimlos, Green Chem., 2019, 21, 4217–4230 RSC.
- M. B. Griffin, G. A. Ferguson, D. A. Ruddy, M. J. Biddy, G. T. Beckham and J. A. Schaidle, ACS Catal., 2016, 6, 2715–2727 CrossRef CAS.
- A. Eschenbacher, A. Saraeian, B. H. Shanks, P. A. Jensen, C. Li, J. Ø. Duus, A. B. Hansen, U. V. Mentzel, U. B. Henriksen, J. Ahrenfeldt and A. D. Jensen, Sustainable Energy Fuels, 2020, 4, 1991–2008 RSC.
- K. Wang, D. C. Dayton, J. E. Peters and O. D. Mante, Green Chem., 2017, 19, 3243–3251 RSC.
- S. Wan, T. Pham, S. Zhang, L. Lobban, D. Resasco and R. Mallinson, AIChE J., 2013, 59, 2275–2285 CrossRef CAS.
- K. Murugappan, C. Mukarakate, S. Budhi, M. Shetty, M. R. Nimlos and Y. Román-Leshkov, Green Chem., 2016, 18, 5548–5557 RSC.
- M. A. Machado, S. He, T. E. Davies, K. Seshan and V. Teixeira da Silva, Catal. Today, 2018, 302, 161–168 CrossRef CAS.
- P. Cross, K. Wang, J. Weiner, E. Reid, J. Peters, O. Mante and D. C. Dayton, Energy Fuels, 2020, 34, 4678–4684 CrossRef CAS.
-
A. Dutta, M. K. Iisa, M. Talmadge, C. Mukarakate, M. B. Griffin, E. C. Tan, N. Wilson, M. M. Yung, M. R. Nimlos and J. A. Schaidle, Ex Situ Catalytic Fast Pyrolysis of Lignocellulosic Biomass to Hydrocarbon Fuels: 2019 State of Technology and Future Research, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2020 Search PubMed.
- S. Boonyasuwat, T. Omotoso, D. E. Resasco and S. P. Crossley, Catal. Lett., 2013, 143, 783–791 CrossRef CAS.
- T. O. Omotoso, B. Baek, L. C. Grabow and S. P. Crossley, ChemCatChem, 2017, 9, 2612 CrossRef CAS.
- P. M. de Souza, L. Nie, L. E. Borges, F. B. Noronha and D. E. Resasco, Catal. Lett., 2014, 144, 2005–2011 CrossRef CAS.
- M. B. Pecha, E. Ramirez, G. M. Wiggins, D. Carpenter, B. Kappes, S. Daw and P. N. Ciesielski, Energy Fuels, 2018, 32, 10683–10694 CrossRef CAS.
- E. Ranzi, P. E. A. Debiagi and A. Frassoldati, ACS Sustainable Chem. Eng., 2017, 5, 2867–2881 CrossRef CAS.
- E. Ranzi, P. E. A. Debiagi and A. Frassoldati, ACS Sustainable Chem. Eng., 2017, 5, 2882–2896 CrossRef CAS.
- V. S. Bharadwaj, M. B. Pecha, L. Bu, V. L. Dagle, R. A. Dagle and P. N. Ciesielski, Catal. Today, 2019, 338, 141–151 CrossRef CAS.
- L. D. Dellon, C.-Y. Sung, D. J. Robichaud and L. J. Broadbelt, Ind. Eng. Chem. Res., 2019, 58, 15173–15189 CrossRef CAS.
- O. Levenspiel, Ind. Eng. Chem. Res., 1999, 38, 4140–4143 CrossRef CAS.
-
J. B. Rawlings and J. G. Ekerdt, Chemical reactor analysis and design fundamentals, Nob Hill Pub., 2002 Search PubMed.
-
H. S. Fogler, Elements of chemical reaction engineering, Pearson PTG, London, England, UK, 6th edn, 2021 Search PubMed.
- N. Jurtz, M. Kraume and G. D. Wehinger, Rev. Chem. Eng., 2019, 35, 139–190 Search PubMed.
- E. W. Thiele, Ind. Eng. Chem. Res., 1939, 31, 916–920 CrossRef CAS.
- A. M. Lattanzi, M. B. Pecha, V. S. Bharadwaj and P. N. Ciesielski, Chem. Eng. J., 2020, 380, 122507 CrossRef CAS.
- J. R. Kremer, D. N. Mastronarde and J. R. McIntosh, J. Struct. Biol., 1996, 116, 71–76 CrossRef CAS.
-
PyMOL, The PyMOL Molecular Graphics System, 2017, Version 2.0 Search PubMed.
- E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef CAS.
- A. Oasmaa, Y. Solantausta, V. Arpiainen, E. Kuoppala and K. Sipilä, Energy Fuels, 2010, 24, 1380–1388 CrossRef CAS.
- A.-C. Johansson, H. Wiinikka, L. Sandström, M. Marklund, O. G. W. Öhrman and J. Narvesjö, Fuel Process. Technol., 2016, 146, 9–19 CrossRef CAS.
- E. Hoekstra, R. J. M. Westerhof, W. Brilman, W. P. M. Van Swaaij, S. R. A. Kersten, K. J. A. Hogendoorn and M. Windt, AIChE J., 2012, 58, 2830–2842 CrossRef CAS.
- S. Ergun, Chem. Eng. Prog., 1952, 48, 89–94 CAS.
- F. Logist, P. Saucez, J. Van Impe and A. V. Wouwer, Chem. Eng. J., 2009, 155, 603–616 CrossRef CAS.
- A. Vande Wouwer, P. Saucez and W. Schiesser, Ind. Eng. Chem. Res., 2004, 43, 3469–3477 CrossRef CAS.
- A. V. Wouwer, P. Saucez, W. Schiesser and S. Thompson, J. Comput. Appl. Math., 2005, 183, 245–258 CrossRef.
- P. Saucez, L. Some and A. V. Wouwer, Appl. Math. Comput., 2009, 215, 1821–1829 CrossRef.
- K. K. Sirkar, Chem. Eng. Sci., 1974, 29, 863–869 CrossRef CAS.
- J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, SIAM J. Control, 1998, 9, 112–147 Search PubMed.
- C. Mukarakate, X. Zhang, A. R. Stanton, D. J. Robichaud, P. N. Ciesielski, K. Malhotra, B. S. Donohoe, E. Gjersing, R. J. Evans and D. S. Heroux, Green Chem., 2014, 16, 1444–1461 RSC.
- J. D. Adjaye and N. N. Bakhshi, Biomass Bioenergy, 1995, 8, 131–149 CrossRef CAS.
- J. D. Adjaye and N. N. Bakhshi, Biomass Bioenergy, 1995, 8, 265–277 CrossRef CAS.
- J. Klinger, D. L. Carpenter, V. S. Thompson, N. Yancey, R. M. Emerson, K. R. Gaston, K. Smith, M. Thorson, H. Wang, D. M. Santosa and I. Kutnyakov, ACS Sustainable Chem. Eng., 2020, 8(7), 2793–2805 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0re00339e |
| ‡ Fig. 1 is reprinted (adapted) from Chemical Engineering 380, Aaron M. Lattanzi, M. Brennan Pecha, Vivek S. Bharadwaj, Peter N. Ciesielski, Beyond the effectiveness factor: Multi-step reactions with intraparticle diffusion limitations, 1, Copyright (2020), with permission from Elsevier. |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Kristiina
Iisa
*a,
Kristiina
Iisa
 a,
Michael
Griffin
a,
Michael
Griffin
 a,
Calvin
Mukarakate
a,
Calvin
Mukarakate
 a,
Richard
French
a,
Richard
French
 a,
Bruce
Adkins
b,
Vivek S.
Bharadwaj
a,
Bruce
Adkins
b,
Vivek S.
Bharadwaj
 a,
Meagan
Crowley
a,
Meagan
Crowley
 a,
Thomas D.
Foust
a,
Joshua A.
Schaidle
a,
Thomas D.
Foust
a,
Joshua A.
Schaidle
 a and
Peter N.
Ciesielski
a and
Peter N.
Ciesielski
 *a
*a


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C) of 12, a 7.1 h run time, with 0.5 wt% Pt/TiO2 catalyst, a weight hourly space velocity of 1.5 g biomass per g catalyst h−1, and a 50%/50% clean pine (CP)/forest residue (FR) wood blend as the biomass feed. The pyrolysis temperature was 500 °C and the average internal temperature of the VPU was 450 °C. The biomass ultimate analysis and further analytical details are included in the ESI.† Yields from the pyrolysis + HDO reactor were compared to results from pyrolysis alone. Further experimental data collected for the same catalytic conditions with B
C) of 12, a 7.1 h run time, with 0.5 wt% Pt/TiO2 catalyst, a weight hourly space velocity of 1.5 g biomass per g catalyst h−1, and a 50%/50% clean pine (CP)/forest residue (FR) wood blend as the biomass feed. The pyrolysis temperature was 500 °C and the average internal temperature of the VPU was 450 °C. The biomass ultimate analysis and further analytical details are included in the ESI.† Yields from the pyrolysis + HDO reactor were compared to results from pyrolysis alone. Further experimental data collected for the same catalytic conditions with B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 6 and 21 as well as a data set for a 1 wt% Pt on the same TiO2 support and 100% clean pine as feed at B
C of 6 and 21 as well as a data set for a 1 wt% Pt on the same TiO2 support and 100% clean pine as feed at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3 were used to verify the model. The equations used to calculate lumped product yields across the VPU are detailed in the ESI.†
C 3 were used to verify the model. The equations used to calculate lumped product yields across the VPU are detailed in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal site ratio is 4.9.
metal site ratio is 4.9.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12), the pyrolysis reactor converted 89% of 50/50 CP/FR wood into volatile and gaseous species that pass into the HDO reactor (Table 1), with the remainder being char. However, not all of the vapors are expected to participate in the catalytic upgrading reactions in the subsequent VPU reactor. Here, light gases (LG), light condensables (LC), and water vapor from pyrolysis were considered to pass through the VPU without being majorly transformed, as the yields of these families increase after the HDO. They may couple but appear to remain in the same category.
C 12), the pyrolysis reactor converted 89% of 50/50 CP/FR wood into volatile and gaseous species that pass into the HDO reactor (Table 1), with the remainder being char. However, not all of the vapors are expected to participate in the catalytic upgrading reactions in the subsequent VPU reactor. Here, light gases (LG), light condensables (LC), and water vapor from pyrolysis were considered to pass through the VPU without being majorly transformed, as the yields of these families increase after the HDO. They may couple but appear to remain in the same category.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, kg/kg
C, kg/kg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, kg/kg
C, kg/kg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 experiments were summed together, and for OX all tracked species were also summed together (Fig. 6). The component groups analyzed by GC × GC were also divided into the same families (LMW PV, OX, HC), (Table 2), and the final yields for each family were calculated. The RGA data provides transient intensities representing these three primary vapor chemical families whose integrals are normalized to equal the yield of each lumped product. The light gases and light condensables were also monitored throughout the experimental runs; the additional light gases formed during VPU were tracked as a separate product family (LG); the additional condensables formed were divided into OX or HC depending on the compound. Thus the data was transformed to represent cumulative yield of products as a function of time based on total LMW PV fed during the experiment for the base case of biomass to catalyst (B
C 12 experiments were summed together, and for OX all tracked species were also summed together (Fig. 6). The component groups analyzed by GC × GC were also divided into the same families (LMW PV, OX, HC), (Table 2), and the final yields for each family were calculated. The RGA data provides transient intensities representing these three primary vapor chemical families whose integrals are normalized to equal the yield of each lumped product. The light gases and light condensables were also monitored throughout the experimental runs; the additional light gases formed during VPU were tracked as a separate product family (LG); the additional condensables formed were divided into OX or HC depending on the compound. Thus the data was transformed to represent cumulative yield of products as a function of time based on total LMW PV fed during the experiment for the base case of biomass to catalyst (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C) ratio of 12 with a 0.5 wt% Pt/TiO2. In addition, the final yield of coke (CK) and additional water formed (WAT) was available. The final yields of each compound family based on the LMW PV from non-catalytic pyrolysis are shown in Fig. 5. The equations for determining the lumped yields are listed in the ESI.†
C) ratio of 12 with a 0.5 wt% Pt/TiO2. In addition, the final yield of coke (CK) and additional water formed (WAT) was available. The final yields of each compound family based on the LMW PV from non-catalytic pyrolysis are shown in Fig. 5. The equations for determining the lumped yields are listed in the ESI.†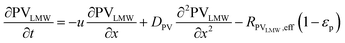
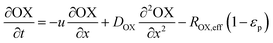
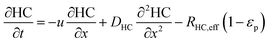
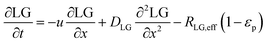
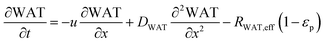
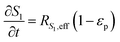
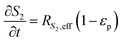
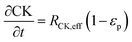
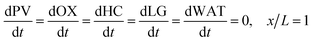
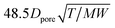
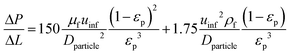
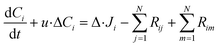
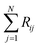 is the sum of reactions consuming i, and
is the sum of reactions consuming i, and 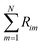 is the sum of reactions forming i, and Ji is the flux of species i. Assuming no advection and using spherical coordinates the equation becomes
is the sum of reactions forming i, and Ji is the flux of species i. Assuming no advection and using spherical coordinates the equation becomes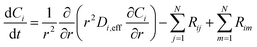
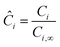
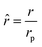
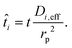

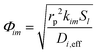
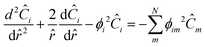
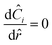
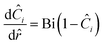
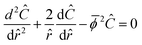
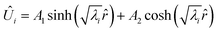
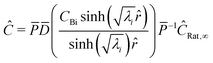
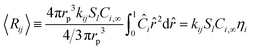
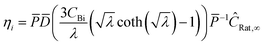
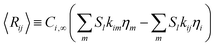
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catalyst ratio of 12. Note that these rate constants are for 450 °C and are independent of the catalyst porosity and particle size. Results from this optimization are shown in Table 4. A comparison of model predictions of lumped yields vs. experimental lumped yields vs. time is shown in Fig. 8, wherein the model and experiment match well and trend towards deactivation together.
catalyst ratio of 12. Note that these rate constants are for 450 °C and are independent of the catalyst porosity and particle size. Results from this optimization are shown in Table 4. A comparison of model predictions of lumped yields vs. experimental lumped yields vs. time is shown in Fig. 8, wherein the model and experiment match well and trend towards deactivation together.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 6 and 21 and an experiment with a catalyst with twice the platinum loading (1%), a different feed (100% clean pine vs. a 50/50 blend of forest residues and pine), and B
C of 6 and 21 and an experiment with a catalyst with twice the platinum loading (1%), a different feed (100% clean pine vs. a 50/50 blend of forest residues and pine), and B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3. Changing the feedstock was accounted for by reviewing product characterization of the raw pyrolysis vapors. Doubling of the active sites was accounted for in the model by doubling S1 and S2 concentrations. In other tested simulations not presented here, doubling of a single catalytic site only resulted in behavior that did not match the experiments. This does not prove there are exactly two sites, but it does hint that that is the general physical phenomenon here.
C 3. Changing the feedstock was accounted for by reviewing product characterization of the raw pyrolysis vapors. Doubling of the active sites was accounted for in the model by doubling S1 and S2 concentrations. In other tested simulations not presented here, doubling of a single catalytic site only resulted in behavior that did not match the experiments. This does not prove there are exactly two sites, but it does hint that that is the general physical phenomenon here.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 the model matches with experiments within the error, as expected. At B
C 12 the model matches with experiments within the error, as expected. At B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 6 and 21, which had no replicates, the model predicts yields with an accuracy of 5% with the largest error being in the most abundant product OX. At a B
C of 6 and 21, which had no replicates, the model predicts yields with an accuracy of 5% with the largest error being in the most abundant product OX. At a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 21, the model predicts lower values for HC, OX and LG, but over predicts CK and PV. This could be because the experiment was done in two cycles. Cycle 1 was run until a B
C of 21, the model predicts lower values for HC, OX and LG, but over predicts CK and PV. This could be because the experiment was done in two cycles. Cycle 1 was run until a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C of 12 and cycle 2 was done the following day from B
C of 12 and cycle 2 was done the following day from B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 to 21. The catalyst was left in N2 flow overnight and was reduced in H2 prior to running cycle 2, which reactivated some active sites. This may explain the discrepancies in the coke yields and shows the need for a thorough examination of coke formation and degradation over these catalysts.
C 12 to 21. The catalyst was left in N2 flow overnight and was reduced in H2 prior to running cycle 2, which reactivated some active sites. This may explain the discrepancies in the coke yields and shows the need for a thorough examination of coke formation and degradation over these catalysts.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 experiment with 50/50 CP/FR matches within the experimental error. More interestingly, the variance between experiment and model is reduced for the 1% Pt B
C 12 experiment with 50/50 CP/FR matches within the experimental error. More interestingly, the variance between experiment and model is reduced for the 1% Pt B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 3 with clean pine. For light gas the model predicts 26% vs. experimental 28%; for water the model predicts 27% vs. experimental 23%; for breakthrough of reactant LMW PV the model predicts 2% vs. experimental 1%; for HC the model predicts 4.4% vs. experimental 4%; for OX the model predicts 13% vs. experimental 14%; and for coke the model predicts 0.4% vs. experimental 2.5%. For such a different experimental condition, these predictions exceeded expectations and show that while there is room for improvement, the existing model has valuable predictive capabilities. One of the limitations of this modeling approach is that the coke formation reaction rates were fit to final yields, not time-resolved yields. This could explain why the coke yields are not as accurate across different operating conditions than the other lumped chemical groups. Future modeling work exploring time-resolved coke yields and axial profiles would greatly improve the validity of this modeling approach. However, in general it is logical that if coke is formed from reactive pyrolysis vapors, then it is likely to accumulate near the entrance where there is a higher concentration of these compounds.
C 3 with clean pine. For light gas the model predicts 26% vs. experimental 28%; for water the model predicts 27% vs. experimental 23%; for breakthrough of reactant LMW PV the model predicts 2% vs. experimental 1%; for HC the model predicts 4.4% vs. experimental 4%; for OX the model predicts 13% vs. experimental 14%; and for coke the model predicts 0.4% vs. experimental 2.5%. For such a different experimental condition, these predictions exceeded expectations and show that while there is room for improvement, the existing model has valuable predictive capabilities. One of the limitations of this modeling approach is that the coke formation reaction rates were fit to final yields, not time-resolved yields. This could explain why the coke yields are not as accurate across different operating conditions than the other lumped chemical groups. Future modeling work exploring time-resolved coke yields and axial profiles would greatly improve the validity of this modeling approach. However, in general it is logical that if coke is formed from reactive pyrolysis vapors, then it is likely to accumulate near the entrance where there is a higher concentration of these compounds.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C 12 with 0.5% Pt on TiO2 when the reactor diameter is less than 3.2 cm with particle sizes up to 5 mm, also shown in Fig. 10. This “sweet spot” would allow for longer operation before regeneration, less catalyst, and /or lower catalyst loading.
C 12 with 0.5% Pt on TiO2 when the reactor diameter is less than 3.2 cm with particle sizes up to 5 mm, also shown in Fig. 10. This “sweet spot” would allow for longer operation before regeneration, less catalyst, and /or lower catalyst loading.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C
C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g
g