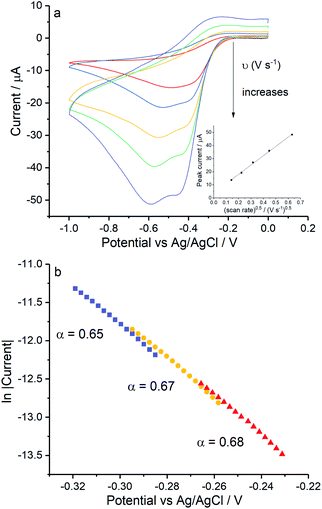
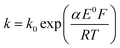Open Access Article
Open Access ArticleThe oxygen reduction reaction at silver electrodes in high chloride media and the implications for silver nanoparticle toxicity†
Yanjun
Guo
,
Minjun
Yang
,
Ruo-Chen
Xie
and
Richard G.
Compton
 *
*
Physical and Theoretical Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, Oxford, OX1 3QZ, UK. E-mail: Richard.Compton@chem.ox.ac.uk
First published on 6th November 2020
Abstract
The oxygen reduction reaction (ORR) at neutral pH in various aqueous chloride-containing solutions was investigated voltammetrically. In particular, the ORR was performed in high chloride containing aqueous media including authentic and synthetic seawater under oxygen saturated conditions and compared with that in aqueous nitrate and perchlorate media. The experimental voltammograms revealed a two-electron process forming hydrogen peroxide in low chloride media. In contrast, high concentration chloride solutions, including both synthetic and authentic seawater showed an increase of overpotential, accompanied by a splitting of the voltammetric peak into two one-electron features indicating the formation of superoxide in the first step and its release from the silver-solution interface. The implications for silver nanoparticle toxicology are discussed given the markedly greater toxicity of superoxide over peroxide and the high levels of chloride in biological media as well as in seawater.
Introduction
Provoked by increasing concern over environmental changes much attention is currently focussed on sustainable energy investigations. One such focus concerns those fuel cells where the Oxygen Reduction Reaction (ORR) has been extensively studied as the cathodic reaction. In general, the ORR can be either a 4-electron transfer process (eqn (1)) or a 2 + 2 electron – double step process involving hydrogen peroxide (H2O2) formation (eqn (2) and (3)).1–5 This production of hydrogen peroxide as an intermediate or product decreases the overall cell efficiency, but precious metals (notably Pt) are required as a catalyst layer to realise the former route, which increases the capital cost of energy devices.2| O2 + 4e− + 4H+ ⇌ 2H2O | (1) |
| O2 + 2e− + 2H+ ⇌ H2O2 | (2) |
| H2O2 + 2e− + 2H+ ⇌ 2H2O | (3) |
Accordingly attention has been turned to alternative materials, among which silver is considered a potential catalyst for anion exchange membrane fuel cells.6 The replacement of Pt catalysts usually requires alkaline conditions to achieve lower overpotentials for the O2/O2−˙ redox couple.7–9 In the low pH region, the reaction on silver involves both 2e− and 4e− pathways with less H2O2 generated as the overpotential increases. In alkaline solution, however, the overpotential drops significantly and reaction follows a 4e− pathway predominately.10–12 The first electron transfer to oxygen regardless of pH is recognized as the rate determining step (RDS).13,14
It is clearly evidenced that H2O2 formation is involved in the ORR on Ag in neutral solution and the pathways at least in part follow, proposed by Neumann et al.,15 though the mechanism is sensitive to the surface oxidation state and morphology as well as the electrode potential.16 In particular, as a common oxygen reduction catalyst, the ORR on silver may involve catalytic decomposition of H2O2 alongside or as an alternative to the rapid electroreduction of peroxide to water (eqn (4)–(8)).17
| O2 + e− ⇌ O2−˙ (RDS) | (4) |
| O2−˙ + H2O + e− ⇌ HO2− + OH− | (5) |
| HO2− + H2O ⇌ H2O2 + OH− | (6) |
The formation of hydrogen peroxide is followed by catalytic decomposition
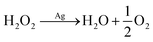 | (7) |
| H2O2 + 2H+ + 2e− → 2H2O | (8) |
Note that eqn (5) might occur directly as written or as a CE (homogeneous chemical reaction followed by an electron transfer step) sequence in which superoxide first reacts with water to form ˙OOH and OH− followed by reduction of ˙OOH.
The European consumption of AgNPs reached 35 tons per year in 2014 with global demand steadily increasing towards an estimated value of 600 tons per year in 2020.18 The main applications of AgNPs exploit their antiviral, antimicrobial and anti-inflammatory properties19–24 but the extensive scale of use has driven concerns on its toxicity to the natural environment given the likely release of large quantities of silver nanoparticles into the environment. At the nanoscale, the ORR on silver is especially interesting in so far that it concerns the nanotoxicology of silver nanoparticles (AgNPs). This in turn has led to mechanistic studies of nanoparticle dissolution and antibacterial behaviour.25
AgNPs kill bacteria via damaging membrane structures and intracellular biomolecules by possible mechanisms including AgNPs attachment to the membrane, catalytic formation of reactive oxygen species (ROS) and silver ion dissolution.26–28 All of those are sensitive to the local chemical environment. The oxidative dissolution of AgNPs in aqueous solution can be favoured by the presence of Cl−, I− and phosphate anions29 although the release of Ag+ can however simultaneously be inhibited by trace amounts of chloride due to formation of AgCl layers at the nanoparticle surface.30 The combined anion effects influencing both thermodynamics and kinetics hint at the complexity of silver nanotoxicology in natural media where, for example, it is observed that AgNPs are relative stable with less Ag+ dissolution and ROS formed in environments such as authentic human saliva.31
Does size matter? It is generally believed that AgNPs have higher antibacterial activity32 compared to bulk silver – which is thought not toxic at all. One explanation of the size dependence of the toxicity of silver is in terms of the change of ORR pathways resulting from competition between the particle-size-controlled mass transport and the heterogeneous decomposition rate. Batchelor-McAuley et al.33 proposed a mechanism for the size dependency based on the insight that the dissolution of Ag as Ag+ cations is coupled with the reduction of oxygen at the surface of the dissolving nanoparticle. As noted above in (eqn (4)–(8)), the ORR on Ag proceeds via the formation of hydrogen peroxide followed by the further heterogeneous chemical decomposition of this intermediate to form water. By comparing the rate of the hydrogen peroxide transformation into water with the rate of its diffusion away from the particle it was concluded that a switchover in products occurred when the two rates matched. Note that the size dependence arises since the mass transport coefficient (kMT) for the loss of hydrogen peroxide is given by D/r where D is the diffusion coefficient of H2O2 and r is the particle radius. Thus, hydrogen peroxide ‘escapes’ more easily from smaller particles than from larger ones (eqn (9)–(11)).
| O2 + 2e− + 2H+ → H2O2 | (9) |
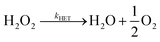 | (10) |
 | (11) |
Cyclic voltammetry data for the ORR on silver provided the relevant heterogeneous rate constant (kHET = 0.013 cm s−1 at 25 °C) for the formation of water. This allowed estimation of the particle radius, r, for the switch over from hydrogen peroxide formation to water formation to be in the region of ca. 10 microns consistent with independent observations.15,33,34
The analysis leading to eqn (9)–(11) proposed by Batchelor-McAuley et al. assumes that the products of the ORR on silver are either water or hydrogen peroxide. From a toxicity point of view, it is to note that, H2O2 is less reactive compared to other ROS in the absence of light or trace metal ions such as iron and copper (eqn (12) and (13)).35
| FeII + H2O2 → FeIII + ˙OH + OH− | (12) |
| CuI + H2O2 → CuII + ˙OH + OH− | (13) |
In contrast the superoxide radical ion. O2−˙, although not as reactive as its protonated form, ˙OOH (pKa = 4.8), is highly toxic at physiological pH; the reaction of O2−˙ with H2O2 and reactions with nitric oxide radical (eqn (14)–(16)) can lead to formation of a short-lived and highly aggressive ROS, hydroxyl radicals ˙OH.36–38 The ˙OH radical, with a reduction potential reported at 2.31 V,39 is a strongly oxidizing reagent and can kill a diverse range of single-cellular phytoplankton at a near-mass-transport limited rate.40
| ˙ON + O2−˙ → ONOO− | (14) |
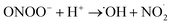 | (15) |
| H2O2 + O2−˙ → O2 + ˙OH + OH− | (16) |
Moreover, superoxide O2−˙ and hydroxyl radicals ˙OH react with most biomolecules in its path including lipids, proteins, and DNA. In reactions with saturated compounds, hydroxy radicals ˙OH can abstract hydrogen atoms from carbon–hydrogen bonds forming a stronger OH bond and radical propagation (eqn (17) and (18)).35–37,41 An example is the lipid peroxidation, the product of which is harmful to membrane-associated proteins,42 causing damage to cell structures and their functionality until the reaction terminates.43
| RH + ˙OH → R˙ + H2O | (17) |
| RC(O)H + ˙OH → RC(O)˙ + H2O | (18) |
Given the enhanced reactivity of O2−˙ and ˙OH as compared to hydrogen peroxide H2O2, it is interesting to focus further on the nature of the chemistry involved in the ORR at silver since this lies at the heart of Ag nanoparticle toxicology. In particular the issue of whether the process leads to H2O2 or O2−˙ (protonated or otherwise) may have toxicological implications. In this paper we generate a fundamental understanding of the ORR in chloride containing media including seawater to explore the possible fate of silver nanoparticles in those media. We recognise also that biological systems contain high levels of chloride, for example saliva (10 to 43 mM)44 and blood (96 to 106 mM),45 and focus on the likely associated chemistry.
Thus, this paper aims to explore ORR in aqueous chloride media including seawater on bulk silver electrodes, compare it with other aqueous salt solutions and assess any implications for the nanotoxicology of silver nanoparticles. To our knowledge, it is the first paper of the ORR mechanism study on silver in seawater. Furthermore, the change of mechanism and of overall chemistry revealed below has implications for the effects of the silver in biological media which typically contain high chloride levels as well as in seawater.
Results and discussion
We explore the ORR at both glassy carbon and silver electrodes considering aqueous electrolyte ranging from chloride free to high chloride media such as seawater. The presence of chloride is shown to profoundly alter the mechanism of the reaction at silver electrodes with the formation of superoxide rather than hydrogen peroxide. The implications for nano-toxicology are assessed in the light of the inferred changed chemistry.O2 reduction on glassy carbon electrodes
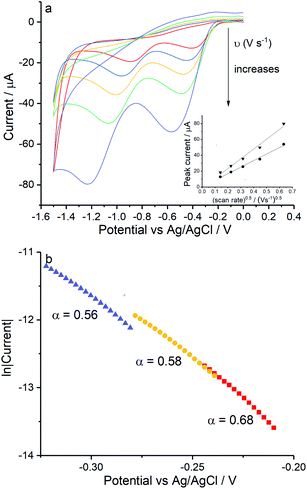
Reduction of oxygen saturated solution (CO2 = 1.26 mM)46 was performed on a glassy carbon macroelectrode in a simple synthetic seawater. The composition of the latter is given in Table S1 in ESI Section 2† along with the composition of authentic seawater47,48 from which it can be seen that the solution studied contained the major components of seawater but that minor components were excluded. Voltammograms were recorded for scan rates varying from 0.02 V s−1 to 0.4 V s−1 (Fig. 1) and revealed broad irreversible reduction peaks at −0.5 V and −1.0 V at 0.05 V s−1 measured relative to a Ag/AgCl ([Cl−] = 3.5 M) reference electrode indicating the probable formation of hydrogen peroxide and water respectively in the two voltammetric features. This first voltammetric wave in seawater solution is consistent with the fully electrochemically irreversible Randles–Ševčík equation, assuming that the first electron transfer is rate determining, where the variation of the peak current (Ip) with the square root of the scan rate (v) is:| Ip = 2.99 × 105neffα1/2ADO21/2CO2v1/2 | (19) |
The diffusion coefficients of oxygen in various aqueous media are given in Table S2 (ESI Section 2†). The values vary widely discouraging further quantitative analysis including the separation of the number of electrons transferred and the diffusion coefficient. Moreover and in particular, comparison of experiment with the literature on the basis of GC electrodes is challenging due to the complexity of the pH dependency and the surface sensitivity of ORR pathways on glassy carbon electrode. The influence of carbon centres at the electrode surface on mechanism and its pH responses has been reported by Zhang et al.,49 which not only presents the vital importance of the amount and oxidative condition of adsorption sites but also the possibility of parallel mechanisms under different pH conditions. In particular for synthetic seawater during the reduction process, hydroxide ions are generated near the electrode and since no buffer is present the local pH can be markedly changed which likely alters the mechanism as a function of both potential and possibly scan rate. Thus, quantitative analysis based on the simple Randles–Ševčík equation and associated Tafel analysis is potentially misleading. In the following section we consider silver electrodes where surface adsorption of reactive oxygen species is less likely.
O2 reduction on silver electrodes
The study of the ORR in seawater at silver electrodes mixes a potentially complex electrochemical mechanism, as discussed above, with a medium containing many different chemical species as is evident from Table S1.† The first step towards examining the reaction in seawater is to simplify the problem by analysing signals in electrolytes such as alkali metal nitrate and perchlorate solutions as is discussed in the following section.O2 reduction on Ag electrodes in 0.1 M KNO3 and 0.1 M NaClO4
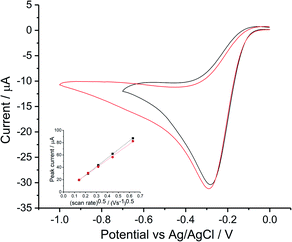
Reductive voltammetry studies in oxygen saturated 0.1 M KNO3 and 0.1 M NaClO4 were performed on a silver macroelectrode with varying scan rates from 0.02 V s−1 to 0.4 V s−1 (Fig. S2, ESI Section 3†). Voltammograms for 0.5 V s−1 are plotted in Fig. 2.Consistency was found between the irreversible (voltammetrically and chemically)50 peak for perchlorate and for nitrate; both achieved a maximum current at −0.3 V vs. Ag/AgCl([Cl−] = 3.5 M). Transfer coefficients were evaluated as 0.75 ± 0.03 and 0.69 ± 0.04 in KNO3 and NaClO4 respectively. The dependence of the peak current on scan rate followed the irreversible form of Randles–Ševčík equation (Fig. 2 inlay). Analysis using the diffusion coefficient of 1.96 × 10−9 m2 s−1 (ref. 15) and oxygen solubility (CO2 = 1.26 mM) whilst noting the wide range of values in Tables S2 and S4 (ESI Section 2†) suggests a likely 2e− transfer for the first reductive peak.
The results are consistent with a proposed mechanism with a rate determining step producing superoxide followed by its fast reaction with water (eqn (4) and (5)) with a further electron transfer. Interestingly, whilst the use of pure oxygen to saturate the solution leads us to infer the operation of a two electron process we note that in air saturated solutions, containing roughly one fifth the level of dissolved oxygen, a larger number of electrons, neff = 3.3,15 is observed. A heterogeneous disproportionation of hydrogen peroxide leads to some water formation.15 The difference may reflect different levels of proton release or a change in the silver surface the morphology of which is likely to markedly influence the heterogeneous disproportionation.
On the basis of the investigations obtained from simple electrolyte solutions, explorations of the ORR in authentic and synthetic seawater were next carried out.
O2 reduction in seawater
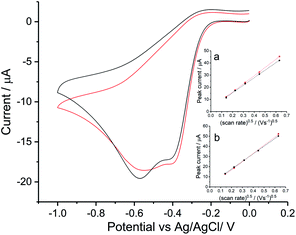
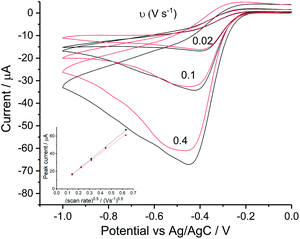
To investigate the ORR mechanism in seawater, reduction of oxygen on a silver macro-disc electrode was carried out in standard synthetic seawater and filtered authentic seawater from Scotland (see Table S1† for chemical compositions) with varying scan rates from 0.02 V s−1 to 0.4 V s−1 (Fig. S3 in ESI Section 4†). Voltammograms for 0.05 V s−1 are plotted in Fig. 3. The synthetic seawater suitably mimics the authentic seawater sample. However, in comparison with the reduction wave observed in nitrate and perchlorate solutions, both voltammetric signals here are shifted to a higher overpotential by ca. 0.1 V and most interestingly split into separated peaks at −0.4 V and −0.6 V vs. Ag/AgCl([Cl−] = 3.5 M).Tafel analysis of the initial part of the voltammetric waves gave transfer coefficients of 0.71 ± 0.05 in authentic seawater and 0.68 ± 0.01 in synthetic seawater. This is in excellent agreement with Neumann et al.15 who found that α = 0.7 in 0.1 M NaClO4. Comparison of the magnitudes of the peak currents for oxygen saturated solutions between Fig. 2 and 3 suggests that the two-electron feature seen for the simple nitrate and perchlorate electrolytes has split into two partly overlapping one electron features in addition to being shifted to higher overpotential. The first peak, necessarily approximately given the overlapping with the second peak, was analysed using the Randles–Sevcik equation. Using the above estimates of DO2 = 1.96 × 10−9 m2 s−1 (ref. 15) and CO2 = 1.26 mM together with the transfer coefficient values above a single electron transfer process at −0.4 V in seawater was inferred. Similarly, values of neff = 1.05 ± 0.07 (authentic seawater) and neff = 1.05 ± 0.04 (synthetic seawater) for the second reduction reaction were inferred. Thus the two electron voltammetric wave seen for nitrate and perchlorate electrolytes splits into two waves in seawater and seawater-like media with the formation of superoxide inferred as the product of the first wave.
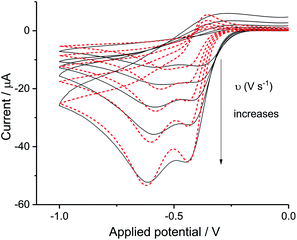
Digisim modelling of the voltammetry in synthetic seawater
The split peak seen for seawater was next fitted with the commercial simulation software DigiSim51 to confirm the inferences of the last paragraph. Experimental cyclic voltammograms as presented in Fig. 4 for synthetic seawater were modelled using the mechanism in eqn (4) and (5).The transfer coefficient and standard electrochemical rate constant data reported in Table 1 correspond to the best-fit approximation of the cyclic voltammograms obtained over the full scan rate range in Fig. 4 using these parameters to fit each voltammogram. Notice that the second reduction process is irreversible and modelled within the Butler–Volmer formalism the current response is described by a combined parameter 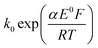 52,53 where k0 and E0 are the electrochemical constant and formal potential for each reduction step.
52,53 where k0 and E0 are the electrochemical constant and formal potential for each reduction step.
A satisfactory fit of experimental (solid line) and simulated (dot line) is obtained with standard electron transfer rate constants k0 of 1.0 cm s−1 and 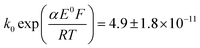 cm s−1 for the 1st and 2nd peak respectively. The significant error in the latter value was from simulation of voltammogram at 0.02 V s−1. In particular for the first wave, the high rate constant gave an apparent electrochemically quasi-reversible behaviour so that the value of 0.5 in Table 1 simply reflects the modelling of the voltammetry rather than being a measurement of the Tafel coefficient. Herein, the precise value of transfer coefficient used is less important since in the limit of full reversibility the apparent transfer coefficient tends to unity.54 The combination of a high k0 and the assumed transfer coefficient gives a qualitatively good fit and the peak potential was well described by the set formal potential i.e. −0.4 V vs. Ag/AgCl, especially during fast scan rates. A consistent value of E0(O2/O2−˙) = −0.395 V vs. Ag/AgCl was reported by Baxendale et al.,55 similarly, E0(O2/O2−˙) = −0.385 ± 0.02 V vs. Ag/AgCl was determined for neutral solutions by Hoppenol et al.56 Noticeably, the value of E0(O2/O2−˙) applied here is pH independent, and the follow up chemistry results in proton consumption.
cm s−1 for the 1st and 2nd peak respectively. The significant error in the latter value was from simulation of voltammogram at 0.02 V s−1. In particular for the first wave, the high rate constant gave an apparent electrochemically quasi-reversible behaviour so that the value of 0.5 in Table 1 simply reflects the modelling of the voltammetry rather than being a measurement of the Tafel coefficient. Herein, the precise value of transfer coefficient used is less important since in the limit of full reversibility the apparent transfer coefficient tends to unity.54 The combination of a high k0 and the assumed transfer coefficient gives a qualitatively good fit and the peak potential was well described by the set formal potential i.e. −0.4 V vs. Ag/AgCl, especially during fast scan rates. A consistent value of E0(O2/O2−˙) = −0.395 V vs. Ag/AgCl was reported by Baxendale et al.,55 similarly, E0(O2/O2−˙) = −0.385 ± 0.02 V vs. Ag/AgCl was determined for neutral solutions by Hoppenol et al.56 Noticeably, the value of E0(O2/O2−˙) applied here is pH independent, and the follow up chemistry results in proton consumption.
Overall the voltammetry is consistent with the interpretation, as suggested in the previous section, of two partly overlapping diffusional voltammetric peaks corresponding first to the formation of superoxide and second to peroxide. The possible chemical cause for the split is considered in the next section which focusses on the role of the chloride ions present in seawater.
The Cl− concentration effect on the ORR at Ag electrodes
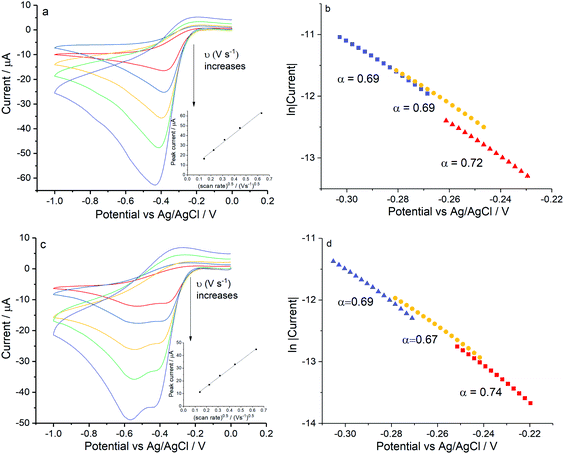
In the light of the differences between the data shown in Fig. 2 and 3 in which the solution composition varied from chloride free to chloride rich, the reduction of oxygen on a silver macro-disc electrode was carried out first in aqueous potassium chloride solutions of 0.1 M and 0.42 M. Second the solution containing 0.42 M NaCl and 9.39 mM KCl was studied and third a solution containing 0.42 M NaCl, 9.39 mM KCl and 54.6 mM MgCl2. The latter corresponds to the levels of chloride, sodium, magnesium and potassium in seawater. Finally, oxygen reduction was conducted in 0.54 M KCl solution corresponding to the total chloride level seen in seawater so as to clarify the role of chloride in the absence of Mg2+.Voltammograms in KCl solutions were recorded with varying scan rates from 0.02 V s−1 to 0.4 V s−1 as plotted in Fig. 5. Where in both solutions, despite the different chloride concentrations the reductive currents were essentially the same although there is a broadening of the peak at the higher chloride concentrations. Tafel analysis gives almost identical transfer coefficients of the two concentration as listed in Table 2. Using the values of CO2 = 1.26 mM and DO2 = 1.96 × 10−9 m2 s−1 (assuming these are salinity independent in this modelling), the effective number of electrons transferred in 0.42 M KCl is noticeably smaller (1.33 ± 0.15) as compared to 1.47 ± 0.02 in 0.1 M KCl. Apart from decrease in electrons transferred, the peak shifted to higher overpotential in 0.1 M KCl (−0.42 ± 0.02 V) and 0.42 M KCl (−0.44 ± 0.03 V) as compared to the value of −0.30 ± 0.05 V as observed in 0.1 M KNO3 and −0.29 ± 0.02 V in 0.1 M NaClO4. Consequently, the clear split of the voltammetric peak seen in seawater was inferred to relate to additional species present in the latter in addition to 0.42 M NaCl. Hence seawater level concentrations of KCl and MgCl2 were added stepwise into 0.42 M NaCl solution.
| Solution composition | [Cl−]/M | α | n eff | Number of peaks |
|---|---|---|---|---|
| 0.1 M KNO3 | 0.00 | 0.75 ± 0.03 | 1.64 ± 0.03 | 1 |
| 0.1 M NaClO4 | 0.00 | 0.69 ± 0.04 | 1.65 ± 0.02 | 1 |
| 0.1 M KCl | 0.10 | 0.65 ± 0.02 | 1.47 ± 0.02 | 1 |
| 0.42 M KCl | 0.42 | 0.66 ± 0.05 | 1.33 ± 0.15 | 1 |
| 0.42 M NaCl, 9.39 mM KCl, 54.6 mM MgCl2 | 0.54 | 0.70 ± 0.04 | 0.93 ± 0.04 | 2 |
| 0.54 M KCl | 0.54 | 0.67 ± 0.02 | 1.07 ± 0.10 | 2 |
Firstly, experiments were conducted in solution consisting 0.42 M NaCl and 9.39 mM KCl (Fig. 6a) and then with addition of 54.6 mM MgCl2 (Fig. 6c) under the same scan rate range as above. As can be seen, a single reductive peak was recorded for all scan rates in the first solution whereas the further addition of magnesium chloride caused the splitting into two peaks. Given that the transfer coefficient is almost a constant in both cases (Fig. 6b and d), the only change observed in the voltammetric response was the decrease in effective number of electrons transferred at the potential of the first peak, neff at −0.4 V (from 1.35 ± 0.13 to 0.93 ± 0.04).
Table 2 summarises the above described ORR results on silver and correlates the progressive increase in the chloride concentration with a decrease in the effective number of electrons transferred. Note that the transfer coefficient remains approximately constant throughout and suggestive of the quasi-reversible formation of superoxide. The apparent number of electrons transferred drops steadily with increased chloride concentration again signalling the developing formation of the superoxide ion ultimately in a distinct one electron wave. Overall, data in Table 2 is consistent with a quasi-reversible formation of superoxide (reaction (4)) prior to the slowing of the reaction (5) followed up until the extent that in seawater two peaks appear. Interestingly the voltammetric waves seen in nitrate and perchlorate media are seen at less negative potentials than in chloride media. This suggests that the following chemical step occurs very rapidly under these conditions and the voltammetric reduction wave is shifted to less negative potentials.52,53
Lastly, control experiments in chloride concentrations equivalent to Fig. 6d (ca. 0.54 M KCl) were conducted in Fig. 7 to clarify if the peak splitting is due to the increased chloride level or to the presence of Mg(II). Importantly, the splitting of the reduction wave and the potential of the first electron transferred in pure KCl solution are in line with that in the mixed solution (Fig. 6d). The transfer coefficient is comparable in 0.54 M KCl solution (0.67 ± 0.02) to that in the magnesium containing solution (0.70 ± 0.04), and the effective number of electrons transferred has a value of 1.07 ± 0.10 at −0.4 V. Moreover, possible effects from high ionic strength were excluded by performing the reduction of oxygen in 0.54 M KNO3 at 0.02 V s−1 and 0.4 V s−1 where only a single two electron wave was seen at a silver electrode (data not shown).Overall these experiments confirms that the presence of two peaks on silver is due to the chloride rich conditions rather than the presence of magnesium cations.
Physicochemical origins of the peak splitting
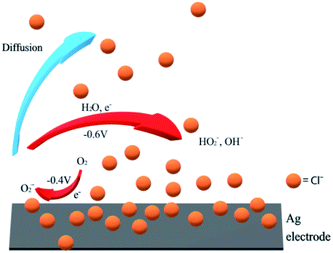
The peak splitting requires the presence of very high concentrations of chloride for silver electrodes. We note that chloride adsorption on silver has been widely reported.57–60 The chloride can form adlayers on the silver electrode surface and significantly increase the double layer capacitance.58 Hence it is not surprising to find voltammetric signals at silver electrodes affected in concentrated chloride solutions like seawater (ca. 0.54 M Cl−). However, but since capacitive effects are apparent even at low concentrations of 1 mM, the simplest explanation of the effect is a slower follow up reaction57–60 and the escape of the superoxide from the interface. The superoxide is formed at electrode potentials immediately negative of the thermodynamic reduction potential consistent with the quasi-reversible character of the observed voltammetry of the first peak in the split wave. The new peak at ca. −0.6 V in cyclic voltammetry reflects the change of the electrode mechanism. We suggest that eqn (5) involves first a chemical step in which superoxide reacts with water to form hydroxide and ˙OOH radicals followed by electron transfer to ˙OOH. If this chemical step is slowed at the chloride rich interface then this is consistent with the observation of electrochemically reversible superoxide formation. It is also consistent with the development of an overpotential as compared to chloride free media (since the follow up reactions which shift the reversible oxygen/superoxide wave to less negative potentials occur more slowly with high chloride concentrations). Finally the absence of ˙OOH (and OH− (ref. 61)) in the vicinity of the electrode prevents the second step leading to hydrogen peroxide. Rather a different route to the formation of the latter occurs, at a more negative potential possibly as given in eqn (22) and Fig. 8.| O2 + e− ⇌ O2−˙ (−0.4 V) | (20) |
| O2−˙ → bulk (diffusion) | (21) |
| O2−˙ + H2O + e− ⇌ HO2− + OH− (−0.6 V) | (22) |
Implications for silver nanoparticle toxicology
The above experiments show that the reduction of oxygen on silver results in most electrolyte solutions in an overall two electron process leading to the formation of hydrogen peroxide. However in seawater which contains high levels of chloride the formation of superoxide ions has been evidenced. This in turn suggests the likely formation of superoxide in seawater when Ag nanoparticles dissolve. We note that a previous study confirmed that the high concentration of chloride not only promotes dissolution of AgNPs by forming AgClx(1−x) (ref. 33) but also correlates to higher nanoparticle toxicity consistent with superoxide formation rather than generation of the less toxic hydrogen peroxide. In addition, the dissolution of AgNPs under UV irradiation confirmed higher bacteria death rates in 0.5 M chloride solution as compared to solution containing less chloride.62 Despite fast aggregation of particles reported under high chloride concentration, the higher oxidative stress observed by Li et al. is thus possibly attributed to the increased production of superoxide, the major precursor of rest ROS. Overall, silver nanoparticles in the presence of concentrate chloride may likely be more toxic, in consistent with above-discussed experiments in seawater, though interpretations should be of course, made very carefully when considering nanotoxicology in real cases.Conclusions
The mechanistic study of oxygen reduction reaction in neutral chloride solution in particular seawater was conducted on a silver macrodisc electrode via cyclic voltammetry. Compared to alkaline metal nitrate solution, the reduction in seawater is shifted to higher overpotential and split into 2 steps. Simulation results from Digisim suggest the mechanism in seawater involves quasi reversible formation of the superoxide ion. Depending on the concentration of chloride present, further reduction of superoxide was slowed at least locally to the extent that superoxide escapes from the interface before it can react further on the voltammetric timescale, thus, ultimately for chloride levels above 0.5 M two peaks emerge signalling the formation of superoxide. Unlike ORR in nitrate or perchlorate solutions, the proposed mechanism implies superoxide formation in seawater, and indicates the likelihood of enhanced nanotoxicology of AgNPs in marine and in biological systems, which are typically of high chloride concentration.Experimental
Chemical reagents
All chemicals were used as received from Sigma Aldrich unless stated otherwise. Filtered Scottish seawater was purchased from SAMS (Scottish Marine Institute, Argyll, UK). Solutions were degassed with nitrogen gas (N2, 99.998%, BOC Gases plc, Guildford, UK) or oxygen gas (O2, BOC Gases plc, Guildford, UK) for 15 min prior to each voltammetric experiment. The gas flow during degassing is sufficiently fast such that the voltammetric features corresponding to a saturated level of N2 or O2 is consistently observed or each experiment. All the solutions were prepared using deionised water with a resistivity of 18.2 MΩ cm at 25 °C (Millipore).Electrochemical analysis
All electrochemical measurements were performed in a conventional three-electrode cell consisting of a platinum wire counter electrode, a Ag/AgCl reference electrode (in 3.5 M KCl solution) and a working electrode (WE). A glassy carbon macro-electrode (GC, radius 1.49 mm, BAS, Technical, UK) and a silver macro-disc electrode (Ag, homemade, radius 1.36 mm) calibrated as described in ESI (Fig. S1, ESI Section 1†) were used as working electrodes. Both electrodes were polished using a sequence of 1.0, 0.3 and 0.05 micron alumina lapping compounds (Bucher, Germany). Measurements were performed using a μAutolab II potentiostat (Metrohm-Autolab BV, Utrecht, Netherlands) under 25 °C. A constant temperature of 25 ± 0.5 °C was maintained by a thermostated water bath.Oxygen reduction reaction on macro-electrodes
Cyclic voltammetry at various scan rates was performed to measure the kinetics of oxygen reduction on a macro glassy carbon and a macro silver WE. The experiments were conducted in the following freshly prepared solutions; oxygen saturated 0.1 M sodium perchlorate, 0.1 M potassium nitrate, 0.1 M and 0.42 M potassium chloride, simple synthetic seawater solution (0.42 M sodium chloride, 9.39 mM potassium chloride and 54.6 mM magnesium chloride) and synthetic seawater prepared using a standard recipe in literature.47,48 The analysed potential range was 0 V to −0.7 V for the potassium nitrate solution and 0 to −1.0 V for other solutions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. Y. acknowledges funding via an EPSRC Industrial CASE award (EP/N509711/1).References
- C. Hu and L. Dai, Angew. Chem., Int. Ed. Engl., 2016, 55, 11736–11758 CrossRef CAS.
- Y. Nie, L. Li and Z. Wei, Chem. Soc. Rev., 2015, 44, 2168–2201 RSC.
- M. Shao, Q. Chang, J. P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116, 3594–3657 CrossRef CAS.
- L. Dai, Y. Xue, L. Qu, H. J. Choi and J. B. Baek, Chem. Rev., 2015, 115, 4823–4892 CrossRef CAS.
- X. Ge, A. Sumboja, D. Wuu, T. An, B. Li, F. W. T. Goh, T. S. A. Hor, Y. Zong and Z. Liu, ACS Catal., 2015, 5, 4643–4667 CrossRef CAS.
- H. Erikson, A. Sarapuu and K. Tammeveski, ChemElectroChem, 2019, 6, 73–86 CrossRef CAS.
- M. Chatenet, L. Genies-Bultel, M. Aurousseau, R. Durand and F. Andolfatto, J. Appl. Electrochem., 2002, 32, 1131–1140 CrossRef CAS.
- B. B. Blizanac, P. N. Ross and N. M. Marković, J. Phys. Chem. B, 2006, 110, 4735–4741 CrossRef CAS.
- N. Ramaswamy and S. Mukerjee, Adv. Phys. Chem., 2012, 2012, 491604 Search PubMed.
- J. M. Linge, H. Erikson, A. Kasikov, M. Rähn, V. Sammelselg and K. Tammeveski, Electrochim. Acta, 2019, 325, 134922 CrossRef CAS.
- L. Tammeveski, H. Erikson, A. Sarapuu, J. Kozlova, P. Ritslaid, V. Sammelselg and K. Tammeveski, Electrochem. Commun., 2012, 20, 15–18 CrossRef CAS.
- A. Treshchalov, H. Erikson, L. Puust, S. Tsarenko, R. Saar, A. Vanetsev, K. Tammeveski and I. Sildos, J. Colloid Interface Sci., 2017, 491, 358–366 CrossRef CAS.
- D. Sepa, M. Vojnovic and A. Damjanovic, Electrochim. Acta, 1970, 15, 1355–1366 CrossRef CAS.
- A. Qaseem, F. Y. Chen, X. Q. Wu and R. L. Johnston, Catal. Sci. Technol., 2016, 6, 3317–3340 RSC.
- C. C. M. Neumann, E. Laborda, K. Tschulik, K. R. Ward and R. G. Compton, Nano Res., 2013, 6, 511–524 CrossRef CAS.
- N. A. Shumilova, G. V. Zhutaeva and M. P. Tarasevich, Electrochim. Acta, 1966, 11, 967–974 CrossRef CAS.
- P. K. Adanuvor, J. Electrochem. Soc., 1988, 135, 2509–2517 CrossRef CAS.
- J. Pulit-Prociak and M. Banach, Open Chem., 2016, 14, 76–91 CAS.
- S. M. Dizaj, F. Lotfipour, M. Barzegar-Jalali, M. H. Zarrintan and K. Adibkia, Mater. Sci. Eng., C, 2014, 44, 278–284 CrossRef CAS.
- G. Franci, A. Falanga, S. Galdiero, L. Palomba, M. Rai, G. Morelli and M. Galdiero, Molecules, 2015, 20, 8856–8874 CrossRef CAS.
- A. J. Huh and Y. J. Kwon, J. Controlled Release, 2011, 156, 128–145 CrossRef CAS.
- H. H. Lara, E. N. Garza-Treviño, L. Ixtepan-Turrent and D. K. Singh, J. Nanobiotechnol., 2011, 9, 30 CrossRef CAS.
- R. Vazquez-Muñoz, B. Borrego, K. Juárez-Moreno, M. García-García, J. D. Mota Morales, N. Bogdanchikova and A. Huerta-Saquero, Toxicol. Lett., 2017, 276, 11–20 CrossRef.
- P. L. Nadworny, J. Wang, E. E. Tredget and R. E. Burrell, J. Inflammation, 2010, 7, 13 CrossRef.
- P. A. Holden, J. P. Schimel and H. A. Godwin, Curr. Opin. Biotechnol., 2014, 27, 73–78 CrossRef CAS.
- S. Tang and J. Zheng, Adv. Healthcare Mater., 2018, 7, 1701503 CrossRef.
- N. Beyth, Y. Houri-Haddad, A. Domb, W. Khan and R. Hazan, J. Evidence-Based Complementary Altern. Med., 2015, 2015, 246012 Search PubMed.
- C. Marambio-Jones and E. M. V. Hoek, J. Nanopart. Res., 2010, 12, 1531–1551 CrossRef CAS.
- D. V. Navolotskaya, H. S. Toh, C. Batchelor-McAuley and R. G. Compton, Chemistryopen, 2015, 4, 595–599 CrossRef CAS.
- B. J. Plowman, K. Tschulik, E. Walport, N. P. Young and R. G. Compton, Nanoscale, 2015, 7, 12361–12364 RSC.
- K. Ngamchuea, C. Batchelor-McAuley and R. G. Compton, Nanotoxicology, 2018, 12, 305–311 CrossRef CAS.
- Y. N. Slavin, J. Asnis, U. O. Häfeli and H. Bach, J. Nanobiotechnol., 2017, 15, 65 CrossRef.
- C. Batchelor-McAuley, K. Tschulik, C. Neumann, E. Laborda and R. G. Compton, Int. J. Electrochem. Sci., 2014, 9, 1132 Search PubMed.
- F. W. Campbell, S. R. Belding, R. Baron, L. Xiao and R. G. Compton, J. Phys. Chem. C, 2009, 113, 9053–9062 CrossRef CAS.
- J. Lee, N. Koo and D. B. Min, Compr. Rev. Food Sci. Food Saf., 2004, 3, 21–33 CrossRef CAS.
- R. A. Larson and J. M. McCord, Crit. Rev. Environ. Sci. Technol., 1978, 8, 197–246 CAS.
- A. M. Pisoschi and A. Pop, Eur. J. Med. Chem., 2015, 97, 55–74 CrossRef CAS.
- H. J. Forman and N. Haugaard, Trends Biochem. Sci., 1982, 7, 279 CrossRef CAS.
- M. B. Koryckadahl and T. Richardson, CRC Crit. Rev. Food Sci. Nutr., 1978, 10, 209–241 CrossRef CAS.
- M. Yang, C. Batchelor-McAuley, L. Chen, Y. Guo, Q. Zhang, R. E. M. Rickaby, H. A. Bouman and R. G. Compton, Chem. Sci., 2019, 10, 7988–7993 RSC.
- G. Buonocore, S. Perrone and M. L. Tataranno, Semin. Fetal Neonatal Med., 2010, 15, 186–190 CrossRef.
- J. C. M. Riley and H. R. Behrman, Proc. Soc. Exp. Biol. Med., 1991, 198, 781–791 CrossRef CAS.
- B. Kalyanaraman, Redox Biol., 2013, 1, 244–257 CrossRef CAS.
- J. H. Thaysen, N. A. Thorn and I. L. Schwartz, Am. J. Physiol., 1954, 178, 155–159 CrossRef CAS.
- H. K. Walker, W. D. Hall and J. W. Hurst, in Clinical Methods: The History, Physical, and Laboratory Examinations, ed.H. K. Walker, W. D. Hall and J. W. Hurst, Butterworths, Boston, 3rd edn, 1990, ch. 197 Search PubMed.
- K. Shimizu, L. Sepunaru and R. G. Compton, Chem. Sci., 2016, 7, 3364–3369 RSC.
- F. M. M. Morel, J. G. Rueter, D. M. Anderson and R. R. L. Guillard, J. Phycol., 2008, 15, 135–141 CrossRef.
- N. M. Price, G. I. Harrison, J. G. Hering, R. J. Hudson, P. M. V. Nirel, B. Palenik and F. M. M. Morel, Biol. Oceanogr., 1989, 6, 443–461 Search PubMed.
- H. Zhang, C. Lin, L. Sepunaru, C. Batchelor-McAuley and R. G. Compton, J. Electroanal. Chem., 2017, 799, 53–60 CrossRef CAS.
- J. M. Savéant and C. Costentin, in Elements of Molecular and Biomolecular Electrochemistry, 2019, vol. 285–381, 383–437, pp. 81–181, DOI:10.1002/9781119292364.ch2.
- DigiSim (Professional version 3.0b), Bioanalytical Systems, Inc., West Lafayette, 2013 Search PubMed.
- A. J. Bard, Electrochemical methods : fundamentals and applications, Wiley, New York, 1980 Search PubMed.
- R. G. Compton and C. E. Banks, Understanding voltammetry, Imperial College Press, London, 2011 Search PubMed.
- W. J. Albery and W. Albery, Electrode Kinetics, Clarendon Press, 1975 Search PubMed.
- J. H. Baxendale, M. D. Ward and P. Wardman, Trans. Faraday Soc., 1971, 67, 2532–2537 RSC.
- W. H. Koppenol, D. M. Stanbury and P. L. Bounds, Free Radic. Biol. Med., 2010, 49, 317–322 CrossRef CAS.
- G. Aloisi, A. M. Funtikov and T. Will, J. Electroanal. Chem., 1994, 370, 297–300 CrossRef CAS.
- V. I. Birss and C. K. Smith, Electrochim. Acta, 1987, 32, 259–268 CrossRef CAS.
- B. M. Jović, V. D. Jović and D. M. Dražić, J. Electroanal. Chem., 1995, 399, 197–206 CrossRef.
- M. S. Zei, J. Electroanal. Chem. Interfacial Electrochem., 1991, 308, 295–307 CrossRef CAS.
- B. B. Blizanac, P. N. Ross and N. M. Markovic, Electrochim. Acta, 2007, 52, 2264–2271 CrossRef CAS.
- Y. Li, J. Zhao, E. Shang, X. Xia, J. Niu and J. Crittenden, Environ. Sci. Technol., 2018, 52, 4842–4849 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04295a |
| This journal is © The Royal Society of Chemistry 2021 |