A DNA nanopillar as a scaffold to regulate the ratio and distance of mimic enzymes for an efficient cascade catalytic platform

Abstract

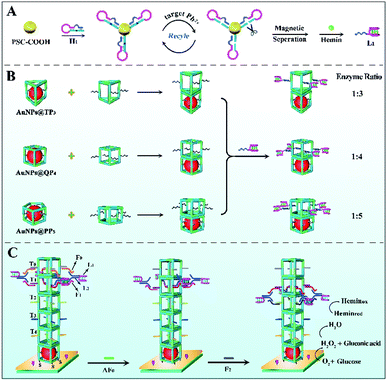
Herein, a rigid 3D DNA nanopillar was used to investigate the influence of spatial organization on the cascade activity in multienzyme systems, realizing controllable regulation of the mimic enzyme ratio and spacing for acquiring a high-efficiency enzyme cascade catalytic platform. Initially, the ratio of mimic enzyme AuNPs (glucose oxidase-like activity) and hemin/G-quadruplex DNAzyme (peroxidase-like activity) fixed at the designed position was adjusted by changing the number of edges in a DNA polyhedron, resulting in an optimal mimic enzyme ratio of 1 : 4 with a quadrangular prism as the scaffold. Notably, the DNA nanopillar formed by quadrangular prism layer-by-layer assembly acted as a track for directional and controllable movement of a bipedal DNA walker based on the toehold mediated strand displacement reaction (TSDR), which endowed the assay system with continuous enzyme spacing regulation compared with previous enzyme cascade systems that induced inflexible operation. Furthermore, enzyme mimetics in this work circumvented the drawbacks of natural enzymes, such as time-consuming purification processes and poor thermal stability. As a proof of concept, the proposed dual regulation strategy of cascade enzymes was applied in the ultrasensitive electrochemical detection of Pb²⁺, which provided a new route to fabrication of high-performance artificial enzyme cascade platforms for ultimate application in bioanalysis and biodiagnostics.

---

Introduction

Enzyme cascade, which embraces multiple enzymatic reactions in one pot without isolation of intermediates has a wide range of potential applications in bioanalysis,^1–7 biosensors^8,9 and biodiagnostics.^10–15 Indeed, the co-immobilization of cascade enzymes on a platform is one of the most straightforward protocols to mimic sequential enzyme reactions.^16–19 However, random enzyme distribution in traditional approaches brought many challenges such as the overlap of enzyme active sites, mismatch of the optimal enzyme ratio and inappropriate interenzyme distances, thereby leading to an inferior mass transport of reactants and intermediates among enzymes with significantly reduced catalytic efficiency. Accordingly, besides the inherent catalytic activity, cascade enzymes with a rational spatial arrangement (e.g., enzyme spacing and ratio) are crucial to achieve highly efficient cascade catalysis, which has been the focus of researchers in recent years but remains challenging.

To date, DNA nanostructures, such as origami,^20,21 tetrahedra²² and nanotweezers,²³ have emerged as promising scaffolds to tether cascade enzymes with an equivalent ratio and regulate enzyme spacing at nanoscale on account of their structural programmability and accurate addressability. Despite these successes, the uncontrolled stoichiometric ratio of cascade enzymes does not favor better cooperation of the first and second enzymatic reactions, and thus ineffective diffusion of intermediates in enzyme cascade processes limited catalytic efficiency. Recently, although some reports have studied the influence of the enzyme ratio on the cascade catalytic efficiency, where the enzyme ratios can be regulated by changing the amount of enzymes,^24–26 such strategies usually required the co-assembly of multiple enzymes without separated space, which led to increased obstacles for enzyme cascade reactions caused by too close enzyme spacing. In addition, such strategies were mainly focused on natural enzymes, which suffered from complicated purification processes and poor thermal stability that restricted their further application.^27,28 As a result, rational engineering of artificial enzyme cascade systems with a controlled enzyme ratio and spacing is urgent for high-performance cascade catalytic efficiency, which has rarely been investigated to the best of our knowledge.

In this work, using AuNPs (glucose oxidase-like activity) and hemin/G-quadruplex DNAzyme (peroxidase-like activity) as model mimic enzymes, a DNA nanopillar acted as a scaffold to control the enzyme ratio and continuously regulate the enzyme spacing for construction of an efficient mimic enzyme cascade system. As expressed in Scheme 1B, the ratio of mimic enzyme fixed at the designed position was effectively controlled by changing the number of edges in the DNA polyhedron, and thus an optimal scaffold quadrangular prism (QP₄) was obtained. Importantly, the 3D DNA nanopillar, assembled layer-by-layer by AuNPs@DNA cages and various QP₄ (Scheme S2†), could be used as a track for controllable movement of the bipedal DNA walker that was formed by hemin/G-quadruplex DNAzyme and ssDNA L₂ based on the toehold mediated strand displacement reaction, resulting in the continuous regulation of enzyme spacing for further improving cascade catalytic efficiency. Moreover, mimic enzymes exhibited comparable activity and better stability in comparison with natural enzymes. Such a dual regulation strategy of mimic enzymes with improved catalytic efficiency was applied in the fabrication of an electrochemical sensing platform for ultrasensitive Pb²⁺ detection, which gives impetus to exploit a new generation of high-performance mimic enzyme cascade platforms for application in bioanalysis and biodiagnostics.

Scheme 1 Schematic illustration of (A) DNAzyme-assisted cleavage recycling amplification; (B) optimization of the enzyme ratio between AuNPs and hemin/G-quadruplex DNAzyme; (C) construction procedure of biosensor sensing based on enzyme cascade catalytic amplification.

Experimental section

Preparation of different 3D DNA nanostructures and AuNPs@DNA cage complexes

The different 3D DNA nanostructures were successfully assembled via a clip-by-clip approach²⁹ (Scheme S1†). In detail, the equimolar amounts of all required DNA clips were mixed in 1× TAMg buffer (40 mM Tris and 12.5 mM MgCl₂·6H₂O, pH 7.8) for a final concentration of 1 μM for each oligonucleotide. The mixture was heated at 95 °C for 5 minutes, and 80 °C for 5 minutes, and then cooled down to 4 °C at a rate of −1 °C/5 min (6.5 h). Finally, R₃/R₄/R₅ pre-activated by 50 mM DTT and three different DNA cages were mixed together for 2 h to synthesize trigonal prism TP₃, quadrangular prism QP₄ and pentagonal prism PP₅, respectively. Indeed, thiolated strands R₃/R₄/R₅ were used to bind DNA cages to an electrochemically-deposited gold thin film (depAu) on glassy carbon electrodes (GCE).

For the preparation of ssDNA-modified AuNPs (DNA–AuNPs), 100 μL of 10 μM thiolated ssDNA in 1× TBEN buffer (90 mM Tris, 90 mM boric acid, 1.1 mM EDTA and 100 mM NaCl, pH 8.3) was incubated with 50 mM DTT solution for 40 min to reduce the S–S bond, followed by mixing with the as-synthesized 400 μL of AuNP solution with a diameter of 4 nm (Fig. S1A†). After the incubation of 12 h, DNA–AuNPs were obtained by centrifugal precipitation and re-dispersed in PBS (0.1 M, pH 7.4). For the encapsulation of DNA–AuNPs into the DNA cages, DNA–AuNPs and various DNA cages (TP₃-15A, QP₄-15A, or PP₅-15A) with ratios in a range of 2 : 1 to 1 : 2 were mixed together in 1× TAMg buffer, which were then incubated overnight at room temperature to form AuNPs@DNA cage complexes.

The preparation of the bipedal DNA walker

Before use, hairpin DNA 1 (H₁) was heated up at 90 °C for 5 min, and then slowly cooled to room temperature. After that, H₁ (40 μL, 20 μM) was added into 60 μL pre-activated carboxylated-magnetic polystyrene microsphere (PSC–COOH) solution (EDC/NHS) to covalently connect amino-terminated H₁ on the PSC–COOH surface. Whereafter, different concentrations of Pb²⁺ were added into above solution for 30 min of reaction at 37 °C. The supernatant was collected by magnetic separation and further added into 40 μL HEPES buffer (500 mM HEPES and 500 mM NaOH, pH 7.4) containing 100 mM KCl and 0.2 mM hemin to react at 25 °C for 30 min, thereby resulting in the formation of hemin/G-quadruplex DNAzyme (L₁) for an electrochemical signal through direct electrocatalysis. Finally, L₁ was mixed with L₂ (10 μM) and reacted for 30 min to acquire the bipedal DNA walker (as shown in Scheme 1C).

Fabrication process of the biosensor

The pretreated mirror-like GCE was first electrodeposited in HAuCl₄ solution (−0.2 V, 30 s) to obtain a depAu layer. Afterward, the prepared AuNPs@DNA cages were assembled on depAu/GCE via a Au–S bond (10 h, 4 °C). After blocking with 1% HT for 40 min, DNA nanostructures with various walker tracks were self-assembled on the above electrode surface layer-by-layer for generation of the DNA nanopillar, accompanied by the addition of the bipedal DNA walker and corresponding fuels. Ultimately, the designed biosensor was submerged in 2 mL phosphate buffered solution (PBS, 0.1 M Na₂HPO₄, 0.1 M NaH₂PO₄ and 0.1 M KCl, pH 7.4) containing 4 mM glucose to observe the differential pulse voltammetry (DPV) response.

Results and discussion

Characterization of various nanomaterials

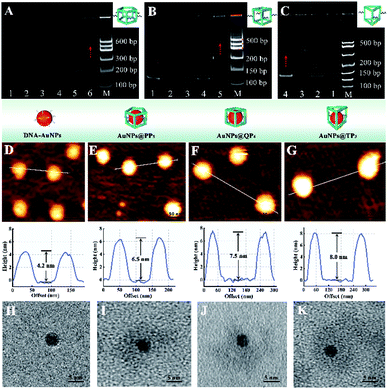
Polyacrylamide gel electrophoresis (PAGE) was employed to evaluate the successful assembly of different DNA cages. As exhibited in Fig. 1A, lanes 1–5 represented the ssDNA of P₅₁, P₅₂, P₅₃, P₅₄, and P₅₅, respectively. After five ssDNA self-assembling into PP₅, lane 6 showed a slower migration rate than ssDNA because of the high molecular weight of PP₅ (575 bp), which corresponded to the standard DNA marker, confirming the successful formation of PP₅. Similarly, Fig. 1B and C also demonstrated successful self-assembly of QP₄ (460 bp) and TP₃ (390 bp), respectively.

Fig. 1 Native PAGE analysis of different 3D DNA nanostructures including (A) pentagonal prism PP₅, (B) quadrangular prism QP₄, and (C) trigonal prism TP₃. (D–G) AFM images of DNA–AuNPs and various AuNPs@DNA cages, scale bars: 50 nm. (H–K) TEM images of DNA–AuNPs and various AuNPs@DNA cages.

The various AuNPs@DNA cages were characterized by atomic force microscopy (AFM) and the results were displayed in Fig. 1D–G. After encapsulation of AuNPs, the obtained AuNPs@DNA cages showed a significantly increased diameter (6.5–8.0 nm) compared with free DNA–AuNPs (∼4.2 nm), which confirmed that AuNPs were successfully encapsulated in three DNA cages, respectively. In addition, transmission electron microscopy (TEM) was also used to characterize the prepared AuNPs@DNA cages. In the enlarged views of Fig. 1H–K, obvious DNA coronas could be observed outside the highly electron dense core of AuNPs, indicating the feasibility of the encapsulation process.

The mechanism of stepwise movement for the bipedal DNA walker

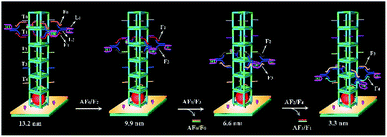
The system contained four components (Fig. 2): a bipedal DNA walker, track (T₀, T₁, T₂, T₃, and T₄), fuel strands and antifuel strands (AF₀, AF₁, and AF₂). The bipedal DNA walker could be joined to the track through base pairing with fuel strands. After introduction of corresponding antifuel strands, the fuel strands were removed through strand–displacement reactions and they liberated the walker leg for the next step. Here, the stepwise movement of the bipedal DNA walker from the top to bottom on the DNA nanopillar track could achieve continuous and dynamic regulation of cascade catalytic efficiency based on the toehold-mediated strand displacement. It was worth noting that each walking step of the bipedal DNA walker represented different interenzyme distances between AuNPs (glucose oxidase-like activity) and hemin/G-quadruplex DNAzyme (HRP-mimicking DNAzyme), which were 13.2 nm, 9.9 nm, 6.6 nm, and 3.3 nm, respectively. As a result, the optimized interenzyme distance was obtained for efficient cascade catalytic amplification.

Fig. 2 Principle of the walking process based on toehold-mediated strand displacement.

Influence of different enzyme ratios and interenzyme distances on catalytic efficiency

For the mimic enzyme-catalyzed cascade reaction, AuNPs with GOx-like activity first catalyzed the oxidation of glucose to gluconic acid with the accompanying formation of H₂O₂, which was then reduced by HRP-mimicking DNAzyme, and lastly an electrochemical signal was generated by direct electrocatalysis. In a typical enzyme cascade reaction, appropriate enzyme ratios and interenzyme distances could enhance the local concentration of substrates and overcome intermediate decomposition, resulting in high cascade catalytic efficiency.³⁰ Therefore, three various DNA nanostructures as scaffolds were used to regulate the enzyme ratio in this work (Fig. 3A). We found that QP₄ as a scaffold for the immobilization of mimic enzymes with a AuNPs/HRP-mimicking DNAzyme ratio of 1 : 4 showed the highest DPV signal (part b) compared with TP₃ and PP₅ as scaffolds (part a and c). Therefore, QP₄ was chosen as the most suitable scaffold in subsequent experiments. In addition, different interenzyme distances induced by stepwise walking of the bipedal DNA walker were optimized to investigate the effect of the interenzyme distance on the enzyme cascade catalytic efficiency. As displayed in Fig. 3B, an interenzyme distance of 9.9 nm demonstrated superior electrocatalytic performance in comparison to other interenzyme distances, which was thus employed as the optimal distance between AuNPs and HRP-mimicking DNAzyme.

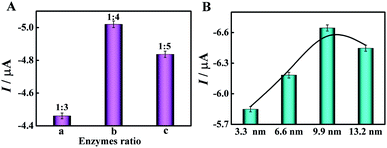Fig. 3 Effect of (A) different enzyme ratios and (B) different interenzyme distances between AuNPs and HRP-mimicking DNAzyme on cascade catalytic efficiency.

Catalytic efficiency of different enzyme cascade systems

For evaluating the catalytic efficiency of various enzyme cascade systems with single factor and two-factor regulation, different biosensors were operated in PBS (pH = 7.4) containing 4 mM glucose. As shown in Fig. 4, the enzyme cascade system with two-factor regulation (enzyme ratio and spacing) showed a much greater DPV peak current than the enzyme cascade system with single factor regulation (enzyme ratio or spacing), highlighting the excellent catalytic efficiency of the dual regulation strategy, which greatly facilitated the mass transport of reactants and intermediates among enzymes.

Fig. 4 DPV curves of the cascade enzyme systems with different factor regulation: (A) enzyme ratio, (B) enzyme spacing, and (C) enzyme ratio and spacing.

Analytical performance of the designed biosensor

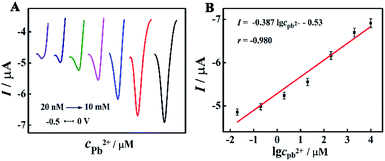
The analytical performance of the designed biosensor was evaluated by DPV measurements under optimal conditions. Along with the increase of the target Pb²⁺ concentration from 20 nM to 10 mM, the DPV response was gradually enhanced (Fig. 5A). Fig. 5B demonstrated an excellent linear relationship between the DPV signals and the logarithm of the Pb²⁺ concentration, and the linear equation was I (μA) = −0.387 lg c_Pb²⁺ – 0.53 (r = −0.980). The detection limit was found to be 5.5 nM via the 3σ rule. In addition, a comparison of this approach with other methods for Pb²⁺ detection was summarized in Table S2 (in the ESI†). It can be obviously seen that the proposed biosensor exhibited remarkable sensing performance, ascribing to highly efficient enzyme cascade amplification with an optimized enzyme ratio and interenzyme distance.

Fig. 5 (A) DPV signals of the proposed biosensor with various concentrations of Pb²⁺: 20 nM, 200 nM, 2 μM, 20 μM, 200 μM, 2 mM, and 10 mM. (B) Linear relationship of DPV currents versus the logarithm of the Pb²⁺ concentration. The error bars represented the standard deviations of three repetitive measurements.

Analysis of Pb²⁺ in human serum

For real sample analysis, various concentrations of Pb²⁺ were mixed with 50-fold diluted serum samples to execute a recovery test. It was illustrated in Table 1 that the recoveries ranged from 99.1% to 105%, confirming the satisfactory applicability of this approach in real samples.

Table 1 Recovery results of Pb²⁺ added in human serum samples (n = 3)

Sample number	Added/μM	Found/μM	Recovery/%	RSD/%
1	2	2.1	105	4.7
2	20	20.4	102	4.5
3	200	198.1	99.1	3.9
4	2000	1996.8	99.8	3.5

---

The serum samples of healthy people were obtained from the Southwest Hospital (Chongqing, China). Informed consent was obtained in all cases. The study was performed in strict accordance with the principles of the International Ethical Guidelines on Biomedical Research Involving Human Subjects, and was approved by the Medical Ethics Committee of the Chongqing Medical Association.

Conclusions

To summarize, we constructed a high-performance artificial enzyme cascade platform for electrochemical Pb²⁺ detection based on dual regulation of the enzyme spacing and ratio. Compared with traditional enzyme cascade efficiency regulation strategies, our method offered distinctive advantages as follows: (i) the ratio of AuNPs and hemin/G-quadruplex DNAzyme was adjusted by changing the number of edges in the DNA polyhedron for enhanced cascade catalytic activity; (ii) the as-developed rigid DNA nanopillar served as an enzyme-immobilization scaffold for continuous interenzyme distance regulation by controllable and directional movement of the bipedal DNA walker, which endowed the assay system with excellent enzyme cascade catalytic efficiency; (iii) the utilization of mimic enzymes could avoid the intrinsic drawbacks of natural enzymes. Such a strategy aimed to improve the cascade catalytic efficiency to a certain extent based on two-factor regulation of the enzyme ratio and spacing. Moreover, this general protocol is expected to facilitate further development of high-performance artificial enzyme cascade systems for bioanalysis and biosensing applications. For example, CeO₂ (GOx-like activity)/gold nanoclusters (peroxidase-like activity) can be used as model mimic enzymes, where the ratio and distance of cascade enzymes are regulated in a reaction system for improved cascade catalytic efficiency. Moreover, other small molecules such as proteins or nucleic acid can achieve quantitative analysis by replacing Pb²⁺-dependent DNAzymes with corresponding aptamers or nucleic acid.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the NNSF of China (21974108, 21775124 and 21675129), the Fundamental Research Funds for the Central Universities (XDJK2019B022, XDJK2020TY002), and the Chongqing Natural Science Foundation (cstc2018jcyjAX0085).

Notes and references

1. J. Liang, F. Mazur, C. Tang, X. Ning, R. Chandrawati and K. Liang, J. Chem. Sci., 2019, 10, 7852–7858.
2. Y. H. Chen, G. L. Ke, Y. L. Ma, Z. Zhu, M. H. Liu, Y. Liu, H. Yan and C. Y. James Yang, J. Am. Chem. Soc., 2018, 140, 8990–8996.
3. M. M. Li, S. Qiao, Y. L. Zheng, Y. H. Andaloussi, X. Li, Z. J. Zhang, A. Li, P. Cheng, S. Q. Ma and Y. Chen, J. Am. Chem. Soc., 2020, 142, 6675–6681.
4. P. Zhang, D. Sun, A. Cho, S. Weon, S. Lee, J. Lee, J. W. Han, D. P. Kim and W. Choi, Nat. Commun., 2019, 10, 940.
5. T. H. Kim, S. H. Kang, J. E. Han, E. J. Seo, E. Y. Jeon, G. E. Choi, J. B. Park and D. K. Oh, ACS Catal., 2020, 10, 4871–4878.
6. M. Vázquez-González, C. Wang and I. Willner, Nat Catal., 2020, 3, 256–273.
7. E. Kumari, S. Görlich, N. Poulsen and N. Kröger, Adv. Funct. Mater., 2020, 30, 2000442.
8. Y. Liu, Y. L. Zheng, Z. Chen, Y. L. Qin and R. Guo, Small, 2019, 15, 1804987.
9. X. X. Xiao, H. Q. Xia, R. R. Wu, L. Bai, L. Yan, E. Magner, S. Cosnier, E. Lojou, Z. G. Zhu and A. H. Liu, Chem. Rev., 2019, 119, 9509–9558.
10. H. Wang, Z. Zhao, Y. Liu, C. Shao, F. Bian and Y. Zhao, Sci. Adv., 2018, 4, eaat2816.
11. L. Yue, S. Wang, V. Wulf and I. Willner, Nat. Commun., 2019, 10, 1–10.
12. B. C. Buddingh, J. Elzinga and J. C. M. Van Hest, Nat. Commun., 2020, 11, 1652.
13. Q. Wu, Z. He, X. Wang, Q. Zhang, Q. C. Wei, S. Q. Ma, C. Ma, J. Li and Q. G. Wang, Nat. Commun., 2019, 10, 240.
14. B. J. H. M. Rosier, A. J. Markvoort, B. G. Audenis, J. A. L. Roodhuizen, A. den Hamer, L. Brunsveld and T. F. A. de Greef, Nat Catal., 2020, 3, 295–306.
15. A. Fischer, S. Lilienthal, M. Vazquez-Gonzalez, M. Fadeev, Y. S. Sohn, R. Nechushtai and I. Willner, J. Am. Chem. Soc., 2020, 142, 4223–4234.
16. W. Chen, M. Vazquez-González, A. Zoabi, R. Abu-Reziq and I. Willner, Nat Catal., 2018, 1, 689–695.
17. S. Zhang, C. Wang, H. Chang, Q. Zhang and Y. Cheng, Sci. Adv., 2019, 5, eaaw4252.
18. W. H. Chen, G. F. Luo, M. Vázquez-González, R. Cazelles, Y. S. Sohn, R. Nechushtai, Y. Mandel and I. Willner, ACS Nano, 2018, 12, 7538–7545.
19. C. Wang, A. Fischer, A. Ehrlich, Y. Nahmias and I. Willner, Chem. Sci., 2020, 11, 4516–4524.
20. T. A. Ngo, E. Nakata, M. Saimura and T. Morii, J. Am. Chem. Soc., 2016, 138, 3012–3021.
21. W. P. Klein, R. P. Thomsen, K. B. Turner, S. A. Walper, J. Vranish, J. Kjems, M. G. Ancona and I. L. Medintz, ACS Nano, 2019, 13, 13677–13689.
22. P. Song, J. W. Shen, D. K. Ye, B. J. Dong, F. Wang, H. Pei, J. B. Wang, J. Y. Shi, L. H. Wang, W. Xue, Y. R. Huang, G. Huang, X. L. Zuo and C. H. Fan, Nat. Commun., 2020, 11, 838.
23. A. C. Stelson, M. H. Liu, C. A. E. Little, C. J. Long, N. D. Orloff, N. Stephanopoulos and J. C. Booth, Nat. Commun., 2019, 10, 1–9.
24. C. W. Chiang, X. Y. Liu, J. W. Sun, J. W. Guo, L. Tao and W. P. Gao, Nano Lett., 2020, 20, 1383–1387.
25. S. Q. Fan, B. Liang, X. X. Xiao, L. Bai, X. J. Tang, E. Lojou, S. Cosnier and A. H. Liu, J. Am. Chem. Soc., 2020, 142, 3222–3230.
26. S. Lim, G. A. Jung, D. J. Glover and D. S. Clark, Small, 2019, 15, 1805558.
27. Y. Tian, J. R. Lhermitte, L. Bai, T. Vo, H. L. L. Xin, H. L. Li, R. P. Li, M. Fukuto, K. G. Yager and J. S. Kahn, Nat. Mater., 2020, 19, 1–8.
28. V. Smeets, W. Baaziz, O. Ersen, E. M. Gaigneaux, C. Boissiere, C. Sanchez and D. P. Debecker, Chem. Sci., 2020, 11, 954–961.
29. X. Luo, P. Chidchob, J. F. Rahbani and H. F. Sleiman, Small, 2018, 14, 1702660.
30. Y. H. Chen, G. L. Ke, Y. L. Ma, Z. Zhu, M. H. Liu, Y. Liu, H. Yan and C. J. Yang, J. Am. Chem. Soc., 2018, 140, 8990–8996.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc03584j

---