Open Access Article
Open Access ArticleMechanistic insight of KBiQ2 (Q = S, Se) using panoramic synthesis towards synthesis-by-design†
Rebecca
McClain
 a,
Christos D.
Malliakas
a,
Christos D.
Malliakas
 a,
Jiahong
Shen
b,
Jiangang
He
a,
Jiahong
Shen
b,
Jiangang
He
 b,
Chris
Wolverton
b,
Chris
Wolverton
 b,
Gabriela B.
González
b,
Gabriela B.
González
 c and
Mercouri G.
Kanatzidis
c and
Mercouri G.
Kanatzidis
 *a
*a
aDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA. E-mail: m-kanatzidis@northwestern.edu
bDepartment of Materials Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA
cDepartment of Physics, DePaul University, Chicago, Illinois 60614, USA
First published on 23rd November 2020
Abstract
Solid-state synthesis has historically focused on reactants and end products; however, knowledge of reaction pathways, intermediate phases and their formation may provide mechanistic insight of solid-state reactions. With an increased understanding of reaction progressions, design principles can be deduced, affording more predictive power in materials synthesis. In pursuit of this goal, in situ powder X-ray diffraction is employed to observe crystalline phase evolution over the course of the reaction, thereby constructing a “panoramic” view of the reaction from beginning to end. We conducted in situ diffraction studies in the K–Bi–Q (Q = S, Se) system to understand the formation of phases occurring in this system in the course of their reactions. Powder mixtures of K2Q to Bi2Q3 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1.5
1 and 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios were heated to 800 °C or 650 °C, while simultaneously collecting diffraction data. Three new phases, K3BiS3, β-KBiS2, and β-KBiSe2, were discovered. Panoramic synthesis showed that K3BiQ3 serves an important mechanistic role as a structural intermediate in both chalcogen systems (Q = S, Se) in the path to form the KBiQ2 structure. Thermal analysis and calculations at the density functional theory (DFT) level show that the cation-ordered β-KBiQ2 polymorphs are the thermodynamically stable phase in this compositional space, while Pair Distribution Function (PDF) analysis shows that all α-KBiQ2 structures have local disorder due to stereochemically active lone pair expression of the bismuth atoms. The formation of the β-KBiQ2 structures, both of which crystallize in the α-NaFeO2 structure type, show a boundary where the structure can be disordered or ordered with regards to the alkali metal and bismuth. A cation radius tolerance for six-coordinate cation site sharing of
1 ratios were heated to 800 °C or 650 °C, while simultaneously collecting diffraction data. Three new phases, K3BiS3, β-KBiS2, and β-KBiSe2, were discovered. Panoramic synthesis showed that K3BiQ3 serves an important mechanistic role as a structural intermediate in both chalcogen systems (Q = S, Se) in the path to form the KBiQ2 structure. Thermal analysis and calculations at the density functional theory (DFT) level show that the cation-ordered β-KBiQ2 polymorphs are the thermodynamically stable phase in this compositional space, while Pair Distribution Function (PDF) analysis shows that all α-KBiQ2 structures have local disorder due to stereochemically active lone pair expression of the bismuth atoms. The formation of the β-KBiQ2 structures, both of which crystallize in the α-NaFeO2 structure type, show a boundary where the structure can be disordered or ordered with regards to the alkali metal and bismuth. A cation radius tolerance for six-coordinate cation site sharing of 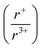 ∼ 1.3 is proposed. The mechanistic insight the panoramic synthesis technique provides in the K–Bi–Q system is progress towards the overarching goal of synthesis-by-design.
∼ 1.3 is proposed. The mechanistic insight the panoramic synthesis technique provides in the K–Bi–Q system is progress towards the overarching goal of synthesis-by-design.
Introduction
The discovery of new materials has led to revolutions in many scientific and technological fields, such as magnetism,1 radiation detection,2 optics,3–6 superconductivity,7,8 lithium-ion batteries,9,10 thermoelectrics,11 and phase-change memory.12 Traditionally, materials discovery of inorganic structures involves exploratory synthesis to identify compounds using heuristically determined reaction conditions, where the compounds are isolated and identified upon completion of the reaction. Within this paradigm, it is unclear whether the desired products form upon heating, cooling, or while dwelling at maximum temperature, or if metastable, short-lived products appear and re-dissolve during the reaction. In situ diffraction techniques are a powerful tool that enable the observation of transient phases during the reaction in efforts towards materials discovery. Moreover, observing these transient phases leads to mechanistic understanding of the reaction; thereby advancing efforts to more rationally design or discover solid-state materials.13–16 In particular, rational design is crucial to the pursuit of structural complexity for many fields, such as in thermoelectrics to achieve materials with lower thermal conductivity17 and in nonlinear optics for large second harmonic generation.5 To fully realize the potential for rational synthetic design, a comprehensive long-term approach to analyze solid-state reactions at all stages of the reaction is required.A powerful tool that provides full awareness of phase identity and phase evolution during a reaction is in situ powder X-ray diffraction. This technique enables the direct observation of all crystalline phases, including intermediate ones, during a solid-state synthesis.18,19 This “panoramic” view of the phase space explored during the reaction enables an understanding of the reaction pathway required to form the final products. To this end, in situ powder X-ray diffraction promotes the discovery of new materials and increased mechanistic understanding of solid-state chemistry.
However, simply conducting in situ powder X-ray diffraction on systems in isolation is not sufficient to achieve the generalized understanding of solid-state reaction dynamics necessary to maximize the potential for discovery. Comprehensive studies of multiple closely related compositions and systems are needed to paint a full picture of reactions that can then be extended to new systems. Therefore, the aggregation of mechanistic data describing material formation and progression of intermediate phases is the first step to determining reaction pathways for rational synthesis.13,14,20–24 This technique must therefore be applied to a broad, diverse set of systems and phases spaces. Once these reaction pathways of these systems are cataloged and codified, they can be data mined for design principles among similar reaction types.13 With reaction types and assembly rules, predictive power of material synthesis can be achieved, leading to intentional synthesis of targeted materials with chosen, desired properties.25
In situ powder X-ray diffraction has been utilized for various interests such as materials discovery18,19,26 and mechanism elucidation,25,27–33 as well as the investigation of metathesis reactions,27,34 self-propagating high temperature syntheses,14,25,28 phase change,14,35 decomposition,36 and crystallization.14,25,28 This approach has shown success in discovering new materials, even in systems that were previously investigated.18,19 Furthermore, it has been shown that, by using mechanistic insight from in situ studies, the reaction pathway can be influenced.30 Studies focused on building a database of reaction formation and mechanistic understanding for a specific reaction type can be combined in aggregate towards the goal of rational synthesis.
A promising phase space to study is in the A–Pn–Q systems, where A is an alkali metal, Pn is a pnictogen such as bismuth or antimony, and Q is a chalcogenide,37,38 as many are reported structures and have been of interest for their thermoelectric39–45 and optical5,35,46,47 properties. Moreover, a number of the known compounds are isostructural disordered analogues, such as KBiS2, NaBiS2, NaBiSe2, KBiSe2, and NaSbS2, while ordered phases contain similar structural motifs.48–50 Investigation of this family of structures expands the library of known materials, reaction pathways, and understanding of structure–property relationships. Reaction pathways can then be compared within this phase space to understand their design principles. The combination of experimental observation and computational data-mining can accelerate materials discovery and expedite the development of the mechanistic understanding required to achieve rational synthesis of materials.23,51
Herein, we have applied this in situ diffraction technique using both in-house and synchrotron sources to the K–Bi–S and K–Bi–Se system, by monitoring the reaction between the respective binaries, K2Q and Bi2Q3 (Q = S, Se). Powder mixtures were heated to 800 °C or 650 °C, while diffraction data was simultaneously collected. From this investigation, we found that the two systems share an isostructural intermediate phase, K3BiQ3. The presence of this intermediate phase in both reactions suggests K3BiQ3 is mechanistically important for KBiQ2 formation from the binary starting materials. Two additional compounds were discovered: β-KBiS2 and β-KBiSe2. These compounds crystallize in the α-NaFeO2 structure type and are cation-ordered polymorphs of the known rocksalt ternaries. The ability of KBiQ2 to form both a disordered and ordered phase, while NaBiQ2 and RbBiQ2 crystallize in the rocksalt and α-NaFeO2 type structures, respectively, suggests that there is a cation radius tolerance 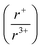 of 1.33 or greater for high symmetry rocksalt formation. This work is one of the pioneer studies in proposing a tolerance factor for a chalcogenide system.52–54 We have also performed density functional theory (DFT) calculations to show that the cation-ordered β-KBiQ2 polymorphs are thermodynamically stable and demonstrated that DFT can be used as a complimentary tool in the panoramic studies to determine the phase stabilities.
of 1.33 or greater for high symmetry rocksalt formation. This work is one of the pioneer studies in proposing a tolerance factor for a chalcogenide system.52–54 We have also performed density functional theory (DFT) calculations to show that the cation-ordered β-KBiQ2 polymorphs are thermodynamically stable and demonstrated that DFT can be used as a complimentary tool in the panoramic studies to determine the phase stabilities.
Experimental section
Reagents
Chemicals in this work were used as-obtained: bismuth metal (99.99%, American Elements), sulfur, (sublimed, 99.99%, Spectrum), selenium pellets (99.99%, American Elements), potassium metal (99.5%, Aldrich), glassy carbon (99.9%, Aldrich). K2S and K2Se were synthesized using stoichiometric amounts of the elements in liquid ammonia as described elsewhere.47Synthesis
Physical measurements
PXRD data used for K3BiS3 Rietveld refinement was collected at room temperature on a STOE-STADI-P powder diffractometer equipped with an asymmetric curved germanium monochromator (pure-CuKα1 radiation, λ = 1.54056 Å) and one-dimensional silicon strip detector (MYTHEN2 1K from DECTRIS). The line focused Cu X-ray tube was operated at 40 kV and 40 mA. Powder was packed in a 3 mm metallic mask and sandwiched between two polyimide layers of tape. Intensity data from 3 to 124° 2θ were collected over a period of 45 min. The instrument was calibrated against a NIST Silicon standard (640d) prior to the measurement.
High resolution synchrotron powder diffraction data were collected using beamline 11-BM at the Advanced Photon Source (APS), Argonne National Laboratory using an average wavelength of 0.4577 Å. Discrete detectors covering an angular range from 2 to 24° 2θ are scanned over a 6° 2θ range, with data points collected every 0.001° 2θ and scan speed of 0.01° s−1.
GSAS-II was used to calibrate the sample-to-detector distance, detector alignment, and instrumental resolution parameters using a NIST CeO2 standard and to integrate the data (ref. 56). The empty Kapton capillary signal was subtracted from each scattering data pattern using PDFgetX3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 prior to obtaining the Pair Distribution Functions (PDFs). PDFgui58 was used to fit PDFs in the range 2 Å < r < 30 Å. Subgroups were generated using the Bilbao Crystallographic Server;59–61 space groups investigated included R
57 prior to obtaining the Pair Distribution Functions (PDFs). PDFgui58 was used to fit PDFs in the range 2 Å < r < 30 Å. Subgroups were generated using the Bilbao Crystallographic Server;59–61 space groups investigated included R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Pm
m, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, C2/m, P
m, C2/m, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, I4/mmm, Pn
m1, I4/mmm, Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, P3221.
m, P3221.
Computational methods
All DFT calculations are performed using the projector augmented wave (PAW) method,62,63 as implemented in the Vienna Ab initio Simulation Package (VASP).64,65 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional66 and a plane wave basis set with a cutoff energy of 520 eV were used. A Γ-centered k-mesh with ≈8000 k-points per reciprocal atom (KPPRA) was used to sample the Brillouin zone. The Open Quantum Material Database (OQMD)51,67 was used for convex hull construction. To calculate the formation energy of the cation-disordered KBiQ2Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures, a 32-atom special quasi-random structure (SQS)68 was generated by using the Monte Carlo algorithm (mcsqs) as implemented in the Alloy Theoretic Automated Toolkit (ATAT).69,70 The cluster correlations used to define the SQS were specified using a distance-based cutoff of all 2-, 3-, and 4-body clusters with a maximum distance of 5–6 Å. To calculate the effective band structure of the K/Bi disordered cubic phase (Fm
m structures, a 32-atom special quasi-random structure (SQS)68 was generated by using the Monte Carlo algorithm (mcsqs) as implemented in the Alloy Theoretic Automated Toolkit (ATAT).69,70 The cluster correlations used to define the SQS were specified using a distance-based cutoff of all 2-, 3-, and 4-body clusters with a maximum distance of 5–6 Å. To calculate the effective band structure of the K/Bi disordered cubic phase (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), a 2 × 2 × 2 supercell was generated based on the perfect rocksalt structure with bismuth and potassium alternatively stacking along the [111] direction. The potassium and bismuth atoms are then randomly distributed in the supercell to simulate the cation-disordered KBiQ2Fm
m), a 2 × 2 × 2 supercell was generated based on the perfect rocksalt structure with bismuth and potassium alternatively stacking along the [111] direction. The potassium and bismuth atoms are then randomly distributed in the supercell to simulate the cation-disordered KBiQ2Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures. Effective band structures were recovered from the supercell calculations using the band unfolding technique proposed by Medeiros et al.71,72
m structures. Effective band structures were recovered from the supercell calculations using the band unfolding technique proposed by Medeiros et al.71,72
Results and discussion
Panoramic synthesis KBiS2
The synthesis of KBiS2 has been previously reported using potassium carbonate, elemental bismuth, and elemental sulfur.48,73 KBiS2 crystallizes in the simple rocksalt structure,48,73 where potassium and bismuth have equivalent occupancy in the sodium site and sulfur is in the chloride site. Moreover, the K–Bi–S phase space is of interest for thermoelectric materials74 and photovoltaics,75 in efforts towards rational design within this phase space, we began with this simple structure.To monitor the reaction progression in the K–Bi–S system, panoramic syntheses were conducted using a commercial STOE high-temperature furnace (HT) attachment for a STOE STADI-MP powder X-ray diffractometer. In previously reported syntheses, an excess of potassium starting material was used to form KBiS2, therefore a ratio of 1.5 K2S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
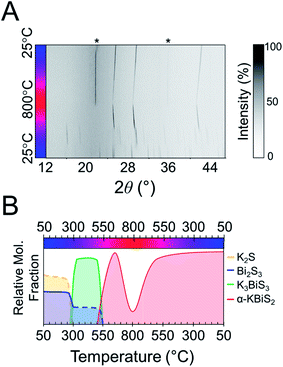
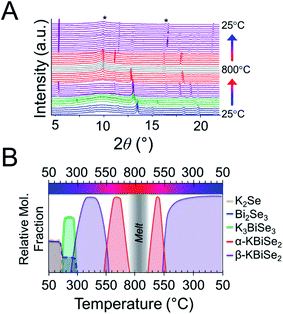
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi2S3 is used.73 The reaction has a maximum temperature of 800 °C. The overlaid diffraction patterns from the panoramic synthesis are shown in Fig. 1A. Phases are identified primarily through pattern matching. A schematic of the reaction pathway with relative mole fractions of the phases is shown in Fig. 1B. The relative mole fraction of the starting material amorphous K2S was determined according to the experimental loading of the material. It is useful to regard the reaction between K2S and Bi2S3 as a Lewis acid–base reaction in which K2S is the base and Bi2S3 is the acid. In this context, basic activity increases with the K2S fraction and acidic activity increases with the Bi2S3. The end crystalline products are KBiS2 and cristobalite, a high temperature polymorph of SiO2. The ground amorphous silica, which was used as a spacer to protect the glass tip of the capillary, crystallized after reaching temperatures above 700 °C. To avoid this, all subsequent panoramic syntheses in this system have a maximum temperature of 650 °C. An intermediate phase is observed during the reaction, appearing at 270 °C and disappearing at 510 °C as the product, KBiS2, emerges. The intermediate phase was isolated ex situ as described in the Experimental section and determined to be K3BiS3via Rietveld refinement (Fig. S1 and Tables S1–S4†).
1 Bi2S3 is used.73 The reaction has a maximum temperature of 800 °C. The overlaid diffraction patterns from the panoramic synthesis are shown in Fig. 1A. Phases are identified primarily through pattern matching. A schematic of the reaction pathway with relative mole fractions of the phases is shown in Fig. 1B. The relative mole fraction of the starting material amorphous K2S was determined according to the experimental loading of the material. It is useful to regard the reaction between K2S and Bi2S3 as a Lewis acid–base reaction in which K2S is the base and Bi2S3 is the acid. In this context, basic activity increases with the K2S fraction and acidic activity increases with the Bi2S3. The end crystalline products are KBiS2 and cristobalite, a high temperature polymorph of SiO2. The ground amorphous silica, which was used as a spacer to protect the glass tip of the capillary, crystallized after reaching temperatures above 700 °C. To avoid this, all subsequent panoramic syntheses in this system have a maximum temperature of 650 °C. An intermediate phase is observed during the reaction, appearing at 270 °C and disappearing at 510 °C as the product, KBiS2, emerges. The intermediate phase was isolated ex situ as described in the Experimental section and determined to be K3BiS3via Rietveld refinement (Fig. S1 and Tables S1–S4†).
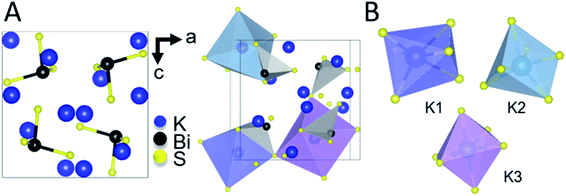
The intermediate phase, K3BiS3, shown in Fig. 2, crystallizes in the cubic Na3AsS3 structure type (space group P213; a = b = c = 9.4425(1) Å) and is isostructural to K3SbS3 and Na3SbS3.76 The formation of an intermediate phase of this composition is surprising because it implies a reaction of K2S and Bi2S3 in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, which is a more basic condition than what is being used in this reaction, where the ratio is 3
1 ratio, which is a more basic condition than what is being used in this reaction, where the ratio is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. This suggests that K3BiS3 is a kinetic product.
2. This suggests that K3BiS3 is a kinetic product.
K3BiS3 has two structural motifs: trigonal-pyramidal BiS3 units and distorted octahedral KS6 units. The isolated pyramidal molecule of [BiS3]3− makes the structure of K3BiS3 essentially molecular. We synthesized this intermediate ex situ using the conditions identified by the panoramic synthesis experiments and refined its structure using Rietveld refinement (Fig. S1†). The trigonal-pyramidal units of BiS3 have bond lengths and bond angles of 2.593(7) Å and 99.2(3)°, respectively. The distorted KS6 octahedra exhibit three different coordination environments, shown in different colors in Fig. 2B. The distortion of the octahedra give rise to a range of bond lengths between 3.11(2) and 3.53(1) Å. The distorted octahedra of K1, shown in blue, is capped by a bismuth and shares a corner with the three other BiS3 units in the structure. K2, in turquoise, is edge-sharing with three BiS3 units, while K3, shown in purple, is exclusively corner-sharing with the BiS3 polyhedra.
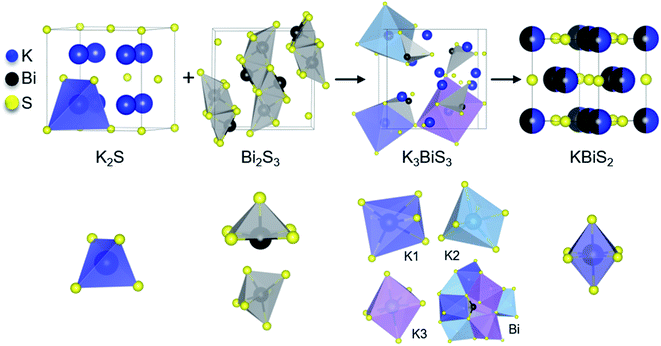
By comparing the structures in the 1.5 K2S + Bi2S3 reaction, shown in Fig. 3, the role of K3BiS3 as an intermediate phase in the formation of KBiS2 is examined. The coordination environment of potassium can be described as a gradual progression from tetrahedral to octahedral. In the starting material, the potassium cation begins in the K2S anti-fluorite structure consisting of KS4 tetrahedra with bond lengths of 3.191 Å,77 and over the course of the reaction expands to the distorted KS6 octahedra in K3BiS3. By the final product, potassium forms ideal KS6 octahedra in KBiS2. Of note, the K–S bond lengthens in K3BiS3, before shortening to 3.02 Å in the final Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure.78 In contrast, the bismuth coordination sphere does not undergo a gradual progression. In fact, bismuth undergoes an unexpected decrease in coordination number from square pyramidal and distorted octahedral to trigonal pyramidal, before transitioning to octahedral in KBiS2. In K3BiS3, bismuth stereochemically expresses its lone pair into a void created by the potassium cations, then no longer expresses its lone pair in the final product, KBiS2. The bismuth precursor, Bi2S3, contains square-pyramidal BiS5 units and distorted BiS6 octahedra, as illustrated in Fig. 3. Three different Bi–S bond lengths are present in the BiS5 units. The bond lengths in the basal plane are divided equally between 2.74(1) and 2.96(1) Å, while the apical Bi–S in BiS5 is the shortest bond length in the structure at 2.56(1) Å.77 The BiS6 octahedra has two bond lengths at 2.67(1) Å, another two at 2.96(1) Å, as well as one at 3.05(1) and 2.69(1) Å. The Bi–S bond length shortens to 2.62(1) Å in K3BiS3, before increasing to 3.02 Å in KBiS2. A concurrent shortening of the Bi–S bonds and lengthening of the K–S bonds in K3BiS3 is likely a result of the concomitant separation of the Bi2S3 chains and incorporation of the KS4 units. Owing to its utility as a structural transition framework, K3BiS3 therefore can be considered a structural intermediate for the formation of KBiS2.
m structure.78 In contrast, the bismuth coordination sphere does not undergo a gradual progression. In fact, bismuth undergoes an unexpected decrease in coordination number from square pyramidal and distorted octahedral to trigonal pyramidal, before transitioning to octahedral in KBiS2. In K3BiS3, bismuth stereochemically expresses its lone pair into a void created by the potassium cations, then no longer expresses its lone pair in the final product, KBiS2. The bismuth precursor, Bi2S3, contains square-pyramidal BiS5 units and distorted BiS6 octahedra, as illustrated in Fig. 3. Three different Bi–S bond lengths are present in the BiS5 units. The bond lengths in the basal plane are divided equally between 2.74(1) and 2.96(1) Å, while the apical Bi–S in BiS5 is the shortest bond length in the structure at 2.56(1) Å.77 The BiS6 octahedra has two bond lengths at 2.67(1) Å, another two at 2.96(1) Å, as well as one at 3.05(1) and 2.69(1) Å. The Bi–S bond length shortens to 2.62(1) Å in K3BiS3, before increasing to 3.02 Å in KBiS2. A concurrent shortening of the Bi–S bonds and lengthening of the K–S bonds in K3BiS3 is likely a result of the concomitant separation of the Bi2S3 chains and incorporation of the KS4 units. Owing to its utility as a structural transition framework, K3BiS3 therefore can be considered a structural intermediate for the formation of KBiS2.
To explore if the formation of rocksalt KBiS2 persists, an increase in amount of Bi2S3 relative to K2S was investigated. The overlaid diffraction patterns and reaction map of the 1 K2S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi2S3 panoramic synthesis are shown in Fig. 4A and B, respectively. As before, K3BiS3 forms first and appears between 240–250 °C, which is similar to the formation temperature of 270 °C in the K2S-rich reactions featuring a ratio of 1.5
1 Bi2S3 panoramic synthesis are shown in Fig. 4A and B, respectively. As before, K3BiS3 forms first and appears between 240–250 °C, which is similar to the formation temperature of 270 °C in the K2S-rich reactions featuring a ratio of 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The continued formation of K3BiS3 before the crystallization of KBiS2, despite a different final product, corroborates that this kinetic intermediate is mechanistically important for the formation of the rocksalt structure. The KBiS2 rocksalt structure emerges at ca. 435 °C. The rocksalt phase persists through the maximum temperature and, on cooling, a third phase is observed starting between 465–480 °C. KBiS2 persists until approximately 300 °C on cooling, where the third phase is the sole final product.
1. The continued formation of K3BiS3 before the crystallization of KBiS2, despite a different final product, corroborates that this kinetic intermediate is mechanistically important for the formation of the rocksalt structure. The KBiS2 rocksalt structure emerges at ca. 435 °C. The rocksalt phase persists through the maximum temperature and, on cooling, a third phase is observed starting between 465–480 °C. KBiS2 persists until approximately 300 °C on cooling, where the third phase is the sole final product.
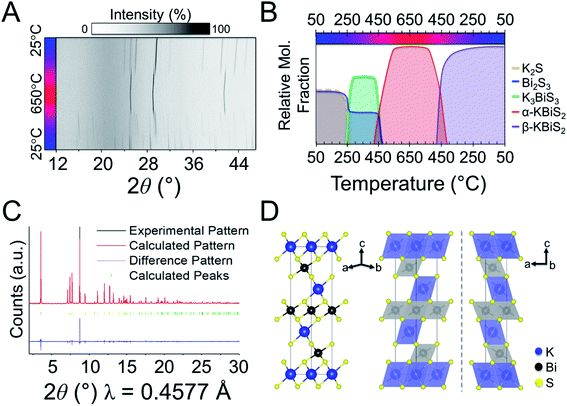
The third and final phase in this reaction is a cation-ordered polymorph of KBiS2 in the rhombohedral α-NaFeO2 structure type (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, a = b = 4.12983(3) Å, c = 22.09484(17) Å). The structure of the KBiS2 polymorph, hereafter named β-KBiS2, was determined using Rietveld refinement on synchrotron PXRD data (Fig. 4C). β-KBiS2 is an ordered rocksalt that is isostructural to RbBiS2.79 In this structure type, cation trigonal anti-prisms are connected through edge-sharing as in the disordered rocksalt structure (Fig. 4D).80 The layers alternate between CdCl2-type [BiS2]− layers and potassium cations. It is notable that the ordered R
m, a = b = 4.12983(3) Å, c = 22.09484(17) Å). The structure of the KBiS2 polymorph, hereafter named β-KBiS2, was determined using Rietveld refinement on synchrotron PXRD data (Fig. 4C). β-KBiS2 is an ordered rocksalt that is isostructural to RbBiS2.79 In this structure type, cation trigonal anti-prisms are connected through edge-sharing as in the disordered rocksalt structure (Fig. 4D).80 The layers alternate between CdCl2-type [BiS2]− layers and potassium cations. It is notable that the ordered R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m forms only when stoichiometric amounts of bismuth and potassium precursors are used; an excess of just 5% of K2S yields the rocksalt structure (Fig. S3†). The original synthesis for the cation-disordered Fm
m forms only when stoichiometric amounts of bismuth and potassium precursors are used; an excess of just 5% of K2S yields the rocksalt structure (Fig. S3†). The original synthesis for the cation-disordered Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m KBiS2 (now called α-KBiS2) also uses an excess of the potassium precursor, K2CO3.73 This suggests that an excess of potassium may have a role in destabilizing the lower symmetry structure.
m KBiS2 (now called α-KBiS2) also uses an excess of the potassium precursor, K2CO3.73 This suggests that an excess of potassium may have a role in destabilizing the lower symmetry structure.
Thermal analysis data of β-KBiS2 shown in Fig. S5† and Density Functional Theory (DFT) calculations, described further below, corroborate the experimental evidence that cation-ordered β-KBiS2 is the thermodynamically stable phase. The endothermic peak at ca. 480 °C upon heating and broad exothermic peak at ca. 405 °C upon cooling in the thermal analysis data indicate β-KBiS2 undergoes a phase transition. The temperature of these peaks corresponds to the transition temperature for the α-KBiS2 to β-KBiS2 transition in Fig. 4A. This, in conjunction with the identity of the post-thermal analysis product as β-KBiS2, confirms these signals result from phase transitions from a low to high temperature phase. Moreover, DFT calculations show that cation-ordered β-KBiS2 sits on the convex hull and, thus, is the thermodynamically stable phase, while cation-disordered α-KBiS2 sits at 75 meV per atom above the convex hull (i.e. above β-KBiS2).
Panoramic synthesis of KBiSe2
KBiSe2 is reported to crystallize in the rocksalt structure and was hypothesized to proceed through a similar mechanism to α-KBiS2 owing to their isostructural nature. The panoramic synthesis on 1 K2Se + 1 Bi2Se3 was conducted and is illustrated in Fig. 5. Different colors are used to highlight different phases that form during the reaction, beginning with the starting materials in blue. At 195 °C, again the analogous material, K3BiSe3, forms (Fig. S6;†P213; a = b = c = 9.773(2) Å).49 The appearance of K3BiSe3 (indicated in green) as an intermediate phase also in the selenide analogue reaction supports that this molecular salt phase may be important mechanistically to the reaction path.The reaction selectivity of K3BiQ3 (Q = S, Se) directly proceeding the formation of the KBiQ2 ternary is postulated to be structural in origin as opposed to energetic. In situ studies observing the phase formation found the composition of the first transient phase to be that which yielded the largest energy release81 or the fastest energy release.30 The former does not apply for these chalcogenide systems as the formation of K3BiQ3 is less energetically favorable than the β-KBiQ2 phases. Specifically, the formation energies of K3BiS3 and K3BiSe3 are calculated to be −48 meV per atom and −28 meV per atom below the convex hull, respectively, while those of β-KBiQ2 are −68 meV per atom and −60 meV per atom below the hull for the sulfide and selenide, respectively. The alpha phases have positive formation energies relative to the convex hull according to DFT calculations and are, therefore, considered unstable. K3BiQ3 also does not provide the fastest energy release as diffusion must occur for this phase to form as compared to KBiQ2. The precursor loadings in this work are 3 K2S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Bi2S3 (e.g. 1.5
2 Bi2S3 (e.g. 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and 1 K2Q
1) and 1 K2Q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi2Q3 (Q= S, Se). The precursors were sieved and thoroughly mixed, such that the average contact between particles are expected to mirror that of the loading ratio. Correspondingly, no notably K2Q-rich or poor areas are expected. The fastest energy release would therefore be the formation of KBiQ2, however, K3BiQ3 reproducibly forms first in both chalcogenide system regardless of loading ratio. The formation of the K3BiQ3 structural intermediate therefore cannot be easily rationalized by current thermodynamic or kinetic theories. However, the formation of the potassium-rich intermediate, persistent even in relatively potassium-poor reactant loading, underscores that this compound is necessary for the formation of the KBiQ2 ternary in these conditions.
1 Bi2Q3 (Q= S, Se). The precursors were sieved and thoroughly mixed, such that the average contact between particles are expected to mirror that of the loading ratio. Correspondingly, no notably K2Q-rich or poor areas are expected. The fastest energy release would therefore be the formation of KBiQ2, however, K3BiQ3 reproducibly forms first in both chalcogenide system regardless of loading ratio. The formation of the K3BiQ3 structural intermediate therefore cannot be easily rationalized by current thermodynamic or kinetic theories. However, the formation of the potassium-rich intermediate, persistent even in relatively potassium-poor reactant loading, underscores that this compound is necessary for the formation of the KBiQ2 ternary in these conditions.
The structural intermediate, K3BiSe3, shown in green in Fig. 5, persists until a new phase emerges at 285 °C, shown in purple. This new phase disappears at 555 °C before reappearing at 525 °C on cooling as the final product. This phase is isostructural to β-KBiS2 and hereafter called β-KBiSe2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, a = b = 4.26442 (1) Å, c = 23.0290(1) Å). When β-KBiSe2 disappears, the known rocksalt structure-type α-KBiSe2 begins to emerge. Upon cooling, β-KBiSe2 reappears by 500 °C. In order to isolate α-KBiSe2, the product was quenched at 650 °C and annealed. Attempts to synthesize α-KBiSe2 using the binaries without quenching, even with an excess of K2Se, were unsuccessful.
m, a = b = 4.26442 (1) Å, c = 23.0290(1) Å). When β-KBiSe2 disappears, the known rocksalt structure-type α-KBiSe2 begins to emerge. Upon cooling, β-KBiSe2 reappears by 500 °C. In order to isolate α-KBiSe2, the product was quenched at 650 °C and annealed. Attempts to synthesize α-KBiSe2 using the binaries without quenching, even with an excess of K2Se, were unsuccessful.
The overall reaction pathway in the selenide and sulfide systems is similar. Both systems proceed through a K3BiQ3 (Q = S, Se) intermediate. The coordination sphere of potassium increases from an anti-fluorite tetrahedron to distorted octahedra in K3BiSe3, as it does in the sulfide system. The coordination sphere of bismuth in the selenide system, however, decreases during the intermediate phase from an octahedron in Bi2Se3, shown in Fig. S7,† to trigonal pyramidal in the discrete ions in K3BiSe3, before returning to an octahedron in both the highly dense ordered and the disordered rocksalt type KBiSe2. The formation temperature of the selenide ternaries is observed lower than that of the sulfide likely as a result of the lower melting points of the selenide binaries, the higher basicity of K2Se than K2S, and the more polarizable anionic framework of the selenium ternary, which facilitates ion mobility.82 Similar to the KBiS2 system, thermal analysis (Fig. S8†) and DFT calculations show that the ordered, α-NaFeO2 type polymorph of KBiSe2 is the thermodynamically stable phase. Comparable to its sulfur analogue, cation-disordered α-KBiSe2 sits 76 meV per atom above the ordered, stable β-KBiS2 phase.
Investigation of local structure
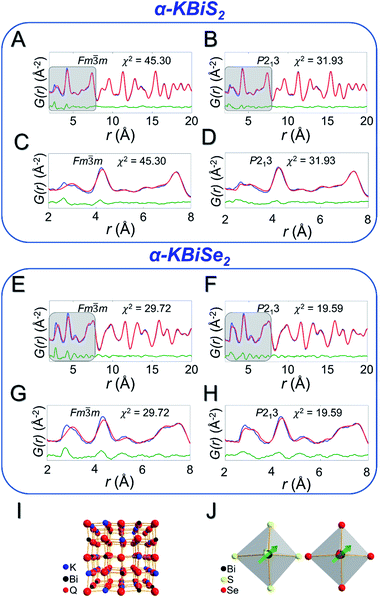
Local off-centering from ns2 lone pairs has been demonstrated previously for materials containing heavy main-group elements as for example the emphanisis effects in PbQ.83–88 The structure of the titular KBiQ2 compounds is therefore expected to be locally distorted as a result of stereochemical activity of the Bi3+ lone pair, while the global structure remains in the rocksalt or α-NaFeO2 structure type for the alpha and beta phases, respectively. Pair distribution function (PDF) analysis confirms that the data are well fit using Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m for α-KBiS2 and α-KBiSe2 at long r ranges (Fig. 6A and E). However, the split of the first PDF peak is not well fit, as shown in Fig. 6C and G. The Bilbao Crystallographic Server59–61 was used to generate possible subgroups of space group Fm
m for α-KBiS2 and α-KBiSe2 at long r ranges (Fig. 6A and E). However, the split of the first PDF peak is not well fit, as shown in Fig. 6C and G. The Bilbao Crystallographic Server59–61 was used to generate possible subgroups of space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m assuming the Wyckoff positions 4a and 8c. Those subgroups were used to fit the PDF data. The short range (r < 6 Å) were better fit using the lower symmetry space group P213 with partial site occupations in a cubic lattice cell as shown in Fig. 6B, D, F, and H. The split in the first coordination shell was better modeled by off-centering the atoms from the ideal rocksalt positions as illustrated in Fig. 6I and J.
m assuming the Wyckoff positions 4a and 8c. Those subgroups were used to fit the PDF data. The short range (r < 6 Å) were better fit using the lower symmetry space group P213 with partial site occupations in a cubic lattice cell as shown in Fig. 6B, D, F, and H. The split in the first coordination shell was better modeled by off-centering the atoms from the ideal rocksalt positions as illustrated in Fig. 6I and J.
Optical properties of α- and β-KBiQ2
As the ratio of K2Q to Bi2Q3 becomes stoichiometric in the syntheses, the final product transitions from α-KBiQ2 to β-KBiQ2 with band gap energies of 0.84(2) eV and 1.09(2) eV, respectively, for the selenides (red, Fig. 7A) and 1.23(2) eV and 1.55(2) eV for the sulfides (blue, Fig. 7A). As the compounds undergo a decrease in symmetry moving from the disordered α-KBiQ2 to the ordered β-KBiQ2, we observe a subsequent increase in band gap. The dimensional reduction from the ordering of β-KBiQ2 into layers of [BiQ2]− and K+ (Fig. 7B) yields a blue shift in the experimental band gap, as similarly observed for other semiconductors.84,89Fig. 7C shows the energies of the valence band maxima for α-KBiQ2 and β-KBiQ2 measured using a Kelvin Probe (see Experimental section) as well as for four well-known semiconductors (Si, CdTe, methylammonium lead iodide (MAPbI3), and TiO2) for reference. The energies of the conduction band minima are included and were extrapolated using the valence band maxima energies and experimental or known band gaps.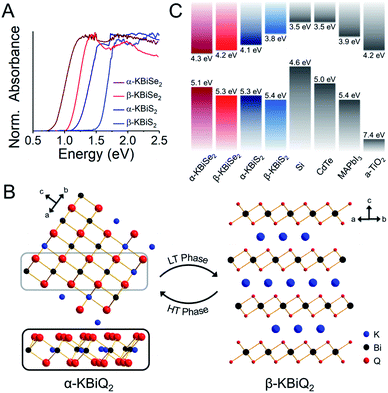 | ||
Fig. 7 (A) Experimental band gaps for the known α-KBiQ2 (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and discovered β-KBiQ2 phases (R m) and discovered β-KBiQ2 phases (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). (B) Illustration of dimension reduction from the 3D covalent framework in the high temperature (HT) phase, α-KBiQ2, to the layered 2D covalent framework in the low temperature (LT) phase, β-KBiQ2. For both structures, only covalent bonds (e.g. Bi–Q bonds) are shown. The site distribution of bismuth and potassium in α-KBiQ2 was randomized, while constrained to maintain equivalent amounts of the cations. The inset for α-KBiQ2 tilts the indicated portion of the structure to highlight the 3D connectivity through the plane. (C) Depiction of valence band maxima, conduction band minima, and band gap energies for α-KBiQ2, β-KBiQ2, Si,90,91 CdTe,92 MAPbI3,93 and TiO2 (anatase).94,95 m). (B) Illustration of dimension reduction from the 3D covalent framework in the high temperature (HT) phase, α-KBiQ2, to the layered 2D covalent framework in the low temperature (LT) phase, β-KBiQ2. For both structures, only covalent bonds (e.g. Bi–Q bonds) are shown. The site distribution of bismuth and potassium in α-KBiQ2 was randomized, while constrained to maintain equivalent amounts of the cations. The inset for α-KBiQ2 tilts the indicated portion of the structure to highlight the 3D connectivity through the plane. (C) Depiction of valence band maxima, conduction band minima, and band gap energies for α-KBiQ2, β-KBiQ2, Si,90,91 CdTe,92 MAPbI3,93 and TiO2 (anatase).94,95 | ||
Calculation of thermodynamic stability and electronic band structure
DFT calculations were performed to determine the thermodynamic stabilities and electronic structures of the α-KBiQ2 and β-KBiQ2 materials. When compiling the phase diagram for the K–Bi–S and K–Bi–Se phase spaces in Fig. 8A and B, all the related compounds stored in the Open Quantum Materials Database51 are considered and the grand canonical linear programming (GCLP) is used to construct the thermodynamic stability convex hull. The energy calculation for the structure of KBi6.33S10 and its partial occupancies39 is computationally intensive; thus, the compound is included in the phase diagram assuming it has T = 0 K stability. Notably, all ternary phases discovered to date in these phase diagrams lay along the K2Q–Bi2Q3 composition line, including the titular compounds. The intermediate phases, K3BiS3 and K3BiSe3, are also on the convex hull, and hence are considered thermodynamically stable ground state phases at T = 0 K. Our calculations show that the ordered phases, β-KBiS2 and β-KBiSe2, are on the convex hull, while the disordered α-KBiS2 and α-KBiSe2 structures are 75 and 76 meV per atom above the hull, respectively. This indicates the beta phases are the thermodynamically stable polymorphs, while the alpha phases are metastable. This agrees with the experimental observations as the beta phases are stable at room temperature, while the alpha phases form at high temperature.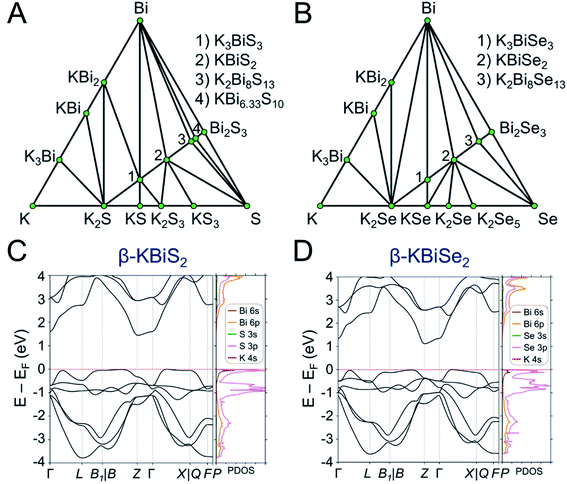 | ||
Fig. 8 Phase diagram of (A) K–Bi–S and (B) K–Bi–Se phase space. The band structure and partial density of states (PDOS) of (C) β-KBiS2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and (D) β-KBiSe2 (R m) and (D) β-KBiSe2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). m). | ||
The band structures of β-KBiS2 and β-KBiSe2 are shown in Fig. 8C and D, respectively. These two materials are indirect band gap semiconductors with calculated band gaps of 1.45 and 1.12 eV for β-KBiS2 and β-KBiSe2, respectively, using PBE functional method. These are consistent with the experimental band gaps of 1.55(2) eV and 1.09(2) eV as well as the expectation of the more electronegative sulfur analogue having a wider band gap than the selenium. For both β-KBiQ2 phases, the conduction band minimum is at the Z point of the Brillouin zone, while the valence band maxima are in the region along Γ–L, Z–B and Γ–X directions. The conduction band maximum is primarily comprised of the bismuth 6pz orbital with contribution from the sulfur 3s orbital (Fig. S10†). The bismuth 6s and sulfur 3p orbitals form the valence band maxima regions (Fig. S10†). The Γ–L and Γ–X direction have more contribution from the sulfur 3px orbital and the bismuth 6s, sulfur 3px and 3py orbitals, respectively. Overall, the conduction band is far more dispersive than the top of the valence band as shown in Fig. 8C and D, indicating that, in the beta phase, the charge transport of electrons would be far more efficient than that of holes. The partial density of states (PDOS) shows that the relatively flat valence band maxima is a consequence of the localized S/Se p orbitals that make up this band.
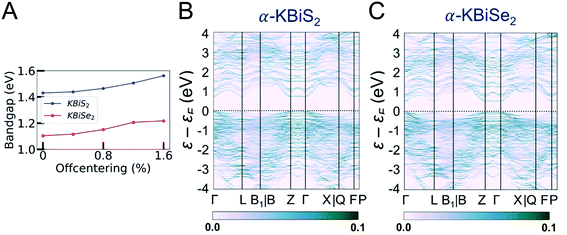
In order to understand the electronic structures of the alpha phases, the effects of bismuth off-centering and K/Bi disorder must be separated. The band gaps of the rocksalt-ordered KBiQ2 as a function of coherent bismuth off-centering are shown in Fig. 9A. As the off-centering of bismuth from its ideal positions increases, the band gaps of α-KBiS2 and α-KBiSe2 are calculated to increase. The disordering of α-KBiQ2 is simulated by randomly arranging potassium and bismuth atoms in supercells and the calculated band gaps using the same PBE functional method are 0.77 and 0.58 eV for α-KBiS2 and α-KBiSe2, respectively. The band structures of the alpha phases are shown in Fig. 9B and C. Both dimensional reduction89 and stereochemical lone pair expression,84 manifesting as cation ordering (Fig. 7B) and presenting as the off-centering of the bismuth atom, increase the band gap. Therefore, the band gaps of these compounds observed at finite temperature is a combination of these two effects (i.e. increasing the temperature yields a reduction in cation ordering and, on the other hand, an increase in off-centering). The comparative lower value for the experimental band gaps of disordered α-KBiQ2 than those of the ordered β-KBiQ2 materials indicates the influence of ordering has a larger effect than that of off-centering on the band gap, which is consistent with our calculations.
Comparison of A–Bi–Q
When looking at ABiQ2 (A = alkali metal, Q = S, Se, Te) compounds, simultaneous trends of decreasing symmetry and dimensionality are observed as the size of the alkali metal increases relative to bismuth (Fig. 10). As we move across the sulfides in Fig. 10D, the [BiQ2]1− framework is progressively broken up by the increasingly larger alkali metal illustrated in Fig. 10A–C. This is consistent with the so-called “counterion effect,” where, given an anionic framework, a countercation can induce a specific structural change as result of steric effects as a function of its size.96–99 Previous work5,97 has shown that the smaller the countercation, the higher the dimensionality and the higher coordination numbers of the metal in the covalent framework.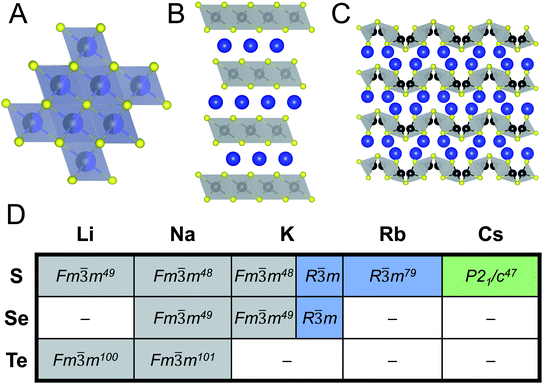 | ||
Fig. 10 Representative illustrations of ABiQ2 (A = alkali metal, Q = S, Se, Te) structures that crystallize in the (A) rocksalt structure type (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), (B) α-NaFeO2 structure type (R m), (B) α-NaFeO2 structure type (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), and (C) CsSbS2 structure type (P21/c). Monovalent cation shown in blue, trivalent cation in black, and chalcogenide in yellow. (D) Chart of ABiQ2 compounds reported in literature47–49,79,100,101 and in this paper. m), and (C) CsSbS2 structure type (P21/c). Monovalent cation shown in blue, trivalent cation in black, and chalcogenide in yellow. (D) Chart of ABiQ2 compounds reported in literature47–49,79,100,101 and in this paper. | ||
As the alkali metal increases in size, there is a decrease in dimensionality in agreement with the counterion effect that results from the end of site-sharing for the alkali metal and pnictogen.96,97 The previously reported lithium, sodium, and potassium ABiQ2 compounds crystallize in the rocksalt structure with the alkali metal and bismuth sharing the same octahedral cation site, shown in Fig. 10A. As observed in this work, KBiS2 and KBiSe2 can be directed to crystallize in the β-phase (Fig. 10B), which is in the α-NaFeO2 structure type. DFT mixing entropy calculations, shown in Fig. S13,† corroborate these experimental results and underscore that the rocksalt structure cannot be stabilized by finite temperature compared to the α-NaFeO2 structure type. This structure consists of [BiS2]− layers stacked perpendicular to the c-axis and separated by K+ cations (Fig. 10B). The potassium ternary marks an inflection point of site-sharing of bismuth and the alkali metal, as the rubidium and cesium ternaries also do not exhibit site-sharing of the two cations. The framework here transitions from a three dimensional covalent framework to a two dimensional layered framework, as highlighted previously in Fig. 7B. RbBiS2 crystallizes in the α-NaFeO2 structure type, similar to β-KBiS2 and β-KBiSe2, where bismuth and potassium separately occupy sites in alternate layers. RbBiSe2 was synthesized using a 1.5 Rb2Se![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi2Se3 ratio and is indexed to be in the R
1 Bi2Se3 ratio and is indexed to be in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. CsBiS2 crystallizes in the CsSbS2 structure type (P21/c), shown in Fig. 10C. This structure exemplifies the transition from a 2D covalent framework to a 1D framework as it comprises extended, corrugated [BiS2]− chains separated by Cs+ atoms.
m space group. CsBiS2 crystallizes in the CsSbS2 structure type (P21/c), shown in Fig. 10C. This structure exemplifies the transition from a 2D covalent framework to a 1D framework as it comprises extended, corrugated [BiS2]− chains separated by Cs+ atoms.
With potassium acting as an inflection point in the ABiQ2 system, there is a region of stability for six-coordinate site-sharing of bismuth and alkali metal corresponding to a cation radii ratio 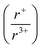 of 1.33 or less, using Shannon ionic radii.102 For ratios higher than 1.33, the cation-ordered structure forms (e.g. RbBiS2, RbBiSe2, and CsBiS2). A similar cation radii tolerance is found in the ALnS254 and AAn2Q6103 structures (A = alkali metal or Tl, Ln = lanthanide, An = Th, U, Np), thus supporting the plausibility of this proposed site-sharing tolerance. Inspection of antimony analogues corroborates the cation radii tolerance for metal site sharing. NaSbS2 forms in both the rocksalt structure50 and in the KSbS2 structure type.104 The
of 1.33 or less, using Shannon ionic radii.102 For ratios higher than 1.33, the cation-ordered structure forms (e.g. RbBiS2, RbBiSe2, and CsBiS2). A similar cation radii tolerance is found in the ALnS254 and AAn2Q6103 structures (A = alkali metal or Tl, Ln = lanthanide, An = Th, U, Np), thus supporting the plausibility of this proposed site-sharing tolerance. Inspection of antimony analogues corroborates the cation radii tolerance for metal site sharing. NaSbS2 forms in both the rocksalt structure50 and in the KSbS2 structure type.104 The 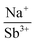 ratio is 1.3, which within approximation agrees with the previous trend for bismuth. KSbS2 crystallizes only in a cation-ordered structure and is not observed in a disordered rocksalt phase; the radius ratio for potassium and antimony
ratio is 1.3, which within approximation agrees with the previous trend for bismuth. KSbS2 crystallizes only in a cation-ordered structure and is not observed in a disordered rocksalt phase; the radius ratio for potassium and antimony 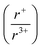 in KSbS2 is 1.8, thereby following the proposed cation radii tolerance.105
in KSbS2 is 1.8, thereby following the proposed cation radii tolerance.105
To demonstrate the robustness of the tolerance factor, the total energies of the three prototypes (Fig. 10A–C) were calculated for all reported structures in Fig. 10D and their accuracy were subsequently compared to the room-temperature structures. The DFT-calculated predictions found that at T = 0 K all structures are most stable in the ordered α-NaFeO2 structure type. Notably, the energy difference for CsBiS2 between the rhombohedral and monoclinic structures, as shown in Table S13,† is quite small (≤10 meV per atom) at 0 K and, thus, the monoclinic CsSbS2 (P21/c) structure type is very likely stabilized by temperature. The transition temperature between the rocksalt and α-NaFeO2 structure types, and therefore their temperature dependence, were investigated by introducing ideal mixing entropy (i.e. the configurational entropy) to the T = 0 K energies and fitting the transition temperatures using the experimental transition temperature of KBiS2. As shown in Table S14,† the calculated transition temperatures follow the disorder-to-order trend predicted by the tolerance factor. The lithium ternaries have a transition temperature below room temperature, indicating that the rocksalt phase would be present at room temperature. The sodium ternaries have similarly low transition temperatures, while the potassium, rubidium, and cesium ternaries have a transition temperature of over ∼700 K, thus confirming the robustness of the proposed tolerance factor.
Understanding and employing this proposed cation radii tolerance profitably impacts the numerous fields using ternary chalcogenide semiconductors. More specifically, alkali metal pnictogen chalcogenide ternaries are of interest for thermoelectrics and non-linear optics. In the field of thermoelectrics, binary chalcogenide semiconductors (i.e. GeQ, SnQ, PbQ) that crystallize in the rocksalt structure type have historically been of great interest. Current studies now capitalize on structure–property relationships to optimize properties by exploring solid solutions of rocksalt materials.44,45 These solid solutions of rocksalt structures reduce the lattice thermal conductivity in the thermoelectric material through phonon scattering as well as exploit band gap engineering. The proposed cation radii ratio 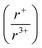 , therefore, provides guidance for the compositional requirements to form a cation-disordered APnQ2 ternary (A = alkali metal, Pn = Sb, Bi, Q = S, Se) that may then be mixed with another rocksalt structure. For non-linear optical materials, noncentrosymmetry is a structural requirement. The probability of achieving a noncentrosymmetric space group greatly increases with cation ordering as well as expression of the pnictogen ns2 lone pair. Therefore, the proposed cation radii ratio can similarly be used to guide cation selection criterion for non-linear optical materials.
, therefore, provides guidance for the compositional requirements to form a cation-disordered APnQ2 ternary (A = alkali metal, Pn = Sb, Bi, Q = S, Se) that may then be mixed with another rocksalt structure. For non-linear optical materials, noncentrosymmetry is a structural requirement. The probability of achieving a noncentrosymmetric space group greatly increases with cation ordering as well as expression of the pnictogen ns2 lone pair. Therefore, the proposed cation radii ratio can similarly be used to guide cation selection criterion for non-linear optical materials.
Conclusion
In this work, panoramic synthesis is shown to be a valuable tool for materials discovery and mechanistic insight into structure formation of KBiS2 and KBiSe2. Three new compounds were identified, K3BiS3, β-KBiS2, and β-KBiSe2. The KBiQ2 however do not form directly. The appearance of K3BiQ3 (Q = S, Se) preceding the formation of KBiQ2 suggests that this compound is mechanistically important as an intermediate in the reaction pathway. K3BiQ3 serves as a transition point for the potassium coordination environment and for cation intermixing. The observation of the KBiQ2 as both a rocksalt and α-NaFeO2 type structure, while NaBiQ2 and RbBiQ2 crystallize in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space groups, respectively, suggests that there is a cation radius tolerance
m space groups, respectively, suggests that there is a cation radius tolerance 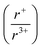 of 1.33 or greater for high symmetry rocksalt formation. Thermal analysis data and DFT calculations show that the cation-ordered polymorphs are the thermodynamically stable phases, while PDF analysis shows that the structures have local off-centering from stereochemically active 6s2 lone pair expression on the bismuth. DFT calculations also corroborate the increase in band gap from α-KBiQ2 to β-KBiQ2 as a result of dimensional reduction. By continuing to develop and catalog reactions using in situ diffraction techniques, we can work to expand our mechanistic understanding and predictive power towards the ultimate goal of synthesis-by-design.
of 1.33 or greater for high symmetry rocksalt formation. Thermal analysis data and DFT calculations show that the cation-ordered polymorphs are the thermodynamically stable phases, while PDF analysis shows that the structures have local off-centering from stereochemically active 6s2 lone pair expression on the bismuth. DFT calculations also corroborate the increase in band gap from α-KBiQ2 to β-KBiQ2 as a result of dimensional reduction. By continuing to develop and catalog reactions using in situ diffraction techniques, we can work to expand our mechanistic understanding and predictive power towards the ultimate goal of synthesis-by-design.
Author contributions
The idea for this project was conceived by M. G. K. and R. M. The manuscript was written by R. M. and M. G. K. with input from all authors. R. M. conducted all syntheses, structure solutions, and optical characterizations. C. D. M. assisted with optimizing the in situ experimental set-up, conducted the Pair Distribution Function (PDF) experiments, and provided fruitful conversations for refinements. J. S. and J. H. ran all DFT calculations under the guidance of C. W. The PDF analyses were completed by G. B. G. The overall project was supervised by M. G. K.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Science Foundation through the MRSEC program (NSF-DMR 1720139) at the Materials Research Center. Use was made of the IMSERC Facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-1542205), the State of Illinois, and International Institute for Nanotechnology (IIN). Use of the computational resources were provided by the Quest high performance computing facility at Northwestern University. The authors thank Dr Kyle M. McCall for helpful discussions. Use of the Advanced Photon Source (11-BM-B and 11-ID-B beamline) at Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract no. DE-AC02-06CH11357.References
- M. Sagawa, S. Fujimura, N. Togawa, H. Yamamoto and Y. Matsuura, J. Appl. Phys., 1984, 55, 2083–2087 CrossRef CAS.
- T. E. Schlesinger, J. E. Toney, H. Yoon, E. Y. Lee, B. A. Brunett, L. Franks and R. B. James, Mater. Sci. Eng., R, 2001, 32, 103–189 CrossRef.
- J. D. Bierlein and H. Vanherzeele, J. Opt. Soc. Am. B, 1989, 6, 622–633 CrossRef CAS.
- H. P. Maruska and J. J. Tietjen, Appl. Phys. Lett., 1969, 15, 327–329 CrossRef CAS.
- I. Chung and M. G. Kanatzidis, Chem. Mater., 2014, 26, 849–869 CrossRef CAS.
- T. T. Tran, H. Yu, J. M. Rondinelli, K. R. Poeppelmeier and P. S. Halasyamani, Chem. Mater., 2016, 28, 5238–5258 CrossRef CAS.
- M. K. Wu, J. R. Ashburn, C. J. Torng, P. H. Hor, R. L. Meng, L. Gao, Z. J. Huang, Y. Q. Wang and C. W. Chu, Phys. Rev. Lett., 1987, 58, 908–910 CrossRef CAS.
- Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296–3297 CrossRef CAS.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373 CrossRef CAS.
- S. R. Ovshinsky, Phys. Rev. Lett., 1968, 21, 1450–1453 CrossRef.
- L. Soderholm and J. F. Mitchell, APL Mater., 2016, 4, 053212 CrossRef.
- N. Pienack and W. Bensch, Angew. Chem., Int. Ed. Engl., 2011, 50, 2014–2034 CrossRef CAS.
- J. R. Chamorro and T. M. McQueen, Acc. Chem. Res., 2018, 51, 2918–2925 CrossRef CAS.
- H. Kohlmann, Eur. J. Inorg. Chem., 2019, 2019, 4174–4180 CrossRef CAS.
- D.-Y. Chung, K.-S. Choi, L. Iordanidis, J. L. Schindler, P. W. Brazis, C. R. Kannewurf, B. Chen, S. Hu, C. Uher and M. G. Kanatzidis, Chem. Mater., 1997, 9, 3060–3071 CrossRef CAS.
- D. P. Shoemaker, Y. J. Hu, D. Y. Chung, G. J. Halder, P. J. Chupas, L. Soderholm, J. F. Mitchell and M. G. Kanatzidis, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10922–10927 CrossRef CAS.
- A. S. Haynes, C. C. Stoumpos, H. Chen, D. Chica and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 10814–10821 CrossRef CAS.
- A. J. Martinolich, J. A. Kurzman and J. R. Neilson, J. Am. Chem. Soc., 2016, 138, 11031–11037 CrossRef CAS.
- A. J. Martinolich and J. R. Neilson, Chem. Mater., 2017, 29, 479–489 CrossRef CAS.
- X. Jia, A. Lynch, Y. Huang, M. Danielson, I. Lang'at, A. Milder, A. E. Ruby, H. Wang, S. A. Friedler, A. J. Norquist and J. Schrier, Nature, 2019, 573, 251–255 CrossRef CAS.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS.
- M. G. Kanatzidis, Inorg. Chem., 2017, 56, 3158–3173 CrossRef CAS.
- R. I. Walton and D. O'Hare, Chem. Commun., 2000, 2283–2291, 10.1039/B007795J.
- A. Bhutani, J. A. Schiller, J. L. Zuo, J. N. Eckstein, L. H. Greene, S. Chaudhuri and D. P. Shoemaker, Chem. Mater., 2017, 29, 5841–5849 CrossRef CAS.
- A. J. Martinolich and J. R. Neilson, J. Am. Chem. Soc., 2014, 136, 15654–15659 CrossRef CAS.
- A. E. Terry, G. B. M. Vaughan, Å. Kvick, R. I. Walton, A. J. Norquist and D. O'Hare, Synchrotron Radiat. News, 2002, 15, 4–13 CrossRef.
- S. J. Moorhouse, Y. Wu, H. C. Buckley and D. O'Hare, Chem. Commun., 2016, 52, 13865–13868 RSC.
- Z. Jiang, A. Ramanathan and D. P. Shoemaker, J. Mater. Chem. C, 2017, 5, 5709–5717 RSC.
- S. S. Bhella, S. P. Shafi, F. Trobec, M. Bieringer and V. Thangadurai, Inorg. Chem., 2010, 49, 1699–1704 CrossRef CAS.
- R. J. Lundgren, L. M. D. Cranswick and M. Bieringer, J. Solid State Chem., 2006, 179, 3599–3606 CrossRef CAS.
- S. P. Shafi, R. J. Lundgren, L. M. D. Cranswick and M. Bieringer, J. Solid State Chem., 2007, 180, 3333–3340 CrossRef CAS.
- J. B. Wiley and R. B. Kaner, Science, 1992, 255, 1093–1097 CrossRef CAS.
- A. S. Haynes, F. O. Saouma, C. O. Otieno, D. J. Clark, D. P. Shoemaker, J. I. Jang and M. G. Kanatzidis, Chem. Mater., 2015, 27, 1837–1846 CrossRef CAS.
- D. Friedrich, M. Schlosser, C. Näther and A. Pfitzner, Inorg. Chem., 2018, 57, 5292–5298 CrossRef CAS.
- M. G. Kanatzidis, Acc. Chem. Res., 2005, 38, 359–368 CrossRef CAS.
- A. Mrotzek and M. G. Kanatzidis, Acc. Chem. Res., 2003, 36, 111–119 CrossRef CAS.
- M. G. Kanatzidis, T. J. McCarthy, T. A. Tanzer, L.-H. Chen, L. Iordanidis, T. Hogan, C. R. Kannewurf, C. Uher and B. Chen, Chem. Mater., 1996, 8, 1465–1474 CrossRef CAS.
- L. Iordanidis, P. W. Brazis, C. R. Kannewurf and M. G. Kanatzidis, MRS Online Proc. Libr., 1998, 545, 65–74 CrossRef.
- D.-Y. Chung, T. Hogan, P. Brazis, M. Rocci-Lane, C. Kannewurf, M. Bastea, C. Uher and M. G. Kanatzidis, Science, 2000, 287, 1024–1027 CrossRef CAS.
- D.-Y. Chung, T. P. Hogan, M. Rocci-Lane, P. Brazis, J. R. Ireland, C. R. Kannewurf, M. Bastea, C. Uher and M. G. Kanatzidis, J. Am. Chem. Soc., 2004, 126, 6414–6428 CrossRef CAS.
- V. Bazakutsa, N. Gnidash, E. Pod'Yachaya, L. Voinova and N. Kravtsova, Russ. Phys. J., 1991, 34, 992–996 Search PubMed.
- T. J. Slade, T. P. Bailey, J. A. Grovogui, X. Hua, X. Zhang, J. J. Kuo, I. Hadar, G. J. Snyder, C. Wolverton, V. P. Dravid, C. Uher and M. G. Kanatzidis, Adv. Energy Mater., 2019, 9, 1901377 CrossRef.
- T. J. Slade, J. A. Grovogui, S. Hao, T. P. Bailey, R. Ma, X. Hua, A. Guéguen, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 7021–7031 CrossRef CAS.
- T. K. Bera, J. I. Jang, J.-H. Song, C. D. Malliakas, A. J. Freeman, J. B. Ketterson and M. G. Kanatzidis, J. Am. Chem. Soc., 2010, 132, 3484–3495 CrossRef CAS.
- T. J. McCarthy, S. P. Ngeyi, J. H. Liao, D. C. DeGroot, T. Hogan, C. R. Kannewurf and M. G. Kanatzidis, Chem. Mater., 1993, 5, 331–340 CrossRef CAS.
- J. W. Boon, Recl. Trav. Chim. Pays-Bas, 1944, 63, 32–34 CrossRef CAS.
- G. Gattow and J. Zemann, Z. Anorg. Allg. Chem., 1955, 279, 324–327 CrossRef CAS.
- J. Olivier-Fourcade, E. Philippot and M. Maurin, Z. Anorg. Allg. Chem., 1978, 446, 159–168 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- Y. Peng, Q. Sun, H. Chen and W.-J. Yin, J. Phys. Chem. Lett., 2019, 10, 4566–4570 CrossRef CAS.
- J.-P. Sun, G. C. McKeown Wessler, T. Wang, T. Zhu, V. Blum and D. B. Mitzi, Chem. Mater., 2020, 32, 1636–1649 CrossRef CAS.
- J. Fabry, L. Havlak, M. Dusek, P. Vanek, J. Drahokoupil and K. Jurek, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 360–371 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- P. Juhas, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef CAS.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS.
- M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS.
- M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128 CrossRef.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr. Cryst. Mater., 2006, 221, 15 CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS.
- A. Van de Walle, P. Tiwary, M. De Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS.
- A. van de Walle, Calphad, 2009, 33, 266–278 CrossRef CAS.
- P. V. C. Medeiros, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 041407 CrossRef.
- P. V. C. Medeiros, S. S. Tsirkin, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 041116 CrossRef.
- O. Glemser and M. Filcek, Z. Anorg. Allg. Chem., 1955, 279, 321–323 CrossRef CAS.
- B. Chen, C. Uher, L. Iordanidis and M. G. Kanatzidis, Chem. Mater., 1997, 9, 1655–1658 CrossRef CAS.
- R. E. Brandt, V. Stevanović, D. S. Ginley and T. Buonassisi, MRS Commun., 2015, 5, 265–275 CrossRef CAS.
- C. Pompe and A. Pfitzner, Z. Anorg. Allg. Chem., 2013, 639, 296–300 CrossRef CAS.
- C. West, Z. Kristallogr. Cryst. Mater., 1934, 88, 97–115 CAS.
- B. Gabrel'yan, A. Lavrentiev, I. Y. Nikiforov and V. Sobolev, J. Struct. Chem., 2008, 49, 788–794 CrossRef.
- Y. V. Voroshilov, E. Y. Peresh and M. I. Golovei, Chem. Informationsdienst, 1972, 3, 777–778 Search PubMed.
- G. C. Mather, C. Dussarrat, J. Etourneau and A. R. West, J. Mater. Chem., 2000, 10, 2219–2230 RSC.
- M. Bianchini, J. Wang, R. J. Clément, B. Ouyang, P. Xiao, D. Kitchaev, T. Shi, Y. Zhang, Y. Wang, H. Kim, M. Zhang, J. Bai, F. Wang, W. Sun and G. Ceder, Nat. Mater., 2020, 19, 1088–1095 CrossRef CAS.
- A. R. West, Solid State Chemistry and its Applications, Wiley, 2nd edn, 2014 Search PubMed.
- E. Rathore, R. Juneja, S. P. Culver, N. Minafra, A. K. Singh, W. G. Zeier and K. Biswas, Chem. Mater., 2019, 31, 2106–2113 CrossRef CAS.
- D. H. Fabini, G. Laurita, J. S. Bechtel, C. C. Stoumpos, H. A. Evans, A. G. Kontos, Y. S. Raptis, P. Falaras, A. Van der Ven, M. G. Kanatzidis and R. Seshadri, J. Am. Chem. Soc., 2016, 138, 11820–11832 CrossRef CAS.
- G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Chem. Sci., 2017, 8, 5628–5635 RSC.
- E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis and S. J. L. Billinge, Science, 2010, 330, 1660 CrossRef.
- K. R. Knox, E. S. Bozin, C. D. Malliakas, M. G. Kanatzidis and S. J. L. Billinge, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 014102 CrossRef.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- J. Androulakis, S. C. Peter, H. Li, C. D. Malliakas, J. A. Peters, Z. Liu, B. W. Wessels, J.-H. Song, H. Jin, A. J. Freeman and M. G. Kanatzidis, Adv. Mater., 2011, 23, 4163–4167 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press LLC, Boca Raton, FL, 99th edn, 2018 Search PubMed.
- W. Bludau, A. Onton and W. Heinke, J. Appl. Phys., 1974, 45, 1846–1848 CrossRef CAS.
- G. Fonthal, L. Tirado-Mejía, J. I. Marín-Hurtado, H. Ariza-Calderón and J. G. Mendoza-Alvarez, J. Phys. Chem. Solids, 2000, 61, 579–583 CrossRef CAS.
- I. Spanopoulos, I. Hadar, W. Ke, Q. Tu, M. Chen, H. Tsai, Y. He, G. Shekhawat, V. P. Dravid, M. R. Wasielewski, A. D. Mohite, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 5518–5534 CrossRef CAS.
- V. Stevanović, S. Lany, D. S. Ginley, W. Tumas and A. Zunger, Phys. Chem. Chem. Phys., 2014, 16, 3706–3714 RSC.
- H. Tang, H. Berger, P. E. Schmid, F. Lévy and G. Burri, Solid State Commun., 1993, 87, 847–850 CrossRef CAS.
- M. G. Kanatzidis, Phosphorus, Sulfur Silicon Relat. Elem., 1994, 93, 159–172 CrossRef.
- K.-W. Kim and M. G. Kanatzidis, J. Am. Chem. Soc., 1998, 120, 8124–8135 CrossRef CAS.
- Y.-J. Lu and J. A. Ibers, Comments Inorg. Chem., 1993, 14, 229–243 CrossRef CAS.
- E. G. Tulsky and J. R. Long, Chem. Mater., 2001, 13, 1149–1166 CrossRef CAS.
- A. F. Trippel, V. B. Lazarev and S. I. Berul, Zh. Neorg. Khim., 1978, 23, 707–710 CAS.
- B. Eisenmann and H. Schäfer, Z. Anorg. Allg. Chem., 1979, 456, 87–94 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- D. E. Bugaris, D. M. Wells, J. Yao, S. Skanthakumar, R. G. Haire, L. Soderholm and J. A. Ibers, Inorg. Chem., 2010, 49, 8381–8388 CrossRef CAS.
- K. Cenzual, L. M. Gelato, M. Penzo and E. Parthe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 433–439 CrossRef.
- H. A. Graf and H. Schäfer, Z. Anorg. Allg. Chem., 1975, 414, 211–219 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2003740–2003742. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04562d |
| This journal is © The Royal Society of Chemistry 2021 |