Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Signal-enhanced real-time magnetic resonance of enzymatic reactions at millitesla fields†
Sergey
Korchak
 ab,
Anil P.
Jagtap
ab and
Stefan
Glöggler
*ab
ab,
Anil P.
Jagtap
ab and
Stefan
Glöggler
*ab
aNMR Signal Enhancement Group, Max-Planck-Insitute for Biophysical Chemistry, Am Faßberg 11, 37077 Göttingen, Germany. E-mail: stefan.gloeggler@mpibpc.mpg.de
bCenter for Biostructural Imaging of Neurodegeneration of UMG, Von-Siebold-Str. 3A, 37075 Göttingen, Germany
First published on 30th October 2020
Abstract
The phenomenon of nuclear magnetic resonance (NMR) is widely applied in biomedical and biological science to study structures and dynamics of proteins and their reactions. Despite its impact, NMR is an inherently insensitive phenomenon and has driven the field to construct spectrometers with increasingly higher magnetic fields leading to more detection sensitivity. Here, we are demonstrating that enzymatic reactions can be followed in real-time at millitesla fields, three orders of magnitude lower than the field of state-of-the-art NMR spectrometers. This requires signal-enhancing samples via hyperpolarization. Within seconds, we have enhanced the signals of 2-13C-pyruvate, an important metabolite to probe cancer metabolism, in 22 mM concentrations (up to 10.1% ± 0.1% polarization) and show that such a large signal allows for the real-time detection of enzymatic conversion of pyruvate to lactate at 24 mT. This development paves the pathways for biological studies in portable and affordable NMR systems with a potential for medical diagnostics.
Introduction
Nuclear magnetic resonance (NMR) is a versatile technique routinely applied in chemical analysis, structural biology and for medical diagnosis.1–3 Due to small energy differences of nuclear spin populations only a few spins per million contribute to the observable NMR signal even in state-of-the-art superconducting high-field magnets.3 Overpopulating one specific spin state beyond thermal equilibrium limitations allows enhancing NMR signals by several orders of magnitude. This process is referred to as hyperpolarization.4–28 While hyperpolarization has gained a lot of attention in the past decades, especially in biological sciences and in combination with high-field NMR and magnetic resonance imaging (MRI), it also offers potential for technological advances at very low to zero magnetic fields and not only for typical Faraday detectors.29–31 It especially offers potential for more sensitive magnetic field sensor technologies that have matured in recent years and include: atomic magnetometers (AM),32–36 superconducting quantum interferences devices (SQUIDs)37–39 and nitrogen vacancy (NV) diamond magnetometers.40–47 All of these sensors operate best at very low magnetic fields ranging from several millitesla (SQUID and NV magnetometers) to zero-field (AM), the so-called zero and ultra-low field regime (ZULF) starting on the order of 10 millitesla. It was shown, that NMR spectroscopy can be performed with all of the described sensors in the ZULF regime.32,33,37,41 In order to obtain sufficient signal, prepolarization at high magnetic fields or long averaging times are necessary. Additionally, some examples were demonstrated in which hyperpolarization enhances signals that can be rapidly detected at low magnetic fields.29–31,33,39 Although the hyperpolarized metabolites were Faraday detected at as low as 47 mT field and even in vivo,29 no enzymatic conversion in millitesla fields resolving different metabolites and desired kinetic parameters was demonstrated. Proof of principle experiments to monitor enzymatic reactions would pave pathways for efficient, low-cost and portable analytical and medical devices with the potential to detect the metabolism of single cells in real-time via e.g. NV-diamond sensors.In this article, we demonstrate that the enzymatic conversion of hyperpolarized 2-13C-pyruvate into 2-13C-lactate can be monitored in real-time at millitesla fields. Pyruvate is an important metabolite and is currently investigated in clinical hyperpolarization studies as a probe for cancer.28 Even at such low magnetic fields, we obtain high-resolution NMR spectra containing information of different chemical moieties via the chemical shift parameter and the electron-mediated spin–spin (J-) coupling. Based on the highly resolved real-time NMR experiments we are able to devise kinetic parameters of the enzymatic pyruvate–lactate conversion in a portable low field (millitesla) NMR system without the requirement of a dedicated high-field magnet.
In our study, we have accomplished to hyperpolarize 2-13C-pyruvate-d3 (Fig. 1) within seconds using para-hydrogen induced polarization (PHIP)9,10,13 to 10.1% ± 0.1% in 22 mM concentrations. PHIP relies on the conversion of singlet spin order of para-hydrogen into observable magnetization.17 This can be performed via a pairwise hydrogen addition to unsaturated bonds. As unsaturated precursors are not available for many relevant metabolites, the concept of PHIP-SAH (PHIP by means of sidearm hydrogenation) was introduced.13 It requires to combine a metabolite of interest and an unsaturated side chain as a chemical precursor. The side chain can be hydrogenated with para-hydrogen and the spin order subsequently transferred to a nucleus of interest within the metabolite. Rapid chemical cleavage of the side chain releases the metabolite for biological investigations. Here, we have achieved the efficient hyperpolarization of 2-13C-pyruvate-d3 with para-hydrogen by combining a rational side chain design and polarization transfer via the ESOTHERIC experiment (efficient spin order transfer to heteronuclei via relayed INEPT chains).19,20 Details on the procedure are described in the ESI.† One feature to achieve high levels of polarization was to deuterate the pyruvate to remove additional 1H–13C-couplings, which may affect the pulsed transfer experiment. The transfer was conducted in a commercial spectrometer at 7 T.19 The hyperpolarization results of 22 mM 2-13C-pyruvate-d3 are depicted in Fig. 1. Overall we achieve an average polarization of 10.1% which corresponds to a signal enhancement of about 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900-fold compared to the thermal spectrum at a magnetic field of B0 = 7 T or about 5 million enhancement factor at 24 mT.
900-fold compared to the thermal spectrum at a magnetic field of B0 = 7 T or about 5 million enhancement factor at 24 mT.
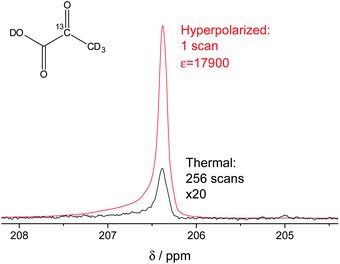 | ||
Fig. 1 Signal enhanced 2-13C-pyruvate-d3. Red: 13C-NMR spectrum of hyperpolarized free 2-13C-pyruvate-d3 detected at B0 = 7 T and 320 K in a single scan with a 90° pulse after hydrolysis of the hydrogenation product using a carbonate solution (pH ∼ 10). Black: Thermally polarized 13C-NMR spectrum of the same sample and at the same conditions with 256 scans, 300 s repetition time and 20-fold enlarged. The signal enhancement corresponds to 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900-fold at the given field. The hyperpolarization here corresponds to 10.2% with 10.1% on average over 3 experiments. Only a minor amount of side products are seen after hydrolysis (see also Fig. S5†). 900-fold at the given field. The hyperpolarization here corresponds to 10.2% with 10.1% on average over 3 experiments. Only a minor amount of side products are seen after hydrolysis (see also Fig. S5†). | ||
Results and discussion
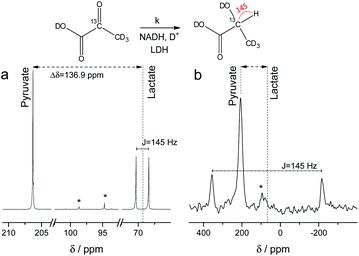
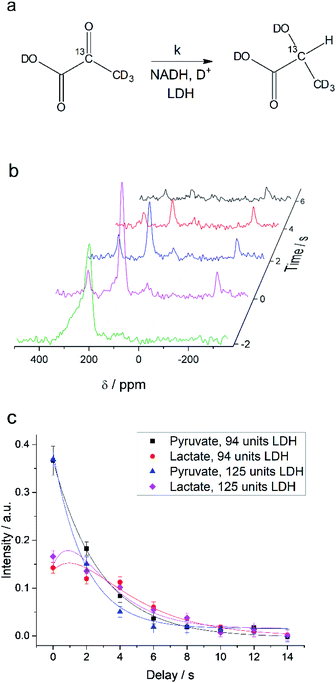
NMR setups working at millitesla magnetic fields experience lower chemical shift resolution, because the chemical shift is linear dependent on the magnetic field. However, the spin–spin interaction is independent of the magnetic field and in particular heteronuclear J-couplings such as the 1H–13C-coupling can be resolved even at zero-field to perform high-resolution NMR.48 We are exploring this fact here to distinguish between 2-13C-pyruvate-d3 and 2-13C-lactate-d3. Since the perdeuterated pyruvate does not contain any 1H–13C couplings we expect one major peak that is slightly broadened by the three deuterium interacting with the 13C spin. When 2-13C-pyruvate is enzymatically converted into 2-13C-lactate in the presence of protonated nicotinamide adenine dinucleotide (NADH), one proton is introduced into the molecule leading to a dominant 1H–13C coupling of 145 Hz. The difference in J-couplings of these pyruvate and lactate can then be used to distinguish them even without chemical shift difference. We have explored this pyruvate–lactate conversion starting from hyperpolarized 2-13C-pyruvate-d3 and the results for experiments at high-field (7 T) and low-field (24 mT) are depicted in Fig. 2. Hyperpolarized 2-13C-pyruvate-d3 is transformed into 2-13C-lactate-d3 under the action of lactate dehydrogenase (LDH) in presence of the reduced form of nicotinamide adenine dinucleotide (NADH). At high field (Fig. 2a), the 13C species of 2-13C-pyruvate-d3 and 2-13C-lactate-d3 are well separated by a large chemical shift difference of 136.9 ppm which corresponds to a frequency difference of about 10 kHz (B0 = 7 T). In addition, the large heteronuclear 1H–13C-coupling is observed. At low field (Fig. 2b), the large heteronuclear J-coupling of lactate allows to distinguish it from the pyruvate signal. We note that we achieve a linewidth of 4 Hz for 13C in our low field setup which is a limitation given by the stability of the applied current source and residual couplings to the deuterons. The homogeneity hence amounts to 15 ppm (with residual 2H–13C J-coupling broadening) over the sample volume. Due to the large chemical shift difference of 136.9 ppm and a field homogeneity of 15 ppm, we are even able to resolve the chemical shift difference between lactate and pyruvate. At 24 mT, the frequency difference amounts to 27.4 Hz which is well above the linewidth and hence resolvable as indicated in Fig. 2b. Additionally, the observable chemical shift difference allows to distinguish the desired peaks from minor cleavage side-products and the hydrated form of pyruvate. Overall, the hyperpolarized spectra at 24 mT yield the same information in single scan experiments as in the high magnetic field.Interconversion of hyperpolarized pyruvate and lactate is currently investigated in hyperpolarized cancer studies as sensor for elevated metabolism.28 This metabolic step is promoted by lactate dehydrogenase and is schematically depicted in Fig. 3a. At 24 mT we are able to follow this conversion in real-time (Fig. 3b) due to the possibility of distinguishing 2-13C-pyruvate and 2-13C-lactate via the heteronuclear J-coupling and chemical shift difference. In Fig. 3c we show averaged decay curves of 2-13C-pyruvate-d3 and build-up of 2-13C-lactate-d3 derived from low-field experiments. The real-time dynamics for each repetition are shown in the ESI.† In Fig. 3b, we have acquired a signal of the initial 2-13C-pyruvate-d3 with a low flip angle pulse and before addition of the enzyme. After injection of the enzyme the reaction starts and the lactate signals appear. We probe the reaction in increments of two seconds following small flip angles leaving the most magnetization intact, thus allowing for deriving a parameter to evaluate the reaction kinetics (Fig. 3c).
Evaluating the kinetics of pyruvate to lactate have been a challenging task in pure enzymatic reactions with LDH over the past decades.49 Fortunately, no substrate inhibition under our conditions were operative because the pyruvate is freshly generated by hydrolysis and has no time to form a ternary complex with NAD+ and LDH during 16 s of the overall enzymatic reaction time.50 At low concentrations, first order reaction takes place according to the Michaelis–Menten equation. Due to the so obtained concentration dependence of pyruvate we have investigated whether a first order derived kinetic model is suitable to extract relevant reaction parameters of the reaction.51 We would like to note that the obtained apparent reaction rate constant will only serve as a parameter to differentiate between LDH concentrations. Assuming excess of NADH and first order kinetics with respect to the pyruvate concentration, the reaction catalyzed by LDH is the following:
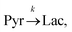 | (1) |
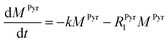 | (2) |
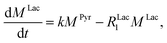 | (3) |
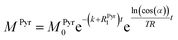 | (4) |
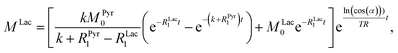 | (5) |
With respect to the kinetic model we would like to emphasize, that the conversion rates differ by only 25% which is proportional to the LDH concentration indicating that thus determined reaction constant k can serve as measure of quantity of the enzyme. As a result, the presented experiments demonstrate that the real-time kinetics of enzymatic conversion can be measured and kinetic parameters determined via hyperpolarized NMR at very low magnetic fields. The fits for each real-time experiment are shown in the ESI† where different LDH concentrations provide different conversion rate constants.
Experimental
Unsaturated precursor of 2-13C pyruvate was synthesized according to procedure described in the ESI† and in the literature. All non-synthesized chemicals were obtained from Sigma-Aldrich. Lactate dehydrogenase is from porcine heart. A solution of 1 μL of the precursor in 0.1 ml C2H5OD (44 mM) together with hydrogenation catalyst ([1,4-bis(diphenylphosphino)butane] (1,5-cyclooctadiene)rhodium(I) tetrafluoroborate) (1 mM) was placed into a 5 mm NMR tube and was hydrogenated with 83% para-enriched hydrogen gas (Bruker PHG 90) inside the 5 mm probehead of a 7 T Bruker (Avance III) spectrometer at 320 K. The hydrogen gas was delivered to the solution using a home-build, automated setup. Using a modified ESOTHERIC pulse sequence, the polarization was transferred from protons to the 2-13C-enriched pyruvate moiety. Then 0.1 ml 100 mM Na2CO3 solution in D2O was added to cleave the side chain and to obtain free and hyperpolarized pyruvate. The enzymatic reaction was conducted inside the low field setup after transfer of the sample. 0.3 mL 30 μL mL−1 LDH (94 units per experiment) or 40 μL mL−1 LDH (125 units per experiment), 20 mM NADH and 20% HEPES (1 M) dissolved in D2O was added to hyperpolarized pyruvate solution to initiate the conversion. The low field setup consists of a custom made temperature stabilized electromagnet generating a 24 mT field using a commercial power supply with 10 ppm stability. The low field spectrometer is a Magritek Kea.2 More experimental details and synthetic procedures can be found in the ESI.†Conclusions
In this work we have introduced the feasibility to perform real-time kinetic experiments of an enzymatic conversion combining hyperpolarization and NMR at very low magnetic fields (millitesla) utilizing distinctive spin–spin couplings of the metabolites. Foremost, our realization was achieved due to the possibility to obtain highly polarized 2-13C-pyruvate-d3 generated in seconds using para-hydrogen. Modeling the acquired data allowed us to obtain the rate constant of the enzymatic conversion from pyruvate to lactate that follows LDH concentration. This reaction is especially relevant because a prominent pyruvate–lactate metabolism is observed in cancer cells and tumors and hyperpolarized pyruvate (1-13C- and 2-13C-pyruvate) is being assessed in clinical studies for disease detection. It is worth to mention that our approach is not limited to perdeuterated pyruvate but can be applied to protonated 1-13C- and 2-13C-pyruvate by further optimizing the ESOTHERIC pulse sequence. As a consequence of our results, we believe that a series of new applications will emerge allowing for portable low field magnetic resonance to detect diseases in combination with hyperpolarization. This includes affordable low field magnetic resonance imaging (MRI) devices.55 Lastly, we foresee that analytical possibilities will be unlocked for ZULF-NMR in the future. This can be achieved by combining the presented method with highly sensitive detection schemes that include the EHQE (external-high-quality-enhanced) NMR approach for Faraday detection56 or the use of SQUIDs, atomic magnetometers and NV diamond magnetometers with the potential to measure real-time kinetics of metabolites in single cells.32–47Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding by the Max Planck Society and German Research Foundation (DFG) with grant number 418416679 and 426677227. We furthermore thank Dr Belov and the team of the synthesis facility and Rainer Schürkötter, Andreas Pucher-Diehl and the members of the precision mechanics team of the Max Planck Institute for Biophysical Chemistry for upscaling of the pyruvate precursor and help in building the low field NMR setup.Notes and references
- H. Günther, NMR Spectroscopy: Basic Principles, Concepts and Applications in Chemistry, 2013 Search PubMed.
- J. Cavanagh, W. J. Fairbrother, A. G. Palmer III and N. J. Skelton, Protein NMR Spectroscopy: Principles and Practice, Academic Press, 2nd edn, 2006 Search PubMed.
- R. W. Brown, Y. C. N. Cheng, E. M. Haake, M. R. Thompson and R. Venkatesan, Magnetic resonance imaging: physical principles and sequence design, Wiley, 2014 Search PubMed.
- V. S. Bajaj, M. L. Mak-Jurkauskas, M. Belenky, J. Herzfeld and R. G. Griffin, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9244–9249 CrossRef CAS.
- T. R. Eichhorn, Y. Takado, N. Salameh, A. Capozzi, T. Cheng, J.-N. Hyacinthe, M. Mishkovsky, C. Roussel and A. Comment, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18064 CrossRef CAS.
- X. Ji, A. Bornet, B. Vuichoud, J. Milani, D. Gajan, A. J. Rossini, L. Emsley, G. Bodenhausen and S. Jannin, Nat. Commun., 2017, 8, 13975 CrossRef CAS.
- A. Nardi-Schreiber, A. Gamliel, T. Harris, G. Sapir, J. Sosna, J. M. Gomori and R. Katz-Brull, Nat. Commun., 2017, 8, 341 CrossRef.
- S. Düwel, C. Hundshammer, M. Gersch, B. Feuerecker, K. Steiger, A. Buck, A. Walch, A. Haase, S. J. Glaser, M. Schwaiger and F. Schilling, Nat. Commun., 2017, 8, 15126 CrossRef.
- C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648 CrossRef CAS.
- T. C. Eisenschmid, R. U. Kirss, P. P. Deutsch, S. I. Hommeltoft, R. Eisenberg, J. Bargon, R. G. Lawler and A. L. Balch, J. Am. Chem. Soc., 1987, 109, 8089–8091 CrossRef CAS.
- M. Goldman, H. Jóhannesson, O. Axelsson and M. Karlsson, C. R. Chim., 2006, 9, 357–363 CrossRef CAS.
- R. W. Adams, J. A. Aguilar, K. D. Atkinson, M. J. Cowley, P. I. P. Elliott, S. B. Duckett, G. G. R. Green, I. G. Khazal, J. López-Serrano and D. C. Williamson, Science, 2009, 323, 1708–1711 CrossRef CAS.
- F. Reineri, T. Boi and S. Aime, Nat. Commun., 2015, 6, 5858 CrossRef CAS.
- S. Narasimhan, S. Scherpe, A. Lucini Paioni, J. Van Der Zwan, G. E. Folkers, H. Ovaa and M. Baldus, Angew. Chem., 2019, 131, 13103–13107 CrossRef.
- J. Eills, E. Cavallari, C. Carrera, D. Budker, S. Aime and F. Reineri, J. Am. Chem. Soc., 2019, 141, 20209–20214 CrossRef CAS.
- T. Theis, M. L. Truong, A. M. Coffey, R. V. Shchepin, K. W. Waddell, F. Shi, B. M. Goodson, W. S. Warren and E. Y. Chekmenev, J. Am. Chem. Soc., 2015, 137, 1404–1407 CrossRef CAS.
- J.-B. Hövener, A. N. Pravdivtsev, B. Kidd, C. R. Bowers, S. Glöggler, K. V. Kovtunov, M. Plaumann, R. Katz-Brull, K. Buckenmaier, A. Jerschow, F. Reineri, T. Theis, R. V. Shchepin, S. Wagner, P. Bhattacharya, N. M. Zacharias and E. Y. Chekmenev, Angew. Chem., Int. Ed., 2018, 57, 11140–11162 CrossRef.
- E. Cavallari, C. Carrera, M. Sorge, G. Bonne, A. Muchir, S. Aime and F. Reineri, Sci. Rep., 2018, 8, 8366 CrossRef.
- S. Korchak, S. Yang, S. Mamone and S. Glöggler, ChemistryOpen, 2018, 7, 344–348 CrossRef CAS.
- S. Korchak, S. Mamone and S. Glöggler, ChemistryOpen, 2018, 7, 672–676 CrossRef CAS.
- M. Suefke, S. Lehmkuhl, A. Liebisch, B. Blümich and S. Appelt, Nat. Phys., 2017, 13, 568 Search PubMed.
- P. T. Judge, E. L. Sesti, L. E. Price, B. J. Albert, N. Alaniva, E. P. Saliba, T. Halbritter, S. T. Sigurdsson, G. B. Kyei and A. B. Barnes, J. Phys. Chem. B, 2020, 124, 2323–2330 CrossRef CAS.
- G. Zhang, S. Ahola, M. H. Lerche, V.-V. Telkki and C. Hilty, Anal. Chem., 2018, 90, 11131–11137 CrossRef CAS.
- J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef.
- K. Golman, R. i. t. Zandt, M. Lerche, R. Pehrson and J. H. Ardenkjaer-Larsen, Cancer Res., 2006, 66, 10855–10860 CrossRef CAS.
- S. E. Day, M. I. Kettunen, F. A. Gallagher, D.-E. Hu, M. Lerche, J. Wolber, K. Golman, J. H. Ardenkjaer-Larsen and K. M. Brindle, Nature Medicine, 2007, 13, 1382–1387 CrossRef CAS.
- S. Jannin, A. Bornet, R. Melzi and G. Bodenhausen, Chem. Phys. Lett., 2012, 549, 99–102 CrossRef CAS.
- S. J. Nelson, J. Kurhanewicz, D. B. Vigneron, P. E. Z. Larson, A. L. Harzstark, M. Ferrone, M. van Criekinge, J. W. Chang, R. Bok, I. Park, G. Reed, L. Carvajal, E. J. Small, P. Munster, V. K. Weinberg, J. H. Ardenkjaer-Larsen, A. P. Chen, R. E. Hurd, L.-I. Odegardstuen, F. J. Robb, J. Tropp and J. A. Murray, Sci. Transl. Med., 2013, 5, 198ra108 Search PubMed.
- A. M. Coffey, K. V. Kovtunov, D. A. Barskiy, I. V. Koptyug, R. V. Shchepin, K. W. Waddell, P. He, K. A. Groome, Q. A. Best, F. Shi, B. M. Goodson and E. Y. Chekmenev, Anal. Chem., 2014, 86, 9042–9049 CrossRef CAS.
- A. M. Coffey, R. V. Shchepin, M. L. Truong, K. Wilkens, W. Pham and E. Y. Chekmenev, Anal. Chem., 2016, 88, 8279–8288 CrossRef CAS.
- A. M. Coffey, M. A. Feldman, R. V. Shchepin, D. A. Barskiy, M. L. Truong, W. Pham and E. Y. Chekmenev, J. Magn. Reson., 2017, 281, 246–252 CrossRef CAS.
- D. A. Barskiy, M. C. D. Tayler, I. Marco-Rius, J. Kurhanewicz, D. B. Vigneron, S. Cikrikci, A. Aydogdu, M. Reh, A. N. Pravdivtsev, J.-B. Hovener, J. W. Blanchard, T. Wu, D. Budker and A. Pines, Nat. Commun., 2019, 10, 1–9 CrossRef CAS.
- T. Theis, P. Ganssle, G. Kervern, S. Knappe, J. Kitching, M. Ledbetter, D. Budker and A. Pines, Nat. Phys., 2011, 7, 571–575 Search PubMed.
- M. Ledbetter, I. Savukov, D. Budker, V. Shah, S. Knappe, J. Kitching, D. Michalak, S. Xu and A. Pines, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2286–2290 CrossRef CAS.
- I. Kominis, T. Kornack, J. Allred and M. V. Romalis, Nature, 2003, 422, 596–599 CrossRef CAS.
- H. Dang, A. C. Maloof and M. V. Romalis, Appl. Phys. Lett., 2010, 97, 151110 CrossRef.
- R. McDermott, A. H. Trabesinger, M. Mück, E. L. Hahn, A. Pines and J. Clarke, Science, 2002, 295, 2247–2249 CrossRef CAS.
- B. Inglis, K. Buckenmaier, P. SanGiorgio, A. F. Pedersen, M. A. Nichols and J. Clarke, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19194–19201 CrossRef CAS.
- S.-J. Lee, K. Jeong, J. H. Shim, H. J. Lee, S. Min, H. Chae, S. K. Namgoong and K. Kim, Sci. Rep., 2019, 9, 1–8 CrossRef.
- C. Müller, X. Kong, J.-M. Cai, K. Melentijević, A. Stacey, M. Markham, D. Twitchen, J. Isoya, S. Pezzagna and J. Meijer, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- D. R. Glenn, D. B. Bucher, J. Lee, M. D. Lukin, H. Park and R. L. Walsworth, Nature, 2018, 555, 351–354 CrossRef CAS.
- A. Ajoy, B. Safvati, R. Nazaryan, J. Oon, B. Han, P. Raghavan, R. Nirodi, A. Aguilar, K. Liu and X. Cai, Nat. Commun., 2019, 10, 1–12 CrossRef CAS.
- P. Kehayias, A. Jarmola, N. Mosavian, I. Fescenko, F. M. Benito, A. Laraoui, J. Smits, L. Bougas, D. Budker and A. Neumann, Nat. Commun., 2017, 8, 1–8 CrossRef CAS.
- J. Smits, J. T. Damron, P. Kehayias, A. F. McDowell, N. Mosavian, I. Fescenko, N. Ristoff, A. Laraoui, A. Jarmola and V. M. Acosta, Sci. Adv., 2019, 5, eaaw7895 CrossRef CAS.
- D. B. Bucher, D. P. A. Craik, M. P. Backlund, M. J. Turner, O. B. Dor, D. R. Glenn and R. L. Walsworth, Nat. Protoc., 2019, 2707–2747 CrossRef CAS.
- A. Ajoy, K. Liu, R. Nazaryan, X. Lv, P. R. Zangara, B. Safvati, G. Wang, D. Arnold, G. Li and A. Lin, Sci. Adv., 2018, 4, eaar5492 CrossRef.
- G. Balasubramanian, I. Chan, R. Kolesov, M. Al-Hmoud, J. Tisler, C. Shin, C. Kim, A. Wojcik, P. R. Hemmer and A. Krueger, Nature, 2008, 455, 648–651 CrossRef CAS.
- S. Appelt, F. Häsing, U. Sieling, A. Gordji-Nejad, S. Glöggler and B. Blümich, Phys. Rev. A, 2010, 81, 023420 CrossRef.
- P. Tang, J. Xu, C. L. Oliveira, Z. J. Li and S. Liu, J. Enzyme Inhib. Med. Chem., 2017, 32, 564–571 CrossRef CAS.
- J. Everse, R. E. Barnett, C. J. Thorne and N. O. Kaplan, Arch. Biochem. Biophys., 1971, 143, 444–460 CrossRef CAS.
- H. Zeng, Y. Lee and C. Hilty, Anal. Chem., 2010, 82, 8897–8902 CrossRef CAS.
- C. Taglang, D. E. Korenchan, C. von Morze, J. Yu, C. Najac, S. Wang, J. E. Blecha, S. Subramaniam, R. Bok, H. F. VanBrocklin, D. B. Vigneron, S. M. Ronen, R. Sriram, J. Kurhanewicz, D. M. Wilson and R. R. Flavell, Chem. Commun., 2018, 54, 5233–5236 RSC.
- B. T. Chung, H.-Y. Chen, J. Gordon, D. Mammoli, R. Sriram, A. W. Autry, L. M. Le Page, M. Chaumeil, P. Shin, J. Slater, C. T. Tan, C. Suszczynski, S. Chang, Y. Li, R. A. Bok, S. M. Ronen, P. Ez Larson, J. Kurhanewicz and D. B. Vigneron, J. Magn. Reson., 2019, 106617, DOI:10.1016/j.jmr.2019.106617.
- J. M. Park, S. Josan, T. Grafendorfer, Y.-F. Yen, R. E. Hurd, D. M. Spielman and D. Mayer, NMR Biomed., 2013, 26, 1197–1203 CrossRef CAS.
- D. E. Waddington, T. Boele, R. Maschmeyer, Z. Kuncic and M. S. Rosen, Sci. Adv., 2020, 6, eabb0998 CrossRef CAS.
- M. Suefke, A. Liebisch, B. Blümich and S. Appelt, Nat. Phys., 2015, 11, 767–771 Search PubMed.
- S. Korchak, M. Emondts, S. Mamone, B. Blümich and S. Glöggler, Phys. Chem. Chem. Phys., 2019, 21, 22849–22856 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedure and characterization, NMR experiments. See DOI: 10.1039/d0sc04884d |
| This journal is © The Royal Society of Chemistry 2021 |