Molecular control over vitrimer-like mechanics – tuneable dynamic motifs based on the Hammett equation in polyimine materials

Abstract

In this work, we demonstrate that fine-grained, quantitative control over macroscopic dynamic material properties can be achieved using the Hammett equation in tuneable dynamic covalent polyimine materials. Via this established physical-organic principle, operating on the molecular level, one can fine-tune and control the dynamic material properties on the macroscopic level, by systematic variation of dynamic covalent bond dynamics through selection of the appropriate substituent of the aromatic imine building blocks. Five tuneable, crosslinked polyimine network materials, derived from dianiline monomers with varying Hammett parameter (σ) were studied by rheology, revealing a distinct correlation between the σ value and a range of corresponding dynamic material properties. Firstly, the linear correlation of the kinetic activation energy (E_a) for the imine exchange to the σ value, enabled us to tune the E_a from 16 to 85 kJ mol⁻¹. Furthermore, the creep behaviour (γ), glass transition (T_g) and the topology freezing transition temperature (T_v), all showed a strong, often linear, dependence on the σ value of the dianiline monomer. These combined results demonstrate for the first time how dynamic material properties can be directly tuned and designed in a quantitative – and therefore predictable – manner through correlations based on the Hammett equation. Moreover, the polyimine materials were found to be strong elastic rubbers (G′ > 1 MPa at room temperature) that were stable up to 300 °C, as confirmed by TGA. Lastly, the dynamic nature of the imine bond enabled not only recycling, but also intrinsic self-healing of the materials over multiple cycles without the need for solvent, catalysts or addition of external chemicals.

---

Introduction

Dynamic covalent (DC) bonds, which combine chemical strength with reversible formation under conditions of equilibrium control,¹ have gained a tremendous interest in several sub-disciplines of chemistry, such as in self-assembly of macromolecular architectures, reversible formation of molecular cages and containers, and in the design of molecular motors.^1–6 In recent years, DC chemistry has also become an important tool for the development of new ‘smart’ polymer materials that are, for example, renewable, self-healing, reprocessable or shape transformable.^7–13 When DC bonds are included into crosslinked polymeric materials, covalent adaptable networks (CANs) can be synthesised.^14,15 These CANs are thermosets, as they are covalently crosslinked polymer networks. However, in contrast to non-reversible classical thermosets, CANs can be recycled and reprocessed due to bond exchange reactions (BERs) of the DC bonds. Several BERs in polymers have been investigated, like transesterifications,^16,17 reversible Diels–Alder reactions,^18–21 disulphide exchange,^22–25 boronic ester exchange,^26–29 urea exchange,^30,31 and imine exchange.^32–36

While the choice of type of BER can affect the dynamic material properties, other, more fine-grained approaches are still needed to allow careful, bottom-up design of dynamic polymer materials. In this regard it should be noted that the dynamics of the reversible covalent bonds within CANs are a key factor in the function of a dynamic polymeric material.³⁷ Control over the material properties at the macroscopic level can thus be traced back to controlling the behaviour of the dynamic covalent bonds at the molecular level.^{7,14,31,38,39} In other research domains, such as liquid-crystalline materials,^40,41 supramolecular chemistry,⁴² organic photovoltaic devices,^43,44 colloidal systems,⁴⁵ and metamaterials,^46–48 this hierarchical translation of (molecular) structure to macroscopic material properties has already proven essential in offering bottom-up material design. However, for CANs this approach is still underexplored. Therefore, a core topic of interest for the tunability of CANs and their corresponding designability, is to find a delicate handle on how small changes in the molecular structure of the polymer can be translated to changes in – and ultimately control over – macroscopic physical properties of the material.³⁷ A number of promising initial efforts has already been made to tune the material properties of CANs and broaden their range of applications. Recent examples include the effect of sterics and degree of crosslinking for poly(alkylurea-urethane) networks,³¹ choice of electronically activated crosslinkers for thiol-yne⁴⁹ and thiol-ene⁵⁰ networks, and the effect of telechelic neighbouring groups in boronic ester transesterifications.²⁶ Additionally, the introduction of block copolymer vitrimers showed to be an effective method for topology control over viscoelastic flow.⁵¹ These studies show a promising guide for molecular tunability of CANs, however a systematic, more quantitative approach, that even allows for correlation of a given dynamic material property to a molecular descriptor, has yet to be designed. Herein, we show that the established physical-organic, molecule-based, concept defined by the Hammett equation^52–55 can be exploited to achieve quantitatively predictable and subtle chemical control over macroscopic material properties. Our results indicate that introduction of the Hammett equation in polyimines offers a powerful toolbox for making cheap, tuneable, and recyclable materials suitable for a wide range of applications.

Imines – sometimes referred to as Schiff bases⁵⁶ – are commonly synthesised via a condensation reaction of an aldehyde and amine. This reaction is reversible, and is very dependent on the stability of the imine bond.⁴ When water is removed, or when the imine bond is sufficiently stable, this reverse reaction can be prevented. Imines show two more reversible exchange reactions: transimination, which requires free amine groups, and imine metathesis, which occurs between two imines.⁵ Once these exchangeable imine bonds are included into a polymer matrix, a dynamic polyimine CAN is constructed.^32,57 Polyimine CANs have gained a tremendous interest in research and industry due to the potential to synthesis strong yet recyclable materials.^32,58,59 They are also favourable materials, as a broad variety of monomers is commercially available, as well as for the potential to obtain these from bio-based sources.^60,61 Polyimine materials have been studied for a broad variety of applications, like fire-resistance,^62,63 3D printing,⁶⁴ sensing,^65,66 CO₂ capture,^67–69 antibacterial coatings,⁷⁰ and in the production of electronic skins.⁷¹

Some attempts in tuning the material properties of polyimines have been documented: for example by tuning the degree of crosslinking,^72,73 sub-chain composition,^36,59,74,75 solvent,^34,76 or metal-coordination.^35,65,77 These attempts have produced a number of interesting results, but focussed more on the composition of the polymer matrix rather than on the dynamics of the imine bond itself. Therefore, we propose to tune the intrinsic dynamics of the DC bonds in polyimines via the electronic effect of substituted aromatic imines, derived from anilines. The reactivity of these imines depends on the nature of the substituent on the aromatic ring, as can be described by the Hammett equation.^52,53 Kovaříček and Lehn demonstrated a similar Hammett equation-based concept by studying the imine exchange in small molecules, finding differences in exchange rates varying by more than three orders of magnitude for different substituents.⁷⁸ Similarly, Schultz and Nitschke relied on the Hammett equation to control imine exchange reactions in multistep transformation in Cu(I):imine complexes.⁷⁹ An extension of such control over DC bond exchange, based on the Hammett equation, to imine-derived polymers can therefore offer a (systematically) controllable molecular handle for material tunability on the macroscopic level.

To demonstrate the extensive control over material properties offered by substituent effect in CANs, we selected a set of tuneable dianiline monomers (XDAs), where the effective (i.e. tuneable) substituents are the bridging atoms between the two aniline moieties (Chart 1). These tuneable dianiline monomers are ideal building blocks for polymeric materials, given their wide commercial availability, and the option to focus exclusively on electronic (rather than mixed electronic-steric) effects. To complete the network formation of our tuneable polyimine P-XDA materials, terephthalaldehyde (TA), tris(2-aminoethyl)amine (TREN) and 4,7,10-trioxa-1,13-tridecanediamine (TOTDDA) were included.

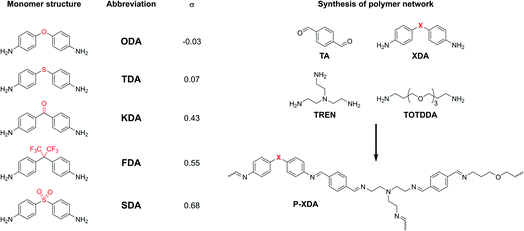Chart 1 (Left) Overview of tuneable dianiline monomers and (Right) construction of the polyimine network. Dianiline monomers will be referred to by their abbreviation (XDA) and the corresponding polymers will be referred by the same abbreviation, but preceded by the letter ‘P’ (P-XDA). The value for the Hammett parameter (σ) for each of the XDA monomers was taken from structurally highly related reference compounds (Chart S1†).^53,54

For this study, five dianiline monomers were selected from a list of commercially available dianilines, based on a wide range of electron-donating or -withdrawing effects that the bridging moieties provide. These effects are expressed by their corresponding Hammett parameter (σ), where a higher σ value relates to a more electron-withdrawing effect (σ values are listed in Chart 1). As the imine bonds are stabilised by resonance via the aromatic rings, we hypothesised that more electron-donating substituents (lower σ) result in more stable and electron-rich imine bonds, and therefore, create tougher materials when incorporated into a polyimine network.

We quantitatively verify these hypotheses here by showing a direct correlation between the Hammett parameter and a range of material properties of direct relevance, such as glass transition temperature, topology freezing temperature, relaxation behaviour and kinetic activation energy for the imine exchange. The correlation of the Hammett parameter to various material properties thus shows to be a delicate, yet directly applicable handle to tune the dynamic behaviour of polyimine CANs. Furthermore, material recycling over multiple cycles was achieved without loss in material properties, and without the need of catalysts or other reagents. Also autonomous self-healing behaviour was observed as cut samples were able to regrow back together and retain their material properties.

Results and discussion

Small-molecule exchange studies

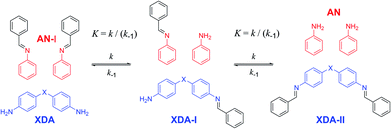
As a proof of concept, small-molecule studies were initially carried out for all tuneable dianilines before their inclusion into polymers. The correlation between the σ value of the substituent on the aniline ring and the equilibrium constant (K) of the exchange reaction (Scheme 1) was first investigated using ¹H NMR spectroscopy. A reference imine (AN-I) from benzaldehyde and aniline was synthesised and dissolved in CDCl₃. To this solution 0.5 equivalents of the tuneable dianiline (XDA) was added to obtain a 1 : 1 imine : amine ratio.

Scheme 1 Exchange reaction of aromatic imine with tuneable dianiline monomers. For the equilibrium studies (to determine K) 0.5 equivalents of XDA, with respect to AN-I was added to obtain a 1 : 1 imine : amine ratio. For the kinetic studies (to determine k) 5 equivalents of XDA were added to obtain a 1 : 10 imine : amine ratio.

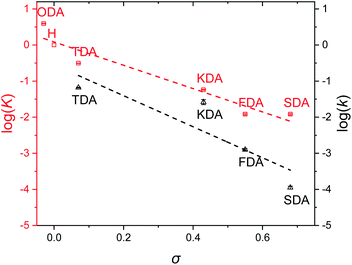
Once equilibrium had been reached, the overall equilibrium constant (K) was calculated via integration of the relevant ¹H NMR signals of the presented compounds, assuming the two consecutive exchange reactions occur independently from each other (Table S1†).⁷⁹ To obtain a Hammett plot, the obtained K values for all dianilines were plotted on a logarithmic scale as a function of σ (Fig. 1, red squares).^54,55 A trendline was then fitted through the individual data points, showing a linear correlation in which a lower σ results in a higher log K value. As a lower σ translates to a more electron-donating effect, this effectively means that more strongly electron-donating substituents push the equilibrium reaction (Scheme 1) towards the right (formation of XDA-II). The Hammett reaction constant (ρ) – representing the sensitivity of the reaction towards the substituent effect – was determined from the slope of the fit to be −3.1 ± 0.3.⁸⁰ Such a value is typical for reactions in which aromatic ring conjugated electrons are involved in forming a new bond.⁸⁰

Fig. 1 Hammett plots of imine exchange reactions for studied tuneable dianilines, showing the equilibrium constant (K, red squares) and the rate constant (k, black triangles) as a function of σ. The correlations are visualised by fitting a linear trendline. For the kinetic studies, the solvent was changed from CDCl₃ to acetone-d₆ as a consequence of poorer solubility of the dianilines due to the higher required concentration. For the same reason, ODA was excluded from this experiment.

Reaction rate constants (k) were also obtained for the dianiline monomers to investigate their dependence on the Hammett parameter. For this experiment, the same exchange reaction (Scheme 1) was carried out. However, the reference imine (AN-I) was reacted with 5 equivalents of dianiline (meaning 10 equivalents of amine groups) to obtain a pseudo first-order reaction. The conversion of the AN-I into XDA-II was followed over time by ¹H NMR, typically from the imine proton signal (Fig. S1–S5†). From this data, the first-order rate constant (k) was determined for all tuneable dianilines, and subsequently plotted as a function of σ (Fig. 1, black triangles). Despite some deviations for individual data points from the overall trendline, which we attribute to solubility issues, a clear dependence of the rate constant on the Hammett parameter was observed. It should be noted that the observed poor solubility will not be present once the monomers are included into a (solvent-free) bulk polymer matrix.

From the kinetic data it was observed that when σ increased, the reaction rates of the exchange reaction decreased significantly. For example, the conversion of the reaction with TDA after 5 hours was already at 91%, whereas the conversion of SDA was only at 2% at that time, leading to a k for TDA (6.6·10⁻² min⁻¹) that was about 600 times higher than that for SDA (1.1·10⁻⁴ min⁻¹). These large differences in imine exchange rates, in addition to the observed changes in exchange equilibrium and stability of the imine bond, already demonstrate the potential for a Hammett exchange-based control over dynamic material properties once these imines are integrated in polymer networks.

Design of the polymer network

To synthesise the tuneable polyimine materials, each of the tuneable dianilines (XDAs) was reacted with terephthalaldehyde (TA). Next, tris(2-aminoethyl)amine (TREN) and 4,7,10-trioxa-1,13-tridecanediamine (TOTDDA) were added (Chart 1). TREN was used as the crosslinking agent, while TOTDDA was added to increase flexibility of the polymer chains. The latter is important because without this “flexibility agent” the polymer chains become very rigid due to the short chain lengths and high aromatic content,^58,62,81 even to the extent that it would disturb the chains to freely move, which would decrease the occurrence of the bond exchange reaction. Three initial variations of the composition of the polyimine network were prepared in which the dianiline contents were 10%, 20% or 30% of the total amine content. Using rheology, a temperature sweep experiment was performed on the three samples to evaluate the viscous and elastic contribution to the material properties. To quantify this, we plotted the tan(δ) as a function of the temperature (Table S2 and Fig. S9†). The 20% dianiline material resulted in the most desirable material for our tunability studies, as the 30% variant was already very rigid and lacked a clear temperature dependence, whereas the 10% material showed a fast drop in viscosity at relatively low temperatures, and thus limiting the tuneable range of the materials. The crosslinker (TREN) concentration was set at 5.0% (note that TREN has 3 amine groups, meaning an effective amine concentration of 7.5 mol%, in relation to the bisaldehyde monomer). TOTDDA was added as the remaining component to reach 100% of amines. Terephthalaldehyde was added in a 1 : 1 amine : aldehyde ratio to fully react all amines to imines. This was done to stimulate the imine metathesis exchange mechanism,⁸² and minimise occurrence of transimination reactions. Furthermore, due to the aromatic conjugation of the imines, they were stable enough to minimise retro-imination.^5,33 Therefore, we assumed that imine metathesis would be the main mechanism of exchange. This hypothesis is further supported by exchange studies on aromatic imine model compounds that revealed a non-catalysed, associative metathesis-based exchange for aromatic imines at room temperature.³³ Although we cannot fully rule out contribution of the other exchange pathways (i.e. transimination or retro-imination), for example due to trace amounts of amine and/or water.

The associative exchange mechanism is generally considered necessary for vitrimer-like materials to maintain a constant crosslinking density,⁸³ with the small proviso that for some previously reported materials it was observed that the rubbery plateau can be lost and flow can be observed.⁸⁴ To verify that a constant crosslinking degree was maintained in our P-XDA materials, a frequency sweep rheological experiment at four different temperatures was performed (Fig. S18†). The observation that, at all given temperatures, the G′ reached a plateau of similar value indicates that the crosslinking degree in the network remained constant. This observation is suggestive of an associative exchange mechanism, as a dissociative mechanism would typically result in a decrease in the crosslinking density,⁸⁵ although some dissociative CANs have been shown to display very similar vitrimer-like behaviour as common associative CANs,^86–88 which has raised the question whether the term vitrimer should be used selectively for associative CANs.⁸⁹

Full conversion of the polymer network was further concluded from FT-IR spectroscopy (Fig. S8†), as disappearance of the aldehyde signal at 1700 cm⁻¹ and concomitant appearance of the imine signal at 1640 cm⁻¹ could be observed. Furthermore, by rheology measurements it was established that all polymers had reached their gel point at room temperature (tan(δ) < 1 at 20 °C, see Fig. S17†).

From an environmental point of view, it is noteworthy to mention that our polyimine materials could be synthesised at room temperature using minimal amounts of solvent (∼5 mL THF per gram of synthesised product material), without the need for any catalysts or other reagents, and with water as the only side product, which could easily be removed from the polymer materials in a drying oven. The full experimental procedures are included in the ESI.†

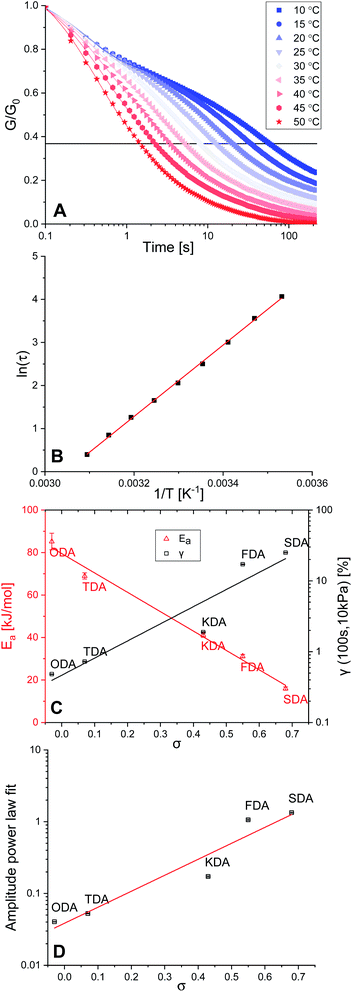
Stress relaxation and activation energies

Crosslinked polymers were synthesised for all five tuneable XDAs, and moulded into films with a 0.40 mm thickness and 10 mm diameter. To study the mechanical properties of the polymers, firstly a rheology experiment was conducted in which a constant angular strain (1%) was applied to the films, and the relaxation modulus (G) was followed over time. Normalisation of the data (G/G₀) was performed to obtain the stress relaxation curves. Stress relaxation curves were obtained for every sample at temperatures from 10–50 °C, with 5 °C increments. The data for P-TDA are shown in Fig. 2A as a representative example; the results for the other samples can be found in the ESI (Fig. S10–S14 and Table S3†). The relaxation time (τ) was taken as the point where G/G₀ reached 1/e (≈0.37), according to the Maxwell model for stress relaxation (G/G₀ = exp[−t/τ]).⁹⁰

Fig. 2 (A) Normalised stress relaxation curves of P-TDA at different temperatures. (B) Arrhenius plot of P-TDA, based on the data shown in (A). (C) Plot of E_a (red triangles) and γ (black squares) as a function of σ. (D) Amplitude of the fitted power law creep versus σ. In (C) and (D) a linear trendline was fitted as guide to the eye.

By plotting ln(τ) versus the reciprocal temperature (1/T) an Arrhenius plot was constructed (Fig. 2B). As the slope of the Arrhenius plot equals E_a/R, the kinetic activation energy (E_a) could be calculated for each of the P-XDA materials. Subsequently, plotting E_aversus the corresponding σ values of the dianiline monomers resulted in a rather striking linear relation (Fig. 2C, red triangles), with the activation energy between the lowest and highest studied Hammett parameter differing by more than a factor 5. The distinct trend that can be seen is that by increasing the electron-donating effect of the aniline substituent, the E_a increases as well, whereas more electron-withdrawing substituents decrease the E_a. This corresponds to our observation that electron-donating effects stabilise the imine bond, and therefore, increase the energy required for the exchange reaction. As the E_a follows a linear trend with the Hammett parameter, to first approximation, a desired activation energy can be directly translated into the corresponding σ value needed to achieve this energy.

Next, a creep test was carried out in which the polymer films were exposed to a constant stress of 10 kPa, and the strain (γ) was measured over time (Fig. S15 and Table S4†). By comparing the strain of the materials at a fixed point in time (here: 100 s) we observed an increase in the amount of strain when σ increases as well (Fig. 2C, black squares). We found that all materials displayed creep reminiscent of Andrade creep,^91,92 but with a different sublinear power law time dependence, in which strain grows with a diffusive exponent of 0.5–0.6. Deviations from the Andrade creep exponent have been observed in other glassy materials.⁹³ Importantly, the creep amplitude correlated directly with the Hammett parameter (Fig. 2D), and is most likely sensitive to the applied stress and temperature,⁹⁴ just like other creep phenomena,⁹⁵ offering a wide range of tunability. Consequently, we observed that also the extent of creep becomes precisely tuneable as a dynamic mechanical material property by selection of the appropriate Hammett parameter (i.e. choice of dianiline monomer).

Thermal properties

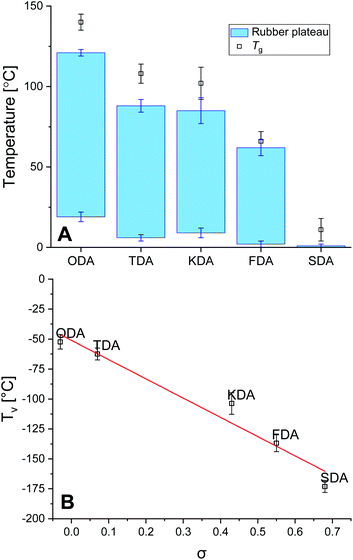
The thermal stability of the P-XDA materials was tested using thermographic analysis (TGA). A sample of every P-XDA material was prepared, and was gradually heated from 30 to 900 °C with a temperature ramp of 1 °C min⁻¹ (Fig. S16†). The temperature at which 5% weight loss of the materials was observed (T_g5%), was determined for all materials. From the results it could be concluded that all materials showed a similar T_g5% of 298 ± 6 °C. This indicates that independently of the choice of dianiline monomer, the materials remained stable at temperatures up to ∼300 °C.

The glass transition temperature (T_g) and rubbery domain of the materials were determined using rheology via a temperature sweep (0–150 °C) experiment at a constant angular frequency of 1 Hz and strain of 0.1%. Storage (G′) and loss (G′′) moduli were measured as function of the temperature, and tan(δ) was calculated as G′′/G′ (Fig. S17†). The materials with the most electron-donating substituents (P-ODA and P-TDA) displayed a peak in tan(δ), and therefore T_g was derived from the top of this peak.³⁶ For the materials with more electron-withdrawing groups (P-KDA, P-FDA and P-SDA), a point in temperature was reached at which the G′ rapidly dropped to 0. For these materials T_g was determined at the point where tan(δ) = 1.¹⁴ From the determined T_g values (Fig. 3A), a trend can be observed in which the P-XDA materials showed a lower T_g when the electron-withdrawing effect of the substituents increased (increase in σ). This is in line with the results obtained from the small-molecule studies, for which the electron-withdrawing substituents resulted in a less stable imine bond, requiring less energy for bond exchange.

Fig. 3 (A) Rubbery plateaus and T_g for the P-XDA materials, as determined by rheology measurements. (B) Plot of T_v as function of σ value of the corresponding substituents of dianiline monomer (a linear line was fitted to the data points).

The rubbery domain of the materials was determined from the plateau region in G′ before it reached the T_g (Fig. 3A).¹⁴ From the determined temperature region of the rubbery plateau we can conclude that – apart from the most electron-withdrawing P-SDA – the materials displayed rubbery behaviour in an ambient atmosphere at room temperature. Secondly, the lower temperature of the rubbery state remained similar for all materials roughly in the range of 0–20 °C, whereas the upper temperature decreased when the electron-withdrawing effect of the substituents increases.

Another important parameter for vitrimer-like materials is the topology freezing transition temperature (T_v). As previously defined,⁹⁶ the T_v is the temperature at which the network topology of the material is considered frozen due the absence of required bond exchange reactions. For vitrimer-like materials this frozen state is considered at the point at which the viscosity (η) reaches 10¹² Pa s. In order to determine the T_v for our P-XDA materials the data from the stress relaxation and temperature response were combined. Firstly, the stress relaxation time (τ_v) at T_v was determined using the following equation:³¹

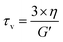where η = 10¹² Pa s, and G′ represents the storage modulus of the rubbery plateau, obtained from the temperature sweeps.

Next, the fitted Arrhenius curves from the stress relaxation experiment (Fig. S10–S14†) were extrapolated to the point for which τ = τ_v, allowing the corresponding temperature T_v to be determined. Note that the T_v is a hypothetical parameter that is derived from extrapolation, and should be treated as a parameter belonging to the specific exchange reaction present within the material.³⁷ Once the T_v for every material was determined, these values were plotted as a function of σ to reveal a distinct linear trend between the two parameters, with T_v decreasing for increasing σ values (Fig. 3B). We also observed that the T_v values for all materials lay relatively far below their T_v values, which indicates that the bond exchange reaction can occur at very low temperatures, and independent of the composition of the polymer network.⁹⁶ The trend we see in the T_v of the P-XDA materials suggests that the required heat for the bond exchange reaction to either occur or not can be tuned via the Hammett parameter.

Solvent resistance

The solvent resistance of the P-XDA materials was tested by submerging each polymer in a relatively large excess of solvent (20 mg polymer in 2 mL solvent) and leaving it for 5 days at room temperature in a closed vial. Afterwards, the solid was separated from the liquid, and the remaining mass of the solid was determined after drying. Fig. 4 shows the remaining mass as a fraction of the initial mass of the sample for all tested solvents. As the two most electron-withdrawing materials (P-SDA and P-FDA) were too viscous for this type of experiment, only the three most electron-donating materials (P-KDA, P-TDA and P-ODA) could be tested.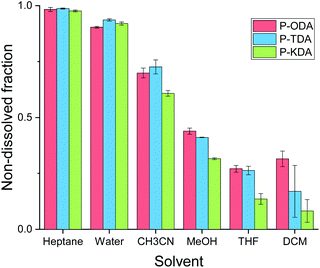

Fig. 4 Overview of non-soluble fractions for P-ODA, P-TDA and P-KDA polymers after immersion (at room temperature) in the corresponding solvent for 5 days.

The results showed that the materials have a strong resistance against water and heptane (>0.90 non-dissolved fraction), and only partially to acetonitrile (0.61–0.73 non-dissolved fraction), methanol (0.32–0.44 non-dissolved fraction), THF (0.14–0.27 non-dissolved fraction), and dichloromethane (0.08–0.32 non-dissolved fraction). From the obtained results we could not infer the presence of a σ-dependent solvent resistance of the materials, although indications can be observed for methanol, THF and dichloromethane. While partial dissolution of the polymer was observed for some solvents, ¹H NMR analysis of the soluble material (Fig. S19 and S20†) revealed the absence of any aldehyde species. This suggests that a dissociative retro-imination process (i.e. imine hydrolysis) is not the main driving force for the polymer dissolution. Instead, we suggest that the partial network dissolution could have been caused by formation of loops that separate one portion of the network from another, as recently proposed by Elling and Dichtel in their discussion of the – still not fully understood – solubility of vitrimer(-like) materials.⁸⁵

The poor solubility results indicate that reprocessing via redissolving the materials is not suitable, but their relatively good resistance against several common solvents enables applications where the material is exposed to small amounts of solvent or for short time intervals, for example in washing steps or condensed environments. Reprocessing of the materials remained still possible by other means, such as heating (see next section).

Recycling and self-healing

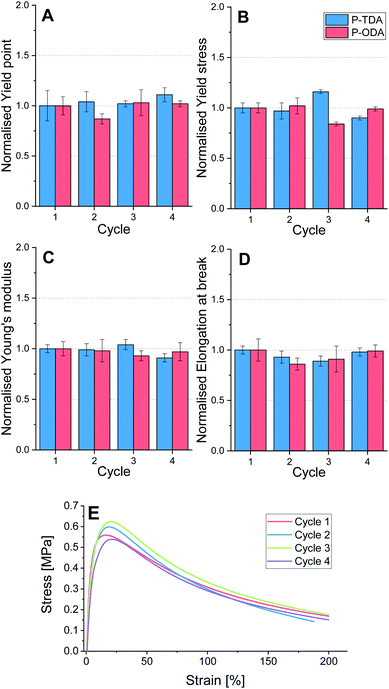
To test the applicability of this type of tuneable polyimine networks as strong, yet recyclable materials, P-TDA and P-ODA were evaluated because of their higher relative strength compared to the other three materials. Both P-TDA and P-ODA were recycled up to three times to establish whether material properties could be recovered. For each cycle the material was cut into small pieces and then hot-pressed (100 °C, 1 MPa, 15 min) into bars of 15 × 10 × 1.0 mm dimension (see ESI for further experimental details†). Dynamic mechanical analysis (DMA) was used to stretch the materials with a constant stretching speed of 10% per minute, and the stress (MPa) was measured as a function of the strain (%) until the sample broke. For each cycle, four samples were measured and the average values for yield point (%), yield stress (MPa), elongation at break (%) and Young's modulus (MPa) were determined (Tables S7 and S8†). The data for both P-TDA and P-ODA were normalised for better comparison, and are presented in Fig. 5.

Fig. 5 Recycling test of P-TDA (blue, left bars) and P-ODA (red, right bars), showing normalised data over multiple cycles for (A) yield point, (B) yield stress, (C) Young's modulus, and (D) Elongation at break. Cycle 1 corresponds to the pristine material and cycles 2–4 represent each of the following recycling steps. (E) Stress–strain curves of representative samples of P-TDA from each recycling step.

Despite some small deviations in the obtained data, most likely as a result of natural variability, no systematic decrease in any of these material properties was observed over multiple cycles. Therefore, we concluded that recyclability of the materials over multiple cycles is possible without loss in material properties.

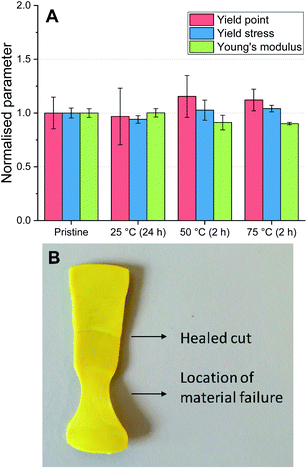
The degree of autonomous self-healing of the P-TDA material was also investigated. For this experiment, bars of the same dimensions as used for the recycling experiments were prepared. The bars were then cut in half, and the two halves were placed back into the mould with the cut edges touching. The samples were left in the mould (in a horizontal position), but this time without applying external pressure so that the materials were left to self-heal (see ESI for further experimental details†). The experiment was carried out at 25 °C, 50 °C and 75 °C. After the samples were cooled back down to room temperature, DMA was used to determine the material properties of the healed materials (Fig. 6A and Table S9†).

Fig. 6 (A) Material properties of self-healed P-TDA materials at 25, 50 and 75 °C, compared to the pristine material. The materials healed at 25 °C required 24 hours to heal, whereas the samples at 50 °C and 75 °C required only 2 hours; data were normalised to the pristine material. (B) P-TDA material that was cut, healed, and then stretched. The location of material failure, as a result of an applied strain, is different from the location of the healed cut.

For all of the healed materials, the yield point (red, left column), yield stress (blue, middle column) and Young's modulus (green, right column) were comparable to the pristine material. Furthermore, by stretching the materials, the location at which the break or flow appeared was different from where the material was initially cut (Fig. 6B). The samples heated at 50 °C and 75 °C were fully healed after 2 hours, while the healing at 25 °C was eventually achieved after 24 hours due to the slower bond exchange at lower temperatures. It is worthwhile to stress that no external chemicals, solvents or catalysts were required, and as such, these materials are capable of autonomous self-healing.

Conclusions

We developed a precise way to tune the dynamic mechanical and thermal properties of dynamic covalent polyimine CANs via the electronic effect of dianiline monomers based on the Hammett equation. This allowed for the first time a direct and quantitative correlation of a simple, molecule-based physical parameter to macroscopic material properties. In more detail: the relaxation time (τ), kinetic activation energy (E_a), creep (γ), glass transition (T_g) and topology freezing (T_v) could all be tuned via the Hammett parameter (σ) of the dianiline monomer. This opens the potential for simply picking the desired macroscopic properties for a CAN material, and then obtaining that property via the selection of the required dianiline monomer using only the σ value of the substituent from a large list of available substituents. We also hypothesise that such a Hammett equation-based guiding principle can be extended to other polymer networks, irrespectively of whether their bond exchange reactions occur via an associative or a dissociative mechanism.

Furthermore, our tuneable polyimine materials show potential to be used for applications in daily life as common rubbers due their stable rubbery state, which could be tuned to over 100 °C based on the choice of dianiline monomer. TGA also showed that all materials were stable from degradation up to 300 °C. Additionally, recycling and intrinsic self-healing without loss of material properties were realised without addition of an external chemical, solvent or catalyst.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Herman de Beukelaer (Wageningen Food & Biobased Research) for his assistance in the TGA measurements. The Netherlands Organisation for Scientific Research (NWO) is acknowledged for funding (NWO Vidi grant 016.Vidi.189.031 to M. M. J. S.).

Notes and references

1. S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Angew. Chem., Int. Ed., 2002, 41, 898–952.
2. P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J.-L. Wietor, J. K. M. Sanders and S. Otto, Chem. Rev., 2006, 106, 3652–3711.
3. N. M. Rue, J. Sun and R. Warmuth, Isr. J. Chem., 2011, 51, 743–768.
4. M. E. Belowich and J. F. Stoddart, Chem. Soc. Rev., 2012, 41, 2003–2024.
5. C. D. Meyer, C. S. Joiner and J. F. Stoddart, Chem. Soc. Rev., 2007, 36, 1705–1723.
6. R. Tian, X. Fan, S. Liu, F. Li, F. Yang, Y. Li, Q. Luo, C. Hou, J. Xu and J. Liu, Macromol. Rapid Commun., 2020, 41, 1900586.
7. J. M. Winne, L. Leibler and F. E. Du Prez, Polym. Chem., 2019, 10, 6091–6108.
8. G. M. Scheutz, J. J. Lessard, M. B. Sims and B. S. Sumerlin, J. Am. Chem. Soc., 2019, 141, 16181–16196.
9. Y. Jin, Z. Lei, P. Taynton, S. Huang and W. Zhang, Matter, 2019, 1, 1456–1493.
10. W. Zou, J. Dong, Y. Luo, Q. Zhao and T. Xie, Adv. Mater., 2017, 29, 1606100.
11. C. J. Kloxin, T. F. Scott, B. J. Adzima and C. N. Bowman, Macromolecules, 2010, 43, 2643–2653.
12. F. García and M. M. J. Smulders, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 3551–3577.
13. N. J. Van Zee and R. Nicolaÿ, Prog. Polym. Sci., 2020, 104, 101233.
14. C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161–7173.
15. M. Podgórski, B. D. Fairbanks, B. E. Kirkpatrick, M. McBride, A. Martinez, A. Dobson, N. J. Bongiardina and C. N. Bowman, Adv. Mater., 2020, 32, 1906876.
16. D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968.
17. M. Capelot, D. Montarnal, F. Tournilhac and L. Leibler, J. Am. Chem. Soc., 2012, 134, 7664–7667.
18. N. Bai, K. Saito and G. P. Simon, Polym. Chem., 2013, 4, 724–730.
19. M. Fan, J. Liu, X. Li, J. Zhang and J. Cheng, Ind. Eng. Chem. Res., 2014, 53, 16156–16163.
20. Y. Min, S. Huang, Y. Wang, Z. Zhang, B. Du, X. Zhang and Z. Fan, Macromolecules, 2015, 48, 316–322.
21. Q.-T. Li, M.-J. Jiang, G. Wu, L. Chen, S.-C. Chen, Y.-X. Cao and Y.-Z. Wang, ACS Appl. Mater. Interfaces, 2017, 9, 20797–20807.
22. M. Pepels, I. Filot, B. Klumperman and H. Goossens, Polym. Chem., 2013, 4, 4955–4965.
23. J. Canadell, H. Goossens and B. Klumperman, Macromolecules, 2011, 44, 2536–2541.
24. Z. Q. Lei, H. P. Xiang, Y. J. Yuan, M. Z. Rong and M. Q. Zhang, Chem. Mater., 2014, 26, 2038–2046.
25. L. Imbernon, E. K. Oikonomou, S. Norvez and L. Leibler, Polym. Chem., 2015, 6, 4271–4278.
26. O. R. Cromwell, J. Chung and Z. Guan, J. Am. Chem. Soc., 2015, 137, 6492–6495.
27. J. J. Cash, T. Kubo, A. P. Bapat and B. S. Sumerlin, Macromolecules, 2015, 48, 2098–2106.
28. A. Breuillac, A. Kassalias and R. Nicolaÿ, Macromolecules, 2019, 52, 7102–7113.
29. M. Röttger, T. Domenech, R. van der Weegen, A. Breuillac, R. Nicolaÿ and L. Leibler, Science, 2017, 356, 62–65.
30. Z. Wang, S. Gangarapu, J. Escorihuela, G. Fei, H. Zuilhof and H. Xia, J. Mater. Chem. A, 2019, 7, 15933–15943.
31. L. Zhang and S. J. Rowan, Macromolecules, 2017, 50, 5051–5060.
32. P. Taynton, K. Yu, R. K. Shoemaker, Y. Jin, H. J. Qi and W. Zhang, Adv. Mater., 2014, 26, 3938–3942.
33. Z. Q. Lei, P. Xie, M. Z. Rong and M. Q. Zhang, J. Mater. Chem. A, 2015, 3, 19662–19668.
34. A. Chao, I. Negulescu and D. Zhang, Macromolecules, 2016, 49, 6277–6284.
35. F. García, J. Pelss, H. Zuilhof and M. M. J. Smulders, Chem. Commun., 2016, 52, 9059–9062.
36. P. Taynton, C. Zhu, S. Loob, R. Shoemaker, J. Pritchard, Y. Jin and W. Zhang, Polym. Chem., 2016, 7, 7052–7056.
37. M. Guerre, C. Taplan, J. M. Winne and F. E. Du Prez, Chem. Sci., 2020, 11, 4855–4870.
38. R. J. Wojtecki, M. A. Meador and S. J. Rowan, Nat. Mater., 2010, 10, 14–27.
39. P. Chakma and D. Konkolewicz, Angew. Chem., Int. Ed., 2019, 58, 9682–9695.
40. Y.-J. Choi, Y. Lee, G. Bang, J. Jeong, N. Kim, J.-H. Lee and K.-U. Jeong, Adv. Funct. Mater., 2019, 29, 1905214.
41. L. T. Roling, J. Scaranto, J. A. Herron, H. Yu, S. Choi, N. L. Abbott and M. Mavrikakis, Nat. Commun., 2016, 7, 13338.
42. T. Shiraki, M. Morikawa and N. Kimizuka, Angew. Chem., Int. Ed., 2008, 47, 106–108.
43. M. D. Perez, C. Borek, S. R. Forrest and M. E. Thompson, J. Am. Chem. Soc., 2009, 131, 9281–9286.
44. V. V. Brus, J. Lee, B. R. Luginbuhl, S.-J. Ko, G. C. Bazan and T.-Q. Nguyen, Adv. Mater., 2019, 31, 1900904.
45. M. Gerth and I. K. Voets, Chem. Commun., 2017, 53, 4414–4428.
46. X. W. Sha, E. N. Economou, D. A. Papaconstantopoulos, M. R. Pederson, M. J. Mehl and M. Kafesaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115404.
47. X. Yu, J. Zhou, H. Liang, Z. Jiang and L. Wu, Prog. Mater. Sci., 2018, 94, 114–173.
48. K. Bertoldi, V. Vitelli, J. Christensen and M. van Hecke, Nat. Rev. Mater., 2017, 2, 17066.
49. N. Van Herck, D. Maes, K. Unal, M. Guerre, J. M. Winne and F. E. Du Prez, Angew. Chem., Int. Ed., 2020, 59, 3609–3617.
50. B. M. El-Zaatari, J. S. A. Ishibashi and J. A. Kalow, Polym. Chem., 2020, 11, 5339–5345.
51. J. J. Lessard, G. M. Scheutz, S. H. Sung, K. A. Lantz, T. H. Epps and B. S. Sumerlin, J. Am. Chem. Soc., 2020, 142, 283–289.
52. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103.
53. L. P. Hammett, Chem. Rev., 1935, 17, 125–136.
54. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
55. C. Hansch, A. Leo, S. H. Unger, K. H. Kim, D. Nikaitani and E. J. Lien, J. Med. Chem., 1973, 16, 1207–1216.
56. H. Schiff, Liebigs Ann., 1864, 131, 118–119.
57. C. Luo, Z. Lei, Y. Mao, X. Shi, W. Zhang and K. Yu, Macromolecules, 2018, 51, 9825–9838.
58. H. Zheng, Q. Liu, X. Lei, Y. Chen, B. Zhang and Q. Zhang, J. Mater. Sci., 2019, 54, 2690–2698.
59. H. Li, J. Bai, Z. Shi and J. Yin, Polymer, 2016, 85, 106–113.
60. S. Dhers, G. Vantomme and L. Avérous, Green Chem., 2019, 21, 1596–1601.
61. H. Geng, Y. Wang, Q. Yu, S. Gu, Y. Zhou, W. Xu, X. Zhang and D. Ye, ACS Sustainable Chem. Eng., 2018, 6, 15463–15470.
62. S. Wang, S. Ma, Q. Li, W. Yuan, B. Wang and J. Zhu, Macromolecules, 2018, 51, 8001–8012.
63. Y. Liu, Y. Zhang, Z. Cao and Z. Fang, Ind. Eng. Chem. Res., 2012, 51, 11059–11065.
64. X. He, Z. P. Lei, W. Zhang and K. Yu, 3D Print. Addit. Manuf., 2019, 6, 31–39.
65. J. Pignanelli, B. Billet, M. Straeten, M. Prado, K. Schlingman, M. J. Ahamed and S. Rondeau-Gagné, Soft Matter, 2019, 15, 7654–7662.
66. M. Kathan, C. Jurissek, P. Kovaříček and S. Hecht, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 2378–2382.
67. J. Leclaire, G. Husson, N. Devaux, V. Delorme, L. Charles, F. Ziarelli, P. Desbois, A. Chaumonnot, M. Jacquin, F. Fotiadu and G. Buono, J. Am. Chem. Soc., 2010, 132, 3582–3593.
68. J. Wang, I. Senkovska, M. Oschatz, M. R. Lohe, L. Borchardt, A. Heerwig, Q. Liu and S. Kaskel, J. Mater. Chem. A, 2013, 1, 10951–10961.
69. C. Xu, Z. Bacsik and N. Hedin, J. Mater. Chem. A, 2015, 3, 16229–16234.
70. X. Xu, S. Ma, J. Wu, J. Yang, B. Wang, S. Wang, Q. Li, J. Feng, S. You and J. Zhu, J. Mater. Chem. A, 2019, 7, 15420–15431.
71. Z. Zou, C. Zhu, Y. Li, X. Lei, W. Zhang and J. Xiao, Sci. Adv., 2018, 4, eaaq0508.
72. Y. Liu, Z. Tang, J. Chen, J. Xiong, D. Wang, S. Wang, S. Wu and B. Guo, Polym. Chem., 2020, 11, 1348–1355.
73. R. Hajj, A. Duval, S. Dhers and L. Avérous, Macromolecules, 2020, 53, 3796–3805.
74. R. Mo, J. Hu, H. Huang, X. Sheng and X. Zhang, J. Mater. Chem. A, 2019, 7, 3031–3038.
75. P. Taynton, H. Ni, C. Zhu, K. Yu, S. Loob, Y. Jin, H. J. Qi and W. Zhang, Adv. Mater., 2016, 28, 2904–2909.
76. C. Zhu, C. Xi, W. Doro, T. Wang, X. Zhang, Y. Jin and W. Zhang, RSC Adv., 2017, 7, 48303–48307.
77. S. Wang, S. Ma, Q. Li, X. Xu, B. Wang, K. Huang, Y. liu and J. Zhu, Macromolecules, 2020, 53, 2919–2931.
78. P. Kovaříček and J.-M. Lehn, J. Am. Chem. Soc., 2012, 134, 9446–9455.
79. D. Schultz and J. R. Nitschke, J. Am. Chem. Soc., 2006, 128, 9887–9892.
80. J. Clayden, N. Greeves and S. G. Warren, Organic Chemistry, Oxford University Press, Oxford, New YorK, 2nd edn, 2012.
81. H. Zheng, Q. Liu, X. Lei, Y. Chen, B. Zhang and Q. Zhang, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 2531–2538.
82. M. Ciaccia, R. Cacciapaglia, P. Mencarelli, L. Mandolini and S. Di Stefano, Chem. Sci., 2013, 4, 2253–2261.
83. W. Denissen, J. M. Winne and F. E. Du Prez, Chem. Sci., 2016, 7, 30–38.
84. W. Denissen, I. De Baere, W. Van Paepegem, L. Leibler, J. Winne and F. E. Du Prez, Macromolecules, 2018, 51, 2054–2064.
85. A. Jourdain, R. Asbai, O. Anaya, M. M. Chehimi, E. Drockenmuller and D. Montarnal, Macromolecules, 2020, 53, 1884–1900.
86. M. M. Obadia, A. Jourdain, P. Cassagnau, D. Montarnal and E. Drockenmuller, Adv. Funct. Mater., 2017, 27, 1703258.
87. P. Chakma, Z. A. Digby, M. P. Shulman, L. R. Kuhn, C. N. Morley, J. L. Sparks and D. Konkolewicz, ACS Macro Lett., 2019, 8, 95–100.
88. P. Chakma, C. N. Morley, J. L. Sparks and D. Konkolewicz, Macromolecules, 2020, 53, 1233–1244.
89. B. R. Elling and W. R. Dichtel, ACS Cent. Sci., 2020, 6, 1488–1496.
90. P. W. Atkins and J. De Paula, Physical Chemistry, W.H. Freeman and Company, New York, 9th edn, 2010.
91. E. N. D. C. Andrade and F. T. Trouton, Proc. R. Soc. A, 1910, 84, 1–12.
92. E. N. D. C. Andrade and A. W. Porter, Proc. R. Soc. A, 1914, 90, 329–342.
93. M. Siebenbürger, M. Ballauff and T. Voigtmann, Phys. Rev. Lett., 2012, 108, 255701.
94. J. M. Hutchinson, Prog. Polym. Sci., 1995, 20, 703–760.
95. M. E. Kassner and M. T. Pérez-Prado, Prog. Mater. Sci., 2000, 45, 1–102.
96. M. Capelot, M. M. Unterlass, F. Tournilhac and L. Leibler, ACS Macro Lett., 2012, 1, 789–792.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05458e

---