Open Access Article
Open Access ArticleVisually precise, low-damage, single-cell spatial manipulation with single-pixel resolution†
Qi
Zhang
a,
Yunlong
Shao
a,
Boye
Li
a,
Yuanyuan
Wu
a,
Jingying
Dong
a,
Dongtang
Zhang
 a,
Yanan
Wang
a,
Yong
Yan
a,
Xiayan
Wang
a,
Yanan
Wang
a,
Yong
Yan
a,
Xiayan
Wang
 *a,
Qiaosheng
Pu
*a,
Qiaosheng
Pu
 *b and
Guangsheng
Guo
*a
*b and
Guangsheng
Guo
*a
aCenter of Excellence for Environmental Safety and Biological Effects, Beijing Key Laboratory for Green Catalysis and Separation, Department of Chemistry and Biology, Beijing University of Technology, Beijing 100124, China. E-mail: xiayanwang@bjut.edu.cn; gsguo@bjut.edu.cn
bDepartment of Chemistry, Lanzhou University, Lanzhou, Gansu 730000, China. E-mail: puqs@lzu.edu.cn
First published on 2nd February 2021
Abstract
The analysis of single living cells, including intracellular delivery and extraction, is essential for monitoring their dynamic biochemical processes and exploring intracellular heterogeneity. However, owing to the 2D view in bright-field microscopy and optical distortions caused by the cell shape and the variation in the refractive index both inside and around the cells, achieving spatially undistorted imaging for high-precision manipulation within a cell is challenging. Here, an accurate and visual system is developed for single-cell spatial manipulation by correcting the aberration for simultaneous bright-field triple-view imaging. Stereo information from the triple view enables higher spatial resolution that facilitates the precise manipulation of single cells. In the bright field, we resolved the spatial locations of subcellular structures of a single cell suspended in a medium and measured the random spatial rotation angle of the cell with a precision of ±5°. Furthermore, we demonstrated the visual manipulation of a probe to an arbitrary spatial point of a cell with an accuracy of <1 pixel. This novel system is more accurate and less destructive for subcellular content extraction and drug delivery.
Introduction
The manipulation of single cells plays an important role in the field of biomedicine and single-cell analysis,1–3 especially in intracellular drug delivery and content extraction techniques that use a tip such as in gene editing, ex vivo cell-based therapies, organelle transplantation, and subcellular omics.4–6 Most of these require that a micron-sized cell is accurately punctured by a pipette at a specific spatial position or organelle without affecting the cell viability. However, this is challenging.7,8By reducing the size of the pipette tip, the accuracy of intracellular manipulation can be improved and cell damage can be reduced in traditional micromanipulation.9,10 However, the difference in refractive index of the intracellular components, the culture solution,11 and the round shape of the cell may lead to a shift in the focal point and other optical distortions.12 The precise control of the micropipette or other type of microprobe inside a cell is difficult when using a normal microscopic system, and is heavily dependent on the skill of the operator,13 especially when the cell diameter is smaller than 25 μm.14,15 Through the design of a microfluidic chip, the space of its microchannel structure contains the single cell,16,17 improving the success rate of the puncture and enabling accurate intracellular injection. However, the position of the puncture cannot be controlled. Using fluorescence imaging for reconstruction in three dimensions will improve the accuracy of spatial manipulation.18,19 However, in the time needed for fluorescence imaging, which includes image acquisition, the processing time is usually larger than that needed for micromanipulation or other dynamic cellular processes, which limits its use in micromanipulation.20 Xu et al. have proposed a new type of stereo vision micromanipulation system. Unlike the existing kinds of research that use on the micro- or nanoscale that have been reported in recent years, their proposed system can offer depth information more directly.21,22 However, it is difficult for this system to achieve accurate manipulation of micron-sized single cells in terms of imaging quality and resolution.
Currently, the fluid force microscope is a powerful tool for micromanipulation.7,23,24 It can accurately determine whether to penetrate the cell or the nucleus according to the change in the membrane breaking force. However, the puncture process is not visualized,20 which means that the accurate manipulation of organelles other than the nucleus and cytoplasm may not be possible.25 In addition, it is not suitable for the puncture of a suspended single cell. Therefore, developing a faster way of spatially locating organelles and being able to accurately locate the microprobe visually inside either an adhered or a suspended cell is of great significance for studying single cells and is still a grand challenge.
Multiple-view imaging can be used to expand the measurable range of a system,26 and obtain spatial information through the use of more lenses for additional views.27–30 Simultaneous multi-angle imaging has been implemented in fluorescence 3D imaging;31 however, the use of spatial imaging for the accurate manipulation and location of a nanotip probe with regard to a specific point within a cell, which may be dynamically changing, has not been reported. For accurate probe operation and single-cell manipulation, a delicately designed system that has sufficient operating space for free movement of the probe under a bright field and the capability of continuous 3D information acquisition is needed.
In this work, we propose a single-cell spatial manipulation system based on a simultaneous multi-angle imaging system for the observation of a single cell or organelle. The system possesses the capability of aberration–correction in the bright field and allows the precise operation of a microprobe with submicrometer resolution. Combining three long-working-distance objectives (100×) with the aberration-corrected sample chamber and angle-corrected illumination source, we have constructed a simultaneous triple-view spatial resolution micromanipulation (STSRM) system for multi-angle spatial imaging under the bright field, allowing the fully functional micromanipulation of a cell or probe with high accuracy. Simply and quickly, the system can achieve spatial positioning of the subcellular structure of a single suspended cell and obtain the 3D rotation angle of that cell. The system provides a universal platform for the fast and accurate 3D manipulation of a single cell, allowing precise operation of a probe that can greatly enhance the performance of single-cell analysis. The device can also be used in single-cell genome editing, ex vivo cell-based therapies, and subcellular omics.
Results and discussion
Construction of the STSRM system
To achieve precise, visual spatial manipulation of a single cell, simultaneous bright-field triple-view imaging can be adopted for fast and label-free micromanipulation. The principle of the system is shown in Fig. 1. The exact position of the micropipette can be easily determined by images taken at three different angles. Three are needed since two angles may not be enough for obtaining the real position. In addition, using images from three different angles (in the planes xy, ln, and mn) allows the exact coordinates of the pipette tip or other observation subject to be determined (STSRM system positioning principle†). This system setup avoids micromanipulation problems such as a low success rate and high cell damage caused by a lack of effective information about the spatial location of the tip, cell, and organelles.32 Compared with traditional micromanipulation (Fig. S1†), the positional accuracy can be improved greatly because the optical distortions for each view angle can be corrected using the images obtained from the other two angles.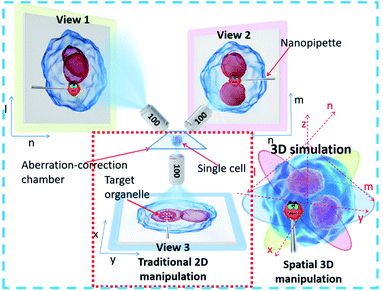 | ||
| Fig. 1 Schematic diagram of the STSRM system for micromanipulation. The spatial position of the organelle, pipette, and the cell can be determined by their relative position from different views. | ||
Bright-field imaging with high magnification commonly uses a vertical (traditional) or horizontal single view,33–35 which cannot provide enough steric information. The main challenge for this system lies in the steric constraints from objectives, illumination source, and the microprobe. For its versatility, our system was set up on a traditional inverted microscope frame. Two orthogonal and symmetric optical paths were arranged above the sampling plate. Dry objectives with higher numerical apertures (one at 100×, WD = 4.5 mm, NA = 0.8, and another at 100×, WD = 10 mm, NA = 0.6) were selected to reduce the steric constraints between the objectives so that the illumination sources could be properly arranged. An operating volume of >6.8 cm3 was reserved for the sample and probe placement, which helped to prevent irremediable damage of the lens surface caused by physical contact with the tip during manipulation. For intense and uniform illumination, a surface-mounted light-emitting diode was placed between the orthogonally installed objectives to serve as the light source for the bottom view, and a rigid optical fiber was used to adjust the transmission light of the two upper views. The focus of each objective could be tuned independently (Fig. 2a).
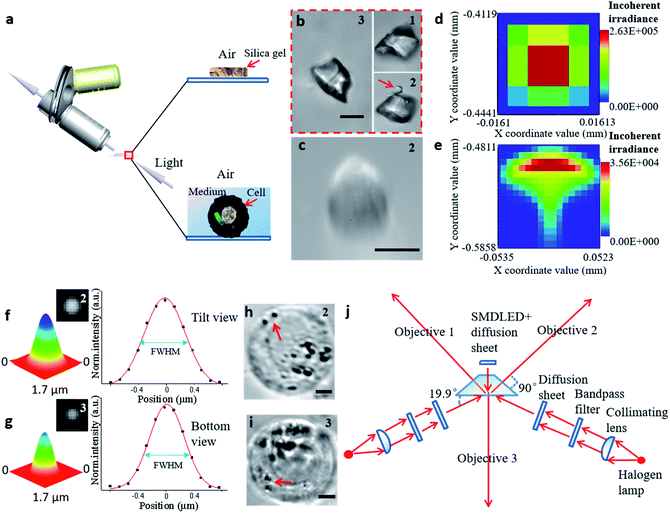 | ||
| Fig. 2 The process of establishing the STSRM system. (a) Observation of samples in different media by inclined microscope objective. (b) Triple-view image of silica gel particle in air. The number in the upper right corner of each picture represents the objective viewpoint: (1) from the upper left; (2) from the upper right; and (3) from the bottom. (Scale bar: 10 μm.) (c) Image of the cell showing aberrations in the tilt view. (Scale bar: 10 μm.) (d and e) Analog distribution of light passing through the air (d) and a 1 mm-thick liquid layer (e). (f and g) Point-spread function determination using 100 nm fluorescent beads in the sample chamber (Fig. S5†): normalized 3D surface distribution, top view FWHM = (527 ± 9 nm, 669 ± 23 nm) (f), and bottom view FWHM = 542 ± 14 nm (g) by Gaussian fitting. (h and i) Suspended A546 cell in the sample chamber, top view (h) and bottom view (i). The red arrow represents two bacteria. (Scale bar: 5 μm.) (j) Schematic diagram of the proposed optical lighting system with aberration correction. | ||
To illustrate the applicability of the system for subjects that have an irregular shape, a grain of silica gel was imaged at three different angles (Fig. 2b), which implies that the triple-angle system provides more morphological information. In particular, a tiny pellet attached to the particle (marked with a red arrow) could only be seen clearly through objective 2, which implies that some details may be lost even with a dual-angle device. This result demonstrates the capability and necessity of the triple-angle system for analyzing steric information.
For cell imaging, however, the situation can be more challenging. To image a cell in a medium, the medium has to be spread over a supporting surface. When coaxial illumination was applied, the image was mostly blurred under the inclined view with the 100× objective lens (Fig. 2c). Based on the principle of the optical path in geometrical optics, the sample in the medium on the supporting surface cannot be perfectly imaged by views 1 and 2 (Fig. S2†). Here, the optical path difference can be expressed as Δs = |f(θ, n1, n2, h)|, where θ is the aperture angle, n1 and n2 are the refractive index of medium 1 and medium 2, respectively, and h is the height of medium 2. If the aperture angle and the refractive index of the medium are known, Δs is dependent on h, and the smaller the value of h, the better the imaging. We simulated each imaging mode, including the light distribution passing through air (Fig. 2d) and a high liquid level (Fig. 2e). According to these simulation results, the image in the inclined view cannot be perfect. Non-symmetric light distribution in the meridional plane and the sagittal plane (Fig. 2e) causes serious aberration (similar to comatic aberration). To correct this, we designed a sample chamber with a shape similar to a triangular prism (Fig. S3†) to make the optical axis perpendicular to the medium for correcting serious aberration. The prism-like chamber ensures that the light transmission is of a uniform distribution and is more compatible with micromanipulation than that probed by a cylindrical or cuboid chamber.28,36 For each imaging mode, we compared the simulated light distribution, the modulation transfer function, and experimental pictures (Fig. S4†). The imaging quality was improved by using a thin liquid layer or after aberration correction for both simulation and experimental results. We also tested the point-spread function of the fluorescent beads in the sample chamber to confirm the elimination of similar comatic aberration and to calculate the full width at half-maximum (FWHM) of the intensity curve (Fig. 2f and g). The resolution of objective 3 only decreased by about 110 nm and that for objectives 1 and 2 was not affected when the thickness of the glass was 100 μm. Even when the sample distance was 1 mm, the resolution obtained at objectives 1 and 2 decreased by only 140 nm. The image resolution could approach the theoretical value (343 × 457 × 457 nm for viewpoints 3, 2, and 1, respectively) if the thickness of the glass and the volume of the chamber were reduced (Fig. S5†). Furthermore, we designed a new, compact illuminating unit for simultaneously imaging cells under the bright field, where the angle between the illuminating light and the horizontal direction was 19.9° (Fig. 2j and S6†). Compared with the tilt view without aberration correction (Fig. 2c),21,22,37 the imaging quality was significantly improved (Fig. 2h), and the 3D distribution of bacteria (marked with a red arrow) could be clearly distinguished in different views (Fig. 2h and i).
Monitoring a single cell with irregular motion
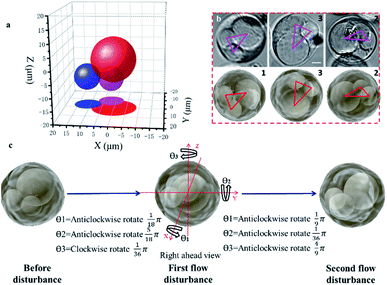
Observing the spatial distribution and transformation of cell nuclei is helpful for tracking the differentiation of single cells; in addition, the known spatial distribution of the nuclei will improve the precision of organelle biopsy and reduce cell damage by eliminating the need for inaccurate subjective estimations to be made by the microscope operator.32,38 With the STSRM system, the spatial distribution of multiple nuclei could be determined and the random 3D rotation angle of a cell can be tracked directly with high accuracy. After A549 cells had been cultured for some time, it was observed that some had a multinucleated giant cell morphology, shown by multiple nuclei and an enlarged size. A549 cells are epithelial cells, and the fusion between epithelial cells produces multinucleated giant cells. Here, one of these multinucleated giant cells (Fig. S7a†) in an A549 cell suspension was used to examine the capability of the proposed system together with simulations. Having only Z-slice images (Fig. S7b†), it is impossible to obtain accurate spatial information about the nuclei within any of the single views because the measurement accuracy of the Z-axis could be up to 10 μm.39 With the STSRM system, however, the shape and relative motion of these nuclei could be well estimated. In each view, we selected the appropriate focus plane to see every nucleus clearly and recorded images simultaneously. The contour of the nucleus was fitted to a circle or ellipse (Fig. S7c†). The centroid coordinates of each nucleus in the three views were extracted from the fitted shape so that the spatial positions of the nuclei were determined (Fig. 3a). The spatial distributions and outlines of the nuclei in the triple view were simulated, and the nuclei in each simulated view were obtained (Fig. S7c†). Because of the confinement imposed by the cytoskeleton,40 the nuclei are bound within the cell, and the internal structure of the cell should therefore remain stable after rotation. To verify the positioning accuracy, we disturbed the liquid slightly, through the addition of 2 μL DMEM, to make the suspended cells roll by a small angle. The process was simulated based on the center of the cells since A549 cells belong to a spherical single-shell model.41 When the red triangle (connection of centroids) in the three simulations (as seen in Fig. 3b) overlapped with the magenta triangle in the three experiments, the simulated rotation was stopped, and after repeated disturbances of the cells the experimental results were highly consistent with the simulated data, showing a matching angle accuracy of ±5° (Fig. 3b and S7d†). By comparing the simulated and experimental results we were also able to calculate the random spatial rotation angle of the cell (Fig. 3c and Movie S1†), which is impossible when just any single view is available. When the cell rotates to a certain angle, all nuclei can be seen clearly by each objective (around the depth of field (DOF)) at the same time (Fig. 3b), and so the spatial distribution of the nuclei could be determined from just one group of images captured simultaneously.Accurately judging single-cell spatial puncture through visualization
Accurate control of the movement of a microprobe (i.e. puncturing with an aspiration needle, optical fiber tip, etc.) is essential for measuring or operating at a specific location in a cell. An adequate DOF for the movement of the microprobe is an essential requirement. In the STSRM system, the DOF of the long-working-distance objectives used is approximately five times larger than those with a high NA, e.g., 1.4, which can be described as follows:42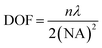 | (1) |
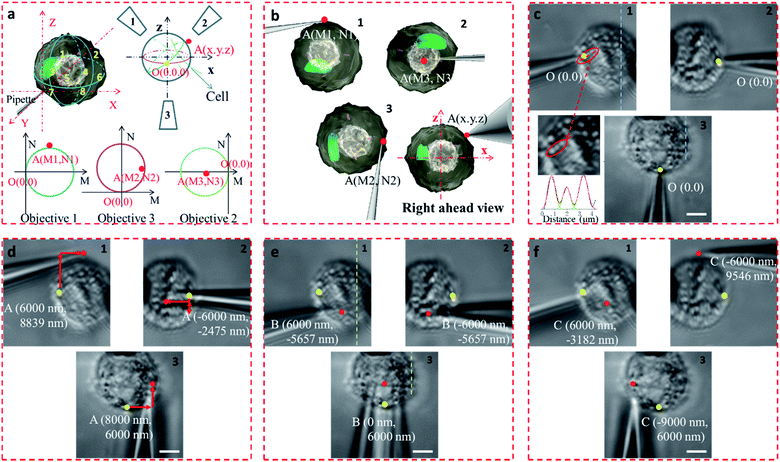
In the proposed setup, the larger DOF ensures sufficient resolution for the movement of the microprobe. The microprobe was carried by a high-precision 3D nanomanipulator, which was controlled using the LabVIEW program based on its spatial coordinates. The relationship between the 3D- and 2D-coordinates in the plane of each view was determined through coordinate transformation (Fig. S8†). First, the accurate movement of the probe tip was demonstrated. If the probe tip position is initially set at O (0, 0, 0), then the position of any point in the space can be defined as A (x, y, z). For example, point A was on the surface of the cell, between quadrants 2 and 4 (Fig. 4a and b). If the microprobe moves in a straight line, it may cause some damage to the cell. With the aid of 3D coordinates, the path can be delicately designed to avoid damage.
The precision of the system is therefore important. If bend and vibration can be avoided, the minimum displacement accuracy of the probe is determined by the translation stage, which is 1 nm. The observation precision is dependent on the image resolution. The position of the microprobe tip was deduced through the contour of the microprobe in the optical image, and the exact shape of the microprobe near its tip was confirmed by scanning electron microscopy (Fig. S9†). The diameter of the quartz tip was ∼120 nm (internal diameter ∼70 nm). Based on the results from multiple images, the position of the tip could be determined with an accuracy of <1 pixel, which represents 65 nm in this system. We defined the initial position of the microprobe tip in each view as O (0, 0). When the cell was fixed by the micropipette and the view was in focus (Fig. 4c), the details of the cell with its variations in shape and size could be seen, and the FWHM of the pixel intensity of the three adjacent dots was 671, 683, and 789 nm (Fig. 4c).
The STSRM system can greatly assist judging the exact position of the microprobe tip. When the tip reached point A (8000, 6000, 4500 nm), typical images were taken at three different views as shown in Fig. 4d. If just one or even two views are used (with objectives 2 and 3), it is hard to judge if the tip is at the correct position. The experimental results showed good agreement with the simulations for the tip position relative to the cell (Fig. 4b and Movie S2†), which clearly demonstrates the convenience of the proposed device. Different final positions of the tip were then examined: point B (0, 6000, −8000 nm) below the cell and on the edge of quadrants 7 and 8 (Fig. 4e); and point C (−9000, 6000, 4500 nm) on the edge of quadrants 1 and 3 (Fig. 4f). By watching the location of the tip and the deformation of the cell, we could judge whether or not the tip contacted the cell directly. When the tip was moved to quadrant 3 of the cell (Fig. 5a and b), the tip and the cell were in the focal plane in all three views. More visual information showed that the cell was punctured. It could be seen that a deformation (yellow arrow) was caused by the tip in the three images, and a shift in the focal plane (red arrow) was caused by contact force in the images for objectives 1, 2, and 3. Through image analysis, the plot profiles in Fig. 5c (blue and green dashed lines in the images for objective 1 of Fig. 4c and e, respectively) and Fig. 5d (in objective 3 images of Fig. 4c and e) show that the cell had almost no displacement (<1 pixel), and that the tip did not touch the cell using this resolution. The plot profile in Fig. 5e (blue and green dashed lines in the images for objective 1 of Fig. 5a and b, respectively) and Fig. 5f (in objective 3 images of Fig. 5a and b) show a significant displacement (∼1 μm and 500 nm) caused by puncturing. When the displacement in the direction of the puncture was ∼390–520 nm (6–8 pixels), all cells were punctured, as verified by fluorescence injection (n = 7) (Fig. 5f inset and S10†). These experiments have proved that it is not difficult for the nanotip (∼120 nm diameter) to penetrate the cell when the cell is fixed. Through our studies on the location of the tip, changes in the displacement, deformation of the cell, and verification through fluorescence (Fig. 5 and S10†), precise spatial penetration can be achieved. The experimental results have shown that, compared with a single-view setup, the spatial puncture of a single cell in this triple-view system can provide lots of different information.
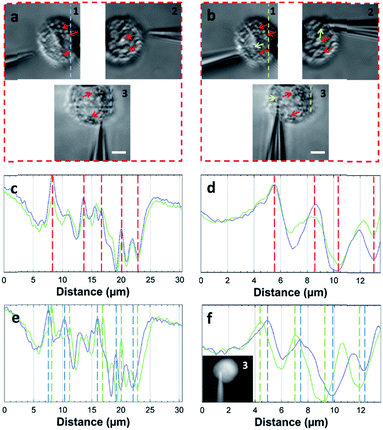 | ||
| Fig. 5 Single-cell puncture process and image analysis. (a) The tip is in the front of the cell. (b) The tip is moved to quadrant 3 of the cell. It can be seen that deformation (yellow arrow) of the cell was caused by the tip, and the shift of the focal plane (red arrow) was caused by the contact force in objectives 1, 2, and 3. Plot profiles (c) (blue and green dashed line in the images of objective 1 of Fig. 4c and e) and (d) (objective 3 images of Fig. 4c and e) show almost no cell displacement, and the plot profiles (e) (blue and green dashed lines in the images of objective 1 of a and b) and (f) (objective 3 images of (a) and (b)) show significant displacement (∼1 μm and 500 nm). The penetration can be verified by displacement and injection of a fluorescent solution into the cell (f) (Fig. S10†). (Scale bar: 5 μm.) | ||
Alternative puncture path to reduce physical cell damage
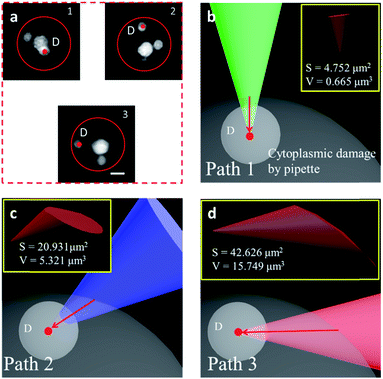
We have shown that the STSRM system is compatible with the fluorescence mode. A combination of the cell contour in bright field mode and with the organelles in fluorescence mode is shown in Fig. 6a. Studying the spatial relationship between the target point D (the centroid of an organelle) and the cell contour, we can easily establish a movement path for the probe that causes less damage to the cell whilst monitoring the process in real time. We simulated the puncturing process by targeting point D inside the cell with a nanotip (diameter 100 nm, cone angle 30°). Three paths (Fig. 6b–d) were demonstrated by adjusting the tilt angle of the tip, and the volume of the damage from the tip movement was evaluated by Boolean calculation. Apparently, if a bottom view is used, we will not realize that the puncture path will bring different degrees of cell damage. Damage is more obvious in images from objective 2; meanwhile, the volume (V) and surface area (S) values of path 3 are three times and twice those obtained using path 2, respectively (Fig. 6c and d). In this case, path 1 is the best (Fig. 6b) as it causes only 1/23.7 of the volume damage and 1/9 of the surface area damage of path 3. If the tip used had a larger diameter or cone angle, the damage caused by the paths would be more significant. The choice of path is therefore critical for minimizing damage to the cytomembrane, ion dynamic equilibrium, and intracellular actin.43 In addition, correct selection of the probe tip and observation of its movement are necessary for preventing damage to the tip itself, especially if a nanotip is used. To verify cell viability, 15 cells were punctured and, after 24 hours, it was verified that the cells were still alive by trypan blue staining (Fig. S11†). Based on these observations the proposed system has great application potential.Conclusions
The traditional optical microscope only provides 2D positioning of an object, manipulation, and 2D verification of the rotation angle.44,45 Our STSRM system can achieve the simple and rapid, label-free spatial positioning of objects such as organelles in a freely suspended single cell using a nanopipette. Irregular spatial movement information can be obtained for single-cell dynamics, and accurate spatial puncture of a suspended single cell can be achieved for content extraction to reveal the intracellular spatial heterogeneity of metabolism. For less destructive manipulation of cells, the tip size used is typically a concern.10,46 However, as the manufacture of ever-smaller tips becomes increasingly difficult and the optical resolution that is achievable with smaller tip diameters is limited (to >30 nm),20 the pursuit of even smaller tips becomes ineffective. It is noteworthy that damage to the cells could be reduced greatly by choosing the best puncture path according to the known spatial position of the target. By referring to nanopipette cone angles given in the literature,9,46 it can be calculated that the diameter of the perforation is more than 1 μm when the puncture depth is 5 μm, which would cause severe damage to a cell. Therefore, choosing the right path is absolutely necessary. Possible applications of the STSRM system also include drug delivery for subcellular organelles, gene engineering, and combination with nanoelectrochemistry for in situ single-cell analysis.47Compared with a phase-contrast microscope (PC) and a differential interference contrast microscope (DIC), the STSRM system has several advantages. Experiments have shown that the success rate of microinjection in the bright field is higher than with PC and DIC.48 In addition, the PC is suitable for thin samples and not for spherical cells. Although the samples used for DIC can be slightly thicker, and a 3D view can be produced that is useful for micromanipulation, DIC may be limited by the DOF of suspended cells and it lacks spatial location and some morphology information because it uses a single objective. By contrast, the STSRM system can provide accurate spatial positioning and additional morphology information for constructing a stereo vision, which can be of great value for single-cell analysis. Furthermore, the STSRM system shows potential in the research in translational medicine and precision cancer medicine.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Natural Science Foundation of China (Grant No. 21527808, 21625501, and 21936001), the Beijing Outstanding Young Scientist Program (BJJWZYJH01201910005017), the Beijing Municipal High-Level Innovative Team Building Program (IDHT20180504), and the Analysis Center of Chemical Performance of Beijing University of Technology.Notes and references
- S. Campuzano, B. Esteban-Fernandez de Avila, P. Yanez-Sedeno, J. M. Pingarron and J. Wang, Chem. Sci., 2017, 8, 6750–6763 RSC.
- Y. Qin, L. Wu, T. Schneider, G. S. Yen, J. Wang, S. Xu, M. Li, A. L. Paguirigan, J. L. Smith, J. P. Radich, R. K. Anand and D. T. Chiu, Angew. Chem., Int. Ed., 2018, 57, 11378–11383 CrossRef CAS.
- S. Mao, Q. Zhang, W. Liu, Q. Huang, M. Khan, W. Zhang, C. Lin, K. Uchiyama and J. M. Lin, Chem. Sci., 2019, 10, 2081–2087 RSC.
- H. X. Wang, M. Li, C. M. Lee, S. Chakraborty, H. W. Kim, G. Bao and K. W. Leong, Chem. Rev., 2017, 117, 9874–9906 CrossRef CAS.
- P. Tiefenboeck, J. AhKim and J.-C. Leroux, Adv. Drug Delivery Rev., 2018, 132, 3–15 CrossRef CAS.
- Q. Huang, S. Mao, M. Khan, W. Li, Q. Zhang and J.-M. Lin, Chem. Sci., 2020, 11, 253–256 RSC.
- O. Guillaume-Gentil, R. V. Grindberg, R. Kooger, L. Dorwling-Carter, V. Martinez, D. Ossola, M. Pilhofer, T. Zambelli and J. A. Vorholt, Cell, 2016, 166, 506–516 CrossRef CAS.
- S. G. Higgins and M. M. Stevens, Science, 2017, 356, 379–380 CrossRef CAS.
- B. P. Nadappuram, P. Cadinu, A. Barik, A. J. Ainscough, M. J. Devine, M. Kang, J. Gonzalez-Garcia, J. T. Kittler, K. R. Willison, R. Vilar, P. Actis, B. Wojciak-Stothard, S. H. Oh, A. P. Ivanov and J. B. Edel, Nat. Nanotechnol., 2019, 14, 80–88 CrossRef CAS.
- J. Song, C. H. Xu, S. Z. Huang, W. Lei, Y. F. Ruan, H. J. Lu, W. Zhao, J. J. Xu and H. Y. Chen, Angew. Chem., Int. Ed., 2018, 57, 13226–13230 CrossRef CAS.
- G. Vizsnyiczai, A. Buzas, B. Lakshmanrao Aekbote, T. Fekete, I. Grexa, P. Ormos and L. Kelemen, Biomed. Opt. Express, 2020, 11, 945–962 CrossRef CAS.
- B. P. Bratton and J. W. Shaevitz, PLoS One, 2015, 10, e0134616 CrossRef.
- S. Permana, E. Grant, G. M. Walker and J. A. Yoder, IEEE ASME Trans. Mechatron., 2016, 21, 2391–2404 Search PubMed.
- Y. T. Chow, S. Chen, C. Liu, C. Liu, L. Li, C. W. M. Kong, S. H. Cheng, R. A. Li and D. Sun, IEEE ASME Trans. Mechatron., 2016, 21, 838–850 Search PubMed.
- A. Shakoor, M. Xie, T. Luo, J. Hou, Y. Shen, J. K. Mills and D. Sun, IEEE Trans. Biomed. Eng., 2019, 66, 2210–2222 Search PubMed.
- A. Adamo and K. F. Jensen, Lab Chip, 2008, 8, 1258–1261 RSC.
- C. K. Yun, J. W. Hwang, T. J. Kwak, W. J. Chang, S. Ha, K. Han, S. Lee and Y. S. Choi, Lab Chip, 2019, 19, 580–588 RSC.
- H. Liu, J. Wen, Y. Xiao, J. Liu, S. Hopyan, M. Radisic, C. A. Simmons and Y. Sun, ACS Nano, 2014, 8, 3821–3828 CrossRef CAS.
- C. S. Hansel, S. W. Crowder, S. Cooper, S. Gopal, M. Joao Pardelha da Cruz, L. de Oliveira Martins, D. Keller, S. Rothery, M. Becce, A. E. G. Cass, C. Bakal, C. Chiappini and M. M. Stevens, ACS Nano, 2019, 13, 2913–2926 CrossRef CAS.
- K. Yum, N. Wang and M. F. Yu, Nanoscale, 2010, 2, 363–372 RSC.
- Z. Nan and Q. Xu, 2017 IEEE Int. Conf. Rob. Biomimetics, pp. 1106–1111 Search PubMed.
- Q. Xu, in Micromachines for Biological Micromanipulation, Springer International Publishing, 2018, pp. 209–223 Search PubMed.
- O. Guillaume-Gentil, T. Rey, P. Kiefer, A. J. Ibanez, R. Steinhoff, R. Bronnimann, L. Dorwling-Carter, T. Zambelli, R. Zenobi and J. A. Vorholt, Anal. Chem., 2017, 89, 5017–5023 CrossRef CAS.
- J. Dehullu, J. A. Vorholt, P. N. Lipke and Y. F. Dufrene, Trends Microbiol., 2019, 27, 728–730 CrossRef CAS.
- S. Boeynaems, S. Alberti, N. L. Fawzi, T. Mittag, M. Polymenidou, F. Rousseau, J. Schymkowitz, J. Shorter, B. Wolozin, L. Van Den Bosch, P. Tompa and M. Fuxreiter, Trends Cell Biol., 2018, 28, 420–435 CrossRef CAS.
- M. Wang, Y. Yin, D. Deng, X. Meng, X. Liu and X. Peng, Opt. Express, 2017, 25, 19408–19421 CrossRef.
- Y. Wu, P. Wawrzusin, J. Senseney, R. S. Fischer, R. Christensen, A. Santella, A. G. York, P. W. Winter, C. M. Waterman, Z. Bao, D. A. Colon-Ramos, M. McAuliffe and H. Shroff, Nat. Biotechnol., 2013, 31, 1032–1038 CrossRef CAS.
- R. K. Chhetri, F. Amat, Y. Wan, B. Hockendorf, W. C. Lemon and P. J. Keller, Nat. Methods, 2015, 12, 1171–1178 CrossRef CAS.
- M. Guo, Y. Li, Y. Su, T. Lambert, D. D. Nogare, M. W. Moyle, L. H. Duncan, R. Ikegami, A. Santella, I. Rey-Suarez, D. Green, A. Beiriger, J. Chen, H. Vishwasrao, S. Ganesan, V. Prince, J. C. Waters, C. M. Annunziata, M. Hafner, W. A. Mohler, A. B. Chitnis, A. Upadhyaya, T. B. Usdin, Z. Bao, D. Colon-Ramos, P. La Riviere, H. Liu, Y. Wu and H. Shroff, Nat. Biotechnol., 2020, 38, 1337–1346 CrossRef CAS.
- Y. Wu, A. Kumar, C. Smith, E. Ardiel, P. Chandris, R. Christensen, I. Rey-Suarez, M. Guo, H. D. Vishwasrao, J. Chen, J. Tang, A. Upadhyaya, P. J. La Riviere and H. Shroff, Nat. Commun., 2017, 8, 1452 CrossRef.
- Y. Wu, P. Chandris, P. W. Winter, E. Y. Kim, V. Jaumouille, A. Kumar, M. Guo, J. M. Leung, C. Smith, I. Rey-Suarez, H. Liu, C. M. Waterman, K. S. Ramamurthi, P. J. La Riviere and H. Shroff, Optica, 2016, 3, 897–910 CrossRef CAS.
- W. Gao, A. Shakoor, L. Zhao, Z. Jiang and D. Sun, IEEE Robot. Autom. Lett., 2019, 4, 231–238 Search PubMed.
- O. Chaudhuri, S. H. Parekh, W. A. Lam and D. A. Fletcher, Nat. Methods, 2009, 6, 383–387 CrossRef CAS.
- Y. Fu, R. Kunz, J. Wu and C. Dong, PLoS One, 2012, 7, e30721 CrossRef CAS.
- C. Dong and X. X. Lei, J. Biomech, 2000, 33, 35–43 CrossRef CAS.
- A. D. Baik, X. L. Lu, J. Qiu, B. Huo, E. M. Hillman, C. Dong and X. E. Guo, Biophys. J., 2010, 99, 2812–2820 CrossRef CAS.
- S. Zappe, M. Fish, M. P. Scott and O. Solgaard, Lab Chip, 2006, 6, 1012–1019 RSC.
- M. M. Villone, P. Memmolo, F. Merola, M. Mugnano, L. Miccio, P. L. Maffettone and P. Ferraro, Lab Chip, 2018, 18, 126–131 RSC.
- J. Liu, Z. Zhang, X. Wang, H. Liu, Q. Zhao, C. Zhou, M. Tan, H. Pu, S. Xie and Y. Sun, IEEE Robot. Autom. Lett., 2017, 2, 499–505 Search PubMed.
- D. A. Fletcher and R. D. Mullins, Nature, 2010, 463, 485–492 CrossRef CAS.
- L. Huang, P. Zhao and W. Wang, Lab Chip, 2018, 18, 2359–2368 RSC.
- J. M. Behm, J. C. Hemminger and K. R. Lykke, Anal. Chem., 1996, 68, 713–719 CrossRef CAS.
- M. P. Stewart, A. Sharei, X. Ding, G. Sahay, R. Langer and K. F. Jensen, Nature, 2016, 538, 183–192 CrossRef CAS.
- P. Benhal, J. G. Chase, P. Gaynor, B. Oback and W. Wang, Lab Chip, 2014, 14, 2717–2727 RSC.
- M. Habaza, M. Kirschbaum, C. Guernth-Marschner, G. Dardikman, I. Barnea, R. Korenstein, C. Duschl and N. T. Shaked, Adv. Sci., 2017, 4, 1600205 CrossRef.
- P. Actis, M. M. Maalouf, H. J. Kim, A. Lohith, B. Vilozny, R. A. Seger and N. Pourmand, ACS Nano, 2014, 8, 546–553 CrossRef CAS.
- Y. L. Ying, Z. Ding, D. Zhan and Y. T. Long, Chem. Sci., 2017, 8, 3338–3348 RSC.
- J. Liu, V. Siragam, Z. Gong, J. Chen, M. D. Fridman, C. Leung, Z. Lu, C. Ru, S. Xie, J. Luo, R. M. Hamilton and Y. Sun, IEEE Trans. Biomed. Eng., 2015, 62, 119–125 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05534d |
| This journal is © The Royal Society of Chemistry 2021 |