Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the crystal chemistry of inorganic nitrides: crystal-chemical parameters, bonding behavior, and opportunities in the exploration of their compositional space†
Olivier C.
Gagné
 *
*
Earth and Planets Laboratory, Carnegie Institution for Science, Washington, D.C. 20015, USA. E-mail: ogagne@carnegiescience.edu
First published on 15th February 2021
Abstract
The scarcity of nitrogen in Earth's crust, combined with challenging synthesis, have made inorganic nitrides a relatively unexplored class of compounds compared to their naturally abundant oxide counterparts. To facilitate exploration of their compositional space via a priori modeling, and to help a posteriori structure verification not limited to inferring the oxidation state of redox-active cations, we derive a suite of bond-valence parameters and Lewis acid strength values for 76 cations observed bonding to N3−, and further outline a baseline statistical knowledge of bond lengths for these compounds. Examination of structural and electronic effects responsible for the functional properties and anomalous bonding behavior of inorganic nitrides shows that many mechanisms of bond-length variation ubiquitous to oxide and oxysalt compounds (e.g., lone-pair stereoactivity, the Jahn–Teller and pseudo Jahn–Teller effects) are similarly pervasive in inorganic nitrides, and are occasionally observed to result in greater distortion magnitude than their oxide counterparts. We identify promising functional units for exploring uncharted chemical spaces of inorganic nitrides, e.g. multiple-bond metal centers with promise regarding the development of a post-Haber–Bosch process proceeding at milder reaction conditions, and promote an atomistic understanding of chemical bonding in nitrides relevant to such pursuits as the development of a model of ion substitution in solids, a problem of great relevance to semiconductor doping whose solution would fast-track the development of compound solar cells, battery materials, electronics, and more.
Introduction
The predominance and variety of oxide and oxysalt compounds as minerals in Earth's crust means that they were inevitably among the first materials to be methodically characterized and examined for interesting properties, occupying scientists for decades in trying to decipher, reproduce, and enhance their behavior. Conversely, inorganic nitrides, here defined as ionic/covalent compounds with N3− as the main anion, are a relatively unexplored class of compounds owing to (1) the scarcity of nitrogen minerals in Earth's crust due to various biological and geological transport processes drawing nitrogen away from the crust1 (not limited to their reaction with water to form hydroxides and ammonia2), and (2) challenging synthesis.3Systematic investigation of nitrides began in the late 1930s with the work of Juza and collaborators who mainly focused on lithium compounds for their relative ease of preparation.4–6 Rapid progression in the synthesis and characterization of nitride compounds followed the introduction of several new methods of preparation in the 1980s. This sudden burst of interest eventually led to the successful synthesis of many compounds suited to single-crystal X-ray diffraction, resulting in collection of significantly more accurate bond lengths compared to those determined via powder diffraction.7 Several reviews on the descriptive crystal chemistry of inorganic nitrides followed2,8–14 (more recent reviews include those of Höhn & Niewa for non-main group elements,15 and Tareen et al. for mixed ternary transition metal nitrides16), and the chemistry of nitrides was soon likened to that of silicates;10 the term nitridometalate was introduced to describe compounds containing covalent complex anions [MxNy]z− (in relation to oxometallates, commonly called oxyanions in the Earth sciences),11,12 reflecting the richness of chemistries to come. New classes of inorganic nitrides that were initially considered to be scientific curiosities have since been described as functionally diverse groups of materials, not limited to the nitridosilicates,8,17 oxynitrididosilicates18 and perovskite-related oxynitrides.19,20
In parallel to developments occurring in the bulk, the past decades saw binary III–V nitrides gain notoriety as semiconductors due to a trove of desirable properties largely associated with their wide, direct, and highly tunable band gaps. These properties include high temperature and power operation, high breakdown voltages, high thermal conductivity, high phonon frequency, low noise generation, and resilience to both large electric fields and hostile thermal/chemical environments, thus making these compounds attractive for a wide range of electronic and optoelectronic applications of commercial and industrial interest.21–26 More recently, ternary II–IV-N2 nitrides were introduced,27–29 thus providing additional compositional (and structural) flexibility for fine-tuning these properties.
Nitrides sensu lato provide a great opportunity for materials discovery owing to their unique electronic and bonding characteristics. Large-scale computational and synthetic efforts are underway to explore their compositional space. These compounds are being investigated for properties arising from both their bulk and trace/minor element composition spanning energy conversion and storage,30 solar-driven CO2 reduction (e.g. in Z-scheme-inspired photoelectrochemical cells),31 in quantum information processing,32 as alternatives to metals, metal oxides and metal sulfides in heterogeneous catalysis,33 as piezoelectric34,35 and photoluminescent36 materials, electrocatalysts,37,38 electrochemical sensors,39 photocatalysts,40,41 photovoltaics,42–44 photodetectors,45,46 light-emitting diodes,47,48 thermoelectrics,34,49 superconductors,50–52 as hard coating53 and ultrahard materials54 (in their pernitride form), etc., demonstrating the importance of an adequate understanding of their chemical bonding – a feat typically achieved in the bulk, and applied locally in studying point defects. With a relatively slow start compared to oxides and oxysalts, it is no surprise that some of the most exciting properties of these materials are currently being realized, and that much promise lies ahead in the exploratory synthesis of functional inorganic nitrides.
The present work is premised on a distillation of crystallographic knowledge for inorganic nitrides, with the goal of facilitating their characterization and design. Such pursuits have been eased by the bond-valence model for many classes of inorganic compounds, which is for example used to screen compounds in pymatgen55 and to infer the oxidation state of redox-active ions56 under the umbrella of the Materials Project.57 Most recently, the bond-topological nature of the bond-valence model was featured in showing how bond-length variation (thus polyhedral distortion) is an inherent, predictable and quantifiable by-product of chemical bonding in inorganic solids58 (polyhedral distortion having crucial implications with regard to the functional properties of various types of materials not limited to ferroelectricity,59,60 piezoelectricity,59,61 flexoelectricity,62 second-order nonlinear optical behavior,59,63 negative thermal expansion,64 and photoluminescence65,66). However, the parameterization of the bond-valence model is largely incomplete for cations bonded to N3−, and the quality of published bond-valence parameters is not established. In this work, we use the method of Gagné & Hawthorne67 to derive new bond-valence parameters for nitrides, provide a scale of Lewis acidity for nitrides, and further outline a baseline statistical knowledge of bond lengths for cations bonded to N3−; these data serve as a contribution to our gradual efforts of systematizing chemical bonding behavior in solids, toward modernizing Shannon's set of ionic radii68 (see ref. 58 and 69–72 for bond-length statistics of cations bonded to O2−; in prep for cations bonded to S2−, Se2− and/or Te2−), and are a useful aid to structure verification and the design of physically realistic crystal structures. In the second part of this work, we explore new venues for the exploratory synthesis of functional inorganic nitrides, using the systematic nature of this dataset to identify plausible ion configurations likely to lead to new and promising functional units to be transposed across various chemical spaces. Considering that the pairwise bonding data given herein are independent of their chemical environment, the type of analysis advanced in this work may be extended to other fields whose functional units may differ from those covered in this article, e.g. coordination chemistry, mineralogy, biochemistry, etc.
Dataset
We used the Inorganic Crystal Structure Database (ICSD) to extract bond-length data for elements bonded to N3− as a function of oxidation state and coordination number. Data collection criteria are those outlined by Gagné & Hawthorne:69 (1) publication date ≥ 1975; (2) R1 ≤ 0.06; (3) the site of interest is fully occupied by the cation; (4) all bonds involve ions at fully occupied sites; (5) the cation and anion sites of interest show no positional disorder; (6) crystallographic data were measured at ambient conditions; (7) no data from powder, electron or synchrotron diffraction were included; (8) for H, only neutron-diffraction data were collected. The procedure used to determine the coordination polyhedron in ambiguous cases is also that of Gagné & Hawthorne.69Following data collection, we examined structures with questionable bond-lengths and/or mean bond-lengths for various problems (e.g. positional/substitutional disorder, inconsistent (an)isotropic displacement parameters, high standard deviations on bond lengths, etc.) and discarded data which could not be confidently confirmed.
Whereby bond-valence parameters may be derived for mixed-anion coordination polyhedra (see ESI†), we also collected bonding data for cations bonded to both N3− and O2−; the final dataset used to derive the bond-valence parameters given in Table 1 consists of 6770 bond lengths hand-picked from 1436 coordination polyhedra from 720 crystal-structure refinements, covering 76 cations bonded to N3− (and possibly also O2−). The dataset that omits mixed-anion data accounts for 4048 bond lengths taken from 875 cation coordination polyhedra; these data and their basic statistics are reported in Table 2 and will be discussed further below.
| Ion | No. of coordination polyhedra | Average observed coordination numberb | S a (v.u.) | Std. dev. on Sa | R o (Å) | B (Å) | RMSD (v.u.) | Method of derivation (1-CN ions)c | |
|---|---|---|---|---|---|---|---|---|---|
| a Neutron-diffraction data. b Data from mixed-anion coordination polyhedra are omitted in the calculation of AOCN and Sa; more detail on these data are given in Table 2. c 1: Ro fixed to predicted value, 2: B fixed to family average, 3: B fixed to 0.399 Å. | |||||||||
| H+ | 30 | 0.935 | 0.572 | 0.032 | |||||
| Li+ | 83 | 3.63 (6) | 0.275 (4) | 0.070 | 1.713 | 0.312 | 0.111 | ||
| Be2+ | 2 | 3.5 (2) | 0.57 (3) | 0.08 | 1.537 | 0.301 | 0 | ||
| B3+ | 51 | 2.43 (6) | 1.24 (3) | 0.33 | 1.467 | 0.321 | 0.079 | ||
| C4+ | 270 | 2.76 (2) | 1.45 (1) | 0.22 | 1.401 | 0.261 | 0.094 | ||
| N5+ | 6 | 2 | 2.5 | 1.51 | 0.345 | 0.027 | |||
| Na+ | 74 | 5.29 (6) | 0.189 (2) | 0.027 | 1.62 | 0.546 | 0.098 | ||
| Mg2+ | 7 | 4 | 0.5 | 1.83 | 0.37 | 0.252 | |||
| Al3+ | 11 | 4.20 (9) | 0.71 (2) | 0.10 | 1.772 | 0.413 | 0.187 | ||
| Si4+ | 58 | 4.02 (1) | 0.995 (2) | 0.036 | 1.742 | 0.422 | 0.175 | 3 | |
| P5+ | 80 | 4 | 1.25 | 1.72 | 0.414 | 0.307 | |||
| S4+ | 10 | 2 | 2 | 1.781 | 0.328 | 0.081 | 2 | ||
| S6+ | 46 | 1.731 | 0.366 | 0.075 | |||||
| K+ | 67 | 6.46 (9) | 0.155 (2) | 0.028 | 1.892 | 0.543 | 0.122 | ||
| Ca2+ | 43 | 5.13 (7) | 0.390 (5) | 0.074 | 2.114 | 0.435 | 0.214 | ||
| V2+ | 1 | 6 | 1/3 | 1.779 | 0.405 | — | 1 | ||
| V3+ | 2 | 4.5 (5) | 0.67 (7) | 0.22 | 1.815 | 0.33 | 0 | ||
| V5+ | 1 | 4 | 1.25 | 1.93 | 0.399 | — | 2 | ||
| Cr2+ | 1 | 6 | 1/3 | 1.816 | 0.372 | — | 1 | ||
| Cr3+ | 26 | 5.8 (1) | 0.522 (9) | 0.075 | 1.796 | 0.403 | 0.061 | ||
| Cr5+ | 1 | 4 | 1.25 | 1.844 | 0.399 | — | 2 | ||
| Cr6+ | 2 | 4 | 1.5 | 1.924 | 0.399 | 0.075 | 2 | ||
| Mn2+ | 25 | 5.3 (1) | 0.377 (9) | 0.064 | 1.874 | 0.328 | 0.141 | ||
| Mn3+ | 3 | 3 | 1 | 1.759 | 0.399 | 0.124 | 2 | ||
| Mn5+ | 2 | 4 | 1.25 | 1.906 | 0.399 | 0.063 | 2 | ||
| Fe2+ | 15 | 5.2 (2) | 0.39 (1) | 0.10 | 1.719 | 0.427 | 0.084 | ||
| Fe3+ | 3 | 4.3 (3) | 0.69 (6) | 0.20 | 1.74 | 0.687 | 0.059 | ||
| Co+ | 1 | 2 | 0.5 | 1.472 | 0.399 | — | 2 | ||
| Co2+ | 9 | 4.7 (2) | 0.429 (1) | 0.09 | 1.626 | 0.485 | 0.049 | ||
| Co3+ | 66 | 6 | 0.5 | 1.686 | 0.399 | 0.062 | 2 | ||
| Ni2+ | 19 | 4.6 (1) | 0.44 (1) | 0.09 | 1.611 | 0.457 | 0.054 | ||
| Cu+ | 9 | 2.2 (1) | 0.45 (3) | 0.13 | 1.539 | 0.399 | 0.2 | 2 | |
| Cu2+ | 17 | 5.5 (2) | 0.36 (1) | 0.06 | 1.577 | 0.515 | 0.129 | ||
| Zn2+ | 29 | 3.85 (7) | 0.51 (1) | 0.10 | 1.792 | 0.293 | 0.264 | ||
| Ga3+ | 4 | 4.5 (2) | 0.67 (3) | 0.13 | 1.858 | 0.318 | 0.164 | ||
| Ge4+ | 2 | 1.891 | 0.422 | 0.014 | 3 | ||||
| Se6+ | 2 | 1.945 | 0.422 | 0.067 | 3 | ||||
| Rb+ | 29 | 7.7 (1) | 0.130 (2) | 0.023 | 1.914 | 0.639 | 0.039 | ||
| Sr2+ | 32 | 5.8 (2) | 0.35 (1) | 0.12 | 2.269 | 0.441 | 0.215 | ||
| Y3+ | 5 | 6 | 0.5 | 2.114 | 0.399 | 0.055 | 2 | ||
| Nb5+ | 12 | 4.3 (1) | 1.15 (3) | 0.20 | 2.052 | 0.404 | 0.057 | ||
| Mo6+ | 13 | 4 | 1.5 | 1.97 | 0.265 | 0.129 | |||
| Ru3+ | 8 | 6 | 0.5 | 1.816 | 0.399 | 0.02 | 2 | ||
| Rh3+ | 5 | 6 | 0.5 | 1.795 | 0.399 | 0.023 | 2 | ||
| Pd2+ | 5 | 4 | 0.5 | 1.767 | 0.399 | 0.033 | 2 | ||
| Ag+ | 18 | 2.5 (1) | 0.41 (2) | 0.12 | 1.926 | 0.277 | 0.089 | ||
| Cd2+ | 8 | 6 | 1/3 | 1.889 | 0.399 | 0.048 | 2 | ||
| Sn2+ | 1 | 3 | 2/3 | 1.965 | 0.438 | — | 2 | ||
| Sn4+ | 4 | 6 | 2/3 | 2 | 0.438 | 0.003 | 2 | ||
| Cs+ | 24 | 9.5 (1) | 0.106 (1) | 0.021 | 1.979 | 0.67 | 0.077 | ||
| Ba2+ | 53 | 6.68 (9) | 0.299 (4) | 0.067 | 2.432 | 0.405 | 0.171 | ||
| La3+ | 21 | 8.00 (0.08) | 0.375 (4) | 0.037 | 2.177 | 0.52 | 0.192 | ||
| Ce3+ | 11 | 8.40 (8) | 0.357 (3) | 0.021 | 2.162 | 0.469 | 0.157 | 2 | |
| Ce4+ | 1 | 6 | 2/3 | 2.237 | 0.469 | — | 2 | ||
| Pr3+ | 3 | 7 | 3/7 | 2.129 | 0.469 | 0.183 | 2 | ||
| Nd3+ | 8 | 6.7 (2) | 0.45 (1) | 0.06 | 2.051 | 0.555 | 0.256 | ||
| Sm3+ | 7 | 7 | 3/7 | 2.042 | 0.469 | 0.119 | 2 | ||
| Eu2+ | 5 | 8.4 (4) | 0.24 (1) | 0.07 | 1.952 | 0.587 | 0.089 | ||
| Eu3+ | 3 | 6 | 0.5 | 2.238 | 0.275 | 0.279 | |||
| Gd3+ | 2 | 2.064 | 0.38 | 0.017 | |||||
| Tb3+ | 3 | 2.042 | 0.415 | 0.019 | |||||
| Dy3+ | 1 | 1.978 | 0.469 | — | 2 | ||||
| Ho3+ | 2 | 6 | 0.5 | 2.097 | 0.391 | 0.25 | 1 | ||
| Er3+ | 4 | 6 | 0.5 | 2.057 | 0.498 | 0.138 | |||
| Yb3+ | 3 | 6.3 (1) | 0.474 (8) | 0.035 | 1.928 | 0.584 | 0.19 | ||
| Lu3+ | 1 | 6 | 0.5 | 1.966 | 0.487 | — | 1 | ||
| Hf4+ | 1 | 8 | 0.5 | 2.023 | 0.399 | — | 2 | ||
| Ta5+ | 5 | 4 | 1.25 | 2.047 | 0.399 | 0.038 | 2 | ||
| W6+ | 27 | 4 | 1.5 | 2.026 | 0.399 | 0.089 | 2 | ||
| Pt2+ | 15 | 4 | 0.5 | 1.817 | 0.351 | 0.063 | |||
| Au+ | 2 | 2 | 0.5 | 1.743 | 0.399 | 0.187 | 2 | ||
| Tl+ | 8 | 6.88 (8) | 0.145 (2) | 0.013 | 2.114 | 0.493 | 0.03 | ||
| Pb2+ | 2 | 6.0 (3) | 0.33 (2) | 0.06 | 2.058 | 0.529 | 0 | ||
| Bi3+ | 3 | 2.066 | 0.438 | 0.018 | 2 | ||||
| U4+ | 1 | 8 | 0.5 | 2.129 | 0.422 | — | 3 | ||
| U6+ | 2 | 2.035 | 0.422 | 0.053 | 3 | ||||
| Mean RMSD n ≥ 10 | 0.122 | ||||||||
| Mean RMSD weighted by number of CP | 0.120 | ||||||||
| Ion | Coordination number | Number of coordination polyhedraa | Number of bonds | Mean bond-length (Å) | Standard deviation (Å) | Range (Å) | Maximum bond-length (Å) | Minimum bond-length (Å) |
|---|---|---|---|---|---|---|---|---|
| a Numbers in parentheses are for mixed (O2− and N3−) coordination polyhedra. Statistical results given here do not include these data. | ||||||||
| H+ | 2 | 0 (29) | 0 (58) | |||||
| 3 | 0 (1) | 0 (3) | ||||||
| Li+ | 2 | 11 | 22 | 1.947 | 0.025 | 0.078 | 1.990 | 1.912 |
| 3 | 12 | 36 | 2.121 | 0.029 | 0.125 | 2.181 | 2.056 | |
| 4 | 43 (10) | 172 (40) | 2.148 | 0.103 | 0.690 | 2.613 | 1.923 | |
| 5 | 2 (2) | 10 (10) | 2.240 | 0.185 | 0.681 | 2.722 | 2.041 | |
| 6 | 3 | 18 | 2.255 | 0.039 | 0.094 | 2.302 | 2.208 | |
| Be2+ | 3 | 1 | 3 | 1.660 | 0.026 | 0.059 | 1.683 | 1.624 |
| 4 | 1 | 4 | 1.746 | 0.014 | 0.038 | 1.770 | 1.732 | |
| B3+ | 2 | 31 | 62 | 1.337 | 0.017 | 0.096 | 1.383 | 1.287 |
| 3 | 12 (3) | 36 (9) | 1.473 | 0.029 | 0.143 | 1.545 | 1.402 | |
| 4 | 4 (1) | 16 (4) | 1.557 | 0.019 | 0.052 | 1.570 | 1.518 | |
| C4+ | 2 | 33 (4) | 66 (8) | 1.226 | 0.061 | 0.188 | 1.325 | 1.137 |
| 3 | 103 (130) | 309 (390) | 1.326 | 0.017 | 0.119 | 1.395 | 1.276 | |
| N5+ | 2 | 2 | 4 | 1.194 | 0.000 | 0.000 | 1.194 | 1.194 |
| 3 | 0 (4) | 0 (12) | ||||||
| Na+ | 4 | 6 (5) | 24 (20) | 2.417 | 0.052 | 0.200 | 2.538 | 2.338 |
| 5 | 12 (7) | 60 (35) | 2.594 | 0.196 | 0.783 | 3.116 | 2.333 | |
| 6 | 16 (26) | 96 (156) | 2.562 | 0.113 | 0.640 | 3.022 | 2.382 | |
| 7 | 0 (2) | 0 (14) | ||||||
| Mg2+ | 4 | 4 | 16 | 2.121 | 0.049 | 0.162 | 2.198 | 2.036 |
| 6 | 0 (3) | 0 (18) | ||||||
| Al3+ | 4 | 9 | 36 | 1.898 | 0.043 | 0.144 | 1.984 | 1.840 |
| 6 | 1 (1) | 6 (6) | 2.044 | 0.006 | 0.015 | 2.052 | 2.037 | |
| Si4+ | 4 | 46 (11) | 184 (44) | 1.738 | 0.039 | 0.288 | 1.941 | 1.653 |
| 5 | 1 | 5 | 1.943 | 0.259 | 0.588 | 2.287 | 1.699 | |
| P5+ | 4 | 28 (52) | 112 (208) | 1.624 | 0.030 | 0.151 | 1.711 | 1.560 |
| S4+ | 2 | 9 (1) | 18 (2) | 1.552 | 0.020 | 0.069 | 1.596 | 1.527 |
| S6+ | 4 | 0 (46) | 0 (184) | |||||
| K+ | 4 | 1 | 4 | 2.688 | 0.025 | 0.061 | 2.709 | 2.648 |
| 5 | 1 | 5 | 2.907 | 0.165 | 0.424 | 3.134 | 2.710 | |
| 6 | 19 (6) | 114 (36) | 2.894 | 0.112 | 0.509 | 3.210 | 2.701 | |
| 7 | 0 (12) | 0 (84) | ||||||
| 8 | 6 (15) | 48 (120) | 3.115 | 0.236 | 0.898 | 3.703 | 2.805 | |
| 9 | 0 (6) | 0 (54) | ||||||
| 10 | 1 | 10 | 3.083 | 0.305 | 0.844 | 3.638 | 2.794 | |
| Ca2+ | 4 | 9 | 36 | 2.491 | 0.031 | 0.115 | 2.526 | 2.411 |
| 5 | 16 (1) | 80 (5) | 2.526 | 0.113 | 0.510 | 2.823 | 2.313 | |
| 6 | 11 (4) | 66 (24) | 2.563 | 0.107 | 0.616 | 2.965 | 2.349 | |
| 7 | 0 (1) | 0 (7) | ||||||
| 9 | 1 | 9 | 2.770 | 0.072 | 0.155 | 2.823 | 2.668 | |
| V2+ | 6 | 1 | 6 | 2.224 | 0.000 | 0.000 | 2.224 | 2.224 |
| V3+ | 3 | 1 | 3 | 1.815 | 0.007 | 0.017 | 1.825 | 1.808 |
| 6 | 1 | 6 | 2.044 | 0.005 | 0.012 | 2.051 | 2.039 | |
| V5+ | 4 | 1 | 4 | 1.842 | 0.016 | 0.038 | 1.851 | 1.813 |
| Cr2+ | 6 | 1 | 6 | 2.224 | 0.000 | 0.000 | 2.224 | 2.224 |
| Cr3+ | 3 | 1 | 3 | 1.798 | 0.046 | 0.097 | 1.863 | 1.766 |
| 6 | 11 (14) | 66 (84) | 2.078 | 0.025 | 0.193 | 2.158 | 1.965 | |
| Cr5+ | 4 | 1 | 4 | 1.755 | 0.002 | 0.004 | 1.757 | 1.753 |
| Cr6+ | 4 | 2 | 8 | 1.763 | 0.013 | 0.031 | 1.780 | 1.749 |
| Mn2+ | 4 | 3 | 12 | 2.109 | 0.032 | 0.095 | 2.166 | 2.071 |
| 5 | 1 (1) | 5 (5) | 2.306 | 0.326 | 0.827 | 2.958 | 2.131 | |
| 6 | 6 (14) | 36 (84) | 2.241 | 0.044 | 0.247 | 2.417 | 2.170 | |
| Mn3+ | 3 | 3 | 9 | 1.760 | 0.025 | 0.059 | 1.798 | 1.739 |
| Mn5+ | 4 | 2 | 8 | 1.818 | 0.007 | 0.015 | 1.825 | 1.810 |
| Fe2+ | 3 | 3 | 9 | 1.899 | 0.026 | 0.080 | 1.941 | 1.861 |
| 4 | 1 | 4 | 2.008 | 0.000 | 0.000 | 2.008 | 2.008 | |
| 6 | 9 (2) | 54 (12) | 2.196 | 0.032 | 0.128 | 2.274 | 2.146 | |
| Fe3+ | 3 | 1 | 3 | 1.730 | 0.000 | 0.000 | 1.730 | 1.730 |
| 4 | 1 | 4 | 1.957 | 0.000 | 0.000 | 1.957 | 1.957 | |
| 6 | 1 | 6 | 2.207 | 0.000 | 0.000 | 2.207 | 2.207 | |
| Co+ | 2 | 1 | 2 | 1.749 | 0.000 | 0.000 | 1.749 | 1.749 |
| Co2+ | 4 | 4 | 16 | 1.963 | 0.011 | 0.035 | 1.983 | 1.948 |
| 6 | 2 (3) | 12 (18) | 2.181 | 0.005 | 0.010 | 2.186 | 2.176 | |
| Co3+ | 6 | 36 (30) | 216 (180) | 1.963 | 0.013 | 0.115 | 2.007 | 1.892 |
| Ni2+ | 4 | 10 | 40 | 1.928 | 0.025 | 0.141 | 2.014 | 1.873 |
| 6 | 4 (5) | 24 (30) | 2.127 | 0.026 | 0.085 | 2.164 | 2.079 | |
| Cu+ | 2 | 8 | 16 | 1.875 | 0.022 | 0.084 | 1.931 | 1.847 |
| 4 | 1 | 4 | 1.977 | 0.000 | 0.000 | 1.977 | 1.977 | |
| Cu2+ | 4 | 1 (1) | 4 (4) | 1.941 | 0.012 | 0.032 | 1.953 | 1.921 |
| 5 | 0 (2) | 0 (10) | ||||||
| 6 | 3 (10) | 18 (60) | 2.185 | 0.288 | 0.843 | 2.722 | 1.879 | |
| Zn2+ | 2 | 3 | 6 | 1.860 | 0.013 | 0.032 | 1.874 | 1.842 |
| 4 | 23 (2) | 92 (8) | 1.984 | 0.038 | 0.180 | 2.086 | 1.906 | |
| 6 | 1 | 6 | 2.136 | 0.000 | 0.000 | 2.136 | 2.136 | |
| Ga3+ | 4 | 3 | 12 | 1.952 | 0.040 | 0.159 | 2.063 | 1.904 |
| 6 | 1 | 6 | 2.079 | 0.012 | 0.035 | 2.099 | 2.064 | |
| Ge4+ | 4 | 0 (2) | 0 (8) | |||||
| Se6+ | 4 | 0 (2) | 0 (8) | |||||
| Rb+ | 6 | 6 | 36 | 3.080 | 0.104 | 0.441 | 3.347 | 2.906 |
| 7 | 1 (1) | 7 (7) | 3.085 | 0.099 | 0.315 | 3.191 | 2.876 | |
| 8 | 14 (3) | 112 (24) | 3.263 | 0.193 | 0.806 | 3.764 | 2.958 | |
| 9 | 0 (1) | 0 (9) | ||||||
| 10 | 1 | 10 | 3.484 | 0.308 | 0.804 | 3.915 | 3.111 | |
| 11 | 0 (1) | 0 (11) | ||||||
| 12 | 1 | 12 | 3.568 | 0.283 | 0.605 | 3.773 | 3.168 | |
| Sr2+ | 4 | 9 | 36 | 2.641 | 0.030 | 0.137 | 2.682 | 2.545 |
| 5 | 6 | 30 | 2.691 | 0.122 | 0.460 | 2.940 | 2.480 | |
| 6 | 9 (1) | 54 (6) | 2.749 | 0.150 | 0.708 | 3.216 | 2.508 | |
| 7 | 1 (1) | 7 (7) | 2.916 | 0.229 | 0.601 | 3.221 | 2.620 | |
| 8 | 1 (1) | 8 (8) | 2.977 | 0.299 | 0.811 | 3.379 | 2.568 | |
| 10 | 2 | 20 | 2.999 | 0.248 | 0.810 | 3.380 | 2.570 | |
| 13 | 1 | 13 | 3.268 | 0.311 | 1.024 | 3.730 | 2.706 | |
| Y3+ | 6 | 5 | 30 | 2.394 | 0.050 | 0.174 | 2.478 | 2.304 |
| Nb5+ | 4 | 10 | 40 | 1.963 | 0.024 | 0.110 | 2.026 | 1.916 |
| 6 | 2 | 12 | 2.126 | 0.003 | 0.006 | 2.129 | 2.123 | |
| Mo6+ | 4 | 11 (1) | 44 (4) | 1.864 | 0.031 | 0.149 | 1.951 | 1.802 |
| 5 | 0 (1) | 0 (5) | ||||||
| Ru3+ | 6 | 8 | 48 | 2.092 | 0.005 | 0.019 | 2.101 | 2.082 |
| Rh3+ | 6 | 3 (2) | 18 (12) | 2.071 | 0.007 | 0.024 | 2.078 | 2.054 |
| Pd2+ | 4 | 5 | 20 | 2.044 | 0.015 | 0.060 | 2.079 | 2.019 |
| Ag+ | 2 | 9 (2) | 18 (4) | 2.125 | 0.026 | 0.108 | 2.192 | 2.084 |
| 3 | 2 | 6 | 2.266 | 0.099 | 0.295 | 2.445 | 2.150 | |
| 4 | 2 | 8 | 2.277 | 0.024 | 0.085 | 2.316 | 2.231 | |
| 5 | 0 (1) | 0 (5) | ||||||
| 6 | 0 (2) | 0 (12) | ||||||
| Cd2+ | 6 | 4 (4) | 24 (24) | 2.341 | 0.044 | 0.227 | 2.466 | 2.239 |
| Sn2+ | 3 | 1 | 3 | 2.143 | 0.019 | 0.042 | 2.170 | 2.128 |
| Sn4+ | 6 | 4 | 24 | 2.177 | 0.000 | 0.001 | 2.178 | 2.177 |
| Cs+ | 6 | 1 | 6 | 3.187 | 0.000 | 0.000 | 3.187 | 3.187 |
| 7 | 2 | 14 | 3.342 | 0.135 | 0.393 | 3.549 | 3.156 | |
| 8 | 5 (1) | 40 (8) | 3.396 | 0.146 | 0.641 | 3.818 | 3.177 | |
| 9 | 2 (1) | 18 (9) | 3.479 | 0.242 | 0.839 | 3.940 | 3.101 | |
| 10 | 5 | 50 | 3.559 | 0.185 | 0.836 | 4.034 | 3.198 | |
| 11 | 1 | 11 | 3.665 | 0.242 | 0.698 | 4.068 | 3.370 | |
| 12 | 5 (1) | 60 (12) | 3.642 | 0.145 | 0.448 | 3.827 | 3.379 | |
| Ba2+ | 4 | 1 | 4 | 2.738 | 0.065 | 0.155 | 2.798 | 2.643 |
| 5 | 6 (1) | 30 (5) | 2.868 | 0.088 | 0.388 | 3.041 | 2.653 | |
| 6 | 13 (1) | 78 (6) | 2.896 | 0.156 | 0.768 | 3.375 | 2.607 | |
| 7 | 16 | 112 | 2.960 | 0.177 | 0.771 | 3.447 | 2.676 | |
| 8 | 7 | 56 | 3.059 | 0.234 | 0.846 | 3.519 | 2.673 | |
| 9 | 0 (3) | 0 (27) | ||||||
| 10 | 0 (3) | 0 (30) | ||||||
| 11 | 0 (1) | 0 (11) | ||||||
| 14 | 1 | 14 | 3.293 | 0.226 | 0.665 | 3.490 | 2.825 | |
| La3+ | 6 | 1 (1) | 6 (6) | 2.531 | 0.006 | 0.013 | 2.535 | 2.522 |
| 7 | 1 (1) | 7 (7) | 2.607 | 0.151 | 0.397 | 2.834 | 2.437 | |
| 8 | 8 (3) | 64 (24) | 2.698 | 0.104 | 0.553 | 2.965 | 2.412 | |
| 9 | 3 (3) | 27 (27) | 2.770 | 0.154 | 0.621 | 3.098 | 2.477 | |
| Ce3+ | 8 | 3 (2) | 24 (16) | 2.646 | 0.120 | 0.486 | 2.849 | 2.363 |
| 9 | 2 (4) | 18 (36) | 2.740 | 0.192 | 0.713 | 3.133 | 2.420 | |
| Ce4+ | 6 | 1 | 6 | 2.427 | 0.000 | 0.000 | 2.427 | 2.427 |
| Pr3+ | 7 | 1 | 7 | 2.572 | 0.081 | 0.236 | 2.691 | 2.455 |
| 8 | 0 (1) | 0 (8) | ||||||
| 9 | 0 (1) | 0 (9) | ||||||
| Nd3+ | 6 | 2 | 12 | 2.497 | 0.062 | 0.164 | 2.571 | 2.407 |
| 8 | 1 (3) | 8 (24) | 2.589 | 0.005 | 0.010 | 2.594 | 2.584 | |
| 9 | 0 (2) | 0 (18) | ||||||
| Sm3+ | 7 | 1 | 7 | 2.477 | 0.046 | 0.162 | 2.544 | 2.382 |
| 8 | 0 (5) | 0 (40) | ||||||
| 9 | 0 (1) | 0 (9) | ||||||
| Eu2+ | 6 | 2 | 12 | 2.599 | 0.106 | 0.279 | 2.715 | 2.436 |
| 8 | 1 | 8 | 2.861 | 0.256 | 0.681 | 3.235 | 2.554 | |
| 10 | 1 | 10 | 2.928 | 0.214 | 0.717 | 3.246 | 2.529 | |
| 12 | 1 | 12 | 2.993 | 0.048 | 0.135 | 3.059 | 2.924 | |
| Eu3+ | 6 | 1 | 6 | 2.463 | 0.002 | 0.003 | 2.464 | 2.461 |
| 8 | 0 (1) | 0 (8) | ||||||
| 9 | 0 (1) | 0 (9) | ||||||
| Gd3+ | 9 | 0 (2) | 0 (18) | |||||
| Tb3+ | 8 | 0 (3) | 0 (24) | |||||
| Dy3+ | 8 | 0 (1) | 0 (8) | |||||
| Ho3+ | 6 | 1 | 6 | 2.417 | 0.104 | 0.274 | 2.609 | 2.335 |
| 8 | 0 (1) | 0 (8) | ||||||
| Er3+ | 6 | 1 (2) | 6 (12) | 2.401 | 0.056 | 0.165 | 2.525 | 2.360 |
| 8 | 0 (2) | 0 (16) | ||||||
| Yb3+ | 6 | 2 | 12 | 2.366 | 0.046 | 0.124 | 2.417 | 2.293 |
| 7 | 1 | 7 | 2.397 | 0.138 | 0.403 | 2.664 | 2.261 | |
| Lu3+ | 6 | 1 | 6 | 2.304 | 0.021 | 0.042 | 2.325 | 2.283 |
| Hf4+ | 8 | 1 | 8 | 2.327 | 0.148 | 0.295 | 2.474 | 2.179 |
| Ta5+ | 4 | 5 | 20 | 1.959 | 0.027 | 0.106 | 2.008 | 1.902 |
| W6+ | 4 | 26 (1) | 104 (4) | 1.868 | 0.054 | 0.218 | 1.972 | 1.754 |
| Pt2+ | 4 | 4 (11) | 16 (44) | 2.049 | 0.008 | 0.030 | 2.065 | 2.035 |
| Au+ | 2 | 2 | 4 | 2.020 | 0.006 | 0.013 | 2.025 | 2.012 |
| Tl+ | 6 | 2 | 12 | 3.039 | 0.167 | 0.571 | 3.385 | 2.814 |
| 7 | 5 | 35 | 3.117 | 0.240 | 0.913 | 3.664 | 2.751 | |
| 8 | 1 | 8 | 3.204 | 0.239 | 0.762 | 3.542 | 2.780 | |
| Pb2+ | 5 | 1 | 5 | 2.559 | 0.125 | 0.313 | 2.622 | 2.309 |
| 7 | 1 | 7 | 2.724 | 0.064 | 0.155 | 2.822 | 2.667 | |
| Bi3+ | 8 | 0 (3) | 0 (24) | |||||
| U4+ | 8 | 1 | 8 | 2.424 | 0.040 | 0.080 | 2.464 | 2.384 |
| U6+ | 7 | 0 (2) | 0 (14) | |||||
Derivation of bond-valence parameters
While the first proposal of a relation between bond length and bond strength can be attributed to Pauling,73 the first universal two-body correlation between these variables was described by Brown and Shannon74 in what ultimately developed into the bond-valence model.75 The bond-valence relation was initially proposed as an inverse power equation74 and later reformulated to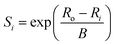 | (1) |
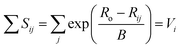 | (2) |
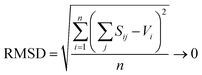 | (3) |
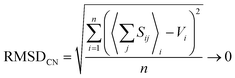 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weighting scheme between RMSD and RMSDCN of Gagné & Hawthorne to derive the bond-valence parameters of Table 1. A detailed discussion of the method used to derive bond-valence parameters for mixed-anion cation coordination polyhedra, and those observed in a single coordination number, is given in the ESI† alongside complementary verification of anion bond-valence sums for the full set of parameters.
1 weighting scheme between RMSD and RMSDCN of Gagné & Hawthorne to derive the bond-valence parameters of Table 1. A detailed discussion of the method used to derive bond-valence parameters for mixed-anion cation coordination polyhedra, and those observed in a single coordination number, is given in the ESI† alongside complementary verification of anion bond-valence sums for the full set of parameters.
Comparison to O2− bond-valence parameters
For the 40 cations for which both Ro and B were refined, the mean increase in Ro and B are 0.064 and 0.023 Å, respectively, in comparison to the parameters of Gagné & Hawthorne.67 When weighting these changes by the number of coordination polyhedra used for each ion, these numbers are 0.092 and −0.011 Å, respectively. The largest change is for Li+: for O2−, Ro = 1.062, B = 0.642 Å, and for N3−, Ro = 1.713, B = 0.312 Å. This variation is an artifact of a shallow RMSD global minimum (typical of alkali and alkaline-earth metals), whereby large changes in the bond-valence parameters lead to only slight changes in RMSD. A lower value of Ro for N3−vs. O2− is usually associated with an increased value for B, and vice versa.Comparison with published bond-valence parameters
We compared the parameters of this work to the set of soft bond-valence parameters of Chen & Adams77 which they adapted to the first coordination shell (but did not evaluate for anion bond-valence sums). Fewer bond-valence parameters are given by these authors for nitrides, allowing comparison for 25 pairs of bond-valence parameters. Whereby the valence-sum rule applies equally to cations and anions, and good agreement for cation bond-valence sums (BVS) in no way implies good agreement for anion BVS, our evaluation necessarily covers both cation and anion BVS. For a set of 25 reliable crystal structures selected for this purpose, the mean anion RMSD observed for the parameters of this work and those of Chen & Adams are 0.236 v.u. and 0.258 v.u., respectively. For cation BVS, the mean cation RMSD over the 25 ion pairs is 0.118 v.u. for the parameters of this work, and 0.219 v.u. for the parameters of Chen & Adams. Weighting by the number of coordination polyhedra, these values are 0.136 and 0.369 v.u., respectively, thus validating the derivation method of Gagné & Hawthorne.67On deriving bond-valence parameters
We stress that there is no good alternative to ensuring the quality of bond-valence parameters other than to verify their performance over a large number of crystal-structure refinements.With strong correlation between the ratio of bond-valence parameter Ro and mean-bond-length as a function of the nth ionization energy of the cation,67 it may be tempting to derive bond-valence parameters for ion pairs without empirical data taking the mean-bond-length to be equal to the sum of the constituent ionic radii. However, this practice is fraught with uncertainty due to (1) large uncertainty associated with Shannon's ionic radii (the subject of upcoming work), and (2) the risk involved in fixing bond-valence parameter Ro instead of B (even where experimental data are available).67 It is for these reasons that we have refrained from predicting bond-valence parameters which cannot be verified via high-quality experimental data. Even where such data are available, one may easily be misled into reporting “high-quality” bond-valence parameters if their quality is not checked against anion bond-valence sums.
Derivation of Lewis acid strengths
Pearson's concept of hard and soft acids and bases (HSAB)78,79 may be conveniently transposed and quantified onto the bond-valence scale as| Sa = V/Ni | (5) |
As Lewis acid strength is dependent upon the base against which it is measured,85 we derive a scale of Lewis acidity for 77 cations bonded to N3− (Table 1) to complement the dataset of Gagné & Hawthorne for cations bonded to O2−.86 On average, Lewis acid strength values increase by 0.115 v.u. for cations bonded to N3−vs. O2−, due to generally lower observed cation coordination numbers. Notable discrepancies result from a favored tetrahedral over octahedral coordination for such ions as Nb5+, Mo6+, and W6+ when bonded to N3−.
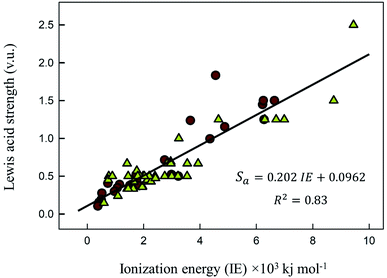
Correlation with ionization energy
In Fig. 1 we show the correlation between Lewis acid strength and the nth ionization energy for the 64 cations reported here (n < 10 coordination polyhedra marked by triangles). Linear fit (solid line) to all data gives R2 = 0.83. For n ≥ 10 coordination polyhedra (25 cations), the best-fit equation becomes| Sa = 0.315 × IE0.807 | (6) |
We also note a high correlation (R2 = 0.96) between the ratio 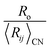 and Lewis acidity (Table 1)
and Lewis acidity (Table 1)
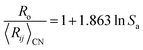 | (7) |
Bond-length variation
We generally observe much narrower bond-length ranges for nitrides than we do for oxides and oxysalts. This observation is likely due to a combination of the nascent sampling of the compositional space of inorganic nitrides and a focus by experimentalists on simple compositions and structures as a result of the significant challenges associated with synthesizing and growing these compounds. In fact, of the 18 transition metal configurations with bond-length range > 0.75 Å when bonded to O2−,58 only three configurations are observed in our dataset for nitrides: [6]Mn2+ (n = 6), with bond lengths 2.170–2.417 Å, [6]Cu2+ (n = 3), with bond lengths 1.879–2.722 Å, and [6]Nb5+ (n = 2), with bond lengths 2.123–2.129 Å; this compares to bond-length ranges of 0.837, 0.893 and 0.777 Å when bonded to O2−,58 respectively. Furthermore, the absence of any substantial bond-length variation in many ion configurations bonded to N3− is a result of their observation in (relatively) highly symmetrical structures with inherently little to no variation in a priori bond lengths, which was recently demonstrated to be the most common cause of bond-length variation in inorganic solids by Gagné & Hawthorne.58There are 66 cations overlapping this work and that of Gagné & Hawthorne for oxides58,69–72 from which we can directly compare mean bond-length and average observed coordination number. We find that cation–N3− mean bond-lengths are on average 0.027 Å longer than their O2− counterparts (0.034 Å when weighting these differences by the number of N3− coordination polyhedra per cation) with mean bond-length differences varying between 0.318 Å shorter (Ag+) and 0.196 Å longer (Hf4+) when bonded to N3−. The average observed coordination number is 1.078 lower for cations bonded to N3−vs. O2− (1.159, weighted).
Comparing the data on the basis of ion configurations (i.e. as a function of oxidation state and coordination number), the average increase in mean bond-length for N3− coordination polyhedra is 0.118 Å (0.106 Å when weighting these differences by the number of N3− coordination polyhedra per cation), over 112 overlapping ion configurations. In comparison, the ionic radii for [4]N3− and [4]O2− are 1.46 and 1.38 Å, respectively.68 Thus, our data show a slightly more pronounced increase in mean bond-lengths for N3−vs. O2− than predicted via the addition of ionic radii, with the largest increase for [12]Rb+ (0.339 Å) and largest decrease for [4]Ag+ (−0.120 Å).
We do not observe structures with N–H⋯N complexes in our neutron diffraction dataset; only N–H⋯O (n = 25) and O–H⋯N (n = 4). For N–H bonds, the average length is 0.999 Å with a range of 0.915–1.025 Å; for N⋯H bonds, the average length is 2.269 Å, with a range of 2.034–2.610 Å.
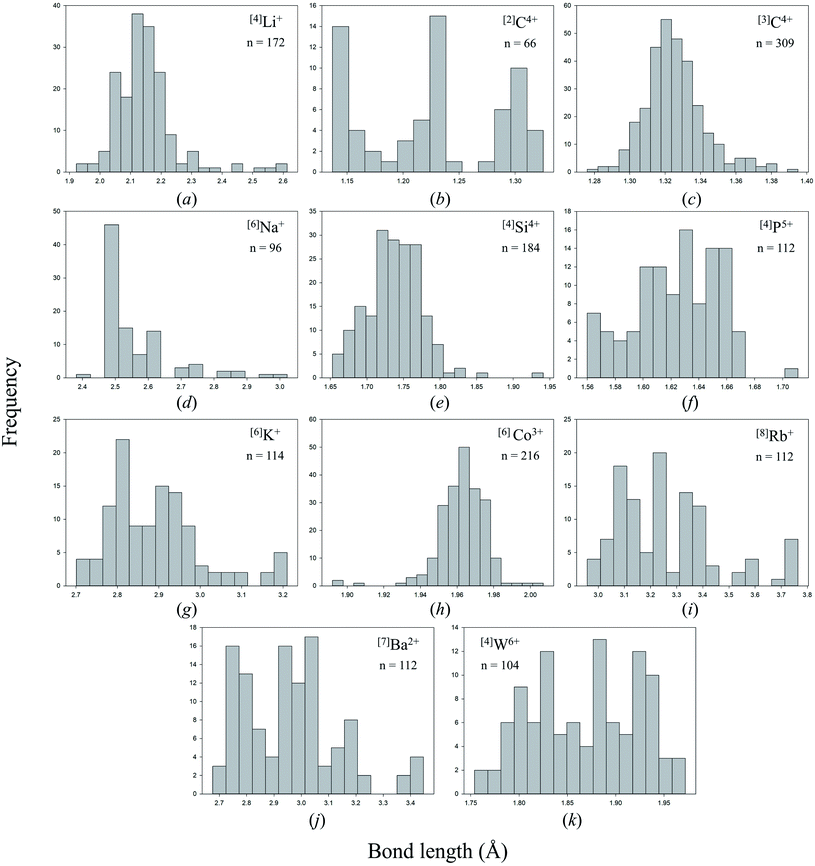
Anomalous bond-length distributions
Bond lengths are expected to form positively skewed Gaussian distributions as a result of the interplay between Coulomb attraction and Born repulsion for ion pairs (Fig. 2c gives such an example for [3]C4+ bonded to N3−). Gagné & Hawthorne state that deviations from such shape are the result of bond-topological, electronic and/or crystal-structure effects,58 which they go on to describe for all cations of the periodic table observed bonding to O2− in inorganic structures.58,69–72 Notable examples of anomalous bond-length distributions include a tri-modal distribution for [4]P5+–O2− bonds,70 caused by varying bond-valence requirements as a function of the degree of polymerization of the [PO4]3− oxyanion (i.e. bond-topological effects), a tri-modal distribution for [6]Mo6+–O2− bonds,58 arising from a combination of pseudo Jahn–Teller and bond-topological effects, and anomalously long tails at longer bond lengths for penta-coordinated ion configurations of Cr2+, Co2+ and Cu2+, also caused by pseudo Jahn–Teller and bond-topological effects.58Fig. 2 shows bond-length distributions for the data of Table 2 (cations bonded solely to N3−) for n > 100 bond lengths and a few more interesting configurations. Due to a general paucity of data, partly due to the difficulty of growing inorganic nitrides as single crystals, few ion configurations have sufficient data for a distinct shape to arise from their bond-length distribution.
Visual inspection of these bond-length distributions shows departure from regular behavior for a handful of ion configurations. For the [2]C4+ configuration (Fig. 2c), we observe a tri-modal distribution of bond lengths with peaks at ∼1.15, ∼1.22 and ∼1.31 Å. Converting these bond lengths into bond valences gives 2.62, 2.00 and 1.42 v.u., respectively. Thus, the peak at ∼1.22 Å arises from symmetrical bonds of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N carbodiimide units, such as in the structure of SrCN2 (ref. 87) (75040) with a priori (observed) bond valences 2 × 2 v.u. (1.933 and 1.985) for C4+ (6 × 1/3 v.u. for Sr2+) calculated using the method of Gagné & Hawthorne88 (Table S2†). The two other peaks of Fig. 2c are complementary, with bond-valence sum ≈ 4 v.u.; they result from N–C
N carbodiimide units, such as in the structure of SrCN2 (ref. 87) (75040) with a priori (observed) bond valences 2 × 2 v.u. (1.933 and 1.985) for C4+ (6 × 1/3 v.u. for Sr2+) calculated using the method of Gagné & Hawthorne88 (Table S2†). The two other peaks of Fig. 2c are complementary, with bond-valence sum ≈ 4 v.u.; they result from N–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N cyanamide units, for example in Ag+N(CN)2 (ref. 89) (843) with a priori (observed) bond valences 1.5 (1.524) and 2.5 (2.626) v.u. for C4+, and 2 × 0.5 (0.511) v.u. for Ag+. Thus, this result shows that bond valences are not perfectly distributed into a [3 + 1] v.u. arrangement in cyanamide units; a bond-valence of 3 v.u. would require a bond length of 1.115 Å.
N cyanamide units, for example in Ag+N(CN)2 (ref. 89) (843) with a priori (observed) bond valences 1.5 (1.524) and 2.5 (2.626) v.u. for C4+, and 2 × 0.5 (0.511) v.u. for Ag+. Thus, this result shows that bond valences are not perfectly distributed into a [3 + 1] v.u. arrangement in cyanamide units; a bond-valence of 3 v.u. would require a bond length of 1.115 Å.
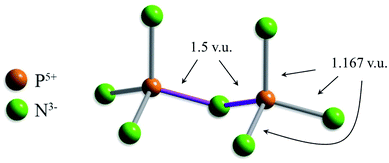
Two other bond-length distributions are observed with slight irregularities; those of [4]P5+, and [4]W6+ (Fig. 2f and k, respectively). In both instances, the root cause for irregularity is non-local bond-topological asymmetry. For these ion configurations, competition between the bond-valence constraints of the cation and its bonded anions requires uneven distribution of bond valences (thus bond lengths; eqn (1)) in cation and/or anion coordination polyhedra. This mechanism of bond-length variation was described for [4]P5+ bonded to O2− by Gagné & Hawthorne,70 and was later extended to transition metals and described under the umbrella of bond-topological effects.58 For example, [4]P5+ ideally forms 4 bonds that are 1.25 v.u. in strength; however, the ideal bond strengths for a bridging [2]N3− ion are 2 × 1.5. v.u. Thus, for polymerization into corner-sharing dimers, [4]P5+ adapts to the bond-valence requirement of [2]N3− and increase the strength of one bond to 1.5 v.u., weakening the three other bonds to 1.167 v.u (Fig. 3). For a chain of corner-sharing tetrahedra, [4]P5+ adjusts to 2 × 1.5 and 2 × 1 v.u.—so and so forth for different combinations of degrees of polymerization, number of shared vertices, and varying coordination number of the bridging anion(s). These different combinations result in multiple maxima in the bond-length distribution of cations prone to bond-topological effects; full rationalization of the shape of their bond-length distributions is achieved via the calculation of a priori bond valences for their constituent crystal structures. In our dataset, [4]P5+ and [4]W6+ are observed to polymerize into oligomers, chains, rings, sheets, clusters and frameworks, and we do not resolve the bond-valence requirements of each scenario here.
While other apparent instances of multi-modality observed in Fig. 2 result from paucity of data, our full dataset abounds with subtle bonding irregularities that allow a glimpse into the intriguing bonding properties of nitrides sensu lato, of which many bear technological importance. In the next part of this work, we examine structural and electronic effects associated with anomalous bond lengths in our dataset, thus shifting our focus toward uncovering less traditional bonding properties of inorganic nitrides that offer promising opportunities in the exploration of their bulk compositional space.
Opportunities for bulk exploratory synthesis
On the exploration of new compositional spaces
This past decade has seen a rapid increase in the development of high-throughput (HT) computational methods applied to materials discovery. These methods, usually rooted in Density Functional Theory (DFT) and/or Machine Learning (ML), allow screening of large compositional spaces in search of yet-to-be-observed compounds with desired functional properties. A growing number of HT studies include experimentally validated predictions (see a list compiled by Jain et al. for DFT90),28,91–96 partly owing to their suitability to synthesizability analysis3,28,97–99—an emerging concept used to curb the difficulty of predicting the outcome of chemical reactions in the solid state.Today, rapid increase in available computational power has by-and-large transformed the problem of in silico exploration from one of computational feasibility to one of a priori identifying compositional spaces of interest100,101—a pursuit that has historically been realized via rules of crystal chemistry102,103 and heuristic concepts. However, several issues cloud the exploration of new compositional spaces via DFT approaches, separate from the difficulties traditionally associated with the theory itself (e.g. strongly correlated systems, substitutional disorder, ground state calculations that ignore a potentially non-negligible entropic contribution to structure stability,104etc.). For example, while exploration of extensive compositional spaces is currently manageable for ternary phases (as most recently evidenced by the work of Sun et al.28), quaternary-and-higher compositional spaces are exponentially more computationally expensive for they require their stability be evaluated against an exponentially large number of stoichiometrically feasible phases of lower order. Current approaches are further limited to a relatively small set of known elementary, binary, and ternary crystal structures which may not necessarily conform to the chemical compositions investigated. Nonetheless, these problems are largely temporal, and should progressively lessen with an ever-increasing supply of computational power and the incremental discovery of new crystal structures.
A more difficult (yet hardly discussed) problem is the fundamental inability of DFT to model energetically degenerate and pseudo-degenerate electronic states, whereby vibronic coupling giving rise to Jahn–Teller (and pseudo Jahn–Teller) distortions do not conform to the Born–Oppenheimer and adiabatic approximations underpinning DFT.105,106 This is problematic with regard to the startling extent to which vibronic coupling occurs in inorganic solids, as recently shown by Gagné & Hawthorne via large-scale bond-length dispersion analysis for oxides and oxysalts;58 of 147 configurations of transition metal ions observed bonding to O2−, 52 configurations were observed with anomalous bond-length distributions, 46 of which partially or entirely due to vibronic coupling. Pending development of vibronic patches to DFT methods for HT investigation (e.g. ref. 107) and widescale evaluation of their efficacy, complementing DFT calculations with different approaches could possibly attenuate the vibronic coupling problem; for example, prediction of non-centrosymmetric behavior is within the purview of machine learning, which has been used in combination with DFT calculations to insulate promising non-centrosymmetric compositions from large compositional spaces (e.g. Ruddlesden–Popper oxides108). The practice of combining DFT and machine learning approaches was recently reviewed by Schleder et al.109
Notwithstanding the above, HT computing should not be mistaken for a one-stop solution to the multi-faceted issue of exploratory synthesis.110 While HT methods play a critical role in fast-tracking materials discovery via the identification of “missing compounds” and the calculation of their properties,28,100 they are limited to rehashing data derived from known chemical spaces; navigating the totality of all existing compositional and structural spaces is categorically intractable for state-of-the-art HT methods.111 Thus, the discovery of new compositional spaces and of next-generation materials largely continues to lie in the ingenuity of the crystal and synthetic chemists. This assertion is particularly relevant to the exploration of inorganic nitrides, whose remarkable range of metastability suggests an exceptionally broad spectrum of observable compositions.97 Combined with the main takeaways of our bond-length dispersion analysis, this proposition leads us to affirm that the chemical potential of inorganic nitrides has barely been scratched, thus pressing the need for exploration outside known compositional spaces.
Below, we use the systematic nature of our bond-length dispersion analysis to identify various functional building blocks for integration into new compositions and crystal structures. Such an approach has disproportionate potential for leading to new disruptive compounds, and could advantageously be integrated into HT approaches to a priori identify areas of interest in lieu of expanding resources in low-return chemical spaces. Further integration of the data from Tables 1 and 2 may be used to rapidly verify the structural validity of these modeled compounds before expanding resources on them.
New compositional spaces for the exploratory synthesis of inorganic nitrides
In light of the recent extensive review of the crystal chemistry of oxides and oxysalts by Gagné & Hawthorne,58,69–72 we investigate our dataset of inorganic nitride structures for the occurrence of bond topological, electronic and/or crystal-structure effects, placing emphasis on the functional properties resulting from these effects. Compositional and structural divergences are expected between the compounds making up these two datasets. For example, lower cation coordination numbers are expected in inorganic nitrides due to the larger size of N3−vs. O2− (as evidenced by our comparison of mean bond lengths between N3− and O2− structures, above). We further expect (and observe) similar or lower oxidation states for cations in inorganic nitrides since O2− is better at stabilizing high metal oxidation states as a result of its higher electronegativity (3.44 vs. 3.04 for N), or alternatively, higher electron affinity.112 Furthermore, the reduced ionicity of the chemical bonds made by N3− allows formation of exceptionally strong and localized bonds that can lock-in energetically unfavorable atomic arrangements;97 this is particularly relevant to electronegative p-block and d-block elements.In addition to our principal dataset, we surveyed the chemical behavior of inorganic nitrides in coordination complexes; many molecular features of coordination complexes are preserved as they incorporate into crystal structures, and the carrying of their electronic properties is often more important than the steric constraints of space-group symmetry and long-range order.113 A chemically intuitive treatment of chemical bonding thus follows from the common simplifying assumption of no translational symmetry,114,115 allowing the study of molecular fragments via ligand field theory; the slight loss in accuracy (effectively, losing information on “additional” bonding schemes that arise in extended solids as a result of electron delocalization) is greatly overcome by substantial gains in chemical intuition at a local scale, resulting in transferable insight useful to the exploration of new compositional spaces. As such, bonding knowledge derived in coordination chemistry poses as powerful inspiration to solid-state syntheses.116
We organize our discussion into five phenomenological compositional spaces holding promise for the exploratory synthesis of bulk functional inorganic nitrides (summarized in Table 3), and encourage expansion of this kind of analysis to different chemical subfields whose functional units may differ in composition. In contrast to HT methods, the intent of the following subsections is not to identify specific chemical compositions and/or crystal structures, but to unearth new and promising compositional spaces from an otherwise intractable combinatorial space of chemistries to be used as starting points for more concrete computational and/or synthetic investigations.
| Confirmed (O2−)58,69–72 | Confirmed (N3−) | To be investigated (N3−)a | Relation to O2− |
|---|---|---|---|
| a Includes cations of high oxidation state (OS) that may be challenging to achieve experimentally. | |||
| Full-fledged multiple-bond formation (>1.95 v.u.) | |||
| [3]N5+, [4]Cl7+, [4]V5+, [4]Cr6+, [5,6]Mo5+, [4–6]Mo6+, [6]W6+, [4–5]Re7+, [4–5]Os8+, [6–8]U6+ | [2]C4+, [2]N5+, [2]S4+, [5]Mo6+, [4]W6+ | V4+, V5+, Cr5,6+, Nb5+, Mo5+, Tc7+, Ta5+, Re7+, Os8+, U6+ | χ N3− < χO2−; multiple-bond formation facilitated for N3−. Triple bond impossible for O2−; special geometry required for N3− |
| (>1 v.u.: Ti4+, Se4,6+, As5+, Br5,7+, Te4,6+, I5,7+, W5+, Os6,7+, Bi5+, Np5,6,7+) | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Coupled electronic-vibrational degeneracy: the Jahn–Teller effect | |||
| [6]Cr2+, [6]Mn3+, [6]Cu2+ | [3]Cr3+, [6]Co3+, [6]Cu2+ | [6]V3+, [6]Cr2+, [6]Mn3+, [6]Fe2+, [3]Fe3+, [6]Co2+, [6]Mo5+, [6]Os7+ | χ N3− < χO2−; increased covalency thus distortion magnitude for N3− |
| Minor: [6]Co2+, [6]V3+ and [6]Mo5+, [6]Os7+ | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Coupled electronic-vibrational near-degeneracy: the pseudo Jahn–Teller effect | |||
| [4–7]Ti4+, [4–6]V5+, [6–10,12]Y3+, [6–10]Zr4+, [4–8]Nb5+, [4–6]Mo6+, [6–8]Hf4+, [6–7]Ta5+, [4–6]W6+, [4–6]Re7+, [4–6]Os8+. Minor: [6–8]Sc3+, [5–6]V4+, [4]Cr6+, [4]Mn7+, [6–10,12]Y3+; [5]Cr2+, [5]Co2+, [5]Cu2+, [6]Zn2+, [6]Cd2+, [6]Hg2+ | [6]Y3+, [4]Mo6+, [8]Hf4+, [4]Ta5+, [4]W6+ | Sc3+, Ti4+, Zr4+ | χ N3− < χO2−; optimal match of atomic orbital energies shifted to cations of lower electronegativity. Increased covalency thus distortion magnitude for N3− |
| Observed, but distortion magnitude inconclusive due to paucity of data: [4]V5+, [4]Cr6+, [4,6]Nb5+ | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Lone-pair stereoactivity | |||
| [3]P3+, [3]S4+, [2,4]Cl3+, [3]Cl5+, [3–8]As3+, [4–10]Se4+, [6–8]Br5+, [3–9]Sn2+, [3–9]Sb3+, [3–12]Te4+, [6–9]I5+ | [6–8]Tl+, [3]Sn2+, [5,7]Pb2+ | Sn2+, As3+, Sb3+, Se4+; possibly In+, Ge2+, Te4+, Bi3+ | χ N3− < χO2−; optimal match of atomic orbital energies shifted to cations of lower electronegativity |
| Minor: [3–12]Tl+, [3–12]Pb2+, [3–10,12]Bi3+ | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Polymerization: [4] M 6+ configuration | |||
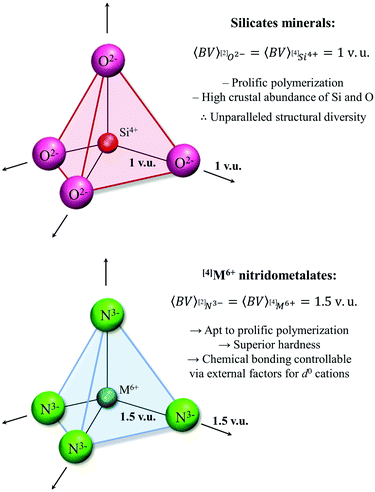
| [4]Si4+, [4]Ge4+, [4]Ti4+, [4]Cr4+ | [4]Mo6+, [4]W6+ | [4]S6+, [4]Se6+, [4]Cr6+ | Cation OS/CN ratio of 1.5 required for prolific polymerization via[2]N3−, vs. a ratio of 1 for [2]O2− |
Multiple-bond formation
One of the primary causes of bond-length variation in inorganic solids is the formation of “multiple bonds” between ion pairs.58 Inorganic nitrides are exciting materials for in-depth study of this phenomenon and its ensuing properties, for they are a rare class of solid-state compounds where triple-bond formation (i.e. up to 3 v.u. in strength) is possible. In inorganic nitrides, multiple-bond formation is commonly observed for metal nitrido complexes, i.e. coordination complexes which contain one or more atoms of nitrogen bound only to transition metals. In these complexes, multiple-bond formation (commonly called “double” or “triple” bonds) occurs via mixing of anion p orbitals and unfilled metal d and/or f orbitals.117,118Coordination compounds containing nitrido complexes are ubiquitous in chemical literature, largely driven by the desire to improve our understanding of the mechanism of nitrogen fixation (which is assumed to undergo nitrido-complex formation).119 Comprehensive reviews bring into light the remarkable chemical versatility of doubly- and triply-bonded N3−.120–124 Despite this wealth of information, very few compounds containing double or triple M–N bonds have been synthesized and characterized in the solid state. Of the 137 cation configurations we observe bonded solely to N3− (Table 2), only four configurations are observed with one or more structures containing a bond valence > 1.95 v.u.; three are non-metals, the other is [4]W6+ (including oxynitrides only adds one configuration to this tally: [5]Mo6+). In comparison, Gagné & Hawthorne report 17 of 461 cation configurations with bond valence > 1.95 v.u. (i.e. discrete terminal double bonds to O2−) in oxide and oxysalt structures, 12 of which for transition metals (Fig. 4).58 Although inorganic nitrides have the ability to make terminal bonds up to 3 v.u. in strength, we observe no such bonds in our dataset. The strongest metal bond observed is for [5]Mo6+ in oxynitride Na5Mo6+O4N125 (55113) with a Mo6+–N3− distance of 1.719 Å, representing a bond valence of 2.583 v.u.
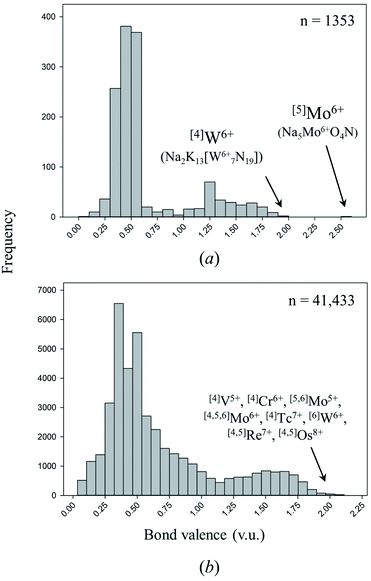 | ||
| Fig. 4 Distribution of bond valences for all transition-metal configurations observed in (a) this work, (b) the dataset of Gagné & Hawthorne for transition metals bonded to O2−. | ||
Evidently, the potential for making strong terminal bonds to N3− is untapped; combined with the incredible variety of known nitrido complexes spanning most metals of the periodic table (including U118,126), doubly and triply-bonded inorganic nitrides are promising candidates for exploratory synthesis. Such compounds may not only be helpful in clarifying the mechanism of N2 reduction, but could possibly be used as heterogeneous catalysts in the development of a post-Haber–Bosch process proceeding at milder reaction conditions; the remarkable diversity of known nitrido-complex compounds shows considerable promise for fine tuning the kinetics of N2 and H2 activation. Metal-nitrido coordination complexes have also been reported as a key component to the catalytic oxidation of water,127 alkanes,128 alkenes and alcohols,129 thus showing further promise for their use as solid-state catalysts.
There are 66 of 76 cations and 112 of 137 cation configurations overlapping this work and that of Gagné & Hawthorne for oxides and oxysalts,58,69–72 whereby non-overlapping configurations primarily result from the preference of inorganic nitrides for lower cation oxidation states and/or coordination numbers. Based on the similar crystal-chemical behavior of these classes of compounds, their significant overlap in cation configurations, and the isoelectronic nature of N3− and O2−, we assume that cation configurations yet-to-be-observed in inorganic nitrides with equal or lower oxidation states and/or coordination numbers than their oxide and oxysalt counterparts either result from challenging synthesis or lack of synthetic attempts. Comparing the dataset of Gagné & Hawthorne against the present work for cation configurations with bonds > 1 v.u., we conclude that promising opportunities for multiple bond-formation (1–3 v.u.) in inorganic nitrides include cations such as Ti4+, V4+, As5+, Se4,6+, Br5+,7+, Mo5+, Tc7+, Te4,6+, I5,7+, W5+, Re7+, Os6,7,8+, Bi5+, U6+ and Np5,6,7+; further syntheses are also warranted for V5+, Cr5,6+, Nb5+, Mo6+, Ta5+ and W6+.
Coupled electronic-vibrational degeneracy: the Jahn–Teller effect
The Jahn–Teller effect (JTE) is a mechanism of symmetry-breaking that results from strong electron–vibrational (vibronic) and electron–phonon interactions in molecules and crystals, respectively,130 and is characterized by energetically favorable occupancy of electronic states ensuing degeneracy breaking polyhedral distortion. Although the JTE is commonly observed in coordination complexes of N3− (including nitrido complexes,131 which are for example used as single-molecule magnets132), research into the material properties resulting from the JTE has historically focused on oxide and oxysalt compounds, including colossal magnetoresistance,133 superconductivity,134 improved electrochemical performance of cathode materials (via the “opening” of diffusion channels),135,136 and magnetic-dielectric bistability.106Gagné & Hawthorne's recent bond-length dispersion analysis for transition metals bonded to O2− identifies 4 out of 52 typically highly distorted ion configurations where coupled electronic-vibrational degeneracy is the principal underlying cause of bond-length variation, [6]Cr2+, [6]Mn3+, [6]Cu2+ and [6]Os7+, and an additional three configurations where it is a minor contributing factor: [6]Co2+, [6]V3+ and [6]Mo5+. Considering the lower electronegativity of N vs. O (which entails more covalent bonds to transition metals) and the isoelectronic nature of these ligands, there is reason to believe that the above ion configurations (and possibly others) may experience the JTE with larger distortion magnitude when bonded to N3−.
In the present dataset, we observe three cation configurations (bonded solely to N3−) for which anomalous bond lengths can be attributed to the JTE: [3]Cr3+, [6]Co3+ (weak) and [6]Cu2+ (strong). Ion configurations [6]Mn3+, [6]Os7+ and [6]Mo5+ have yet to be observed, while [6]Cr2+ and [6]V3+ are each observed in one structure, refined as regular octahedra, and [6]Co2+ observed in two structures, also refined as regular octahedra. [3]Cr3+ is observed in Ca3Cr3+N3 (40205) with bond lengths 2 × 1.766 and 1.863 Å.137[6]Co3+ ([Ar]3d6) is observed in (NH3)5Co3+NCSCo3+(CN)5H2O (4094), with two anomalously short bond lengths of 1.907 and 1.932 Å in trans configuration, and 4 equatorial bonds ranging 1.972–1.977 Å,138 and in (Co3+(NH3)6)(Np5+O2(C2O4)2)(H2O)1.5 (155531) with two short bond lengths of 1.892 and 1.894 Å in trans configuration and 4 equatorial bonds ranging 1.937–1.970 Å (spin unknown in both structures).139[6]Cu2+ ([Ar]3d9) is observed in three structures bonded solely to N3−, and ten structures in mixed proportions with O2−. The Jahn–Teller effect is observed in all cases, to a largely varying extent, and where the two weakest bonds (<0.2 v.u.) are always to O2−. For the three Cu2+N6 octahedra, the observed bond lengths are 4 × 2.061 and 2 × 2.612 Å for Cu(NH3)4)(Ag(SCN)3 (10065),140 4 × 1.997 and 2 × 2.369 Å in Cu[B(CN)4]2 (415546),141 and 2 × 1.879, 2 × 1.965 and 2 × 2.722 Å for K2CuFe(CN)6 (99499).142
The surprisingly large range of bond lengths observed for the latter structure, 0.843 Å, appears to support the case for higher distortion magnitude in inorganic nitrides; of 365 polyhedra observed bonding to O2− by Gagné & Hawthorne,58 only one is observed with a larger range of bond lengths, 0.870 Å, for mrázekite Bi23+Cu32+(OH)2O2(PO4)2(H2O)2 (71934).143
To verify that the large variation of bond lengths is not due (or partly due) to non-local bond-topological asymmetry in K2CuFe(CN)6, we calculate values of Δtopol and Δcryst for the Cu2+N6 octahedron using the method of Gagné & Hawthorne;58Δtopol is calculated as the mean (absolute) weighted deviation between the bond valences of a given polyhedron and that of its regular variety with equidistant bond lengths, i.e. its Pauling bond strength, and Δcryst is calculated as the mean (absolute) weighted deviation between the a priori and observed bond valences—thus encompassing all effects not arising from bond-topological arguments. We calculate Δtopol = 0.008 and Δcryst = 0.199 v.u. for the Cu2+N6 octahedron (Fig. 5); these values clearly indicate that bond-length variation is overwhelmingly due to the JTE, supporting the suggestion of larger distortion magnitude for cations bonded to N3− (a priori bond valences are given in Table S2†). The untapped potential for highly distorted Cu2+ polyhedra (and other JT-active cations) may have important implications in the design of oxynitride and/or nitride counterparts to cuprate superconductors, with a handful of layered oxynitride144 and nitride superconductors already known for d0 transition metals.145,146
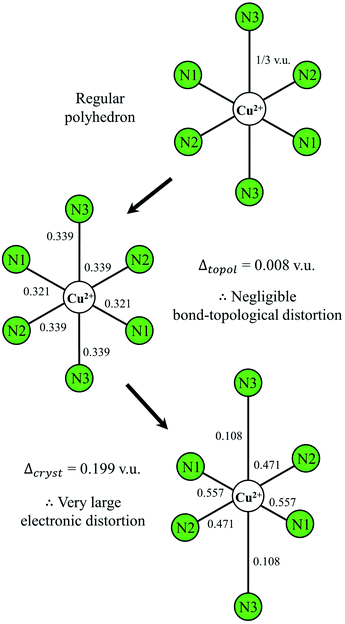 | ||
| Fig. 5 Effect of bond-topological and electronic effects on polyhedral distortion for the Cu2+N6 octahedron in K2CuFe(CN)6. All values are in valence units. | ||
Our dataset contains two cations that seem to be JT-inactive in octahedral coordination to N3− with d4 and d7 electronic configurations: [6]Cr2+ and [6]Co2+. [6]Cr2+ ([Ar]d4, n = 1) is observed in [Cr2+(NH3)6]I2 (78860)147 with reported high spin configuration, refined as a regular octahedron. [6]Co2+ ([Ar]d7, n = 2) is observed in [Co2+(NH3)6](PF6)2 (30704; spin unknown)148 with bond lengths 6 × 2.186 Å, nearly identical to those of [Co2+(NH3)6]Br2 (78864)147 (6 × 2.176 Å) with Co2+ in high spin configuration. In comparison, both [6]Cr2+ and [6]Co2+ are dominatingly high spin in oxides,58 making [6]Cr2+ strongly JT-active (with clear-cut bi-modal bond-length distribution) and [6]Co2+ weakly JT-active (unimodal bond-length distribution). It is possible that the observation of regular Co2+/Cr2+N6 octahedra is due to the dynamic JTE, which was shown to be present in Co2+N6 terpyridine complexes by Kremer et al.149 In oxynitride Co2+(H2O)2Ni2+(CN)4·4H2O (59366; spin unknown),150 bond distances are 2 × 2.095 and 2 × 2.101 Å to N3−, and 2 × 2.128 Å to O2− (0.380, 0.376 and 0.319 v.u. respectively); in Cs2Co2+(S8(Re3+(CN))6)(H2O)2 (89491),151 bond distances are 2.052 (0.390) and 2.092 (0.351) to O2−, and 4 × 2.161 Å (0.332 v.u.) to N3−, indicating that [6]Co2+ may be JT-active when bonded to a mixture of O2− and N3−.
Other cations prone to the JTE and warranting further investigation include Fe2+, Co3+, V3+ and Mo5+ in octahedral coordination (weak); the observation of [6]Mn3+ (strong) seems less likely as Mn3+ appears to prefer lower coordination numbers when bonded to N3−. Cations with lower coordination numbers (e.g.[3]Fe3+ (ref. 152)) do present further opportunity to study the JTE in inorganic nitrides, although bond-length variations associated with lower coordination numbers are usually modest.
Coupled electronic-vibrational near-degeneracy: the pseudo Jahn–Teller effect
The pseudo Jahn–Teller effect (PJTE) is a mechanism of symmetry breaking that results from the vibronic mixing of (two or more) electronic states sufficiently close in energy to interact under nuclear displacement.130,153 Vibronic mixing usually (but not necessarily) occurs between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), with a distortion mode having the same symmetry as the HOMO to LUMO transition.153 Although occurrence of the PJTE is not encumbered by a priori limitations such as electronic configuration, the PJTE is primarily observed for d0 transition metals, with resulting non-centrosymmetric behavior responsible for a host of technologically relevant properties including ferroelectricity,59,154 ferromagnetism,155 multiferroicity,156 piezoelectricity,59 photocatalysis,157 nonlinear optics,59,63 magnetic-dielectric bistability,106etc. The PJTE is of particular interest to materials design, for the structural instability resulting from this effect can be controlled by means of electronic rearrangements induced by redox processes, electromagnetic fields, external pressure, and more,153 with potential applications spanning bistable atomic switches,158–160 and control over sorption characteristics of catalysts to move beyond the Sabatier principle.161Because vibronic phenomena do not conform to the Born–Oppenheimer and adiabatic approximations, the modeling of JTE- and PJTE-active compounds is ill-suited to DFT investigation and requires careful treatment that precludes high-throughput analysis.106 For this reason, the derivation of empirical trends and use of heuristic concepts is particularly important to the exploration of this phenomenon. Gagné & Hawthorne recently showed that the PJTE is the 2nd most frequently encountered cause of bond-length variation in transition metals when bonded to O2− (after bond-topological effects).58 In their work, the PJTE is observed as the main reason underlying anomalous bond-length distributions (in terms of shape and/or range) for 29 of 52 transition metal configurations, in addition to 11 ion configurations for which it is present in minor yet significant ways, covering electronic configurations d0, d4, d7, d9 and d10, and coordination numbers [4]–[10]. Because studies covering PJTE-active cations have almost exclusively focused on oxides and oxysalts, our understanding of this phenomenon is particularly lagging in inorganic nitrides, where few syntheses incorporating d0 transition metals have been attempted (with the exception of the group of Kazuhiko Maeda who studied a handful of oxynitrides with d0 transition metals as photocatalytic materials162).
Because PJTE instabilities can be of any symmetry within the group representation (thus are indiscriminate of coordination number), occurrence of the PJTE can be reduced to a problem of energy gap between interacting electronic states. In their study of octahedrally coordinated d0 transition metals, Kunz & Brown163 observed an increasing degree of distortion with decreasing HOMO–LUMO gap, which in turn correlates to the size and charge of the d0 cation (this trend was later described in terms of electronegativity,164 whereby more electronegative cations lead to larger distortions when bonded to O2−). While similar behavior is expected for nitrides, the lower electronegativity of N (3.04) compared to O (3.44) entails a shift of the electronic states of N3− to higher energies, thus affecting the HOMO–LUMO gap (and distortion magnitude) compared to O2−. As a result, the occurrence of PJT-driven distortion for bonds made to N3− are shifted to cations of lower electronegativity in relation to O2− for a better match of orbital energies. In addition, the lower electronegativity of N (closer to that of transition metals) entails potential for larger distortion magnitude (measured as Δcryst) owing to increased covalency of the M–N bond. However, others factors (e.g. nearest-neighbor identity153,164) may have an overwhelming effect on the energy gap of the interacting states. While rationalizing the occurrence of the PJTE via quantum mechanical arguments is now commonplace, predicting the occurrence of a PJT distortion from simple crystal-chemical principles remains an open problem.
Table 4 summarizes bond-length information for ion configurations prone to the PJTE overlapping the present dataset and that of Gagné & Hawthorne for oxides and oxysalts.58 Italicised entries are for ion configurations where the PJTE is a minor contributor to bond-length variation in oxides and oxysalts; for example, the effect of polymerization on bond length variation is much larger than that of the PJTE for [4]V5+ when bonded to O2−. To precisely evaluate the relative distortion magnitude for cations bonded to N3−vs. O2−, one would ideally quantify the proportion of bond-length variation due to the PJTE via the method of Gagné & Hawthorne,58i.e., by removing the bond-topological contribution to bond-length variation (example given for Cu2+ above). Unfortunately, too few crystal structures are available to comprehensively calculate Δtopol and Δcryst indices in inorganic nitrides. However, the few crystal structures suited to the calculation of these indices are in support of a shift of the occurrence of the PJTE to cations of lower electronegativity, and hint at larger distortion magnitude for the same cation configurations (data compared to Table S2† of Gagné & Hawthorne58). For example, Δtopol = 0 and Δcryst = 0.177 v.u. for [8]Hf4+ in Hf34+N4 (97997),165 with bond-length range 0.295 Å; in Li4(Ta5+N3) (412585),166Δtopol = 0.083 and Δcryst = 0.084 v.u. for [4]Ta5+, with bond-length range 0.106 Å. Distortion magnitudes attributable to the PJTE are still large for higher-electronegativity transition metals: in LiBa4(Mo26+N7) (74822),167Δtopol = 0.079 and 0.095 and Δcryst = 0.230 and 0.123 v.u. for two crystallographically distinct [4]Mo6+ sites, with bond-length ranges 0.149 and 0.111 Å, respectively; in LiBa4(W26+N7) (74823),167Δtopol = 0.081 and 0.091 and Δcryst = 0.101 and 0.064 v.u. for two crystallographically distinct [4]W6+ sites, with bond-length ranges 0.138 and 0.110 Å, respectively (all a priori bond valences in Table S2† herein).
| Ion configuration | Electronic configuration | Sample size bonded to N3−/O2−a | Mean bond-length range bonded to N3−/O2−a (Å) |
|---|---|---|---|
| a Oxide data taken from Gagné & Hawthorne.58 b Not observed bonded to O2−. | |||
| [4] V 5+ | d0 | 1/345 | 0.038/0.118 |
| [4] Cr 6+ | d0 | 2/169 | 0.024/0.120 |
| [6]Zn2+ | d10 | 1/193 | 0/0.169 |
| [6]Y3+ | d0 | 5/25 | 0.096/0.081 |
| [4]Nb5+ | d0 | 10/2 | 0.049/0.117 |
| [6]Nb5+ | d0 | 2/240 | 0/0.290 |
| [4] Mo 6+ | d0 | 11/434 | 0.068/0.069 |
| [6] Cd 2+ | d10 | 4/135 | 0.067/0.140 |
| [8]Hf4+ | d0 | 1/7 | 0.295/0.163 |
| [4]Ta5+ | d0 | 5/0b | 0.0464/— |
| [4]W6+ | d0 | 26/35 | 0.124/0.053 |
Based on these observations, exploratory synthesis of PJTE-active inorganic nitrides appears promising for the exploitation of their functional properties. Common d0 transition metals warranting investigation and missing from our dataset (some due to our stringent collection/filtering criteria) include Sc3+, Ti4+, and Zr4+; these elements are particularly promising candidates for PJT-induced distortion in inorganic nitrides owing to their low electronegativity.
Lone-pair stereoactivity
Lone-pair stereoactivity is an electronic phenomenon associated with the observation of highly anisotropic coordination polyhedra for p-block cations with ns2np0 electron configuration. Lone-pair stereoactivity has been described as the causal mechanism for a multitude of material properties not limited to ultra-low thermal conductivity (a property most relevant to the development of next-generation thermoelectrics168),169 second-harmonic generation response,170–172 piezoelectricity,61,173 pyroelectricity,173,174 ferroelectricity,175,176 ferromagnetism,177 multiferroicity,178 dielectric behavior,179 photocatalysis,157,180 and the photovoltaic effect.181Lone-pair (LP) stereoactivity originates from strong interaction between the cation s and anion p orbitals leading to a high energy antibonding state which, via distortion of the structure, may interact with empty cation p orbitals to form a localized electronic state where the lone pair resides.182 As such, LP stereoactivity essentially amounts to a special case of the PJTE (see above), where crucial variables include a (vibronic) distortion mode with net positive overlap between the cation p and mixed cation s and anion p states, and favorable interaction between cation s and p states for the formation of the interacting antibonding state (the energy of which being strongly dependent on that of the anion p states). Thus, LP stereoactivity (vs. inertness) is strongly a function of ligand identity; for example, the increasing energy of p states with increasing period has been demonstrated to reduce mixing with cation s states to the point of quenching the effect.183,184 It follows that anions have a “sweet spot” of cation s and p atomic orbital energies for which the occurrence and magnitude of lone-pair stereoactivity is maximized, where the initial cation s and anion p interaction determines how much stabilization (if any) may be achieved via interaction with empty cation p orbitals. Other factors influencing the occurrence and magnitude of lone-pair stereoactivity include the s character of the antibonding orbital (the higher the s character of the antibonding state, the better it is stabilized via mixing with the cation p state) and relativistic effects for period 6 cations, whereby relativistic contraction of the 6s orbital reduces mixing with anion p states, leading to more diffuse lone pairs and less distorted structures.185
Much like the PJTE, predicting the occurrence of LP stereoactivity for a given composition/structure requires consideration of orbital energy, symmetry and spatial overlap, thus eludes simple crystal-chemical principles; however, trends may be derived to maximize the probability of observing this phenomenon in new syntheses where full composition and/or structure is not known a priori. Trends in atomic orbital energy are particularly relevant in this regard. DFT calculations for a series of simple oxides have shown that the energy of the O 2p state cuts in-between that of the s state of group 13 metals for periods 5 and 6 in way that leaves mixing with In+ (group 14) unfavorable and Tl+ (group 15) marginally favorable.182,186 Mixing becomes more favorable with increasing group number along these periods (i.e. with decreasing energy of the metal s state), making group 14 and 15 cations (Sn2+/Sb3+ and Pb2+/Bi3+, bar relativistic effects) most susceptible to stereoactive lone-pair formation when bonded to O2−. By this principle, the relatively higher-energy s state of period 4 p-block elements may be inferred to require further decrease in energy to best mix with the O 2p orbitals, thus making group 15 and 16 most prone to LP stereoactivity (particularly As3+) for this period. Such propositions are in-line with the results of the bond-length dispersion analysis of Gagné & Hawthorne for non-metals70 and metalloids/post-transition metals.71
Considering that the 2p states of N are slightly more energetic than those of O (due to its lower electronegativity), we presume that LP stereoactivity may be possible for cations with higher-energy states such as In+/Ge2+, is most likely for ions Sn2+, As3+, Sb3+ and Se4+, and is less likely for late-period, higher group elements.
There are unfortunately too few data available to verify this statement; while literature abounds with well-characterized structures containing one or more stereoactive lone pairs for oxides and oxysalts, and to a lesser extent chalcogenides and halides, very few structures have been reported with stereoactive lone-pair electrons when bonded to N3−. Presumably, this paucity of data is due to the relatively nascent exploration of (functional) inorganic nitrides. Our dataset contains no data for As3+, Se4+, Sb3+, Te4+ Bi3+, or any relevant group 17 cations. Only one coordination polyhedron was recorded for Sn2+, in Li(Sn(NH2)3) (50467),187 with three short bonds 2.128, 2.132 and 2.170 Å in length and a stereoactive lone pair occupying the 4th apex of a tetrahedron. For period 6 ions, eight coordination polyhedra were recorded for Tl+ and two for Pb2+; in all cases, short bonds are concentrated in one hemisphere, away from the lone pair, while long bonds (if any) are present in the other. Thus, all p-block cations with ns2np0 electron configuration are observed with a stereoactive lone-pair in the present dataset, in sharp contrast to oxides and oxysalts; this result is promising for the exploitation of the functional properties resulting from lone-pair stereoactivity in inorganic nitrides. Lone-pair stereoactivity is further observed in coordination complexes for Ge2+,188 and in mixed coordination with Cl− for Se4+ (ref. 189) and Te4+,190,191 showcasing additional opportunities for the solid state.
The [4]M6+ configuration
Earth's remarkable mineral diversity has been attributed to a number of factors spanning geochemical, crystal-chemical and thermodynamic considerations including efficient elemental concentration mechanisms, peculiar electronic behavior for certain elements, mineral stability ranges, etc.83,192,193 A less-discussed factor enabling mineral diversity is the ability of a (strongly bonded) structural unit to polymerize into a variety of motifs (e.g. as oligomers, chains, rings, clusters, sheets, frameworks) inter-linked via weakly bonded constituents. This concept is best illustrated for silicate minerals; there are currently 5600+ minerals approved by the International Mineralogical Association, 1550+ of which contain Si and O as essential elements (http://rruff.info/ima/). What are the salient characteristics of the SiO4 unit that lead to such remarkable diversity? From the valence-sum rule (eqn (2)), we may deduce that the two bonds made by a bridging [2]O2− ion are ideally 1 v.u. in strength. Similarly, [4]Si4+ ideally makes four bonds 1 v.u. in strength. With the bond-valence requirements of [4]Si4+ perfectly matching those of [2]O2− (see the valence-matching principle, above), the SiO4 unit freely polymerizes via one, two, three or four corners in a theoretically infinite number of motifs, leading to a remarkably stable and diverse class of minerals that accounts for ∼90% of Earth's crustal composition by volume.194 In inorganic nitrides, the analogous bond-valence requirements for a bridging [2]N3− anion are 2 × 1.5 v.u.; thus, hexavalent cations are required for polymerization of corner-sharing tetrahedra to result in proliferation of structural motifs (i.e. 4 × 1.5. v.u. = 6 v.u.), hence the significance of the [4]M6+ configuration in inorganic nitrides (Fig. 6).Porous materials (e.g. zeolites) are an important class of functional materials for which corner-sharing polymerization of the M6+N4 unit shows promise for exploratory synthesis. Zeolites are known for their remarkable catalytic and sorption characteristics,195,196 offering the ability to carry and optimize specific reactions via partial substitution of the cations making up the structural unit according to their Lewis acidity (Table 1).197 Although framework structures based on the M6+N4 unit have been synthesized,198 successful incorporation of N3− as the major anion in a zeolite structure has so far only been achieved in the presence of stoichiometric oxygen for oxynitridophosphates (in NPO199 and NPT200), and otherwise for zeolite-like (pore-less) nitridophosphates201 and nitridosilicates.202 Interestingly, framework structures based on the M6+N4 units may exhibit further interesting properties as a result of the pseudo Jahn–Teller effect for d0 transition metals such as Mo6+ and W6+ (e.g. ferroelectricity, ferromagnetism, piezoelectricity, magnetic-dielectric bistability; see above), thus possibly providing external control on molecular selectivity for catalytic reactions and adsorption/desorption processes.
Polymerization of the M6+N4 unit also shows promise for the synthesis of ultrahard materials. The hardness of inorganic nitrides is known to be intimately linked to their bond strength;203,204 for example, the hardness of cubic BN (boron nitride), where all bonds are 0.75 v.u. in strength, is only slightly lesser than that of diamond (with bulk modulus 400 vs. 440 GPA, respectively).205,206 Notwithstanding synthetic feats, the synthesis of M6+N2 nitrides with bonds 1.5. v.u. in strength (e.g. Mo6+N2 and W6+N2, analogous to SiO2) could lead to new ultrahard materials and ultra-wide-band-gap semiconductors. In addition to their refractory nature, the characteristically high hardness of inorganic nitrides has already been applied to the development of reinforced cements and concretes for different forms of BN.207,208
We observe five ions with [4]M6+ configuration in our dataset: S6+, Cr6+, Se6+, Mo6+ and W6+. Both the [4]S6+ and [4]Se6+ configurations are only observed in oxynitrides thus far, either as [M6+O2N2]4− or [M6+O3N]3−, while the [Cr6+N4]6− unit has yet to be observed as a product of polymerization. More interesting is the [WN4]6− unit, which is observed to polymerize into dimers in LiBa4[W26+N7] (74823),167 6-membered rings in K14W66+N16NH (75033),209 chains in Na5X[(W6+N3)2] with X = Rb+ or Cs+ (55534),210 sheets in Na2K13[W76+N19] (81764)211 and into a framework structure in Cs5[Na(W46+N10)] (50002).212 Fewer works have studied the polymerization of the [MoN4]6− unit; dimers have been described in LiBa4[Mo26+N7]·BaCl2 (72400)213 and in LiBa4[Mo26+N7] (74822).167 Evidently, much of the potential of the [4]M6+ configuration in inorganic nitrides lies ahead.
Conclusion
Following several decades of progressive syntheses primarily driven by new and improved methods of preparation, inorganic nitrides recently matured into a thriving class of inorganic solids with a promising set of functional properties akin to oxide and oxysalt compounds. This work uses structure–property relationships to identify some of the most promising uncharted compositional spaces for inorganic nitrides bearing functional properties, and further provides basic, universal parameters helpful to the verification of high-throughput computational results and the design and characterization of nitrides sensu lato.Whereby chemical-bonding insight gained in the bulk carries well into the study of the local scale, an immediate opportunity enabled by the crystal-chemical data and analyses provided herein regards the study of point defects in semiconductors, more precisely, the (bottleneck) activation of their useful properties via extrinsic doping. Considering that doping success typically relies on comfortable substitutional incorporation of foreign ions into the host crystal structure, a logical next step may be to use the data and insight provided herein as stepping stones toward an atomistic understanding of the factors underlying ion substitution in solids – a problem whose solution would fast-track the development of next-generation solar cells, battery materials, electronics, and the many more semiconductor-based technologies we've come to depend on.
Further developments for this class of compounds will surely follow from strong symbiosis between theoretical, synthetic and computational chemists by way of identifying, understanding, and exploiting the structural underpinnings of their functional properties and energetics.
Notes
Relevant ICSD codes included in parentheses in text.Funding sources
This work was supported by a Banting post-doctoral fellowship from the Natural Sciences and Engineering Research Council of Canada, and a Carnegie post-doctoral fellowship from the Carnegie Institution for Science to OCG.Conflicts of interest
There are no conflicts to declare.References
- B. Mysen, Nitrogen in the Earth: abundance and transport, Prog. Earth Planet. Sci., 2019, 6, 38 CrossRef.
- N. E. Brese and M. O'Keeffe, Crystal chemistry of inorganic nitrides, in Complexes, Clusters and Crystal Chemistry, Springer-Verlag, 1992, vol. 79, pp. 307–378 Search PubMed.
- W. Sun, et al., Thermodynamic routes to novel metastable nitrogen-rich nitrides, Chem. Mater., 2017, 29, 6936–6946 CrossRef CAS.
- R. Juza and H. Hahn, Über die kristallstrukturen von Cu3N, GaN und InN metallamide und metallnitride, Z. Anorg. Allg. Chem., 1938, 239, 282–287 CrossRef CAS.
- R. Juza and H. Hahn, Über die Kristallstrukturen von Zn3N2, Cd3N2 und Ge3N4. Metallamide und metallnitride. IX. Mitteilung, Z. Anorg. Allg. Chem., 1940, 244, 125–132 CrossRef CAS.
- H. Hahn and R. Juza, Untersuchungen über die nitride von cadmium, gallium, indium und germanium. Metallamide und metallnitride. VIII. Mitteilung, Z. Anorg. Allg. Chem., 1940, 244, 111–124 CrossRef CAS.
- W. H. Baur, Effective ionic radii in nitrides, Crystallogr. Rev., 1987, 1, 59–83 CrossRef.
- R. Marchand, Y. Laurent, J. Guyader, P. L'Haridon and P. Verdier, Nitrides and oxynitrides: Preparation, crystal chemistry and properties, J. Eur. Ceram. Soc., 1991, 8, 197–213 CrossRef CAS.
- W. Schnick, Solid-state chemistry with nonmetal nitrides, Angew. Chem., Int. Ed. Engl., 1993, 32, 806–818 CrossRef.
- R. Niewa and H. Jacobs, Group V and VI alkali nitridometalates: a growing class of compounds with structures related to silicate chemistry, Chem. Rev., 1996, 96, 2053–2062 CrossRef CAS.
- R. Kniep, Ternary and quaternary metal nitrides: A new challenge for solid state chemistry, Pure Appl. Chem., 1997, 69, 185–192 CAS.
- R. Niewa and F. J. DiSalvo, Recent developments in nitride chemistry, Chem. Mater., 1998, 10, 2733–2752 CrossRef CAS.
- D. H. Gregory, Structural families in nitride chemistry, J. Chem. Soc., Dalton Trans., 1999, 259–270 RSC.
- D. H. Gregory, Nitride chemistry of the s-block elements, Coord. Chem. Rev., 2001, 215, 301–345 CrossRef CAS.
- P. Höhn and R. Niewa, Nitrides of non-main group elements, in Handbook of Solid State Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2017, pp. 251–359 Search PubMed.
- A. K. Tareen, G. S. Priyanga, S. Behara, T. Thomas and M. Yang, Mixed ternary transition metal nitrides: A comprehensive review of synthesis, electronic structure, and properties of engineering relevance, Prog. Solid State Chem., 2019, 53, 1–26 CrossRef CAS.
- W. Schnick and H. Huppertz, Nitridosilicates - A significant extension of silicate chemistry, Chem.–Eur. J., 1997, 3, 679–683 CrossRef CAS.
- M. Zeuner, S. Pagano and W. Schnick, Nitridosilicates and oxonitridosilicates: from ceramic materials to structural and functional diversity, Angew. Chem., Int. Ed., 2011, 50, 7754–7775 CrossRef CAS.
- S. G. Ebbinghaus, et al., Perovskite-related oxynitrides – Recent developments in synthesis, characterisation and investigations of physical properties, Prog. Solid State Chem., 2009, 37, 173–205 CrossRef CAS.
- A. Fuertes, Chemistry and applications of oxynitride perovskites, J. Mater. Chem., 2012, 22, 3293 RSC.
- H. Morkoç, Nitride Semiconductors and Devices, Springer Berlin Heidelberg, 1999, vol. 32 Search PubMed.
- P. Pampili and P. J. Parbrook, Doping of III-nitride materials, Mater. Sci. Semicond. Process., 2017, 62, 180–191 CrossRef CAS.
- R. A. Ferreyra, C. Zhu, A. Teke and H. Morkoç, Group III Nitrides, in Springer Handbook of Electronic and Photonic Materials, ed. S. Kasap and P. Capper, Springer International Publishing, 2017, p. 1, DOI:10.1007/978-3-319-48933-9_31.
- N. Izyumskaya, et al., Recent Development of Boron Nitride towards Electronic Applications, Adv. Electron. Mater., 2017, 3, 1600485 CrossRef.
- P. P. Paskov and B. Monemar, Point defects in group-III nitrides, in Defects in Advanced Electronic Materials and Novel Low Dimensional Structures, Elsevier, 2018, pp. 27–61, DOI:10.1016/B978-0-08-102053-1.00002-8.
- M. Shur, Wide band gap semiconductor technology: State-of-the-art, Solid-State Electron., 2019, 155, 65–75 CrossRef CAS.
- Y. Hinuma, et al., Discovery of earth-abundant nitride semiconductors by computational screening and high-pressure synthesis, Nat. Commun., 2016, 7, 11962 CrossRef CAS.
- W. Sun, et al., A map of the inorganic ternary metal nitrides, Nat. Mater., 2019, 18, 732–739 CrossRef CAS.
- S. R. Bauers, et al., Ternary nitride semiconductors in the rocksalt crystal structure, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 14829–14834 CrossRef CAS.
- Y. Zhong, et al., Transition metal carbides and nitrides in energy storage and conversion, Adv. Sci., 2016, 3, 1500286 CrossRef.
- S. K. Kuk, et al., Continuous 3D Titanium Nitride Nanoshell Structure for Solar-Driven Unbiased Biocatalytic CO2 Reduction, Adv. Energy Mater., 2019, 9, 1900029 CrossRef.
- T. T. Tran, K. Bray, M. J. Ford, M. Toth and I. Aharonovich, Quantum emission from hexagonal boron nitride monolayers, Nat. Nanotechnol., 2016, 11, 37–41 CrossRef CAS.
- A.-M. Alexander and J. S. J. Hargreaves, Alternative catalytic materials: carbides, nitrides, phosphides and amorphous boron alloys, Chem. Soc. Rev., 2010, 39, 4388 RSC.
- P. Eklund, S. Kerdsongpanya and B. Alling, Transition-metal-nitride-based thin films as novel energy harvesting materials, J. Mater. Chem. C, 2016, 4, 3905–3914 RSC.
- S. Mertin, et al., Piezoelectric and structural properties of c-axis textured aluminium scandium nitride thin films up to high scandium content, Surf. Coat. Technol., 2018, 343, 2–6 CrossRef CAS.
- L. Wang, R.-J. Xie, T. Suehiro, T. Takeda and N. Hirosaki, Down-Conversion Nitride Materials for Solid State Lighting: Recent Advances and Perspectives, Chem. Rev., 2018, 118, 1951–2009 CrossRef CAS.
- J. Xie and Y. Xie, Transition metal nitrides for electrocatalytic energy conversion: Opportunities and challenges, Chem.–Eur. J., 2016, 22, 3588–3598 CrossRef CAS.
- C. Walter, et al., A molecular approach to manganese nitride acting as a high performance electrocatalyst in the oxygen evolution reaction, Angew. Chem., 2018, 130, 706–710 CrossRef.
- C. You, et al., Fe2Ni2N nanosheet array: An efficient non-noble-metal electrocatalyst for non-enzymatic glucose sensing, Nanotechnology, 2017, 28, 365503 CrossRef.
- W.-J. Ong, L.-L. Tan, Y. H. Ng, S.-T. Yong and S.-P. Chai, Graphitic carbon nitride (g-C3N4)-based photocatalysts for artificial photosynthesis and environmental remediation: Are we a step closer to achieving sustainability?, Chem. Rev., 2016, 116, 7159–7329 CrossRef CAS.
- M. Xiao, B. Luo, M. Lyu, S. Wang and L. Wang, Photocatalysis: Single-crystalline nanomesh tantalum nitride photocatalyst with improved hydrogen-evolving performance, Adv. Energy Mater., 2018, 8, 1770138 CrossRef.
- Y. Wu, P. Lazic, G. Hautier, K. Persson and G. Ceder, First principles high throughput screening of oxynitrides for water-splitting photocatalysts, Energy Environ. Sci., 2013, 6, 157–168 RSC.
- A. Zakutayev, Design of nitride semiconductors for solar energy conversion, J. Mater. Chem. A, 2016, 4, 6742–6754 RSC.
- J. Häusler, R. Niklaus, J. Minár and W. Schnick, Ammonothermal synthesis and optical properties of ternary nitride semiconductors Mg-IV-N2, Mn-IV-N2 and Li-IV2-N3 (IV=Si, Ge), Chem.–Eur. J., 2018, 24, 1686–1693 CrossRef.
- S. Krishna, A. Sharma, N. Aggarwal, S. Husale and G. Gupta, Ultrafast photoresponse and enhanced photoresponsivity of indium nitride based broad band photodetector, Sol. Energy Mater. Sol. Cells, 2017, 172, 376–383 CrossRef CAS.
- M. Zhang, et al., High performance self-powered ultraviolet photodetectors based on electrospun gallium nitride nanowires, Appl. Surf. Sci., 2018, 452, 43–48 CrossRef CAS.
- M. Kneissl and J. Rass, III-Nitride Ultraviolet Emitters: Technology and Applications, Springer International Publishing, 2016, DOI:10.1007/978-3-319-24100-5.
- P. Pust, et al., Narrow-band red-emitting Sr[LiAl3N4]:Eu2+ as a next-generation LED-phosphor material, Nat. Mater., 2014, 13, 891–896 CrossRef CAS.
- I. Ohkubo and T. Mori, Two-dimensional layered complex nitrides as a new class of thermoelectric materials, Chem. Mater., 2014, 26, 2532–2536 CrossRef CAS.
- C. Wang, et al., A new ZrCuSiAs-type superconductor: ThFeAsN, J. Am. Chem. Soc., 2016, 138, 2170–2173 CrossRef CAS.
- T. Shiroka, et al., High-Tc superconductivity in undoped ThFeAsN, Nat. Commun., 2017, 8, 156 CrossRef CAS.
- Z.-C. Wang, et al., Enhanced superconductivity in ThNiAsN, Europhys. Lett., 2017, 118, 57004 CrossRef.
- L. Aihua, D. Jianxin, C. Haibing, C. Yangyang and Z. Jun, Friction and wear properties of TiN, TiAlN, AlTiN and CrAlN PVD nitride coatings, Int. J. Refract. Met. Hard Mater., 2012, 31, 82–88 CrossRef.
- V. S. Bhadram, D. Y. Kim and T. A. Strobel, High-pressure synthesis and characterization of incompressible titanium pernitride, Chem. Mater., 2016, 28, 1616–1620 CrossRef CAS.
- S. P. Ong, et al., PYthon MATerials GENomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- D. Waroquiers, et al., Statistical analysis of coordination environments in oxides, Chem. Mater., 2017, 29, 8346–8360 CrossRef CAS.
- A. Jain, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: Results for the transition metals and quantification of the factors underlying bond-length variation in inorganic solids, IUCrJ, 2020, 7, 581–629 CrossRef.
- P. S. Halasyamani and K. R. Poeppelmeier, Noncentrosymmetric oxides, Chem. Mater., 1998, 10, 2753–2769 CrossRef CAS.
- R. E. Cohen, Origin of ferroelectricity in perovskite oxides, Nature, 1992, 358, 136–138 CrossRef CAS.
- F. Yu, et al., High-performance, high-temperature piezoelectric BiB3O6 crystals, J. Mater. Chem. C, 2015, 3, 329–338 RSC.
- L. H. Wang, et al., Piezoelectricity and local structural distortions in (Na0.5Bi 0.5)1−xSrxTiO3-Bi12TiO20 flexoelectric-type polar ceramics, Appl. Phys. Lett., 2012, 101, 062903 CrossRef.
- B.-L. Wu, C.-L. Hu, F.-F. Mao, R.-L. Tang and J.-G. Mao, Highly Polarizable Hg2+ Induced a Strong Second Harmonic Generation Signal and Large Birefringence in LiHgPO4, J. Am. Chem. Soc., 2019, 141, 10188–10192 CrossRef CAS.
- B. A. Marinkovic, et al., Correlation between AO6 Polyhedral Distortion and Negative Thermal Expansion in Orthorhombic Y2Mo3O12 and Related Materials, Chem. Mater., 2009, 21, 2886–2894 CrossRef CAS.
- S. Miao, et al., Effect of Al/Si substitution on the structure and luminescence properties of CaSrSiO4:Ce3+ phosphors: analysis based on the polyhedra distortion, J. Mater. Chem. C, 2015, 3, 4616–4622 RSC.
- M. Chen, Z. Xia, M. S. Molokeev, T. Wang and Q. Liu, Tuning of Photoluminescence and Local Structures of Substituted Cations in xSr2Ca(PO4)2–(1 –x)Ca10Li(PO4)7:Eu2+ Phosphors, Chem. Mater., 2017, 29, 1430–1438 CrossRef CAS.
- O. C. Gagné and F. C. Hawthorne, Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 562–578 CrossRef.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: Alkali and alkaline-earth metals, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 602–625 CrossRef.
- O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: Results for the non-metals and discussion of lone-pair stereoactivity and the polymerization of PO4, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 79–96 CrossRef.
- O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: Metalloids and post-transition metals, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 63–78 CrossRef.
- O. C. Gagné, Bond-length distributions for ions bonded to oxygen: Results for the lanthanides and actinides and discussion of the f-block contraction, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 49–62 CrossRef.
- L. Pauling, Atomic radii and interatomic distances in metals, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- I. D. Brown and R. D. Shannon, Empirical bond-strength–bond-length curves for oxides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, 29, 266–282 CrossRef CAS.
- I. D. Brown, The Chemical Bond in Inorganic Chemistry: The Bond Valence Model, Oxford University Press, 2016 Search PubMed.
- I. D. Brown and D. Altermatt, Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247 CrossRef.
- H. Chen and S. Adams, Bond softness sensitive bond-valence parameters for crystal structure plausibility tests, IUCrJ, 2017, 4, 614–625 CrossRef CAS.
- R. G. Pearson, Hard and soft acids and bases, HSAB, part 1: Fundamental principles, J. Chem. Educ., 1968, 45, 581 CrossRef CAS.
- R. G. Pearson, Hard and soft acids and bases, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- I. D. Brown and A. Skowron, Electronegativity and Lewis acid strength, J. Am. Chem. Soc., 1990, 112, 3401–3403 CrossRef CAS.
- I. D. Brown, The Bond-Valence Method: An Empirical Approach to Chemical Structure and Bonding, in Structure and Bonding in Crystals, ed. M. O'Keeffe and A. Navrotsky, Elsevier, 1981, vol. 2, pp. 1–30 Search PubMed.
- F. C. Hawthorne and M. Schindler, Understanding the weakly bonded constituents in oxysalt minerals, Z. Kristallogr. - Cryst. Mater., 2008, 223, 41–68 CAS.
- F. C. Hawthorne, Toward theoretical mineralogy: A bond-topological approach, Am. Mineral., 2015, 100, 696–713 CrossRef.
- F. C. Hawthorne, A bond-topological approach to theoretical mineralogy: Crystal structure, chemical composition and chemical reactions, Phys. Chem. Miner., 2012, 39, 841–874 CrossRef CAS.
- G. N. Lewis, Acids and bases, J. Franklin Inst., 1938, 226, 293–313 CrossRef.
- O. C. Gagné and F. C. Hawthorne, Empirical Lewis acid strengths for 135 cations bonded to oxygen, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 956–961 CrossRef.
- U. Berger and W. Schnick, Syntheses, crystal structures, and vibrational spectroscopic properties of MgCN2, SrCN2, and BaCN2, J. Alloys Compd., 1994, 206, 179–184 CrossRef CAS.
- O. C. Gagné, P. H. J. Mercier and F. C. Hawthorne, A priori bond-valence and bond-length calculations in rock-forming minerals, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 470–482 CrossRef.
- D. Britton and Y. M. Chow, The crystal structure of silver dicyanamide, AgN(CN)2, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 697–699 CrossRef.
- A. Jain, Y. Shin and K. A. Persson, Computational predictions of energy materials using density functional theory, Nat. Rev. Mater., 2016, 1, 15004 CrossRef CAS.
- A. O. Oliynyk, et al., High-Throughput Machine-Learning-Driven Synthesis of Full-Heusler Compounds, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- Y. Zhuo, A. Mansouri Tehrani, A. O. Oliynyk, A. C. Duke and J. Brgoch, Identifying an efficient, thermally robust inorganic phosphor host via machine learning, Nat. Commun., 2018, 9, 4377 CrossRef.
- A. Mansouri Tehrani, et al., Machine Learning Directed Search for Ultraincompressible, Superhard Materials, J. Am. Chem. Soc., 2018, 140, 9844–9853 CrossRef CAS.
- F. Ren, et al., Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments, Sci. Adv., 2018, 4, eaaq1566 CrossRef.
- D. Xue, et al., Accelerated search for materials with targeted properties by adaptive design, Nat. Commun., 2016, 7, 11241 CrossRef CAS.
- P. V. Balachandran, B. Kowalski, A. Sehirlioglu and T. Lookman, Experimental search for high-temperature ferroelectric perovskites guided by two-step machine learning, Nat. Commun., 2018, 9, 1668 CrossRef.
- W. Sun, et al., The thermodynamic scale of inorganic crystalline metastability, Sci. Adv., 2016, 2, e1600225 CrossRef.
- M. A. Jansen, Concept for Synthesis Planning in Solid-State Chemistry, Angew. Chem., Int. Ed., 2002, 41, 3746–3766 CrossRef CAS.
- F. T. Szczypiński, S. Bennett and K. E. Jelfs, Can we predict materials that can be synthesised?, Chem. Sci., 2021, 12, 830–840 RSC.
- G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Finding Nature's Missing Ternary Oxide Compounds Using Machine Learning and Density Functional Theory, Chem. Mater., 2010, 22, 3762–3767 CrossRef CAS.
- B. Meredig, et al., Combinatorial screening for new materials in unconstrained composition space with machine learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- V. M. Goldschmidt, Die Gesetze der Krystallochemie, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- L. Pauling, The principles determining the structure of complex ionic crystals, J. Am. Chem. Soc., 1929, 51, 1010–1026 CrossRef CAS.
- C. M. Rost, et al., Entropy-stabilized oxides, Nat. Commun., 2015, 6, 8485 CrossRef CAS.
- I. B. Bersuker, Limitations of density functional theory in application to degenerate states, J. Comput. Chem., 1997, 18, 260–267 CrossRef CAS.
- I. B. Bersuker, The Jahn–Teller and pseudo Jahn–Teller effect in materials science, J. Phys.: Conf. Ser., 2017, 833, 012001 CrossRef.
- M. C. Palenik, B. I. Dunlap and D. Gunlycke, Jahn–Teller effect in density-functional theory, Phys. Rev. A, 2019, 99, 022502 CrossRef CAS.
- P. V. Balachandran, J. Young, T. Lookman and J. M. Rondinelli, Learning from data to design functional materials without inversion symmetry, Nat. Commun., 2017, 8, 14282 CrossRef CAS.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, JPhys Mater., 2019, 2, 032001 CrossRef CAS.
- S. Curtarolo, et al., The high-throughput highway to computational materials design, Nat. Mater., 2013, 12, 191–201 CrossRef CAS.
- P. V. Balachandran, Machine learning guided design of functional materials with targeted properties, Comput. Mater. Sci., 2019, 164, 82–90 CrossRef CAS.
- W. A. Nugent and J. M. Mayer, Metal-Ligand Multiple Bonds: The Chemistry of Transition Metal Complexes Containing Oxo, Nitrido, Imido, Alkylidene, or Alkylidyne Ligands, Wiley-Interscience, 1988 Search PubMed.
- I. B. Bersuker, Electronic Structure and Properties of Transition Metal Compounds: Introduction to the Theory, John Wiley & Sons, Inc., 2010 Search PubMed.
- J. K. Burdett, From bonds to bands and molecules to solids, Prog. Solid State Chem., 1984, 15, 173–255 CrossRef CAS.
- H. W. Roesky, I. Haiduc and N. S. Hosmane, Organometallic Oxides of Main Group and Transition Elements Downsizing Inorganic Solids to Small Molecular Fragments, Chem. Rev., 2003, 103, 2579–2596 CrossRef CAS.
- S. A. Sunshine, D. A. Keszler and J. A. Ibers, Coordination chemistry and the solid state, Acc. Chem. Res., 1987, 20, 395–400 CrossRef CAS.
- K. Meyer, J. Bendix, E. Bill, T. Weyhermüller and K. Wieghardt, Molecular and Electronic Structure of Nitridochromium(V) Complexes with Macrocyclic Amine Ligands, Inorg. Chem., 1998, 37, 5180–5188 CrossRef CAS.
- D. M. King, et al., Synthesis and Structure of a Terminal Uranium Nitride Complex, Science, 2012, 337, 717–720 CrossRef CAS.
- Y. Nishibayashi, Recent Progress in Transition-Metal-Catalyzed Reduction of Molecular Dinitrogen under Ambient Reaction Conditions, Inorg. Chem., 2015, 54, 9234–9247 CrossRef CAS.
- W. P. Griffith, Transition metal nitrido complexes, Coord. Chem. Rev., 1972, 8, 369–396 CrossRef CAS.
- K. Dehnicke and J. Strähle, Nitrido Complexes of Transition Metals, Angew. Chem., Int. Ed. Engl., 1992, 31, 955–978 CrossRef.
- K. Dehnicke and J. Strähle, The Transition Metal-Nitrogen Multiple Bond, Angew. Chem., Int. Ed. Engl., 1981, 20, 413–426 CrossRef.
- J. F. Berry, Terminal nitrido and imido complexes of the late transition metals, Comments Inorg. Chem., 2009, 30, 28–66 CrossRef CAS.
- R. Eikey, Nitrido and imido transition metal complexes of Groups 6–8, Coord. Chem. Rev., 2003, 243, 83–124 CrossRef CAS.
- N. Arumugam, E. M. Peters and M. Jansen, Synthesis and structure of sodium tetraoxo nitrido molybdate, Na5MoO4N, Z. Naturforsch., B: Chem. Sci., 2004, 59, 274–276 CAS.
- M. Falcone, L. Chatelain, R. Scopelliti, I. Živković and M. Mazzanti, Nitrogen reduction and functionalization by a multimetallic uranium nitride complex, Nature, 2017, 547, 332–335 CrossRef CAS.
- L. Ma, et al., Cerium(IV)-Driven Water Oxidation Catalyzed by a Manganese(V)-Nitrido Complex, Angew. Chem., Int. Ed., 2015, 54, 5246–5249 CrossRef CAS.
- S.-M. Yiu, W.-L. Man and T.-C. Lau, Efficient Catalytic Oxidation of Alkanes by Lewis Acid/[OsVI(N)Cl4]− Using Peroxides as Terminal Oxidants. Evidence for a Metal-Based Active Intermediate, J. Am. Chem. Soc., 2008, 130, 10821–10827 CrossRef CAS.
- M. Chen, et al., Catalytic oxidation of alkanes by a (salen)osmium(VI) nitrido complex using H2O2 as the terminal oxidant, Chem. Commun., 2015, 51, 13686–13689 RSC.
- I. B. Bersuker, The Jahn–Teller effect, Cambridge University Press, 2006 Search PubMed.
- G. E. Cutsail III, et al., EPR, ENDOR, and Electronic Structure Studies of the Jahn–Teller Distortion in an FeV Nitride, J. Am. Chem. Soc., 2014, 136, 12323–12336 CrossRef.
- M. Ding, et al., A low spin manganese(IV) nitride single molecule magnet, Chem. Sci., 2016, 7, 6132–6140 RSC.
- A. P. Ramirez, Colossal magnetoresistance, J. Phys.: Condens. Matter, 1997, 9, 8171–8199 CrossRef CAS.
- H. Keller, A. Bussmann-Holder and K. A. Müller, Jahn–Teller physics and high-Tc superconductivity, Mater. Today, 2008, 11, 38–46 CrossRef CAS.
- H. Kim, et al., Anomalous Jahn–Teller behavior in a manganese-based mixed-phosphate cathode for sodium ion batteries, Energy Environ. Sci., 2015, 8, 3325–3335 RSC.
- X. Li, et al., Jahn–Teller Assisted Na Diffusion for High Performance Na Ion Batteries, Chem. Mater., 2016, 28, 6575–6583 CrossRef CAS.
- D. A. Vennos, M. E. Badding and F. J. DiSalvo, Synthesis, structure, and properties of a new ternary metal nitride, Ca3CrN3, Inorg. Chem., 1990, 29, 4059–4062 CrossRef CAS.
- F. R. Fronczek and W. P. Schaefer, Crystal Structure of p-Thiccyanato-[pentaamminecobalt(III)]pentacyanocobalt(III) Monohydrate, Inorg. Chem., 1975, 14, 2066–2070 CrossRef CAS.
- I. A. Charushnikova, N. N. Krot and I. N. Polyakova, Crystal structure of a double oxalate of Np(V) and Co(NH3)63+, Co(NH3)6NpO2(C2O4)2·1.5H2O, Radiochemistry, 2005, 47, 540–544 CrossRef CAS.
- L. Shihsiung and H. Chinling, Cu(NH3)4Ag(SCN)3, Kexue Tongbao, 1980, 25, 835–838 CrossRef.
- M. Neukirch, S. Tragl, H.-J. Meyer, T. Küppers and H. Willner, M[B(CN)4]2: Zwei neue tetracyanoborate mit zweiwertigen kationen (M = Zn, Cu), Z. Anorg. Allg. Chem., 2006, 632, 939–944 CrossRef CAS.
- C. Loos-Neskovic, et al., Structure of copper-potassium hexacyanoferrate(II) and sorption mechanisms of cesium, J. Solid State Chem., 2004, 177, 1817–1828 CrossRef CAS.
- T. Ridkosil, V. Srein, J. Fabry, J. Hybler and B. A. Maximov, Mrazekite, Bi2Cu3(OH)2O2(PO4)2, a new mineral species and its crystal structure, Can. Mineral., 1992, 30, 215–224 CAS.
- G. Tobías, J. Oró-Solé, D. Beltrán-Porter and A. Fuertes, New Family of Ruddlesden–Popper Strontium Niobium Oxynitrides: (SrO)(SrNbO2−xN)n (n = 1, 2), Inorg. Chem., 2001, 40, 6867–6869 CrossRef.
- S. Yamanaka, H. Kawaji, K. Hotehama and M. Ohashi, A new layer-structured nitride superconductor. Lithium-intercalated β-zirconium nitride chloride, LixZrNCl, Adv. Mater., 1996, 8, 771–774 CrossRef CAS.
- S. Yamanaka, High-Tc Superconductivity in Electron-Doped Layer Structured Nitrides, Annu. Rev. Mater. Sci., 2000, 30, 53–82 CrossRef CAS.
- R. Eßmann, et al., Isotype Strukturen einiger Hexaamminmetall(II)-halogenide von 3d-Metallen: [V(NH3)6]I2, [Cr(NH3)6]I2, [Mn(NH3)6]Cl2, [Fe(NH3)6]Cl2, [Fe(NH3)6]Br2, [Co(NH3)6]Br2 und [Ni(NH3)6]Cl2, Z. Anorg. Allg. Chem., 1996, 622, 1161–1166 CrossRef.
- S. Kummer and D. Babel, Strukturverfeinerungen an den Cobalt(II)hexammin-Komplexen [Co(NH3)6](BF4)2 und [Co(NH3)6](PF6)2, Z. Naturforsch., B: Chem. Sci., 1984, 39, 1118–1122 Search PubMed.
- S. Kremer, W. Henke and D. Reinen, High-spin-low-spin equilibriums of cobalt(2+) in the terpyridine complexes Co(terpy)2X2·nH2O, Inorg. Chem., 1982, 21, 3013–3022 CrossRef CAS.
- T. Niu, G. Crisci, J. Lu and A. J. Jacobson, Diaquacobalt tetracyanonickelate tetrahydrate, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1998, 54, 565–567 CrossRef.
- N. G. Naumov, A. V. Virovets, Yu. I. Mironov, S. B. Artemkina and V. E. Fedorov, Synthesis and crystal structure of new layered cluster cyanides Cs2M(Re6S8(CN)6).2(H2O) (M = Mn(2+), Fe(2+), Co(2+), Cd(2+)): size control over framework dimension, Ukr. Khim. Zh., 1999, 65, 21–27 CAS.
- R. B. King, The chemical bonding topology of ternary and quaternary transition metal nitrides containing low-coordinate metal atoms, Can. J. Chem., 1995, 73, 963–971 CrossRef CAS.
- I. B. Bersuker, Pseudo-Jahn–Teller effect—A two-state paradigm in formation, deformation, and transformation of molecular systems and solids, Chem. Rev., 2013, 113, 1351–1390 CrossRef CAS.
- I. B. Bersuker, Vibronic (pseudo Jahn–Teller) theory of ferroelectricity: Novel aspects and applications, Ferroelectrics, 2018, 536, 1–59 CrossRef CAS.
- J. M. D. Coey, d0 ferromagnetism, Solid State Sci., 2005, 7, 660–667 CrossRef CAS.
- C. Xu, et al., Pressure-Induced Multiferroics via Pseudo Jahn–Teller Effects and Novel Couplings, Adv. Funct. Mater., 2017, 27, 1604513 CrossRef.
- A. Kudo and S. Hijii, H2 or O2 evolution from aqueous solutions on layered oxide photocatalysts consisting of Bi3+ with 6s2 configuration and d0 transition metal ions, Chem. Lett., 1999, 1103–1104 CrossRef CAS.
- N. J. Szymanski, L. N. Walters, D. Puggioni and J. M. Rondinelli, Design of Heteroanionic MoON Exhibiting a Peierls Metal-Insulator Transition, Phys. Rev. Lett., 2019, 123, 236402 CrossRef CAS.
- R. Yang, et al., Synaptic plasticity and memory functions achieved in a WO3−x-based nanoionics device by using the principle of atomic switch operation, Nanotechnology, 2013, 24, 384003 CrossRef.
- P. Garcia-Fernandez and I. B. Bersuker, Class of Molecular and Solid State Systems with Correlated Magnetic and Dielectric Bistabilities Induced by the Pseudo Jahn–Teller Effect, Phys. Rev. Lett., 2011, 106, 246406 CrossRef.
- A. Kakekhani and S. Ismail-Beigi, Ferroelectric-Based Catalysis: Switchable Surface Chemistry, ACS Catal., 2015, 5, 4537–4545 CrossRef CAS.
- K. Maeda, (Oxy)nitrides with d0-electronic configuration as photocatalysts and photoanodes that operate under a wide range of visible light for overall water splitting, Phys. Chem. Chem. Phys., 2013, 15, 10537 RSC.
- M. Kunz and I. D. Brown, Out-of-center distortions around octahedrally coordinated d0 transition metals, J. Solid State Chem., 1995, 115, 395–406 CrossRef CAS.
- P. S. Halasyamani, Asymmetric cation coordination in oxide materials:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Influence of lone-pair cations on the intra-octahedral distortion in d0 transition metals, Chem. Mater., 2004, 16, 3586–3592 CrossRef CAS.
Influence of lone-pair cations on the intra-octahedral distortion in d0 transition metals, Chem. Mater., 2004, 16, 3586–3592 CrossRef CAS. - A. Zerr, G. Miehe and R. Riedel, Synthesis of cubic zirconium and hafnium nitride having Th3P4 structure, Nat. Mater., 2003, 2, 185–189 CrossRef CAS.
- R. Niewa, D. A. Zherebtsov, H. Borrmann and R. Kniep, Preparation and Crystal Structure of Li4[TaN3], Z. Anorg. Allg. Chem., 2002, 628, 2505–2508 CrossRef CAS.
- P. Höhn, R. Kniep and J. Maier, LiBa4[Mo2N7] und LiBa4[W2N7]: Neue nitridomolybdate/wolframate (YI) mit dinieren tetraeder-anionen, Z. Naturforsch., B: Chem. Sci., 1994, 49, 5–8 Search PubMed.
- W. Lai, Y. Wang, D. T. Morelli and X. Lu, From Bonding Asymmetry to Anharmonic Rattling in Cu12Sb4S13 Tetrahedrites: When Lone-Pair Electrons Are Not So Lonely, Adv. Funct. Mater., 2015, 25, 3648–3657 CrossRef CAS.
- M. D. Nielsen, V. Ozolins and J. P. Heremans, Lone pair electrons minimize lattice thermal conductivity, Energy Environ. Sci., 2013, 6, 570–578 RSC.
- K. M. Ok and P. S. Halasyamani, The Lone-Pair Cation I5+ in a Hexagonal Tungsten Oxide-Like Framework: Synthesis, Structure, and Second-Harmonic Generating Properties of Cs2I4O11, Angew. Chem., Int. Ed., 2004, 43, 5489–5491 CrossRef CAS.
- T. Hu, L. Qin, F. Kong, Y. Zhou and J.-G. Mao, Ln3Pb3(IO3)13(μ3-O) (Ln = La–Nd): New Types of Second-Order Nonlinear Optical Materials Containing Two Types of Lone Pair Cations, Inorg. Chem., 2009, 48, 2193–2199 CrossRef CAS.
- C.-F. Sun, C.-L. Hu and J.-G. Mao, PbPt(IO3)6(H2O): a new polar material with two types of stereoactive lone-pairs and a very large SHG response, Chem. Commun., 2012, 48, 4220 RSC.
- H.-Y. Chang, S.-H. Kim, P. S. Halasyamani and K. M. Ok, Alignment of Lone Pairs in a New Polar Material: Synthesis, Characterization, and Functional Properties of Li2Ti(IO3)6, J. Am. Chem. Soc., 2009, 131, 2426–2427 CrossRef CAS.
- T. Sivakumar, H. Y. Chang, J. Baek and P. S. Halasyamani, Two New Noncentrosymmetric Polar Oxides: Synthesis, Characterization, Second-Harmonic Generating, and Pyroelectric Measurements on TlSeVO5 and TlTeVO5, Chem. Mater., 2007, 19, 4710–4715 CrossRef CAS.
- W. Bi, N. Leblanc, N. Mercier, P. Auban-Senzier and C. Pasquier, Thermally Induced Bi(III) Lone Pair Stereoactivity: Ferroelectric Phase Transition and Semiconducting Properties of (MV)BiBr5 (MV= methylviologen), Chem. Mater., 2009, 21, 4099–4101 CrossRef CAS.
- J. X. Zhang, et al., Microscopic Origin of the Giant Ferroelectric Polarization in Tetragonal-like BiFeO3, Phys. Rev. Lett., 2011, 107, 147602 CrossRef CAS.
- R. Seshadri and N. A. Hill, Visualizing the Role of Bi 6s “Lone Pairs” in the Off-Center Distortion in Ferromagnetic BiMnO3, Chem. Mater., 2001, 13, 2892–2899 CrossRef CAS.
- N. A. Hill, Density Functional Studies of Multiferroic Magnetoelectrics, Annu. Rev. Mater. Res., 2002, 32, 1–37 CrossRef CAS.
- X. Wang, H. Wang and X. Yao, Structures, Phase Transformations, and Dielectric Properties of Pyrochlores Containing Bismuth, J. Am. Ceram. Soc., 1997, 80, 2745–2748 CrossRef CAS.
- J. Yu and A. Kudo, Effects of Structural Variation on the Photocatalytic Performance of Hydrothermally Synthesized BiVO4, Adv. Funct. Mater., 2006, 16, 2163–2169 CrossRef CAS.
- W.-J. Yin, J.-H. Yang, J. Kang, Y. Yan and S.-H. Wei, Halide perovskite materials for solar cells: a theoretical review, J. Mater. Chem. A, 2015, 3, 8926–8942 RSC.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Stereochemistry of post-transition metal oxides: revision of the classical lone pair model, Chem. Soc. Rev., 2011, 40, 4455 RSC.
- A. Walsh and G. W. Watson, Influence of the Anion on Lone Pair Formation in Sn(II) Monochalcogenides: A DFT Study, J. Phys. Chem. B, 2005, 109, 18868–18875 CrossRef CAS.
- A. Walsh and G. W. Watson, The origin of the stereochemically active Pb(II) lone pair: DFT calculations on PbO and PbS, J. Solid State Chem., 2005, 178, 1422–1428 CrossRef CAS.
- M. W. Stoltzfus, P. M. Woodward, R. Seshadri, J.-H. Klepeis and B. Bursten, Structure and Bonding in SnWO4, PbWO4, and BiVO4: Lone Pairs vs. Inert Pairs, Inorg. Chem., 2007, 46, 3839–3850 CrossRef CAS.
- A. Walsh, The origin of structural distortions in metal ceramics, Trinity College, School of Chemistry, Dublin, Ireland, 2006 Search PubMed.
- N. Scotti, F. Flacke, R. Ludwig and H. Jacobs, Lithiumtriamidostannat(II), Li[Sn(NH2)3] - Synthese und kristallstruktur, Z. Anorg. Allg. Chem., 1998, 624, 1395–1399 CrossRef CAS.
- A. C. Filippou, P. Portius and G. Kociok-Köhn, Germanium(II) azides: synthesis and crystal structure of TpAGeN3 [TpA = hydrotris(3,5-dimethylpyrazol-1-yl)borato], Chem. Commun., 1998, 21, 2327–2328 RSC.
- C. Lau, et al., Se2NBr3, Se2NCl5, Se2NCl6−: New Nitride Halides of Selenium(III) and Selenium(IV), Chem.–Eur. J., 1996, 2, 1373–1378 CrossRef CAS.
- D. K. Kennepohl, H.-G. Schmidt, M. Noltemeyer and H. W. Roesky, Preparation and Characterization of F3Te(map) and the Structure of Cl3Te(map) (map = 2-(methylamino)pyridinato), Z. Naturforsch., B: Chem. Sci., 1992, 47, 5–8 CAS.
- R. S. Laitinen, A. Maaninen and J. Pietikäinen, Selenium- and Tellurium-Containing Chalcogen Nitrides, Phosphorus, Sulfur Silicon Relat. Elem., 1998, 136, 397–412 CrossRef.
- R. M. Hazen, E. S. Grew, R. T. Downs, J. Golden and G. Hystad, Mineral ecology: chance and necessity in the mineral diversity of terrestrial planets, Can. Mineral., 2015, 53, 295–324 CrossRef CAS.
- A. G. Christy, Causes of anomalous mineralogical diversity in the Periodic Table, Mineral. Mag., 2015, 79, 33–49 CrossRef.
- W. A. Deer, R. A. Howie and J. Zussman, Introduction to the Rock-Forming Minerals, Mineralogical Society of Great Britain and Ireland, 2013 Search PubMed.
- W. J. Roth, P. Nachtigall, R. E. Morris and J. Čejka, Two-Dimensional Zeolites: Current Status and Perspectives, Chem. Rev., 2014, 114, 4807–4837 CrossRef CAS.
- B. M. Weckhuysen and J. Yu, Recent advances in zeolite chemistry and catalysis, Chem. Soc. Rev., 2015, 44, 7022–7024 RSC.
- M. Moliner, State of the art of Lewis acid-containing zeolites: lessons from fine chemistry to new biomass transformation processes, Dalton Trans., 2014, 43, 4197–4208 RSC.
- R. Niewa and H. Jacobs, Cs5[Na{W4N10}]: The first framework nitridotungstate(VI), Z. Anorg. Allg. Chem., 1996, 622, 881–884 CrossRef CAS.
- S. Correll, O. Oeckler, N. Stock and W. Schnick, LixH12xyz[P12OyN24y]Clz—An Oxonitridophosphate with a Zeolitelike Framework Structure Composed of 3-Rings, Angew. Chem., Int. Ed., 2003, 42, 3549–3552 CrossRef CAS.
- S. J. Sedlmaier, et al., Unprecedented Zeolite-Like Framework Topology Constructed from Cages with 3-Rings in a Barium Oxonitridophosphate, J. Am. Chem. Soc., 2011, 133, 12069–12078 CrossRef CAS.
- W. Schnick and J. Lücke, Zn7[P12N24]Cl2—A Sodalite with a Phosphorus–Nitrogen Framework, Angew. Chem., Int. Ed. Engl., 1992, 31, 213–215 CrossRef.
- H. Huppertz and W. Schnick, Ba2Nd7Si11N23—A Nitridosilicate with a Zeolite-Analogous Si–N Structure, Angew. Chem., Int. Ed. Engl., 1997, 36, 2651–2652 CrossRef CAS.
- F. Gao, R. Xu and K. Liu, Origin of hardness in nitride spinel materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 052103 CrossRef.
- A. Šimůnek and J. Vackář, Hardness of Covalent and Ionic Crystals: First-Principle Calculations, Phys. Rev. Lett., 2006, 96, 085501 CrossRef.
- M. Grimsditch, E. S. Zouboulis and A. Polian, Elastic constants of boron nitride, J. Appl. Phys., 1994, 76, 832–834 CrossRef CAS.
- Z. Pan, H. Sun, Y. Zhang and C. Chen, Harder than Diamond: Superior Indentation Strength of Wurtzite BN and Lonsdaleite, Phys. Rev. Lett., 2009, 102, 055503 CrossRef.
- M. A. Rafiee, et al., Hexagonal Boron Nitride and Graphite Oxide Reinforced Multifunctional Porous Cement Composites, Adv. Funct. Mater., 2013, 23, 5624–5630 CrossRef CAS.
- W. Wang, S. J. Chen, F. Basquiroto de Souza, B. Wu and W. H. Duan, Exfoliation and dispersion of boron nitride nanosheets to enhance ordinary Portland cement paste, Nanoscale, 2018, 10, 1004–1014 RSC.
- D. Ostermann and H. Jacobs, Synthesis and crystal structure of the potassium imido nitrido polytungstate(VI) K14W6N16NH, J. Alloys Compd., 1994, 206, 15–19 CrossRef CAS.
- R. Niewa and H. Jacobs, Na5Rb[(WN3)2] and Na5Cs[(WN3)2], two new sodium nitrido tungstates(VI) with the heavier alkali metals rubidium and cesium, J. Alloys Compd., 1996, 234, 171–177 CrossRef CAS.
- R. Niewa and H. Jacobs, Na2K13[W7N19] the first nitrido tungstate(VI) with layers of corner-sharing nitrogen tetrahedra around tungsten, J. Alloys Compd., 1996, 236, 13–18 CrossRef CAS.
- R. Niewa and H. Jacobs, Cs5[Na{W4N10}]: The first framework nitridotungstate(VI), Z. Anorg. Allg. Chem., 1996, 622, 881–884 CrossRef CAS.
- A. Gudat, R. Kniep and J. Maier, LiBa4[Mo2N7]·BaCl2: Dimere anionen [Mo2N7]9− durch kondensationsreaktion von Ba3[MoN4] in LiCl-Schmelzen, Z. Naturforsch., B: Chem. Sci., 1992, 47, 1363–1366 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Method for deriving and verifying bond-valence parameters and two tables cited in text (Tables S1 and S2) listing structures used in anion bond-valence sum verification and a priori bond valences of selected crystal structures. See DOI: 10.1039/d0sc06028c |
| This journal is © The Royal Society of Chemistry 2021 |