Open Access Article
Open Access ArticleConformational analysis by UV spectroscopy: the decisive contribution of environment-induced electronic Stark effects†
Jeremy
Donon
,
Sana
Habka
,
Michel
Mons
 ,
Valérie
Brenner
,
Valérie
Brenner
 and
Eric
Gloaguen
and
Eric
Gloaguen
 *
*
LIDYL, CEA, CNRS, Université Paris Saclay, CEA Saclay, Bât 522, 91191 Gif-sur-Yvette, France. E-mail: eric.gloaguen@cea.fr
First published on 5th January 2021
Abstract
UV chromophores are frequently used as probes of the molecular structure. In particular, they are sensitive to the electric field generated by the molecular environment, resulting in the observation of Stark effects on UV spectra. While these environment-induced electronic Stark effects (EI-ESE) are already used for conformational analysis in the condensed phase, this work explores the potential of such an approach when performed at much higher conformational resolution in the gas phase. By investigating model alkali benzylacetate and 4-phenylbutyrate ion pairs, where the electric field applied to the phenyl ring is chemically tuned by changing the nature of the alkali cation, this work demonstrates that precise conformational assignments can be proposed based on the correlation between the conformation-dependent calculated electric fields and the frequency of the electronic transitions observed in the experimental UV spectra. Remarkably, the sole analysis of Stark effects and fragmentation patterns in mass-selected UV spectra provided an accurate and complete conformational analysis, where spectral differences as small as a few cm−1 between electronic transitions were rationalized. This case study illustrates that the identification of EI-ESE together with their interpretation at the modest cost of a ground state electric field calculation qualify UV spectroscopy as a powerful tool for conformational analysis.
1. Introduction
Conformational analysis aims at elucidating the tridimensional structure of flexible molecular objects. It includes the structure elucidation of flexible molecules as well as issues dealing with supramolecular organization. This is a more or less difficult matter that can be treated at different levels, which range from the rough identification of the dominant conformation among a limited set of likely candidates, to the full characterization of the conformational distribution of a complex mixture. Numerous spectroscopic methods exist and are often combined with theoretical models or calculations to achieve these goals.1 Among these experimental methods, those using UV light are rather accessible and can be applied to various liquid or gas samples. These techniques rely on UV chromophores, which are probes sensitive to their environment. This is illustrated in the condensed phase by fluorescence resonance energy transfer (FRET), which is used to accurately document the distance between two distinct UV chromophores,2 or electronic circular dichroism (ECD), which can document structural changes at the protein scale based on the relative disposition of UV chromophores.3 In the gas phase, where FRET4 and ECD5 may also be used, UV based-techniques applied to cold samples achieve a better spectral resolution, making them particularly sensitive to subtle changes in the chromophore environment. In particular, a UV spectrum with a standard resolution of a few cm−1 allows to disentangle the electronic transitions of a mixture of conformers, which can be further characterized by e.g. their fragmentation pattern using mass spectrometry.6 A higher spectral resolution can sometimes be decisive to directly identify conformers by measuring the rotational contour of their electronic transition.7,8 For relatively simple systems, UV spectra with full rotational resolution can be recorded and provide unambiguous conformational assignments.9 While spectral resolution is a precious help, conformer-selectivity, i.e. the individual spectroscopic characterization of each conformer, is a sophistication, which is often required to perform a complete analysis of a conformational mixture. Conformer-selective UV spectra may be recorded by using UV/UV double resonance techniques,10 but conformer-selection can also be achieved using ion mobility.11 Otherwise, UV chromophores take a critical part in the conformer-selection process for other types of spectroscopy, like conformer-selective IR12–14 or photoinduced dynamics,15 and in the measurement of the fractional abundances of a conformational mixture,16 which can be considered as the ultimate goal of conformational analysis.While UV spectroscopy is widely used, it is often not enough to perform an advanced conformational analysis without being coupled to other techniques like mass spectrometry or IR spectroscopy. In this line, a possible complementary diagnosis is provided by electronic Stark spectroscopy (ESS), which consists of recording UV spectra when the sample is placed in a controlled, homogeneous external electric field. Given the electric fields technically achievable (<0.1 GV m−1),17 the resulting Stark shifts are often modest (less than a few cm−1) and preferably suit the conformational analyses carried out in the gas phase with high-resolution,18 although such investigations can sometimes also be performed in the condensed phase.19,20 Beyond ESS, electronic Stark effects (ESE) may simply result from the electric fields generated by the molecular environment of the UV chromophore itself. These electric fields are much larger (up to ∼10 GV m−1) and induce significant ESE that can be more easily observed in UV spectra.21 The interest of these environment-induced ESE (EI-ESE) is two-fold: they can be used to tune the electric field applied to a UV chromophore by changing its environment in a controlled way (e.g. solvent,22 chemical substitution23), echoing an ESS experiment; conversely, a UV chromophore can serve as a probe to monitor its electrostatic environment.21 Ultimately, these UV probes, once calibrated by ESS experiments, can be used to make an in situ measurement of the absolute value of the electric field, which is a conformation-dependent observable.24 While conformational analyses in the condensed phase have relied on EI-ESE for a long time,24 those conducted in the gas phase surprisingly did not exploit this possibility so far.
In this context, the present work aims at exploring to what extent EI-ESE can be used to perform conformational analyses in the gas phase. Following a recent exploratory study on alkali phenylacetate ion pairs, (M+, PA−) with M = Li, Na, K, Rb and Cs, for which a significant quadratic electronic Stark effect was observed along the series,23 the present study applies the same approach to the conformational analysis of more complex ion pairs, i.e. alkali benzylacetate (M+, BA−) for M = Li, Na, K, Rb and alkali 4-phenylbutyrate (M+, PB−) for M = Li and Na. This approach relies on the correlation between the experimental energy of the electronic transitions and the calculated electric field generated by the environment of the UV chromophore. These ion pairs of general formula (M+, Ph–(CH2)n–CO2−) are made of a UV probe, i.e. the phenyl ring, which experiences the large and chemically tuned electric fields generated by the -(CH2)n-CO2− M+ moiety, where the carboxylate group makes a contact ion pair with an alkali counter ion. They are thus ideal systems to reveal EI-ESE and use them for conformational analysis purposes. In addition, they can also be considered as general models for the numerous systems containing a UV chromophore surrounded by polar groups, which will be illustrated by the consistency of the present results with that previously obtained on benzylacetic acid (Ph–(CH2)2–CO2H).7 In contrast, n-alkylbenzenes Ph–(CH2)n–CH3, where the phenyl ring is surrounded by a nonpolar moiety, represent an interesting nonpolar reference for a direct comparison with the ion pairs investigated. In this respect, the conformational analysis of n-alkylbenzenes,25 carried out at the cost of an advanced theoretical and experimental investigation of the CH stretch modes, is a particularly useful asset for this study. While the conformational analysis of (Li+, BA−) and (Li+, PB−) from conformer-selective IR spectra in the CO2− stretch region already provided partial assignments,26 the approach used in this work will not only enable us to complete the analysis, extend it to other systems and rationalize UV spectra, but will also demonstrate its ability to extract unique structural pieces of information, revealing UV spectroscopy as an even more precious tool for conformational analysis.
2. Methodology
2.1 Experiments
Gas phase ion pairs were produced by laser desorption27 (frequency-doubled Nd:YAG laser, 10 Hz, 0.1–3 mJ per pulse, Minilite Continuum) of a pellet made of the desired salt mixed with graphite, according to a procedure detailed previously (ESI of ref. 26). The plume of desorbed material seeded a pulsed supersonic molecular beam (General Valve, 1 mm diameter nozzle, repetition rate 10 Hz) of a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 He
30 He![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ne gas mixture (back pressure 18 bar), which cooled the vaporized species enough to both trap them in their conformational minima and record vibrationally-cold spectra. UV spectra were obtained by resonant 2-photon ionization (R2PI) induced by a wavelength-scanned laser pulse from a Nd:YAG-pumped (Powerlite Continuum, 100 mJ per pulse at 355 nm) dye laser (Narrow Scan Radiant dyes, 700 μJ per pulse). These ions were generated at the interaction region of a reflectron mass-spectrometer and further detected by microchannel plates. Conformer-selective IR spectra were recorded by scanning the wavelength of an IR pump pulse from a Nd:YAG-pumped (Continuum Surelite, 650 mJ per pulse at 1064 nm) optical parametric oscillator/amplifier (OPO KTP/OPA KTA) Laservision equipped with a difference frequency generation (DFG) stage (∼1 mJ per pulse in the 1300–1700 cm−1 range), while the wavelength of the UV probe pulse was tuned on the electronic transition of the targeted conformer according to a procedure detailed elsewhere.28 IR and UV spectra were recorded on the mass channel corresponding to that of the most abundant isotopologue for each system.
Ne gas mixture (back pressure 18 bar), which cooled the vaporized species enough to both trap them in their conformational minima and record vibrationally-cold spectra. UV spectra were obtained by resonant 2-photon ionization (R2PI) induced by a wavelength-scanned laser pulse from a Nd:YAG-pumped (Powerlite Continuum, 100 mJ per pulse at 355 nm) dye laser (Narrow Scan Radiant dyes, 700 μJ per pulse). These ions were generated at the interaction region of a reflectron mass-spectrometer and further detected by microchannel plates. Conformer-selective IR spectra were recorded by scanning the wavelength of an IR pump pulse from a Nd:YAG-pumped (Continuum Surelite, 650 mJ per pulse at 1064 nm) optical parametric oscillator/amplifier (OPO KTP/OPA KTA) Laservision equipped with a difference frequency generation (DFG) stage (∼1 mJ per pulse in the 1300–1700 cm−1 range), while the wavelength of the UV probe pulse was tuned on the electronic transition of the targeted conformer according to a procedure detailed elsewhere.28 IR and UV spectra were recorded on the mass channel corresponding to that of the most abundant isotopologue for each system.
2.2 Calculations
Explorations of the potential energy surfaces were performed based on both the previous work on (Li+, BA−) and (Li+, PB−),26 and additional considerations about the dihedral angles around C–C single bonds. Geometry optimizations were further carried out at the RI-B97-D3/dhf-TZVPP level,29–31 unless specified otherwise, using Turbomole32,33 (more details on Turbomole options in ESI†). Numerical harmonic frequency calculations were performed at the same level. Harmonic frequencies, f0th, were further corrected to obtain mode-dependent34 frequencies, fth, scaled by two linear functions,35,36fth = 0.9272f0th + 137.9 cm−1 for the (CO2−)anti stretch, and fth = 1.1431f0th − 164.3 cm−1 for the (CO2−)sym stretch, determined previously37 from a set of carboxylate-containing conformers assigned in the literature. Electric field calculations were performed at the RI-B97-D3(BJ)/def2-QZVPP level29,31,38,39 on RI-B97-D3(BJ)-abc/dhf-TZVPP optimized structures, unless specified otherwise (Turbomole options detailed in ESI†).3. (M+, BA−) ion pairs
3.1 Theoretical conformers
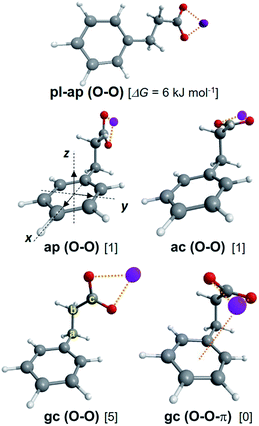
Following the experimental and theoretical study of the lithium benzylacetate ion pair, (Li+, BA−),26 the series (Na+, BA−), (K+, BA−), (Rb+, BA−) was investigated similarly. The lowest energy minima of the RI-B97-D3/dhf-TZVPP potential energy surface are reported in Table 1. The structure of these minima is mainly characterized by three dihedrals CorthoCipsoCaCb, CipsoCaCbCc and CaCbCcO (Fig. 1). For the majority of these minima, the CorthoCipsoCaCb angle is such that the CipsoCaCb plane is almost perpendicular to the phenyl ring plane. For a few conformers, however, not only Cb belongs to the phenyl ring plane, but also all the other heavy atoms. In this latter case, the label pl will be used to specify the planar structure of these conformations in order to distinguish them from the former set of conformers. The label gauche (g±) is used for CipsoCaCbCc angles lying between 0 and ±120°, and anti (a) otherwise. The label periplanar, p (resp. clinalc), will be used when one of the CaCbCcO dihedrals lies between −30 and 30° (resp. between 30° and 90° or between −30° and −90°). In addition, the type and number of non-covalent interactions that the anion makes with the cation M+ are indicated by specific labels: one or two “O” when M+ strongly interacts with one or two oxygen atoms of carboxylate, respectively, and “π” when M+ non-covalently binds to the aromatic ring. For all systems, the conformational distribution is made of five conformers ap, ac, g+c, g−c and pl-ap. Conformers g+c and g−c being enantiomers that cannot be distinguished by the spectroscopic methods employed, only g+c is reported under the label gc (Fig. 1 and Table 1). While for M = Li, conformers are of type O–O, the conformational distribution for Na, K and Rb is made of a mixture of conformers of type O–O (pl-ap, ap and ac) and type O–O-π (gc). Along the (M+, BA−) series, conformer gc thus changes from type O–O to O–O-π when the cation is large enough to enable simultaneous non-covalent interactions between the carboxylate and the phenyl ring.| System | Label | Type | CipsoCaCbCc | CaCbCcO | ΔG(300 K) | |Ex| | Conf. | σ 0(ππ*) |
|---|---|---|---|---|---|---|---|---|
| a Partial optimization with a fixed CipsoCaCbCc angle at the RI-B97-D3/dhf-TZVPP level. Electric field calculations were further carried out from this geometry at the RI-B97-D3(BJ)/def2-QZVPP level. b Optimization at the RI-B97-D3(BJ)-abc/dhf-TZVPP level. c Extracted from Fig. 1 in Hewett et al.25 d The O atom of the CaCbCcO dihedral corresponds to that of the carbonyl group. e Values taken from ref. 7. | ||||||||
| (Li+, BA−) | ap | O–O | 180 | 3 | 0 | 2.64 | B | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558.7 558.7 |
| ac | O–O | 180 | 89 | 2 | 2.34 | |||
| gc | O–O | 65 | 40 | 1 | 2.66 | A | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597.2 597.2 |
|
| pl-ap | O–O | 180 | −3 | 6 | ||||
| (Na+, BA−) | ap | O–O | 180 | 1 | 1 | 3.29 | B | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511.7 511.7 |
| ac | O–O | 180 | 89 | 1 | 3.01 | |||
| gc | O–O | 65 | 42 | 5 | 3.26 | A | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563.8 563.8 |
|
| gc | O–O-π | 41 | 59 | 0 | ||||
| pl-ap | O–O | 180 | 0 | 6 | ||||
| (K+, BA−) | ap | O–O | 180 | 1 | 5 | 3.73 | B | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473.0 473.0 |
| ac | O–O | 180 | 89 | 5 | 3.49 | |||
| gc | O–O-π | 46 | 53 | 0 | C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557.5 557.5 |
||
| pl-ap | O–O | 180 | −1 | 10 | ||||
| (Rb+, BA−) | ap | O–O | 179 | −7 | 5 | 3.82 | B | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461.2 461.2 |
| ac | O–O | 180 | 89 | 4 | 3.58 | |||
| gc | O–O-π | 47 | 52 | 0 | C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571.5 571.5 |
||
| pl-ap | O–O | 180 | −1 | 8 | ||||
| n-Propylbenzene | a | 180b | 2.13 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592c 592c |
||||
| g | 63b | 2.09 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543c 543c |
|||||
| Benzylacetic acid | ap | 181b | 1b,d | 1.32 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 627e 627e |
|||
| gc | 70b | 34b,d | 1.33 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649e 649e |
||||
3.2 UV spectroscopy
Fig. 2 presents the R2PI-UV spectra recorded on the relevant mass channels for each ion pair. From the IR spectra of the CO2− stretches recorded in a previous study,26 it is known that the two main electronic transitions observed on the (Li+, BA−) parent ion channel correspond to two different conformers, A, assigned to the gc (O–O) conformer, and B assigned to another O–O conformer.26 However, the nearly indistinguishable theoretical IR spectra of the O–O conformers prevent us to identify B, illustrating the need of an alternative approach to push further the conformational analysis.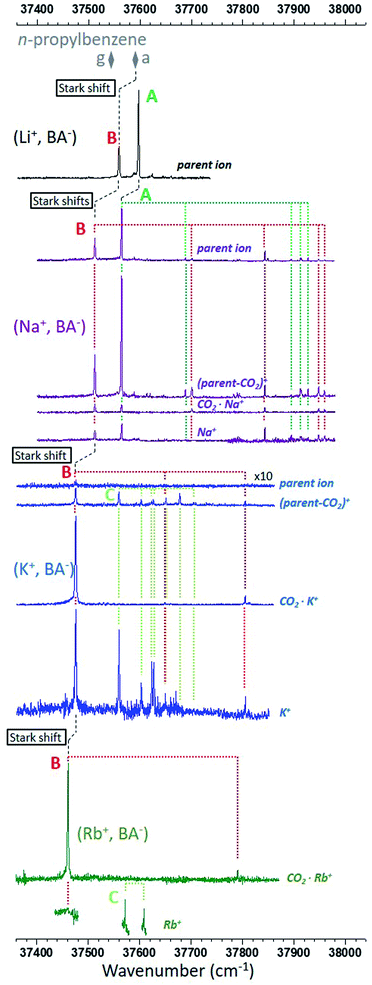 | ||
| Fig. 2 R2PI ion signals recorded in the ππ* origin spectral region of the phenyl ring. The mass channels, identified by their most representative ion of same m/z, are shown for each type of ion pair from top to bottom: (Li+, BA−) in black,26 (Na+, BA−) in purple, (K+, BA−) in blue and (Rb+, BA−) in dark green. The most intense electronic and vibronic transitions are assigned to three types of conformer, A in green, B in red, and C in light green. The origin transitions of both conformers g and a of n-propylbenzene are also reported (grey diamonds). Stark shifts are marked with dashed black lines (see text for details). | ||
The electronic spectrum of (Na+, BA−) is also made of two main transitions and looks like that of (Li+, BA−), except that: (i) transitions are red-shifted by 30–50 cm−1; (ii) the signal is spread over four mass channels corresponding to that of the parent ion, a decarboxylated parent ion noted (parent-CO2)+, the CO2·Na+ ion, and the sodium cation, Na+. This fragmentation pattern is consistent with a decarboxylation induced by the ionization of the phenyl ring (Fig. S0†), which is analogous to that already proposed to explain the fragmentation observed for (Li+, PA−).26 The similarities of the (Na+, BA−) spectrum with that of (Li+, BA−) lead us to label the main transitions A and B accordingly. A close examination reveals that the relative intensities between these transitions vary with the mass channel, confirming that A and B correspond to two different species: the largest A/B ratio is observed on the (parent-CO2)+ mass channel, whereas the smallest ratio is found on the CO2·Na+ channel where both conformers have origin transitions of similar intensities. The same observation can be made for several vibronic bands, enabling us to assign them to A or B (Fig. 2).
Similarly, the transitions observed in the electronic spectrum of (K+, BA−) can be sorted in two sets according to their fragmentation pattern. A first set can be clearly seen on the CO2·K+ mass channel, without any contribution from the other set. Its vibronic spectral pattern, resembling that of conformer B of (Na+, BA−) red-shifted by 39 cm−1, qualifies this set to receive the same label. On the (parent-CO2)+ and K+ channels, this set is mixed with another one, mostly made of a quasi-harmonic vibrational progression, nσvib, where σvib is the harmonic component of a 20 cm−1 vibrational mode and n the vibrational quantum number (Fig. S1†). The transitions corresponding to n = 0, 2, 3, 4, 5, 6 can be observed on the (parent-CO2)+ mass channel, the missing n = 1 transition suggesting that its Franck–Condon factor is probably too weak for its detection with our experimental setup. The K+ mass channel only shows the first part of the progression (n = 0, 2, 3), which will be tentatively explained later on. The second set of transitions is thus quite different from that of A or B, and is assigned a label C.
Finally, spectra were also recorded for (Rb+, BA−). Only the CO2·Rb+ (Fig. 1) mass channel has a complete spectrum. Indeed, the signal-to-noise ratio on the Rb+ mass channel was too poor to consider long scans, only a few critical spectral regions were targeted and shown on Fig. 1; no signal was detected on the parent ion mass channel; the (parent-CO2)+ ion mass channel was useless due to the presence of an intense ion signal coming from a neighbor mass channel. The CO2·Rb+ mass channel shows a signature compatible with that of the series of conformers B, that of (Rb+, BA−) being the most red-shifted. Two more transitions separated by 37 cm−1 are seen on the Rb+ mass channel in the spectral region where the conformer C would be expected, with an energy difference similar to that observed between transitions n = 0 and 2 of (K+, BA−) (43 cm−1). These transitions are thus labeled accordingly.
3.3 Conformational assignment
The low frequency mode responsible for the vibrational progression of conformer C in (K+, BA−) is an indication of a folded species where the phenyl ring is non-covalently bound to another part of the system, a situation that only occurs for the O–O-π conformer according to the theoretical study (Section 3.1). As IR spectroscopy of the CO2− stretches is appropriate to distinguish between O–O-π and O–O conformers,26 conformer-selective IR spectra (Fig. S2†) were recorded and compared to calculated frequencies (Table S1†), and provided an additional support for the assignment of C to the gc (O–O-π) conformer. The same assignment for conformer C of (Rb+, BA−) is very likely, although IR experiments were not possible due to the weak signal.Conformer A of (Li+, BA−) being already assigned to gc (O–O), the same assignment is proposed for (Na+, BA−). With this assignment, the experimental spectra along the series of systems show that these conformers gc (O–O) are only present for the light cations Li+ and Na+, and are replaced by gc (O–O-π) for the heavier cations K+ and Rb+. This evolution can be interpreted by considering both the cation size and the constraints needed to fold the anion enough for the cation to simultaneous bind to the phenyl ring and the carboxylate group: the smaller the cation, the less stable gc (O–O-π) relative to gc (O–O). This picture is only partly supported by RI-B97-D3/dhf-TZVPP calculations, which found a gc (O–O) conformer only for Li+, and gc (O–O-π) conformers for the other cations. In the case of Na+, the false prediction gc (O–O-π) instead of the observed gc (O–O) is ascribed to the limitation of the level of calculation in accurately describing the subtle competition between the cation–π and cation–anion interactions in these gc conformers (Fig. S3†). This flaw, however, did not generate any further issue in the analysis of the larger (M+, PB−) systems presented in Section 4.
By elimination, conformer B can be assigned either to ap, ac or pl-ap. Its origin transition redshifts from Li+ to Rb+ (Fig. 2), in a very similar way to what was previously observed for the (M+, PA−) ion pairs series, for M going from Li to Cs.23 These redshifts were interpreted as Stark shifts induced by the increasing electric field generated by the (M+, ˙CH2–CO2−) radical at the centre of the phenyl ring for M going down the group of alkali cations. A classical analysis of the Stark effects proved to account for the observations, therefore a more sophisticated quantum-mechanical treatment40 was not needed. Using the same approach on (M+, BA−) systems, the electric field generated by the (M+, ˙CH2–CH2–CO2−) radical is reported in Tables 1 and S2† for conformers ap and ac. pl-ap sharing the same (M+, ˙CH2–CH2–CO2−) geometry with ap, no specific calculation for this conformer was needed, which also means that these two conformers cannot be discriminated by EI-ESE. As investigated previously for (M+, PA−) ion pairs, this electric field in (M+, BA−) is oriented mainly along the x axis in each conformer (Table S2,† see Fig. 1 for axes definition) and the difference between the dipole moments of the excited and ground states (Δμ) can be neglected,23 leading at the second order to the following relation between the Stark shift (Δσ), the Planck's constant (h), the speed of light (c), the electric field (E), the difference between the polarizability tensors of the excited and ground states of the phenyl ring (Δα), and their components along the x axis (Ex and Δαxx):
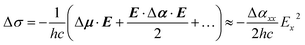 | (1) |
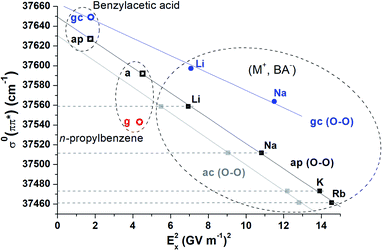
Fig. 3 reports the origin electronic transitions of conformers B along the alkali cation series, plotted as a function of Ex2 for either ap or ac. Both sets (black and grey solid squares respectively) show a linear behaviour as expected from eqn (1), and demonstrate that the experimental shift observed for conformers B along the (M+, BA−) series of systems can indeed be interpreted as a consistent series of quadratic Stark shifts (Fig. 1). Although it is not possible to assign B to ap or ac from these datasets yet, the comparison of these systems with n-propylbenzene and benzylacetic acid is expected to be helpful. Indeed, n-propylbenzene and benzylacetic acid are made of a –CH2–CH2–CH3 and –CH2–CH2–COOH moiety respectively, which are analogous to the –CH2–CH2–CO2− M+ moiety of (M+, BA−), where the ionic group –CO2−M+ is replaced by either a methyl or carboxylic group. These substitutions lead to a change of the electric field experienced by the phenyl ring, and thus induce a shift of its electronic transition according to eqn (1). The electric field generated by the ˙CH2–CH2–CH3 or ˙CH2–CH2–COOH systems at the center of the phenyl ring is reported in Table 1 for conformer a of n-propylbenzene and ap of benzylacetic acid. Their origin electronic transition are known,7,25 enabling us to add these conformers to Fig. 3 (black open squares). Their alignment with the linear correlation of conformers ap of (M+, BA−) makes a consistent set where all electronic transitions of these conformers are governed by quadratic Stark effects. In contrast, conformers a and ap of n-propylbenzene and benzylacetic acid are not aligned with the set of conformers ac, forbidding such a rationalisation. From that observation, conformers B can be assigned to ap or pl-ap. If a final assignment of B to ap is only suggested by its lower relative energy at this stage (Table 1), it will be further confirmed by considering its fragmentation pattern, which will be discussed in Section 4 dedicated to the (M+, PB−) ion pairs.
3.4 Stark effects, molecular interactions and probing distance
Unlike a Stark spectroscopy experiment where Stark shifts of a given molecular system are induced by an external electric field, the electric field applied to the UV chromophore, i.e. the phenyl ring, is here generated by the second moiety of the system, i.e. a non-covalent molecular object covalently bound to the chromophore. While all types of molecular interactions occur between these two moieties, the fact that electronic shifts observed on the first moiety can be rationalized by only considering the electric field generated by the second moiety (Fig. 3, black) means that only electrostatic and polarization interactions contribute to these shifts, namely Stark shifts, whereas dispersion or repulsion have a negligible contribution. Furthermore, the first significant permanent moment of the phenyl being a quadrupole, the variation of the electrostatic term between the two moieties results from a quadrupole–dipole interaction, which is expected to be weak compared to that of the polarization term in the distance range considered. Therefore, Stark shifts in these systems can be mainly ascribed to the sole variation of the polarization of the phenyl ring induced by changes, i.e. substitution or conformational isomerization, occurring in the second moiety of the system. Conversely, any shift observed while the electric field is unchanged, is likely due to variations in dispersive and/or repulsive interactions.These considerations lead us to focus the discussion on conformers g of n-propylbenzene and gc of benzylacetic acid, (Li+, BA−) and (Na+, BA−) (Fig. 3, red and blue respectively). First, in the case of n-propylbenzene, the redshift of conformer g relative to a (49 cm−1) was formerly assigned to an interaction between the phenyl ring and the methyl group, which is stronger in g than in a due to a shorter interaction distance in the former (shortest interatomic distance, SID = 281 pm, see Fig. S4†).25,41 Remarkably, the phenyl ring experiences an almost identical electric field from the –CH2–CH2–CH3 moiety in both conformers (Table 1, Fig. 3). Consequently, a Stark effect cannot account for the redshift, which must result mainly from dispersion and/or repulsion variations. Similarly, the almost identical electric fields calculated for conformers gc and ap in benzylacetic acid, (Li+, BA−) or (Na+, BA−) cannot account for the difference between their electronic origin transitions. In these cases, the group –COOH or –CO2−M+ is much closer to the phenyl ring in gc (SID in the 270–280 pm range) than in ap (Fig. S4†). Interestingly, such dispersive/repulsive interactions typical of gc lead to a blue shift of 20 to 50 cm−1 in the case of benzylacetic acid or ion pairs, compared to a redshift of 49 cm−1 for n-propylbenzene g conformers. In contrast, the shifts observed within the set of a/ap conformers (Fig. 3, black) are fully explained by an EI-ESE, and thus by a pure phenyl ring polarization effect excluding any contribution from dispersion or repulsion. Indeed, in that case, the SID between the phenyl ring and the group varying within this set, namely –CH3, –COOH or –CO2−M+, is larger than 422 pm, i.e. a much larger distance than the previous considered cases where structural changes occurred closer than 281 pm from the phenyl ring.
When comparing electronic transitions of two species differing by either a substitution or a conformational change, the latter discussion showed the importance of considering the SID between the phenyl ring and the closest chemical group where the difference lies. When changes occur at sufficiently large SIDs, variations of dispersion/repulsion are negligible enough to assimilate these changes to a simple variation of the electric field applied to the phenyl ring. Stark shifts may then be easily identified on the electronic spectra and provide fruitful information as shown above. At short SIDs, dispersion and repulsion blur this simple picture, and one needs to disentangle each contribution to the electronic shifts. The notion of short vs. large SIDs depends in principle on the nature of the interacting partners and is directly related to the accuracy needed for the analysis of the electronic spectrum. In the case of the systems investigated above, SIDs of ∼280 pm lead to dispersion/repulsion-induced electronic shifts of several tens of wavenumbers, whereas at SIDs larger than 430 pm, they are negligible (less than a few wavenumbers) compared to the Stark shifts considered, according to the good correlation obtained on Fig. 3 (black set, standard deviation < 2 cm−1). In this context, the case of gc conformers of benzylacetic acid, (Li+, BA−) and (Na+, BA−) (Fig. 3, blue set, standard deviation > 4 cm−1) is interesting to point out. With an intermediate SID of 386 pm (CorthoH⋯Li distance), it is legitimate to discuss if the differences between the electronic transitions of this set can be considered as a Stark shift, or not. While the transition redshifts from benzylacetic acid to (Na+, BA−), as expected for a Stark shift induced by the increase of electric field according to eqn (1), one notices that the slope defined by these systems (Fig. 3 blue line) is different from that obtained for the a/ap set of conformers (black line). As this slope is determined by a quantity intrinsic to the phenyl ring of BA−, Δαxx, a different slope for gc conformers lead us to conclude that the electronic shift between their transitions does not result from a pure Stark effect and contains contributions of dispersive/repulsive interactions.
These considerations on the typical probing distances of the phenyl chromophore used as a Stark probe open up interesting perspectives in terms of conformational assignment based on electronic spectroscopy only. In order to explore the potential of this approach, it has been tested on more complex systems, namely (Li+, PB−) and (Na+, PB−), where the alkyl chain of PB− exhibits one more methylene group than BA−. Before, the next section will benefit from these assignments to rationalize the fragmentation patterns observed for the (M+, BA−) systems.
3.5 Rationalization of the fragmentation patterns
Fig. 2 and S5† show that the fragmentation patterns of the (M+, BA−) systems are extremely sensitive to the nature of the M+ cation, and also depends on the nature of the conformer. Several trends can be observed, and are tentatively rationalized here:– The intensity of the parent ion channel decreases drastically along the alkali series in favour of several fragment ion channels. This increasing reactivity of the parent ion can be associated to the decreasing energy of the ionic bond of the ion pair when going down the alkali series (from ∼700 to 500 kJ mol−1, see Table S3†). Indeed, in a context where the fragmentation pattern suggests a decarboxylation where the ionic bond is broken, the stronger the ionic bond, the less reactive the parent ion.
– The (parent-CO2)+ and CO2·M+ channels (steps 2 and 4 on Fig. S0,† respectively) both result from the decarboxylation of the parent ion, but the ratio between these channels strongly depends on the conformer for both M = Na and K, and appears to be related to the proximity of the cation to the phenyl ring. Indeed, for the gc (O–O-π) conformer (C) of (K+, BA−) where the cation is non-covalently bound to the phenyl ring (CorthoK distance = 362 pm), there is no signal on the CO2·K+ mass channel, presumably due to a better stabilization of K+ by a cation-π bond42 in the (parent-CO2)+ fragment. In the gc (O–O) conformer (A), Na+ does not significantly interact with the phenyl ring (CorthoNa distance = 455 pm). However, their relative proximity (Fig. 1 and S4†) lead to a significant signal on the (parent-CO2)+ channel, whereas the contribution of the CO2·Na+ mass channel remains small. Finally, for conformers ap (B), the contribution of the CO2·M+ channel is more important, likely due to a quite remote position of the cation relative to the phenyl ring (e.g. CipsoNa distance = 637 pm), which does not favor the (parent-CO2)+ channel. A stronger cation–π interaction with Na+ compared to K+,42 can also explain a relatively smaller contribution of the CO2·M+ mass channel in the former.
– The M+ channel could also result from the decarboxylation induced by the removal of a π electron from the phenyl ring (step 3 on Fig. S0†). However, such an assignment would not be consistent with the different spectra recorded for the (K+, BA−) O–O-π conformer on the K+ and (parent-CO2)+ channels. Indeed, the last vibronic bands of the progression are missing on the K+ channel, suggesting that a dark, ultrafast relaxation path competes with the formation of K+ ions, whereas such a competition is not seen on the (parent-CO2)+ fragment. Thus, K+ ions would more likely be formed after a photoexcitation of the ππ* state towards a highly excited state of the neutral, which would eventually autoionize when the amount of vibrational energy is not large enough to trigger an ultrafast relaxation towards dark states of the neutral.
4. (M+, PB−) ion pairs
4.1 Theoretical conformers
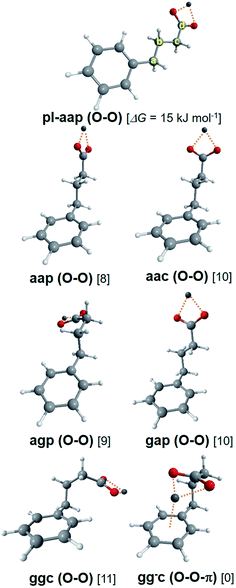
Theoretical conformers of (M+, PB−) ion pairs for M = Li and Na are listed in Table 2 and shown on Fig. 4 with the same nomenclature as that previously used for the successive dihedral angles of the (M+, BA−) ion pairs. (Li+, PB−) and (Na+, PB−) have very similar conformational distributions made of one O–O-π conformer, predicted as the most stable by at least 8 kJ mol−1, and six O–O conformers aap, aac, agp, gap, ggc and pl-ap together with their indistinguishable enantiomers when applicable. It is thus expected from these calculations that the O–O-π conformer will dominate the UV spectrum of these systems, in contrast to (Li+, BA−) and (Na+, BA−) where the methylene chain is too short to make the O–O-π conformer stable enough to be detected.| System | Label | Type | CipsoCaCbCc | CaCbCcCd | CbCcCdO | ΔG(300 K) | |Ex| | Conf. | σ 0(ππ*) |
|---|---|---|---|---|---|---|---|---|---|
| a Partial optimization with a fixed dihedral angle around the CcCd bond at the RI-B97-D3(BJ)-abc/dhf-TZVPP level. Electric field calculations were further carried out from this geometry at the RI-B97-D3(BJ)/def2-QZVPP level. b Optimization at the RI-B97-D3(BJ)-abc/dhf-TZVPP level. c Extracted from Fig. 1 in Hewett et al.25 | |||||||||
| (Li+, PB−) | aap | O–O | 180 | 179 | −5 | 8 | 2.54 | D | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570.4 570.4 |
| aac | O–O | 180 | 180 | 90 | 10 | 2.38 | F | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576.5 576.5 |
|
| agp | O–O | −177 | 68 | 21 | 9 | 2.60 | C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 554.7 554.7 |
|
| gap | O–O | 65 | −178 | 17 | 10 | 2.32 | |||
| gac | O–O | 63 | 178 | 89 | 2.13 | E | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523.8 523.8 |
||
| ggc | O–O | 66 | 63 | 61 | 11 | 2.34 | |||
| gg−c | O–O-π | 71 | −66 | −52 | 0 | A | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.4 156.4 |
||
| pl-aap | O–O | 180 | 180 | 5 | 15 | B | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561.3 561.3 |
||
| (Na+, PB−) | aap | O–O | 180 | 180 | −2 | 14 | 2.99 | D | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544.0 544.0 |
| aac | O–O | 180 | 179 | −84 | 13 | 2.85 | F | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557.9 557.9 |
|
| agp | O–O | −177 | 68 | 20 | 14 | 3.03 | C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537.3 537.3 |
|
| gap | O–O | 65 | −178 | 16 | 16 | 2.71 | |||
| gac | O–O | 63 | 178 | 90 | 2.52 | E | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501.5 501.5 |
||
| ggc | O–O | 66 | 62 | 60 | 16 | 2.77 | |||
| gg−c | O–O-π | 71 | −69 | −55 | 0 | A | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 292.7 292.7 |
||
| pl-aap | O–O | 179 | 180 | −2 | 20 | B | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 533.5 533.5 |
||
| n-Butylbenzene | aa | 180b | 180b | 2.20 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584c 584c |
||||
| ag | −177b | 65b | 2.16 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581c 581c |
|||||
| ga | 64b | −180b | 2.11 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521c 521c |
|||||
| gg | 61b | 65b | 2.10 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 522c 522c |
|||||
4.2 UV spectroscopy
Fig. 5 presents the R2PI-UV spectra recorded for (Li+, PB−) and (Na+, PB−). As expected from their theoretical conformational distributions, both systems display similarities: vibrational progressions point to a conformer labelled A; a pattern made of five transitions labelled from B to F following the decreasing intensity order. The previous study of (Li+, PB−) assigned A to the O–O-π conformer,26 while conformer-selective IR spectra revealed that the remaining pattern of transitions was made of different conformers assigned to the O–O type. On these bases, the same conclusions can be drawn for (Na+, PB−), as conformer-selective IR spectra (Fig. S6 and Table S4†) support these assignments without providing any additional information. However, a first comparison with the UV spectrum of n-butylbenzene25 is useful for assignment purposes. Indeed, the transitions of g· conformers (· standing for a non-defined value of the dihedral angle) are red-shifted relative to a· by ∼60 cm−1 due to the interaction between the methylene group CcH2 and the phenyl ring. The same type of interactions being at play in conformers g·· in (Li+, PB−) and (Na+, PB−), their transition is also expected to be red-shifted relative to conformers a··. Transition E being red-shifted by at least 30 cm−1 relative to all the other O–O conformers in both systems, it is then assigned to a conformer g··, while B C D and F are assigned to a·· conformers.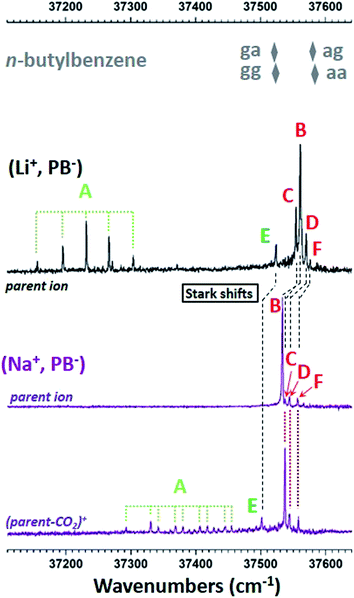 | ||
| Fig. 5 R2PI ion signals recorded in the ππ* spectral region of the phenyl ring. Mass channels, identified by their most representative ion of same m/z, are shown for each type of ion pair from top to bottom: (Li+, PB−) in black,26 (Na+, PB−) in purple. The most intense transitions are assigned to three types of conformers, A in light green, B, C, D, F in red, and E in dark green. Please note that conformer A of (Li+, PB−) is the only conformer of this system significantly detected on the (parent-CO2)+ mass channel with an intensity similar to that of the parent ion mass channel (Fig. S7†). The origin transitions of the four conformers aa, ag, ga and gg of n-butylbenzene are also reported (grey diamonds). Stark shifts are also marked with dashed black lines (see text for details). | ||
4.3 Fragmentation pattern
Several trends previously observed in the (M+, BA−) series can be seen in the fragmentation patterns of (Li+, PB−) and (Na+, PB−). First, (Na+, PB−) ion pairs fragment more efficiently than (Li+, PB−), which is consistent with a weaker ionic bond in the former species. Second, the fragmentation pattern of the (Na+, PB−) ion pairs depends on their conformation (Fig. 5 and S8†). A and E conformers undergo extensive fragmentation, which is consistent with their respective assignment to O–O-π and g·· (O–O) species according to the rationalization conducted on the (M+, BA−) series showing a stronger (parent-CO2)+ channel for gc than for ap (Section 3.5 and Fig. S5†). C, D, F are conformers that are mainly detected on the (parent-CO2)+ fragment, but are also clearly visible on the parent ion. Such a pattern is compatible with a·· conformers, with the difference that fragmentation into the (parent-CO2)+ channel tends to be higher than for their (Na+, BA−) ap analogue. Conformer B, in turn, is only detected on the parent ion mass channel, which is particularly intriguing in a context where (i) such a behavior was not encountered in (Na+, BA−) and (ii) fragmentation seems to be similar or higher in (Na+, PB−) than in (Na+, BA−) for all the other conformers. Looking for a reason forbidding the fragmentation of B, we examined how the decarboxylation reaction could be impacted by the symmetry of the conformers. On one side, this decarboxylation breaks the CcCd bond, and thus involves an electron transfer from the σ(CcCd) orbital. On the other side, this process is induced by the photoionization of the phenyl ring, and is thus triggered by the removal of one electron from the π orbitals of the phenyl ring, π(phenyl). Given that these two orbitals are remote, this reaction must also involve other orbitals like σ orbitals of the C–C single bonds between Cipso and Cc. While a low symmetry enables a non-zero overlap between all these orbitals for most conformers, this does not happen in the pl-aap conformer, where π(phenyl) has a zero overlap with all σ(CC) orbitals due to the Cs symmetry group of these species where the plane defined by the heavy atoms is plane of symmetry. In this case, the decarboxylation cannot be triggered by the π-hole, which could explain that pl-aap is not reactive compared to all the other conformers. On these grounds, (Na+, PB−) B is assigned to pl-aap. A close examination of the much less reactive (Li+, PB−) species also support the same assignment (Fig. S7†). Finally, looking back at conformers B of the (M+, BA−) series with this new awareness, its significant fragmentation points to an assignment to ap rather than pl-ap for which no fragmentation is expected.4.4 Conformational analysis using EI-ESE
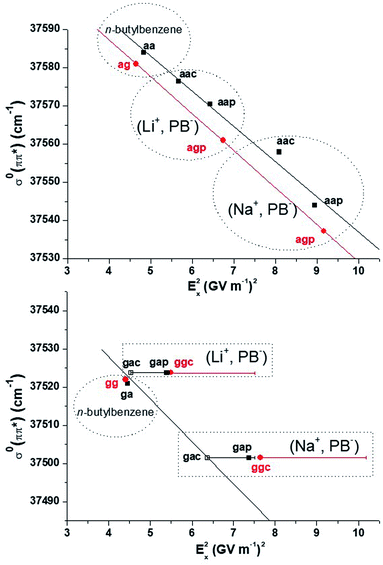
Conformers A and B being assigned, we are left with partial assignments of C, D, F to a·· conformers, and E to a g·· (O–O) conformer. According to the theoretical study, C, D and F must then be assigned to aap, aac or agp. These three theoretical conformers display indeed significantly different electric fields (Table 2 and S5†), which suggest that a EI-ESE can spread their electronic transitions over a spectral range compatible with that of conformers C D F. It is then legitimate to propose an assignment of these conformers based on an increasing electric field and decreasing electronic transition energy order according to eqn (1): F to aac, D to aap, and C to agp. However, one still needs to examine if these assignments are consistent with a quadratic Stark effect, not only to rationalize the electronic shifts within these conformers for one system, but also between all the related systems, i.e. (Li+, PB−), (Na+, PB−) and n-butylbenzene.25 If we first examine the correlation for the four aa· conformers of the ion pairs and the aa conformer of n-butylbenzene (Fig. 6 top, black), it is as good as that observed for the a and ap conformers (Fig. 3, black set), or the (M+, PA−) systems.23 If ag and agp conformers are added to this picture (Fig. 6 top, red), they also appear to follow a quadratic Stark effect, but do not seem to form a fully-consistent set with conformers aa and aa·. As seen previously for (M+, BA−), intramolecular interactions could be responsible for this behavior (Section 3.4). Indeed, the conformational changes between aa/aa· and ag/agp conformers occur at a short SID (CorthoH⋯O distances in the 370 pm range for agp), forbidding a global interpretation of their electronic spectra based on Stark shifts only. Consequently, the significant splitting of the triplet CDF compared to the nearly degenerate aa ag doublet in n-butylbenzene (Fig. 5) can only partly be ascribed to the increased electric field range experienced by the phenyl ring.Conformers E remain to be assigned either to gap or ggc according to the theoretical study. The redshift of transition E between (Li+, PB−) and (Na+, PB−) looks very similar to that observed for the multiplet BCDF (Fig. 5), and suggests again a quadratic Stark effect. The comparison with n-butylbenzene, however, provides a striking fact: the transition of (Li+, PB−) lies within only a few cm−1 to the blue of that of n-butylbenzene ga or gg conformers (Table 2, Fig. 5), whereas the difference of the calculated electric field between both systems should lead to a quadratic Stark effect with a significant redshift, making this set not consistent, whatever the assignment of E to gap or ggc (solid symbols in Fig. 6, bottom). In this context, the energy profiles of the ga· and gg· rotamers around the CbCcCdO angle (Fig. S9b and c†) reveal a remarkably low theoretical energy barrier to the rotation, especially for rotamers ga· (1.5 kJ mol−1). As the level of theory employed cannot provide such an accuracy on the calculated energy, other rotamers than gap or ggc should also be considered for the assignment of E. Indeed, the electric field profiles of these rotamers display large variations (Fig. S9†), which are reported on Fig. 6 (horizontal bars). Assuming again a quadratic Stark effect, it appears that an assignment of E to gac species for both (Li+, PB−) and (Na+, PB−) is the only possibility to form an aligned, i.e. consistent, set of conformers including n-butylbenzene ga or gg.
Finally, a detailed analysis of the fragmentation patterns of conformers C D F of (Na+, PB−) is consistent with the assignment provided by the analysis of Stark effects presented above. Indeed, conformer C, assigned to agp, displays a more significant fragmentation than transitions D and F (Fig. 5 and S8†) assigned to aap and aac. This observation is in line with the higher fragmentation of conformers with a gauche dihedral already pointed out (Fig. 2 and Section 3.5).
5. Final discussion
The conformational analysis presented above led us to sort conformers of several systems (ion pairs, benzylacetic acid or n-alkylbenzenes) in different sets, within which the electronic shifts between their origin transitions are simply governed by quadratic Stark effects. Both this study and that previously published on (M+, PA−) ions pairs23 demonstrate that conformers which share the same structure around the phenyl ring up to ∼430 pm always belong to the same set. In other words, the phenyl ring can be used as a Stark probe to accurately document structural changes beyond 430 pm in all these systems. In turn, if a substitution or a conformational change occurs closer to the phenyl ring, other effects involving dispersion and/or repulsion may contribute to shift electronic transitions.σ 0(ππ*) of the sets discussed in this work are plotted as a function of Ex2 in Fig. S10† and linearly fitted. The resulting parameters of these fits together with that of pl-aap conformers and the (M+, PA−) series23 are shown in Table 3, namely the offset (σ00) and Δαxx, which is directly related to the slope according to eqn (1).
| Conformer sets | Number of conformers in the set | Chain length | σ 00 | Δαxx |
|---|---|---|---|---|
| aa/aap/aac | 5 | 4C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 ± 5 629 ± 5 |
3.7 ± 0.1 |
| ag/agp | 3 | 4C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 ± 1 626 ± 1 |
3.8 ± 0.1 |
| ga/gg/gac | 4 | 4C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 ± 6 570 ± 6 |
4.3 ± 0.3 |
| pl-aap | 2 | 4C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 634 |
4.5 |
| a/ap | 5 | 3C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649 ± 2 649 ± 2 |
5.1 ± 0.1 |
| (M+, PA−) | 5 | 2C | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 ± 10 541 ± 10 |
10.1 ± 0.2 |
When the chain attached to the phenyl ring contains 4 carbon atoms (4C), the values found for Δαxx are rather homogeneous. The determination of Δαxx is independent on the conformation, as expected from the measurement of an intrinsic property of the phenyl ring in these systems. It can be noted that the Δαxx value obtained for the ga/gg/gac set is remarkably consistent with the others, strengthening the assignment of transitions E to gac conformers initially based on the sole linearity of the set (Section 4.4, Fig. 6). These Δαxx values are also consistent with that measured in the condensed phase for toluene from solvatochromic measurements in n-alkanes, i.e. Δ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) = (Δαxx + Δαyy + Δαzz)/3 = 2.9 ± 2.3 × 10−40 J m2 V−2.22 However, when looking at the 3C and 2C sets, Δαxx is found to increase respectively at 5.1 and 10.1 × 10−40 J m2 V−2, which correspond to significant variations if compared to αxx of the benzene ground state measured at 13.1 × 10−40 J m2 V−2.43,44 These results suggest that the polarizability properties of the phenyl ring are affected by the short alkyl chain bearing the carboxylate group in BA− and PA−, pointing out a through-bond effect rather than a through-space effect.
= (Δαxx + Δαyy + Δαzz)/3 = 2.9 ± 2.3 × 10−40 J m2 V−2.22 However, when looking at the 3C and 2C sets, Δαxx is found to increase respectively at 5.1 and 10.1 × 10−40 J m2 V−2, which correspond to significant variations if compared to αxx of the benzene ground state measured at 13.1 × 10−40 J m2 V−2.43,44 These results suggest that the polarizability properties of the phenyl ring are affected by the short alkyl chain bearing the carboxylate group in BA− and PA−, pointing out a through-bond effect rather than a through-space effect.
For each set of Table 3, σ00 is, according to eqn (1), the upper value of the origin ππ* transition, which is reached when a zero electric field is applied to a phenyl ring surrounded by the vicinal environment characterizing the set considered. It is interesting to note that, beyond this concept underlying σ00, its value can sometimes be approached, e.g. in the case of the origin ππ* transition of phenylacetic acid23 recorded at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 cm−1 (σ00 = 37
535 cm−1 (σ00 = 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 cm−1 for the (M+, PA−) set). By definition, σ00 does not depend on EI-ESE, and depends on the dispersive/repulsive interactions between the phenyl ring and the neighboring groups. For instance, the comparison between the ga/gg/gac and aa/aap/aac sets shows that σ00 shifts to the red by 59 cm−1, which can be mainly ascribed to dispersive/repulsive interactions between the methylene group CcH2 and the phenyl ring. More generally, large variations of σ00 are observed between sets where structural differences occur close to the phenyl ring. Taking the aa/aap/aac set as a reference, the (M+, PA−) and ga/gg/gac sets both display structural differences in the 270–320 pm range from the phenyl ring, inducing significant σ00 redshifts of respectively ∼90 cm−1 and ∼60 cm−1 (Table 3).
541 cm−1 for the (M+, PA−) set). By definition, σ00 does not depend on EI-ESE, and depends on the dispersive/repulsive interactions between the phenyl ring and the neighboring groups. For instance, the comparison between the ga/gg/gac and aa/aap/aac sets shows that σ00 shifts to the red by 59 cm−1, which can be mainly ascribed to dispersive/repulsive interactions between the methylene group CcH2 and the phenyl ring. More generally, large variations of σ00 are observed between sets where structural differences occur close to the phenyl ring. Taking the aa/aap/aac set as a reference, the (M+, PA−) and ga/gg/gac sets both display structural differences in the 270–320 pm range from the phenyl ring, inducing significant σ00 redshifts of respectively ∼90 cm−1 and ∼60 cm−1 (Table 3).
In summary, the origin ππ* transition of a phenyl ring in a given environment, σ0, can be simply predicted by the relation σ0(E) = σ00 + Δσ(E), where Δσ is given by eqn (1). The knowledge of σ00, which depends on the phenyl ring and its nearest neighbors, Δα, which is intrinsic to the phenyl ring of the system considered, and E the electric field applied to the phenyl ring by its environment is sufficient to easily determine σ0. According to the discussions above, the nearest neighbors that contribute to shift electronic transitions by more than a few wavenumbers through dispersive and/or repulsive interactions are the chemical groups typically lying within ∼430 pm from the phenyl ring. Such a decomposition of a UV probe environment in two parts, i.e. the nearest and remote interacting partners, has proven to be beneficial for both the conformational analysis and the rationalization of experimental UV spectra, but could equally be interesting in the frame of a theoretical approach. Indeed, the calculation of σ00 at an advanced level of theory, or its semi-empirical estimation, paves the way to an accurate prediction of electronic transitions in large species, the role of the remote environment, covalently bond to the UV probe or not, being equivalent to that of a simple electric field applied to the UV probe, and thus much easier to model.
6. Conclusions
This article presents a method aiming at accurately interpreting UV spectra based on the calculation of the electric field applied to the UV probe by its intermolecular or intramolecular environment. Illustrated on the UV spectra of isolated ion pairs compared to that of n-alkylbenzenes and benzylacetic acid, this original approach enabled us to reveal several EI-ESE, either shifts of electronic transitions between different systems or multiplet splittings between conformers within the same system. This work demonstrated several advantages of such an approach:– The identification of EI-ESE greatly facilitates conformational analysis. They appear especially fruitful when they are the main cause of shifts and splittings, i.e. within sets of systems where UV probes share the same vicinal environment (within 430 pm from the phenyl probes considered in this work). Indeed, EI-ESE, once identified, can be used to strengthen a tentative assignment, push the analysis further by assigning more conformers, or just improve the consistency of the conformational analysis.
– Electronic shifts of a few cm−1 can be reliably interpreted. The correlations found between the experimental electronic transitions and the square of the calculated electric field experienced by the phenyl probe are indeed good enough to make the approach so accurate. An electronic shift of Δσ ≈ 10 cm−1 typically corresponds to a variation of the electric field ΔE2 ≈ 1 GV2 m−2 for E in the 0–14 GV2 m−2 range, illustrating the sensitivity of the phenyl probe, as well as the modest accuracy needed on the calculation of E to reach a satisfactory correlation. This accuracy is far better than that reached by CC2 calculations to predict adiabatic electronic transitions, the relative errors being typically of the order of ∼100 cm−1 for the phenyl chromophore.45,46
– Remarkably, identifying EI-ESE in our work, together with taking Franck–Condon and fragmentation patterns into account, enabled a complete conformational analysis based on UV spectroscopy only. While conformer-selective IR spectroscopy is legitimately considered as a powerful source of structural information, the cost of these experiments and their related frequency calculations appear useless in this study, i.e. when systems sharing structural similarities around the UV probe are already known. In comparison, the analysis of EI-ESE brought decisive structural information at the relatively much lower cost of an electric field calculation in the ground state.
– Considering EI-ESE can also lead to challenge the rather advanced theoretical methods used to describe the structure of flexible molecular systems. The sensitivity of the phenyl probe to the electric field variation induced by the rotation of the carboxylate group enabled us to bring to light flaws of the theoretical potential energy surface. The corresponding dihedral angle appeared to be better predicted by electronic spectroscopy than by calculation, echoing the use of Stark effects to monitor larger structural changes in proteins.17
While the electric field variations induced by the conformational changes of the ionic groups made EI-ESE particularly obvious in ion pairs, any UV probe attached to, or simply surrounded by, ions or polar groups can efficiently help with the conformational analysis of a large set of systems. While this approach works well with phenyl, its application to other UV chromophores may not be as simple due to several issues: the presence of a significant permanent electric dipole on the chromophore (e.g. in phenol), or an electric field not aligned with one of the main axis of the chromophore can make eqn (1) more complex; the calculation of the electric field at a single point may not be enough for larger chromophores (e.g. indole), and/or when the elecric field is highly inhomogeneous introducing new terms in eqn (1).49 In this respect, further studies will benefit from the numerous medium-size systems of biological interest already investigated in the gas phase by UV spectroscopy47,48 in order to assess the potential of this approach to accurately determine the conformation of biomolecules. Judging by the present results, a systematic investigation of EI-ESE in electronic spectra already appears quite promising regarding both the fruitful information gained on the molecular structure and the moderate computational effort required.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. G. acknowledges ANR (grant ANR-16-CE29-0017), GENCI-TGCC (projects A0050807524 and p615), and Labex PALM (ANR-10-LABX-0039-PALM) for their support.References
- A. Mazzanti and D. Casarini, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 613 CAS.
- R. Roy, S. Hohng and T. Ha, Nat. Methods, 2008, 5, 507 CrossRef CAS.
- D. M. Rogers, S. B. Jasim, N. T. Dyer, F. Auvray, M. Refregiers and J. D. Hirst, Chem, 2019, 5, 2751 CAS.
- S. Daly, F. Poussigue, A. L. Simon, L. MacAleese, F. Bertorelle, F. Chirot, R. Antoine and P. Dugourd, Anal. Chem., 2014, 86, 8798 CrossRef CAS.
- A. Hong, H. Jang, C. Jeong, M. C. Choi, J. Heo and N. J. Kim, J. Phys. Chem. Lett., 2016, 7, 4385 CrossRef CAS.
- J. S. Brodbelt, L. J. Morrison and I. Santos, Chem. Rev., 2020, 120, 3328 CrossRef CAS.
- J. A. Dickinson, P. W. Joireman, R. W. Randall, E. G. Robertson and J. P. Simons, J. Phys. Chem. A, 1997, 101, 513 CrossRef CAS.
- Y. H. Lee, J. W. Jung, B. Kim, P. Butz, L. C. Snoek, R. T. Kroemer and J. P. Simons, J. Phys. Chem. A, 2004, 108, 69 CrossRef CAS.
- M. Becucci and S. Melandri, Chem. Rev., 2016, 116, 5014 CrossRef CAS.
- A. M. Rijs and J. Oomens, IR Spectroscopic Techniques to Study Isolated Biomolecules, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, 2015, vol. 364, p. 1 Search PubMed.
- T. R. Rizzo and O. V. Boyarkin, Cryogenic Methods for the Spectroscopy of Large, Biomolecular Ions, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, 2015, vol. 364, p. 43 Search PubMed.
- E. Gloaguen and M. Mons, Isolated Neutral Peptides, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, 2015, vol. 364, p. 225 Search PubMed.
- S. Bakels, M. P. Gaigeot and A. M. Rijs, Chem. Rev., 2020, 120, 3233 CrossRef CAS.
- E. Gloaguen, M. Mons, K. Schwing and M. Gerhards, Chem. Rev., 2020, 120, 12490 CrossRef CAS.
- S. Soorkia, C. Jouvet and G. Grégoire, Chem. Rev., 2020, 120, 3296 CrossRef CAS.
- T. S. Zwier, J. Phys. Chem. A, 2006, 110, 4133 CrossRef CAS.
- S. D. Fried and S. G. Boxer, Acc. Chem. Res., 2015, 48, 998 CrossRef CAS.
- M. Wilke, C. Brand, J. Wilke and M. Schmitt, J. Mol. Spectrosc., 2017, 337, 137 CrossRef CAS.
- M. Chattoraj, B. A. King, G. U. Bublitz and S. G. Boxer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8362 CrossRef CAS.
- L. L. Premvardhan, S. Wachsmann-Hogiu, L. A. Peteanu, D. J. Yaron, P. C. Wang, W. Wang and A. G. MacDiarmid, J. Chem. Phys., 2001, 115, 4359 CrossRef CAS.
- M. Drobizhev, S. Tillo, N. S. Makarov, T. E. Hughes and A. Rebane, J. Phys. Chem. B, 2009, 113, 12860 CrossRef CAS.
- I. Renge, Chem. Phys., 1992, 167, 173 CrossRef CAS.
- J. Donon, S. Habka, V. Vaquero-Vara, V. Brenner, M. Mons and E. Gloaguen, J. Phys. Chem. Lett., 2019, 10, 7458 CrossRef CAS.
- S. G. Boxer, J. Phys. Chem. B, 2009, 113, 2972 CrossRef CAS.
- D. M. Hewett, S. Bocklitz, D. P. Tabor, E. L. Sibert, M. A. Suhm and T. S. Zwier, Chem. Sci., 2017, 8, 5305 RSC.
- S. Habka, V. Brenner, M. Mons and E. Gloaguen, J. Phys. Chem. Lett., 2016, 7, 1192 CrossRef CAS.
- F. Piuzzi, I. Dimicoli, M. Mons, B. Tardivel and Q. Zhao, Chem. Phys. Lett., 2000, 320, 282 CrossRef CAS.
- E. Gloaguen, H. Valdes, F. Pagliarulo, R. Pollet, B. Tardivel, P. Hobza, F. Piuzzi and M. Mons, J. Phys. Chem. A, 2010, 114, 2973 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 19 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143 CrossRef CAS.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com Search PubMed.
- TURBOMOLE V7.2 2017, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com, accessed Oct 2019 Search PubMed.
- Y. Bouteiller, J. C. Poully, C. Desfrançois and G. Grégoire, J. Phys. Chem. A, 2009, 113, 6301 CrossRef CAS.
- H. S. Biswal, Y. Loquais, B. Tardivel, E. Gloaguen and M. Mons, J. Am. Chem. Soc., 2011, 133, 3931 CrossRef CAS.
- R. J. Plowright, E. Gloaguen and M. Mons, ChemPhysChem, 2011, 12, 1889 CrossRef CAS.
- S. Habka, T. Very, J. Donon, V. Vaquero-Vara, B. Tardivel, F. Charnay-Pouget, M. Mons, D. J. Aitken, V. Brenner and E. Gloaguen, Phys. Chem. Chem. Phys., 2019, 21, 12798 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS.
- H. E. Wagie, J. C. Woehl and P. Geissinger, Theor. Chem. Acc., 2016, 135, 114 Search PubMed.
- J. B. Hopkins, D. E. Powers and R. E. Smalley, J. Chem. Phys., 1980, 72, 5039 CrossRef CAS.
- D. A. Dougherty, Science, 1996, 271, 163 CrossRef CAS.
- M. Okruss, R. Muller and A. Hese, J. Chem. Phys., 1999, 110, 10393 CrossRef CAS.
- G. R. Alms, A. K. Burnham and W. H. Flygare, J. Chem. Phys., 1975, 63, 3321 CrossRef CAS.
- M. S. Dupuy, E. Gloaguen, B. Tardivel, M. Mons and V. Brenner, J. Chem. Theory Comput., 2020, 16, 601 CrossRef.
- M. Mališ, Y. Loquais, E. Gloaguen, H. S. Biswal, F. Piuzzi, B. Tardivel, V. Brenner, M. Broquier, C. Jouvet, M. Mons, N. Došlić and I. Ljubić, J. Am. Chem. Soc., 2012, 134, 20340 CrossRef.
- J.-P. Schermann, Spectroscopy and modeling of biomolecular building blocks, Elsevier, 2008 Search PubMed.
- O. V. Boyarkin, Int. Rev. Phys. Chem., 2018, 37, 559 Search PubMed.
- A. J. Stone, Molecules in Electrostatic Fields, in The Theory of Intermolecular Forces, Clarendron Press, Oxford, 1996, pp. 12–35 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc06074g |
| This journal is © The Royal Society of Chemistry 2021 |