Open Access Article
Open Access ArticleSingle molecule force spectroscopy reveals the context dependent folding pathway of the C-terminal fragment of Top7†
Jiayu
Li
,
Guojun
Chen
,
Yabin
Guo
,
Han
Wang
 and
Hongbin
Li
and
Hongbin
Li
 *
*
Department of Chemistry, University of British Columbia, Vancouver, BC V6T 1Z1, Canada. E-mail: hongbin@chem.ubc.ca
First published on 23rd December 2020
Abstract
Top7 is a de novo designed protein with atomic level accuracy and shows a folded structure not found in nature. Previous studies showed that the folding of Top7 is not cooperative and involves various folding intermediate states. In addition, various fragments of Top7 were found to fold on their own in isolation. These features displayed by Top7 are distinct from those of naturally occurring proteins of a similar size and suggest a rough folding energy landscape. However, it remains unknown if and how the intra-polypeptide chain interactions among the neighboring sequences of Top7 affect the folding of these Top7 fragments. Here we used single-molecule optical tweezers to investigate the folding–unfolding pathways of full length Top7 as well as its C-terminal fragment (CFr) in different sequence environments. Our results showed that the mechanical folding of Top7 involves an intermediate state that likely involves non-native interactions/structure. More importantly, we found that the folding of CFr is entirely dependent upon its sequence context in which it is located. When in isolation, CFr indeed folds into a cooperative structure showing near-equilibrium unfolding–folding transitions at ∼6.5 pN in OT experiments. However, CFr loses its autonomous cooperative folding ability and displays a folding pathway that is dependent on its interactions with its neighboring sequence/structure. This context-dependent folding dynamics and pathway of CFr are distinct from those of naturally occurring proteins and highlight the critical importance of intra-chain interactions in shaping the overall energy landscape and the folding pathway of Top7. These new insights may have important implications on the de novo design of proteins.
Introduction
Through natural evolution, proteins have evolved into the workhorses of cells to perform a diverse range of biological functions in today's complex lives.1–3 To carry out their particular tasks, proteins need to fold rapidly and reliably into their specific structures to avoid disease-causing misfolding and aggregations. How the natural evolution shapes the sequence and structure of proteins to ensure that proteins accomplish this feat remains largely elusive.4,5Over the last two decades, the fast progress of computational biology tools has made it possible to de novo design proteins with designed three-dimensional structures from scratch, including those not found in naturally occurring proteins, offering an alternative approach to natural evolution to design proteins.6–8 Such computational studies have started to reveal interesting findings that are not found in naturally occurring proteins, thus offering an invaluable perspective to gain insight into the unique impact of natural evolution on protein folding and functions.6–10
Top7 is the first de novo designed globular protein that has atomic level accuracy in its designed structure.11 Top7 contains 92 amino acid (aa) residues and adopts a unique α/β fold that is not observed in nature (Fig. 1A). Although the three-dimensional structure of Top7 achieved atomic-level accuracy with the computational design, its folding dynamics, as revealed by ensemble chemical denaturation studies and computational studies,12–17 exhibited features that are distinct from those of similar-sized natural globular proteins, likely due to the fact that the Top7 sequence and structure lack an evolutionary history. Most notably, the folding of Top7 is a non-cooperative process and involves intermediate states and non-native interactions, suggesting a very rugged folding energy landscape. Moreover, fragments of Top7 were found to be able to fold independently and/or associate to form dimers.12 Given the fact that similar-sized natural globular proteins undergo a cooperative folding transition, i.e. a two-state process with a single energy barrier between the folded and unfolded state, it is plausible that the smooth energy landscape and the highly cooperative folding transition of natural globular proteins have resulted from the natural selection.12,14
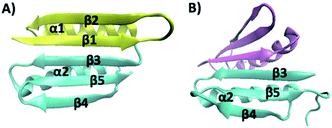 | ||
| Fig. 1 (A) Three-dimensional structure of Top7 (PDB code: 1QYS). Top7 is a de novo designed 92-residue protein composed of five β-strands and two α-helices. (B) Three-dimensional structure of the CFr (PDB code: 2GJH). The CFr forms an antiparallel homo-dimer, and each CFr folds into a structure that is similar to the CFr in Top7. The two CFrs are colored differently. | ||
Although ensemble studies have provided invaluable insights into the folding of Top7, inter-molecular interactions between different Top7 molecules inevitably complicate the understanding of kinetic processes of Top7, making it difficult to compare them with computational studies, including the de novo design and molecular dynamics (MD) simulations of folding pathways, which are carried out essentially on individual Top7 molecules. To offer a direct comparison with computational studies, it is desirable to investigate the folding–unfolding of Top7 one molecule at a time.
Moreover, although some fragments of Top7 can fold individually, it remains unknown if these fragments can serve as independent folding units in Top7, and if and how the neighboring sequences affect the folding of these fragments in Top7. To address these important questions, the C-terminal fragment of Top7 is an appealing model system. It was found that the isolated C-terminal fragment (CFr) was able to form a stable symmetric antiparallel homo-dimer that resembles the packing of the Top7 hydrophobic core, with each CFr folding into a structure similar to that in Top7 (Fig. 1B).12 And MD simulations of Top7 showed that the CFr can always form in the simulation trajectories as a stable intermediate.13,15 However, it remains unknown if the C-terminal fragment serves as an independent folding unit in the folding of full sequence Top7. Here, we used single-molecule optical tweezers to investigate the folding–unfolding pathway of Top7 and the C-terminal fragment one molecule at a time.
Over the past two decades, single-molecule force spectroscopy has evolved into a powerful tool to investigate the protein folding–unfolding mechanism at the single-molecule level.18–20 By mechanically stretching a protein from its two specific residues, the protein can be unfolded along a well-defined reaction coordinate defined by the stretching force. Atomic force microscopy (AFM), optical tweezers (OT) and magnetic tweezers experiments are among the most widely used single molecule force spectroscopy techniques. The mechanical unfolding of Top7 was investigated by using single-molecule AFM and steered molecular dynamics simulations.21 It was found that Top7 unfolded in an apparent two-state fashion by sliding β-strand 1 against strand 3.21 However, due to limited force resolution, the folding of Top7 was not directly observed in AFM experiments. Recently, Top7 was used as a handle in studying the release of ribosome-nascent protein chains. It was found that Top7 could refold upon relaxation.22 However, no detailed analysis or mechanistic study of the folding of Top7 was carried out. Here, by combining single molecule OT with protein engineering techniques, we investigated the mechanical unfolding and folding of Top7 and the C-terminal fragment in different sequence environments of Top7. Our study revealed that the unfolding and refolding of Top7 involve an intermediate state, which is likely mediated by non-native interactions. We found that the folding pathway of the CFr is strongly dependent upon the sequence context, and intramolecular interactions within the Top7 polypeptide chain play a critical role in modulating the overall folding/unfolding mechanisms of Top7. Our study highlights the importance and complexity of the rugged energy landscape for the folding of the C-terminal fragment as well as the full-length Top7.
Materials and methods
Protein engineering
The gene of Top7 was a kind gift from Prof. David Baker. Polymerase chain reaction (PCR) was carried out to endow Top7 with a 5′ BamHI restriction site and 3′ BglII and KpnI sites. The gene of the CFr of Top7 was constructed via standard PCR, and the gene of Top7(G42C) was constructed via standard site-directed mutagenesis methods using the Top7 gene as a template. NuG2-Top7(G42C), Top7(G42C)-NuG2 and GB1-CFr-GB1 were constructed following a stepwise digestion and ligation scheme based on identity of the sticky ends generated from the BamHI and BglII restriction sites. The genes of Top7, GB1-CFr-GB1, NuG2-Top7(G42C) and Top7(G42C)-NuG2 were then subcloned into modified pQE80L (Qiagen, Valencia, CA) expression vectors, which allow for adding either an N-terminal cysteine or a C-terminal cysteine, or both, onto the protein. All the sequences were confirmed by direct DNA sequencing.The recombinant proteins were overexpressed in the Escherichia coli strain DH5α. After inoculation with 3 mL of preculture, the cells were grown in 200 mL of 2.5% Luria–Bertani media containing 100 μg mL−1 ampicillin at 37 °C and 225 rpm. When the OD600 of the culture reached ∼0.7, protein overexpression was induced with 0.5 mM isopropyl-β-D-1-thiogalactopyranoside (Thermo Fisher Scientific, Waltham, MA) and the protein expression continued for 4 h. Then, the cells were pelleted by centrifugation at 4000g for 10 min at 4 °C and resuspended in 10 mL of phosphate-buffered saline (PBS) buffer (10 mM, pH 7.4). After adding 10 μL of protease inhibitor cocktail (Sigma-Aldrich, St. Louis, MO), 100 μL of 50 mg mL−1 lysozyme from egg white (Sigma-Aldrich, St. Louis, MO), 1 mL of 10% (w/v) Triton X-100 (VWR, Tualatin, OR), and 50 μL of 1 mg mL−1 DNase I (Sigma-Aldrich, St. Louis, MO) and RNase A (Bio Basic Canada Inc, Markham, ON), the cells were lysed for 40 min on ice. Cell debris was then removed by centrifugation at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g at 4 °C, and the supernatant was loaded into a Co2+ affinity chromatography column (Takara Bio USA Inc, Mountain View, CA). After washing the column with 50 mL of washing buffer (10 mM PBS, 300 mM NaCl, 7 mM imidazole, pH 7.4), the protein was eluted with 2 mL of elution buffer (10 mM PBS, 300 mM NaCl, 250 mM imidazole, pH 7.4).
000g at 4 °C, and the supernatant was loaded into a Co2+ affinity chromatography column (Takara Bio USA Inc, Mountain View, CA). After washing the column with 50 mL of washing buffer (10 mM PBS, 300 mM NaCl, 7 mM imidazole, pH 7.4), the protein was eluted with 2 mL of elution buffer (10 mM PBS, 300 mM NaCl, 250 mM imidazole, pH 7.4).
Preparation of the DNA–protein chimera
Double-strand DNA (dsDNA) handles were prepared via the methods described previously.23 Briefly, two dsDNA handles of 802 and 558 bp were generated via regular PCR amplification. dsDNA handles were allowed to react with 4-(N-maleimidomethyl)cyclohexanecarboxylic acid N-hydroxysuccinimide ester (SMCC, Sigma-Aldrich, St. Louis, MO) overnight to introduce the maleimide group into the end of the dsDNA handles. Then, the freshly expressed proteins, which were reduced with 1 mM tris(2-carboxyethyl) phosphine (TCEP) (Sigma-Aldrich, St. Louis, MO) for 1 hour, were diluted to ∼3 μM by using Tris buffer (20 mM Tris, 150 mM NaCl, pH 7.4). 1 μL of the diluted protein was added to 1 μL of mixed dsDNA handles (both are at 3 μM). The thiol–maleimide reaction was carried out at room temperature overnight. The formed dsDNA–protein chimera was diluted with Tris buffer (20 mM Tris, 150 mM NaCl, pH 7.4) to ∼10 nM and made ready for the optical tweezers experiment.OT experiments
The OT experiments were carried out using a Minitweezers setup, which was described previously.23,24 The liquid chamber of the optical tweezers was filled with Tris buffer (20 mM Tris, 150 mM NaCl, pH 7.4) to provide the working environment. In a typical experiment, 1 μL of 0.5% streptavidin modified polystyrene beads (1% w/v, 1 μm, Spherotech Inc, Lake Forest, IL) was diluted to 3 mL and injected into the fluid chamber. A single streptavidin modified polystyrene bead was captured using a laser beam and then held using a micro pipette tip within the chamber. 1 μL of 5 nM DNA–protein chimera was allowed to react with 5 μL of 0.1% antidigoxigenin modified polystyrene beads (0.5% w/v, 2 μm, Spherotech Inc, Lake Forest, IL) for 30 min at room temperature. The mixture was then diluted to 3 mL and injected into the chamber. A single anti-digoxigenin (anti-Dig) modified polystyrene bead was captured by the laser trap. The laser trap controlled the movement of the anti-dig bead against the streptavidin modified polystyrene bead fixed on the pipette tip to carry out the force-extension experiments.Calculating the kinetics of unfolding/folding of proteins
We used the method proposed by Oesterhelt et al. and dwell-time distribution analysis to extract the folding and unfolding rate constants at different forces from the force–distance curves.25 The curves were divided into time windows (Δt) that are small enough so that the force can be considered constant within the time window. The probability of protein folding/unfolding within Δt can be calculated as P(F) = N(F)/M(F), where N(F) is the total number of all the folding or unfolding events at a force of F, and M(F) is the total number of time windows at a force of F. The rate constant of protein folding/unfolding at a force of F can be calculated as k(F) = P(F)/Δt.Results
The unfolding of Top7 involves overcoming two energy barriers
To investigate the unfolding–folding behavior of full length Top7 (termed Top71–92), we constructed a protein–DNA chimera, dsDNA-Top71–92-dsDNA, in which Top7 is flanked by two dsDNA handles at its both termini. Stretching this protein–DNA chimera allowed us to stretch Top7 from its N- and C-termini directly. Fig. 2A shows the representative force–distance curves of the protein–DNA chimera at a pulling speed of 5 nm s−1. Stretching Top71–92 resulted in a clear unfolding event of Top7 in the force–distance curve. The mechanical unfolding of Top71–92 occurred in a broad range of forces (from 10 to 40 pN) with an average of 26 pN at a pulling speed of 5 nm s−1 (Fig. 2C). Fitting the force–extension relationships of Top7 using the worm-like chain model (WLC) of polymer elasticity26 yielded a contour length increment (ΔLc) of ∼29.8 nm upon unfolding (Fig. 2C inset), which was close to that expected from the complete unfolding of Top7 (92 aa × 0.36 nm/aa − 3.0 nm = 30.1 nm, where 0.36 nm/aa is the length of an aa residue and 3.0 nm is the distance between the N- and C-termini of Top7). This result indicated that the unfolding of Top7 occurred via an apparent two-state pathway, a result that is similar to the AFM results.21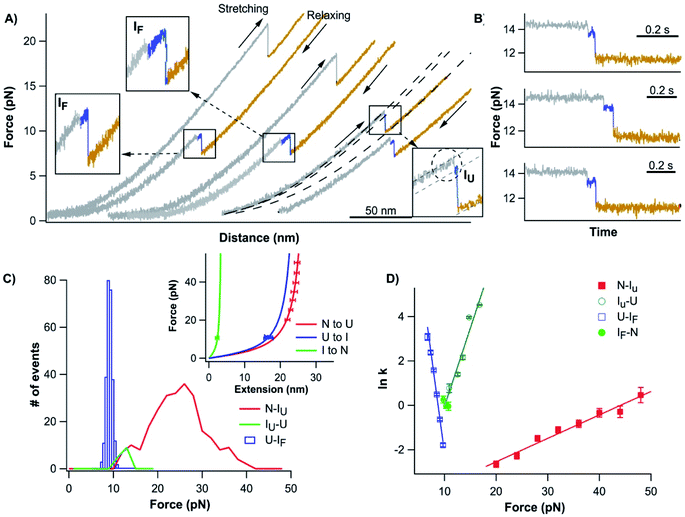 | ||
| Fig. 2 Folding–unfolding signatures of Top7. (A) Representative force–distance curves of Top7 at a pulling speed of 5 nm s−1. An unfolding intermediate (circled in the inset) can be observed when Top7 unfolds at relatively low forces (<15 pN), while a folding intermediate can almost always be observed. For clarity, the first two pairs of curves are offset horizontally relative to each other. (B) The unfolding of Top7 shows a short-lived intermediate state when the unfolding occurred at lower force (<15 pN). Force–time curves clearly show the intermediate state (colored in blue). In (A) and (B), the curve of the folded state of Top7 is colored in grey, the intermediate in blue and the unfolded state in brown. (C) Force histograms of the folding–unfolding of Top7 at a pulling speed of 5 nm s−1. The inset shows the force–extension curves of the unfolded polypeptide chains released/contracted from given unfolding/folding events (symbols) and the WLC fits to these curves. WLC fits (solid lines) to the experimental data revealed a persistence length of 0.8 nm and a ΔLc of 29.8 ± 0.1 nm (red curve) between native and unfolded states, a ΔLc of 26.7 ± 0.4 nm (blue curve) between the intermediate and the unfolded state, and a ΔLc of 3.9 ± 0.1 nm (green curve) between the native state and the intermediate state. (D) Force-dependent folding–unfolding rates measured for Top7. The solid lines are fits of the Bell–Evans model to the experimental data. The resultant unfolding/folding rate constant and distance to the transition state are tabulated in Table 1. | ||
The unfolding force of Top7 is sensitive to the pulling speed (Fig. S1†). Using the method proposed by Oesterhelt25 we directly measured the unfolding rate constants α(F) of Top7 as a function of stretching force. Fitting the α(F)–F relationship to the Bell–Evans model yielded a spontaneous unfolding rate constant at zero force (α0) of 0.009 s−1 and the unfolding distance between the native state and transition state (Δxu) is 0.43 nm (Fig. 2D). These parameters are close to those estimated using the well-established Monte Carlo simulation protocols (Fig. S1†). These results suggested that the native state of Top7 is brittle and has a short distance to the transition state.
It is interesting to note that although most Top7 unfolded in an apparent two-state fashion (93%), ∼7% of the unfolding events involved a short-lived unfolding intermediate state (Fig. 2A, circled, and Fig. S2†). The unfolding intermediate IU has a ΔLc of ∼4 nm (Fig. 2C inset). It is also of note that the IU was observed only when Top7 unfolded at relatively low forces (<15 pN, Fig. 2C). This observation raised the question if the unfolding of Top7 involves two unfolding barriers, and the unfolding intermediate IU was also involved in the apparent two-state pathway but was too short-lived to be observed in our OT experiments due to the limited temporal resolution. To address this issue, we stretched Top7 to a force of ∼15 pN and held it there for an extended period of time to unfold Top7 (aka. constant distance experiment). It is interesting that under this experimental protocol, ∼95% (121/128) of the unfolding events of Top7 did show a short-lived intermediate state IU (Fig. 2B). This result strongly indicated that the unfolding of Top7 involved a high energy intermediate state and thus follows a three-state unfolding pathway. When Top7 unfolded at high forces, the energy landscape is tilted by the stretching force to the point that the intermediate IU is too short-lived to be observed (Fig. S3†). This result revealed the roughness of the unfolding energy landscape of Top7. The unfolding kinetics of IU–U was obtained by analysing the lifetime of the IU at low forces (<15 pN) from both constant speed and constant distance experiments. IU events that occurred at higher forces were not included in the analysis due to the missing of IU events that are too short-lived to be detected at higher forces.
The folding of Top7 involves an obligatory folding intermediate
After the mechanical unfolding of Top7, the unfolded Top7 was relaxed to allow Top7 to refold. We observed that all Top7 molecules were able to refold back to their native state at ∼10 pN. The folding occurred in a narrow range of forces at the given pulling speed (Fig. 2C), which is in sharp contrast with the broad distribution of the unfolding forces (ESI†). The refolding force is also less sensitive to the pulling speed (Fig. S1†). It is of note that the folding occurred in a narrow range of forces in a number of other proteins also, and may be a generic phenomenon for protein folding against a stretching force27–33 (ESI†). Moreover, in the subsequent consecutive stretching–relaxation cycles, Top7 can undergo unfolding and refolding for tens of cycles without any folding fatigue, suggesting that the folding of Top7 is robust and of high fidelity.The folding of Top7 almost always occurred in a three-state manner (∼94%, 1170/1246), involving a folding intermediate state IF. In the first step, Top7 refolded into an intermediate state showing a contour length increment of ΔLc of 27 nm, which corresponds to the folding of ∼89% of the full sequence of Top7. In the second step, the folding intermediate state IF folded into the complete native structure (showing a ΔLc of 3.9 nm). As the IF has a similar Lc to the IU (∼7 nm, Fig. S2†), it is likely that they have the same structure. However, further experiments are needed to confirm this point. The folding intermediate IF is relatively short-lived, resulting in the observation that the folding intermediate state was best resolved in slow pulling experiments. At high pulling speed experiments, the folding intermediate state tended to smear out. These results clearly indicate that the folding of Top7 is not a simple cooperative process, instead, it involves an intermediate state. In rare occasions during relaxation, the folding intermediate state If was observed to return back to the unfolded state (Fig. S4†).
Using the Oesterhelt method, we measured the folding rate constant as a function of force (Fig. 2D). Fitting the experimental data with the Bell–Evans model yielded a spontaneous folding rate constant (βU–IF) of 1.7 × 106 s−1 and a folding distance of 6.8 nm between the unfolded and IF states. It is worth noting that we used the Bell–Evans model to extract the folding rate constant largely due to its simplicity. Recent studies suggested that the energetics associated with the collapse of the unfolded polypeptide chain also plays an important role in determining the observed folding kinetics.29,34 Folding rate constants extracted using such models will likely differ from those extracted using the Bell–Evans model, and the latter may have a large uncertainty.
The intermediate states may involve non-native interactions
The intermediate states found in naturally occurring small globular proteins are often structural motifs of the protein and can be identified and pin-pointed by single-molecule force spectroscopy techniques.35,36 In order to identify the structural origin of the intermediate states, we attempted to examine which part of the Top7 structure could give rise to a ΔLc of 3.9 nm.Top7 has a symmetrical structure consisting of a 5-stranded β-sheet and two α-helices (Fig. 1A). The two terminal β-strands, β-1 and β-5, connect the other three β-strands together, thus keeping the β-sheet intact. Moreover, there are more contacts within the C-terminal half of Top7 (CTh, β-3-α-2-β-4-β-5, colored in yellow in Fig. 1), making it significantly more compact than the N-terminal half (NTh, β-1-β-2-α-1, colored in cyan in Fig. 1). MD simulations and ensemble experiments showed that the C-terminal half is stable on its own and can form a stable homo-dimer.
Considering that the end-to-end distance of Top7 increases during the pulling experiment and the secondary structure connectivity and extensibility, the structural unraveling events that could happen to lengthen Top7 are listed in Table 2. Evidently, none of the unraveling events of β-hairpins would give rise to a ΔLc as small as ∼4 nm. However, it is of note that the unraveling of α-helix 1or 2 could lead to a ΔLc of ∼4 nm. It is of note that a previous MD simulation study on the folding of Top7 predicted that the last folding step involved the formation of α-helix 1 and the packing of the N-terminal half onto the C-terminal half.15 This simulation study would lend support to the possibility that the intermediate state arises from the unraveling of the α-helix 1.
| k 0 (s−1) | Δx (nm) | ||
|---|---|---|---|
| a The data are presented as average ± standard deviation. N. D.: not determined. Rate constants k and distance to the transition state were determined by fitting the force-dependent rate constant to the Bell–Evans model. | |||
| Top7 | N → IU | 0.009 ± 0.002 | 0.43 ± 0.03 |
| IU → U | (8.4 ± 13) × 10−4 | 2.89 ± 0.44 | |
| U → IF | (1.7 ± 1.1) × 106 | 6.76 ± 0.33 | |
| IF → N | N.D. | N.D. | |
| CFr | N → U | 0.029 ± 0.028 | 3.71 ± 0.58 |
| U → N | (1.1 ± 1.3) × 106 | 7.09 ± 0.76 | |
| CTh | N → I | (3.1 ± 2.5) × 10−5 | 2.16 ± 0.09 |
| I → U | 0.12 ± 0.24 | 1.19 ± 0.38 | |
| U → I | (5.6 ± 6.1) × 105 | 4.08 ± 0.36 | |
| I → N | 20.3 ± 2.7 | 2.63 ± 0.10 | |
| Unravelled structural element | ΔLc (nm) |
|---|---|
| β1 & β2 | 11.7 |
| β4 & β5 | 9.5 |
| α1 | 4.0 |
| α2 | 4.2 |
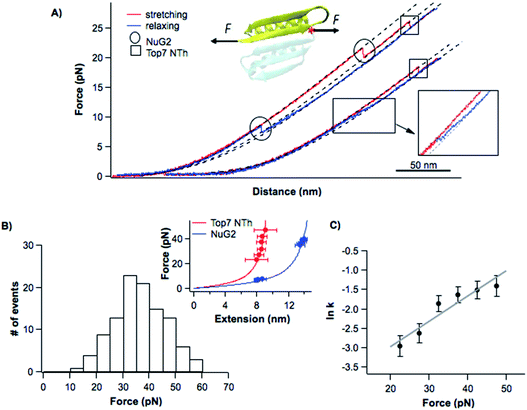
To test this possibility, we stretched the N-terminal half (NTh) of Top7 using OT. For this, we stretched Top7 between its N-terminus and residue 42, which is located in the loop linking α-helix 1 to the C-terminal half. We constructed Cys-NuG2-Top7-G42C (termed Top71–42), in which the well-characterized NuG2 domain serves as a fingerprint domain for identifying single-molecule stretching events.31 Stretching Top71–42 resulted in force–distance curves with two clear unfolding events (Fig. 3A).
The unfolding and folding events indicated using the circles are due to the fingerprint domain NuG2, as they showed the characteristic signatures of the unfolding/folding of NuG2 (with a ΔLc of ∼17 nm, and unfolding force at ∼20–40 pN and folding force at ∼8 pN).31 The unfolding event indicated with the square can thus be attributed to the NTh. The unfolding of the NTh displayed a ΔLc of ∼11 nm, which is very close to the ΔLc expected from the unraveling of the NTh (42 aa × 0.36 nm/aa − 3 nm = 12.3 nm, where 3 nm is the distance between the N- and Cys42) (Fig. 3B inset), suggesting that the unfolding corresponds to the complete unfolding of the NTh. The unfolding of the NTh occurred in a clear two-state fashion without any accumulated intermediate state. Furthermore, the folding of the NTh did not show any clear two-state-like folding event, instead, a continuous “hump-like” feature was observed at ∼10 pN, during which the force–distance curve gradually deviated from that expected from a polypeptide chain (Fig. 3A inset). While this hump-like folding behavior has been observed for some other proteins before, its nature remains unknown, probably relevant to the formation of frustrated local structures by short-range interactions.33,36 The fact that no unfolding/folding event with a ΔLc of 4.2 nm was observed suggested that the intermediate state observed in Top71–92 is unlikely to originate from the (un)folding of the α-helix 1. This result also suggested that the intermediate states may involve non-native interactions/motifs that are different from those in the folded Top7 structure.
C-terminal fragment of Top7 can fold on its own
Having examined the folding–unfolding pathways of the full sequence Top7, we now examine the folding behavior of the C-terminal fragment of Top7, CFr, in isolation using OT. To do so, we built a chimera, cys-GB1-CFr-GB1-cys, in which the well-characterized GB1 served as a fingerprint for identifying single-molecule stretching events.37 When a GB1-CFr-GB1 molecule was captured and stretched from its N- and C-termini by the OT (even if the CFr forms a dimer with another GB1-CFr-GB1), only a single GB1-CFr-GB1 was held in the OT as soon as the CFr was mechanically unfolded, as the unfolding of the CFr would lead to the dissociation of the CFr dimer and the dissociated CFr would diffuse away. This way, the effect of dimerization can be readily eliminated in our OT experiments. Stretching cys-GB1-CFr-GB1-cys resulted in representative force–distance curves shown in Fig. 4A, which were characterized by rapid unfolding–folding fluctuations at ∼6 pN followed by one or two unfolding events at higher forces (often higher than ∼35 pN). The unfolding events colored in green correspond to the unfolding of the fingerprint GB1 domain, which is known to be mechanically stable.37 Then, the rapid unfolding–folding fluctuations at ∼6 pN (colored in red) can be readily assigned to the CFr. Since GB1 unfolded at higher forces (often higher than 35 pN), we limited the stretching force to less than 20 pN so that only the CFr was unfolded in the force–distance curve. In such curves, the rapid unfolding–folding transitions of the CFr can be clearly observed (Fig. 4B), suggesting that the CFr folded on its own and can undergo near-equilibrium unfolding–folding transitions. The near-equilibrium unfolding–folding of the CFr was also evidenced by its unfolding and refolding force distributions, which gave an average unfolding force of 7.2 pN and a folding force of 6.0 pN at a pulling speed of 50 nm s−1, respectively (Fig. 4C). The ΔLc is ∼18 nm, close to the ΔLc expected from the complete unfolding of the CFr (50 aa × 0.36 nm/aa − 0.8 nm = 17.2 nm, where 0.8 nm is the distance between the N- and C-termini of the CFr). Using the Oesterhelt method, we determined the force-dependency of the unfolding and folding rate constants (Fig. 4D). Fitting the data to the Bell–Evans model yielded a spontaneous unfolding rate constant of 0.03 s−1 and a folding rate constant of 1.1 × 106 s−1, and a Δxu of 3.7 nm and Δxf of 7.1 nm, respectively.The rapid unfolding–folding transition was best displayed in constant force experiments (Fig. S5A†). When holding the CFr at 6.5 pN, rapid transition between the folded and unfolded states was clearly observed, with ∼50% occupancy of the folded and unfolded states, indicating that the unfolding and folding reached equilibrium at ∼6.5 pN. By changing the stretching force, the occupancy of the folded/unfolded states changed accordingly. Analyzing the dwell time of the folded states and unfolded states, we directly measured the unfolding and folding kinetics (Fig. S5B†). Fitting the mechanical Chevron plots to the Bell–Evans model yielded the kinetics parameters for the unfolding and folding reactions which are similar to those measured using the Oesterhelt method (Fig. 4D).
In rare occasions, we also observed complex force–distance curves of cys-GB1-CFr-GB1-cys, which contained up to four GB1 unfolding events. Such curves were likely due to the stretching of a dimer of GB1-CFr-GB1, which were crosslinked by a disulfide bond (Fig. S6†).
Comparing the folding behavior of the CFr with that of wt Top7, it is clear that although the CFr can fold in isolation, the CFr does not function as an independent folding unit, as the folding intermediate state (with a ΔLc of 27 nm) in wt Top7 involves a stretch of at least 72 aa, which is significantly longer than the CFr alone. Moreover, this result implied that the folding behavior of the CFr is significantly affected by the neighboring sequence of Top7 in the unfolded state.
Folded N-terminal half can modulate the folding of the C-terminal half
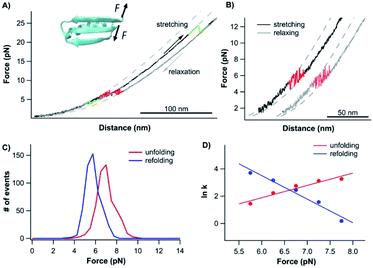
To further examine the role of neighboring sequences in the folding of the CFr, we also investigated the unfolding–folding behavior of the CFr in Top7 by stretching the Top7 from its residues 42 and 92 (Top742–92). The C-terminal half of Top7 is termed CTh, to distinguish it from the CFr in isolation. For this, we constructed Top7(G42C)-NuG2-cys.Fig. 5A shows the typical force–distance curves of the CTh. The unfolding of the CTh occurred between ∼15 and 25 pN in a two-state and three-state fashion with a total ΔLc of ∼17.5 nm, which is close to the theoretical value of ∼17.2 nm (50 aa × 0.36 nm/aa − 0.8 nm, where 0.8 nm is the distance between the N- and C-termini of the CTh) (Fig. 5Binset). Similar to wt Top7, the unfolding intermediate of the CTh only occurred when the unfolding occurred at relatively low forces, implying that the apparent two-state unfolding is essentially a three-state unfolding and the unfolding intermediate state was not resolved (Fig. 4B). It is worth pointing out that the unfolding force of the CTh is much higher than that of the CFr, suggesting that the CTh is mechanically stabilized by the folded NTh. Moreover, the folding of the CTh always proceeded in two steps involving a folding intermediate state. The U–I occurred at ∼12 pN with a ΔLc2 of 11 nm, while the I–N transition occurred at ∼5 pN with a ΔLc1 of ∼7 nm, respectively (Fig. 5A and B). The unfolding and folding pathways appeared to be reversible, suggesting that the unfolding and refolding go through the same transition state.
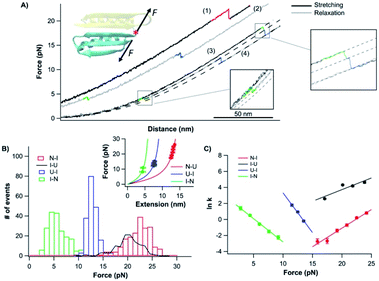 | ||
| Fig. 5 Folding–unfolding behavior of the CTh. (A) Force–distance curves of the CTh at a pulling speed of 20 nm s−1. The unfolding of the CTh occurred following an apparent two-state (curve 1) and three-state pathway (curve 3). The folding of the CTh always followed a three-state pathway involving an intermediate state. For clarity, curves 1 and 2 are horizontally offset relative to each other. Dashed lines are pseudo-WLC fits to the data. The inset shows the schematics of stretching the CTh along residue 42 and the C-terminus of Top7. (B) Force histograms for unfolding and folding of the CTh at a pulling speed of 20 nm s−1. The inset shows the WLC analysis of the ΔLcs of the unfolding/refolding events of the CTh. WLC fits (solid lines) to the experimental data revealed a ΔLc of 17.5 ± 0.1 nm (red curve) between the native and the unfolded states, a ΔLc1 of 7.4 ± 0.3 nm (green curve) between the native and the intermediate state, and a ΔLc2 of 11.4 ± 0.1 nm (blue curve) between the intermediate and the unfolded state. (C) Force-dependent folding–unfolding rates for the CTh. Solid lines are fits of the Bell–Evans model to the data. Fitting parameters are tabulated in Table 1. | ||
It is of note that the ΔLc1 of the unfolding event coincided with that expected from the unfolding of the β-hairpin (β strands 4 and 5), which gives rise to a ΔLc of 6.2 nm (18 aa × 0.36 nm/aa − 0.8 nm), and the subsequent unfolding of β-strand 3 and α-helix 2. This result suggested that during refolding, the β-strand 3 and α-helix 2 folded first against a high stretching force, followed by the folding and packing of the β-hairpin (β strands 4 and 5).
In the steered molecular dynamics simulation trajectories of the mechanical unfolding of the CTh, the NTh was observed to retain its secondary structure for an extended period of time (0.6 ns) after the CTh unraveled (Fig. S7†). Although this observation remains to be validated experimentally, our results for the folding of the CTh suggested that the NTh may serve as a folding nucleus to greatly facilitate the folding of the β-strand 3 and α-helix 2, upon which the β hairpin (β strands 4 and 5) can then fold and pack. Compared with the cooperative folding behavior of the CFr, the interactions with the neighboring N-terminal domain significantly stabilized the β-strand 3 and α-helix 2, and made the C-terminal domain not a cooperative folding/unfolding unit.
Discussion
The folding pathway of the CFr is context dependent: multifaceted folding behavior
As a de novo designed protein, Top7 displays some distinct properties from naturally occurring proteins of a similar size, with one being that multiple fragments of Top7 are able to fold into stable substructures and form homodimers, while fragments of naturally occurring small globular proteins are seldom stable in isolation.12 The CFr is one such fragment. The CFr is even an obligate dimer under most experimental conditions with an extremely low dissociation constant (2 × 10−19 M).38 This strong dimerization effect may bring potential interferences to traditional ensemble folding–unfolding experiments, in which domain dissociation and folding–unfolding signals intertwine and become indistinguishable.Using single molecule OT, here we investigated the folding behavior of the C-terminal fragment of Top7 in three different sequence environments one molecule at a time. By eliminating the influence of intermolecular interactions, our results provide unambiguous insights that are intrinsic to the CFr alone. Our results showed that the CFr is a folding chameleon, and its folding behavior is strongly dependent on the sequence context in which the CFr is located. In isolation, the CFr is an autonomous two-state folder, which can undergo rapid folding and unfolding transitions. The folding and unfolding reached equilibrium at ∼6.5 pN. However, when the CFr is placed next to other sequences (both folded and unfolded), the folding behavior of the CFr (which is the CTh in the full sequence Top7) changed considerably and the CFr is no longer a cooperative two-state folder. These results suggested that the neighboring sequences had a pronounced effect on modeling the energy landscape of the CFr.
In the presence of a possibly folded N-terminal half (NTh), the CFr changes itself from a two-state folder to a three-state folder. Clearly, the interactions with the NTh significantly stabilized the portion (β-strand 3 and α-helix 2) of the CTh next to the NTh and effectively broke the folding cooperativity of the CFr, making β-strand 3 and α-helix 2 fold first and unfold last in the folding and unfolding pathways of the CFr. Moreover, the interactions with the NTh also have a significant impact on the deformability of the folded state of the CFr. In isolation, the native state of the CFr is highly malleable (with a Δxu of ∼4 nm). The interactions with the NTh significantly rigidified the folded state of the CFr in Top7, as evidenced by its small Δxu (∼2 nm).
Moreover, when the CFr is in the full sequence of Top7, the CFr no longer behaves as an autonomous folder. The folding/unfolding intermediate state of Top7 comprises at least 85% of the total sequence of Top7, and most likely includes the CFr. Although the CFr contains more contacts than the NTh in the folded state, it remains unclear how the unfolded N-terminal half affects the behavior of the CFr. The fact that the unfolding/folding intermediate state likely contains non-native interactions makes it more difficult to elucidate the detailed folding mechanism of wt Top7.
These results suggest that the folding of the CFr is strongly context-dependent, thus making the CFr multifaceted in terms of its folding pathway. To some extent, such a multifaceted feature is similar to the chameleon behavior of proteins, via which the same protein (or a short peptide sequence) can assume different conformations. Such chameleon behavior has been reported in numerous proteins,39–42 such as those related to GB1.39,40 Previously, molecular dynamics simulations suggested that the α-helix segment of the CFr has chameleonicity, which helps the CFr to fold via a caching mechanism.16,43 Our results now extend the chameleon behavior of the CFr to the dynamic folding behavior of the whole CFr. This context-dependent folding pathway is unique to Top7, and highlights the complexity of the folding pathways of Top7 and the importance of intramolecular interactions in the folding of Top7.
However, the detailed mechanism via which intramolecular interactions within the sequence of Top7 modulate the overall folding energy landscape remains to be elucidated. Although the folding of Top7 is not cooperative, the interactions between different parts of Top7 are an important feature governing the structure and folding dynamics of Top7. Elucidating the interactions that cause the CFr to lose its ability to fold independently in the full sequence Top7 will help find ways to further smooth the energy landscape and improve the overall folding cooperativity of Top7.
Conclusions
Using optical tweezers, here we investigated the folding of the de novo designed Top7 as well as its C-terminal fragment. Our results demonstrated that the folding pathway of the C-terminal fragment is context-dependent, a feature distinct from that of naturally occurring proteins. Depending on its neighboring sequences of Top7, the folding of the C-terminal fragment shows a drastically different folding pathway and kinetics. Our results highlight the critical importance of the intra-polypeptide chain interactions in shaping the energy landscape of the C-terminal fragment of Top7.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada. J. L. and H. W. acknowledge the fellowship support from the NSERC NanoMat CREATE program.Notes and references
- J. M. Thornton, C. A. Orengo, A. E. Todd and F. M. Pearl, J. Mol. Biol., 1999, 293, 333 CrossRef CAS.
- C. Pál, B. Papp and M. J. Lercher, Nat. Rev. Genet., 2006, 7, 337 CrossRef.
- P. B. Chi and D. A. Liberles, Protein Sci., 2016, 25, 1168 CrossRef CAS.
- A. I. Jewett, V. S. Pande and K. W. Plaxco, J. Mol. Biol., 2003, 326, 247 CrossRef CAS.
- C. Debes, M. Wang, G. Caetano-Anolles and F. Grater, PLoS Comput. Biol., 2013, 9, e1002861 CrossRef CAS.
- E. G. Baker, G. J. Bartlett, K. L. Porter Goff and D. N. Woolfson, Acc. Chem. Res., 2017, 50, 2085 CrossRef CAS.
- R. Das and D. Baker, Annu. Rev. Biochem., 2008, 77, 363 CrossRef CAS.
- N. Koga, R. Tatsumi-Koga, G. Liu, R. Xiao, T. B. Acton, G. T. Montelione and D. Baker, Nature, 2012, 491, 222 CrossRef CAS.
- J. H. Han, S. Batey, A. A. Nickson, S. A. Teichmann and J. Clarke, Nat. Rev. Mol. Cell Biol., 2007, 8, 319 CrossRef CAS.
- B. Kuhlman and D. Baker, Curr. Opin. Struct. Biol., 2004, 14, 89 CrossRef CAS.
- B. Kuhlman, G. Dantas, G. C. Ireton, G. Varani, B. L. Stoddard and D. Baker, Science, 2003, 302, 1364 CrossRef CAS.
- A. L. Watters, P. Deka, C. Corrent, D. Callender, G. Varani, T. Sosnick and D. Baker, Cell, 2007, 128, 613 CrossRef CAS.
- Z. Zhang and H. S. Chan, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2920 CrossRef CAS.
- M. Scalley-Kim and D. Baker, J. Mol. Biol., 2004, 338, 573 CrossRef CAS.
- Z. Zhang and H. S. Chan, Biophys. J., 2009, 96, L25 CrossRef CAS.
- S. Mohanty, J. H. Meinke and O. Zimmermann, Proteins, 2013, 81, 1446 CrossRef CAS.
- S. Neelamraju, S. Gosavi and D. J. Wales, J. Phys. Chem. B, 2018, 122, 12282 CrossRef CAS.
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491 CrossRef CAS.
- W. Ott, M. A. Jobst, C. Schoeler, H. E. Gaub and M. A. Nash, J. Struct. Biol., 2017, 197, 3 CrossRef CAS.
- Y. Javadi, J. M. Fernandez and R. Perez-Jimenez, Physiology, 2013, 28, 9 CrossRef CAS.
- D. Sharma, O. Perisic, Q. Peng, Y. Cao, C. Lam, H. Lu and H. Li, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9278 CrossRef CAS.
- D. H. Goldman, C. M. Kaiser, A. Milin, M. Righini, I. Tinoco Jr and C. Bustamante, Science, 2015, 348, 457 CrossRef CAS.
- X. Zhang, K. Halvorsen, C. Z. Zhang, W. P. Wong and T. A. Springer, Science, 2009, 324, 1330 CrossRef CAS.
- http://www.tweezerslab.unipr.it/ .
- L. Oberbarnscheidt, R. Janissen and F. Oesterhelt, Biophys. J., 2009, 97, L19 CrossRef CAS.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759 CrossRef CAS.
- H. Chen, G. Yuan, R. S. Winardhi, M. Yao, I. Popa, J. M. Fernandez and J. Yan, J. Am. Chem. Soc., 2015, 137, 3540 CrossRef CAS.
- J. Fang, A. Mehlich, N. Koga, J. Huang, R. Koga, X. Gao, C. Hu, C. Jin, M. Rief, J. Kast, D. Baker and H. Li, Nat. Commun., 2013, 4, 2974 CrossRef.
- S. Guo, Q. Tang, M. Yao, H. You, S. Le, H. Chen and J. Yan, Chem. Sci., 2018, 9, 5871 RSC.
- S. Le, X. Hu, M. Yao, H. Chen, M. Yu, X. Xu, N. Nakazawa, F. M. Margadant, M. P. Sheetz and J. Yan, Cell Rep., 2017, 21, 2714 CrossRef CAS.
- H. Lei, C. He, C. Hu, J. Li, X. Hu, X. Hu and H. Li, Angew. Chem., Int. Ed., 2017, 56, 6117 CrossRef CAS.
- M. Yao, B. T. Goult, B. Klapholz, X. Hu, C. P. Toseland, Y. Guo, P. Cong, M. P. Sheetz and J. Yan, Nat. Commun., 2016, 7, 11966 CrossRef.
- G. Zoldak, J. Stigler, B. Pelz, H. Li and M. Rief, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18156 CrossRef CAS.
- R. Berkovich, S. Garcia-Manyes, J. Klafter, M. Urbakh and J. M. Fernandez, Biochem. Biophys. Res. Commun., 2010, 403, 133 CrossRef CAS.
- M. Bertz and M. Rief, J. Mol. Biol., 2008, 378, 447 CrossRef CAS.
- H. Wang, X. Gao, X. Hu, X. Hu, C. Hu and H. Li, Biochemistry, 2019, 58, 4751 CrossRef CAS.
- L. Fu, H. Wang and H. Li, CCS Chem., 2019, 1, 138 CAS.
- G. Dantas, A. L. Watters, B. M. Lunde, Z. M. Eletr, N. G. Isern, T. Roseman, J. Lipfert, S. Doniach, M. Tompa, B. Kuhlman, B. L. Stoddard, G. Varani and D. Baker, J. Mol. Biol., 2006, 362, 1004 CrossRef CAS.
- P. A. Alexander, Y. He, Y. Chen, J. Orban and P. N. Bryan, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11963 CrossRef CAS.
- D. L. Minor Jr and P. S. Kim, Nature, 1996, 380, 730 CrossRef CAS.
- L. L. Porter and L. L. Looger, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5968 CrossRef CAS.
- H. Tidow, T. Lauber, K. Vitzithum, C. P. Sommerhoff, P. Rosch and U. C. Marx, Biochemistry, 2004, 43, 11238 CrossRef CAS.
- S. Mohanty, J. H. Meinke, O. Zimmermann and U. H. Hansmann, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8004 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc06344d |
| This journal is © The Royal Society of Chemistry 2021 |