Open Access Article
Open Access ArticleAnalyzing mechanisms in Co(I) redox catalysis using a pattern recognition platform†
Tianhua
Tang
,
Christopher
Sandford
 ,
Shelley D.
Minteer
,
Shelley D.
Minteer
 * and
Matthew S.
Sigman
* and
Matthew S.
Sigman
 *
*
Department of Chemistry, University of Utah, 315 South 1400 East, Salt Lake City, Utah 84112, USA. E-mail: sigman@chem.utah.edu; minteer@chem.utah.edu
First published on 17th February 2021
Abstract
Redox catalysis has been broadly utilized in electrochemical synthesis due to its kinetic advantages over direct electrolysis. The appropriate choice of redox mediator can avoid electrode passivation and overpotential, which strongly inhibit the efficient activation of substrates in electrolysis. Despite the benefits brought by redox catalysis, establishing the precise nature of substrate activation remains challenging. Herein, we determine that a Co(I) complex bearing two N,N,N-tridentate ligands acts as a competent redox catalyst for the reduction of benzyl bromide substrates. Kinetic studies combining electroanalytical techniques with multivariable linear-regression analysis were conducted, disclosing an outer-sphere electron-transfer mechanism, which occurs in concert with C–Br bond cleavage. Furthermore, we apply a pattern recognition platform to distinguish between mechanisms in the activation of benzyl bromides, found to be dependent on the ligation state of the cobalt(I) center and ligand used.
1. Introduction
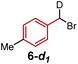
Redox catalysis, also known as indirect electrolysis, has been widely used in both bulk electrolysis and electrochemical analysis.1 Instead of the direct reduction of a substrate at the electrode, the redox mediator is first reduced at the electrochemical surface and subsequently transfers an electron to the substrate in bulk solution, regenerating the initial oxidation state of the mediator.1a–c Accordingly, adding a catalytic amount of the redox mediator leads to differentiated electron-transfer kinetics, with reduction of the organic substrate becoming a homogeneous redox event occurring away from the electrode/electrolyte interface.1d,e Switching from direct electrolysis to redox catalysis, problems of electrode passivation as well as the requirement for an overpotential to activate substrates, which can strongly reduce the efficiency of electrolysis, can be addressed.1e This allows the oxidation or reduction process of a substrate to take place at a decreased potential. Multiple reports harness this electrochemical strategy to reduce aliphatic halides with transition metal complexes owing to the importance of the alkyl radical generated for alkylation and cross-coupling reactions.2,3 However, it remains challenging to identify the inner- or outer-sphere nature of the reduction of the carbon–halogen bond by the metal,4 a differentiation that is key to understanding directions for optimization of the redox catalyst.As part of our efforts to develop a global understanding of the intricate factors that impact the mechanism of fundamental organometallic steps such as the reduction of alkyl halides, we previously demonstrated that a Co(I) complex bearing an N,N-bidentate ligand can activate benzyl bromides through an inner-sphere electron-transfer process (halogen-atom abstraction, Scheme 1a).5,6 Accordingly, we next questioned whether it is possible to manipulate the nature of substrate reduction by switching to Co(I) complexes bearing N,N,N-tridentate ligands. Herein, we uncover an alternative outer-sphere activation pathway for benzyl bromides in the presence of electrogenerated Co(I) complexes bearing the 2,6-bis(pyrazol-1-yl)pyridine ligand (BPP, 3), depicted in Scheme 1b. Cyclic voltammetric studies identified the existence of a catalytic waveform,7 in agreement with the catalytic reduction of benzyl bromides to benzyl radicals by the Co(I) complex, and detailed kinetic studies unveiled trends in substrate variation consistent with an outer-sphere electron-transfer mechanism. This mechanistic proposal, distinctive from our previously studied system,6 was further supported by multivariable linear-regression (MLR) analysis,8 enabling us to identify that the electron transfer occurs in a concerted fashion with dissociation of bromide from the substrate. In addition, with the combination of the electroanalytical techniques7 and statistical modeling,8 we establish a pattern recognition platform for rapidly distinguishing between the activation mechanisms of different metal complexes (Scheme 1b),9 a tool that we anticipate will be broadly applied in the rational design of new organometallic reactions.
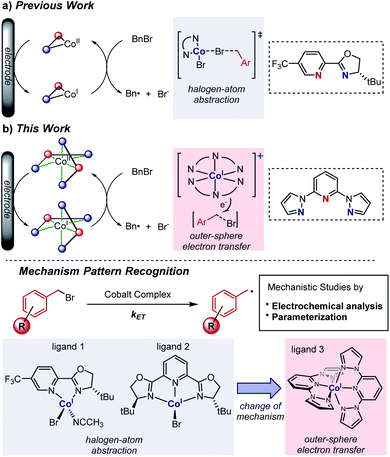 | ||
| Scheme 1 Mechanistic investigations into the reaction of Co(I) complexes with benzyl bromides, conducted (a) previously, and (b) in this work. | ||
2. Results and discussion
2.1. Characterization of a reversible electron-transfer process by a bis-ligated cobalt complex
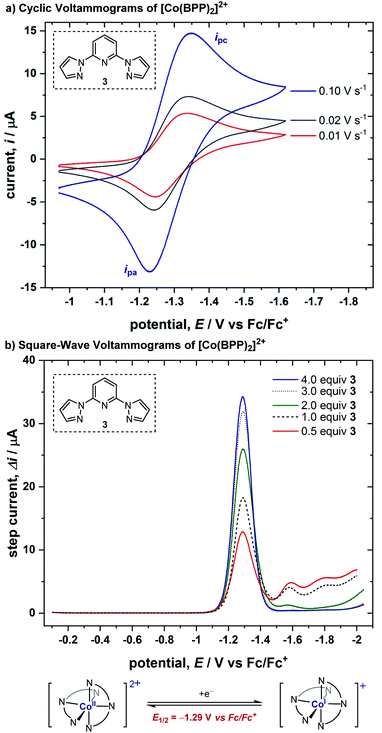
We conducted cyclic voltammetric (CV) studies with a solution containing 1 equiv. of CoBr2 and 2 equiv. of BPP ligand 3. A reversible electron transfer with E1/2 = −1.29 V (vs. Fc/Fc+) was discovered, where the ratio of peak currents in the forward (ipc) and reverse (ipa) scans did not decrease even when the scan rate was low (ipa/ipc = 0.81 at 0.01 V s−1) (Fig. 1a). Cyclic voltammograms in the presence of varied equivalents of ligand demonstrated that this reversible response originates from the Co(II)/Co(I) redox cycle of a bis-ligated cobalt complex (for more details, see ESI†). Moreover, square-wave voltammograms (SWVs) were obtained from solutions of 1 mM CoBr2 after sequential additions of ligand 3 (Fig. 1b). The SWVs show a single peak response from the complex with E1/2 = −1.29 V (vs. Fc/Fc+), consistent with our CV studies. Also, we ascertained that 75% of the cobalt ions in solution were bis-ligated when only two equivalents of the ligand were added (for more details, see ESI†).2.2. Discovery of a catalytic chemical reaction with benzyl bromide
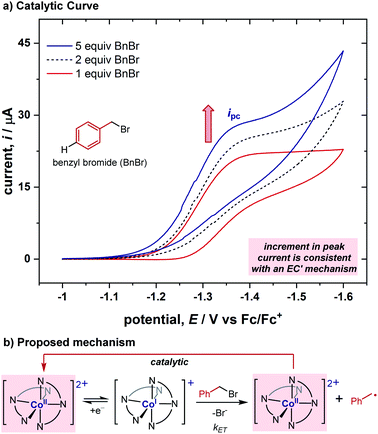
While benzyl bromide itself is not reduced within the redox window where this cobalt complex is reduced (for comparison of substrates' and complex's CVs, see ESI†), after adding 1 equiv. of the benzyl bromide substrate to the cobalt complex solution above, the cyclic voltammogram became irreversible (Fig. 2a), indicating the existence of a chemical reaction step after the electroreduction of the Co(II) complex. This demonstrates this cobalt complex's ability to reduce the benzyl bromide substrate using a less negative potential, sharing a similar feature to redox catalysts previously reported.1 To better understand the reaction between Co(I) and benzyl bromide, we conducted cyclic voltammograms with various concentrations of the substrate (Fig. 2a). A sequential increase in the current was observed upon adding additional equivalents of the substrate. We postulated that the increment of current is derived from the catalytic regeneration of the Co(II) species during the CV timespan, and is consistent with an EC′ mechanism (electrochemical reduction, E, followed by a chemical catalytic step regenerating Co(II), C′, Fig. 2b).10 This EC′ mechanism illustrates that the [Co(BPP)2]2+ complex can act as a redox catalyst in the reduction of benzyl bromides, but the exact nature of the electron transfer through either an inner-sphere or outer-sphere process remained elusive at this stage.2.3. Determination of activation rate constants
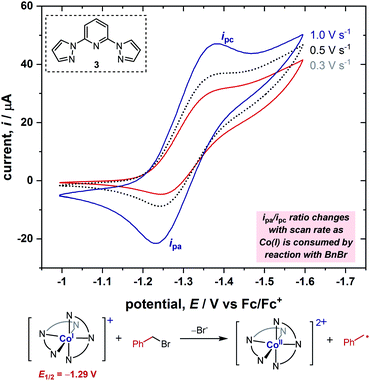
In order to obtain further information on the mechanism of the redox catalysis, we next turned to kinetic studies in which we obtained the rate constants for the reaction between [Co(BPP)2]+ and a range of benzyl bromide substrates, utilizing the same electroanalytical technique as in our previous study.6,7c Using this electroanalytical technique, the second-order rate constant can be derived by calculation of the quantity of Co(I) complex consumed by reaction with benzyl bromide during the CV from the ratio of peak currents, ipa/ipc (Fig. 3). For a more detailed explanation of this method, we direct the reader to previous studies.5,6 This analysis allowed us to measure the rate constant for each substrate in less than 30 minutes, thus enabling us to rapidly conduct kinetic studies with a wide array of substrates.2.4. Hammett studies
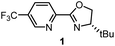
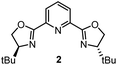
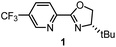
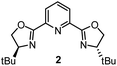
Having determined the relative rate constants for a variety of para-substituted benzyl bromides 4–13, a linear free energy relationship analysis was performed using Hammett σ parameters.11 Correlations were built and compared for substrate behavior between [Co(BPP)2]+ and cobalt complexes bearing the bidentate ligand 5CF3-Pyrox 1 and an alternative tridentate, commonly used ligand, tBu-PyBox 2 (Fig. 4). The Hammett plot for Co(I) ligated by one 5CF3-Pyrox ligand, published previously (Fig. 4a),6 displays a broken Hammett relationship between substrates with electron-rich groups (best correlated with σ+) and those with electron-deficient groups (best correlated with σ−). We previously determined that the non-linearity in this Hammett plot was the result of a halogen-atom abstraction mechanism, along with the reversible binding of the benzylic radical to Co(II). The dominating effect in the transition state of this electron transfer was found to be stabilization of the benzylic radical species. Similar features were found when using the mono-ligated Co(I) complex with tBu-PyBox ligand 2 (Fig. 4b). Indeed, not only did we observe the same broken feature in both correlations, we also identified the same outlier (substrate 12), the explanation for which we presented in our previous report.6 The common features in these two systems suggest that Co(I) with ligand 2 can also activate benzyl bromide through a halogen-atom abstraction mechanism.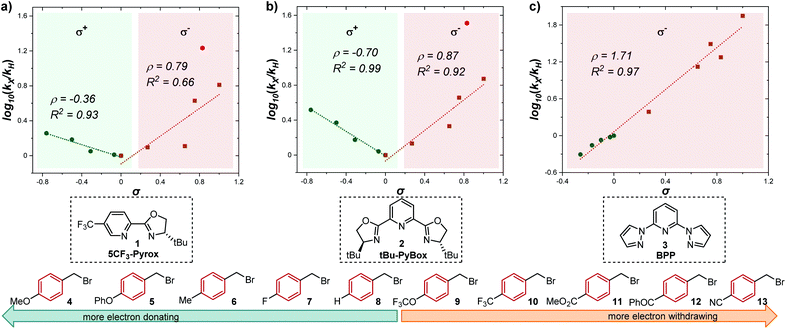 | ||
| Fig. 4 Hammett plots for activation of benzyl bromides by Co(I) complex ligated by (a) 5CF3-Pyrox 1, (b) tBu-PyBox 2, and (c) BPP 3. All three plots use kinetic data from the same substrate set, shown on the bottom of the figure. The lines with negative correlations use σ+ values, while the lines with positive correlations use σ− values.11 | ||
In contrast, the Hammett plot afforded by [Co(BPP)2]+ showed a dramatic difference from that with ligands 1 and 2. Specifically, a singular correlation with σ− was identified to describe the kinetics for both electronically-rich and -poor substrates. Compared with the other two Hammett plots, we postulated that a different mechanism is in operation with ligand 3. The correlation with the σ− parameter indicates a build-up of negative charge in the transition state of the reaction with Co(I), consistent with an outer-sphere electron-transfer mechanism,12 which is further supported by the detailed kinetic studies in the following sections. The different patterns resulting from comparing Hammett plots provide a rapid method to differentiate between mechanistic scenarios. This pattern recognition tool also showcases that the denticity of the ligand is not the primary controlling factor in changing the mechanistic pathway, but rather the number of ligands bound to the metal center (mono- or bis-ligation for complexes bearing tridentate ligands tBu-PyBox 2 and BPP 3, respectively).
2.5. Kinetic isotope effect and secondary substrate effect studies
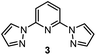
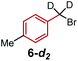
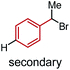
To further differentiate the proposed outer-sphere electron transfer from a halogen-abstraction mechanism, we conducted a kinetic isotope effect (KIE) study,13 as well as an investigation into the effects of changing from primary to secondary benzylic halide substrates. First, rate constants for substrate 6 and deuterated analogues 6-d1 and 6-d2 were measured with each ligand on cobalt, and the results are depicted in Table 1. Normal secondary KIEs were afforded in all systems, which is consistent with a change from sp3 to sp2 hybridization during the reductive cleavage of the C–Br bond. However, the systems using ligand 1 and ligand 2 both have unusually large secondary KIE values, close to or above the theoretical maximum value of ∼1.4 derived from changes in the out-of-plane CH2 bending vibration.14 This large KIE is derived from a formal oxidative addition process, where not only does the first C–Br bond cleavage step contribute to the KIE, but the subsequent radical rebound to Co(II) also impacts this measurement.6 This again supports the similarity of the mechanism with both ligand 1 and ligand 2, which proceeds via a proposed halogen-atom abstraction process. In contrast, ligand 3 gives a statistically-smaller secondary KIE. The difference in magnitude between complexes bearing ligands 3 and 1 suggests that [Co(BPP)2]+ reduces the benzyl bromide substrate by a distinct mechanism, which is in concert with our proposal for an outer-sphere electron-transfer mechanism.Next, we evaluated the effect of changing from a primary benzylic bromide to a secondary substrate (Table 2). Again, we observed a clear distinction in the classification of the mechanisms between ligands 1 and 2, and ligand 3, wherein the former complexes react faster with a secondary substrate, and the latter has a larger rate constant with a primary analogue. The identification of this pattern provides an additional method to rapidly characterize the difference between the two substrate activation mechanisms. The data for complexes bearing ligands 1 and 2 are consistent with a halogen-atom abstraction, whereby secondary substrates react with enhanced rates owing to greater stabilization of the benzylic radical through hyperconjugation. In contrast, within an outer- sphere electron-transfer realm, a higher energy LUMO in the presence of additional electron-donating groups would inhibit the substrates' ability to receive an electron, thus resulting in slower kinetics with secondary substrates, as observed for [Co(BPP)2]+.
2.6. Parameterization of substrates and statistical modeling of kinetic data
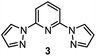
To obtain more detailed mechanistic insight into the electron transfer from [Co(BPP)2]+ to benzyl bromide, we conducted further kinetic studies with the assistance of multivariable linear-regression (MLR) analysis.8 We reasoned that this tool could offer improved identification of the specifics of the electron-transfer mechanism, correlating a broad and diverse data set of substrates into a single model using multiple interpretable DFT-computed parameters. We selected a broader range of substrates to evaluate kinetically, which included diversity in both electronic and steric properties (for a full list of all 46 substrates tested, see ESI†). Additionally, we classified these substrates into three groups (Fig. 5): (1) primary benzylic halides, which do not bear an ortho-substituent, (2) the secondary benzylic halides, and (3) the primary substrates containing one or two ortho-substituents.Considering the reductive nature of the electron transfer from the cobalt complex to the benzylic bromide, where the C–Br bond cleaves during this process,15 we proposed the reaction pathway could be described by two distinct steps: reduction and bond dissociation. As a result, we selected two parameters from the substrates to interrogate, the C–Br bond-dissociation energy (BDE) and the LUMO energy. Additionally, we postulated that BDE could be used to differentiate between two different outer-sphere electron transfer mechanisms.16–18 The outer-sphere electron-transfer reduction of organic substrates with bond dissociation has been reported to occur through two mechanisms, a concerted dissociative electron-transfer mechanism wherein a bond in the substrate is cleaved at the same time as the electron transfer,9,16,17 or a two-step dissociative electron transfer mechanism via a discrete radical anion intermediate.18 In the latter two-step pathway, the kinetic behavior has been explained by Marcus theory, which predicts the relationship between the kinetics and the reorganization energy change during the electron transfer step. In contrast, for a concerted pathway, the energy cost for the broken bond (BDE) is incorporated as another key parameter affecting the kinetics.17 The concerted dissociative electron-transfer theory, modified from Marcus theory,19 was established and developed by Savéant, who derived a semi-quantitative model to calculate the kinetic energy barrier of this process (eqn (1)),16,17
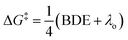 | (1) |
Eqn (1) describes how the intrinsic barrier of a concerted dissociative electron-transfer process is proportional to the bond-dissociation energy. In our study, we identified that the relative rates of both non-ortho primary substrates and secondary substrates are highly correlated with BDE (Fig. 5, R2 = 0.92 in both cases). This is in agreement with eqn (1), supporting a concerted mechanism over a stepwise alternative.17 It should be noted though that there is a clear distinction between the intercepts of these two correlations. Additionally, the BDE does not correlate to the measured rates of ortho-substituted primary substrates (R2 = 0.37). As a result, there are other intrinsic properties of these reactions that are neglected in the correlation with BDE. Thus, we sought to understand these limitations by evaluating alternative parameters.
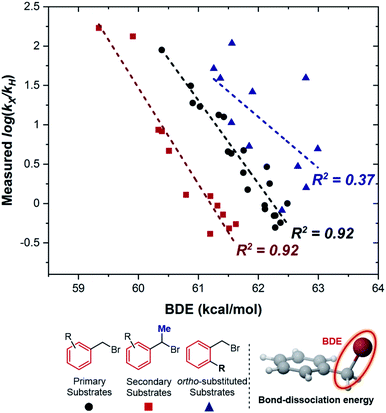
As a consequence, the LUMO energy was tested to interrogate the intrinsic ability of the substrates to undergo electron transfer. This parameter has been previously used to rationalize kinetics in outer-sphere electron transfer, whereby a higher LUMO energy makes reduction less thermodynamically favorable, leading to a concomitant decrease in the rate.20 Once again, we obtained good correlations for both non-ortho primary (Fig. 6a) and secondary (Fig. 6b) benzylic bromides, consistent with an outer-sphere electron-transfer mechanism.
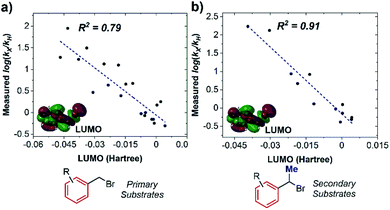
However, when we conducted the same analysis for ortho-substituted substrates, two apparent outliers were identified (Fig. 7a). We hypothesized that this could be a result of changes in substrate reorganization energy for these two anomalies. The reorganization energy, an essential parameter in Marcus theory alongside the driving force of the process, is the energy cost for structural changes of both the reactants and solvent molecules.19 We propose that the dihedral angle of the C–Br bond (referenced to the plane of the phenyl ring) can characterize the substrate reorganization energy, since the C–Br bond must become perpendicular to the aromatic ring in order for concerted cleavage with the electron transfer.17b,21 Accordingly, by introducing this parameter with LUMO into a multivariable fit, an improved correlation with ortho-substituted substrates is observed (Fig. 7b), appropriately accounting for the kinetics of the two initially anomalous performers.
To unify the mechanistic picture, we next sought to pursue a statistical model that could incorporate all of the substrates evaluated. As expected from the above analysis, correlation with the LUMO energy alone does not appropriately account for all the substrate variation (Fig. 8a). However, a multivariable model (Fig. 8b) with good regression statistics (R2 = 0.90, Q2 = 0.86, 4-fold ≈0.85) was found using a combination of the LUMO, BDE, and C–Br bond dihedral angle. Furthermore, this model was validated by a pseudo-randomly selected validation data set (13 out of 43 data points, R2valid. = 0.80), and removal of any of the three parameters leads to a statistically-significant reduction in model statistics (see ESI†).
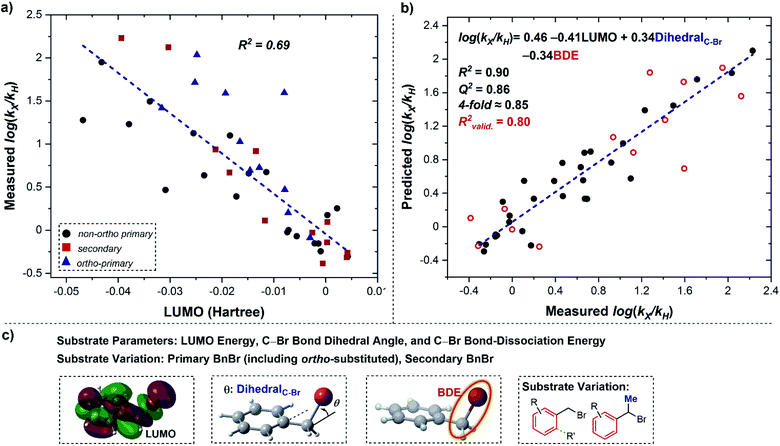 | ||
| Fig. 8 (a) Correlation with substrate LUMO energy. Red squares represent secondary substrates, black circles represent non-ortho primary substrates, and blue triangles represent ortho-substituted primary substrates. (b) The addition of two parameters to formulate a multivariable linear-regression model, the C–Br bond dihedral angle and the C–Br bond-dissociation energy, into the correlation in (a), validated with randomly selected benzyl bromides (open red circles). (c) Description of parameters and substrate classes within Fig. 8. | ||
As discussed above, both the LUMO energy and the C–Br bond dihedral angle are descriptive of an outer-sphere electron-transfer process. The presence of the BDE as a parameter in the model is consistent with a concerted dissociative electron transfer, in contrast to its stepwise counterpart.16,17 As a consequence, the combination of these three terms in the MLR model confirms the key features of a concerted dissociative electron-transfer mechanism, and can be used as a platform to predict rate constants for the reduction of complex alkyl halide substrates in the future.
3. Conclusions
In conclusion, we have investigated the activation of benzyl bromides by a BPP-ligated cobalt(I) complex. Cyclic voltammetric experiments were used to identify that the activation mode occurs through an EC′ mechanism, wherein the cobalt complex acts as a redox catalyst. Results from an assemblage of classic physical organic experiments enabled by electroanalytical analysis exhibited a dramatic contrast in the activation mechanism when compared to cobalt complexes ligated by either Pyrox or PyBox. These results are consistent with a change in mechanism from inner-sphere to outer-sphere electron transfer when the cobalt center is coordinatively saturated and cannot bind the substrate. It also demonstrates the significance of the number of ligands bound to the metal. Further confirmation of the outer-sphere mechanism was afforded by multivariable linear-regression analysis, revealing the concerted nature of the electron transfer in which the C–Br bond is cleaved at the same time as the transfer of the electron. In combination, these results demonstrate the utility of combining electroanalytical techniques with parameterization tools to uncover reaction mechanisms. This is highlighted by using simple Hammett correlations as a pattern recognition platform to rapidly distinguish between different mechanisms in substrate activation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the National Science Foundation Center for Synthetic Organic Electrochemistry for funding (CHE-1740656 and CHE-2002158). M. S. S. thanks the National Science Foundation (CHE-1763436) for initial support of this study. C. S. thanks the EU for Horizon 2020 Marie Skłodowska-Curie Fellowship (grant no. 789399). The support and resources from the Center for High Performance Computing at the University of Utah and the Extreme Science and Engineering Discovery Environment (XSEDE, which is supported by the NSF (ACI-1548562) and provided through allocation TG-CHE190060) are gratefully acknowledged. NMR results included in this report were recorded at the David M. Grant NMR Center, a University of Utah Core Facility. Funds for construction of the Center and the helium recovery system were obtained from the University of Utah and the National Institutes of Health awards 1C06RR017539-01A1 and 3R01GM063540-17W1, respectively. NMR instruments were purchased with the support of the University of Utah and the National Institutes of Health award 1S10OD25241-01.Notes and references
- For reviews on redox catalysis, see: (a) C. P. Andrieux and J.-M. Savéant, Electroanal. Chem., 1986, 2055, 43–58 CrossRef; (b) E. Steckhan, Angew. Chem., Int. Ed., 1986, 25, 683–701 CrossRef; (c) C. P. Andrieux, P. Hapiot and J.-M. Savéant, Chem. Rev., 1990, 90, 723–738 CrossRef CAS; (d) J.-M. Savéant, Chem. Rev., 2008, 108, 2348–2378 CrossRef; (e) R. Francke and R. D. Little, Chem. Soc. Rev., 2014, 43, 2492–2521 RSC.
- For selected studies on nickel-electrocatalyzed functionalization of aliphatic halides, see: (a) M. Durandetti, S. Sibille, J.-Y. Nédélec and J. A. Périchon, Synth. Commun., 1994, 24, 145–151 CrossRef CAS; (b) M. Durandetti, J.-Y. Nédélec and J. Périchon, J. Org. Chem., 1996, 61, 1748–1755 CrossRef CAS; (c) M. Durandetti, J. Périchon and J.-Y. Nédélec, J. Org. Chem., 1997, 62, 7914–7915 CrossRef CAS; (d) R. J. Perkins, D. J. Pedro and E. C. Hansen, Org. Lett., 2017, 19, 3755–3758 CrossRef CAS; (e) R. J. Perkins, A. J. Hughes, D. J. Weix and E. C. Hansen, Org. Process Res. Dev., 2019, 23, 1746–1751 CrossRef CAS; (f) K.-J. Jiao, D. Liu, H.-X. Ma, H. Qiu, P. Fang and T.-S. Mei, Angew. Chem., Int. Ed., 2020, 59, 2565–2576 CrossRef; (g) B. L. Truesdell, T. B. Hamby and C. S. Sevov, J. Am. Chem. Soc., 2020, 142, 5884–5893 CrossRef CAS.
- For selected studies on cobalt-electrocatalyzed functionalization of aliphatic halides, see: (a) D.-L. Zhou, J. Gao and J. F. Rusling, J. Am. Chem. Soc., 1995, 117, 1127–1134 CrossRef CAS; (b) P.-L. Fabre and O. Reynes, Electrochem. Commun., 2010, 12, 1360–1362 CrossRef CAS; (c) C. Costentin, G. Passard, M. Robert and J.-M. Savéant, Chem. Sci., 2013, 4, 819–823 RSC; (d) B.-L. Chen, H.-W. Zhu, Y. Xiao, Q.-L. Sun, H. Wang and J.-X. Lu, Electrochem. Commun., 2014, 42, 55–59 CrossRef CAS.
- (a) J. B. Diccianni and T. Diao, Trends Chem., 2019, 1, 830–844 CrossRef CAS; (b) F. Kreyenschmidt, S. E. Meurer and K. Koszinowski, Chem.–Eur. J., 2019, 25, 5912–5921 CrossRef CAS; (c) A. Guérinot and J. Cossy, Acc. Chem. Res., 2020, 53, 1351–1363 CrossRef; (d) M.-A. N. Nguyen, M. E. Tomasso, D. C. Easter and C. Ji, J. Electrochem. Soc., 2016, 163, G1–G6 CrossRef CAS.
- D. P. Hickey, C. Sandford, Z. Rhodes, T. Gensch, L. R. Fries, M. S. Sigman and S. D. Minteer, J. Am. Chem. Soc., 2019, 141, 1382–1392 CrossRef CAS.
- C. Sandford, L. R. Fries, T. E. Ball, S. D. Minteer and M. S. Sigman, J. Am. Chem. Soc., 2019, 141, 18877–18889 CrossRef CAS.
- (a) C. Sandford, M. A. Edwards, K. J. Klunder, D. P. Hickey, M. Li, K. Barman, M. S. Sigman, H. S. White and S. D. Minteer, Chem. Sci., 2019, 10, 6404–6422 RSC; (b) E. Labbé and O. Buriez, ChemElectroChem, 2019, 6, 4118–4125 CrossRef; (c) L. Polleux, E. Labbé, O. Bruiez and J. Périchon, Chem.–Eur. J., 2005, 11, 4678–4686 CrossRef CAS.
- (a) K. C. Harper and M. S. Sigman, J. Org. Chem., 2013, 78, 2813–2818 CrossRef CAS; (b) M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292–1301 CrossRef CAS.
- For previous electroanalytcal studies on mechanism pattern recognition, see: (a) D. Lexa, J.-M. Savéant, K. B. Su and D.-L. Wang, J. Am. Chem. Soc., 1987, 109, 6464–6470 CrossRef CAS; (b) D. Lexa, J.-M. Savéant, K. B. Su and D.-L. Wang, J. Am. Chem. Soc., 1988, 110, 7617–7625 CrossRef CAS; (c) D. Lexa, J.-M. Savéant, H. J. Schäfer, K.-B. Su, B. Vering and D.-L. Wang, J. Am. Chem. Soc., 1990, 112, 6162–6177 CrossRef CAS.
- (a) J.-M. Savéant, Electrochim. Acta, 1967, 12, 999–1030 CrossRef; (b) C. P. Andrieux, C. Blocman, J. M. Dumas-Bouchiat, F. M'Halla and J. M. Savéant, J. Electroanal. Chem. Interfacial Electrochem., 1980, 113, 19–40 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- (a) J. W. Sease, F. G. Burton and S. C. Nickol, J. Am. Chem. Soc., 1968, 90, 2595–2598 CrossRef CAS; (b) J.-S. Yang, K.-T. Liu and Y. O. Su, J. Phys. Org. Chem., 1990, 3, 723–731 CrossRef CAS.
- M. Gómez-Gallego and M. A. Sierra, Chem. Rev., 2011, 111, 4857–4963 CrossRef.
- A. Streitwieser, R. H. Jagow, R. C. Fahey and S. Suzuki, J. Am. Chem. Soc., 1958, 80, 2326–2332 CrossRef CAS.
- (a) C. P. Andrieus, J.-M. Savéant and K. B. Su, J. Phys. Chem., 1986, 90, 3815–3823 CrossRef; (b) T. Lund and H. Lund, Acta Chem. Scand., 1986, B40, 470–485 CrossRef CAS; (c) T. Lund and H. Lund, Acta Chem. Scand., Ser. B, 1987, 41, 93–102 CrossRef.
- For selected reviews on concerted dissociative electron transfer, see: (a) C. Costentin, M. Robert and J.-M. Savéant, Chem. Phys., 2006, 324, 40–56 CrossRef CAS; (b) A. Houmam, Chem. Rev., 2008, 108, 2180–2237 CrossRef CAS.
- Selected studies on concerted dissociative electron transfer: (a) J.-M. Savéant, J. Am. Chem. Soc., 1987, 109, 6788–6795 CrossRef; (b) C. P. Andrieux, A. L. Gorande and J.-M. Savéant, J. Am. Chem. Soc., 1992, 114, 6892–6904 CrossRef CAS; (c) L. Pause, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 1999, 121, 7158–7159 CrossRef CAS; (d) C. Ji, M. Ahmida, M. Chahma and A. Houmam, J. Am. Chem. Soc., 2006, 128, 15423–15431 CrossRef CAS; (e) C. Costentin, L. Donati and M. Robert, Chem.–Eur. J., 2009, 15, 785–792 CrossRef CAS.
- Selected studies on stepwise dissociative electron transfer: (a) N. Takeda, P. V. Poliakov, A. R. Cook and J. R. Miller, J. Am. Chem. Soc., 2004, 126, 4301–4309 CrossRef CAS; (b) C. Costentin, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2004, 126, 16051–16057 CrossRef CAS; (c) C. Costentin, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2004, 126, 16834–16840 CrossRef CAS.
- (a) R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS; (b) R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- (a) I.-S. H. Lee, D. Stović and M. Kreevoy, J. Am. Chem. Soc., 1988, 110, 3989–3993 CrossRef CAS; (b) A. B. Anderson and T. V. Albu, J. Am. Chem. Soc., 1999, 121, 11855–11863 CrossRef CAS; (c) J. A. Conradie, J. Phys.: Conf. Ser., 2015, 633, 012045 CrossRef; (d) Y. Kunai, A. T. Liu, A. L. Cottrill, V. B. Koman, P. Liu, D. Kozawa, X. Gong and M. S. Strano, J. Am. Chem. Soc., 2017, 139, 15328–15336 CrossRef CAS; (e) S. V. Rosokha, Faraday Discuss., 2017, 203, 315–332 RSC.
- C. Y. Lin, M. L. Coote, A. Gennaro and K. Matyjaszewski, J. Am. Chem. Soc., 2008, 130, 12762–12774 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and methods, experimental cyclic voltammograms and kinetic data, parameters used in the modeling, additional models and correlations, experimental procedures, characterization data and spectra for the synthesis of ligands and substrates, and coordinates of DFT-optimized structures. See DOI: 10.1039/d0sc06725c |
| This journal is © The Royal Society of Chemistry 2021 |