Planar tetracoordinate fluorine atoms

Abstract

Among the list of planar tetracoordinate atoms, fluorine is missing. So far, there are no theoretical or experimental reports suggesting their existence. Herein, we introduce the first six combinations (FIn₄⁺, FTl₄⁺, FGaIn₃⁺, FIn₂Tl₂⁺, FIn₃Tl⁺, and FInTl₃⁺) whose global minima contain a planar tetracoordinate fluorine. The bonding analyses indicate that the interactions between the fluorine and the peripheral atoms are significantly electrostatic, which is also reflected in the electronic delocalization. As opposed to other planar tetracoordinate systems with carbon, nitrogen, or oxygen atoms, the fluorine in the ptFs does not act as a σ-acceptor, restraining any back-donation. On the other hand, σ-electrons show a diatropic response, which would characterize these clusters as σ-aromatic.

---

Introduction

Planar tetracoordinate carbon (ptC) atoms are oddities, they embody a conflict with one of the most important paradigms in organic chemistry, yet some exist in bottles. The long-standing tetrahedral model of van't Hoff and Lebel was first challenged in 1968 when Monkhorst¹ suggested a transition state (TS) with a ptC in the stereomutation of a tetrahedral carbon. Two years later, Hoffmann, Alder, and Wilcox² proposed a few rules for stabilizing such TS based on planar methane's molecular orbital analysis. Schleyer and co-workers adopted this idea to introduce the first structure with a ptC that is energetically more favorable than its tetrahedral counterpart.³ In 1991, Boldyrev and Schleyer predicted various planar tetracoordinate atoms with 18 valence electrons (18ve), such as CAl₂Si₂, OAl₄, NAl₃Si, BAlSi₃, and NAl₄⁻.⁴ In fact, the last one was thereafter experimentally characterized by Nayak et al.⁵ Later, Boldyrev and Simons established that 18ve are required to stabilize a planar form, in which three C-ligand σ-bonds, one C-ligand π-bond, and one ligand–ligand bond take place.⁶ The first neutral pentaatomic ptC molecules with 17 and 18ve experimentally observed in the gas-phase via anion photoelectron spectroscopy and characterized by ab initio computations were CAl₄⁻ and CAl₄²⁻, respectively.^7–9 Although the 18ve valence rule is not universal (a rule is not a law), it proved useful in predicting new planar hypercoordinate atoms.^10–19

So, the theory has played a fundamental role in predicting and understanding these peculiar species.^20–23 Although the list is long, it does not include a theoretically or experimentally reported planar tetracoordinate fluorine (ptF) atom, which does not make sense since the D_4h CAl₄²⁻, NAl₄⁻, and OAl₄ structures are the global minima on their corresponding potential energy surfaces (PESs). Why is the isoelectronic FAl₄⁺ not planar? Is it possible to introduce fluorine into the flat world? Herein, we systematically explored the PESs of all viable pentaatomic clusters containing a fluorine atom combined with main group elements, totaling 18ve and charges from +2 to −2. This amounts to 440 combinations and around 100 000 optimizations. Gratifyingly, we found that the global minima of FIn₄⁺, FTl₄⁺, FGaIn₃⁺, FIn₂Tl₂⁺, FIn₃Tl⁺, and FInTl₃⁺ contain a ptF atom.

Computational details

The systematic exploration of the corresponding PESs was carried out through a modified genetic algorithm, as implemented in the GLobal Optimization of MOlecular Systems (GLOMOS).^24–26 GLOMOS is written in Python and includes stochastic and evolutive methodologies to carry out the global optimization of atomic and molecular clusters, where the local optimizations are solved through an electronic structure code. The initial screening was done at the TPSS²⁷/def2-SVP²⁸ level. All the stationary points were re-minimized and characterized at the TPSS/def2-TZVP level, including Grimme's D3 dispersion²⁹ scheme with Becke-Johnson damping. The final energies were refined at the CCSD(T)³⁰/def2-TZVP level, including the zero-point energy correction at the TPSS-D3(BJ)/def2-TZVP. Thus, the energetic discussion is based on the CCSD(T)/def2-TZVP//TPSS-D3(BJ)/def2-TZVP results. All of these computations were performed with Gaussian 16.³¹

The Wiberg Bond Index (WBI)³² and Natural Population Analysis (NPA)³³ were estimated following the NBO scheme.³⁴ The AdNDP method, developed by Zubarev and Boldyrev,³⁵ was employed for better insight into the bonding of these systems. The AdNDP leads to a partitioning of the charge density into elements with the lowest possible number of atomic centers per electron pair: n-center-two-electron (nc-2e) bonds, including the Lewis bonding elements as core electrons, lone pairs, and 2c–2e bonds.

Also, the analysis of the induced magnetic field^36–38 (B^ind) and induced current density (J^ind)^39–41 was analyzed using the programs Aromagnetic⁴² and GIMIC,^39–41 respectively. The molecular magnetic response to a homogeneous external magnetic field is computed on a rectangular grid with the molecule in its center. These calculations were performed at the TPSS/TZP-DKH⁴³ level.

Bonding and structure

Interestingly, structures with a ptF only arise in clusters formed by substituents exclusively of group 13 (Fig. 1). Let us start with those systems with a single element as ligands, i.e., FX₄⁺ (X = Al, Ga, In, Tl). The planar D_4h form of FAl₄⁺, with F–Al bond lengths (r_F-Al) of 2.214 Å, has two imaginary frequencies. Apparently, the cavity formed by four aluminum atoms is not large enough to accommodate a fluorine atom. The putative global minimum, 18.7 kcal mol⁻¹ lower in energy, is a C_2v aluminum tetrahedron with fluorine at the edge (see Fig. S1†). For the FGa₄⁺ case, the D_4h arrangement (r_F–Ga = 2.238 Å) is a transition state (ν_min = −70 cm⁻¹), 4.5 kcal mol⁻¹ higher in energy than the most stable structure formed by a gallium triangle and a F–Ga fragment. Gratifyingly, the global minimum structures for FIn₄⁺ (r_F–In = 2.415 Å) and FTl₄⁺ (r_F–Tl = 2.533 Å) have the perfect cavity to stabilize a ptF. In other words, the cavity size is critical.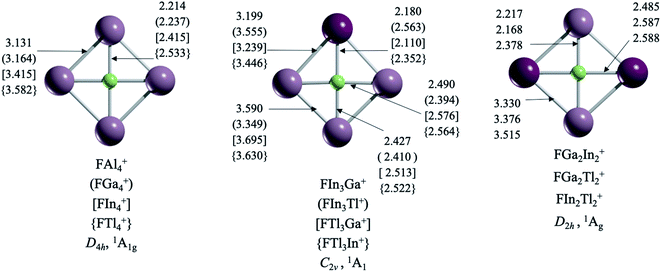

Fig. 1 TPSS-D3(BJ)/def2-TZVP structures of the FX₄⁺ (X = Al, Ga, In, Tl) series. Bond lengths are in Å.

With this in mind, we explored the possibility of combining two elements of group 13 (except boron because it creates a small cavity) to produce more clusters with a ptF. Notably, there is no ptF as the global minimum if the structure contains aluminum. The only ptFs, but as local minima, are FIn₃Al⁺ and FTl₃Al⁺. It might be assumed that replacing a Ga atom in FGa₄⁺ with a heavier element should create a cavity large enough to stabilize a ptF, but it is not so obvious (this only occurs for FGaIn₃⁺). Interestingly, while the putative global minimum of FGaIn₃⁺ (r_F–Ga = 2.180 Å) is a ptF, the ptF isomer for FGaTl₃⁺ (r_F–Ga = 2.110 Å) is 0.6 kcal mol⁻¹ higher in energy than the structure with the tricoordinate fluorine atom. In fact, the F–Ga bond lengths are shortened in clusters containing Tl, reducing the cavity space. So, using larger atoms does not necessarily lead to larger cavities. That is why the three combinations including In and Tl (FIn₂Tl₂⁺, FIn₃Tl⁺, and FInTl₃⁺) are the only ones with perfect cavities for stabilizing a true ptF.

Why are ptFs so elusive compared to their isoelectric analogues CAl₄²⁻, NAl₄⁻, and OAl₄? Table 1 reveals particular trends among planar tetracoordinate atoms surrounded by Al. First, our computations show that going from CAl₄²⁻ to FAl₄⁺, there is a charge decrease on the central atom (from −2.62 |e| to −0.88 |e|) with a charge increment on the peripheral atoms (from +0.16 |e| to +0.47 |e|). So, the charge transfer from the Al₄ skeleton to the central atom is more effective in the fluorine case. In other words, the ionic character between the hypercoordinate center and the metal fragment increases from C to F.

Table 1 NPA charges (q, |e|), valence population, and the total Wiberg bond index of the planar hypercoordinate atom. HOMO–LUMO gap (Δ_H–L, eV) and the lowest vibrational frequency, ν_min

	q	Configuration	WBItotal	Δ H–L (eV)	ν min
FAl4^+	−0.88	2s^1.97 2px^1.97 2py^1.97 2pz^1.97	0.24	1.15	−47
FGa4^+	−0.86	2s^1.97 2px^1.96 2py^1.96 2pz^1.97	0.28	1.13	−71
FIn4^+	−0.88	2s^1.98 2px^1.96 2py^1.96 2pz^1.97	0.24	0.95	33
FTl4^+	−0.87	2s^1.98 2px^1.96 2py^1.96 2pz^1.97	0.25	0.86	28
FGa3In^+	−0.85	2s^1.97 2px^1.96 2py^1.95 2pz^1.97	0.30	0.84	26
FGa3Tl^+	−0.84	2s^1.97 2px^1.95 2py^1.95 2pz^1.96	0.32	0.79	24
FGa2In2^+	−0.84	2s^1.97 2px^1.96 2py^1.95 2pz^1.96	0.31	0.80	30
FGa2Tl2^+	−0.83	2s^1.97 2px^1.96 2py^1.95 2pz^1.96	0.33	0.79	25
FGaIn3^+	−0.87	2s^1.97 2px^1.96 2py^1.97 2pz^1.97	0.26	0.97	42
FGaTl3^+	−0.86	2s^1.97 2px^1.96 2py^1.96 2pz^1.97	0.27	0.89	33
FIn2Tl2^+	−0.88	2s^1.98 2px^1.96 2py^1.96 2pz^1.97	0.25	0.89	10
FIn3Tl^+	−0.88	2s^1.98 2px^1.96 2py^1.96 2pz^1.97	0.25	0.92	25
FInTl3^+	−0.87	2s^1.98 2px^1.96 2py^1.96 2pz^1.97	0.25	0.87	31
CAl4^2−	−2.62	2s^1.60 2px^1.76 2py^1.76 2pz^1.46	2.29	1.55	86
NAl4^−	−2.27	2s^1.79 2px^1.88 2py^1.88 2pz^1.71	1.33	1.79	95
OAl4	−1.68	2s^1.91 2px^1.94 2py^1.94 2pz^1.88	0.63	1.64	94

---

This is also supported by the significant reduction in the total values of the WBI³² of the central atom from 2.29 in CAl₄²⁻ to only 0.24 in FAl₄⁺, which, of course, is a consequence of the electronegativity difference between the peripheral atoms and the corresponding planar tetracoordinate atom. The electron transfer mechanism is less obvious, while carbon acts as σ-acceptor, and this is compensated by the back-donation from its 2p_z electrons to the π-bonding (2s^1.60 2p_x^1.76 2p_y^1.76 2p_z^1.46), the back-donation is null in the fluorine compounds. This is the main reason why these species are so rare. While several ptCs have been predicted and even detected experimentally, only six from 440 compositions contain a planar fluorine atom within the established parameters. For all ptFs, global minimum or not, there is a negligible variation of the fluorine charges and orbital occupancies. The only distinction is a subtle increase in the total WBI values of the gallium clusters due to their relatively short Ga–F bonds. However, the charge transfer is more effective for the global minima, i.e., higher than 0.86 |e| on F. The exception is FAl₄⁺ (−0.88 |e|), but the cavity formed by the aluminum atoms is relatively small. In other words, both cavity size and charge transfer are essential to stabilize the ptF.

AdNDP is a powerful tool for understanding the distribution of electron pairs in the system.³⁵ However, in some cases, several solutions are possible. Our strategy for identifying the most viable ones was to determine those schemes with the highest occupation number (ON). Let us compare two bonding schemes, or solutions, for CAl₄²⁻ and FAl₄⁺. In the first solution (Fig. 2a and b), there are four 2c–2e E-Al σ-bonds (E = C or F), four 3c–2e Al-E-Al σ-bonds, and one π-bond. In both clusters, the σ-bonds remain almost identical, but in the carbon molecule, the π-bond involves the four ligands, whereas, in FAl₄⁺, it is located at the central atom, i.e., it can be reclassified as a lone-pair. The occupation numbers in all cases are higher than 1.95.

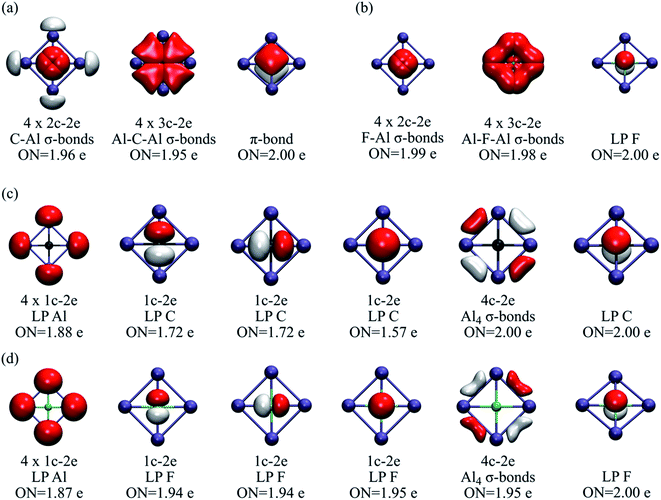Fig. 2 (a) First AdNDP solution for CAl₄²⁻ and (b) FAl₄⁺. (c) Second AdNDP solution for CAl₄²⁻ and (d) FAl₄⁺. ON stands for occupation number.

However, a second solution suggests the absence of back-donation from the central to the peripheral atoms (Fig. 2c and d). This bonding layout can be described by a delocalized 4c–2e σ-bond involving the external ring, one lone-pair on each peripheral atom, and four lone-pairs on the central fluorine, i.e., no overlap between fluoride and the X₄²⁺ skeleton. This is entirely consistent with the charge analysis and WBI values. The residual electrons for the carbon system are 1.47, and in the case of fluorine, only 0.65. These values, along with the corresponding analysis for N and O (Tables S1–S2†), reveal that, along the row, the “ionic” scheme becomes quite competitive. Besides, it should be emphasized that both systems identify the lone pair on the fluorine atom, and most importantly, the number of residual electrons in the ionic scheme varies from 0.65 to 0.35 as it goes from Al to Tl, indicating a proclivity for the scheme bonding with no orbital overlap, i.e., an electrostatic nature between the fluorine and the peripheral atoms.

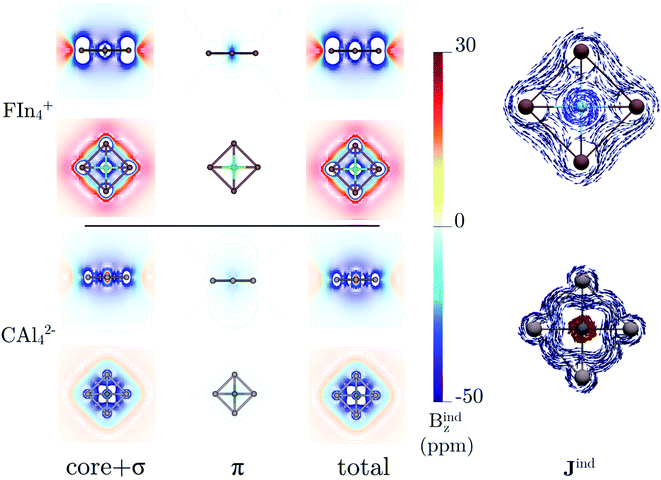
The back-donation absence also has consequences on the magnetic response. Let us compare the induced magnetic field^36–38 of FIn₄⁺ and CAl₄²⁻. In both cases, the magnetic response of the σ- and π-electrons is diatropic, but the first one much stronger compared to that caused by the π-cloud (almost negligible), as Fig. 3 shows. Note that the σ-electrons response of FIn₄⁺ is stronger than in the carbon structure. So, both clusters could be classified as aromatic, predominantly σ-aromatic.⁴⁴ More details about the magnetic response are provided by the induced current density (J^ind).^39–41 For CAl₄²⁻, there is a strong diatropic ring current around the Al₄ skeleton (in deep blue) and a paratropic (counterclockwise) current around the carbon vicinity (in red, see Fig. 3). In contrast, in FIn₄⁺, a local diatropic current is entirely localized at the fluorine atom (light blue). In order to quantify the ring-current strength, the J^ind is integrated into a specific area. For the typical reference system, benzene, the integration plane starts in the center of the ring, intersects the C–C bond ending about 4 Å away. This results in a ring-current strength of 12 nA/T. A ring-current strength of 20.5 (FIn₄⁺) and 13.7 (CAl₄²⁻) nA/T are obtained using the same integration domain. However, these values include the currents located at the central atoms. So, it is mandatory to avoid these local ring-current effects to quantify only the peripheral ring current. The selected integration planes start at 1.2 (FIn₄⁺) and 0.7 Å (CAl₄²⁻) from the central atom, which are inflection J^ind points from the local pathway to a ring current pathway. This provides a ring-current strength of 17.1 nA/T for FIn₄⁺, which is smaller than the corresponding one for CAl₄²⁻ (22.6 nA/T).

Fig. 3 The isolines of the orbital contributions to B_z^ind calculated in the transverse plane and in the molecular plane of FIn₄⁺ and CAl₄²⁻ shown in the left panel. The J^ind vector maps of FIn₄⁺, and CAl₄²⁻ in the right panel. The diatropic and paratropic currents are shown in blue and red, respectively. All the computations were performed at TPSS/TZP-DKH level.

Conclusions

In summary, the exhaustive exploration of the PESs of pentaatomic systems with a fluorine atom and main group elements revealed that only atoms of group 13 as ligands could stabilize a ptF. Among the 440 examined combinations, only six clusters with a ptF are the energy global minimum, two of them with the same element as the ligand, FIn₄⁺ and FTl₄⁺, and the four composite species FGaIn₃⁺, FIn₂Tl₂⁺, FIn₃Tl⁺, and FInTl₃⁺. The bonding analyses indicate that the interactions of fluorine with the peripheral atoms are significantly electrostatic, affecting the electronic delocalization. In other words, as opposed to planar tetracoordinate systems with carbon, nitrogen, or oxygen atoms, the fluorine in the ptFs does not act as a σ-acceptor, restraining any back-donation. This is reflected in the magnetic response. Although ptFs could be characterized as σ-aromatic and with a diatropic external current on the X₄ ring, they also show a diatropic current entirely localized on the central F, as opposed to systems with a ptC. The above implies that the stabilization of these species is through subtle ionic interactions and an adequate cavity to accommodate the central atom, hence its scarcity. We believe that the design and prediction of these species will stimulate the experimental detection of a larger number of bizarre fluorine-containing structures.⁴⁵

Author contributions

G. M. and J. B. conceived the project and wrote the manuscript. G. C.-T., M. O.-I., E. D., and F. O.-C. performed the computational studies in consultation with X. Z., Z.-h. C.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by Grant SEP-Cinvestav-2018-57. F. O.-C. thanks CONACyT (grant Al-S-26876) for financial support and the Cátedras-CONACyT 1024 project. G. C.-T., E. D., M. O.-I. and J. B. thank Conacyt for their PhD fellowships.

References

1. H. J. Monkhorst, Chem. Commun., 1968, 1111–1112.
2. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
3. J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427.
4. P. v. R. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 21, 1536–1538.
5. S. K. Nayak, B. K. Rao, P. Jena, X. Li and L.-S. Wang, Chem. Phys. Lett., 1999, 301, 379–384.
6. A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972.
7. X. Li, L.-S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038.
8. L.-S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687.
9. X. Li, H.-F. Zhang, L.-S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 112, 3776–3778.
10. Z.-H. Cui, Y.-H. Ding, J. L. Cabellos, E. Osorio, R. Islas, A. Restrepo and G. Merino, Phys. Chem. Chem. Phys., 2015, 17, 8769–8775.
11. J. O. C. Jimenez-Halla, Y.-B. Wu, Z.-X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778.
12. R. Grande-Aztatzi, J. L. Cabellos, R. Islas, I. Infante, J. M. Mercero, A. Restrepo and G. Merino, Phys. Chem. Chem. Phys., 2015, 17, 4620–4624.
13. Z.-H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y.-H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141.
14. S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350–12355.
15. M.-H. Wang, X. Dong, Z.-H. Cui, M. Orozco-Ic, Y.-H. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775.
16. A. C. Castro, G. Martínez-Guajardo, T. Johnson, J. M. Ugalde, Y.-B. Wu, J. M. Mercero, T. Heine, K. J. Donald and G. Merino, Phys. Chem. Chem. Phys., 2012, 14, 14764.
17. J.-C. Guo, L.-Y. Feng, J. Barroso, G. Merino and H.-J. Zhai, Chem. Commun., 2020, 56, 8305–8308.
18. J. Xu, X. Zhang, X. Yu, Y.-H. Ding, K. H. Bowen and J. Phys, Chem. Lett., 2017, 8, 2263–2267.
19. J.-C. Guo, L.-Y. Feng, X.-Y. Zhang and H.-J. Zhai, J. Phys. Chem. Lett., 2018, 122, 1138–1145.
20. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
21. V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 1–10.
22. L.-M. Yang, E. Ganz, Z. Chen, Z.-X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501.
23. G. Merino, M. A. Méndez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372.
24. F. Ortiz-Chi and G. Merino, GLOMOS, Mérida, México, 2020.
25. R. Grande-Aztatzi, P. R. Martínez-Alanis, J. L. Cabellos, E. Osorio, A. Martínez and G. Merino, J. Comput. Chem., 2014, 35, 2288–2296.
26. A. Ramirez-Manzanares, J. Peña, J. M. Azpiroz and G. Merino, J. Comput. Chem., 2015, 36, 1456–1466.
27. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
30. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, H. Borkent, W. Laarhoven, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
32. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
33. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
34. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
35. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
36. G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371.
37. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
38. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
39. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
40. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
41. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
42. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, Cinvestav-Mérida, México, 2016.
43. F. E. Jorge, A. Canal Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 064108.
44. S. Fias, Z. Boisdenghien, T. Stuyver, M. Audiffred, G. Merino, P. Geerlings and F. de Proft, J. Phys. Chem. A, 2013, 117, 3556–3560.
45. P. Pröhm, N. Schwarze, C. Muller, S. Steinhauer, H. Beckers, S. M. Rupf and S. Riedel, Chem. Commun., 2021 10.1039/D1CC01088C.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01325d

---