Open Access Article
Open Access ArticleSingle-chain magnet behavior in a finite linear hexanuclear molecule†
Felix
Houard
 a,
Frederic
Gendron
a,
Frederic
Gendron
 a,
Yan
Suffren
a,
Yan
Suffren
 a,
Thierry
Guizouarn
a,
Vincent
Dorcet
a,
Guillaume
Calvez
a,
Thierry
Guizouarn
a,
Vincent
Dorcet
a,
Guillaume
Calvez
 a,
Carole
Daiguebonne
a,
Olivier
Guillou
a,
Carole
Daiguebonne
a,
Olivier
Guillou
 a,
Boris
Le Guennic
a,
Boris
Le Guennic
 a,
Matteo
Mannini
a,
Matteo
Mannini
 b and
Kevin
Bernot
b and
Kevin
Bernot
 *ac
*ac
aUniv Rennes, INSA Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes), UMR 6226, F 35000, Rennes, France. E-mail: kevin.bernot@insa-rennes.fr
bLAboratory for Molecular Magnetism (LA.M.M.), Dipartimento di Chimica “Ugo Schiff”(DICUS), Università degli Studi di Firenze, INSTM, UdR Firenze, Via della Lastruccia n. 3, Sesto Fiorentino (FI), 50019, Italy
cInstitut Universitaire de France, 1 rue Descartes, 75005, Paris, France
First published on 9th July 2021
Abstract
The careful monitoring of crystallization conditions of a mixture made of a TbIII building block and a substituted nitronyl-nitroxide that typically provides infinite coordination polymers (chains), affords a remarkably stable linear hexanuclear molecule made of six TbIII ions and five NIT radicals. The hexanuclear units are double-bridged by water molecules but ab initio calculations demonstrate that this bridge is inefficient in mediating any magnetic interaction other than a small dipolar antiferromagnetic coupling. Surprisingly the hexanuclears, despite being finite molecules, show a single-chain magnet (SCM) behavior. This results in a magnetic hysteresis at low temperature whose coercive field is almost doubled when compared to the chains. We thus demonstrate that finite linear molecules can display SCM magnetic relaxation, which is a strong asset for molecular data storage purposes because 1D magnetic relaxation is more robust than the relaxation mechanisms observed in single-molecule magnets (SMMs) where under-barrier magnetic relaxation can operate.
Introduction
Single-chain magnets (SCMs)1,2 are molecules whose magnetic relaxation is confined in one dimension. An efficient SCM combines a strong interaction between its anisotropic spin carriers with a good magnetic insulation from the neighboring chains.3–5 At low temperature, such topologic and magnetic configurations give rise to a correlation length between spin carriers that can be considered as a 1D magnetic domain on which magnetic information can be encrypted.6The design of new SCMs with enhanced magnetic behavior7–16 relies on the use of coordination chemistry tools and can be performed in two ways. First, the selection of metal centers and their surrounding ligands permits an optimization of the magnetic behavior of the SCMs by enhancing the magnetic anisotropy of the metal ion and/or the ratio between intra- and interchain magnetic interactions.17–19 Second, a careful tuning of the organic ligands can provide new properties to the magnetic chains such as luminescence,20–22 photomagnetic behavior,23–25 magnetic switching,14,26–29 magneto-electric coupling,30,31 magnetochiral dichroism,32 spin helicity,33 or gelation ability.34,35 We have explored this second strategy recently using TbIII ions and nitronyl-nitroxide radicals36–48 substituted by alkyl chains. We showed that the chains of formula [(Tb(hfac)3)6(NITPhOHexyl)5(H2O)2]n (with hfac− = hexafluoroacetylacetonate and NIT-Ph-O-Hexyl = 2-(4′-(hexyloxy)phenyl)-4,4,5,5-tetramethylimidazolin-1-oxyl-3-oxide) can be organized in the crystal packing to form chiral supramolecular nanotubes of single-chain magnets.49 In this paper, we report how chains can be converted into finite hexanuclear species (latter called hexanuclears) with an enhanced SCM behavior.
Results and discussion
Hexanuclear formation process
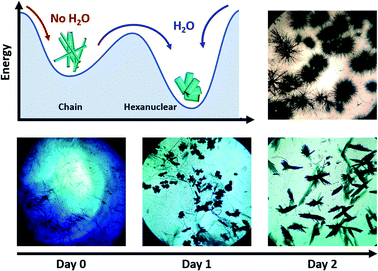
The compound is obtained by the reaction of equimolar amounts of NIT-Ph-O-Hexyl with Tb(hfac)3·2H2O in boiling heptane (see ESI† for details). The reaction mixture crystalizes after three days at ambient temperature.Usually very thin needle-like light green crystals of chains appear but in some rare cases we noticed that plate-like crystals polymorph could be observed during crystal growth (Fig. 1 and S1†). Needle and plates have chemical similarities since they share the same vibrational bands and became quickly amorphous when removed from the mother solution (see Fourier Transform Infra-Red spectroscopy (FTIR) and Powder X-ray Diffraction (PXRD), Fig. S2 and S3†). After a careful screening of the crystallization conditions, we observed that moisture triggers the predominance of plates over needles: crystals of chains always appear first and can be converted into plates in 3 days of slow evaporation if humidity level is high enough (Fig. 1). Based on this observation we have been able to obtain pure batches of plate-like crystals, by conducting crystallization in water-saturated condition in closed vials (see ESI†). Accordingly, what was an awkward by-product in the synthesis of chains, could be rationally investigated.
Crystal structure of the hexanuclears
Crystal structure determination on plate-like crystals suggests the formation of TbIIIhexanuclears of formula [(Tb(hfac)3)6(NITPhOHexyl)5(H2O)2]·CHCl3·C7H16. They crystallize in a monoclinic system, space group P21/n (Tables S1 and S2,†Fig. 2, S3 and S4†). The asymmetric unit is made of five NIT radicals that alternate with six Tb(hfac)3 units to form a linear molecule ended by water capped Tb(hfac)3 units.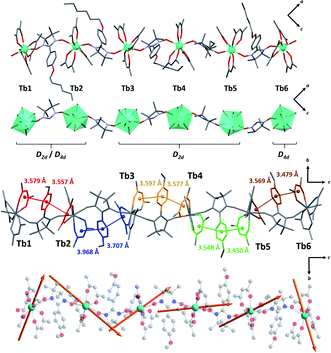 | ||
| Fig. 2 (From top to bottom with solvent molecules, hydrogen and fluorine atoms omitted) Representations of the asymmetric unit; simplified magnetic backbone that highlight the coordination polyhedra; representation of the stacking interactions; representation of the easy axes of the magnetization for the TbIII ground state on the model compound of the hexanuclear (see ESI†). | ||
All TbIII ions are eight coordinated by eight oxygen atoms (six from the hfac− ligands and two from NIT radicals) excepted terminal Tb1 and Tb6 ions where one radical is substituted by a water molecule. Coordination polyhedra are D2d triangular dodecahedra for Tb1, Tb2, Tb3, Tb4 and Tb5 (the first two are also close to D4d square antiprism) and D4d square antiprism for Tb6 (Table S3†). Tb-Orad distances are in the range of 2.36–2.41 Å and shortest intramolecular distance between TbIII ions within the molecule is 8.40 Å. These values are close to the ones reported on chains and highlight the chemical similarities between the two derivatives.
Molecules based on β-diketonate and NIT units usually host numerous π-stacking interaction pathways.50 This is again observed here and inter-centroid distances in the hexanuclears are similar to the one observed in chains (dπ–π = 3.4–3.9 Å) but with more tilted orientations (α = 9.6–24.3°, except for Tb4–Tb5 rings where α = 3.7–4.2°) indicating potentially weaker π-interactions.
The terminal water molecules of two consecutive hexanuclears interact two-by-two in a very similar way as the one observed in the crystalline Tb(hfac)3 dihydrate.51,52 This interaction is tailored by the strong Lewis acidity of the Tb(hfac)3 units that favour interaction between the electron-poor water oxygen atoms of two neighboring molecules. This induces an intermolecular Tb–Tb distance of 6.05 Å that is shorter than the mean value of the intramolecular one (8.40 Å). This will be a key point for the investigation of the magnetic properties of the hexanuclears.
Overall, this non-covalent bonding between consecutive units, coupled with the symmetry operations of the P21/n space group generates a supramolecular arrangement of hexanuclears along the [502] direction (Fig. 3 and 4). Perpendicularly to this direction, shortest Tb–Tb interchain distance is 11.33 Å. This excludes any intermolecular magnetic interactions between the molecules as well as long-range magnetic ordering. Finally, one chloroform and one heptane molecules per asymmetric unit are found (Fig. S4†).
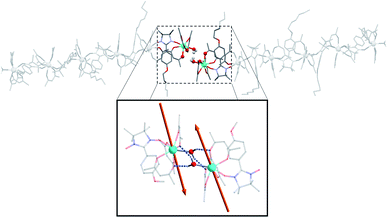 | ||
| Fig. 3 Representation of two neighbouring hexanuclears that stand along the [502] direction, together with the H-bond network between the terminal water molecules highlighted. Tb–Tb distance is 6.05 Å and O⋯H distance is 2.22 and 2.33 Å (fluorine and hydrogen atoms omitted for clarity). (Inset) Representation of the easy axes of the magnetization for the TbIII ground state in the dimer model that simulates the extremities of the hexanuclears (see ESI†). | ||
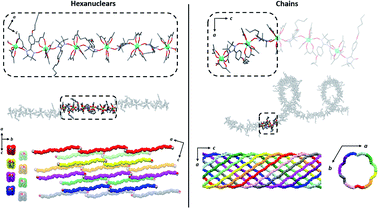 | ||
| Fig. 4 Comparison of the hexanuclears and the chains49 (from top to bottom with solvent molecules, hydrogen and fluorine atoms omitted): representations of the molecules with the asymmetric unit as dotted square; representation of the crystal packing along and perpendicular to the propagation direction of the molecules ([502] direction for the hexanuclears, -axis for the chains). | ||
It is worth comparing the finite hexanuclear molecules obtained here with the previously reported chains.49 At a first glance, one could think that the chains form first and that water molecules cut it in special points to form the finite molecule. However, no obvious “cutting point” can be found on the chains using either the symmetry operation of the space group, the number of repeating asymmetric unit, the Tb coordination polyhedron or the calculated easy-magnetic axes orientation (Fig. 4).
One can also compare the two crystallization routes (Fig. 1): (i) the transformation of chains into hexanuclear units is not strictly a single-crystal-to-single-crystal transformation because it occurs in the mother solution. So, it is likely that the chains decompose and then the presence of water triggers the crystallization of the hexanuclear compounds; (ii) hexanuclear can be obtained directly from the mother solution if the crystallization is conducted in water-saturated conditions. The chain crystals (needles) are not observed but directly the hexanuclear units (platelets).
The crystal packing is also very different (Fig. 4). Hexanuclears are water bridged along the [502] direction and then further stack one over the other. This contrasts with what seen on chains where supramolecular interaction between chains induce a helicity and constrain them to be wrapped eleven by eleven to form supramolecular nanotubes that further stack in a hexagonal lattice.
It can be noted that, as far we tested it, variation of the stoichiometry, the temperature or humidity conditions does not allow controlling the nuclearity of the molecule because as soon as humidity is present during the crystallization, hexanuclears are obtained. This suggests that this species is particularly stable on the thermodynamic point of view. This is rather surprising because linear polynuclear molecules usually tend to form wheels to gain in stability53 even when combined in larger edifices.54
Stability of the hexanuclears: thermal and luminescent characterization
The hexanuclears single-crystals quickly became amorphous when taken off the mother solution. This is due to solvent loss as 10% of the cell volume (Vvoid = 2577 Å3 for a 1.2 Å kinetic radius) is filled with n-heptane and chloroform molecules that quickly evaporate. Despite losing their long-range order and diffracting power, crystals are still robust and can be collected easily. Indeed, SEM images show that crystals are still observable under vacuum conditions (Fig. S1†) and don't collapse into a powder. This is probably because the main intermolecular contacts between the hexanuclear units are via their alkyl chains, not with the crystallization solvent molecules.However, to check that a reliable magnetic measurement can be performed on these amorphous compounds, coupled FTIR spectroscopy and thermogravimetric and thermodifferential analyses (TGA/TDA) have been performed on freshly dried amorphous crystals (Fig. S5 and S6†). They show that the compound is stable up to 124 °C (coordinated water molecules departure) and that no other significant gas emission is observed below 200 °C. This sustains the hypothesis that the fast amorphization is due to crystallization solvent loss (chloroform and heptane) and that the molecular skeleton of the compound is preserved at room temperature (no gas emission before full decomposition of the compound at high temperature).
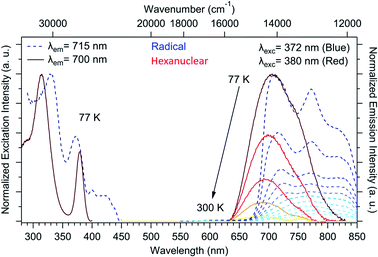
The chemical integrity of the compound can be confirmed using luminescence measurements. Such measurements provide a very sensitive estimation of the stability of NIT-TbIII based compounds49 because both uncoordinated reactants emit in the visible: a line-shaped green emission for the uncoordinated Tb(hfac)3 unit (because of the efficient antenna effect of the β-diketonate ligand)55 and a broad red emission for the NIT radical.56,57 When the two molecules are coordinated, TbIII emission is quenched while the NIT radical emission is blue-shifted by metal–ligand charge transfer (MLCT).57,58 This is what we observed here with no emission of the free TbIII ion and a blue-shifted NIT radical emission (Fig. 5), indicating the efficient Tb-NIT coordination and the absence of uncoordinated TbIII and NIT radical. Moreover, the optical signature of the hexanuclears is different from the ones of the chains (Fig. S7†).
All these thermal and luminescent investigations unambiguously demonstrate that the hexanuclears are preserved upon crystal amorphization and that magnetic investigation can be trustily performed.
Static (dc) magnetic properties
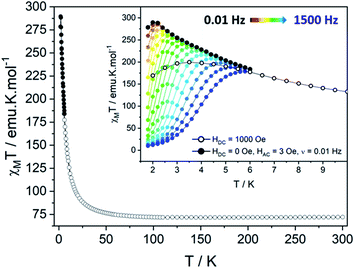
The temperature dependence of the magnetic susceptibility χM has been measured on polycrystalline sample under static field (HDC = 1000 Oe). It shows a χMT(300K) value of 72.02 emu K mol−1, close to the theoretical value χMT(300K) = 72.795 emu K mol−1 expected for 6 TbIII ions and 5 uncoupled NIT radicals (with gS = 2, S = ½, gJ = 3/2 and J = 6). By decreasing the temperature, this value slightly increases until 50 K then sharply reaches a maximum of χMT(dc) = 199.65 emu K mol−1 at 3.5 K. This increase is followed by an abrupt drop due to saturation effects. Hence, a more reliable maximum of χMT(ac) = 289.54 emu K mol−1 is observed at 2 K for ν = 0.019 Hz (HAC = 3 Oe oscillating field). The saturation is also confirmed by the magnetization curve recorded at 2 K that rises very quickly as the field is applied to reach a value of 29.4 μB at 50 kOe (Fig. S8†), slightly lower than the theoretical saturation value expected on a polycrystalline sample (Ms = 32.0 μB). A last confirmation arises from specific heat measurement that does not show any divergence of the specific heat capacity (Cp) in the low temperature region as it can be observed in the presence of long-range magnetic ordering (Fig. S9†).Theoretical description of the hexanuclears and magnetic coupling
The magnetic anisotropy of each of the TbIII centers can be determined by considering either [Tb(hfac)3(NIT)2] units for the central TbIII ions (Tb2, Tb3, Tb4, Tb5) or [Tb(hfac)3(NIT) (H2O)] units for the terminal TbIII ions (Tb1, Tb6) (see ESI for computational details and models Fig. S10†).The calculated relative energies of the states deriving from the 7F6 level of the Tb3+ ion in the model compounds, and the associated EPR g-factors (for the states exhibiting a pseudo-spin S = ½) are given in Table S4.† In all model compounds, the ground state (GS) corresponds to a non-Kramers doublet that derives formally from the MJ states ±6 of the 7F6 level. More precisely, the nature of these states results from an admixture by the crystal-field of the different MJ states. The calculated contributions for the GS wave-function are given in Table S5.† The MJ = ±6 state is the dominant contribution, but a sizable one is calculated from the MJ = ±4 state. Interestingly, the contribution of the MJ = ±6 state into the GS wave-function differs significantly between the six model compounds, in agreement with the small differences observed in the first coordination sphere of the TbIII ions (Table S3†).
The [Tb(1)-NIT2]2− model compound has the lowest MJ = ±6 contribution (76%), leading to the smallest value for the parallel component of the EPR g-factors (g‖ = 16.58). By comparison, the [Tb(5)-NIT-H2O]− model compound exhibits a GS with a EPR g-factor of 17.26 because of the largest contribution (91%) of MJ = ±6 into the wave-function. This is linked with a trend in the modification of the energetic splitting. In [Tb(2)-NIT2]2−, a relatively small energy gap of 16 cm−1 is calculated between the GS and ES1, whereas this energy gap increases to 85 cm−1 for [Tb(5)-NIT-H2O]−. The overall splitting of the 7F6 level also differs between the six building blocks of the hexanuclears, with calculated splitting of 361 and 388 cm−1 for [Tb(5)-NIT-H2O]− and [Tb(6)-NIT-H2O]−, respectively, whereas splitting of 431, 470, 486 and 527 cm−1, are calculated for Tb(1), Tb(2), Tb(4), and Tb(3), respectively.
The orientation of the easy axes of the magnetization for the GS of the six model compounds is shown in Fig. 2 and reveals different orientations. The GS of the model compounds exhibits large magnetic anisotropy, characterized by extremely large parallel components of the EPR g-factors (c.a. 17) and perpendicular components equal to zero. For comparison, a pure MJ = ±6 state would possess a parallel component of 18.0.
For the central Tb centers (Tb2, Tb3, Tb4, Tb5), the easy axis goes mostly along the NIT-Tb-NIT direction as observed on the chains. A very different scenario is observed for the terminal Tb1 and Tb6 atoms. As already observed by some of us on mononuclear molecules59 Tb1 and Tb6 magnetic axes are perpendicular to the Tb-O(water) direction and the plane of the water molecule. The coordinated water is the driving force for the localization of the easy-magnetic axes.
The calculated magnetic susceptibilities and magnetization for the six model compounds are shown in Fig. S11.† At room temperature, very similar χMT values of ca. 11.6 cm3 K mol−1 are calculated for all complexes. Due to a non-magnetic ES1 in [Tb(6)-NIT-H2O]−, the decrease in magnitude of χMT is stronger at very low temperature than in the other compounds. On the other hand, the presence of a very low-lying ES1 in [Tb(1)-NIT2]2− and [Tb(2)-NIT2]2− leads to calculated magnetizations at 2 K that do not reach saturation at 5 Tesla, whereas for the other model compounds, the calculated magnetizations saturate at 4.5 μB.
On 3d-based chains, straightforward ab initio calculations of intrachain coupling constants have been recently reported60 but are unlikely to be directly applicable on the hexanuclears. Indeed, the reliable determination of magnetic interactions on Ln-NIT compounds would require the use of state-of-the-art wave function-based calculations (CASSCF/DDCI) that are challenging even on isolated NIT-YIII-NIT molecules.61 Moreover, the modelization of the magnetic interaction pathways is trickier here because SCM made of NIT radicals and lanthanide ions are known to host nearest (NIT-Ln) and next-nearest (Ln–Ln, and NIT–NIT) neighbor magnetic interactions, the latter being stronger than the former.46 Last, the very large asymmetric unit of the hexanuclears (6 TbIII ions and five radicals) complicate further the study and does not allow for a reliable determination of all of the intramolecular magnetic interactions.
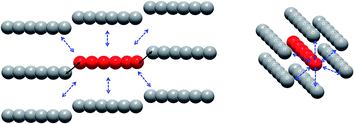
On the intermolecular point of view two main interaction pathways can be considered (Scheme 1): perpendicular (dotted arrows) or along the [502] direction (full arrows). For the first case, the Tb–Tb distance is >11 Å so significant magnetic interaction can be discarded. For the second one, Tb–Tb distance is 6.05 Å and hexanuclear units are water bridged by the terminal water molecules (Fig. 3). Even if specific heat measurements demonstrate that no 3D magnetic ordering is observed, it is crucial to determine the nature and value of a potential interaction to assess if the compound behaves as an alternating chain of coupled hexanuclear units or if hexanuclears are more or less magnetically isolated.
We used the dimer model (Fig. S10†) to calculate the magnetic susceptibility as a function of the temperature (Fig. S12†). At low temperature, the decrease of the χMT product is reinforced by a small intramolecular antiferromagnetic (AFM) interaction between the two Tb3+ ions. Magnetic exchange is neglected because of the large Tb–Tb distance and the isotropic dipolar contribution of the AFM interaction is found of ca. −0.11 cm−1. This value can be readily understood by the almost collinear orientation of the easy magnetic axes as shown on Fig. 3.
Supramolecular interactions are efficient to build SCMs based on 3d metal ions62,63 whereas they are not with 4f ions because of the inner character of their orbitals. Accordingly, the very small dipolar coupling observed between Tb1 and Tb6 ions is unlikely to be strong enough to propagate a correlation length beyond the hexanuclears because it is several orders of magnitude smaller than the ones operating in the molecule as demonstrated on similar NIT-based compound.37,46–48,61 Accordingly, the divergence of the χMT at low temperature (Fig. 6) can be ascribed to the creation of a correlation length that is confined within each hexanuclear.
When the temperature is lowered the χMT product varies as χMT = Ceff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Δξ/kBT) where Ceff is the effective Curie constant, kB the Boltzmann constant and Δξ the correlation energy required to create a domain wall that can be extracted from dc or ac measurements (Δξ(dc) or Δξ(ac), respectively). These values were estimated at Ceff = 66.86 emu K mol−1 and Δξ(dc) = 6.9 ± 0.1 K (R2 = 0.99842) (Fig. S12†). The Δξ(dc) value is comparable to the one observed on the chains derivative (Δξ(dc) = 5.5 ± 0.5 K) (Table 1). We performed diamagnetic doping of the hexanuclears by YIII or LuIII ions to evaluate statistically the dimension of the correlation length. SEM/EDS measurements showed expected Tb/Y or Tb/Lu ratio when pointing at large areas. But as soon as local measurements were taken in spot mode very strong discrepancies occur as a sign of segregation between hexanuclear units made of Tb and others of Y/Lu ions. Consequently, this approach has been dismissed.
exp(Δξ/kBT) where Ceff is the effective Curie constant, kB the Boltzmann constant and Δξ the correlation energy required to create a domain wall that can be extracted from dc or ac measurements (Δξ(dc) or Δξ(ac), respectively). These values were estimated at Ceff = 66.86 emu K mol−1 and Δξ(dc) = 6.9 ± 0.1 K (R2 = 0.99842) (Fig. S12†). The Δξ(dc) value is comparable to the one observed on the chains derivative (Δξ(dc) = 5.5 ± 0.5 K) (Table 1). We performed diamagnetic doping of the hexanuclears by YIII or LuIII ions to evaluate statistically the dimension of the correlation length. SEM/EDS measurements showed expected Tb/Y or Tb/Lu ratio when pointing at large areas. But as soon as local measurements were taken in spot mode very strong discrepancies occur as a sign of segregation between hexanuclear units made of Tb and others of Y/Lu ions. Consequently, this approach has been dismissed.
| Chains | Hexanuclears | |
|---|---|---|
| Δξ(dc) (K) | 5.5 ± 0.5 | 6.9 ± 0.1 |
| ΔI/kB (K)/τI (s) | 29.6 ± 0.5/3.4 ± 0.5 × 10−8 | 27.7 ± 0.1/2.7 ± 0.1 × 10−7 |
| ΔF/kB (K)/τF (s) | 25.5 ± 0.2/2.4 ± 0.3 × 10−7 | 24.4 ± 0.5/1.1 ± 0.2 × 10−6 |
| Δξ(ac) (K) | 4.1 ± 0.7 | 3.3 ± 0.6 |
| T* (K) | 2.1 | 2.4 |
| n (dc and ac) | 17; 5 | 18; 3 |
| α (at 1.8 K) | 0.615 | 0.374 |
| H c (Oe) | 2400 | 4100 |
| M R (μB/%Msat) | 2.09/38% | 19.83/62% |
| T B (K) | 1.39 ± 0.02 | 1.34 ± 0.03 |
Dynamic (ac) magnetic properties
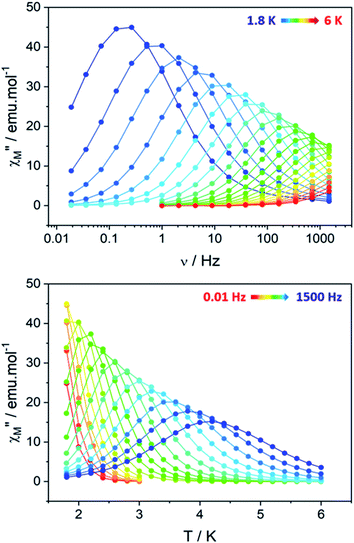
Clear out-of-phase susceptibility (χM′′) signal is observed in absence of dc field at 2 K (Fig. 7, S14–S15†). The magnetic relaxation accelerates when Hdc is increased as expected for an SCM (Fig. S16†).64,65 This is the opposite in-field behavior as the one observed on ferromagnetically-coupled SMM24 that would present an increase of χMT at low temperature but an enhanced in-field dynamic magnetic behavior.The out-of-phase susceptibility χM′′ shows frequency dependence up to 6 K, characteristic of slow relaxation of the magnetization66 with no broadening as one would observed if the six crystallographically independent TbIII ions were not correlated enough and relaxed independently.
The corresponding relaxation times τ were extracted using a generalized Debye model67,68 and fitted according to an Arrhenius law τ = τ0 exp(Δeff/kBT) where Δeff is the effective energy barrier (Table S6†).69
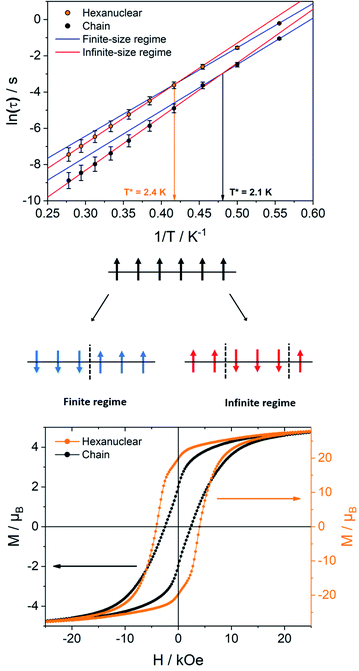
The relaxation dynamics of SCMs is ruled by two thermally activated processes that correspond to the finite- and infinite-magnetic chains when compared to the correlation length.70,71 Their effective energy barriers can be expressed respectively as ΔF = ΔA + Δξ(ac), and ΔI = ΔA + 2Δξ(ac) (with ΔA the anisotropic contribution of the TbIII ion and Δξ(ac) the correlation length extracted from dynamic magnetic measurements). In our case, the finite-regime is characterized by ΔF/kB = 24.4 ± 0.5 K with τF = (1.1 ± 0.2) × 10−6 s (R2 = 0.99884), while for the infinite-regime, ΔI/kB = 27.7 ± 0.1 K with τI = (2.7 ± 0.1) × 10−7 s (R2 = 0.99989), with a crossover temperature between the two regimes at T* = 2.4 K (Fig. 8). Hence, the correlation energy Δξ can be estimated as Δξ(ac) = ΔI − ΔF = 3.3 ± 0.6 K. This value is rather small but is in line with what found on the chains derivative. Δξ can be linked to the average number n of the correlated magnetic anisotropic units through n ≈ 2ξ ≈ exp(Δξ/kBT*). Using Δξ(ac) and given the small values and the large confidence interval, n is comprised between 3 and 5. This is in agreement with the observation of both finite and infinite regimes in this hexanuclear molecule (n = 6).
An extended Debye model16 is applied to determine the distribution (α) of the relaxation times (Table S7†). As a reminder, the α value for an ideal relaxation dynamic tends towards zero (all the molecules share the same single relaxation time τ) while it is 1 for a totally disordered relaxation scheme. In our case, α spread from 0.16 at 4 K to 0.37 at 1.8 K (Fig. S17†) and only one semi-circle is observed ruling out the possibility of an SMM behavior as several relaxations should be observed because the six TbIII ions show different crystal-field splitting and different MJ contributions to the ground-state wavefunction. Additionally, 97% of the sample relaxes slowly at 1.8 K (1 − (χs/χT) = 97% with χs and χT the adiabatic and the isothermal susceptibility, respectively).
The ability of the hexanuclears to store a magnetic information is evaluated by its magnetic hysteresis measurements (Fig. 8). At 0.5 K, a broad opening of the magnetic hysteresis loop is observed (coercive field Hc = 4100 Oe, remnant magnetization Mr = 19.83 μB, 67% of the saturation value). The hysteresis is closed at 2 K (Fig. S18†). Within this range of temperature, the relaxation dynamics is ruled by the finite-size regime and the blocking temperature TB in our operating conditions (magnetic field sweep rate of 15.5 Oe s−1, with a τexp = 21.3 s) can be estimated considering the modified Arrhenius equation TB = ΔF/[kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(τexp/τF)] = 1.34 ± 0.03 K.
ln(τexp/τF)] = 1.34 ± 0.03 K.
It is then clear from all magnetic measurements that the hexanuclears, despite being finite molecules, behave as SCM because they are molecules longer than the correlation length Δξ they are hosting (Fig. 8). Interestingly, this difference between molecule length and correlation length is big enough to allow for the observation of finite and infinite relaxation regimes in the hexanuclears. This shows that spin-reversal can occur at an extremity of the molecule (finite regime) but as well on central position (infinite regime).
Hexanuclears show an enhanced SCM behavior when compared to chains. Indeed, they show a magnetic hysteresis that is steeper with Hc and MR values almost doubled (Fig. 8). A dynamic magnetic relaxation with similar activation energies but slower relaxation times is also observed (Table 1). The reason for this optimized magnetic behavior could reside in the quality of the intra-molecular magnetic coupling between chains and hexanuclears because TbIII magnetic anisotropies are almost similar between chains and hexanuclears. Chains are curled infinite molecules while hexanuclears form linear arrangements of finite molecules (Fig. 4). This second arrangement could favor efficient overlap of magnetic orbitals in the hexanuclears.
Conclusions
This study reports the investigation of what was a randomly appearing by-product of molecular chains and its rational synthesis into stable and pure batches of linear hexanuclear molecule. Its formation is triggered by moisture condition and the so-called hexanuclear shows an SCM behavior. Indeed, we demonstrate that a finite linear molecule can behave as an SCM if its length is big enough when compared to its magnetic correlation length. Additionally, by comparing the hexanuclears with their previously reported infinite counterparts, the chains, we show that the SCM behavior is enhanced in the former. This finding is important in the search for temperature- and air-stable molecules for new molecular data storage devices. Indeed, SCMs host a robust magnetic relaxation that, contrary to the one observed on SMM, is not affected by under-barrier magnetic relaxation. Accordingly, the hexanuclears are promising candidates for surface deposition because they combine a good chemical stability with an SCM magnetic relaxation. This is a strong asset as molecules are far simpler to deposit on surfaces than chains that are insoluble by nature. Indeed, their deposition relies on their partial destruction to form finite objects with large and uncontrolled length distribution. On the contrary, the use of hexanuclears could be a way to form deposits of monodisperse SCM and enhance their ability to self-organize on surface.Author contributions
Felix Houard: PhD in charge of the project. Frederic Gendron: Post-doc in charge of the theoretical calculations and quantum chemical simulations. Yan Suffren: As. Prof. in charge of the luminescence measurements. Thierry Guizouarn: Engineer in charge of very low temperature 3He magnetic measurments. Vincent Dorcet: Crystallographer. Guillaume Calvez: As. Prof. in charge of coupled ATG/IR investigation. Carole Daiguebonne: As. Prof. in charge of crystal structure refinements. Olivier Guillou: Prof. co-conceptor of the study. Boris Le Guennic: CNRS Research Director who coordinate the theoretical calculations and quantum chemical simulations. Matteo Mannini: As. Prof., co-director of F Houard PhD thesis, co-conceptor of the study. Kevin Bernot: As. Prof., co-director of F Houard PhD thesis, co-conceptor of the study, corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by INSA Rennes, CNRS, Rennes Metropole. CDifX is acknowledged for the assistance in crystal structure data collection. Stéphane Freslon is acknowledged for help on STA-FTIR measurements. K. B. acknowledges the Institut Universitaire de France (IUF). F. G. and B. L. G. thank the French GENCI/IDRIS-CINES centres for high-performance computing resources. F. G. and B. L. G. acknowledge the Stratégie d’Attractivité Durable (SAD18006 - LnCPLSMM) for financial support. MM acknowledge MIUR-Italy (“Progetto Dipartimenti di Eccellenza 2018–2022, ref. 96C1700020008” allocated to Department of Chemistry “Ugo Schiff”) and Fondazione Ente Cassa di Risparmio di Firenze (projects Project SPINE-2 2020.1634) for the economic support.Notes and references
- C. Coulon, H. Miyasaka and R. Clérac, in Single-Molecule Magnets and Related Phenomena, ed. R. Winpenny, Springer Berlin Heidelberg, 2006, pp. 163–206 Search PubMed.
- L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750–4758 RSC.
- A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760–1763 CrossRef CAS PubMed.
- G. Poneti, K. Bernot, L. Bogani, A. Caneschi, R. Sessoli, W. Wernsdorfer and D. Gatteschi, Chem. Commun., 2007, 1807–1809 RSC.
- H. Miyasaka, T. Madanbashi, K. Sugimoto, Y. Nakazawa, W. Wernsdorfer, K. Sugiura, M. Yamashita, C. Coulon and R. Clerac, Chem.–Eur. J., 2006, 12, 7029–7040 CrossRef PubMed.
- V. Pianet, M. Urdampilleta, T. Colin, R. Clérac and C. Coulon, Phys. Rev. B, 2017, 96, 214429 CrossRef.
- J.-H. Wang, Z.-Y. Li, M. Yamashita and X.-H. Bu, Coord. Chem. Rev., 2021, 428, 213617 CrossRef CAS.
- J. Yang, Y.-F. Deng and Y.-Z. Zhang, Dalton Trans., 2020, 49, 4805–4810 RSC.
- L. Shi, D. Shao, X.-Q. Wei, K. Dunbar and X. Wang, Angew. Chem., Int. Ed., 2020, 59, 10379–10384 CrossRef CAS PubMed.
- M. Rams, A. Jochim, M. Böhme, T. Lohmiller, M. Ceglarska, M. M. Rams, A. Schnegg, W. Plass and C. Näther, Chem. - Eur. J., 2020, 26, 2837 CrossRef CAS PubMed.
- F. Zhao, Z.-P. Dong, Z.-L. Liu and Y.-Q. Wang, CrystEngComm, 2019, 21, 6958–6963 RSC.
- C. Pichon, N. Suaud, C. Duhayon, N. Guihéry and J.-P. Sutter, J. Am. Chem. Soc., 2018, 140, 7698–7704 CrossRef CAS PubMed.
- C. Pichon, B. Elrez, V. Béreau, C. Duhayon and J. P. Sutter, Eur. J. Inorg. Chem., 2018, 2018, 340–348 CrossRef CAS.
- W. Jiang, C. Jiao, Y. Meng, L. Zhao, Q. Liu and T. Liu, Chem. Sci., 2018, 9, 617–622 RSC.
- Q. Liu, J.-X. Hu, Y.-S. Meng, W.-J. Jiang, J.-L. Wang, W. Wen, Q. Wu, H.-L. Zhu, L. Zhao and T. Liu, Angew. Chem., Int. Ed., 2021, 60, 10537 CrossRef CAS PubMed.
- M. G. F. Vaz, R. A. A. Cassaro, H. Akpinar, J. A. Schlueter, P. M. Lahti and M. A. Novak, Chem. - Eur. J., 2014, 20, 5460–5467 CrossRef CAS PubMed.
- E. Bartolome, J. Bartolome, S. Melnic, D. Prodius, S. Shova, A. Arauzo, J. Luzon, L. Badia-Romano, F. Luis and C. Turta, Dalton Trans., 2014, 43, 10999–11013 RSC.
- X. Zhang, S. Liu, V. Vieru, N. Xu, C. Gao, B. W. Wang, W. Shi, L. F. Chibotaru, S. Gao, P. Cheng and A. K. Powell, Chem. - Eur. J., 2018, 24, 6079–6086 CrossRef CAS PubMed.
- J. Jung, F. Le Natur, O. Cador, F. Pointillart, G. Calvez, C. Daiguebonne, O. Guillou, T. Guizouarn, B. Le Guennic and K. Bernot, Chem. Commun., 2014, 50, 13346–13348 RSC.
- W.-B. Chen, L. Zhong, Y.-J. Zhong, Y.-Q. Zhang, S. Gao and W. Dong, Inorg. Chem. Front., 2020, 7, 3136–3145 RSC.
- M. Al Hareri, Z. Ras Ali, J. Regier, E. L. Gavey, L. D. Carlos, R. A. S. Ferreira and M. Pilkington, Inorg. Chem., 2017, 56(13), 7344–7353 CrossRef CAS PubMed.
- E. Bartolome, J. Bartolome, A. Arauzo, J. Luzon, L. Badia, R. Cases, F. Luis, S. Melnic, D. Prodius, S. Shova and C. Turta, J. Mater. Chem. C, 2016, 4, 5038–5050 RSC.
- R. Ababei, C. Pichon, O. Roubeau, Y.-G. Li, N. Bréfuel, L. Buisson, P. Guionneau, C. Mathonière and R. Clérac, J. Am. Chem. Soc., 2013, 135, 14840–14853 CrossRef CAS PubMed.
- G. Huang, G. Fernandez-Garcia, I. Badiane, M. Camara, S. Freslon, O. Guillou, C. Daiguebonne, F. Totti, O. Cador, T. Guizouarn, B. Le Guennic and K. Bernot, Chem. - Eur. J., 2018, 24, 6983–6991 CrossRef CAS PubMed.
- G. Huang, X. Yi, F. Gendron, B. Le Guennic, T. Guizouarn, C. Daiguebonne, G. Calvez, Y. Suffren, O. Guillou and K. Bernot, Dalton Trans., 2019, 48, 16053–16061 RSC.
- T. Liu, H. Zheng, S. Kang, Y. Shiota, S. Hayami, M. Mito, O. Sato, K. Yoshizawa, S. Kanegawa and C. Duan, Nat. Commun., 2013, 4, 2826 CrossRef.
- N. Hoshino, F. Iijima, G. N. Newton, N. Yoshida, T. Shiga, H. Nojiri, A. Nakao, R. Kumai, Y. Murakami and H. Oshio, Nat. Chem., 2012, 4, 921–926 CrossRef CAS PubMed.
- D.-P. Dong, T. Liu, S. Kanegawa, S. Kang, O. Sato, C. He and C.-Y. Duan, Angew. Chem., Int. Ed., 2012, 51, 5119–5123 CrossRef CAS PubMed.
- M. Hojorat, H. Al Sabea, L. Norel, K. Bernot, T. Roisnel, F. Gendron, B. Le Guennic, E. Trzop, E. Collet, J. R. Long and S. Rigaut, J. Am. Chem. Soc., 2020, 142, 931–936 CrossRef CAS PubMed.
- M. Scarrozza, P. Barone, R. Sessoli and S. Picozzi, J. Mater. Chem. C, 2016, 4, 4176–4185 RSC.
- M. Fittipaldi, A. Cini, G. Annino, A. Vindigni, A. Caneschi and R. Sessoli, Nat. Mater., 2019, 18, 239–334 CrossRef PubMed.
- M. Atzori, F. Santanni, I. Breslavetz, K. Paillot, A. Caneschi, G. L. J. A. Rikken, R. Sessoli and C. Train, J. Am. Chem. Soc., 2020, 142, 13908–13916 CrossRef CAS PubMed.
- I. Mihalcea, M. Perfetti, F. Pineider, L. Tesi, V. Mereacre, F. Wilhelm, A. Rogalev, C. E. Anson, A. K. Powell and R. Sessoli, Inorg. Chem., 2016, 55, 10068–10074 CrossRef CAS PubMed.
- O. Roubeau, A. Colin, V. Schmitt and R. Clérac, Angew. Chem., Int. Ed., 2004, 43, 3283–3286 CrossRef CAS PubMed.
- P. Grondin, O. Roubeau, M. Castro, H. Saadaoui, A. Colin and R. CléRac, Langmuir, 2010, 26, 5184–5195 CrossRef CAS PubMed.
- X. Meng, W. Shi and P. Cheng, Coord. Chem. Rev., 2019, 378, 134–150 CrossRef CAS.
- D. Luneau, Eur. J. Inorg. Chem., 2020, 2020, 597–604 CrossRef CAS.
- J. Sun, J. Xie, L. Li and J.-P. Sutter, Inorg. Chem. Front., 2020, 7, 1949–1956 RSC.
- J. Xie, H.-D. Li, M. Yang, J. Sun, L.-C. Li and J.-P. Sutter, Chem. Commun., 2019, 55, 3398–3401 RSC.
- W. Shi, X. Liu, X. Feng, K. R. Meihaus, X. Meng, Y. Zhang, L. Li, J.-L. Liu, Y.-Q. Zhang, P. Cheng and J. R. Long, Angew. Chem., Int. Ed., 2020, 59, 10610–10618 CrossRef PubMed.
- X. Liu, Y.-X. Wang, Z. Han, T. Han, W. Shi and P. Cheng, Dalton Trans., 2019, 48, 8989–8994 RSC.
- X. Liu, Y. Zhang, W. Shi and P. Cheng, Inorg. Chem., 2018, 57, 13409–13414 CrossRef CAS.
- R. A. A. Cassaro, S. G. Reis, T. S. Araujo, P. M. Lahti, M. A. Novak and M. G. F. Vaz, Inorg. Chem., 2015, 54, 9381–9383 CrossRef CAS PubMed.
- M. G. F. Vaz and M. Andruh, Coord. Chem. Rev., 2021, 427, 213611 CrossRef CAS.
- D. Luneau and P. Rey, Coord. Chem. Rev., 2005, 249, 2591–2611 CrossRef CAS.
- C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369–2388 CrossRef CAS PubMed.
- K. Katoh, K. Kagesawa and M. Yamashita, in World Scientific Reference on Spin in Organics, 2018, pp. 271–344 Search PubMed.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- F. Houard, Q. Evrard, G. Calvez, Y. Suffren, C. Daiguebonne, O. Guillou, F. Gendron, B. Le Guennic, T. Guizouarn, V. Dorcet, M. Mannini and K. Bernot, Angew. Chem., Int. Ed., 2020, 59, 780–784 CrossRef CAS PubMed.
- C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896 RSC.
- I. Y. Bagryanskaya, L. V. Politanskaya and E. V. Tretyakov, Inorg. Chem. Commun., 2016, 66, 47–50 CrossRef CAS.
- Q. Evrard, G. Cucinotta, F. Houard, G. Calvez, Y. Suffren, C. Daiguebonne, O. Guillou, A. Caneschi, M. Mannini and K. Bernot, Beilstein J. Nanotechnol., 2019, 10, 2440–2448 CrossRef CAS PubMed.
- G. A. Timco, T. B. Faust, F. Tuna and R. E. P. Winpenny, Chem. Soc. Rev., 2011, 40, 3067–3075 RSC.
- G. F. S. Whitehead, F. Moro, G. A. Timco, W. Wernsdorfer, S. J. Teat and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2013, 52, 9932–9935 CrossRef CAS PubMed.
- B. Koen, J. C. B. K. A. Gschneidner and V. K. Pecharsky, in Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 2005, pp. 107–272 Search PubMed.
- R. Beaulac, G. Bussiere, C. Reber, C. Lescop and D. Luneau, New J. Chem., 2003, 27, 1200–1206 RSC.
- A. Lannes, M. Intissar, Y. Suffren, C. Reber and D. Luneau, Inorg. Chem., 2014, 53, 9548–9560 CrossRef CAS PubMed.
- C. Lescop, G. Bussiere, R. Beaulac, H. Belisle, E. Belorizky, P. Rey, C. Reber and D. Luneau, J. Phys. Chem. Solids, 2004, 65, 773–779 CrossRef CAS.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- M. Böhme and W. Plass, Chem. Sci., 2019, 10, 9189–9202 RSC.
- J. Jung, M. Puget, O. Cador, K. Bernot, C. J. Calzado and B. Le Guennic, Inorg. Chem., 2017, 56, 6788–6801 CrossRef CAS PubMed.
- M. Ferbinteanu, H. Miyasaka, W. Wernsdorfer, K. Nakata, K.-i. Sugiura, M. Yamashita, C. Coulon and R. Clérac, J. Am. Chem. Soc., 2005, 127, 3090–3099 CrossRef CAS PubMed.
- M. Ding, B. Wang, Z. Wang, J. Zhang, O. Fuhr, D. Fenske and S. Gao, Chem. - Eur. J., 2012, 18, 915–924 CrossRef CAS PubMed.
- C. Coulon, R. Clérac, W. Wernsdorfer, T. Colin, A. Saitoh, N. Motokawa and H. Miyasaka, Phys. Rev. B, 2007, 76, 214422 CrossRef.
- M. G. Pini, A. Rettori, L. Bogani, A. Lascialfari, M. Mariani, A. Caneschi and R. Sessoli, Phys. Rev. B, 2011, 84, 094444 CrossRef.
- C. V. Topping and S. J. Blundell, J. Phys.: Condens. Matter, 2018, 31, 013001 CrossRef PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- C. Dekker, A. F. M. Arts, H. W. de Wijn, A. J. van Duyneveldt and J. A. Mydosh, Phys. Rev. B, 1989, 40, 11243–11251 CrossRef CAS PubMed.
- R. J. Glauber, J. Math. Phys., 1963, 4, 294–307 CrossRef.
- L. Bogani, R. Sessoli, M. G. Pini, A. Rettori, M. A. Novak, P. Rosa, M. Massi, M. E. Fedi, L. Giuntini, A. Caneschi and D. Gatteschi, Phys. Rev. B, 2005, 72 Search PubMed.
- J. H. Luscombe, M. Luban and J. P. Reynolds, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 5852–5860 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: additional structural, thermal, luminescent, theoretical and magnetic data. CCDC 2076378. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc02033a |
| This journal is © The Royal Society of Chemistry 2021 |