Open Access Article
Open Access ArticleDNAzyme- and light-induced dissipative and gated DNA networks†
Jianbang
Wang‡
a,
Zhenzhen
Li‡
a,
Zhixin
Zhou
 a,
Yu
Ouyang
a,
Junji
Zhang
a,
Yu
Ouyang
a,
Junji
Zhang
 b,
Xiang
Ma
b,
Xiang
Ma
 b,
He
Tian
b,
He
Tian
 b and
Itamar
Willner
b and
Itamar
Willner
 *a
*a
aInstitute of Chemistry, The Center for Nanoscience and Nanotechnology, The Hebrew University of Jerusalem, Jerusalem 91904, Israel. E-mail: Itamar.willner@mail.huji.ac.il
bKey Laboratory for Advanced Materials, Joint International Research Laboratory of Precision Chemistry and Molecular Engineering, Feringa Nobel Prize Scientist Joint Research Center, School of Chemistry and Molecular Engineering, Frontiers Center for Materiobiology and Dynamic Chemistry, East China University of Science and Technology, Shanghai 200237, P. R. China
First published on 20th July 2021
Abstract
Nucleic acid-based dissipative, out-of-equilibrium systems are introduced as functional assemblies emulating transient dissipative biological transformations. One system involves a Pb2+-ion-dependent DNAzyme fuel strand-driven network leading to the transient cleavage of the fuel strand to “waste” products. Applying the Pb2+-ion-dependent DNAzyme to two competitive fuel strand-driven systems yields two parallel operating networks. Blocking the competitively operating networks with selective inhibitors leads, however, to gated transient operation of dictated networks, yielding gated catalytic operations. A second system introduces a “non-waste” generating out-of-equilibrium, dissipative network driven by light. The system consists of a trans-azobenzene-functionalized photoactive module that is reconfigured by light to an intermediary state consisting of cis-azobenzene units that are thermally recovered to the original trans-azobenzene-modified module. The cyclic transient photoinduced operation of the device is demonstrated. The kinetic simulation of the systems allows the prediction of the transient behavior of the networks under different auxiliary conditions.
Introduction
Dissipative, out-of-equilibrium processes control many different biological transformations such as proliferation,1 cell motility,2 signal transduction3 and activation of enzymatic networks.4 The operation of out-of-equilibrium reactions requires the continuous input of fuel materials and the generation of “waste” products, or the supply of energy, such as light, heat or electrical energy.5 Lately, substantial research efforts have been directed toward developing out-of-equilibrium chemical transformations.6 For example, the carbodiimide-fueled transient assembly of carboxylic anhydrides,7 or the biocatalytic association or hydrolysis of peptides8 leading to the spatiotemporal formation of fibers, demonstrated biomimetic elements duplicating the native ATP-driven formation and dissociation of actin filaments.The base sequence comprising nucleic acids provides a rich “tool-box” of functional materials that can be integrated into out-of-equilibrium transient systems. Beyond the base-sequence dictated formation of 2D9 and 3D10 nucleic acid structures, functional information can be encoded into the biopolymer, such as sequence-guided biocatalytic transformations, in the presence of enzymes (e.g., specific cleavage by endonucleases11 or nicking enzymes,12 ligation in the presence of ligase13 or polymerization using polymerase14), sequence-specific recognition and binding of ligands (aptamers),15 sequence-dictated catalytic functions16 (e.g., DNAzymes or ribozymes) and sequence-guided structural reconfiguration and reversible switching of DNA nanostructures.17 For example, the fuel strand displacement of duplex nucleic acids and the separation of the displaced duplex with an anti-fuel strand,9b,18 the K+-ion stimulated reconfiguration of guanosine-rich strands into G-quadruplexes and their separation with crown ether,19 the pH-controlled formation and dissociation of T–A·T complexes20 or the light-induced stabilization of duplex DNA with a photoisomerizable intercalator such as trans/cis-azobenzene units21 represent sequence-dictated structural switching of nucleic acids. These sequence-guided functions of nucleic acids were widely applied to develop DNA machines22 and devices, to design materials with switchable stiffness properties for shape-memory and self-healing applications,23 to prepare DNA-modified nanocarriers for controlled drug release,24 to use DNA as a material for logic gate operations and logic circuits,25 and to apply nucleic acids as building blocks of reconfigurable dynamic networks.26 Not surprisingly, the information encoded in DNA was applied to develop out-of-equilibrium transcriptional circuits acting as transcriptional oscillators27 or transcriptional switches, and bistable regulatory networks.28 Also, enzyme-based DNA machines relying on polymerization/endonucleases/nickases were used to generate out-of-equilibrium circuits revealing oscillatory behaviors29 or applied to drive the dissipative reconfiguration of constitutional dynamic networks.30 In addition, fuel-responsive DNA-based aptamers revealing enzyme-guided transient release and uptake of loads31 and light-controlled ATP-fueled out-of-equilibrium DNA ligation cycles32 were demonstrated. In all of these out-of-equilibrium systems enzymes were coupled to the DNA scaffolds. Furthermore, DNA circuits demonstrating the cyclic perturbation and recovery of DNA by strand displacement principles33 were reported, yet this process involved continuous accumulation of waste products. While substantial progress in the development of nucleic acid-based, out-of-equilibrium circuits was demonstrated, the operation of the systems required the participation of enzymes coupled to a DNA scaffold and/or the generation of waste products. Here we wish to report on enzyme-free, out-of-equilibrium circuits and gated dissipative systems. In one circuit, we apply a Pb2+-ion-dependent DNAzyme16a as the catalyst driving the dynamic transient process. Although this system generates a “waste” product, it represents an “all-DNA” catalyst-driven out-of-equilibrium system, and introduces a means to design dynamic circuits of enhanced complexities, e.g., gated transient systems, and transient gated catalytic assemblies. It should be noted that in contrast to previous reports that applied a native enzyme as the catalytic unit to recover the transient, dissipative, regeneration of the system,30,34 we demonstrate now the unprecedented use of a DNAzyme as a catalytic module to recover the networks. The use of a DNAzyme as a catalytic module to operate a dissipative network reveals clear advantages. The sensitivity of native enzymes towards denaturation vs. the robustness of the DNAzyme is certainly superior. Furthermore, the diversity of cofactor-dependent DNAzymes paves the way to construct transient systems of enhanced complexities. In the second system, we design an “all-DNA” out-of-equilibrium circuit that uses light as the energy input to drive the dissipative process without the generation of a waste product. We demonstrate the oscillatory and cyclic operation of the system. Furthermore, we emphasize the significance of kinetic modelling and computational simulations of the experimental results. We demonstrate that the computational modelling of the systems allows us to predict the behaviors of dynamically transient systems under variable auxiliary conditions applied on the systems.
Results and discussion
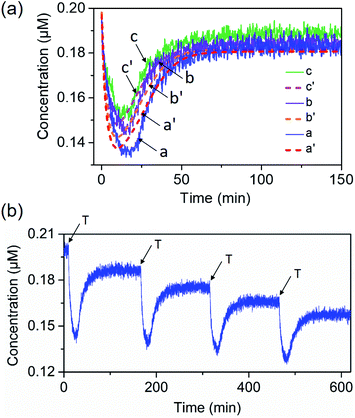
Fig. 1 depicts the Pb2+-ion-dependent DNAzyme-driven dissipative network. The system in its rest state consists of the duplex A/B, where the strand A includes a loop-containing Pb2+-ion-dependent DNAzyme-sequence caged in a duplex structure with strand B. The two strands Cy5-functionalized C and the BHQ2 (quencher)-functionalized D are also included in the system. Under these conditions, Cy5-C is not quenched due to the spatial separation of strands C and D. The addition of the fuel strand T to the system displaces strand B and results in the formation of a Pb2+-ion-dependent DNAzyme/substrate complex A/T. The released strand B is engineered to hybridize with Cy5-C and BHQ2-D, thus forming B/Cy5-C+BHQ2-D supramolecular structures, where the spatial proximity between Cy5 and BHQ2 leads to the quenching of Cy5. The strand T includes, however, the ribonucleobase sequence corresponding to the substrate of the Pb2+-ion-dependent DNAzyme, resulting in, in the presence of Pb2+ ions, the cleavage of T into fragmented T1 and T2 “waste” products and the release of A. The released A leads, however, to the displacement of B from the hybrid complex with B/Cy5-C+BHQ2-D, leading to the depletion and recovery of A/B, the separation of Cy5-C and BHQ2-D, and the recovery of the initial fluorescence of the system. That is, realizing the set of processes involved in the network, and using appropriate concentrations of the constituents, we expect that upon the triggering of the “rest”-state of the network module, a transient time-dependent decay of the fluorescence of Cy5-C will proceed, as a result of the build-up of the B/Cy5-C+BHQ2-D supramolecular complex, followed by the transient recovery of the fluorescence of Cy5-C as a result of the biocatalyzed cleavage of the fuel strand and the separation of the hybrid complex B/Cy5-C+BHQ2-D. Using an appropriate calibration curve and translating the fluorescence changes of Cy5-C into the concentrations of quenched Cy5-C in the complex B/Cy5-C+BHQ2-D structure, Fig. S2,† the transient time-dependent concentration changes of B/Cy5-C+BHQ2-D were evaluated, Fig. 2(a), solid curve (a). The hybrid quenched duplex increases in its content for a time-interval of ca. 15 minutes, followed by a slow dissipative recovery of the original rest state that proceeds for 125 minutes. A control experiment, Fig. S3,† that applied a nucleic acid strand Tc, that lacks the ribonucleobase cleavage site in the strand that binds to the Pb2+-ion-dependent DNAzyme, did not lead to the transient behavior of the system. Triggering the A/B module in the presence of Cy5-C and BHQ2-D with the strand Tc and Pb2+ ions led to the displacement of A/B and the formation of the Cy5-C quenched nanostructure B/Cy5-C+BHQ2-D, yet with no recovery of the initial state.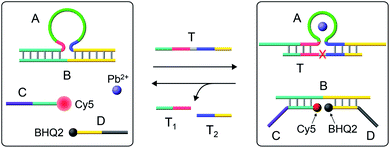 | ||
| Fig. 1 Schematic operation of the Pb2+-ion-dependent DNAzyme-driven dissipative network. (For a further detailed scheme that accounted for the transient dissipative cycle, see Fig. S1†). | ||
The transient operation of the network shown in Fig. 2(a) is a result of a set of competitive reactions, summarized by the kinetic scheme formulated in Fig. S4.† The experimental transient kinetic curve shown in Fig. 2(a), curve (a), was computationally simulated using the kinetic model shown in Fig. S4† and the set of reaction rates formulated in Fig. S5.† The fitted computational simulated transient operation of the dissipative system is provided in Fig. 2(a), curve (a′) (dashed, transient), and the set of derived rate constants involved in the kinetic model are summarized in Table S1.† The computationally simulated results have a value if the rate constants can predict the transient behavior of the system under other auxiliary conditions applied on the network. Furthermore, the set of rate constants that fit the experimental curve might be coincidental and other sets of rate constants might equally account for the experimental curve. To support the validity of the experimental set of rate constants, we searched for the possibility to experimentally derive one of the sub-reaction rate constants evaluated computationally. This was achieved by the experimental evaluation of the k2/k−2 value being a sub-reaction of the model. Indeed, the experimental value of k2/k−2 fits well with the computational value of k2/k−2 (for the results and further discussion, see Fig. S6†). The power of the computational results to predict the experimental behavior of the network under different auxiliary conditions is presented in Fig. 2(a). In these experiments, the concentrations of the triggering strands were altered, and the transient Pb2+-ion-dependent DNAzyme cleavage of the substrate T followed by the formation and transient separation of the B/Cy5-C+BHQ2-D structure through the concentration changes of Cy5 were computationally predicted, Fig. 2(a), curves (b′) and (c′), dashed lines. These results were, then, experimentally validated, Fig. 2(a), curves (b) and (c), solid curves. The experimental results fit well with the predicted computational simulations.
The dynamic transient behavior of the system shown in Fig. 2(a) complies with the basic principle of dissipative reactions that require the introduction of a fuel substrate into the system and its metabolic degradation into “waste” products, that is, the displacement of the A/B duplex with the fuel strand T that yields an energetically favored duplex A/T, and the formation of an intermediate meta-stable complex B/Cy5-C+BHQ2-D. The subsequent DNAzyme-stimulated cleavage of T degrades the fuel strand to “waste” products that restore the original rest system. The dissipative network can be regenerated, and by repeated additions of the fuel strand T, the transient network can be cycled, Fig. 2(b). The cycling of the system is, however, accompanied by the accumulation of the waste products T1 and T2.
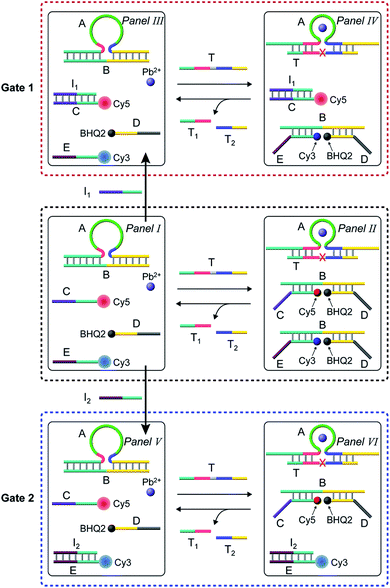
In the next step, the gated operation of two DNAzyme-guided dissipative networks was accomplished, Fig. 3. The duplex structure A/B was mixed with the Cy5-functionalized strand, C, and the Cy3-functionalized strand, E, in the presence of the quencher BHQ2-modified strand D and Pb2+ ions, Panel I. Under these conditions, the fluorescence of Cy5 and Cy3 is switched “ON”. In the presence of the trigger T, the conjugate A/B is separated to yield the Pb2+-ion-dependent DNAzyme/substrate complex A/T, and the separated strand B hybridizes with the fluorophore-functionalized strands C and E and the quencher-modified strand D to competitively yield two fluorescence quenched supramolecular structures B/Cy5-C+BHQ2-D and B/Cy3-E+BHQ2-D, Panel II. The Pb2+ ions triggered cleavage of the substrate T leads to T1 and T2 waste products and to the release of the free strand A that displaces the strand B associated with the two fluorescence-quenched structures, resulting in the competitive transient recovery of the complex A/B and to the regeneration of the fluorescence of Cy5-C and Cy3-E. (For the experimental results and computational simulations of the dissipative network consisting of A/B, Cy3-E and BHQ2-D, see Fig. S7–S10, Table S2† and accompanying discussion). The gating of the two competitive transient systems with the inhibitor I1 results in the hybridization of I1 with the strand Cy5-C, leading to the favored hybridization of the T-triggered displaced strand B associated with the B/Cy3-E+BHQ2-D supramolecular complex, Panels III and IV (Gate 1). Under these conditions, the fluorescence quenched structure B/Cy3-E+BHQ2-D and the accompanying transient are up-regulated while the dissipative process involving Cy5-C is blocked, Panel IV. The degree of the blockage of the Cy5-C network is controlled by the concentration of I1. As the concentration of I1 increases, the extent of blockage of the Cy5-C network is higher and the up-regulation of the Cy3-E dissipative process is intensified. Subjecting the mixture of networks, Panel I, to the inhibitor I2 leads to the hybridization of I2 with Cy3-E, Fig. 3, Panel V (Gate 2). This results in the favored binding of the T-displaced strand B to the Cy5-C+BHQ2-D strand, and to the favored up-regulation of the supramolecular structure B/Cy5-C+BHQ2-D, and to the blockage of the Cy3-E based dynamic network, Panel VI. As the concentration of I2 increases, the blockage of the Cy3-E network is higher and the competitive dissipative process involving Cy5-C is amplified. Thus, in the presence of the inhibitors I1 or I2, the parallel operation of the two dynamic, transient processes is anticipated to be modulated.
Fig. 4 shows the inhibitor-modulated gating of the mixture of the two networks. Fig. 4(a) depicts the transient fluorescence curves corresponding to the competitive operation of the Cy5-C, Panel I and Cy3-E, Panel II, activated systems. The responses of the two transient processes are lowered in their fluorescence as compared to the transients observed for the individual separated networks, consistent with the sharing of the strand B between the two networks. Fig. 4(b) shows the transient fluorescence curves of the Cy5-C active network in Panel III and of the Cy3-E active network, Panel IV, upon subjecting the mixture of networks to variable concentrations of inhibitor I1. As the concentration of I1 increases, the blockage of the Cy5-C active network is intensified, and in parallel, the activity of the Cy3-operating network is enhanced. At a concentration of I1 = 0.2 μM, the network consisting of Cy5-C is fully blocked, whereas the dissipative transient of the Cy3-E network is almost identical to that of the single Cy3-E operating network. Thus, at high concentrations of I1, the gated operation of the B/Cy3-E+BHQ2-D dissipative process is favored. Similarly, subjecting the mixture of networks to the inhibitor I2 leads to the modulated gated inhibition of the B/Cy3-E+BHQ2-D network, and the simultaneous activation of the B/Cy5-C+BHQ2-D network, as displayed in Fig. 4(c). As the concentration of I2 increases, the B/Cy5-C+BHQ2-D dynamic network is intensified, while the B/Cy3-E+BHQ2-D network is decayed, and at a concentration of I2 corresponding to 0.2 μM it is fully depleted, Panel VI. The competitive gated inhibition of the two networks was computationally simulated. A kinetic model that follows the I1/I2 competitive gated inhibition processes was formulated and the set of rate equations following this model are summarized in Fig. S13–S16.† Using the parent common rate constants derived for the individual network systems, the competitive transients shown in Fig. 4(a), Panel I and Panel II, were computationally simulated using the kinetic model shown in Fig. S11 and S12† and the computational results are overlaid on the experimental transients, Fig. S17(a),† Panel I and Panel II. In addition, the transients depicted in Fig. 4(b), Panel III, curve (a) (I1 = 0.06 μM) and Panel IV, curve (a) (I1 = 0.06 μM), were computationally simulated using the kinetic model formulated in Fig. S13 and S14.† The computational curves for the respective transients (a′) (dashed lines) are overlaid on the experimental curves, (a), Fig. S17(b),† Panel III and Panel IV. The set of computationally derived rate constants are summarized in Table S3.† The set of derived rate constants, Table S3,† were used to predict the patterns of the transients at different concentrations of I1 and the transients are presented in Fig. S17(b),† Panel III and Panel IV, curves (b′), (c′) and (d′). The results fit well with the experimental transients. Similarly, the experimental transients corresponding to the I2 inhibited two-network system (I2 = 0.06 μM), curve (a), Panels V and VI, Fig. 4(c), were simulated using the kinetic model summarized in Fig. S15 and S16.† Fig. S17(c),† Panels V and VI, present the respective computationally simulated transients (a′), overlaid on the experimental transients (a). The resulting rate constants are tabulated in Table S4.† The derived rate constants provided in Table S4† were used to predict the patterns of transients of the gated systems at different concentrations of I2, transients (b′), (c′) and (d′). The predicted transients are displayed in Fig. S17(c),† Panels V and VI. Very good agreement between the predicted results and the experimental curves shown in Fig. 4 is demonstrated.
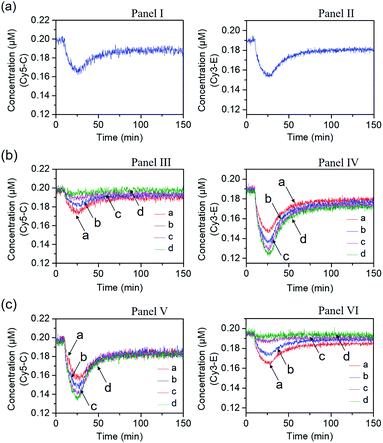 | ||
| Fig. 4 Transients corresponding to the competitive dissipative products associated with the two networks shown in Fig. 3, in the absence and presence of the inhibitors I1 and I2. (a) Transients corresponding to the competitive operation of the two networks in the absence of the inhibitors I1 and I2. Panel I: transient corresponding to B/Cy5-C+BHQ2-D. Panel II: transient corresponding to B/Cy3-E+BHQ2-D. (b) Transients corresponding to the I1-stimulated gating of the two networks, in the presence of variable concentrations of the inhibitor I1, Gate 1; Panel III: transient of B/Cy5-C+BHQ2-D in the presence of different concentrations of I1: (a) I1 = 0.06 μM; (b) I1 = 0.12 μM; (c) I1 = 0.18 μM; (d) I1 = 0.2 μM. Panel IV: transient of B/Cy3-E+BHQ2-D in the presence of different concentrations of I1: (a) I1 = 0.06 μM; (b) I1 = 0.12 μM; (c) I1 = 0.18 μM; (d) I1 = 0.2 μM. (c) Transients corresponding to the I2-stimulated gating of the two networks, in the presence of variable concentrations of the inhibitor I2, Gate 2; Panel V: transient of B/Cy5-C+BHQ2-D in the presence of different concentrations of I2: (a) I2 = 0.06 μM; (b) I2 = 0.12 μM; (c) I2 = 0.18 μM; (d) I2 = 0.2 μM. Panel VI: transient of B/Cy3-E+BHQ2-D in the presence of different concentrations of I2: (a) I2 = 0.06 μM; (b) I2 = 0.12 μM; (c) I2 = 0.18 μM; (d) I2 = 0.2 μM. | ||
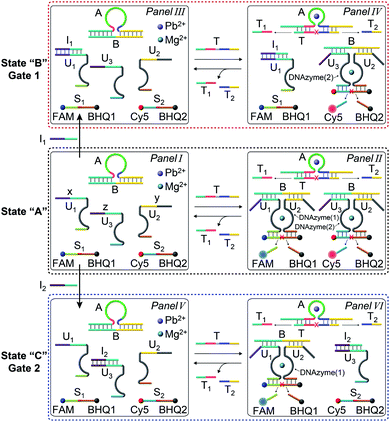
The gated transient system shown in Fig. 3 and 4 yields, however, similar outputs from the two gated states. It would be important, however, to extend the concept to a gated system that generates two different outputs and particularly two different catalytic functions as outputs. This is exemplified in Fig. 5 where a module leading to two different gated catalytic DNAzymes is introduced. The module, state A, includes the duplex A/B, the constituents U1, U2 and U3, being subunits of two different Mg2+-ion-dependent DNAzymes (that are functionalized by tethers x, y, and z, that are activated by the duplex A/B and can be selectively inhibited by the inhibitor I1 or I2), the FAM/BHQ1-modified substrate S1 and the Cy5/BHQ2-modified substrate S2. In the presence of the fuel strand T, the duplex A/B is separated to yield strand B and the Pb2+-ion-dependent DNAzyme/T complex. The released strand B bridges the subunits U1/U2 and U3/U2 to yield two different Mg2+-ion-dependent DNAzymes: DNAzyme(1) and DNAzyme(2), which cleave the substrates S1 and S2 to yield the FAM-fragmented substrate and Cy5-fragmented substrate, as the outputs of the DNAzyme(1) and DNAzyme(2) activities, respectively. The cleavage of strand T within the generated A/T complex releases strand A that displaces the strand B from the two Mg2+-ion-dependent DNAzymes (DNAzyme(1) and DNAzyme(2)), resulting in the transient formation and depletion of the structure A/T and the transient catalytic activities of DNAzyme(1) and DNAzyme(2). Fig. 6(a) shows the concomitant transient catalytic activities of DNAzyme(1), Panel I, and DNAzyme(2), Panel II. Subjecting state “A” to the inhibitor I1, results in the blockage of the constituent U1 leading to state “B” where only the gated operation of DNAzyme(2) is switched “ON” and the catalytic function of DNAzyme(1) is switched “OFF”. Fig. 6(b) shows the gated transient catalytic functions of the system. The catalytic function of DNAzyme(1) is switched “OFF”, Panel III, while the gated transient, dissipative, catalytic function of DNAzyme(2) is switch “ON”, Panel IV. Similarly, the treatment of the reaction module, state “A”, with inhibitor I2, leads to the blocking of subunit U3, prohibiting the formation of DNAzyme(2), and to the activation of the transient catalytic function of DNAzyme(1), state “C”. Fig. 6(c) shows the gated switched “ON” transient dissipative catalytic function of DNAzyme(1), Panel V, while the activity of DNAzyme(2) is fully inhibited, Panel VI.
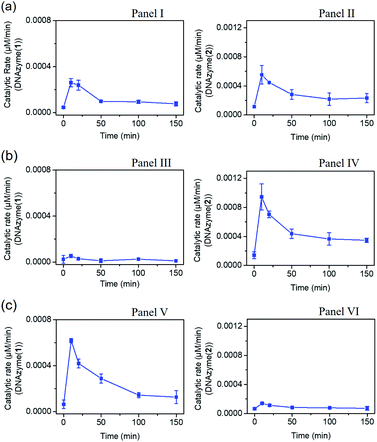 | ||
| Fig. 6 (a) Transient catalytic rates corresponding to the DNAzyme activated by state “A”: Panel I-DNAzyme(1) and Panel II-DNAzyme(2); (b) transient catalytic rates corresponding to the I1 inhibitor, 1 μM, gated system in state “B”: Panel III-DNAzyme(1) and Panel IV-DNAzyme(2); (c) transient catalytic rates corresponding to the I2 inhibitor, 1 μM, gated system in state “C”: Panel V-DNAzyme(1) and Panel VI-DNAzyme(2). The catalytic activities were evaluated by probing the rates of cleavage of the respective substrates by DNAzyme(1) and DNAzyme(2) in the time interval of the transient processes, see Fig. S18.† The fluorescence intensities were translated into molar concentrations of the products using the calibration curves shown in Fig. S19.† In all experiments: A/B, 1 μM, U1 and U3 1 μM each, U2, 2 μM, S1 and S2, 2 μM each, and fuel strand T, 5 μM. | ||
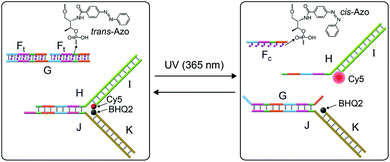
The systems discussed so far applied a fuel strand to trigger the dissipative processes, in the presence of a DNAzyme that transformed the fuel strand into “waste” fragments. This is, certainly, a disadvantage as the cyclic operation of the transient network requires the repeated additions of the fuel strand and the continuous accumulation of waste products. To overcome this limitation, we searched for a method to drive a dissipative network in the absence of a fuel strand, excluding the biocatalyst that leads to the accumulation of “waste” products. The operation of a dissipative network without the generation of “waste” products may be achieved by pumping pulses of energy into the system. Also, the periodic pumping of the energy could lead to an oscillatory transient behavior of the dissipative system. This is exemplified in Fig. 7 with the application of a photo-responsive network that includes azobenzene units as functional components that drive the transient dissipative behavior of the system through the coupled light-induced photoisomerization of the trans-azobenzene to the cis-azobenzene state, followed by the thermal isomerization of the cis-azobenzene to the trans-azobenzene state, Fig. 7. In this system, the dynamic system consists of the duplex between the strand G and two trans-azobenzene functionalized strands Ft, G/(Ft)2, and the Y-shaped DNA module composed of the strands H and J hybridized with the Cy5-I and the BHQ2-K strands. The transient operation of the system is, also, schematically depicted in Fig. 7. The system operates at 55 °C to allow the effective thermal isomerization of the cis-azobenzene units to the trans-state. The irradiation of the rest system, λ = 365 nm (at 55 °C), results in the photoisomerization of the trans-azobenzene intercalator units to the cis-state, leading to the separation of the G/(Ft)2 hybrid. The released strand G displaces the Y-shaped module to yield the separated products H/I and G/J/K and the cis-strand Fc. In the “rest” state, the fluorophore Cy5 is quenched by BHQ2, and the separation of the Y-shaped module yields the H/Cy5-I duplex, where the fluorescence of Cy5 is switched “ON”. The light-induced separation of the Y-shaped structure is rapid (365 nm UV light source, 5 W). The accompanying thermal isomerization of the cis-azobenzene units to the trans-state at 55 °C is substantially slower, and the thermal process results in the slow displacement of strand G by the thermally-generated Ft strand, and the recombination of H/Cy5-I with J/BHQ2-K to form the Y-shaped module, where the fluorescence of Cy5 is quenched. Thus, the transient fluorescence changes of Cy5 provide a readout signal for the dynamic behavior of the system. To allow the dissipative thermally induced full recovery of the system within a reasonable time interval, ca. eight hours, we operated the entire system at 55 °C. In addition, to retain the stabilities of the duplexes H/Cy5-I and G/J/BHQ2-K at 55 °C and prevent their melting, appropriate lengths and base compositions of the respective sequences have to be optimized. Specifically, the strand G has to be sufficiently long to stabilize the duplex G/J/BHQ2-K and this is the reason for the multiple hybridization of G with two Ft strands.
Fig. 8(a), curve (a), solid line, shows the transient operation of the system upon irradiation of the system for 10 minutes and switching off the light source. The fluorescence of the separated product H/Cy5-I increases for ca. 50 minutes and subsequently undergoes thermal recovery to the “rest” state within ca. eight hours. The transient time-dependent concentration changes of H/Cy5-I/J/BHQ2-K were evaluated by translating the fluorescence changes of H/Cy5-I into the concentrations of quenched Cy5-I in the complex Y-shaped structure using an appropriate calibration curve, Fig. S20.† Within the thermal dissipative process, the system was repeatedly irradiated at λ = 365 nm, resulting in cyclic partial transient oscillation events, Fig. 8(b). Also, upon the complete recovery of the rest system, the transient processes could be cycled, Fig. 8(c), without adding any external fuel or generating a “waste” product, highlighting the advantage of operating the dissipative process with a light “energy” input.
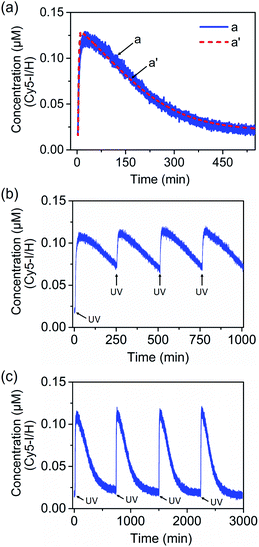 | ||
| Fig. 8 (a) Transient corresponding to the light-induced separation of the Y-shaped DNA module by the strand G generated upon the photoisomerization of the trans-azobenzene units into the cis-state and separation of the G/(Ft)2 scaffold, and the transient recovery of the Y-shaped module upon the thermal transition of Fc into Ft and the regeneration of the G/(Ft)2 scaffold. (b) Cyclic oscillatory operation of the Y-shaped DNA module upon the light-induced pulsed transition of the G/(Ft)2 scaffold into the Fc state within the thermally induced transient recovery of the parent system. (c) Cyclic light-induced operation of the dissipative DNA-based device shown in Fig. 7. | ||
Several control experiments confirmed the supported dissipative process. The irradiation of the system consisting of a Y-shaped H/Cy5-I/J/BHQ2-K system and the duplex G/(Fn)2 scaffold lacking the trans-azobenzene units, did not lead to the activation of the dissipative process, Fig. S21,† indicating that the light-induced photoisomerization of the trans-azobenzene units is, indeed, the trigger for the transient dynamic behaviors of the system. In addition, Fig. S22† depicts the transient behaviors of the Y-shaped H/Cy5-I/J/BHQ2-K system and the G/(Ft)2 photoisomerizable trans-azobenzene duplex scaffold upon the irradiation of the system, λ = 365 nm, at 55 °C, followed by the immediate cooling of the system to 25 °C. The light-induced isomerization of the trans-azobenzene units to the cis-state leads to the efficient separation of the Y-shaped assembly and to the triggered fluorescence changes of Cy5. The cooling down of the system to 25 °C results in, however, the very slow recovery of the initial state, indicating that the thermal isomerization of the cis-azobenzene units coupled to the primary photoisomerization process is, indeed, essential to induce the dissipative cycle of the system.
The photoinduced transient of the system shown in Fig. 8(a), curve (a), was computationally modeled following the kinetic scheme shown in Fig. S23 and S24.† The optimized fit of the simulation is shown in Fig. 8(a), curve (a′), dashed line. The derived set of the computed rate constants is provided in Table S5.† In addition, Fig. S25,† curve (a), depicts the experimental transient system observed upon irradiation, λ = 365 nm, of the “rest” system for a time interval of only 5 minutes. Under these conditions, the yield of the separated strand H/I is lower, ca. 40%. Using the set of rate constants derived for the original computed system, the predictive transient curve for the lower yield generated intermediate H/I was computed, Fig. S26.† An excellent fit between the experimental and predicted computations is demonstrated.
Conclusions
The present study has introduced “all-DNA” dissipative networks. The use of a metal-ion-dependent DNAzyme as a trigger to operate transient, out-of-equilibrium networks paves the way to design out-of-equilibrium “all-DNA” networks of enhanced complexities, such as gated networks, cascaded networks and feedback-driven systems. Specifically, we demonstrated the inhibitor-guided gating of transient, DNAzyme-fueled networks. Besides demonstrating the gating principle, we engineered a dynamic system consisting of two DNAzyme-based modules for the gated, transient operation of selective catalytic DNAzymes. The use of external energy inputs (light) is particularly interesting as it provides a means to operate cyclic dissipative systems without the addition of fuel substrates and the generation of waste products. The use of other auxiliary energy inputs, e.g., electrochemical redox-control of DNA modules, could be an interesting path to follow.Author contributions
J. W. and Z. L. designed the systems, performed the experiments and the computational simulations, and participated in the formulation in the paper. Z. Z. and Y. O. participated in designing the DNA sequences. J. Z. synthesized the azobenzene-modified scaffold. J. Z., X. M. and H. T. participated in the design of the photoresponsive scaffold and in the formulation of the paper. I. W. mentored the project, participated in the design of the experiments and participated in the formulation of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported by the Israel Science Foundation (IW) and by the National Natural Science Foundation of China (NSFC, 22020102006).Notes and references
- (a) A. Desai and T. J. Mitchison, Annu. Rev. Cell Dev. Biol., 1997, 13, 83–117 CrossRef CAS PubMed; (b) L. Rothfield, A. Taghbalout and Y.-L. Shih, Nat. Rev. Microbiol., 2005, 3, 959–968 CrossRef CAS PubMed; (c) A. Martos, M. Jiménez, G. Rivas and P. Schwille, Trends Cell Biol., 2012, 22, 634–643 CrossRef CAS PubMed.
- (a) B. Bugyi and M.-F. Carlier, Annu. Rev. Biophys., 2010, 39, 449–470 CrossRef CAS PubMed; (b) J. T. Parsons, A. R. Horwitz and M. A. Schwartz, Nat. Rev. Mol. Cell Biol., 2010, 11, 633–643 CrossRef CAS PubMed.
- S. O. Rizzoli, EMBO J., 2014, 33, 788–822 CrossRef CAS PubMed.
- (a) S. Debnath, S. Roy and R. V. Ulijn, J. Am. Chem. Soc., 2013, 135, 16789–16792 CrossRef CAS PubMed; (b) J. Boekhoven, W. E. Hendriksen, G. J. Koper, R. Eelkema and J. H. van Esch, Science, 2015, 349, 1075–1079 CrossRef CAS PubMed; (c) G. Ragazzon and L. J. Prins, Nat. Nanotechnol., 2018, 13, 882–889 CrossRef CAS PubMed; (d) M. Tena-Solsona, C. Wanzke, B. Riess, A. R. Bausch and J. Boekhoven, Nat. Commun., 2018, 9, 2044 CrossRef PubMed; (e) A. Goldbeter, Philos. Trans. R. Soc., A, 2018, 376, 20170376 CrossRef PubMed.
- (a) J. M. A. Carnall, C. A. Waudby, A. M. Belenguer, M. C. A. Stuart, J. J.-P. Peyralans and S. Otto, Science, 2010, 327, 1502–1506 CrossRef CAS PubMed; (b) G. M. Whitesides and R. F. Ismagilov, Science, 1999, 284, 89–92 CrossRef CAS PubMed; (c) B. A. Grzybowski and W. T. S. Huck, Nat. Nanotechnol., 2016, 11, 585–592 CrossRef CAS PubMed.
- (a) A. Sorrenti, J. Leira-Iglesias, A. J. Markvoort, T. F. A. de Greef and T. M. Hermans, Chem. Soc. Rev., 2017, 46, 5476–5490 RSC; (b) S. De and R. Klajn, Adv. Mater., 2018, 30, 1706750 CrossRef PubMed; (c) A. Sorrenti, J. Leira-Iglesias, A. Sato and T. M. Hermans, Nat. Commun., 2017, 8, 15899 CrossRef CAS PubMed; (d) S. P. Afrose, S. Bal, A. Chatterjee, K. Das and D. Das, Angew. Chem., Int. Ed., 2019, 58, 15783–15787 CrossRef CAS PubMed; (e) P. Solís Muñana, G. Ragazzon, J. Dupont, C. Z.-J. Ren, L. J. Prins and J. L.-Y. Chen, Angew. Chem., Int. Ed., 2018, 57, 16469–16474 CrossRef PubMed; (f) J. Deng and A. Walther, Adv. Mater., 2020, 32, 2002629 CrossRef CAS PubMed; (g) R. S. M. Rikken, H. Engelkamp, R. J. M. Nolte, J. C. Maan, J. C. M. van Hest, D. A. Wilson and P. C. M. Christianen, Nat. Commun., 2016, 7, 12606 CrossRef CAS PubMed.
- L. S. Kariyawasam and C. S. Hartley, J. Am. Chem. Soc., 2017, 139, 11949–11955 CrossRef CAS PubMed.
- (a) J. Boekhoven, A. M. Brizard, K. N. K. Kowlgi, G. J. M. Koper, R. Eelkema and J. H. van Esch, Angew. Chem., Int. Ed., 2010, 49, 4825–4828 CrossRef CAS PubMed; (b) C. G. Pappas, I. R. Sasselli and R. V. Ulijn, Angew. Chem., Int. Ed., 2015, 54, 8119–8123 CrossRef CAS PubMed.
- (a) P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed; (b) F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- (a) A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS PubMed; (b) R. P. Goodman, I. A. T. Schaap, C. F. Tardin, C. M. Erben, R. M. Berry, C. F. Schmidt and A. J. Turberfield, Science, 2005, 310, 1661–1665 CrossRef CAS PubMed.
- Y. Weizmann, Z. Cheglakov and I. Willner, J. Am. Chem. Soc., 2008, 130, 17224–17225 CrossRef CAS PubMed.
- (a) D. Li, A. Wieckowska and I. Willner, Angew. Chem., Int. Ed., 2008, 47, 3927–3931 CrossRef CAS PubMed; (b) C. Zhang, Z. Wang, Y. Liu, J. Yang, X. Zhang, Y. Li, L. Pan, Y. Ke and H. Yan, J. Am. Chem. Soc., 2019, 141, 17189–17197 CrossRef CAS PubMed.
- (a) L.-M. Lu, X.-B. Zhang, R.-M. Kong, B. Yang and W. Tan, J. Am. Chem. Soc., 2011, 133, 11686–11691 CrossRef CAS PubMed; (b) K. He, W. Li, Z. Nie, Y. Huang, Z. Liu, L. Nie and S. Yao, Chem.–Eur. J., 2012, 18, 3992–3999 CrossRef CAS PubMed.
- F. Wang, C.-H. Lu, X. Liu, L. Freage and I. Willner, Anal. Chem., 2014, 86, 1614–1621 CrossRef CAS PubMed.
- (a) S. E. Osborne, I. Matsumura and A. D. Ellington, Curr. Opin. Chem. Biol., 1997, 1, 5–9 CrossRef CAS PubMed; (b) I. Willner and M. Zayats, Angew. Chem., Int. Ed., 2007, 46, 6408–6418 CrossRef CAS PubMed; (c) A. E. Rangel, A. A. Hariri, M. Eisenstein and H. T. Soh, Adv. Mater., 2020, 32, 2003704 CrossRef CAS PubMed; (d) S. Li, Q. Jiang, S. Liu, Y. Zhang, Y. Tian, C. Song, J. Wang, Y. Zou, G. J. Anderson, J.-Y. Han, Y. Chang, Y. Liu, C. Zhang, L. Chen, G. Zhou, G. Nie, H. Yan, B. Ding and Y. Zhao, Nat. Biotechnol., 2018, 36, 258–264 CrossRef CAS PubMed.
- (a) R. R. Breaker and G. F. Joyce, Chem. Biol., 1994, 1, 223–229 CrossRef CAS PubMed; (b) G. F. Joyce, Angew. Chem., Int. Ed., 2007, 46, 6420–6436 CrossRef CAS PubMed; (c) P. Travascio, A. J. Bennet, D. Y. Wang and D. Sen, Chem. Biol., 1999, 6, 779–787 CrossRef CAS PubMed; (d) R. J. Lake, Z. Yang, J. Zhang and Y. Lu, Acc. Chem. Res., 2019, 52, 3275–3286 CrossRef CAS PubMed.
- (a) F. Wang, X. Liu and I. Willner, Angew. Chem., Int. Ed., 2015, 54, 1098–1129 CrossRef CAS PubMed; (b) N. C. Seeman, Nature, 2003, 421, 427–431 CrossRef PubMed; (c) S. G. Harroun, C. Prévost-Tremblay, D. Lauzon, A. Desrosiers, X. Wang, L. Pedro and A. Vallée-Bélisle, Nanoscale, 2018, 10, 4607–4641 RSC; (d) K. Jiao, B. Zhu, L. Guo, H. Zhou, F. Wang, X. Zhang, J. Shi, Q. Li, L. Wang, J. Li and C. Fan, J. Am. Chem. Soc., 2020, 142, 10739–10746 CrossRef CAS PubMed.
- (a) D. Y. Zhang and G. Seelig, Nat. Chem., 2011, 3, 103–113 CrossRef CAS PubMed; (b) F. C. Simmel, B. Yurke and H. R. Singh, Chem. Rev., 2019, 119, 6326–6369 CAS.
- C.-H. Lu, X.-J. Qi, R. Orbach, H.-H. Yang, I. Mironi-Harpaz, D. Seliktar and I. Willner, Nano Lett., 2013, 13, 1298–1302 CrossRef CAS PubMed.
- Y. Hu, A. Cecconello, A. Idili, F. Ricci and I. Willner, Angew. Chem., Int. Ed., 2017, 56, 15210–15233 CrossRef CAS PubMed.
- (a) H. Asanuma, T. Ito, T. Yoshida, X. Liang and M. Komiyama, Angew. Chem., Int. Ed., 1999, 38, 2393–2395 CrossRef CAS; (b) M. Zhou, X. Liang, T. Mochizuki and H. Asanuma, Angew. Chem., Int. Ed., 2010, 49, 2167–2170 CrossRef CAS PubMed; (c) Q. Yuan, Y. Zhang, T. Chen, D. Lu, Z. Zhao, X. Zhang, Z. Li, C.-H. Yan and W. Tan, ACS Nano, 2012, 6, 6337–6344 CrossRef CAS PubMed.
- (a) C. Teller and I. Willner, Curr. Opin. Biotechnol., 2010, 21, 376–391 CrossRef CAS PubMed; (b) M. K. Beissenhirtz and I. Willner, Org. Biomol. Chem., 2006, 4, 3392–3401 RSC; (c) H. Ramezani and H. Dietz, Nat. Rev. Genet., 2020, 21, 5–26 CrossRef CAS PubMed; (d) J. Bath and A. J. Turberfield, Nat. Nanotechnol., 2007, 2, 275–284 CrossRef CAS PubMed.
- (a) Y. Li and R. Schulman, Nano Lett., 2019, 19, 3751–3760 CrossRef CAS PubMed; (b) M. Vázquez-González and I. Willner, Angew. Chem., Int. Ed., 2020, 59, 15342–15377 CrossRef PubMed; (c) J. S. Kahn, Y. Hu and I. Willner, Acc. Chem. Res., 2017, 50, 680–690 CrossRef CAS PubMed.
- (a) W.-H. Chen, G.-F. Luo, Y. S. Sohn, R. Nechushtai and I. Willner, Adv. Funct. Mater., 2019, 29, 1805341 CrossRef; (b) Y. Wang, J. Yan, N. Wen, H. Xiong, S. Cai, Q. He, Y. Hu, D. Peng, Z. Liu and Y. Liu, Biomaterials, 2020, 230, 119619 CrossRef CAS PubMed; (c) M. Vázquez-González and I. Willner, Langmuir, 2018, 34, 14692–14710 CrossRef PubMed; (d) C.-H. Lu and I. Willner, Angew. Chem., Int. Ed., 2015, 54, 12212–12235 CrossRef CAS PubMed; (e) A. Sarode, A. Annapragada, J. Guo and S. Mitragotri, Biomaterials, 2020, 242, 119929 CrossRef CAS PubMed; (f) A. Fischer, S. Lilienthal, M. Vázquez-González, M. Fadeev, Y. S. Sohn, R. Nechushtai and I. Willner, J. Am. Chem. Soc., 2020, 142, 4223–4234 CrossRef CAS PubMed; (g) C. Wang, M. Vázquez-González, M. Fadeev, Y. S. Sohn, R. Nechushtai and I. Willner, Small, 2020, 16, 2000880 CrossRef CAS PubMed.
- (a) R. Orbach, B. Willner and I. Willner, Chem. Commun., 2015, 51, 4144–4160 RSC; (b) I. Willner, B. Shlyahovsky, M. Zayats and B. Willner, Chem. Soc. Rev., 2008, 37, 1153–1165 RSC; (c) G. Seelig, D. Soloveichik, D. Y. Zhang and E. Winfree, Science, 2006, 314, 1585–1588 CrossRef CAS PubMed; (d) J. Li, A. A. Green, H. Yan and C. Fan, Nat. Chem., 2017, 9, 1056–1067 CrossRef CAS PubMed.
- S. Wang, L. Yue, Z. Shpilt, A. Cecconello, J. S. Kahn, J.-M. Lehn and I. Willner, J. Am. Chem. Soc., 2017, 139, 9662–9671 CrossRef CAS PubMed.
- (a) E. Franco, E. Friedrichs, J. Kim, R. Jungmann, R. Murray, E. Winfree and F. C. Simmel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, E784–E793 CrossRef CAS PubMed; (b) J. Kim and E. Winfree, Mol. Syst. Biol., 2011, 7, 465 CrossRef PubMed.
- S. W. Schaffter and R. Schulman, Nat. Chem., 2019, 11, 829–838 CrossRef CAS PubMed.
- (a) K. Montagne, G. Gines, T. Fujii and Y. Rondelez, Nat. Commun., 2016, 7, 13474 CrossRef CAS PubMed; (b) K. Montagne, R. Plasson, Y. Sakai, T. Fujii and Y. Rondelez, Mol. Syst. Biol., 2011, 7, 466 CrossRef PubMed; (c) M. Luo, M. Xuan, S. Huo, J. Fan, G. Chakraborty, Y. Wang, H. Zhao, A. Herrmann and L. Zheng, Angew. Chem., Int. Ed., 2020, 59, 17250–17255 CrossRef CAS PubMed.
- S. Wang, L. Yue, V. Wulf, S. Lilienthal and I. Willner, J. Am. Chem. Soc., 2020, 142, 17480–17488 CrossRef CAS PubMed.
- (a) E. Del Grosso, G. Ragazzon, L. J. Prins and F. Ricci, Angew. Chem., Int. Ed., 2019, 58, 5582–5586 CrossRef CAS PubMed; (b) E. Del Grosso, A. Amodio, G. Ragazzon, L. J. Prins and F. Ricci, Angew. Chem., Int. Ed., 2018, 57, 10489–10493 CrossRef CAS PubMed.
- (a) J. Deng, D. Bezold, H. J. Jessen and A. Walther, Angew. Chem., Int. Ed., 2020, 59, 12084–12092 CrossRef CAS PubMed; (b) J. Deng and A. Walther, J. Am. Chem. Soc., 2020, 142, 685–689 CrossRef PubMed.
- (a) A. Padirac, T. Fujii and Y. Rondelez, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E3212–E3220 CrossRef CAS PubMed; (b) A. S. Zadorin, Y. Rondelez, G. Gines, V. Dilhas, G. Urtel, A. Zambrano, J.-C. Galas and A. Estevez-Torres, Nat. Chem., 2017, 9, 990–996 CrossRef CAS PubMed; (c) A. S. Zadorin, Y. Rondelez, J.-C. Galas and A. Estevez-Torres, Phys. Rev. Lett., 2015, 114, 068301 CrossRef CAS PubMed; (d) D. Soloveichik, G. Seelig and E. Winfree, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5393–5398 CrossRef CAS PubMed.
- Z. Zhou, Y. Ouyang, J. Wang and I. Willner, J. Am. Chem. Soc., 2021, 143, 5071–5079 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02091a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |