Open Access Article
Open Access ArticlePredicting phosphorescence energies and inferring wavefunction localization with machine learning†
Andrew E.
Sifain‡
 ab,
Levi
Lystrom‡
ab,
Levi
Lystrom‡
 ab,
Richard A.
Messerly
ab,
Richard A.
Messerly
 a,
Justin S.
Smith
a,
Justin S.
Smith
 ab,
Benjamin
Nebgen
ab,
Benjamin
Nebgen
 ac,
Kipton
Barros
ac,
Kipton
Barros
 ab,
Sergei
Tretiak
ab,
Sergei
Tretiak
 abc,
Nicholas
Lubbers
abc,
Nicholas
Lubbers
 *d and
Brendan J.
Gifford
*d and
Brendan J.
Gifford
 *abc
*abc
aTheoretical Division, Los Alamos National Laboratory, Los Alamos, NM, USA 87545. E-mail: giff@lanl.gov
bCenter for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, NM, USA 87545
cCenter for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, NM, USA 87545
dComputer, Computational, and Statistical Sciences Division, Los Alamos National Laboratory, Los Alamos, NM, USA 87545. E-mail: nlubbers@lanl.gov
First published on 29th June 2021
Abstract
Phosphorescence is commonly utilized for applications including light-emitting diodes and photovoltaics. Machine learning (ML) approaches trained on ab initio datasets of singlet–triplet energy gaps may expedite the discovery of phosphorescent compounds with the desired emission energies. However, we show that standard ML approaches for modeling potential energy surfaces inaccurately predict singlet–triplet energy gaps due to the failure to account for spatial localities of spin transitions. To solve this, we introduce localization layers in a neural network model that weight atomic contributions to the energy gap, thereby allowing the model to isolate the most determinative chemical environments. Trained on the singlet–triplet energy gaps of organic molecules, we apply our method to an out-of-sample test set of large phosphorescent compounds and demonstrate the substantial improvement that localization layers have on predicting their phosphorescence energies. Remarkably, the inferred localization weights have a strong relationship with the ab initio spin density of the singlet–triplet transition, and thus infer localities of the molecule that determine the spin transition, despite the fact that no direct electronic information was provided during training. The use of localization layers is expected to improve the modeling of many localized, non-extensive phenomena and could be implemented in any atom-centered neural network model.
Introduction
Molecules that are electronically excited by light or charge injection typically relax non-radiatively to their lowest-energy singlet or triplet excited states.1 Transitions between these singlet and triplet states (intersystem crossing) can be enabled by spin–orbit interactions. Subsequent radiative relaxation from excited-singlet to ground-singlet states leads to fluorescence, which occurs over nanosecond timescales. In contrast, radiative transitions from excited-triplet to ground-singlet states are forbidden on account of the difference in spin multiplicity. This radiative process, known as phosphorescence, occurs over much longer timescales, generally on the order of 10−3 to 100 s.2 The dynamics of low-energy singlet and triplet states form the basis for applications including light-emitting electrochemical cells,3 chemical sensors,4 organic light-emitting diodes (OLEDs),5,6 and photovoltaics.7 For instance, a carefully designed thermally activated delayed fluorescence (TADF) process can be used to harvest energy from triplet to singlet states, raising the efficiency of an OLED to nearly 100%.8 As another example, simultaneous emission from triplet and singlet states in metal–organic polymers can be used to make white light LEDs.9 These examples illustrate the importance of a reliable prediction of triplet state emission energies across a large diversity of molecules capable of guiding experimental efforts toward future optoelectronic technologies.10–12 Computational screening using accurate ab initio calculations, such as density functional theory (DFT), can aid in molecular design.13 However, the computational costs of fully quantum mechanical approaches may restrict both the number and size of molecules that can be sampled efficiently. Machine learning (ML) has newfound relevance in quantum chemistry for accelerating simulations and providing predictions of ab initio quality.14–16 Here, we leverage ML techniques and build an accurate and extensible ML model for phosphorescence energy that is enabled by its ability to account for electron localization associated with the spin transition.ML research has led to predictive models of various molecular properties,17–19 among which are general interatomic potentials of ground state energies.20–23 Such models can be trained to large datasets (e.g., ∼105–106 molecules) containing both equilibrium and off-equilibrium structures. This approach enables the construction of machine learned potential energy surfaces (PESs)24,25 for purposes such as dynamics26 and geometry optimization.27,28 Data curation and model training are computationally demanding tasks,29,30 but once trained, such models not only generate high-fidelity ab initio-quality predictions at low computational costs but also infer relationships within high-dimensional data31 and are transferable to molecules outside of the training dataset.24,31,32 ML for ground state chemistry has been explored at an appreciable depth, achieving models of high-accuracy theories33–35 and extremely large systems.36 However, its use for excited state processes37–39 such as phosphorescence is a new area of research.
The physics involved in describing an excited state transition is fundamentally different however from that of a ground state. For ground states, ML potentials incorporate the extensivity principle which defines the total energy of a molecule as a sum over individual atomic contributions.40 This assumption is physically motivated and has been tested over a large chemical space, and provides the means for attaining transferable and extensible models.24,31,41 However, it breaks down in the case of electronic excitation energies, for which atoms may contribute to the transition energy in a disproportionate way. This disproportionality is evidenced by localized versus delocalized electronic transitions that are prevalent in chemical physics.42–45 In turn, the energy of an excitation does not scale strictly with the size of the molecule. Rather than using extensive predictions, it is reasonable to seek a method that can associate the energy of an excitation with specific regions of the molecule. Such an approach would have wide-ranging applicability since the notion of localization generalizes to many molecular phenomena and systems such as charged species and radicals, and can be potentially applied to a broad class of problems centered around energy and charge carrier transport in molecular materials and solids.
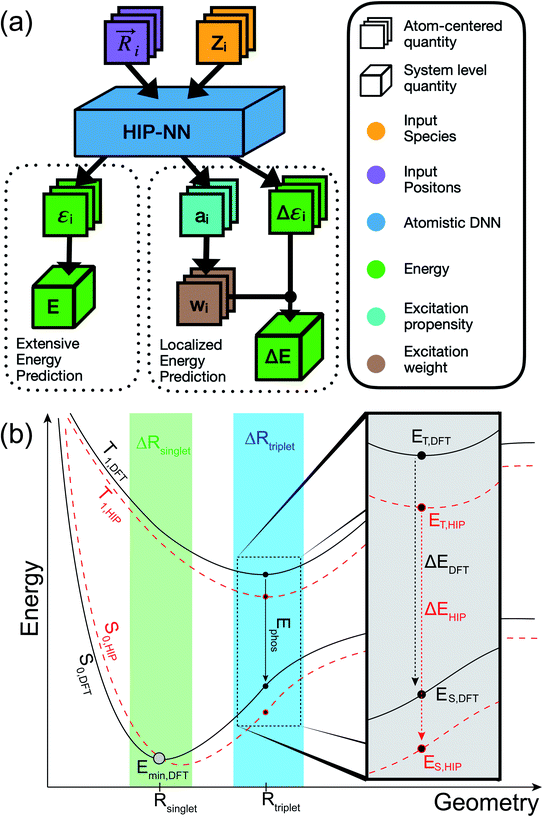
In this work, we develop a model based on the Hierarchical Interacting Particle Neural Network (HIPNN)46 that accurately predicts the singlet–triplet energy gaps in a diverse chemical space of organic compounds at computational speeds that reach over one million times faster than the underlying ab initio method for single-point calculations. HIPNN has previously shown excellent performance for ground state energies,46 partial atomic charges,47 and molecular dipole moments.48 We present new atomistic localization layers that compute a weight for each atom corresponding to the atomic contribution to the molecule's energy gap. The mathematics of these new layers can be likened to the statistical mechanics of a chemical potential, or to the technology of attention mechanisms in the neural network literature.49,50 The localization layers improve phosphorescence energy predictions on an out-of-sample test set of molecules that are larger than those found in the training set and that are known to be phosphorescent from experiment while qualitatively inferring the changes to the electron density due to the transition as shown by direct comparison to reference quantum mechanical spin density calculations. This result is remarkable given that DFT spin density was not provided as a target during training and highlights the added benefit that electronic information could have toward ML models of localized, non-extensive molecular phenomena.
Methods
We start with a brief review of how energy is computed with ML interatomic potentials, including the extensive HIPNN model,46 and describe the new methods in this work. The input descriptors of the molecules are atomic coordinates (Ri) and atomic numbers (Zi), which together define the molecular geometry (R). In extensive HIPNN and several other atomistic neural networks,24,40,46 target energy for geometry R is computed as a sum over atomic energy contributions, | (1) |
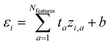 | (2) |
Note that the εi do not represent a direct physical quantity, but rather a factorization or ansatz form of the total energy E, representing the notion that the potential may be taken as a sum of contributions over latent variables εi in the model, and it is a useful ansatz for an extensive total energy. For a single conformation of a system, many values of the εi are compatible with the total energy. However, the machine learning algorithm learns a model of εi so that E will fit a large database of calculations simultaneously. The high-dimensional feature vector zi,a contains information collected from the local environment of that atom, and is also learned, but is less readily interpretable than εi.
This model can be applied in either the singlet ground state (S0) or first triplet excited state (T1). In addition to being trained to energy, our models are also trained to atomic forces. The inclusion of atomic forces as targets has been shown to improve energy predictions.51,52 Throughout the paper, we refer to the extensive HIPNN model that solely employs eqn (1) to compute energy as HIPNN (Scheme 1a, left).
In HIPNN, singlet (ES) and triplet (ET) energies are determined from independent Self-Consistent Field (SCF) calculations, and both ES and ET are learned independently using separate linear prediction with the form of eqn (1). Their difference,
| ΔE = ET − ES | (3) |
We described how one could learn ES and ET and compute ΔE following their predictions (eqn (3)). This approach was carried out for the HIPNN model. Alternatively, one could learn ES and ΔE, with ET defined as ET = ES + ΔE. This definition represents ET as a sum of an extensive (ES) and non-extensive (ΔE) property, the latter of which motivates the HIP-loc model. Atomic forces on the singlet state are the same as those used in the HIPNN model, 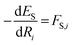 whereas the forces associated with ΔE are calculated as
whereas the forces associated with ΔE are calculated as 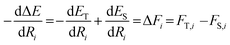 . We now introduce the principal difference between HIPNN and HIP-loc (Scheme 1a). Instead of modeling ΔE as a simple sum over atom-centered energies (eqn (1)), we model it as a non-extensive quantity by weighting atomic energies by normalized weights wi
. We now introduce the principal difference between HIPNN and HIP-loc (Scheme 1a). Instead of modeling ΔE as a simple sum over atom-centered energies (eqn (1)), we model it as a non-extensive quantity by weighting atomic energies by normalized weights wi
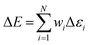 | (4) |
This form is physically motivated by the fact that the electron density may be localized on certain atoms. We show that the inclusion of these weights is instrumental in accurately predicting ΔE, as opposed to eqn (1), which assumes equal atomic contributions. We use a softmax function for wi,
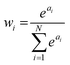 | (5) |
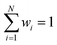 . We predict both Δεi and ai analogously to eqn (2), with linear layers applied to the learned features. Because the weights sum to one, the predicted ΔE is bounded by the extrema of the Δεi, a local quantity that does not intrinsically scale with system size; eqn (4) may be better thought of as a weighted average than as a sum.
. We predict both Δεi and ai analogously to eqn (2), with linear layers applied to the learned features. Because the weights sum to one, the predicted ΔE is bounded by the extrema of the Δεi, a local quantity that does not intrinsically scale with system size; eqn (4) may be better thought of as a weighted average than as a sum.
The form of eqn (4) and (5) are similar to those of attention models49,50 and elementary statistical mechanical models. In a statistical mechanical analogy, the propensity ai plays the role of a (negative) chemical potential, whereas the weights wi are interpreted as a probability derived from the propensity using a Boltzmann weighting, and the excitation corresponds to an observable of the system. Such an analogy gives rise to intuition about the relationship between the propensity and the weights: if the propensities are narrowly distributed, the weights will be roughly evenly distributed across the molecule. If a few propensities are larger than the rest, the weights will be concentrated on those few atoms. In our results, we show that these localization weights effectively infer the region of the triplet excitation, as determined by ab initio spin density calculations.
The molecules of the dataset were randomly sampled from the GDB13 dataset55 and contain C, H, N, O, S, and Cl atoms. Ab initio computations were performed using the ωb97x density functional56 and 6-31g* basis set57 with Gaussian 16.58 All molecules were optimized in vacuum in the T1 state. Thermal conformers (T = 300 K) near the minimum of T1 were obtained with a normal mode sampling scheme.24 Doing so enables learning PESs at molecular conformations near points of stability (Scheme 1b). Subsequent single-point calculations of the entire dataset, including optimized and thermal conformers, were carried out to determine ES and ET. The entire dataset consisted of approximately ∼702k structures with median molecule size of 8 heavy atoms (excluding H) and 16 total atoms with a maximum molecule size of 12 heavy atoms and 30 total atoms (Fig. S2†). A more detailed breakdown of the dataset, including the number of molecules sampled from each GDB dataset, is available in Table S1.†
The trained models were also tested on a challenging set of large aromatic molecules known to be phosphorescent from experiment with median molecule size of 17 heavy atoms (excluding H) and 27 total atoms with a maximum molecule size of 31 heavy atoms and 51 total atoms (Fig. S2†). The compounds of this extensibility set were taken from ref. 59–62 and make up 35 unique compounds and 912 thermal conformers. A sample set of the training and test set compounds is shown in Fig. 1. Further details regarding the neural network architecture and model training can be found in the ESI† under the section labeled Neural Network Architecture and Training Procedure. It is worth noting that a full end-to-end ML-based approach is ultimately desirable for molecular design workflows. Ideally, the ML model should optimize the triplet geometry, which makes up a significant portion of the computational time needed to predict emission energies from first principles. In this work, we concentrate on using localization layers in the modeling of localized, non-extensive properties with emphasis on phosphorescence energies as the application of interest. Thus, we eliminate the error of an ML-based optimization in our results, using geometries obtained by normal mode sampling of conformations near DFT-optimized structures of T1. We do present encouraging results with T1 optimized with ML in ESI,† including the singlet–triplet energy gaps and root-mean-square deviation (RMSD) of the ML-optimized geometries compared with DFT-based optimization.
Results and discussion
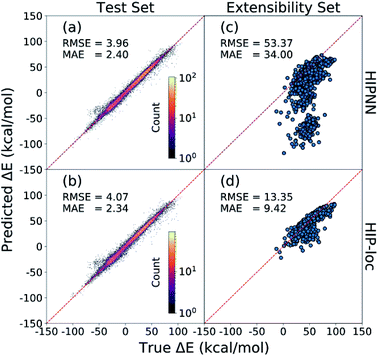
Fig. 2 presents the energy gaps that correspond to molecular geometries near the equilibrium of T1. These geometries are relevant for phosphorescence and will be the focus of our discussion. HIPNN and HIP-loc achieve comparable prediction accuracies on the held-out test set (Fig. 2a and b). Both models exhibit root-mean-square errors (RMSEs) of ∼4 kcal mol−1 and mean-absolute errors (MAEs) of ∼2 kcal mol−1 (or ∼0.1 eV), which are within the error of the DFT method when compared to experimental transition energies.63 These predictions correspond to a median percent error of ∼5% (Fig. S3†). Thus, both HIPNN and HIP-loc attain experimentally informative predictions of Ephos on the held-out test set. Training and testing results for all geometries sampled near the equilibria of S0 and T1 are shown in Fig. S4 and S5.† We also present results of RMSD and energy predictions at geometries optimized with respect to the HIP-loc T1 PES in Fig. S6 and S7.†Despite HIPNN's success of predicting ΔE for molecules with sizes comparable to those found in the training set, its performance substantially worsens for phosphorescent molecules of the extensibility set that consist of on average ∼2× the number of atoms (Fig. S2†). Yet we show that HIP-loc remedies this issue. HIPNN erroneously predicts negative ΔE energies (i.e., T1 is lower in energy than S0) for many molecules, contradicting reference results (Fig. 2c). This result is particularly troublesome given that these are phosphorescent molecules for which DFT correctly predicts T1 to be higher in energy than S0. Altogether, HIPNN's performance on the extensibility set is quite poor with a RMSE of ∼53 kcal mol−1 or ∼2.3 eV, which is well outside the error commonly expected between ab initio and experimental values.63 HIPNN's predictions are especially poor for molecules composed of more than 35 atoms (Fig. S8 and S9†). In contrast, Fig. 2d shows HIP-loc significantly outperforming HIPNN on the extensibility set. The RMSE of HIP-loc results on the extensibility set is ∼13 kcal mol−1, amounting to an ∼4× improvement and median percent error of ∼13% (Fig. S3†). The erroneous negative ΔE energies, predicted by HIPNN (Fig. 2c), are all but eliminated with HIP-loc (Fig. 2d and S10†).
HIP-loc strongly outperforms HIPNN, and the only difference between the two models is the usage of localization layers to model the non-extensive part of ET (i.e., ΔE) by weighting local atomic environments. The extensibility of the model is substantially improved, but relatively large disagreement between HIP-loc and DFT is observed for the largest molecules in the extensibility set comprising several bonded aromatic fragments (Fig. S11†). Nevertheless, HIP-loc's stronger performance demonstrates the importance of model engineering to account for the localized nature of spin transitions. Parity plots for all molecules of the extensibility set, categorized by chemical similarity, are shown in Fig. S11 through S16.†
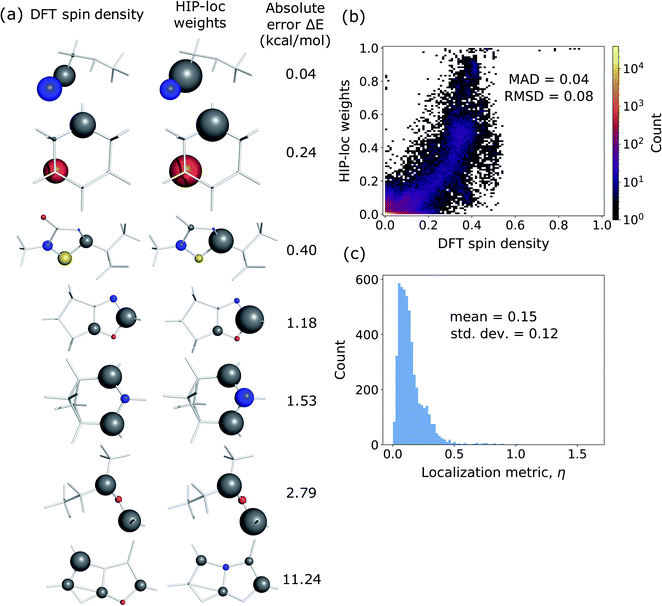
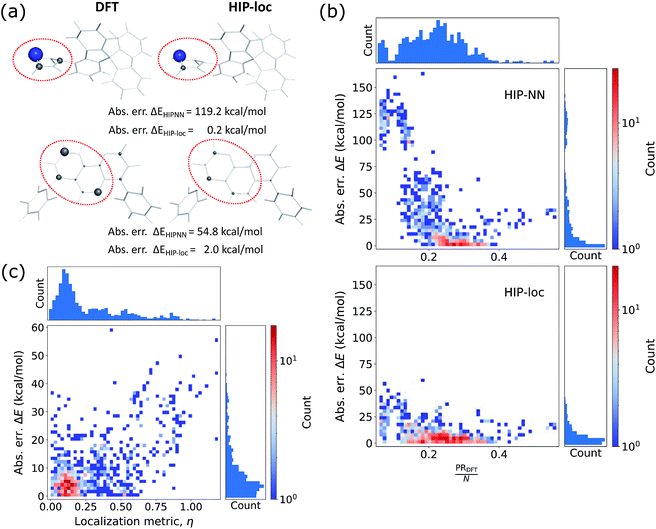
Additionally, we investigated whether the learned localization weights in HIP-loc have some physical significance. We compared the localization weights to DFT spin density differences between the T1 and S0 states. In order to compare the two methods, DFT spin density was approximated as an atom-centered quantity, which we obtained using the Hirshfeld charge partitioning scheme.64Fig. 3a visualizes this comparison for a subset of representative molecules selected from a random sample of the held-out test set. Remarkably, there is qualitative agreement between HIP-loc and DFT for most molecules, suggesting that the HIP-loc localization weights provide physical insight. Moreover, the correspondence between the quantum mechanical and inferred localizations is somewhat correlated with the accuracy in predicted energies; the absolute error in ΔE for the last molecule shown in Fig. 3a is relatively high and, correspondingly, the atom-centered DFT spin density does not as strongly resemble the HIP-loc weights as compared to the other molecules shown. We also find a rough, yet highly significant correlation observed between these learned weights and the DFT spin densities (Fig. 3b). It is important to note that the results of Fig. 3a and b are not meant to assert that learned weights are intrinsically related to spin densities in a rigorous way, especially since they are atom-centered quantities and charge partitioning is ambiguous, but rather that inferring localization through the use of energies and forces across a large dataset leads to similar assignments of localization.
We also analyzed the agreement between the ab initio and inferred localization over a large sample of the held-out test set. For this analysis, we made use of a localization metric η, defined as the ratio of the distance between the centers of localization computed using HIP-loc weights 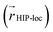 and DFT spin density
and DFT spin density 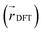 to the radius of gyration (Rg), which quantifies the spatial size of the molecule:
to the radius of gyration (Rg), which quantifies the spatial size of the molecule: 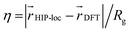 . For η ≪ 1, the centers of localizations are in close proximity to one another, whereas η ∼ 1 signifies that the centers of localization differ by approximately the radius of the molecule and therefore there is very little or no agreement in the predicted localization. See ESI† under Localization Metric for more details. Fig. 3c shows a histogram of η computed for our sample set. The distribution is concentrated at low η (mean = 0.15), indicating that the center of HIP-loc's inferred localization is in close proximity to that determined from DFT for the majority of compounds.
. For η ≪ 1, the centers of localizations are in close proximity to one another, whereas η ∼ 1 signifies that the centers of localization differ by approximately the radius of the molecule and therefore there is very little or no agreement in the predicted localization. See ESI† under Localization Metric for more details. Fig. 3c shows a histogram of η computed for our sample set. The distribution is concentrated at low η (mean = 0.15), indicating that the center of HIP-loc's inferred localization is in close proximity to that determined from DFT for the majority of compounds.
This agreement is also observed for molecules of the phosphorescent extensibility set. Similar to Fig. 3a and 4a visualizes the similarities between DFT and HIP-loc for two example molecules that perform particularly poorly with HIPNN. Additional visualizations of a similar nature are available in ESI Fig. S17 through S20.† The spatial localities associated with the singlet–triplet transitions in these molecules are confined to a relatively small number of atoms compared to the molecules' total number of atoms. This result suggests, albeit not too surprisingly, that the advantages provided by HIP-loc are accentuated in the case of strongly localized transitions. In order to fully probe the improvement provided by HIP-loc for modeling localized versus delocalized transitions, we study the participation ratio (PR). The PR is described as follows: given an N-body wavefunction expanded in terms of atom-localized states 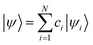 with expansion coefficients ci, the PR is expressed as
with expansion coefficients ci, the PR is expressed as 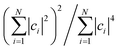 , ranging from 1 (fully localized to a single atom) to N (equally delocalized across all atoms).42 Although we are not working with wavefunctions, we apply the concept of PR to estimate the number of atoms involved in the singlet–triplet transition based on the ab initio (DFT) spin density and thereby quantify the degree of localization. The squares of the expansion coefficients are approximated from the atom-centered DFT spin density (qi):
, ranging from 1 (fully localized to a single atom) to N (equally delocalized across all atoms).42 Although we are not working with wavefunctions, we apply the concept of PR to estimate the number of atoms involved in the singlet–triplet transition based on the ab initio (DFT) spin density and thereby quantify the degree of localization. The squares of the expansion coefficients are approximated from the atom-centered DFT spin density (qi): 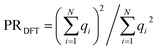 . The PR is complimentary to the previously utilized localization metric η. The latter quantifies the agreement in proximity of the ab initio and ML-inferred centers of localization, whereas the former estimates the number of atoms involved in the transition and is therefore a more appropriate measure of quantifying the degree to which a transition is localized.
. The PR is complimentary to the previously utilized localization metric η. The latter quantifies the agreement in proximity of the ab initio and ML-inferred centers of localization, whereas the former estimates the number of atoms involved in the transition and is therefore a more appropriate measure of quantifying the degree to which a transition is localized.
Fig. 4b shows the relationship between absolute error in ΔE and the degree of localization as computed by PR/N. For molecules in which the density is dispersed more homogeneously across the atoms (or larger PRDFT/N edging closer to ∼1), energy is accurately predicted using eqn (1) of HIPNN. In fact, HIPNN and HIP-loc achieve comparable performance in this regime. However, for molecules in which the density is strongly localized on only a small handful of atoms (or PRDFT/N closer to ∼1/N), HIP-loc is superior. This result underscores the main motivation of our work in that HIPNN does not accurately predict the singlet–triplet energy gap for strongly localized transitions, whereas HIP-loc's localization weights allow the model to weight regions of the molecule that are attributed to the transition, resulting in better energy prediction.
Finally, in order to relate the agreement in the centers of localization to the accuracy in predicted energy, we also show absolute error in ΔE versus η (Fig. 4c). The distribution is concentrated in the regime of low η and low ΔE error, but in contrast to the held-out test set (Fig. 3c), there is also a significant number of molecules that lie in the regime of high η. The distribution of ΔE errors in this high η regime is sporadic and extends to relatively high error. Altogether, these results suggest that robust energy prediction is generally improved when the inferred localization determined by the HIP-loc weights more closely resembles the localization determined by the quantum mechanical spin density.
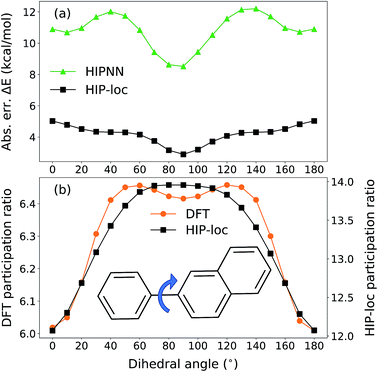
To further demonstrate HIP-loc's feature of localization without changing stoichiometry (and therefore drastically changing total molecular energy), we examined the predicted energy and concomitant variation in localization while scanning a single torsional angle. The set of molecules investigated consists of three to five six-membered aromatic rings and a central carbon–carbon single bond. A relaxed torsional scan over the dihedral angle around the carbon–carbon bond is performed and HIPNN and HIP-loc predictions are made for each conformation. The PR is calculated for both the DFT spin density and HIP-loc weights in order to compare the overall localization using both methods. The analogous form for PRHIP-loc uses HIP-loc weights (wi) in lieu of atom-centered spin density, that is, 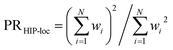 .
.
Our conformational analysis shows that when errors in ΔE predictions are relatively low across the conformational space, localization is accurately predicted by means of the PR. Rotating the molecule's dihedral angle changes its aromaticity and shifts spatial localization of electron density. As a result, the S0 and T1 PESs, as well as the ΔE gap, vary with conformation. Fig. 5a shows absolute error in ΔE as a function of dihedral angle for a representative molecule containing three six-membered aromatic rings, computed with HIPNN and HIP-loc. HIP-loc outperforms HIPNN for all scanned geometries. Additionally, there is qualitative agreement in the trends of the PRs computed using HIP-loc weights and DFT spin density (Fig. 5b). However, HIP-loc infers more delocalized transitions compared to DFT (PR of ∼13 versus ∼6), but in spite of that, for both methods the PR in the planar structure (dihedral of 0° and 180°) is delocalized across atoms on each ring, whereas the PR in the non-planar structure (dihedral of 90°) is localized to slightly more atoms exclusively on the larger ring. The net effect is an increase in PR for the non-planar conformation. An animation in ESI† showing a torsional scan of the molecule in Fig. 5 illustrates this point. Altogether, we find a correspondence between the accuracy of energy prediction and the progression in the degree of localization, quantified by PR. These observations are consistent for all the molecules studied (Fig. S21 through S25†).
Conclusions
In conclusion, machine learning (ML) is becoming an integral part of physical chemistry research and has already made substantial advances in the development of fast and transferable ML potentials for ground state dynamics. Ground state energy can be classified as an extensive property that is represented as a sum over individual atomic contributions whereas electronic excitation energies are best categorized as localized, non-extensive properties that depend on subsets of atoms. In this work, we utilized ML for advancing excited state electronic structure modeling by training a Hierarchical Interacting Particle Neural Network (HIPNN) to predict phosphorescence energy, defined as the gap between the lowest energy triplet and singlet states, at computational speeds that reach over one million times faster than the underlying ab initio method for single-point calculations. Our work improves upon the original version of HIPNN that is based on the extensivity principle, particularly in the case of large aromatic compounds for which their singlet–triplet transition energies do not scale strongly with molecule size.Our main contribution is a new set of localization layers for learning target excitation energies. These localization layers do not depend on the detailed structure of the underlying model and could be implemented in any atom-centered neural network. Combined with HIPNN, the new approach (denoted HIP-loc) defines energy as a weighted sum, where inferred localization weights assigned to the atoms determine the atoms' contribution to the target energy (eqn (4)). This minor yet profound modification substantially improved prediction quality on a more challenging set of experimentally verified phosphorescent compounds that consist of, on average, ∼2× more atoms than the molecules found in the training set. Extensibility is an important practical advantage of the model because it allows screening large molecules for which ab initio calculations are computationally prohibitive. Moreover, the superior energy prediction of HIP-loc over HIPNN was not readily visible on the held-out test set, but only the phosphorescent extensibility set in molecules with strongly localized transitions, showing that the extensibility test provides important characterization of the model's performance. We achieve RMSEs of ∼4 kcal mol−1 (∼5% error) on the held-out test set and ∼13 kcal mol−1 (∼13% error) on the phosphorescent extensibility set (Fig. 2). The physical significance of HIP-loc's localization weights, to our surprise, is that they qualitatively correlate to the quantum mechanical spin density (Fig. 3 and 4). Thus, the model inferred localities of the electron density associated with the singlet–triplet transition in order to make more accurate and transferable prediction of the singlet–triplet energy gap. This result is remarkable given that DFT spin density was not provided as a target during training. Instead, the neural network was provided with somewhat limited information, yet discovered this result nonetheless with a modest change in how target energy is calculated that effectively took into account the relative contribution of the atoms.
The results and performance of the new HIP-loc model lead us to conjecture that predicting localized molecular properties are likely to improve if reference electronic properties (e.g., electron densities) are used explicitly as targets during training. This idea sets the stage for many interesting applications of ML in physical chemistry, where learned properties are dependent on, or correlated to, the spatial distribution of the many-electron wavefunction. We also envision applying localization layers to other localized molecular phenomena and systems such as anions, cations, radicals, or other excited states. Additionally, further improvement of excited state ML potentials for geometry optimization could lend itself useful for a full end-to-end ML-based tool for phosphorescent materials screening.
Data availability
Nebgen, Benjamin (2021): Dataset of Singlet and Triplet Energies and Forces for Organic Molecules. figshare. Dataset. https://doi.org/10.6084/m9.figshare.14736570.v1.Author contributions
A. E. S., L. L., and B. J. G. curated datasets, performed ab initio calculations, analyzed results, made figures, and began the initial draft of the manuscript. L. L. generated the original dataset and trained preliminary models. N. L. developed the HIP-loc model formulation, wrote the corresponding code, and trained models. R. A. M. performed dihedral scan calculations. J. S. S. and K. B. provided valuable discussion and provided directions for analysis, including the idea to analyze DFT spin density. A. E. S., S. T., N. L., and B. J. G. brought the manuscript to a complete form. S. T. and B. N. conceived the task to model excited spin states. All authors contributed to the editing of the final manuscript. B. N., S. T., N. L., and B. J. G. supervised the research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work at Los Alamos National Laboratory (LANL) was supported by the LANL Directed Research and Development (LDRD) funds and performed in part at the Center for Nonlinear Studies (CNLS) and the Center for Integrated Nanotechnologies (CINT), U.S. Department of Energy, Office of Science user facilities. This research used resources provided by the LANL Institutional Computing (IC) Program as well as the LANL Darwin Cluster. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (Contract No. 89233218NCA000001).References
- G. N. Lewis and M. Kasha, J. Am. Chem. Soc., 1944, 66, 2100–2116 CrossRef CAS.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern Molecular Photochemistry of Organic Molecules, 2017 Search PubMed.
- R. D. Costa, E. Ortí, H. J. Bolink, F. Monti, G. Accorsi and N. Armaroli, Angew. Chem., Int. Ed., 2012, 51, 8178–8211 CrossRef CAS PubMed.
- Q. Zhao, C. Huang and F. Li, Chem. Soc. Rev., 2011, 40, 2508 RSC.
- Highly Efficient OLEDs with Phosphorescent Materials, ed. H. Yersin, Wiley, 1st edn, 2007 Search PubMed.
- Y. Tao, C. Yang and J. Qin, Chem. Soc. Rev., 2011, 40, 2943 RSC.
- M. J. Currie, J. K. Mapel, T. D. Heidel, S. Goffri and M. A. Baldo, Science, 2008, 321, 226–228 CrossRef CAS PubMed.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- C.-X. Sheng, S. Singh, A. Gambetta, T. Drori, M. Tong, S. Tretiak and Z. V. Vardeny, Sci. Rep., 2013, 3, 2653 CrossRef PubMed.
- S. Haneder, E. Da Como, J. Feldmann, J. M. Lupton, C. Lennartz, P. Erk, E. Fuchs, O. Molt, I. Münster, C. Schildknecht and G. Wagenblast, Adv. Mater., 2008, 20, 3325–3330 CrossRef CAS.
- S. Mukherjee and P. Thilagar, Chem. Commun., 2015, 51, 10988–11003 RSC.
- Z. An, C. Zheng, Y. Tao, R. Chen, H. Shi, T. Chen, Z. Wang, H. Li, R. Deng, X. Liu and W. Huang, Nat. Mater., 2015, 14, 685–690 CrossRef CAS PubMed.
- J. Hafner, C. Wolverton and G. Ceder, MRS Bull., 2006, 31, 659–668 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- P. O. Dral, J. Phys. Chem. Lett., 2020, 11, 2336–2347 CrossRef CAS PubMed.
- O. A. von Lilienfeld and K. Burke, Nat. Commun., 2020, 11, 4895 CrossRef CAS PubMed.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- A. P. Bartók, S. De, C. Poelking, N. Bernstein, J. R. Kermode, G. Csányi and M. Ceriotti, Sci. Adv., 2017, 3, e1701816 CrossRef PubMed.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. von Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765 CrossRef CAS PubMed.
- T. Mueller, A. Hernandez and C. Wang, J. Chem. Phys., 2020, 152, 050902 CrossRef CAS PubMed.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- Z. Qiao, M. Welborn, A. Anandkumar, F. R. Manby and T. F. Miller, J. Chem. Phys., 2020, 153, 124111 CrossRef CAS PubMed.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924–6935 RSC.
- H. Zhai and A. N. Alexandrova, J. Chem. Theory Comput., 2016, 12, 6213–6226 CrossRef CAS PubMed.
- K. Gubaev, E. V. Podryabinkin, G. L. W. Hart and A. V. Shapeev, Comput. Mater. Sci., 2019, 156, 148–156 CrossRef CAS.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- R. Jinnouchi, K. Miwa, F. Karsai, G. Kresse and R. Asahi, J. Phys. Chem. Lett., 2020, 11, 6946–6955 CrossRef CAS PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- D. Jha, L. Ward, A. Paul, W. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593 CrossRef PubMed.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903 CrossRef.
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Nat. Commun., 2020, 11, 5223 CrossRef CAS PubMed.
- D. Lu, H. Wang, M. Chen, L. Lin, R. Car, W. E, W. Jia and L. Zhang, Comput. Phys. Commun., 2021, 259, 107624 CrossRef CAS.
- J. Westermayr and P. Marquetand, Mach. Learn.: Sci. Technol., 2020, 1, 043001 CrossRef.
- J. Westermayr and P. Marquetand, Chem. Rev., 2020 DOI:10.1021/acs.chemrev.0c00749.
- J. Westermayr, M. Gastegger and P. Marquetand, J. Phys. Chem. Lett., 2020, 11, 3828–3834 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- P. Rowe, V. L. Deringer, P. Gasparotto, G. Csányi and A. Michaelides, J. Chem. Phys., 2020, 153, 034702 CrossRef CAS.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171–3212 CrossRef CAS PubMed.
- T. E. Dykstra, E. Hennebicq, D. Beljonne, J. Gierschner, G. Claudio, E. R. Bittner, J. Knoester and G. D. Scholes, J. Phys. Chem. B, 2009, 113, 656–667 CrossRef CAS PubMed.
- A. N. Panda, F. Plasser, A. J. A. Aquino, I. Burghardt and H. Lischka, J. Phys. Chem. A, 2013, 117, 2181–2189 CrossRef CAS PubMed.
- B. J. Gifford, S. Kilina, H. Htoon, S. K. Doorn and S. Tretiak, Acc. Chem. Res., 2020, 53, 1791–1801 CrossRef CAS PubMed.
- N. Lubbers, J. S. Smith and K. Barros, J. Chem. Phys., 2018, 148, 241715 CrossRef PubMed.
- B. Nebgen, N. Lubbers, J. S. Smith, A. E. Sifain, A. Lokhov, O. Isayev, A. E. Roitberg, K. Barros and S. Tretiak, J. Chem. Theory Comput., 2018, 14, 4687–4698 CrossRef CAS PubMed.
- A. E. Sifain, N. Lubbers, B. T. Nebgen, J. S. Smith, A. Y. Lokhov, O. Isayev, A. E. Roitberg, K. Barros and S. Tretiak, J. Phys. Chem. Lett., 2018, 9, 4495–4501 CrossRef CAS PubMed.
- D. Bahdanau, K. Cho and Y. Bengio, 2014, ArXiv14090473 Cs Stat.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, I. Polosukhin, 2017, ArXiv170603762 Cs.
- A. M. Cooper, J. Kästner, A. Urban and N. Artrith, npj Comput. Mater., 2020, 6, 54 CrossRef CAS.
- J. S. Smith, N. Lubbers, A. P. Thompson and K. Barros, 2020, ArXiv200605475 Cond-Mat Physicsphysics Stat.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- B. Anderson, T.-S. Hy, R. Kondor, 2019, ArXiv190604015, Phys. Stat.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- M. Zander, Angew. Chem., Int. Ed. Engl., 1965, 4, 930–938 CrossRef.
- I. Janić, in Luminescence of Crystals, Molecules, and Solutions, ed. F. Williams, B. Baron, M. Martens and S. P. Varma, Springer US, Boston, MA, 1973, pp. 213–218 Search PubMed.
- E. Clar and W. Schmidt, Tetrahedron, 1976, 32, 2563–2566 CrossRef CAS.
- S. Thiery, D. Tondelier, C. Declairieux, B. Geffroy, O. Jeannin, R. Métivier, J. Rault-Berthelot and C. Poriel, J. Phys. Chem. C, 2015, 119, 5790–5805 CrossRef CAS.
- D. Bousquet, R. Fukuda, D. Jacquemin, I. Ciofini, C. Adamo and M. Ehara, J. Chem. Theory Comput., 2014, 10, 3969–3979 CrossRef CAS PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details regarding ML training procedures and localization metric η. Ab initio energies ES0, ET1, and ΔE as a function of number of atoms, distributions of molecule size for the held-out and extensibility test sets, histograms of percentage error in ΔE prediction on T1 thermal conformers in the held-out and extensibility test sets using HIPNN and HIP-loc, training and testing parity plots of predicted versus true ΔE on thermal conformers sampled around equilibria of S0 and T1 using HIPNN and HIP-loc, RMSD of optimized geometries using the HIP-loc T1 potential and energy error plots at those geometries, absolute errors in ΔE as a function of number of atoms, parity plots of predicted versus true ΔE for the extensibility set categorized by chemical similarity, localization of singlet–triplet transition for select molecules of the extensibility set computed from DFT spin density and HIP-loc weights, conformation-dependent localization of singlet–triplet transitions in molecules with a single torsional angle, and molecular animations of torsional scans including that of the molecule in Fig. 5. See DOI: 10.1039/d1sc02136b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |