Open Access Article
Open Access ArticleDefining the conditions for the development of the emerging class of FeIII-based MRI contrast agents†
Zsolt
Baranyai
 a,
Fabio
Carniato
a,
Fabio
Carniato
 b,
Alessandro
Nucera
b,
Dávid
Horváth
b,
Alessandro
Nucera
b,
Dávid
Horváth
 ac,
Lorenzo
Tei
ac,
Lorenzo
Tei
 b,
Carlos
Platas-Iglesias
b,
Carlos
Platas-Iglesias
 *d and
Mauro
Botta
*d and
Mauro
Botta
 *b
*b
aBracco Research Centre, Bracco Imaging S.p.A., Via Ribes 5, 10010, Colleretto Giacosa, Italy
bDipartimento di Scienze e Innovazione Tecnologica, Università del Piemonte Orientale “A. Avogadro”, Viale T. Michel 11, 15121 Alessandria, Italy. E-mail: mauro.botta@uniupo.it
cDepartment of Physical Chemistry, University of Debrecen, Egyetem tér 1., H-4010, Debrecen, Hungary
dCentro de Investigacións Científicas Avanzadas (CICA), Departamento de Química, Facultade de Ciencias, Universidade da Coruña, 15071 A Coruña, Galicia, Spain. E-mail: carlos.platas.iglesias@udc.es
First published on 26th July 2021
Abstract
Fe(III) complexes are attracting growing interest in chemists developing diagnostic probes for Magnetic Resonance Imaging because they leverage on an endogenous metal and show superior stability. However, in this case a detailed understanding of the relationship between the chemical structure of the complexes, their magnetic, thermodynamic, kinetic and redox properties and the molecular parameters governing the efficacy (relaxivity) is still far from being available. We have carried out an integrated 1H and 17O NMR relaxometric study as a function of temperature and magnetic field, on the aqua ion and three complexes chosen as reference models, together with theoretical calculations, to obtain accurate values of the parameters that control their relaxivity. Moreover, thermodynamic stability and dissociation kinetics of the Fe(III) chelates, measured in association with the ascorbate reduction behaviour, highlight their role and mutual influence in achieving the stability required for use in vivo.
1. Introduction
The success and development of MRI as a diagnostic technique of primary importance has been accompanied and facilitated by the availability of metal-based contrast agents (CAs), which allow very important objectives to be achieved: (i) increase the signal intensity; (ii) decrease image acquisition times; (iii) improve image contrast and thus the diagnosis of different malignancies that could remain undetected using unenhanced procedures; (iv) reduce artefacts and improve cost management. The CAs currently used in clinical practice are small and hydrophilic paramagnetic Gd(III) complexes that accelerate the relaxation rates (R1 and R2) of proximate tissue water protons in regions of agent accumulation.1 In addition to these low molecular weight complexes, many other systems, from polynuclear complexes to sophisticated nanosized structures, supramolecular adducts or theranostic agents, have been designed and developed for bio-medical applications and pre-clinical research.2The success of Gd-based contrast agents (GBCA) was possible thanks to the detailed understanding of the correlation between the efficacy (relaxivity, r1) and the structural and dynamic parameters that characterize these coordination compounds. In summary, the key parameters are the tumbling rate of the complex in solution (1/τR), the exchange rate (kex = 1/τM) of the water molecule in the inner sphere of coordination and its distance (rGdH) from the metal centre, the electronic relaxation times (T1,2e) of the paramagnetic ion and its hydration state (q).1,3 Despite the fact that the clinically used Gd(III) chelates are generally very safe and very well tolerated by patients, there has been recently some concerns related to (i) a new disease, called nephrogenic systemic fibrosis, which was associated with the administration of GBCAs to patients with severely compromised kidney function4 and (ii) the retention of small amounts of Gd in the tissues of patients exposed to multiple MRI scans, although without any evidence that this is associated with clinical harm.5 This has given a boost to exploratory research activities focused on finding alternative contrast enhancer based on different chemical species. One obvious and effective approach is the development of contrast agents based on paramagnetic metal ions with improved tolerability. Among them, Mn(II) has received great attention over the past few years, with some of the complexes showing very promising properties.6 However, while it has been demonstrated that Mn(II)-based MRI probes may have an efficacy quite comparable to that of GBCAs, the challenges remain open in achieving sufficient thermodynamic stability and kinetic inertness for clinical applications.6 More recent reports have also considered the use of high-spin Fe(III) complexes,7 which share the same d5 configuration with the Mn(II) analogues, but with a superior safety profile, since iron is an essential element for life present in 3–5 g in the human body.8 In particular, Schellenberger et al.9 showed that low molecular weight Fe(III) complexes such as [Fe(CDTA)]− provide significant image contrast in vivo and present enhancement kinetics very similar to Gd(DTPA)2−, (Magnevist®) a clinically used agent. Subsequently, Gale10 and Morrow11 reported Fe(III) complexes with relatively high relaxivities at the imaging fields. Alternatively, Fe(II/III) complexes have been used for redox-dependent paramagnetic chemical exchange saturation transfer (PARACEST) applications or 19F MRI thermometers.12,13 Overall, these recent results indicate a promising new way to design novel contrast media for MRI, using an endogenous paramagnetic metal alternative to Gd. Despite these important initial contributions, the mechanisms responsible for water proton relaxation enhancement induced by Fe(III) complexes and the relationships between the molecular parameters that govern r1 and the chemical structure have not been yet deciphered, preventing the development of systems with optimal properties through rational ligand design.
In this paper, we address some basic issues related to the relaxation of the solvent water protons by Fe(III) ions in some model systems, as a necessary initial step towards a detailed evaluation of the efficacy of Fe(III) complexes as diagnostic MRI probes. As stated by S. Koenig over 35 years ago, the Fe(III) ion has the potential to be particularly suitable as an MRI probe due to its relatively large magnetic moment and because it occurs in vivo in a variety of forms.14 Thus, we report here the first detailed 1H and 17O NMR relaxometric analysis, combined with theoretical calculations of four representative Fe(III) complexes: Fe(EDTA)−, Fe(CDTA)−, Fe(DTPA)2− and the aqua ion [Fe(H2O)6]3+. In addition, thermodynamic, kinetic and ascorbate reduction studies on Fe(EDTA)− and Fe(CDTA)− complexes are reported to assess the overall stability of the complexes (Scheme 1).
2. Results and discussion
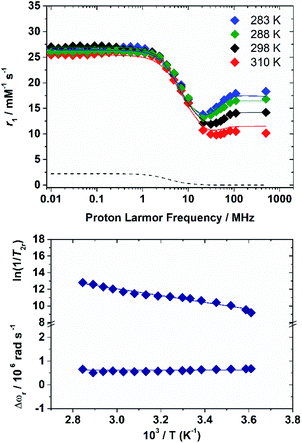
The 1H nuclear magnetic relaxation dispersion (NMRD) profiles recorded for the [Fe(H2O)6]3+ complex, measured over an extended range of Larmor frequencies, are presented in Fig. 1. Since water exchange is a key dynamic parameter that often affects the relaxivity of metal complexes, we also measured 17O transverse relaxation rates and chemical shifts, which provide direct access to kex. These data were obtained at low pH (pH = 0–0.5) to avoid the hydrolysis of the cation and formation of hydroxo-species. 1H NMRD and 17O NMR data were reported several years ago in separate papers.15,16 These studies provided markedly different 298τM values of 0.39 μs (1H NMR) and 14.7 μs and 6.25 ms (17O NMR). The 1H NMRD profiles show a dispersion in the range 1–20 MHz, as typically observed for low-molecular weight Mn(II) and Gd(III) complexes. The relaxivity of [Fe(H2O)6]3+ increases above 20 MHz until ca. 100 MHz, and then remains fairly constant up to 500 MHz. The 17O transverse relaxation data are characteristic of a system in the slow exchange regime, where T2r increases with increasing temperature.Initial attempts to fit the 17O NMR and 1H NMRD data using the same exchange rate failed and provided evidence that proton exchange and the exchange of the whole water molecule occur in different timescales. We therefore carried on a simultaneous fit of the two data sets using the established equations for paramagnetic relaxation17 and assuming two different residence times: 298τHM (1H) and 298τOM (whole water). The 17O NMR data were analysed using the Swift–Connick equations,18 which depend on longitudinal (i = 1) and transverse (i = 2) relaxation times of the electron spin (Tie) as well as 298τOM and the hyperfine coupling constant AO/ℏ. The whole set of equations used for the analysis of the experimental data is reported in the ESI.† Given the large number of parameters that affect the 17O NMR and NMRD data, we estimated some of them with the use of DFT calculations, while some others were fixed to reasonable values. Following our previous work on Mn(II) complexes,19 the 1H and 17O hyperfine coupling constants and the distances between the H atoms of the coordinated water molecules and the paramagnetic centre were estimated from DFT calculations (Table 1). These calculations were performed on [Fe(H2O)6]3+·12H2O, which includes 12 explicit second sphere water molecules. The fit of the data required including a scalar contribution to r1, which depends on the hyperfine coupling constant AH/ħ. The scalar contribution was found to provide a small, but significant (≈10%), contribution at low fields (<1 MHz).
| [Fe(H2O)6]3+d | Fe(EDTA)− | Fe(CDTA)− | |
|---|---|---|---|
| a Additional parameters fixed for fitting: EV = 1 kJ mol−1; 298D = 2.24 × 105 cm2 s−1; ED = 20 kJ mol−1. b Parameters fixed during the fitting procedure. c Values obtained with DFT calculations. d A scalar contribution to relaxivity was included, with AH/ħ fixed to the DFT value of 8.6 × 106 rad s−1. An outer-sphere contribution to the chemical shifts with COS = 0.038 ± 0.007 was considered. Proton exchange is characterized by 298τHM = 756 ± 129 ns and ΔHHH = 28.2 ± 4.1 kJ mol−1 in 0.15 M HNO3 solution. e The activation energy for the modulation of the ZFS EΔ = 7.8 ± 0.5 and 9.8 ± 0.5 kJ mol−1 for Fe(EDTA)− and Fe(CDTA)−. | |||
| 298 r 1 20 MHz [mM−1 s−1] | 12.1 | 2.1 | 2.4 |
| 298 Δ 2 [1020 s−2] | 4.2 ± 0.3 | 27.0 ± 1.4e | 18.1 ± 1.3e |
| 298 τ V [ps] | 5.3 ± 0.3 | 2.8 ± 0.1 | 3.4 ± 0.2 |
| A O/ħ [106 rad s−1] | −99.3b,c | −64.8b,c | −62.8b,c |
| 298 τ OM [ns] | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 3600 000 ± 3600 |
0.9 ± 0.9 | 36 ± 4.4 |
| ΔHM [kJ mol−1] | 31.4 ± 4.4 | 30.5 ± 1.4 | 51.5 ± 9.9 |
| 298 τ R [ps] | 60.7 ± 1.5 | 35.1 ± 1.7 | 48.4 ± 2.3 |
| E R [kJ mol−1] | 17.9 ± 1.0 | 25.2 ± 2.4 | 21.1 ± 2.3 |
| q | 6b | 1b | 1b |
| r FeH [Å] | 2.69b,c | 2.69b,c | 2.70b,c |
| a FeH [Å] | 3.5a | 3.5a | 3.5a |
The residence lifetime of the whole water molecule in the Fe(III) coordination sphere is rather long (298τOM = 25 μs). This can be ascribed to the high charge-to-radius ratio of the cation (cf.298τOM = 35 ns for Mn(II)).20 Water exchange appears to be much faster however than estimated previously by Jordan (298τOM = 6.25 ms).16 The residence lifetime of water protons obtained from 1H NMRD measurements is much shorter (298τHM = 0.76 μs, Table 1), which indicates that 1H exchange receives an important contribution from prototropic exchange under highly acidic conditions, as recently shown for Gd-complexes bearing amide ancillary groups.21 Therefore, the observed exchange rate k can be expressed as 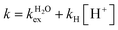 , where
, where 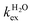 and kH are the rate constants characterizing the exchange of the whole water molecule and the prototropic mechanism, respectively. Since
and kH are the rate constants characterizing the exchange of the whole water molecule and the prototropic mechanism, respectively. Since 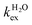 = 4.0 × 104 s−1 and kH = 9.06 × 106 s−1 M−1, the prototropic exchange is expected to provide the main contribution at the acidic pH values required to avoid the hydrolysis of [Fe(H2O)6]3+. These results explain the discrepancies between the data reported earlier on by Merbach and Bertini,15 and indicate that the 298τOM value calculated by Jordan is very inaccurate. Finally, it is worth noting that the calculated kH value is 3–4 times larger than that calculated through a pH-dependent study for a cationic GdDOTA-tetraamide derivative.22
= 4.0 × 104 s−1 and kH = 9.06 × 106 s−1 M−1, the prototropic exchange is expected to provide the main contribution at the acidic pH values required to avoid the hydrolysis of [Fe(H2O)6]3+. These results explain the discrepancies between the data reported earlier on by Merbach and Bertini,15 and indicate that the 298τOM value calculated by Jordan is very inaccurate. Finally, it is worth noting that the calculated kH value is 3–4 times larger than that calculated through a pH-dependent study for a cationic GdDOTA-tetraamide derivative.22
The inner-sphere contribution to relaxivity is given by eqn (1), where q is the number of coordinated water molecules and T1M is the relaxation time of a coordinated water molecule.
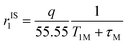 | (1) |
At high magnetic fields (>20 MHz), T1M can be approximated by eqn (2) and (3).
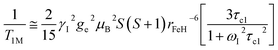 | (2) |
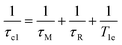 | (3) |
In the case of low molecular weight Mn(II) and Gd(III) complexes τM and T1e are generally in the ns timescale, while τR is in the ps timescale, so that τc1 ≅ τR.1 For [Fe(H2O)6]3+ the relaxation of the electron spin is faster and 298τHM is also relatively long, and thus τc1 receives significant contributions from both T1e and τR at high magnetic fields, explaining the different shapes of the 1H NMRD profiles of Fe(III), Gd(III) and Mn(II) complexes (Fig. 2). In detail, the NMRD profile simulated for Mn(II) shows a dispersion in the range 0.01 to 0.1 MHz related to the scalar contribution to relaxivity. The relaxivity decreases above 1 MHz, reaching a value of ca. 2 mM−1 s−1 above 100 MHz. The lower relaxivity of Mn(II) at high fields is due to the lower value of S(S + 1) compared with Gd(III), an effect partially balanced by a shorter metal–proton distance of the coordinated water molecule (rGdH and rMnH were estimated to be 3.1 and 2.83 Å, respectively).6 The relaxivity simulated for Fe(III) is relatively low at low fields, as a result of a faster electron relaxation. However, r1 calculated at high fields is comparable, or higher, to that of Gd(III), which is explained by the contribution of T1e to τc1, as well as by the short rFeH distance (2.69 Å, as estimated using DFT). From these results we can draw the following important conclusion: small Fe(III) complexes may provide relaxivities quite comparable to those of GBCAs with the same number of coordinated water molecules at the magnetic fields commonly used in MRI.
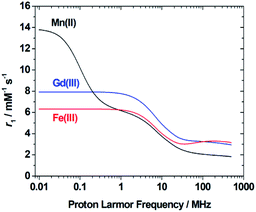 | ||
| Fig. 2 1H NMRD profiles simulated for q = 1 complexes of Fe(III), Mn(II) and Gd(III) using the parameters determined for the corresponding aqua-ions. | ||
Once the relaxometric properties of the [Fe(H2O)6]3+ complex were deciphered, we turned our attention to the complexes with EDTA4− and CDTA4−, which are known to contain a water molecule coordinated to the Fe(III) ion.23 Fe(EDTA)− represents the prototype and model system of monohydrate iron(III) complexes (q = 1), but although some relaxometric data were published in the mid-1980s,24 a complete and in-depth relaxometric study is yet missing. In particular, it is known that at neutral pH the Fe(III) ion is heptacoordinate with a water molecule in its first coordination sphere characterized by a relatively fast exchange rate. We decided to carry out a complete study of this complex, together with the corresponding iron chelates of DTPA and CDTA, combining 1H e 17O NMR relaxometric measurements. Both metal chelates have a well-known pH-dependent chemical speciation (Fig. S3 and S4†), which is reflected in the corresponding dependence of r1 on pH, as shown in Fig. 3. Relaxivity is constant in the acidic zone and up to pH ca. 6.5 for Fe(EDTA)− and 8.5 for Fe(CDTA)−, where deprotonation of the bound water occurs followed by hydrolysis and formation of more complex species.
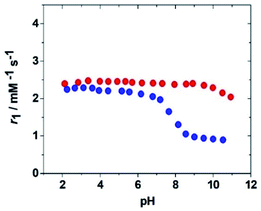 | ||
| Fig. 3 pH dependency of the relaxivity, r1, at 298 K and 20 MHz for the complexes Fe(EDTA)− (blue symbols) and Fe(CDTA)− (red symbols). | ||
Therefore, the relaxometric data were measured at pH = 5.3 where only the species [FeL(H2O)]− is present in solution. To gain insight into the molecular parameters that control the relaxivity of the Fe(III) species, 1H 1/T1 NMRD profiles were recorded at three different temperatures (283, 298 and 310 K) over a range of magnetic field strengths of 2.3 × 10−4 to 3.0 T, which correspond to proton Larmor frequencies of 0.01–127 MHz (Fig. 4). An additional value at 500 MHz was measured using a high-resolution NMR spectrometer. The profiles of the two complexes reproduce the characteristic properties observed for the aqua ion, i.e.: a plateau at low fields, a dispersion around 10 MHz, a minimum around 50–70 MHz followed by a marked increase with the observation frequency to give a large hump centred around 300 MHz. The amplitude of the NMRD profiles (Fig. S11 and S12†) decreases with increasing temperature across the entire range of observed frequencies (0.01–500 MHz). This shows that the residency time of the coordinated water molecule does not influence r1, which implies that the systems are in the condition of fast exchange. This agrees with the conclusions of a previous 17O NMR study.25 Thus, the shape of the profiles confirms that, at magnetic field values of clinical MRI relevance, both molecular tumbling and electron relaxation influence relaxivity. The latter increases with the increase of the applied magnetic field and is therefore responsible for the r1 increase at frequency values greater than 50 MHz. This in an interesting and clearly distinct behaviour from that of the small complexes of Gd(III) and Mn(II).
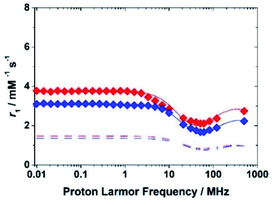 | ||
| Fig. 4 1H NMRD profiles at 298 K for the complexes Fe(EDTA)− (blue symbols) and Fe(CDTA)− (red symbols). The lower dashed curves show the calculated outer-sphere contribution. | ||
The effect of molecular tumbling appears to be relevant in explaining the differences in the profiles of the iron complexes with EDTA and CDTA. In fact, while the molecular mass of Fe(CDTA)− is about 15% greater than that of the EDTA complex, its relaxivity values are about 20–25% higher (at 60 and 120 MHz).
Although there is no clear evidence of an influence of the water exchange rate, kex, in the NMRD profiles, determining the value of this parameter is very important, as it can become a key factor in the development of neutral complexes or macromolecular systems. An estimate of the kex values for the two Fe(III) chelates were obtained about twenty years ago by measuring the temperature dependence of the 17O line broadening over a wide temperature range (273 to 388 K).23
A more accurate assessment is obtained by measuring the temperature dependence of the solvent 17O NMR transverse relaxation rates, R2, and shifts, Δω, of concentrated solutions of the complexes and by performing a simultaneous global fit of the 1H and 17O NMR data.
We collected the data on 4.5 mM solutions of the complexes at pH = 5.5 and 11.75 T (Fig. 5).
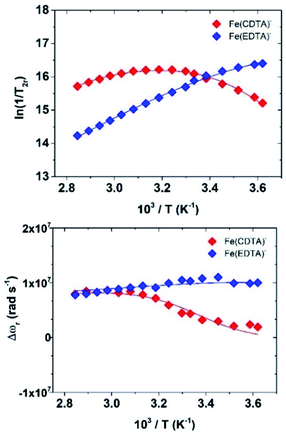
The quantitative analysis of the 1H NMRD and 17O NMR data of Fe(CDTA)− and Fe(EDTA)− was performed in a similar way than for [Fe(H2O)6]3+. The parameters characterizing the outer-sphere contribution (298D, ED and aFeH) were fixed, while the values of AO/ħ and rFeH were estimated with DFT calculations (Table 1). Seven-coordinate complexes with EDTA-like ligands can give rise to two diastereoisomeric forms with capped trigonal prismatic [CTP, Δ(δ)/Λ(λ) enantiomeric pair] and pentagonal bipyramidal [PB, Δ(λ)/Λ(δ) enantiomeric pair] coordination environments.26 Our calculations show that for Fe(CDTA)− the CTP geometry is more stable than the PB one by a Gibbs free energy difference of 23.6 kJ mol−1. However, the two diastereoisomers are virtually isoenergetic in the case of Fe(EDTA)−, with the PB isomer being favoured by only 0.1 kJ mol−1. Thus, the CTP diastereoisomer is likely the only one present in solution for Fe(CDTA)−, while in the case of Fe(EDTA)− both the CTP and PB isomers present significant populations in solution. Nevertheless, the two isomers are characterized by similar AO/ħ and rFeH values (Table S2†). The analysis of the NMRD data did not require including a scalar contribution to relaxivity, which is likely related to low AO/ħ values of the proton nuclei of coordinated water molecules, as suggested by DFT. Finally, the temperature dependence of relaxivity could be well reproduced by allowing the zero-field splitting energy Δ to vary with temperature, following an Arrhenius behaviour with activation energy EΔ. It is well established that relaxation of the electron spin may be the result of both transient and static ZFS contributions. For highly symmetrical complexes such as [Fe(H2O)6]3+, the ZFS energy is very small (CASSCF/NEVPT2 calculations based on a CAS(5,5) active space provide Δ = 0.036 cm−1, Table S2†). In this case electron spin relaxation originates from the transient ZFS, which is associated with transient distortions of the metal coordination environment occurring in solution. The static ZFS corresponds to the averaged value of all configurations existing in solution. The values of Δ2 obtained from the fits of the data correspond to Δ = 0.28 and 0.23 cm−1 for [Fe(EDTA)(H2O)]− and [Fe(CDTA)(H2O)]−, respectively. CASSCF/NEVPT2 calculations give very similar Δ values for the two complexes (∼0.13 cm−1). The calculated values are reasonably close to the experimental ones, taking into account that dynamic effects were not considered in this study.
The values of the rotational correlation times 298τR are quite consistent with the size of the complexes. The longer 298τR value obtained for [Fe(H2O)6]3+ is probably associated with the presence of a well-defined second coordination sphere promoted by the high positive charge density of the metal ion. Water exchange is several orders of magnitude faster in Fe(EDTA)− and Fe(CDTA)− than in the aqua-ion. Water exchange is also considerably faster for Fe(EDTA)− (k298ex = 104 × 107 s−1) than for Fe(CDTA)− (k298ex = 2.8 × 107 s−1). The k298ex value obtained for Fe(CDTA)− is in reasonably good agreement with previous estimates (1.3–1.7 × 107 s−1), while previous works only based on 17O NMR data reported much lower k298ex values for Fe(EDTA)− (6.0–7.2 × 107 s−1).23 The k298ex value determined for Fe(EDTA)− is endowed with a rather large error, as kex provides a significant contribution to T2r only at low temperatures. Nevertheless, our combined 1H and 17O NMR data suggests that previous works underestimated the water exchange rate in Fe(EDTA)−. The lower water exchange rate determined for Fe(CDTA)− can be attributed to the rigidifying effect of the cyclohexyl backbone, which increases the energy cost required to reach the transition state.27
The Fe(III) ion forms with the octadentate ligand DTPA a purely outer sphere (OS) complex (q = 0), hence it represents an effective model to compare the measured r1 values with those calculated for the OS contribution. The NMRD profiles of [Fe(DTPA)]2− were measured in the Larmor frequency range 0.01 to 500 MHz and at temperatures of 283, 298 and 310 K, at neutral pH (Fig. S18†). The experimental and calculated OS profiles are completely similar in shape, while small differences in amplitude are associated with small differences in aFeH and in the parameters of the electron relaxation (Table S3†).
The assessment of the thermodynamic stability and kinetic inertness of the metal-based contrast agents is important to avoid the transmetallation and transchelation reactions with the challenging endogenous components. In particular, Fe(III) complexes can hydrolyse forming hydroxo- and oxo-complexes at high pH values and can be transchelated by transferrins. In fact, transferrins, like serum transferrin (sTf), ovotransferrin (OTf) or lactoferrin (LTf), are strong Fe(III)-binding proteins with one Fe(III)-binding site in each lobe.28 The human sTf and LTf are known to bind Fe(III) with high affinity (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeTf = 22.8, log
KFeTf = 22.8, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFe2Tf = 21.5), which requires the concomitant binding of a synergistic bicarbonate anion.29 Since serum transferrin is normally only 30% saturated with Fe(III), it retains a relatively high capacity to compete with Fe(III)-complexes. Thus, we conducted potentiometric titrations to determine the protonation constants of the ligands (Table S1, details in the ESI†), while spectrophotometric experiments were performed to determine the equilibrium constants that describe solution speciation of the Fe(III)–EDTA and Fe(III)–CDTA systems (Fig. S3 and S4†). The stability constants (I = 0.15 M NaNO3, Table 2) show that the Fe(CDTA)− complex is significantly more stable than Fe(EDTA)−. The stability constants are significantly lower than those determined in 0.1 M KNO3 (log
KFe2Tf = 21.5), which requires the concomitant binding of a synergistic bicarbonate anion.29 Since serum transferrin is normally only 30% saturated with Fe(III), it retains a relatively high capacity to compete with Fe(III)-complexes. Thus, we conducted potentiometric titrations to determine the protonation constants of the ligands (Table S1, details in the ESI†), while spectrophotometric experiments were performed to determine the equilibrium constants that describe solution speciation of the Fe(III)–EDTA and Fe(III)–CDTA systems (Fig. S3 and S4†). The stability constants (I = 0.15 M NaNO3, Table 2) show that the Fe(CDTA)− complex is significantly more stable than Fe(EDTA)−. The stability constants are significantly lower than those determined in 0.1 M KNO3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL = 29.05 and 24.95 for Fe(CDTA)− and Fe(EDTA)−, respectively).25 This indicates that the Na+ ion reduces the stability of Fe(III)-complexes due to its interaction with the ligands. The equilibrium constants characterizing the deprotonation of the coordinated water molecule (log
KFeL = 29.05 and 24.95 for Fe(CDTA)− and Fe(EDTA)−, respectively).25 This indicates that the Na+ ion reduces the stability of Fe(III)-complexes due to its interaction with the ligands. The equilibrium constants characterizing the deprotonation of the coordinated water molecule (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeLH-1) confirm that the hydrolysis does not occur at physiological pH for Fe(CDTA)−, in perfect agreement with the relaxivity pH dependency showed above. At higher pH, complexes form an oxo-bridged dimer. The equilibrium constants characterizing dimer formation (KD and Kd, Table S1†) confirm previous results that pointed to a lower tendency of Fe(CDTA)− to form the oxo-bridged dimer than Fe(EDTA)−.25
KFeLH-1) confirm that the hydrolysis does not occur at physiological pH for Fe(CDTA)−, in perfect agreement with the relaxivity pH dependency showed above. At higher pH, complexes form an oxo-bridged dimer. The equilibrium constants characterizing dimer formation (KD and Kd, Table S1†) confirm previous results that pointed to a lower tendency of Fe(CDTA)− to form the oxo-bridged dimer than Fe(EDTA)−.25
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/kd) characterizing the stability and dissociation reactions of Fe(EDTA)− and Fe(CDTA)− complexes (0.15 M NaNO3, 25 °C)a
2/kd) characterizing the stability and dissociation reactions of Fe(EDTA)− and Fe(CDTA)− complexes (0.15 M NaNO3, 25 °C)a
| Fe(EDTA)− | Fe(CDTA)− | |
|---|---|---|
| a The definitions and equations used for the evaluation of the thermodynamic and kinetic data are reported in the ESI. b From spectrophotometric titrations. c From dissociation experiments. d From ref. 25 (E(NHE) = E(SCE) + 0.242 V). | ||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeL KFeL |
22.14(4) | 24.36(2) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KFeLH-1 KFeLH-1 |
7.51(1)b/7.41(2)c | 9.50(2)b/9.58(4)c |
| k 0 (s−1) | (5 ± 1) ×10−6 | (3.2 ± 0.5) ×10−7 |
| k OH (M−1 s−1) | 1.0 ± 0.2 | (3.6 ± 0.8) ×10−3 |
| k OH 2 (M−2 s−1) | (1.4 ± 0.2) ×103 | 1.2 ± 0.1 |
| k d (s−1) at pH = 7.4 | 2.9 × 10−6 | 2.1 × 10−9 |
| t 1/2 (h) at pH = 7.4 | 66 | 8.9 × 104 |
| E 1/2 [mV vs. SCE]d | −132.5 | −150.5 |
The kinetic inertness of Fe(EDTA)− and Fe(CDTA)− was assessed by transchelation reactions with the HBED ligand, which provided the rates characterizing the spontaneous dissociation k0 and first- and second-order hydroxide-assisted dissociation rates (kOH and kOH2, respectively, Table 2).30 The comparison of the rate constants reported in Table 2 reveals that the spontaneous and the first and second order OH− assisted dissociations of Fe(EDTA)− are about 15, 280 and 1200 times faster than those of Fe(CDTA)−. The significantly slower dissociation of the Fe(CDTA)− is explained by the structural rigidity of the CDTA ligand due to the presence of the cyclohexyl moiety on the ligand backbone,27 as observed for the Mn(II) analogues.31 The dissociation rate constant (kd) of Fe(CDTA)− calculated near to physiological condition (pH = 7.4, 25 °C), is approximately 1000 times lower than that of Fe(EDTA)−, i.e. the former complex is more inert.
It is worth highlighting that for Mn(II) complexes the kinetic inertness is a crucial issue to achieve and typically they follow an acid-assisted dissociation pathway. In general, they tend to form less stable and inert complexes than Fe(III) (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMnEDTA = 12.46; log
KMnEDTA = 12.46; log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMnCDTA = 14.32; t1/2MnEDTA = 0.076 h; t1/2MnCDTA = 12.3 h (pH 7.4)).31
KMnCDTA = 14.32; t1/2MnEDTA = 0.076 h; t1/2MnCDTA = 12.3 h (pH 7.4)).31
Importantly, FeIII-based compounds may participate in the redox cycle by taking the electron from the reducing agent, which is followed by its reduction and the concomitant electron transfer to H2O2 (Fenton reaction). According to the concentration and the redox properties of the possible reducing agents in human blood plasma, ascorbic acid is the most relevant candidate to involve FeIII-complexes into the Fenton reaction.32 The redox stability of Fe(EDTA)− and Fe(CDTA)− was investigated via the reduction of the FeIII-complexes with ascorbic acid monitored by spectrophotometry (pH = 7.4, 25 °C in 0.15 M NaNO3).
According to the kinetic data, the electron-transfer occurs by the formation of the ternary FeIIIL–HA intermediate between the ascorbate anion (HA−) and the FeIIIL complex, likely through the substitution of the inner-sphere water molecule. The formation of a similar ternary Fe(EDTA)–oxalate complex was identified by the pH-potentiometric studies of the Fe(EDTA)–oxalate system (FeIII(EDTA)–Ox: KFeL–Ox = 275 M−1).33 The kHA rate constants characterizing the ascorbate anion assisted reduction of Fe(EDTA)− and Fe(CDTA)− were found to be 8 ± 2 and 3.0 ± 0.2 M−1 s−1 at pH = 7.4. By taking into account the stability of the ternary FeIIIL–HA intermediates (FeIII(EDTA)–HA−: KFeL–HA = 75 ± 15 M−1; FeIII(CDTA)–HA−: KFeL–HA = 40 ± 5 M−1) and the in vivo concentration of the ascorbate anion ([(HA−)] = 43 μM),34 the ascorbate-assisted reduction rate (kobs) and half-lives (t1/2 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/kobs) of Fe(EDTA)− and Fe(CDTA)− are 2.4 × 10−4 and 1.3 × 10−4 s−1, (0.8 and 1.5 hours, respectively). Thus, the half-lives of the complexes near physiological condition are about 83 (Fe(EDTA)−) and 59
2/kobs) of Fe(EDTA)− and Fe(CDTA)− are 2.4 × 10−4 and 1.3 × 10−4 s−1, (0.8 and 1.5 hours, respectively). Thus, the half-lives of the complexes near physiological condition are about 83 (Fe(EDTA)−) and 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (Fe(CDTA)−) times faster upon reduction than in the absence of the reducing agent.
000 (Fe(CDTA)−) times faster upon reduction than in the absence of the reducing agent.
Based on previous studies35,36 the ascorbate-assisted reduction rate constant of FeIIIL complexes is expected to decrease with the electrode potential of FeIIIL, as confirmed by the 1.8 times slower reduction of Fe(CDTA)− with respect to Fe(EDTA)−. Since the electrode potential is correlated to the thermodynamic stability constant of FeIIIL, we emphasize that the thermodynamic properties of the FeIII-complexes play a very important role together to the kinetic ones for their in vivo applications. Ascorbic acid is a strong reducing agent (H2A → A + 2H+ + 2e−E0 = 0.39 V vs. NHE),37 however, the reduction potential is strongly influenced by the pH and the formation of the HA˙ and A˙− radicals as intermediates. Thus, at physiological condition, the electrode potential of the FeIII/FeII-complex redox couple should be lower than −0.2 V vs. NHE to avoid the formation of FeII-complexes and the occurrence of the Fenton reactions.37
3. Conclusions
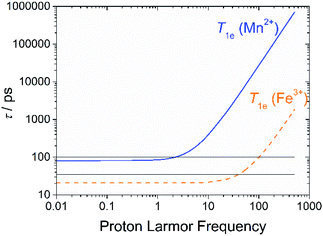
We have shown here that monohydrated Fe(III) complexes are very attractive candidates for the design of efficient MRI contrast agents, in particular at the high magnetic fields of modern clinical scanners and of those used in animal studies. The detailed multinuclear relaxometric analysis over a wide range of proton Larmor frequencies, performed for the first time for Fe(III) complexes, revealed some key differences as compared to related Mn(II) and Gd(III) complexes. The relaxivity of Fe(III) complexes at high fields receives contributions from both τR and T1e, which assume values of the same order of magnitude between ca. 1.5 and 3 T (Fig. 6). On the other hand, T1e is considerably longer for Mn(II) and Gd(III) complexes, hence T1e affects relaxivity only below ∼10 MHz. We anticipate that optimization of both T1e and τR will allow obtaining Fe(III) complexes with effectiveness (relaxivity) even higher than that of the commercially available and clinically used agents.Another important conclusion of the present work is that the properties of Fe(III) contrast agent candidates must be tuned to: (i) increase the pKa of the coordinated water molecule well above physiological pH, (ii) obtain kinetically inert complexes, for example by ligand rigidification, and (iii) shift the reduction potential of the complex out of the biological window (E0 < −0.2 V vs. NHE), to avoid complex dissociation upon reduction and also triggering the Fenton reaction.
In this perspective, coordination chemistry appears to be able to play an important role as two structurally very similar compounds such as the iron(III) complexes of EDTA and CDTA have markedly different pKa values of bound water. The small structural differences between the two chelates also result in significantly different kex values and suggests the possibility of modulating this parameter through a suitable chemical design, as successfully happened in the case of Gd(III) complexes. Even the kinetic inertia seems significantly depend on structural aspects seemingly minor. Then, the CDTA scaffold is clearly better suited for the design of Fe(III)-based MRI contrast agents than it is EDTA.
It will be necessary to understand, at least from an empirical point of view through the collection of a large number of new data, if it is conceivable to optimize the electronic relaxation time with an appropriate design of the ligand as this would allow to increase the relaxation and tune the frequency value corresponding at its maximum value. So, while much remains to be done, we hope that these results may represent useful guidelines for the development of metal-diagnostic probes of improved safety, biotolerability and efficacy.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.Author contributions
CPI and MB conceived and supervised the project. AN carried out the relaxometric study with the assistance of FC and LT. DH and ZB carried out the thermodynamic and kinetic experiments. CPI, AN and MB analysed the relaxometric data. CPI performed the computational study. ZB, LT, CPI and MB wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. C., L. T. and M. B. acknowledge the financial support from Università del Piemonte Orientale (Ricerca locale FAR2019). C.P.-I. thanks Ministerio de Economía y Competitividad (CTQ2016-76756-P) and Xunta de Galicia (ED431B 2020/52) for generous financial support. C.P.-I. also thanks Centro de Supercomputación de Galicia (CESGA) for providing the computer facilities. Z. B. thanks the Doctoral School of Chemistry of the University of Debrecen for the PhD position of D. H. This work was carried out within the framework of the COST CA15209 Action “European Network on NMR Relaxometry”.Notes and references
- (a) A. E. Merbach, L. Helm and E. Toth, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, John Wiley & Sons Ltd, 2nd edn, 2013 CrossRef; (b) J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed.
- (a) E. A. Akam, E. Abston, N. J. Rotile, H. R. Slattery, I. Y. Zhou, M. Lanuti and P. Caravan, Chem. Sci., 2020, 11, 224–231 RSC; (b) M. Botta and L. Tei, Eur. J. Inorg. Chem., 2012, 1945–1960 CrossRef CAS; (c) A. J. L. Villaraza, A. Bumb and M. W. Brechbiel, Chem. Rev., 2010, 110, 2921–2959 CrossRef CAS PubMed; (d) M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed; (e) E. Di Gregorio, L. Lattuada, A. Maiocchi, S. Aime, G. Ferrauto and E. Gianolio, Chem. Sci., 2021, 12, 1368–1377 RSC; (f) C. J. Adams and T. J. Meade, Chem. Sci., 2020, 11, 2524–2530 RSC.
- S. Aime, M. Botta, D. Esteban-Gómez and C. Platas-Iglesias, Mol. Phys., 2019, 117, 898–909 CrossRef CAS.
- (a) J. M. Hazelton, M. K. Chiu and H. H. Abujudeh, Curr. Radiol. Rep., 2019, 7, 5 CrossRef; (b) J. Endrikat, S. Dohanish, N. Schleyer, S. Schwenke, S. Agarwal and T. Balzer, Invest. Radiol., 2018, 53, 541–550 CrossRef PubMed.
- (a) E. Gianolio, E. Di Gregorio and S. Aime, Eur. J. Inorg. Chem., 2019, 137–151 CrossRef CAS; (b) M. Le Fur and P. Caravan, Metallomics, 2019, 11, 240–254 CrossRef CAS PubMed.
- M. Botta, F. Carniato, D. Esteban-Gomez, C. Platas-Iglesias and L. Tei, Future Med. Chem., 2019, 11, 1461–1483 CrossRef CAS PubMed.
- (a) N. Kuznik and M. Wyskocka, Eur. J. Inorg. Chem., 2015, 445–458 Search PubMed; (b) M. F. Tweedle, Radiology, 2018, 286, 409–411 CrossRef PubMed.
- G. J Anderson and D. M. Frazer, Am. J. Clin. Nutr., 2017, 106, 1559S–1566S CrossRef PubMed.
- (a) P. Boehm-Sturm, A. Haeckel, R. Hauptmann, S. Mueller, C. K. Kuhl and E. Schellenberger, Radiology, 2018, 286, 537–546 CrossRef PubMed; (b) J. Xie, A. Haeckel, R. Hauptmann, I. P. Ray, C. Limberg, N. Kulak, B. Hamm and E. Schellenberger, Magn. Res. Med., 2021, 85, 3370–3382 CrossRef CAS PubMed.
- H. Wang, V. Clavijo Jordan, I. A. Ramsay, M. Sojoodi, B. C. Fuchs, K. K. Tanabe, P. Caravan and E. M. Gale, J. Am. Chem. Soc., 2019, 141, 5916–5925 CrossRef CAS PubMed.
- (a) E. M. Snyder, D. Asik, S. M. Abozeid, A. Burgio, G. Bateman, S. G. Turowski, J. A. Spernyak and J. R. Morrow, Angew. Chem., Int. Ed., 2020, 59, 2414–2419 CrossRef CAS PubMed; (b) D. Asik, R. Smolinski, S. M. Abozeid, T. B. Mitchell, S. G. Turowski, J. A. Spernyak and J. R. Morrow, Molecules, 2020, 25, 2291 CrossRef CAS PubMed; (c) A. Patel, D. Asik, E. M. Snyder, A. E. Dilillo, P. J. Cullen and J. R. Morrow, ChemMedChem, 2020, 15, 1050–1057 CrossRef CAS PubMed.
- (a) S. J. Dorazio and J. R. Morrow, Eur. J. Inorg. Chem., 2012, 2006–2014 CrossRef CAS; (b) K. Du, E. A. Waters and T. D. Harris, Chem. Sci., 2017, 8, 4424–4430 RSC; (c) I.-R. Jeon, J. G. Park, C. R. Haney and T. D. Harris, Chem. Sci., 2014, 5, 2461–2465 RSC.
- A. E. Thorarinsdottir, A. I. Gaudette and T. D. Harris, Chem. Sci., 2017, 8, 2448–2456 RSC.
- S. H. Koenig, C. M. Baglin and R. D. Brown III, Magn. Reson. Med., 1985, 2, 283–288 CrossRef CAS PubMed.
- (a) T. W. Swaddle and A. E. Merbach, Inorg. Chem., 1981, 20, 4212–4216 CrossRef CAS; (b) I. Bertini, F. Capozzi, C. Luchinat and Z. Xia, J. Phys. Chem., 1993, 97, 1134–1137 CrossRef CAS.
- M. Grant and R. B. Jordan, Inorg. Chem., 1981, 20, 55–60 CrossRef CAS.
- (a) I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS; (b) N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842–850 CrossRef CAS; (c) J. H. Freed, J. Chem. Phys., 1978, 68, 4034–4037 CrossRef CAS.
- T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307–312 CrossRef CAS.
- G. A. Rolla, C. Platas-Iglesias, M. Botta, L. Tei and L. Helm, Inorg. Chem., 2013, 52, 3268–3279 CrossRef CAS PubMed.
- D. Esteban-Gómez, C. Cassino, M. Botta and C. Platas-Iglesias, RSC Adv., 2014, 4, 7094–7103 RSC.
- L. Leone, M. Boccalon, G. Ferrauto, I. Fabian, Z. Baranyai and L. Tei, Chem. Sci., 2020, 11, 7829–7835 RSC.
- S. Aime, A. Barge, M. Botta, D. Parker and A. S. De Sousa, J. Am. Chem. Soc., 1997, 119, 4767–4768 CrossRef CAS.
- T. Schneppensieper, S. Seibig, A. Zahl, P. Tregloan and R. van Eldik, Inorg. Chem., 2001, 40, 3670–3676 CrossRef CAS PubMed.
- J. Bloch and G. Navon, J. Inorg. Nucl. Chem., 1980, 42, 693–699 CrossRef CAS.
- A. Brausam, J. Maigut, R. Meier, P. A. Szilágyi, H.-J. Buschmann, W. Massa, Z. Homonnay and R. van Eldik, Inorg. Chem., 2009, 48, 7864–7884 CrossRef CAS PubMed.
- J. Maigut, R. Meier, A. Zahl and R. van Eldik, Inorg. Chem., 2008, 47, 5702–5719 CrossRef CAS PubMed.
- (a) E. Balogh, M. Mato-Iglesias, C. Platas-Iglesias, E. Tóth, K. Djanashvili, J. A. Peters, A. de Blas and T. Rodríguez-Blas, Inorg. Chem., 2006, 45, 8719–8728 CrossRef CAS PubMed; (b) G. Tircsó, M. Regueiro-Figueroa, V. Nagy, Z. Garda, T. Garai, F. K. Kalman, D. Esteban-Gómez, E. Tóth and C. Platas-Iglesias, Chem.–Eur. J., 2016, 22, 896–901 CrossRef PubMed.
- Y. Li, B. Liu, Z. Ge and B. Yang, J. Photochem. Photobiol., B, 2008, 91, 137–142 CrossRef CAS PubMed.
- W. R. Harris and V. L. Pecoraro, Biochemistry, 1983, 22, 292–299 CrossRef CAS PubMed.
- A. Vágner, A. Forgács, E. Brücher, I. Tóth, A. Maiocchi, A. Wurzer, H.-J. Wester, J. Notni and Z. Baranyai, Front. Chem., 2018, 6, 170 CrossRef PubMed.
- (a) F. K. Kalman and G. Tircso, Inorg. Chem., 2012, 51, 10065–10067 CrossRef CAS PubMed; (b) K. Pota, Z. Garda, F. K. Kalman, J. L. Barriada, D. Esteban-Gomez, C. Platas-Iglesias, I. Toth, E. Brucher and G. Tircso, New J. Chem., 2018, 42, 8001–8011 RSC.
- (a) W. H. Koppenol and R. H. Hider, Free Radicals Biol. Med., 2019, 133, 3–10 CrossRef CAS PubMed; (b) Y. Turyan and R. Kohen, J. Electroanal. Chem., 1995, 380, 273–277 CrossRef.
- D. Pyreu and E. Kozlovskii, Zh. Neorg. Khim., 2000, 45, 459–464 Search PubMed.
- P. M. May, P. W. Linder and D. R. Williams, J. Chem. Soc., Dalton Trans., 1977, 588–595 RSC.
- M. Taqui-Khan and A. E. Martell, J. Am. Chem. Soc., 1968, 90, 3386–3389 CrossRef PubMed.
- (a) E. Pelizzetti, E. Mentasti and E. Pramauro, Inorg. Chem., 1976, 15, 2898–2900 CrossRef CAS; (b) E. Pelizzetti, E. Mentasti and E. Pramauro, Inorg. Chem., 1978, 17, 1181–1186 CrossRef CAS.
- J. C. Joyner, J. Reichfield and J. A. Cowan, J. Am. Chem. Soc., 2011, 133, 15613–15626 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details: thermodynamic, kinetic and redox studies. Equations used, NMRD profiles and DFT optimized structures. See DOI: 10.1039/d1sc02200h |
| This journal is © The Royal Society of Chemistry 2021 |