Open Access Article
Open Access ArticleComputational and data driven molecular material design assisted by low scaling quantum mechanics calculations and machine learning†
Wei
Li
 *a,
Haibo
Ma
*a,
Haibo
Ma
 *ab,
Shuhua
Li
*ab,
Shuhua
Li
 a and
Jing
Ma
a and
Jing
Ma
 *ab
*ab
aKey Laboratory of Mesoscopic Chemistry of Ministry of Education, Institute of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210023, China. E-mail: majing@nju.edu.cn; wli@nju.edu.cn; haibo@nju.edu.cn
bJiangsu Key Laboratory of Advanced Organic Materials, Jiangsu Key Laboratory of Vehicle Emissions Control, Nanjing University, Nanjing 210023, China
First published on 8th November 2021
Abstract
Electronic structure methods based on quantum mechanics (QM) are widely employed in the computational predictions of the molecular properties and optoelectronic properties of molecular materials. The computational costs of these QM methods, ranging from density functional theory (DFT) or time-dependent DFT (TDDFT) to wave-function theory (WFT), usually increase sharply with the system size, causing the curse of dimensionality and hindering the QM calculations for large sized systems such as long polymer oligomers and complex molecular aggregates. In such cases, in recent years low scaling QM methods and machine learning (ML) techniques have been adopted to reduce the computational costs and thus assist computational and data driven molecular material design. In this review, we illustrated low scaling ground-state and excited-state QM approaches and their applications to long oligomers, self-assembled supramolecular complexes, stimuli-responsive materials, mechanically interlocked molecules, and excited state processes in molecular aggregates. Variable electrostatic parameters were also introduced in the modified force fields with the polarization model. On the basis of QM computational or experimental datasets, several ML algorithms, including explainable models, deep learning, and on-line learning methods, have been employed to predict the molecular energies, forces, electronic structure properties, and optical or electrical properties of materials. It can be conceived that low scaling algorithms with periodic boundary conditions are expected to be further applicable to functional materials, perhaps in combination with machine learning to fast predict the lattice energy, crystal structures, and spectroscopic properties of periodic functional materials.
1 Introduction
High-throughput computations have played important roles in material design in recent years.1–3 The prediction of the structures and properties of newly designed materials is useful to guide molecular syntheses and device fabrication.4–6 For example, theoretical computations have been employed to assist designing layered and inorganic crystals,7 two-dimensional materials,3 energy-related materials,5,8 functional organic materials,6,9 and polymeric materials.10 Both quantum mechanics (QM) and classical molecular mechanics (MM) based molecular simulations are widely employed to compute the material with oligomer/cluster models or periodic boundary conditions (PBCs). PBC calculations are widely applied to atomic and molecular crystals and covalent-bonded three- or two-dimensional inorganic materials.3,7 For many molecular materials (e.g., organic materials with large π-conjugation cores or polymeric materials),6,9,10 QM calculations with a PBC model are still very expensive, due to their large sized cell boxes, and only PBC MM calculations are affordable for high throughput calculations. However, in order to compute the electronic structure properties (such as optical, electrical, or magnetic properties) of materials, to obtain a more accurate material structure or to benchmark the empirical intermolecular potentials, density functional theory (DFT) or even more accurate ab initio electron correlation methods using a cluster model (or a PBC model for molecular materials with small molecules) are required.11,12DFT scales as O(N3-4) with the number of electrons, N, increased and is expensive for large-sized complex material systems.13 To accelerate the design of new materials, a high-throughput screening scheme by integrating multi-scale calculations is employed in computational materials, in which the expensive QM calculations are the bottleneck in the whole computational processes. Conventional QM methods are not available for molecular material systems with thousands of atoms. Higher-level wave function-based electron correlation calculations are even more expensive. The development and implementation of low or even linear scaling QM methods are hence very urgent for material design. The realization of low-scaling DFT or electron correlation calculations is one of the core challenges in the quantum chemistry community in the last two decades. Due to the difficulty in the theoretical treatment of the ground sate and excited states of π-electron delocalized and metal-containing systems, application examples of low or linear scaling methods to materials are far fewer than the computations of water clusters and proteins, as shown in Table S1.† Several low-scaling strategies, such as density matrix-based, local correlation, and fragment-based methods, were used to predict the ground-state energies, structures, and molecular properties of large systems. For example, a local correlation cluster-in-molecule (CIM) method was used to predict the binding energies in aqueous zinc-organic batteries;14 a divide-and-conquer method was developed to optimize the molecular geometries of conjugated oligomers;15 density-functional perturbation theory (DFPT) was employed to compute the polarizabilities of large organic molecules;16 a generalized energy-based fragmentation (GEBF) method was used to predict the infrared (IR) and nuclear magnetic resonance (NMR) spectra of large supramolecular coordination complexes.17
For characterizing the electronic structure features in photophysics and photochemistry, fragment-based methods have been successfully applied in accurately calculating excited states in large systems and condensed phases at a high QM level, ranging from simulating optical spectra of aggregation-induced emission (AIE) in molecular crystal materials18 to elucidating excitonic interactions in the Fenna–Matthews–Olson complex (6853 atoms).19 In addition, ab initio exciton models can be used for the low-cost study of various excited state processes in complex environments, e.g., optical generation of long-range charge-transfer states in electron donor/acceptor heterojunctions20 and singlet fission in crystalline tetracene.21 Moreover, novel low-scaling quantum dynamics methods like time-dependent density matrix renormalization group (tDMRG)22 and multi-configuration time-dependent Hartree (MCTDH)23 were recently employed for the accurate simulation of real-time nonadiabatic dynamics24,25 and ultrafast one- or two-dimensional electronic spectroscopy with vibrational resolution26,27 in complicated systems with a large number of nuclear and electron degrees of freedom, helping build a bridge between theory and experiment in photophysics and photochemistry.
Driven by the fast development of computer science and artificial intelligence, as well as the availability of massive data, efficient data-mining techniques, especially machine learning (ML) approaches, have been widely used in materials science.28–32 The amount of ML-related literature is growing explosively. It is impossible to give a complete list of all those publications, and in Table S2,† we collect some representative applications of ML models in materials. For instance, combining experiments with microscopic structural descriptors and/or computational simulations, quantitative structure–property relationship (QSPR) models can be derived for predicting a variety of properties of materials.33,34 Furthermore, such predictive models can be combined with virtual screening by high throughput computations to accelerate the discovery and development of new functional materials with favourable properties and provide insight into the factors governing these properties.35,36 On the other hand, ML techniques enabled numerous advances for simulating materials previously out of reach due to the computational complexity of traditional electronic-structure methods. Those exciting advances include constructing ML-based force fields (FFs),37 speeding up excited state calculations,38 predicting spectroscopy properties,39 and computer-aided synthesis planning.40
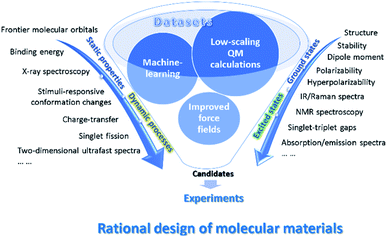
In this review, we will emphasize on computational and data driven molecular material design assisted by low scaling QM calculations and machine learning based on examples from the authors as well as other groups (see Fig. 1). We begin by introducing low scaling ground-state quantum mechanics for the computations of molecular materials, including polymer oligomers, supramolecular complexes, and electrode materials. Then, to treat the excited states in optoelectronic materials, we present low scaling excited-state QM and quantum dynamics (QD) methods and use them to describe microscopic photophysical mechanisms in organic semiconductors. In combination with the low-scaling QM calculations, the improved force fields with the polarizable partial charges or fragment dipole moments are applicable to the simulations of dynamic conformational changes in stimuli-responsive monolayers41 or [2]-rotaxane.42 Furthermore, we introduce the applications of explainable models and deep learning methods to the designs of organic solar cells43 and predictions of molecular or material properties. The efficiency of building the force fields from the low scaling QM-based on-line machine learning force field is also discussed.44,218 Finally, the perspective discusses some directions for further improvement and proposes future lines of this exciting and quickly developing field.
2 Low scaling QM methods for large-sized molecules and aggregates
2.1 Low scaling calculations of ground-state energies and properties
The understanding of ground-state molecular structures, non-covalent interactions or binding energies, and various molecular properties is crucial in the rational design of molecular materials, including oligomers, monolayers on surfaces, molecular crystals, etc. Due to the large size of molecular materials (e.g., polymers and molecular aggregates), empirical force fields are usually employed in their simulations. However, the force field parameters are not always transferable for all the studied materials, especially for charged and π-conjugated polymers. Quantum mechanics calculations are hence required to predict molecular structures and to describe intermolecular interactions without the pre-determination of empirical parameters. DFT is widely used in computational material fields due to the balance between computational cost and accuracy. The lack of long-range attractive terms for describing non-bonded interactions is one of the limitations of some DFT functionals in describing the noncovalent intermolecular interactions in molecular aggregates and super-molecular assembly. To overcome the difficulties and to improve the performance of DFT methods, some functionals, such as B97D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 and ωB97XD,46 were developed to take noncovalent interactions into account. Furthermore, more accurate interaction energies could be obtained by ab initio electron correlation methods, such as second-order Møller–Plesset perturbation theory (MP2) and coupled cluster (CC) theory. However, the conventional electron correlation methods are very expensive for large sized systems due to their high computational scaling with the number of basis functions, Nb, or electrons. For example, the scalings of MP2 and CC singles and doubles (CCSD) methods are O(Nb5) and O(Nb6), respectively. The gold standard CCSD with perturbative triples corrections [CCSD(T)] method even scales as O(Nb7). To alleviate such high computation scales, low (or even linear) scaling quantum chemistry methods were developed for the fast ground-state calculations of large systems.47–49
45 and ωB97XD,46 were developed to take noncovalent interactions into account. Furthermore, more accurate interaction energies could be obtained by ab initio electron correlation methods, such as second-order Møller–Plesset perturbation theory (MP2) and coupled cluster (CC) theory. However, the conventional electron correlation methods are very expensive for large sized systems due to their high computational scaling with the number of basis functions, Nb, or electrons. For example, the scalings of MP2 and CC singles and doubles (CCSD) methods are O(Nb5) and O(Nb6), respectively. The gold standard CCSD with perturbative triples corrections [CCSD(T)] method even scales as O(Nb7). To alleviate such high computation scales, low (or even linear) scaling quantum chemistry methods were developed for the fast ground-state calculations of large systems.47–49
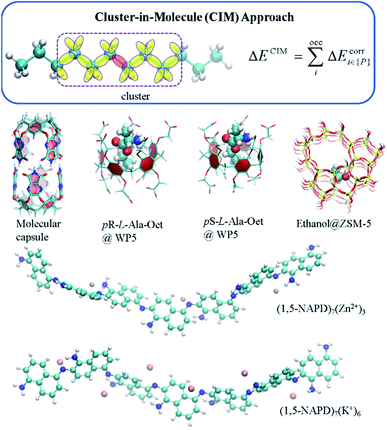
In general, there exist two categories of linear or low scaling algorithms, including “first-principles” methods and fragmentation methods. The “first-principles” methods are further classified in two groups, i.e., linear Hartree–Fock (HF) and DFT algorithms and local correlation methods. In the first-principles based linear or low scaling HF and DFT methods, efficient algorithms are employed to compute integrals or matrix elements. For example, integral screening,50 fast multipole method (FMM),47 order-N exchange method,51 and LinXC scheme52 are employed to compute two-electron integrals, Coulomb matrices, exchange matrices, and exchange–correlation density functional quadrature, respectively. The density matrix search (DMS) approach53 is used to avoid the diagonalization of the Fock matrix. In the local correlation method, the electron correlation equations are approximately solved in the representations of the localized molecular orbital (LMO) or atomic orbital (AO) by neglecting the correlation between spatially distant orbitals. The local correlation method (Fig. 2) was first proposed by Pulay et al. at the MP2 level,54 and generalized by Werner et al. at the CCSD level.55 In the last two decades, the local correlation methods were further developed by various groups.48,56–60 For example, in the CIM approach60–62 developed by us, the correlation energy contributions of occupied LMOs can be approximately obtained from various clusters, each of which consists of only a subset of occupied LMOs and corresponding unoccupied orbitals and atomic basis. In summary, chemical intuition is not involved in the “first-principles” methods and the corresponding program could be a black-box for users. Recently, analytic energy gradients were implemented in the CIM approach, which enables the geometry optimization of large systems with up to 174 atoms.63 The dataset of CIM-MP2 or CIM-CCSD binding energies of supermolecules and molecular aggregates was also reported,64 providing the benchmark data for DFT functional and force-field validations. However, high-order analytical energy derivatives with respect to nuclear coordinates or external electronic (or magnetic) fields are still hard to obtain for the local correlation methods because of requirements of some special integrals.
 | ||
| Fig. 2 Two kinds of linear scaling methods for large sized systems: local correlation methods and fragmentation methods. | ||
On the other hand, fragmentation methods provide a more efficient way to compute the energy or electronic structure properties of large sized systems. In this category, density-matrix based fragmentation and energy-based fragmentation approaches were developed. The density-matrix based fragmentation approach was first proposed by Yang and co-workers in the divide-and-conquer (DC) method at the DFT level,65 which was significantly extended by Nakai and co-workers to various ab initio electron correlation levels.66,67 Within the framework of the density-matrix based approaches, the total density matrix of a target system is obtained from the density matrices or molecular orbitals (MOs) of subsystems. Then, the total ground energy or molecular properties of the total system are computed from the approximate total density matrix. Various density matrix based approaches were also developed, such as the adjustable density matrix assembler (ADMA) method,68 the elongation method,69 and the molecular fractionation with conjugated caps (MFCC) approach.70 The LMO assembler (LMOA) method71 has been proposed with the total density matrix being assembled by the LMOs of the central region of subsystems or electrostatically embedded subsystems.72 However, the density-matrix based methods for large systems require high computational costs of integrals and large resources (memory or disk) for the entire system.
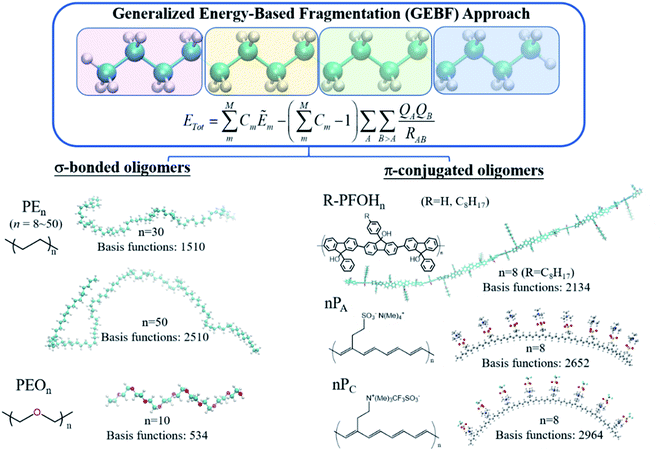
In comparison with density-matrix based approaches, energy-based fragmentation approaches (Fig. 2) need less computational cost and fewer resource requirements for the total system, because in such methods the total ground-state energy (or energy derivatives) of a target system is directly represented as the combination of the corresponding energies (or energy derivatives) of various subsystems.73 Those subsystems could be calculated at both DFT and post-Hartree–Fock levels with existing quantum chemistry packages. In addition, the calculations of subsystems could be coarse-grain paralleled and distributed in different computer nodes, and each subsystem could be fine-grain paralleled with processors within a node. The theoretical framework of molecular fragments was employed to develop QM-based force fields for the simulations of liquids and solutions in the effective fragment potential74 method and explicit polarization75 method, respectively. Based on many-body expansion, Kitaura and co-worker proposed the fragment molecular orbital (FMO) method,76 in which orbitals are employed to saturate the dangling bonds. Energy-based fragmentation methods for the ground-state calculations of large sized molecules are independently proposed by three groups77–79 in 2005. To take long-range electrostatic interactions into account for long oligomer systems with the charged group, we developed an electrostatically embedding scheme by placing point charges at the charge centres in each subsystem calculation.80 Furthermore, by introducing background point charges on those atoms outsides the subsystems, we further proposed the GEBF approach.81 Thus, in our GEBF approach, the ground-state energies (or energy derivatives) of a target molecule could be represented as the linear combination of the corresponding energy (or energy derivatives) of a series of electrostatically embedded subsystems (Fig. 3). In fact, this is a very crucial step in making the linear-scaling fragmentation method applicable to material systems, since many functional materials are highly polar or charged and hence responsive to the stimuli of electric, light, pH and temperature changes. By improving the fragmentation schemes or the constructions of subsystems, the GEBF approach was further applied to a broad range of complex systems with polar or charged groups including polymer oligomers, molecular clusters, ionic liquid clusters, biological systems, and supramolecular complexes.82,83 Other energy-based fragmentation methods, such as the generalized MFCC method,84,85 the molecular tailoring approach,86 the molecules-in-molecules (MIM) method,87 the generalized many-body expansion method,88 have also been developed. To better correlate with experimentally observable properties, the energy-based approaches have been applied to study the relative stabilities and molecular spectroscopic properties (IR/Raman and NMR spectra) of large systems at the levels of HF, DFT, and post-HF methods.73,82,83,89,90
The electronic structure calculations of condensed-phase systems (such as solids, surfaces, and liquids) play important roles in materials science. However, the traditional periodic DFT calculations using plane waves (or Gaussian-type atomic orbitals), which are widely used for condensed phase systems, are much more expensive than the non-periodic DFT calculations of molecules or clusters with similar sizes due to the large number of Bloch vectors under PBCs. On the other hand, due to the dependence of exchange–correlation functionals, DFT calculations may not be accurate enough to describe the relative stabilities of polymorphs, which are usually in the range of 1–2 kcal mol−1. Ab initio electron correlation methods could systematically provide more accurate relative energies. However, periodic electron correlation methods are extremely expensive and are only applicable to model condensed phase systems with several small molecules in a unit cell, even for the PBC-MP2 method. Using the localized Wannier functions in the occupied space, local correlation methods were applied to periodic systems. Those methods include the incremental method,91 the local MP2 method,92 the divide-expand-consolidate method,93 the PBC-CIM method,94 and so on. In the PBC-CIM method developed in our group, the correlation energy per unit cell of a periodic system can be expressed as the summation of the correlation contributions of occupied orbitals within a series of finite-sized clusters.94 Fragmentation methods have also been extended to periodic systems. In such methods, the unit cell energy of a periodic system could be represented as the summation of n-fragment (n = 1, 2, …) energy terms, which could be approximately obtained from the calculations on finite molecular clusters. For instance, the systematic molecular fragmentation and hybrid many-body interaction model could predict the lattice energies or lattice structures of covalent crystals or organic molecular crystals.216,217 A fragment-based QM approach has been used to estimate the lattice energy of benzene crystals at a high-level electron correlation level.95 To take the long-range electrostatic interactions in the infinite crystal environment into account, we have developed a PBC-GEBF method.96,97 In the approach, the ground-state energy or energy derivatives of a periodic system can be evaluated as a linear combination of ground-state energies or energy derivatives of various small nonperiodic subsystems. Here, each subsystem is embedded in the electric field generated by a finite array of background point charges. The PBC-GEBF approach could be employed to predict the lattice energies, crystal structures, and spectroscopic properties of various molecular materials and solutions at various DFT and electron correlation levels.83
Besides the above-mentioned linear scaling DFT and wavefunction-based methods, semiempirical QM methods could also greatly speed up QM calculations by using some empirical parameters to save the computation time of evaluating two-electron integrals. The widely used semiempirical QM methods include Austin model 1 (AM1),98 parametric method 6 (PM6),99 DFT tight-binding methods such as density functional tight-binding (DFTB)100,101 and extended tight-binding (xTB)102 methods. Furthermore, linear scaling semiempirical QM methods could be applied to treat even larger systems. For example, the FMO method has been implemented at the level of DFTB with the third-order expansion (DFTB3), called FMO-DFTB3, which is more than 40 times faster than full DFTB3 for calculating a cellulose sheet containing 1368 atoms.103 Nakai and co-workers have developed the DC-DFTB method for the on-the-fly molecular reaction dynamics simulations of a cubic water box with 256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules.104
000 water molecules.104
2.2 Low scaling excited-state quantum mechanics and quantum dynamics methods
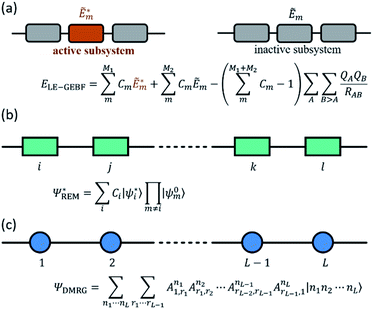
The fundamental physics and chemistry of many optical functional materials ranging from optoelectronic devices to photo-catalysts are governed by light initiated excited-state processes, including photon absorption, radiative and radiationless relaxation, excited-state energy transfer, excited-state charge transfer, etc. Understanding the properties of electronically excited states is impossible to be accomplished without valuable help from quantum chemical and quantum dynamics calculations. However, these theoretical methods for electronic excited states are usually very expensive because their computational costs grow even much faster with the increasing system size than that of ground-state quantum chemical calculations. The upper limit for the applicability of the most common excited-state electronic structure method, time-dependent density functional theory (TDDFT), or even simpler configuration interaction singles (CIS) method, if no further approximations are introduced, is only about 150–200 atoms.105 Therefore, the high demand for interpreting experimental excited-state phenomena and the recent fascinating progress in time-resolved spectroscopy called for the development of novel excited-state theoretical methods for large systems, which was an active research field of quantum chemistry in the last decade.One of the widely used strategies to reduce the costs of excited-state calculations is to utilize local excitation approximation (LEA), in which electronic excitation is restricted to only one specified chromophore. By using various types of localized molecular orbitals, including regional LMOs (RLMOs), natural transition/localized orbitals and absolutely LMOs (ALMOs), to constrain the spatial region of the local excitation, LEA was successfully implemented at the levels of TDDFT and CIS.106–109 In recent years, the great success of linear-scaling fragmentation-based approaches in describing the ground-state also motivated its straightforward extension to excited-state calculations through a combination with LEA.18,110,111 As shown in Fig. 4a, Li et al. also extended the GEBF method to the local excitation GEBF (LE-GEBF) method.83,111 In this method, the localized excited-state energy of a target system can be represented as the combination of the excited-state energies of active subsystems and the ground-state energies of inactive subsystems with an overcounting correction of electrostatic interactions. The LE-GEBF method is employed to describe the solvatochromic shifts of acetone in different solvent environments and the electron absorption spectra of green fluorescence protein (GFP).83,111 Besides the above mentioned fragmentation schemes, the embedding algorithms which incorporate a high-level calculation in the active region of interest and a low-level calculation on its environment are also employed for unravelling the excited-state properties of large systems such as GFP.112 Recently, quickly developed machine learning techniques were also suggested by Chen et al. to be used to further reduce the computational costs of low-level quantum chemical calculations of the large inert regions surrounding the photochemically active space in embedding algorithms.113
Another widely used strategy for low-scaling ground-state calculations, local correlation approximation (LCA), is also applied for describing the excited states of large systems. Taking advantage of the locality of a reduced density matrix gained by the DC method, linear scaling was achieved for TDDFT by using orthogonal atomic orbitals (OAOs) or non-orthogonal LMOs (NOLMOs).114,115 Liu and coworkers116 later developed another linear-scaling TDDFT scheme by making full use of a simple pre-screening of the particle–hole pairs in the fragment LMO (FLMO) representation. Similarly, LCA has been also incorporated into various wavefunction theory (WFT) methods, such as equation-of-motion CCSD (EOM-CCSD),117 second-order approximate coupled-cluster singles and doubles (CC2),118 multi-reference singles and doubles configuration interaction (MRSDCI),119 and CIS120 as well as symmetry adapted cluster configuration interaction (SAC-CI).121 Nakai and coworkers used standard DC-based approaches to evaluate the dynamical polarizability and then described the excited states as the poles of dynamical polarizability.122,123 It has been successfully implemented from the TDDFT level to the coupled cluster linear response (CCLR) level.
At the same time, excitonic models are often used in computational materials science or photochemistry for the qualitative/semi-quantitative investigation of various optoelectronic processes in condensed phases, ranging from photo-absorption/emission, excited-state energy transfer to singlet exciton fission and exciton dissociation.124–131 However, the choice of the parameter values in the excitonic models is usually dependent on the experimental fitting or simple quantum chemical estimation for classical coulombic electrostatic interactions between different chromophores. Obviously, the construction of the excitonic model is non-trivial when each chromophore has more than one excited state involved in the system's optoelectronic process or the short-distance inter-chromophore exchange interaction is non-negligible, and this will greatly decrease the accuracy of the model and also severely restrict the model's application range. In order to better describe the inter-chromophore interactions, Bloch's effective Hamiltonian theory132 can be adopted in conjunction with the numerical renormalization group (NRG) for large correlated systems. Using this strategy, Morningstar and Weinstein133 proposed the contractor renormalization group (CORE) method, in which the general excited-states of the whole system are considered as an assembly of numerous single or multiple local block excitations, and Malrieu and coworkers134 suggested the renormalized excitonic model (REM) to approximate the whole system's low-lying excited states as linear combinations of only single local excitations (Fig. 4b). With this approximation, the dimensions of the effective Hamiltonian matrix of the whole system can be reduced greatly from dN to d × N, where d is the number of local states and N is the total number of blocks. Since 2012, our group has been implementing REM at the ab initio level in conjunction with full CI (FCI), CIS, SAC-CI and TDDFT using orthogonal LMOs (OLMOs) and block canonical molecular orbitals (BCMOs).135–137 The tests of hydrogen chains, polyene, polysilenes, water chains, and benzene aggregates as well as general aqueous systems with polar and nonpolar solutes indicate that the ab initio REM method can give good descriptions of excitation energies for the lowest electronic excitations in large systems with economic computational costs.
On the other hand, the accurate theoretical interpretation of ultrafast time-resolved excited-state spectroscopy experiments relies on full quantum dynamics simulations for the investigated system, which is also computationally prohibitive for realistic molecular systems with a large number of electronic and/or vibrational degrees of freedom. To tackle this so-called curse of dimensionality, many low-scaling quantum dynamics methods using different approximations have been proposed. Among them, tensor product methods138 recently attracted much research interest. For example, MCTDH23 adopts a Tucker decomposition139 scheme to decompose a high-order tensor with a high rank into a set of matrices and one small Tucker core tensor with the same order but a low rank, and accordingly it can be also considered as a high-order single value decomposition (HOSVD).140 However, the Tucker core still suffers from the curse of dimensionality for higher orders, which has been partly overcome by introducing multi-layer MCTDH (ML-MCTDH)141 using a hierarchical Tucker (HT) decomposition. On the other hand, the tensor train decomposition (TT; in the mathematical literature)142 or the equivalent matrix product state representation (MPS; in the physical literature)143 used in the density matrix renormalization group (DMRG)144,145 provides an alternative decomposition algorithm, which decomposes a high-order tensor with a high rank into a product of many local low-order tensors with a one-dimension (1D) topology (Fig. 4c). ML-MCTDH and tDMRG22 have been successfully applied to simulate the dynamics of excited-state energy or charge transfer and the absorption and fluorescence spectra of molecular aggregates,26,27,146–152 demonstrating the great potential for exploring the quantum dynamics of excited-state processes in large chemical systems.
In addition, there also exist various semiempirical excited-state QM methods, such as time-dependent DFTB (TDDFTB) method153 and xTB based simplified Tamm–Dancoff approximation (sTDA-xTB) method.154 A spin-flip TDDFTB (SF-TDDFTB) method is developed to fast determine S0/S1 minimum energy conical intersection (MECI) structures.155 In 2019, Nakai and co-workers implemented a GPU-accelerated DC-TDDFTB method, which could reproduce the experimental absorption and fluorescence spectra of 2-acetylindan-1,3-dione in explicit acetonitrile solution.156
It is not straightforward to precisely compare the accurate and costs of various low scaling QM methods because there usually exist some adjustable parameters for achieving the balance between the accuracy and computational costs. Also, those methods may show different performances for various types of large subsystems. Collins and Bettens have made some comparisons between several typical energy-based fragmentation methods in their review.73 It shows that the absolute errors in the total energies are usually several kJ mol−1 for medium-sized systems and more than 10 kJ mol−1 for large-sized systems such as proteins. By taking the long-range electrostatic interactions into accounts, the computational accuracies are improved for a broad range of large systems, especially for polar or charge systems. Furthermore, for the relative energies (such as binding energies or reaction barriers), which are of chemical interest, the errors are smaller due to the error cancellation. For example, for ten host–guest complexes, the maximum error of the GEBF-DFT binding energies is only 4.4 kJ mol−1, and the maximum error for the relative binding energy between two complexes with the same host molecules is only 0.9 kJ mol−1.157 In local correlation methods, there are some direct comparisons for same large systems.158,159 For example, Li and co-workers have compared resolution-of-identity MP2 (RI-MP2) and CIM-RI-LMP2 methods, which shows that the CIM approach gives better accuracies and efficiencies for quasi one-dimensional peptides.158 Neese and co-workers have compared the accuracies and efficiencies between the domain based local pair-natural orbital (DLPNO) and CIM calculations at the MP2 and CCSD(T) levels for large systems up to 2380 atoms.159 It shows that their efficiencies are similar, while the DLPNO total energy is more accurate for 3-dimensional systems. For a tight CIM parameter, the accuracies of CIM and the DLPNO energy are very close.159 In addition, the fragmentation or local correlation methods are developed to reproduce the corresponding traditional QM methods, and thus their accuracies also depend on the levels of DFT or electron correlation methods. In comparison with “first-principles” DFT methods, DFTB is a semiempirical DFT-based method and additional empirical dispersion corrections need to be added for systems with weak interactions.101
Codes of low scaling ground- and excited-state QM methods are developed by several groups and available in several packages. Some packages are specifically designed for low scaling QM methods, such as ONETEP160 and HONPAS161 based on localized Wannier functions, LSQC162 (including GEBF and CIM), etc. In addition, some low scaling methods, such as FMO, DC, and CIM, are available in the exited GAMESS package;163 local MP2 and CCSD(T) are implemented in the Molpro program;164 DLPNO and CIM methods are included in the ORCA program.165 For periodic systems, low scaling DFT codes are available in Crystal,166 CP2K,167etc. The specific packages for DFTB, such as DFTB+168 and xTB,102 were also widely used to predict the energy and properties of some complicated systems.
3 Applications of low scaling QM methods to complex molecular material systems
In this section, some applications of the methods mentioned in Section 2 are discussed. A thorough overview of the several hundred or even more applications of applying low-scaling QM methods and ML to molecular materials is certainly out of the scope of this review. Also, there exist many methods for inorganic or nanomaterials. As early as 2014, Yang and co-workers have employed a density matrix trace correcting (TC) purification method to compute various electronic properties of hexagonal graphene nanoflakes with up to 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 atoms.169 Recently, Hu and co-workers have applied pole expansion and selected inversion (PEXSI) to calculate the electronic structures of boron nitrogen nanotubes.170 Our aim is not only to show the potential and applicability of different methods and techniques and, by discussing some representative calculations, but also to help the reader to select an appropriate approach for particular molecular material systems.
700 atoms.169 Recently, Hu and co-workers have applied pole expansion and selected inversion (PEXSI) to calculate the electronic structures of boron nitrogen nanotubes.170 Our aim is not only to show the potential and applicability of different methods and techniques and, by discussing some representative calculations, but also to help the reader to select an appropriate approach for particular molecular material systems.
3.1 Polymeric oligomers
Fragmentation based linear scaling methods can treat polymeric oligomers in a direct and economic way. For σ-bonded oligomer chains, such as the widely used polyethylene (PE) and poly(ethylene oxide) (PEO) systems, each repeat unit or several repeat units can be taken as a fragment (Fig. 3).44,171 Such a fragmentation scheme also works well for the π-conjugated chains like polyacetylene and polyfluorenols but the π-bonds cannot be cut during the fragmentation.172,173 An auto fragmentation program was implemented for more complicated molecular aggregate or biological systems with a pre-setting truncate distance for building the subsystems in GEBF calculations.174The combined quantum mechanics and molecular mechanics (QM/MM) method is an efficient method for studying macromolecules in solutions, in which the solute is usually treated by the QM method. The high computational scaling of the QM method is still a bottleneck of QM/MM simulations for macromolecules which require a large QM region. To overcome this difficulty, we have developed a fragment QM/MM method by combining GEBF-based QM and MM calculations for the Born–Oppenheimer molecular dynamics simulations of dilute solutions of macromolecules.171 As for the two selected representative systems, PEO is a water-soluble polymer with extensive industrial applications, and PE is a very important polymer in the plastic industry. GEBF-based QM/MM optimization and MD simulations were performed for PEOn (n = 6–20) and PEn (n = 9–30) in aqueous solutions. As expected, the longer oligomer chains have larger chain flexibility and curling occurs in some local parts of the long σ-bonded oligomer chains.171
π-Conjugated polymers are relatively more rigid than σ-bonded oligomers. The high extent of electron delocalization in π-conjugated aromatic rings brings about the unique optical and electronic properties of various functional material molecules. In addition, the highly directional noncovalent interactions play important roles in the self-assembly behaviour of π-conjugated polymers to fabricate organogels and thin films. We take oligofluorenols, (R)-PFOHn (n = 4 and 8) where R = H (unsubstituted) or OC8H17 (substituted), for side chains as an example. GEBF-B3LYP with the 6-31+G(d) basis set was employed to optimize the oligofluorenols.173 Furthermore, the packing structures for (R)-PFOHn in crystals, amorphous solids and solutions were investigated by polymer consistent force field (PCFF) based MD simulations. Then, for the MD sampled configurations, the ultraviolet/visible (UV/VIS) absorption spectra were computed by the TDDFT and FLMO based TDDFT (FLMO-TDDFT) method.116 The results show that the planar π-conjugated conformations could lead to a red shift in the absorption spectra upon increasing the concentration of solution. The aggregation-induced red-shift of oligofluorenols and the blue-shift of oligothiophenes were rationalized in a unified way.173 Aggregated-configuration engineering could be used to tune the optical properties of electronic devices based on π-conjugated systems.
As mentioned before, the introduction of background point charge into subsystem calculations allows GEBF to give accurate results for charged or highly polar molecules. It can be demonstrated by its application to ionically functionalized polyacetylene analogues, such as poly(tetramethylammonium 2-cyclooctatetraenylethanesulfonate) (PA) and poly[(2-cyclooctatetraenylethyl)trimethylammonium trifluoromethanesulfonate] (PC), which acted as active materials sandwiched between two electrodes (gold nanoparticles). It is very useful in the fabrication of various microelectronic devices, such as light-emitting electrochemical cells and electric current rectifiers. In such devices, the polymer/electrode and polymer/polymer interfaces are really complicated for theoretical simulations. We have combined linear scaling DFT calculations and molecular dynamics (MD) simulations to study the unusual transport properties of an Au|PC|PA|Au junction.172 The energy-based fragmentation approach at the B3LYP/6-31G(d) level was used to optimize the structures of the ionically functionalized oligomers, nPA and nPC (n = 1–8). The all possible cis-configurations of 8PA and 8PC, with the counter ions residing on the same sides of the polyacetylene backbones, are displayed in Fig. 3. Through the oligomer extrapolation of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energies of nPA and nPC as a function of 1/n, the valence band (VB) and conduction band (CB) edges of PA and those of PC were estimated, which are in qualitative agreement with the PBC calculation results.172 The absence of n-doping waves in the voltammetry data of PA in the experiment is rationalized by its high reduction potential or the blocking of effective interfacial electron transfer.
For other oligomers, many density-matrix based or fragment-based linear scaling methods have been employed. For example, Liang and Chen and co-workers have extended the localized-density-matrix (LDM) method for the calculations of nonlinear optical responses (second hyperpolarizability) in large polyacetylene oligomers.175 Kobayashi and Nakai have developed DC-HF and DC-MP2 methods for delocalized or open-shell systems by determining the electrons automatically with a universal Fermi level. Using the approach, the energies of the B–N analogues of oligoacenes (BN-acenes) and their derivatives are comparable with the corresponding conventional values.176 Skylaris and co-workers have used linear scaling DFT in the ONETEP program160 to compute the HOMO and LUMO energies, and the band gap of some long chain oligomers of organic photovoltaics with more than 1000 atoms.177
3.2 Supramolecular complexes and molecular aggregates
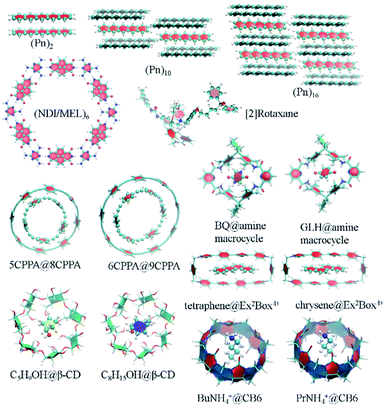
Two-dimensional self-assembled monolayers and supramolecular complexes are important ingredients in the construction of novel smart electronic devices. The packing structures and properties of those molecular aggregates are controlled by non-covalent interactions, whose strength could be calculated by low-scaling QM methods. There are numerous application examples in this direction. Here, we just list some calculation results. Pentacene (Pn) and its functionalized derivatives are widely used building units in high-performance organic thin-film transistors and organic photovoltaics. We have computed the GEBF-MP2 binding energies, Eb, of a series of pentacene (Pn)N aggregates, with up to Pn hexadecamer (N = 16), with the 6-31G(d) basis set (Fig. 5).178 In the (Pn)16 aggregate, the van der Waals and π-stacking interactions are dominant in the non-covalent binding with an Eb of −20.54 kcal mol−1. In contrast, the molecular aggregates with favourable hydrogen bonding (HB) networks usually have larger binding strength. Such a kind of directional HB intermolecular interaction could drive the formation of various packing patterns, such as honeycomb networks, chessboard, and chiral supramolecular structures on the surface or in solutions (Fig. 5). Taking the naphthalene tetracarboxylic di-imide (NDI) and melamine (MEL) binary system as an illustration, these two kinds of π-conjugated molecules constitute a pair of building blocks for constructing hexagonal close-packed architectures. The counterpoise-corrected binding energy of the hexagonal NDI/MEL network including six pairs of NDI/MEL dimers, (NDI/MEL)6, is predicted to be −297.8 kcal mol−1 by GEBF-MP2/6-31G(d) calculations. The triple hydrogen-bonded network is consistent with the image from the scanning tunnelling microscope (STM) on the gold surface.179In addition, the non-covalent interactions of supramolecular host–guest complexes are the driving forces of the supramolecular recognition and self-assembly formation. As a kind of mechanically interlocked molecule being used in molecular devices or nanoscale machines, [2]rotaxane is a <rod|ring> system consisting of a rod (an axle-shaped molecule) and a ring (a macrocyclic compound). The difference in the HB interaction energies between the macrocycle and different binding sites in the long rod of [2]rotaxane is employed to control the shuttling movement.42 In order to accurately predict the binding energies of the supramolecular complexes, we have proposed an efficient way for the constructions of GEBF subsystems to avoid the selection of the whole macrocycle in terms of the cut-off distance from the central guest species.157 In the new scheme, each large primitive subsystem is converted into several overlapped smaller primitive subsystems using an iterative algorithm. Then, the primitive GEBF subsystem for a supramolecule is smaller than before to achieve similar accuracy, and the subsystems in the complex are very similar to those in the host. Thus, more accuracy binding energies could be obtained with smaller but consistent subsystems.157 We have performed GEBF-M06-2X calculations for ten host–guest complexes taken from the S30L dataset,180 including [5]cycloparaphenyleneacetylene (5CPPA) in 8CPPA and 6CPPA in 9CPPA, benzoquinone (BQ) and glycine anhydride (GLH) in the amine macrocycle, cyclopentanol (C5H9OH) and cyclooctanol (C8H15OH) in β-cyclodextrin (β-CD), tetraphene and chrysene in the Ex2Box4+ macrocycle, and protonated butylammonium (BuNH4+) and propylammonium (PrNH4+) in cucurbit[6]uril (CB6) (parts of which are listed in Fig. 5).157 The GEBF approach could reproduce the conventional DFT binding energy and relative binding energy (for two complexes with the same or similar hosts) with the errors being less than 1 kcal mol−1 and 1 kilojoule mol−1, respectively.
In addition to binding energies and packing structures, property predictions are highly desired for bridging the gap between theoretical simulations and experimental measurements of molecular aggregates. By combining GEBF-based ab initio MD (AIMD) and polarizable force field (polar FF)-based MD simulations with variable charges, we investigated the conformational changes and averaged NMR chemical shifts of [2]rotaxane in solution.42 The up-field shifts of NMR signals of rod H-donors are induced by the dipole–dipole interactions between the flexible diethylene glycol chain of the ring and polar acetonitrile solvents, which also leads to the inhomogeneous and directional distribution of the neighbouring solvents. This implies that the interactions between the guest and host or between solvent and solute play an important role in designing novel interlocked systems.42 Recently, in order to treat large systems in solution, the GEBF approach was combined with a universal solvation model based on solute electron density (SMD). The GEBF-SMD approach could compute the solvation energies or predict the relative energies of large systems in solutions.181 In addition, Ochsenfeld and coworkers have employed a linear scaling DFT method to investigate the influence of intra- and intermolecular interactions on the NMR chemical shifts of supramolecular complexes, in which a naphthalene-spaced tweezers molecule is taken as the host with various aromatic, electron-deficient guests.182
Vibrational circular dichroism (VCD) spectra are useful to determine the chiral molecules by the analysis of differential absorption between left- and right-circularly polarized infrared radiation. The conventional QM calculations for the VCD spectra of MD sampled molecular aggregates in amorphous solids or solutions are limited to medium-sized clusters. The GEBF approach was implemented to compute the VCD spectra of (S)-alternarlactam aggregates at the B3PW91/6-31+G(d,p) level, where the VCD signals are obtained from the rotational strength of the GEBF subsystems.183 Hydrogen-bond interactions dominate in the packing configurations at a low density (0.5 g cm−3), and the GEBF calculated VCD spectrum is in good agreement with the experimental result, with signal splitting in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrational regions.183
O stretching vibrational regions.183
Another kind of low scaling method, the CIM approach,61,62 has also been applied to calculate the binding energies of various supramolecular complexes, metal-containing molecular aggregates and zeolites (Fig. 6).60,64 For example, the CIM-MP2 relative energies of different L-amino acid ethyl ester hydrochlorides (L-AA-OEt) in water-soluble pillar[n]arene WP5 were obtained to describe different chiral conformations.184 To understand the mechanism of a chemically self-charging aqueous zinc-organic battery, which consists of a poly(1,5-naphthalenediamine) (i.e., poly(1,5-NAPD)) cathode, a Zn-foil anode and an alkaline electrolyte, the binding energies of (1,5-NAPD)7 with different ions (H+, Zn+, and K+) were calculated by CIM-RI-MP2 with the def2-TZVPD basis set.14 The high level CIM-DLPNO-CCSD(T) binding energies were also obtained for a molecular capsule with multiple hydrogen interactions. With this binding energy as a reference, the results show that several DFT functionals overestimate the binding energies. The binding ability of trapping ethanol molecules in a ZSM-5 zeolite cage is evaluated by CIM-DLPNO-CCSD(T) calculations, which indicates that the M06-2X functional could provide an reasonable binding energy.64 In another way, Jorgensen and co-workers have applied their Massively parallel divide-expand-consolidate RI-MP2 (DEC-RI-MP2) to 1-aza-adamantane-trione (AAT) supramolecular wires including up to 2440 atoms and 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 basis functions.185 Raghavachari and co-workers have employed a multilayer MIM method to study of the energies of foldamers and their complexes with anions. It demonstrates that a two-layer MIM2 model, in which DLPNO-CCSD(T) and DFT with Grimme's dispersion correction (DFT-D3) methods are employed as high and low levels, respectively, could provide accurate binding energies by taking long-range interactions into account.186
440 basis functions.185 Raghavachari and co-workers have employed a multilayer MIM method to study of the energies of foldamers and their complexes with anions. It demonstrates that a two-layer MIM2 model, in which DLPNO-CCSD(T) and DFT with Grimme's dispersion correction (DFT-D3) methods are employed as high and low levels, respectively, could provide accurate binding energies by taking long-range interactions into account.186
To sum up, the improvement of fragmentation schemes and the employment of local correlation methods could yield accurate binding energies of large-sized supramolecular complexes and molecular aggregates at the electron correlation levels.
3.3 Stimuli-responsive monolayers
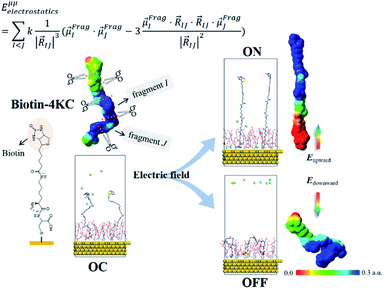
The ordered self-assembly of molecular monolayers on the surface plays an important role in molecular electronics, photonics, and optical devices. The introduction of stimuli-responsive groups into monolayers is an efficient way to fabricate novel smart sensors and drug release systems.41,187–191 An electric field could trigger the moment of the charged head groups or molecular chains of monolayers deposited on substrates. In some cases, the charged oligomer chains are polarized under the electric field. The polarizable force fields are desired to give reasonable descriptions of the electric field driven switching process. GEBF was able to provide variable partial charges or fragment dipoles in response to the conformational changes.As shown in Fig. 7, the energy-based fragmentation method was used on biotin-4KC, i.e., a positively charged tetramer of lysine (K) that is functionalized at one end with the bioactive moiety biotin, which could bind with the neutravidin protein, and at the other end with a cysteine (C), for binding to gold substrates. An electro-switchable surface can be formed by a binary mixed monolayer with biotin-4KC and a short chain of an ethylene glycol-terminated thiol (i.e. (3-mercaptopropyl)tri(ethylene glycol), TEGT), which could fill the space around the biotin-4KC and give enough room for biotin-4KC to switch its backbone under electric field stimuli. Based on the response of a charged molecular backbone of biotin-4KC in such a mixed self-assembled monolayer (SAM), the binding activity of a ligand (biotin) to a protein (neutravidin) can be dramatically changed. It was found that when an upward electric potential (+0.3 V) was applied, high neutravidin protein binding was observed (called ON), while the application of a downward potential (−0.4 V) gave rise to the OFF state with a minimal protein binding ability. Under open circuit (OC) conditions, the protein binding capability was intermediated, lying between the ON and OFF states. The electrostatic potential surfaces of OC, ON, and OFF states indicate the high polarization of charge distribution of the charged biotin-4KC chain under an external electric field. The biotin-4KC chain can be cut into five fragments according to its constituent groups with each fragment containing a lysine or biotin group, which is called fragment I or fragment J, without the loss of generality. For MD sampled configurations, the GEBF-M06-2X calculations were carried out on-the-fly to provide partial charges or fragment dipole moments in a coarse-grained way for polarized force field simulations. For example, the electrostatic interaction energy could be calculated from the dipole–dipole interaction, Eμμelectrostatics, between any two fragment dipoles, 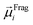 and
and 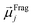 , as shown at the top of Fig. 7. The updated electrostatic interaction energy is used to replace the fixed charge electrostatic term in the traditional force field. It can be found from Fig. 7 that the application of polarizable force field simulations under upward and downward electric fields, respectively, demonstrated the standing straight up (ON) and bending down (OFF) of the biotin-4KC chain, reproducing well the experimental observations.189
, as shown at the top of Fig. 7. The updated electrostatic interaction energy is used to replace the fixed charge electrostatic term in the traditional force field. It can be found from Fig. 7 that the application of polarizable force field simulations under upward and downward electric fields, respectively, demonstrated the standing straight up (ON) and bending down (OFF) of the biotin-4KC chain, reproducing well the experimental observations.189
Polarizable FF models were also applied to simulate the macrocyclic ring at different binding states of [2]-rotaxane, each of which is set as the initial state for GEBF-M06-2X based AIMD simulation to efficiently cut down the computational costs and improve the performance of AIMD simulations.42
3.4 Excited state processes in molecular aggregates
One of the most fundamental issues in discussing about the excited processes in molecular aggregated systems is to accurately describe their absorption and emission spectra, which requires an electronic structure calculation of excited states and/or a Fourier transformation of time correlation functions from a quantum dynamics simulation. In 2014, Ma and Troisi20 predicted direct photo-generation of long-range charge transfer (CT) states in organic photovoltaics through a simulation of the absorption spectra at a tetracene/perylene-3,4,9,10-tetracarboxylic dianhydride (PTCDA) interface by using the REM approach. This was later verified by the experimental assignment of the full CT state absorption spectrum in microcrystalline rubrene/C60.192 Zhang et al.18 employed the electrostatically embedded generalized molecular fractionation (EE-GMF) method, a variant of MFCC, to predict the spectra of a prototype AIE fluorophore: di(p-methoxylphenyl)dibenzofulvene (FTPE), nearly reproducing the experimental optical spectra of FTPE in condensed phases.Applying DMRG into ab initio quantum chemistry Hamiltonian can serve as an efficient and computationally accurate method, for describing the excited state electronic structure properties of strongly correlated systems that require large complete active spaces (CASs) composed of up to 100 active orbitals, which are not accessible by conventional multi-configurational WFT methods. For example, in 2014 Sharma et al.193 computed the individual ground- and excited-state energy levels of [2Fe–2S] and [4Fe–4S] clusters by DMRG calculations with up to 36 active orbitals, suggesting that the low-energy spectrum is very dense due to the presence of many d–d excited states arising from both orbital transitions and spin recouplings. This finding is later supported by indirect experimental evidence from iron L-edge 2p3d resonant inelastic X-ray scattering (RIXS).194 In 2019, Cho et al.195 further performed ultraviolet (UV) absorption spectroscopy and stimulated X-ray Raman spectroscopy (SXRS) for [2Fe–2S] complexes, which complement each other by accessing different parts of the electronic spectrum and together can effectively probe the dense d–d electronic states in the Fe–S clusters. The simulated spectra presented clear signatures of the theoretically predicted dense low-lying excited states within the d–d manifold. Furthermore, the difference in spectral intensity between the absorption-active and Raman-active states provides a potential mechanism to selectively excite states by proper tuning of the excitation pump, to access the electronic dynamics within this manifold.
In recent years, the quick development of the time-dependent series, such as tDMRG method, also promoted the accurate theoretical simulations of spectroscopy in molecular aggregates, especially for systems with strong electron-vibration/phonon couplings. Ren et al.148 computed the vibronically resolved linear absorption and fluorescence spectra of perylene bisimide (PBI) and distyryl benzene (DSB) aggregates by using tDMRG at zero and finite temperature in conjunction with a Holstein model Hamiltonian. The calculations on PBI molecular chains showed that the practical accuracy of tDMRG reaches that of ML-MCTDH at zero temperature. The comparison with n-particle approximation methods on the DSB crystal further shows that tDMRG is not only much more accurate than these approximations but can also practically handle the larger Hilbert spaces arising from increasing the number of vibrational modes to model detailed spectral features. Additionally, it was also shown that appropriate vibronic features in the ultrafast electronic process can be obtained by simulating the two-dimensional (2D) electronic spectrum by virtue of the high computational efficiency of the tDMRG method by Yao et al.,146 by taking an oligothiophene/fullerene heterojunction as an example. Very recently, Gelin and Borrelli further extended tDMRG to the simulation of the time- and frequency-resolved fluorescence spectra of the Fenna–Matthews–Olson antenna complex at room temperature with an account of finite time-frequency resolution in fluorescence detection, orientational averaging, and static disorder.196
Unravelling the microscopic ultrafast dynamic conversion processes in photophysics and/or photochemistry depends on an accurate real-time QD simulation. For example, singlet fission (SF) is a spin-allowed photophysical process that generates two triplet excitons from one singlet excited state and has attracted a lot of research efforts in the past decade.197,198 In recent years, various low-scaling full QD simulations based on MCTDH, tDMRG, or tensor network state (TNS) have been devoted to the theoretical study of both intermolecular and intramolecular SF processes in different molecular crystals or solutions.24,25,199 By employing MCTDH simulations, Tamura et al.24 revealed that the slip-stacked equilibrium packing structure in pentacene derivatives enhances ultrafast SF mediated by a coherent super-exchange mechanism via higher-lying CT states. By contrast, the electronic couplings for singlet fission strictly vanish at the C2h symmetric equilibrium π stacking of rubrene. In this case, singlet fission is driven by excitations of symmetry-breaking intermolecular vibrations, rationalizing the experimentally observed temperature dependence. In addition, tDMRG simulations were also recently adopted by Li et al.200 to obtain a general charge transport picture for organic semiconductors with nonlocal electron-phonon couplings (EPCs). By studying the EPC effect on the carrier mobility, mean free path, optical conductivity, and one-particle spectral function, they located the phonon-assisted (PA), transient localization (TL), and band-like (BL) regimes simultaneously on the transfer integral – nonlocal EPC strength plane. They also identified an intermediate regime, where none of the existing pictures is truly applicable, as a generalization of hopping-band crossover in the Holstein model.
4 Machine learning for molecular materials
The successful applications of low scaling QM calculations and their hybridizations with molecular dynamics simulations in the study of material systems have been collected in the above subsections. Recently, the introduction of various material or QM computation databases and ML methods has changed the traditional “try and error” way to search for novel molecules and materials with desired properties. There are a large number of high throughput screening calculations and ML training and prediction studies for various material systems, and we cannot present all those studies in the review (Table S2†). We only lay emphasis on some selected examples in the three categories of ML methods, i.e., explainable models (with well selected features),201 deep learning (with self-learned representations without the predetermination of feature characters), and on-line or transfer learning (with variable training data sets), as shown in Fig. 8.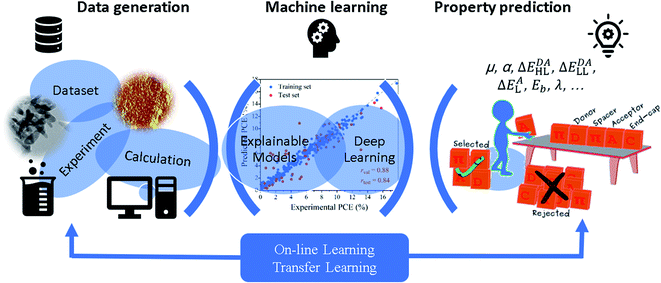 | ||
| Fig. 8 Schematic illustration of explainable machine learning, deep learning, and on-line or transfer learning methods and their applications to predict molecular or material properties. | ||
Driven by the development of computer science and artificial intelligence, as well as the availability of massive data and efficient data-mining techniques, explainable ML approaches have been widely applied in materials science, with an aim to achieve explainable structure–property relationships with several feature descriptors including structural descriptors (e.g., chain length of oligomers, pore size of zeolites, length/diameter ratio of nanoparticles, etc.) and electronic structure descriptors (e.g., dipole moment, polarizability, Frontier molecular orbitals, etc., shown in Fig. 8) without losing the predictive accuracy. For instance, explainable ML models have been learnt to construct QSPR models for predicting different device performances of organic solar cells (OSCs), providing useful suggestions concerning the design of new functional organic materials with desired properties, and contributing to the identification of new OSC materials.202–206 In 2018, we identified 13 important structural and electronic structure descriptors to describe 280 donor molecules by in-depth understanding of the microscopic mechanism of OSCs.207 Among them, one is the structural descriptor (number of unsaturated atoms, Natom), while others, such as polarizability, vertical ionization potential, and hole–electron binding energy, are related to the ground- and excited-state properties obtained by quantum chemical calculations. A range of ML algorithms including K-nearest neighbor (KNN), random forest (RF), gradient boosting (GB), and artificial neural network (ANN) were used to construct regression models for predicting power conversion efficiency (PCE). Both tree-based models obtained remarkable predictive power with Pearson's correlation coefficient (r) exceeding 0.78. In addition to improving the overall performance of organic photovoltaics, it is also necessary to meet the other requirements of specific applications for devices, such as high open-circuit voltage (VOC) for solar-fuel energy conversion and high short-circuit current density (JSC) for solar window applications. To this end, we also constructed ML models to predict the other three important device parameters, VOC, JSC, and filled factor.208 On the basis of an extended experimental data set of 300 donor molecules, the predictive accuracy (r) of the GB model for VOC, JSC and filled factor reached 0.67, 0.66 and 0.71, respectively. Furthermore, we performed high-throughput virtual screening of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 molecules using well-trained ML models.209 All candidates were composed of 32 unique building blocks (four types of units, donor (D), acceptor (A), π-spacer (S) and end-capping (C)) according to ten combinative ways (DA, ADA, DAD, DSA, DSASD, ASDSA, CSDSC, CASDSAC, CDSASDC and CDSAC). In order to derive design rules, an efficient group-combined pair and the most favourable molecular combinations from building blocks were obtained. In addition, the key factors required for highly efficient molecules were clarified. For instance, the energy difference of LUMO+1 and LUMO of donors (ΔL), energy gap (ΔH–L) and Natom of all high-performance dyes have the range of <0.25 eV, <4.25 eV and >60, respectively. Explainable ML methods have been used in many other kinds of materials, and the readers could find more examples in Table S2.†
170 molecules using well-trained ML models.209 All candidates were composed of 32 unique building blocks (four types of units, donor (D), acceptor (A), π-spacer (S) and end-capping (C)) according to ten combinative ways (DA, ADA, DAD, DSA, DSASD, ASDSA, CSDSC, CASDSAC, CDSASDC and CDSAC). In order to derive design rules, an efficient group-combined pair and the most favourable molecular combinations from building blocks were obtained. In addition, the key factors required for highly efficient molecules were clarified. For instance, the energy difference of LUMO+1 and LUMO of donors (ΔL), energy gap (ΔH–L) and Natom of all high-performance dyes have the range of <0.25 eV, <4.25 eV and >60, respectively. Explainable ML methods have been used in many other kinds of materials, and the readers could find more examples in Table S2.†
The interplay between explainable ML models and experiments is becoming more active. Experimental data are important input to obtain an initial guess of descriptor sets, and conversely, the built explainable QSPR model could help experiments to gain inspiration for constructing the chemical combination space of novel materials and fabrication of materials. For example, a new ML framework for simultaneously optimizing D/A molecule pairs and device specifications of OSCs is proposed.210 The structural and electronic properties were further combined with the device bulk properties, which can be measured by atomic force microscope (AFM) experiments. In this way, the built QSPR model achieved unprecedentedly high accuracy and consistency. A large chemical space of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942
942![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 785 D/A pairs is explored to find potential synergistic ones. Favourable device bulk properties such as the root-mean-square of surface roughness for D/A blends and the D/A weight ratio are further screened by grid search methods. This showed that ML can be effective not only for molecular screening but also for experimental parameter optimization for OSCs, which takes an important step further into the practical theoretical guidance in materials engineering. Experimentally observed scanning electron microscope (SEM) or transmission electron microscopy (TEM) pictures are also useful to derive the morphology descriptors of nanoparticles, from which various explainable ML models such as light gradient boosted machine (LightGBM), extreme gradient boosting (XGBoost), support vector machine (SVM), and gradient boosting decision tree (GBDT) could predict the surface energy after being trained with high throughput calculations on different size scales.211
785 D/A pairs is explored to find potential synergistic ones. Favourable device bulk properties such as the root-mean-square of surface roughness for D/A blends and the D/A weight ratio are further screened by grid search methods. This showed that ML can be effective not only for molecular screening but also for experimental parameter optimization for OSCs, which takes an important step further into the practical theoretical guidance in materials engineering. Experimentally observed scanning electron microscope (SEM) or transmission electron microscopy (TEM) pictures are also useful to derive the morphology descriptors of nanoparticles, from which various explainable ML models such as light gradient boosted machine (LightGBM), extreme gradient boosting (XGBoost), support vector machine (SVM), and gradient boosting decision tree (GBDT) could predict the surface energy after being trained with high throughput calculations on different size scales.211
Last but not the least, the synthetic accessibility of screened candidates is an important target of material design. The synthetic accessibility is assessed to identify new efficient and synthetically accessible organic dyes for dye-sensitized solar cells (DSSCs).43 The solubility and viscosity predictions are also very useful for experiments to select appropriate solvents for synthetic experiments. Feature engineering indicated that the molecular size, shape and hydrogen bonding interaction are efficient features to predict the liquid viscosity in a fast way without much loss of accuracy.212
Although the well-behaved features coming from explainable ML methods could provide significant insight for experimentalists in the rational design of different kinds of materials, various deep learning methods have been introduced into chemistry and materials science. In the implementation of deep learning methods, we only need to input the information of atoms, bonds, topology, etc., for each molecule. As mentioned in the above subsection, the functions of novel optical materials and electronic devices are correlated with the descriptors of dipole moment, polarizability, energy levels of the HOMO and the LUMO, and so on. In fact, the accurate prediction of the HOMO and LUMO energy levels is still a big challenge for deep learning methods. To improve the prediction accuracy of HOMO and LUMO energy levels, we proposed an efficient multi-level attention neural network, named DeepMoleNet, for molecular systems to establish an implicit relationship between the molecular structural information and 12 electronic structure properties including dipole moment, polarizability, HOMO, LUMO, HOMO–LUMO gap, zero point vibration energy (ZPVE), electronic spatial extent (<R2>), internal energy at zero and room temperature (U0, U), enthalpy (H), free energy (G), and heat capacity (Cv).213 In addition to these 12 quantum chemistry properties, the atom-centered symmetry functions (ACSFs)214 descriptor is selected as the auxiliary prediction target. Recently, a modified DeepMoleNet model was proposed to study the relative stability of nanoparticles with the introduction of cut-off approximation for treating a complex system.211 It can be expected that the multi-level attention neural network is applicable to high-throughput screening of various chemical species to accelerate the rational design of material candidates.
In addition to the above-mentioned property predictions, machine learning methods have also been introduced in quantum chemical study for the prediction of atomic forces and energies, with the target of constructing accurate force fields and complicated potential energy surfaces. Shen and Yang have combined a QM/MM method and neural network (NN) for direct MD simulations.215 The QM/MM-NN could approximately reproduce the ab initio QM/MM simulated results by saving the computational costs by about 2 orders of magnitude. An on-the-fly GEBF ML approach was developed to construct a machine learning force field for oligomers by employing a Gaussian process without the need for data selection and parameter optimization.44,218 In this approach, only those small GEBF subsystems are employed to construct ML force fields automatically and efficiently. Then, the total energy, gradients, and molecular properties could be obtained from those of GEBF subsystems. With the GEBF-ML force field, long-time MD simulations were performed on various PEn (n = 20, 30, 40, 50). The results show that the full QM energies, forces, and dipole moments of those PE could be accurately reproduced with the GEBF-ML force field. Furthermore, the infrared spectra of PE6 obtained from the GEBF-ML MD simulations are also consistent with those from the corresponding direct AIMD or experimental results. However, the GEBF-ML MD simulations are several orders of magnitude faster than the corresponding direct GEBF-based AIMD simulations. Therefore, on-line and transfer learning force fields could be used for studying the conformation changes or vibration and even electronic spectra of long oligomers.
5 Conclusions
The development of low scaling QM methods and their combination with multiscale models and machine learning techniques has brought about fruitful applications in understanding the microscopic structure of polymeric oligomer chains, self-assembled monolayers, supramolecular complexes, and molecular aggregates in solution or solids and fast predicting various properties for speeding up material design. There are still some challenges as summarized below.It is well known that quantum mechanics and molecular mechanics are the major tools employed in material design. Especially, DFT is widely used to compute the energy, structure, and more properties of various functional materials. However, conventional DFT calculations are still very expensive for those materials with large sizes due to their high scaling. The accuracies of DFT calculations are dependent on the choice of functionals. There are two directions to improve DFT performance for large sized systems. One blooming direction is to use ML to develop more accurate DFT functionals. The generality and transferability of trained models are crucial in this area, which requires the state-of-the-art ML models and an accurate benchmark data set for training and testing the ML derived functionals. Thus, on the other hand, high-level electron correlation methods are needed. But post HF methods are infeasible for large-sized systems and high throughput calculations because of their even higher scaling than that of DFT. For ground-state calculations, low scaling QM methods, such as fragmentation methods and local correlation methods, could speed up DFT calculations and also enable the electron correlation calculations of large systems.
We have illustrated the application of fragmentation approaches to various materials, including polymer oligomers in solutions or solids, supramolecular complexes and their molecular self-assembled, stimuli-responsive materials on surfaces and mechanically interlocked molecules. The fragmentation approaches are simple and effective, and could be extended to various molecular or material properties with the accuracies depending on the parameters for defining local environments. However, for some complex systems such as those containing highly twined, delocalized, or polarizable functional groups, the fragments need to be manually defined. Local correlation approaches could also be employed for the calculations of relative or binding energies of supramolecular complexes. More complicated materials which are difficult to be treated by fragmentation approaches, such as metal oxides, could be computed by the local correlation methods as a black-box. Though analytic energy gradients and geometry optimization are available in the local correlation methods, high-order analytic energy derivatives are too complicated to be implemented until now. Thus, the local correlation methods have not been applied to molecular and material properties such as IR/Raman and NMR spectroscopy, which are useful characterization measurements for material systems. In addition, low scaling QM algorithms need to be improved to treat more complex systems at high QM levels. For example, two low scaling algorithms under periodic boundary conditions, such as PBC-GEBF and PBC-CIM methods, have been developed. These methods are applicable to periodic systems and need to be applied to more functional materials and interfaces. A low scaling QM dataset, such as the GEBF database83 and ExL8 dataset,64 could provide high-accuracy post HF data for both method validation and data driven molecular and material design. More low-scaling QM computation data sets with a wide range of chemical spaces are highly desired.
It has also been stressed that excited-state calculations and dynamics are important for optical functional materials such as optoelectronic devices and photo-catalysts. However, electronic excited-state calculations are much more expensive than the corresponding ground-state calculations. For the excited-state calculations, local excitation or local correlation approximation based on localized molecular orbitals or molecular fragments or excitonic models could be used to accelerate the excited-state calculations. Tensor product methods were employed to speed up the excited-state dynamics. Although the applications of low scaling excited-state methods to investigate the optoelectronic processes in organic photovoltaics have been demonstrated, the further development of quantum dynamics methodologies with an appropriate description of condensed phase environments is highly desired. The collaboration with experimental ultrafast multi-dimensional spectroscopy is also very important to provide insight into the microscopic understanding of electron-vibration coherence.
The combination of low scaling QM methods with force field based molecular dynamics simulations is still a practical way to study the packing structures of very complicated molecular aggregates in a condensed phase. The performance and transferability of the force field parameters are the key issues in material design. Electrostatics polarization could be accurately described with the assistance of the low scaling QM calculations of MD sampled configurations. However, for low-lying excited states and proton transfer reactions, much more studies are required to modify the force field forms and introduce the new idea.
So, a more general way is to apply data-mining techniques and machine learning algorithms to fast predict the energy, force, structure, and properties of functional materials. By using neural networks or other ML algorithms, the optical or electrical properties of materials could be trained from QM computational or experimental databases with some structural descriptors via feature learning. Then, force fields as well as material properties could be directly predicted by the trained ML models. Furthermore, the molecular energies, forces, or electronic structure properties such as HOMO and LUMO energy levels could be directly trained by ML models such as a graph convolutional NN or Gaussian process with molecular descriptors based on molecular geometries. Low scaling QM methods can be expected to accelerate the computational data generation for ML training. For example, an online transfer learning algorithm was developed for predicting the force fields, conformational structures, and IR spectra of polymer oligomers by training GEBF subsystems only.44,218 In the future, the online machine learning force field should also be extended to periodic materials and interfaces by taking infinite long-range electrostatic interactions into accounts. Then, the lattice energy, crystal structures, and spectroscopic properties of periodic materials could be efficiently obtained to assist the design of novel functional materials. Finally, the synthetic accessibility and theoretically designed reaction pathway could guide the experimental fabrications of materials, and in turn, the feedback from experiments could be added into the material datasets to update the ML models for the new design.
Author contributions
J. M. designed the plan and structure of the review article. W. L. and S. L. completed the review of low-scaling QM methods and their applications and ML force fields. H. M. contributed to the methods of excited states and machine learning of organic photovoltaic (OPV) materials. J. M. discussed the interplay between the experiments and simulations of stimuli-responsive monolayers and deep learning study. All authors reviewed and contributed to this manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22033004, 21873046, 22073045, and 21833002) and the Fundamental Research Funds for the Central Universities. The authors would like to thank Ziteng Liu, Yuming Gu, Zheng Cheng, and Kang Liao for their help in collecting the data in Tables S1 and S2.†Notes and references
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- W. Y. Wang, J. Li, W. Liu and Z.-K. Liu, Comput. Mater. Sci., 2019, 158, 42–48 CrossRef.
- X. Zhang, A. Chen and Z. Zhou, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1385 Search PubMed.
- J.-L. Bredas, K. Persson and R. Seshadri, Chem. Mater., 2017, 29, 2399–2401 CrossRef CAS.
- A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 15004 CrossRef CAS.
- R. L. Greenaway and K. E. Jelfs, Adv. Mater., 2021, 33, 2004831 CrossRef CAS PubMed.
- K. T. Butler, J. M. Frost, J. M. Skelton, K. L. Svane and A. Walsh, Chem. Soc. Rev., 2016, 45, 6138–6146 RSC.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185–204 RSC.
- L. Wang, G. Nan, X. Yang, Q. Peng, Q. Li and Z. Shuai, Chem. Soc. Rev., 2010, 39, 423–434 RSC.
- M. Muller and J. J. de Pablo, Annu. Rev. Mater. Res., 2013, 43, 1–34 CrossRef.
- J. A. Elliott, Int. Mater. Rev., 2011, 56, 207–225 CrossRef CAS.
- A. H. Romero, D. C. Allan, B. Amadon, G. Antonius, T. Applencourt, L. Baguet, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, F. Bruneval, G. Brunin, D. Caliste, M. Côté, J. Denier, C. Dreyer, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, F. Jollet, G. Jomard, A. Martin, H. P. C. Miranda, F. Naccarato, G. Petretto, N. A. Pike, V. Planes, S. Prokhorenko, T. Rangel, F. Ricci, G.-M. Rignanese, M. Royo, M. Stengel, M. Torrent, M. J. van Setten, B. Van Troeye, M. J. Verstraete, J. Wiktor, J. W. Zwanziger and X. Gonze, J. Chem. Phys., 2020, 152, 124102 CrossRef CAS PubMed.
- P. Verma and D. G. Truhlar, Trends Chem., 2020, 2, 302–318 CrossRef CAS.
- L. Yan, Y. Zhang, Z. Ni, Y. Zhang, J. Xu, T. Kong, J. Huang, W. Li, J. Ma and Y. Wang, J. Am. Chem. Soc., 2021, 143, 15369–15377 CrossRef CAS PubMed.
- M. Kobayashi, T. Kunisada, T. Akama, D. Sakura and H. Nakai, J. Chem. Phys., 2011, 134, 034105 CrossRef PubMed.
- H. Shang, W. Liang, Y. Zhang and J. Yang, Comput. Phys. Commun., 2021, 258, 107613 CrossRef CAS.
- D. Yuan, Y. Li, W. Li and S. Li, Phys. Chem. Chem. Phys., 2018, 20, 28894–28902 RSC.
- W. Zhang, J. Liu, X. Jin, X. Gu, X. C. Zeng, X. He and H. Li, Angew. Chem., Int. Ed., 2020, 59, 11550–11555 CrossRef CAS PubMed.
- D. S. Kaliakin, H. Nakata, Y. Kim, Q. Chen, D. G. Fedorov and L. V Slipchenko, J. Chem. Theory Comput., 2020, 16, 1175–1187 CrossRef CAS PubMed.
- H. Ma and A. Troisi, Adv. Mater., 2014, 26, 6163–6167 CrossRef CAS PubMed.
- A. F. Morrison and J. M. Herbert, J. Phys. Chem. Lett., 2017, 8, 1442–1448 CrossRef CAS PubMed.
- S. Paeckel, T. Köhler, A. Swoboda, S. R. Manmana, U. Schollwöck and C. Hubig, Ann. Phys., 2019, 411, 167998 CAS.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- H. Tamura, M. Huix-Rotllant, I. Burghardt, Y. Olivier and D. Beljonne, Phys. Rev. Lett., 2015, 115, 107401 CrossRef PubMed.
- F. A. Y. N. Schroder, D. H. P. Turban, A. J. Musser, N. D. M. Hine and A. W. Chin, Nat. Commun., 2019, 10, 1062 CrossRef PubMed.
- X. Xie, Y. Liu, Y. Yao, U. Schollwöck, C. Liu and H. Ma, J. Chem. Phys., 2019, 151, 224101 CrossRef PubMed.
- M. F. Gelin, R. Borrelli and W. Domcke, J. Phys. Chem. Lett., 2019, 10, 2806–2810 CrossRef CAS PubMed.
- S. H. M. Mehr, M. Craven, A. I. Leonov, G. Keenan and L. Cronin, Science, 2020, 370, 101–108 CrossRef CAS PubMed.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631 CrossRef CAS PubMed.
- B. Burger, P. M. Maffettone, V. V Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- B. Mikulak-Klucznik, P. Gołębiowska, A. A. Bayly, O. Popik, T. Klucznik, S. Szymkuć, E. P. Gajewska, P. Dittwald, O. Staszewska-Krajewska, W. Beker, T. Badowski, K. A. Scheidt, K. Molga, J. Mlynarski, M. Mrksich and B. A. Grzybowski, Nature, 2020, 588, 83–88 CrossRef CAS PubMed.
- X. Yang, Y. Wang, R. Byrne, G. Schneider and S. Yang, Chem. Rev., 2019, 119, 10520–10594 CrossRef CAS PubMed.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- A. F. Zahrt, S. V Athavale and S. E. Denmark, Chem. Rev., 2020, 120, 1620–1689 CrossRef CAS PubMed.
- Y. Xu, L. Elcoro, Z.-D. Song, B. J. Wieder, M. G. Vergniory, N. Regnault, Y. Chen, C. Felser and B. A. Bernevig, Nature, 2020, 586, 702–707 CrossRef CAS PubMed.
- J. G. Freeze, H. R. Kelly and V. S. Batista, Chem. Rev., 2019, 119, 6595–6612 CrossRef CAS PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- J. Westermayr and P. Marquetand, Chem. Rev., 2021, 121, 9873–9926 CrossRef CAS PubMed.
- S. Ye, K. Zhong, J. Zhang, W. Hu, J. D. Hirst, G. Zhang, S. Mukamel and J. Jiang, J. Am. Chem. Soc., 2020, 142, 19071–19077 CrossRef CAS PubMed.
- C. W. Coley, W. H. Green and K. F. Jensen, Acc. Chem. Res., 2018, 51, 1281–1289 CrossRef CAS PubMed.
- E. Cantini, X. Wang, P. Koelsch, J. A. Preece, J. Ma and P. M. Mendes, Acc. Chem. Res., 2016, 49, 1223–1231 CrossRef CAS PubMed.
- P. Liu, W. Li, Z. Kan, H. Sun and J. Ma, J. Phys. Chem. A, 2016, 120, 490–502 CrossRef CAS PubMed.
- Y. Wen, L. Fu, G. Li, J. Ma and H. Ma, Sol. RRL, 2020, 4, 2000110 CrossRef CAS.
- Z. Cheng, D. Zhao, J. Ma, W. Li and S. Li, J. Phys. Chem. A, 2020, 124, 5007–5014 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- M. C. Strain, G. E. Scuseria and M. J. Frisch, Science, 1996, 271, 51–53 CrossRef CAS.
- S. Saebo and P. Pulay, Annu. Rev. Phys. Chem., 1993, 44, 213–236 CrossRef CAS.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V Slipchenko, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- D. L. Strout and G. E. Scuseria, J. Chem. Phys., 1995, 102, 8448–8452 CrossRef CAS.
- E. Schwegler and M. Challacombe, J. Chem. Phys., 1996, 105, 2726–2734 CrossRef CAS.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, Chem. Phys. Lett., 1996, 257, 213–223 CrossRef CAS.
- X. Li, J. M. Millam, G. E. Scuseria, M. J. Frisch and H. B. Schlegel, J. Chem. Phys., 2003, 119, 7651–7658 CrossRef CAS.
- S. Saebo and P. Pulay, Chem. Phys. Lett., 1985, 113, 13–18 CrossRef CAS.
- C. Hampel and H. Werner, J. Chem. Phys., 1996, 104, 6286–6297 CrossRef CAS.
- D. Usvyat, L. Maschio and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1357 Search PubMed.
- M. Sparta and F. Neese, Chem. Soc. Rev., 2014, 43, 5032–5041 RSC.
- T. Kjaergaard, P. Baudin, D. Bykov, K. Kristensen and P. Jørgensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1319 Search PubMed.
- Q. Ma and H.-J. Werner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1371 Search PubMed.
- W. Li, Z. Ni and S. Li, Mol. Phy., 2016, 114, 1447–1460 CrossRef CAS.
- S. Li, J. Ma and Y. Jiang, J. Comput. Chem., 2002, 23, 237–244 CrossRef CAS PubMed.
- S. Li, J. Shen, W. Li and Y. Jiang, J. Chem. Phys., 2006, 125, 74109 CrossRef PubMed.
- Z. Ni, Y. Wang, W. Li, P. Pulay and S. Li, J. Chem. Theory Comput., 2019, 15, 3623–3634 CrossRef CAS PubMed.
- Z. Ni, Y. Guo, F. Neese, W. Li and S. Li, J. Chem. Theory Comput., 2021, 17, 756–766 CrossRef CAS PubMed.
- W. Yang, Phys. Rev. Lett., 1991, 66, 1438–1441 CrossRef CAS PubMed.
- M. Kobayashi, T. Akama and H. Nakai, J. Chem. Phys., 2006, 125, 204106 CrossRef PubMed.
- M. Kobayashi and H. Nakai, J. Chem. Phys., 2009, 131, 114108 CrossRef PubMed.
- T. E. Exner and P. G. Mezey, J. Comput. Chem., 2003, 24, 1980–1986 CrossRef CAS PubMed.
- F. L. Gu, Y. Aoki, J. Korchowiec, A. Imamura and B. Kirtman, J. Chem. Phys., 2004, 121, 10385–10391 CrossRef CAS PubMed.
- X. He and J. Z. H. Zhang, J. Chem. Phys., 2005, 122, 031103 CrossRef PubMed.
- W. Li and S. Li, J. Chem. Phys., 2005, 122, 194109 CrossRef PubMed.
- Y. Guo, W. Li and S. Li, Chem. Phys. Lett., 2012, 539–540, 186–190 CrossRef CAS.
- M. A. Collins and R. P. A. Bettens, Chem. Rev., 2015, 115, 5607–5642 CrossRef CAS PubMed.
- J. H. Jensen, P. N. Day, M. S. Gordon, H. Basch, D. Cohen, D. R. Garmer, M. Kraus and W. J. Stevens, Model. Hydrog. Bond, 1994, 569, 139–151 CAS.
- J. Gao, J. Phys. Chem. B, 1997, 101, 657–663 CrossRef CAS.
- K. Kitaura, E. Ikeo, T. Asada, T. Nakano and M. Uebayasi, Chem. Phys. Lett., 1999, 313, 701–706 CrossRef CAS.
- S. Li, W. Li and T. Fang, J. Am. Chem. Soc., 2005, 127, 7215–7226 CrossRef CAS PubMed.
- V. Deev and M. A. Collins, J. Chem. Phys., 2005, 122, 154102 CrossRef PubMed.
- L. Huang, L. Massa and E. Karle, Int. J. Quantum Chem., 2005, 103, 808–817 CrossRef CAS.
- N. Jiang, J. Ma and Y. Jiang, J. Chem. Phys., 2006, 124, 114112 CrossRef PubMed.
- W. Li, S. Li and Y. Jiang, J. Phys. Chem. A, 2007, 111, 2193–2199 CrossRef CAS PubMed.
- S. Li, W. Li and J. Ma, Acc. Chem. Res., 2014, 47, 2712–2720 CrossRef CAS PubMed.
- W. Li, H. Dong, J. Ma and S. Li, Acc. Chem. Res., 2021, 54, 169–181 CrossRef CAS PubMed.
- X. He and J. Z. H. Zhang, J. Chem. Phys., 2006, 124, 184703 CrossRef PubMed.
- X. He, T. Zhu, X. Wang, J. Liu and J. Z. H. Zhang, Acc. Chem. Res., 2014, 47, 2748–2757 CrossRef CAS PubMed.
- S. R. Gadre and V. Ganesh, J. Theor. Comput. Chem., 2006, 05, 835–855 CrossRef CAS.
- N. J. Mayhall and K. Raghavachari, J. Chem. Theory Comput., 2011, 7, 1336–1343 CrossRef CAS PubMed.
- R. M. Richard and J. M. Herbert, J. Chem. Phys., 2012, 137, 064113 CrossRef PubMed.
- K. Raghavachari and A. Saha, Chem. Rev., 2015, 115, 5643–5677 CrossRef CAS PubMed.
- J. M. Herbert, J. Chem. Phys., 2019, 151, 170901 CrossRef PubMed.
- H. Stoll, Chem. Phys. Lett., 1992, 191, 548–552 CrossRef CAS.
- C. Pisani, M. Busso, G. Capecchi, S. Casassa, R. Dovesi, L. Maschio, C. Zicovich-Wilson and M. Schütz, J. Chem. Phys., 2005, 122, 094113 CrossRef CAS PubMed.
- E. Rebolini, G. Baardsen, A. S. Hansen, K. R. Leikanger and T. B. Pedersen, J. Chem. Theory Comput., 2018, 14, 2427–2438 CrossRef CAS PubMed.
- Y. Wang, Z. Ni, W. Li and S. Li, J. Chem. Theory Comput., 2019, 15, 2933–2943 CrossRef CAS PubMed.
- J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Science, 2014, 345, 640–643 CrossRef CAS PubMed.
- T. Fang, W. Li, F. Gu and S. Li, J. Chem. Theory Comput., 2015, 11, 91–98 CrossRef CAS PubMed.
- T. Fang, Y. Li and S. Li, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1297 Search PubMed.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- G. Seifert and J.-O. Joswig, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 456–465 CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- Y. Nishimoto, D. G. Fedorov and S. Irle, Chem. Phys. Lett., 2015, 636, 90–96 CrossRef CAS.
- H. Nishizawa, Y. Nishimura, M. Kobayashi, S. Irle and H. Nakai, J. Comput. Chem., 2016, 37, 1983–1992 CrossRef CAS PubMed.
- D. Mester and M. Kállay, J. Chem. Theory Comput., 2019, 15, 1690–1704 CrossRef CAS PubMed.
- M. Miura and Y. Aoki, J. Comput. Chem., 2009, 30, 2213–2230 CAS.
- R. A. Mata and H. Stoll, J. Chem. Phys., 2011, 134, 034122 CrossRef PubMed.
- C. Zhang, D. Yuan, Y. Guo and S. Li, J. Chem. Theory Comput., 2014, 10, 5308–5317 CrossRef CAS PubMed.
- J. Liu and J. M. Herbert, J. Chem. Theory Comput., 2016, 12, 157–166 CrossRef CAS PubMed.
- X. Jin, W. J. Glover and X. He, J. Chem. Theory Comput., 2020, 16, 5174–5188 CrossRef CAS PubMed.
- W. Li, Y. Li, R. Lin and S. Li, J. Phys. Chem. A, 2016, 120, 9667–9677 CrossRef CAS PubMed.
- G. Macetti and A. Genoni, J. Chem. Theory Comput., 2020, 16, 7490–7506 CrossRef CAS PubMed.
- W.-K. Chen, W.-H. Fang and G. Cui, J. Phys. Chem. Lett., 2019, 10, 7836–7841 CrossRef CAS PubMed.
- C. Yam, S. Yokojima and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 153105 CrossRef.
- G. Cui, W. Fang and W. Yang, Phys. Chem. Chem. Phys., 2010, 12, 416–421 RSC.
- F. Wu, W. Liu, Y. Zhang and Z. Li, J. Chem. Theory Comput., 2011, 7, 3643–3660 CrossRef CAS PubMed.
- T. D. Crawford and R. A. King, Chem. Phys. Lett., 2002, 366, 611–622 CrossRef CAS.
- D. Kats, T. Korona and M. Schütz, J. Chem. Phys., 2006, 125, 104106 CrossRef PubMed.
- T. S. Chwee and E. A. Carter, J. Chem. Theory Comput., 2011, 7, 103–111 CrossRef CAS PubMed.
- Q. Li, Q. Li and Z. Shuai, Synth. Met., 2008, 158, 330–335 CrossRef CAS.
- H. Nakatsuji, T. Miyahara and R. Fukuda, J. Chem. Phys., 2007, 126, 084104 CrossRef PubMed.
- H. Nakai and T. Yoshikawa, J. Chem. Phys., 2017, 146, 124123 CrossRef PubMed.
- T. Yoshikawa, J. Yoshihara and H. Nakai, J. Chem. Phys., 2020, 152, 024102 CrossRef CAS PubMed.
- S. Nishio and Y. Kurashige, J. Chem. Phys., 2019, 151, 084110 CrossRef PubMed.
- S.-H. Lim, T. G. Bjorklund, F. C. Spano and C. J. Bardeen, Phys. Rev. Lett., 2004, 92, 107402 CrossRef PubMed.
- N. J. Hestand, R. V Kazantsev, A. S. Weingarten, L. C. Palmer, S. I. Stupp and F. C. Spano, J. Am. Chem. Soc., 2016, 138, 11762–11774 CrossRef CAS PubMed.
- X. Li, R. M. Parrish, F. Liu, S. I. L. Kokkila Schumacher and T. J. Martínez, J. Chem. Theory Comput., 2017, 13, 3493–3504 CrossRef CAS PubMed.
- J. Wen and H. Ma, Chem. Phys. Lett., 2017, 679, 152–157 CrossRef CAS.
- H. Zhao, Y. Zhao, Y. Song, M. Zhou, W. Lv, L. Tao, Y. Feng, B. Song, Y. Ma, J. Zhang, J. Xiao, Y. Wang, D.-H. Lien, M. Amani, H. Kim, X. Chen, Z. Wu, Z. Ni, P. Wang, Y. Shi, H. Ma, X. Zhang, J.-B. Xu, A. Troisi, A. Javey and X. Wang, Nat. Commun., 2019, 10, 5589 CrossRef CAS PubMed.
- J. A. Green, H. Asha, F. Santoro and R. Improta, J. Chem. Theory Comput., 2021, 17, 405–415 CrossRef CAS PubMed.
- T. Fujita and Y. Mochizuki, J. Phys. Chem. A, 2018, 122, 3886–3898 CrossRef CAS PubMed.
- C. Bloch, Nucl. Phys., 1958, 6, 329–347 CrossRef CAS.
- C. J. Morningstar and M. Weinstein, Phys. Rev. Lett., 1994, 73, 1873–1877 CrossRef CAS PubMed.
- M. Al Hajj, J.-P. Malrieu and N. Guihéry, Phys. Rev. B, 2005, 72, 224412 CrossRef.
- H. Zhang, J. P. Malrieu, H. Ma and J. Ma, J. Comput. Chem., 2012, 33, 34–43 CrossRef CAS PubMed.
- Y. Ma, Y. Liu and H. Ma, J. Chem. Phys., 2012, 136, 024113 CrossRef PubMed.
- Y. Ma and H. Ma, J. Phys. Chem. A, 2013, 117, 3655–3665 CrossRef CAS PubMed.
- T. G. Kolda and B. W. Bader, SIAM Rev., 2009, 51, 455–500 CrossRef.
- L. R. Tucker, Psychometrika, 1966, 31, 279–311 CrossRef CAS PubMed.
- L. De Lathauwer, B. De Moor and J. Vandewalle, SIAM J. Matrix Anal. Appl., 2000, 21, 1253–1278 CrossRef.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- I. V Oseledets, SIAM J. Sci. Comput., 2011, 33, 2295–2317 CrossRef.
- F. Verstraete, V. Murg and J. I. Cirac, Adv. Phys., 2008, 57, 143–224 CrossRef.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef PubMed.
- U. Schollwock, Rev. Mod. Phys., 2005, 77, 259–315 CrossRef CAS.
- Y. Yao, K.-W. Sun, Z. Luo and H. Ma, J. Phys. Chem. Lett., 2018, 9, 413–419 CrossRef CAS PubMed.
- H. Ma, Z. Luo and Y. Yao, Mol. Phys., 2018, 116, 854–868 CrossRef CAS.
- J. Ren, Z. Shuai and G. Kin-Lic Chan, J. Chem. Theory Comput., 2018, 14, 5027–5039 CrossRef CAS PubMed.
- W. Popp, M. Polkehn, R. Binder and I. Burghardt, J. Phys. Chem. Lett., 2019, 10, 3326–3332 CrossRef CAS PubMed.
- A. Baiardi and M. Reiher, J. Chem. Theory Comput., 2019, 15, 3481–3498 CrossRef CAS PubMed.
- W. Li, J. Ren and Z. Shuai, J. Phys. Chem. Lett., 2020, 11, 4930–4936 CrossRef CAS PubMed.
- J. Zheng, J. Peng, Y. Xie, Y. Long, X. Ning and Z. Lan, Phys. Chem. Chem. Phys., 2020, 22, 18192–18204 RSC.
- T. A. Niehaus, D. Heringer, B. Torralva and T. Frauenheim, Eur. Phys. J. D, 2005, 35, 467–477 CrossRef CAS.
- S. Grimme and C. Bannwarth, J. Chem. Phys., 2016, 145, 054103 CrossRef PubMed.
- M. Inamori, T. Yoshikawa, Y. Ikabata, Y. Nishimura and H. Nakai, J. Comput. Chem., 2020, 41, 1538–1548 CrossRef CAS PubMed.
- T. Yoshikawa, N. Komoto, Y. Nishimura and H. Nakai, J. Comput. Chem., 2019, 40, 2778–2786 CrossRef CAS PubMed.
- W. Li, M. Duan, K. Liao, B. Hong, Z. Ni, J. Ma and S. Li, Electron. Struct., 2019, 1, 044003 CrossRef CAS.
- Y. Guo, W. Li and S. Li, J. Phys. Chem. A, 2014, 118, 8996–9004 CrossRef CAS PubMed.
- Y. Guo, U. Becker and F. Neese, J. Chem. Phys., 2018, 148, 124117 CrossRef PubMed.
- J. C. A. Prentice, J. Aarons, J. C. Womack, A. E. A. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M.-M. Dubois, K. K. B. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. O'Regan, M. J. S. Phipps, L. E. Ratcliff, Á. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. M. Hine, A. A. Mostofi, M. C. Payne and C.-K. Skylaris, J. Chem. Phys., 2020, 152, 174111 CrossRef CAS PubMed.
- X. Qin, H. Shang, H. Xiang, Z. Li and J. Yang, Int. J. Quantum Chem., 2015, 115, 647–655 CrossRef CAS.
- W. Li, C. Chen, D. Zhao and S. Li, Int. J. Quantum Chem., 2015, 115, 641–646 CrossRef CAS.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- R. Dovesi, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. Bush, P. D'Arco, Y. Noël, M. Rérat, P. Carbonnière, M. Causà, S. Salustro, V. Lacivita, B. Kirtman, A. M. Ferrari, F. S. Gentile, J. Baima, M. Ferrero, R. Demichelis and M. De La Pierre, J. Chem. Phys., 2020, 152, 204111 CrossRef CAS PubMed.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS PubMed.
- W. Hu, L. Lin, C. Yang and J. Yang, J. Chem. Phys., 2014, 141, 214704 CrossRef PubMed.
- Z. Luo, X. Qin, L. Wan, W. Hu and J. Yang, Front. Chem., 2020, 8, 932 Search PubMed.
- H. Li, W. Li, S. Li and J. Ma, J. Phys. Chem. B, 2008, 112, 7061–7070 CrossRef CAS PubMed.
- H. Cao, T. Fang, S. Li and J. Ma, Macromolecules, 2007, 40, 4363–4369 CrossRef CAS.
- X. Yuan, W. Zhang, L. H. Xie, J. Ma, W. Huang and W. Liu, J. Phys. Chem. B, 2015, 119, 10316–10333 CrossRef CAS PubMed.
- S. Hua, W. Hua and S. Li, J. Phys. Chem. A, 2010, 114, 8126–8134 CrossRef CAS PubMed.
- W. Liang, S. Yokojima and G. Chen, J. Chem. Phys., 2000, 113, 1403–1408 CrossRef CAS.
- M. Kobayashi and H. Nakai, Phys. Chem. Chem. Phys., 2012, 14, 7629 RSC.
- G. Boschetto, H.-T. Xue, J. Dziedzic, M. Krompiec and C.-K. Skylaris, J. Phys. Chem. C, 2017, 121, 2529–2538 CrossRef CAS.
- S. Chen and J. Ma, J. Chem. Phys., 2012, 137, 074708 CrossRef PubMed.
- J. Wen and J. Ma, J. Phys. Chem. C, 2012, 116, 8523–8534 CrossRef CAS.
- R. Sure and S. Grimme, J. Chem. Theory Comput., 2015, 11, 3785–3801 CrossRef CAS PubMed.
- K. Liao, S. Wang, W. Li and S. Li, Phys. Chem. Chem. Phys., 2021, 23, 19394–19401 RSC.
- T. Schaller, U. P. Büchele, F.-G. Klärner, D. Bläser, R. Boese, S. P. Brown, H. W. Spiess, F. Koziol, J. Kussmann and C. Ochsenfeld, J. Am. Chem. Soc., 2007, 129, 1293–1303 CrossRef CAS PubMed.
- N. Jiang, R. X. Tan and J. Ma, J. Phys. Chem. B, 2011, 115, 2801–2813 CrossRef CAS PubMed.
- Y. Chen, L. Fu, B. Sun, C. Qian, R. Wang, J. Jiang, C. Lin, J. Ma and L. Wang, Org. Lett., 2020, 22, 2266–2270 CrossRef CAS PubMed.
- T. Kjaergaard, P. Baudin, D. Bykov, J. J. Eriksen, P. Ettenhuber, K. Kristensen, J. Larkin, D. Liakh, F. Pawłowski, A. Vose, Y. M. Wang and P. Jorgensen, Comput. Phys. Commun., 2017, 212, 152–160 CrossRef CAS.
- S. Debnath, A. Sengupta, K. V. J. Jose and K. Raghavachari, J. Chem. Theory Comput., 2018, 14, 6226–6239 CrossRef CAS PubMed.
- J. Lahann, S. Mitragotri, T.-N. Tran, H. Kaido, J. Sundaram, I. S. Choi, S. Hoffer, G. A. Somorjai and R. Langer, Science, 2003, 299, 371–374 CrossRef CAS PubMed.
- J. Zhao, X. Wang, N. Jiang, T. Yan, Z. Kan, P. M. Mendes and J. Ma, J. Phys. Chem. C, 2015, 119, 22866–22881 CrossRef CAS.
- C. L. Yeung, X. Wang, M. Lashkor, E. Cantini, F. J. Rawson, P. Iqbal, J. A. Preece, J. Ma and P. M. Mendes, Adv. Mater. Interfaces, 2014, 1, 1300085 CrossRef PubMed.
- J. Wen, Z. Tian and J. Ma, J. Phys. Chem. C, 2013, 117, 19934–19944 CrossRef CAS.
- Y. Pei and J. Ma, J. Am. Chem. Soc., 2005, 127, 6802–6813 CrossRef CAS PubMed.
- A. N. Brigeman, M. A. Fusella, Y. Yan, G. E. Purdum, Y.-L. Loo, B. P. Rand and N. C. Giebink, Adv. Energy Mater., 2016, 6, 1601001 CrossRef.
- S. Sharma, K. Sivalingam, F. Neese and G. K.-L. Chan, Nat. Chem., 2014, 6, 927–933 CrossRef CAS PubMed.
- B. E. Van Kuiken, A. W. Hahn, B. Nayyar, C. E. Schiewer, S. C. Lee, F. Meyer, T. Weyhermüller, A. Nicolaou, Y.-T. Cui, J. Miyawaki, Y. Harada and S. DeBeer, Inorg. Chem., 2018, 57, 7355–7361 CrossRef CAS PubMed.
- D. Cho, J. R. Rouxel, S. Mukamel, G. Kin-Lic Chan and Z. Li, J. Phys. Chem. Lett., 2019, 10, 6664–6671 CrossRef CAS PubMed.
- M. F. Gelin and R. Borrelli, J. Chem. Theory Comput., 2021, 17, 4316–4331 CrossRef CAS PubMed.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- Z. Wang, H. Liu, X. Xie, C. Zhang, R. Wang, L. Chen, Y. Xu, H. Ma, W. Fang, Y. Yao, H. Sang, X. Wang, X. Li and M. Xiao, Nat. Chem., 2021, 13, 559–567 CrossRef CAS PubMed.
- S. Mardazad, Y. Xu, X. Yang, M. Grundner, U. Schollwöck, H. Ma and S. Paeckel, 2021, arXiv: 2107.13948.
- W. Li, J. Ren and Z. Shuai, Nat. Commun., 2021, 12, 4260 CrossRef CAS PubMed.
- B. Kailkhura, B. Gallagher, S. Kim, A. Hiszpanski and T. Y.-J. Han, npj Comput. Mater., 2019, 5, 108 CrossRef.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Joule, 2017, 1, 857–870 CrossRef CAS.
- D. Padula, J. D. Simpson and A. Troisi, Mater. Horiz., 2019, 6, 343–349 RSC.
- D. Padula and A. Troisi, Adv. Energy Mater., 2019, 9, 1902463 CrossRef CAS.
- W. Sun, Y. Zheng, K. Yang, Q. Zhang, A. A. Shah, Z. Wu, Y. Sun, L. Feng, D. Chen, Z. Xiao, S. Lu, Y. Li and K. Sun, Sci. Adv., 2019, 5, eaay4275 CrossRef CAS PubMed.
- S.-P. Peng and Y. Zhao, J. Chem. Inf. Model., 2019, 59, 4993–5001 CrossRef CAS PubMed.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 8, 1801032 CrossRef.
- H. Sahu and H. Ma, J. Phys. Chem. Lett., 2019, 10, 7277–7284 CrossRef CAS PubMed.
- H. Sahu, F. Yang, X. Ye, J. Ma, W. Fang and H. Ma, J. Mater. Chem. A, 2019, 7, 17480–17488 RSC.
- Y. Wen, Y. Liu, B. Yan, T. Gaudin, J. Ma and H. Ma, J. Phys. Chem. Lett., 2021, 12, 4980–4986 CrossRef CAS PubMed.
- Z. Liu, Y. Shi, H. Chen, T. Qin, X. Zhou, J. Huo, H. Dong, X. Yang, X. Zhu, X. Chen, L. Zhang, M. Yang, Y. Gao and J. Ma, npj Comput. Mater., 2021, 7, 142 CrossRef CAS.
- Q. Zhu, Y. Gu, L. Hu, T. Gaudin, M. Fan and J. Ma, J. Chem. Phys., 2021, 154, 74502 CrossRef CAS PubMed.
- Z. Liu, L. Lin, Q. Jia, Z. Cheng, Y. Jiang, Y. Guo and J. Ma, J. Chem. Inf. Model., 2021, 61, 1066–1082 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- L. Shen and W. Yang, J. Chem. Theory Comput., 2018, 14, 1442–1455 CrossRef CAS PubMed.
- H. M. Netzloff and M. A. Collins, J. Chem. Phys., 2007, 127(13), 134113 CrossRef PubMed.
- G. J. O. Beran and K. Nanda, J. Phys. Chem. Lett., 2010, 1(24), 3480–3487 CrossRef CAS.
- Z. Cheng, J. Du, L. Zhang, J. Ma, W. Li and S. Li, Phys. Chem. Chem. Phys., 2021 10.1039/D1CP03934B.
Footnote |
| † Electronic supplementary information (ESI) available: Selected studies of using low-scaling quantum mechanics methods or machine learning to study molecular materials. See DOI: 10.1039/d1sc02574k |
| This journal is © The Royal Society of Chemistry 2021 |