 Open Access Article
Open Access ArticleThe electrostatic origins of specific ion effects: quantifying the Hofmeister series for anions†
Kasimir P.
Gregory
 a,
Erica J.
Wanless
a,
Erica J.
Wanless
 a,
Grant B.
Webber
a,
Grant B.
Webber
 b,
Vincent S. J.
Craig
b,
Vincent S. J.
Craig
 c and
Alister J.
Page
c and
Alister J.
Page
 *a
*a
aDiscipline of Chemistry, School of Environmental and Life Sciences, The University of Newcastle, Callaghan, New South Wales 2308, Australia. E-mail: alister.page@newcastle.edu.au
bSchool of Engineering, The University of Newcastle, Callaghan, New South Wales 2308, Australia
cDepartment of Applied Mathematics, Research School of Physics, Australian National University, Canberra, ACT 0200, Australia
First published on 16th October 2021
Abstract
Life as we know it is dependent upon water, or more specifically salty water. Without dissolved ions, the interactions between biological molecules are insufficiently complex to support life. This complexity is intimately tied to the variation in properties induced by the presence of different ions. These specific ion effects, widely known as Hofmeister effects, have been known for more than 100 years. They are ubiquitous throughout the chemical, biological and physical sciences. The origin of these effects and their relative strengths is still hotly debated. Here we reconsider the origins of specific ion effects through the lens of Coulomb interactions and establish a foundation for anion effects in aqueous and non-aqueous environments. We show that, for anions, the Hofmeister series can be explained and quantified by consideration of site-specific electrostatic interactions. This can simply be approximated by the radial charge density of the anion, which we have calculated for commonly reported ions. This broadly quantifies previously unpredictable specific ion effects, including those known to influence solution properties, virus activities and reaction rates. Furthermore, in non-aqueous solvents, the relative magnitude of the anion series is dependent on the Lewis acidity of the solvent, as measured by the Gutmann Acceptor Number. Analogous SIEs for cations bear limited correlation with their radial charge density, highlighting a fundamental asymmetry in the origins of specific ion effects for anions and cations, due to competing non-Coulombic phenomena.
Introduction
It is now over 135 years since Arrhenius first hypothesised the existence of ions from salts, the hypothesis that ultimately won him the 1903 Nobel Prize in chemistry. Within four years of this hypothesis, Franz Hofmeister demonstrated that different salts had varied influence on the stability of hen egg-white albumin protein in water. The ions of some salts destabilised the protein, causing it to aggregate and precipitate from solution, whereas ions of other salts caused the opposite effect, stabilising the protein solution and preventing precipitation. Hofmeister observed the same persistent trends in a range of pharmacological systems, discovering what are now collectively known as specific ion effects (SIEs) – phenomena caused by salts for which the identity of the constituent ions are a determining factor, not just their charge or concentration.Claims that SIEs are as important to our everyday lives as Mendelian genetics1,2 are well-founded. SIEs are ubiquitous throughout the physical, biological, chemical, environmental, and material sciences. They influence key biological functions such as taste,3 cell permeability,4,5 cell movement,6 enzymatic activity,4,7–11 protein stability5,12–14 and perhaps even the origin of life.15 Ion channels that regulate mammalian nervous and cardiovascular systems, as well as metabolic pathways, are ion-specific.16–18 Ion identities play a consequential role in influencing rates of chemical reactions,19 the strengths of acids and bases,20 and even more complex chemical phenomena such as polymer morphology,21–23 metal–organic framework self-assembly,24,25 formation of room temperature ionic liquids26 and other areas of supramolecular chemistry.27 SIEs also have tangible impacts on everyday society, via agriculture,28 energy technologies,29,30 and even by influencing natural geophysical phenomena such as erosion31,32 and the stability of ocean foam33 and glaciers.34,35
Despite their ubiquity and importance, no reliable theory exists for quantitatively predicting SIEs, although progress is being made.2,36–44 Furthermore, alterations or even reversals in SIEs have been observed by changing the solute,45 solvent,46 pH,47 temperature,48 counterion49 or concentration.50 The fact that Hofmeister's original SIE series is so widely and persistently observed, however, suggests that it arises from some as-yet unidentified intrinsic property of ions themselves.51 Several candidates have been explored in this respect,2,52 and while many ion properties correlate well with SIE trends for some ions, there are just as many exceptions, particularly for polyatomic ions (Fig. S1–S4†). It is therefore unclear which correlations are genuine, and which are merely coincidental. For example, while ion polarisability and size have previously been correlated with SIEs,10,40,53 they fail to account for the effects of polyatomic or anisotropic ions such as nitrate (NO3−) and acetate (CH3COO−). SIE trends for anisotropic anions correlate with their Lewis strengths,54 but since the Lewis strength itself is an empirical parameter it cannot be considered an intrinsic ion property.
Results and discussion
Aqueous anion interactions
We consider SIEs from the point of view of fundamental Coulombic interactions. As argued in several reviews,5,40,55 Coulombic interactions will likely dominate interactions between ions and their solvent environment. Quantum chemical calculations also corroborate this hypothesis for anions in water (Fig. S5–S10†), using multiple energy decomposition schemes.56 For molecular ions, these interactions will predominantly arise from the individual atom(s) with the highest charge density, i.e., the ion's ‘active site’ (Fig. 1). Recalling the Coulombic potential arising from two point charges q1 and q2 interacting across a distance R in a vacuum, UE(q,r) = q1q2/(4πε0R), we approximate the electrostatic interaction between an ion's active site atom and its immediate solvent environment via its radial charge density (in units of C m−1),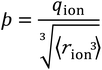 | (1) |
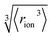 .
.
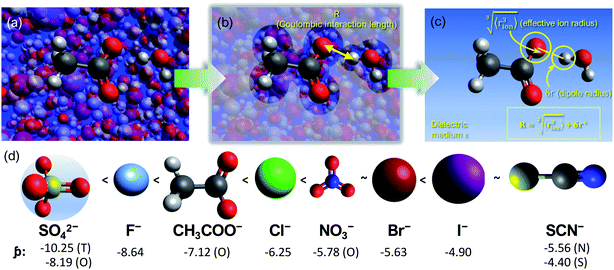 | ||
| Fig. 1 (a) Coulombic interactions in a bulk electrolyte solution are (b) collectively approximated via a single ion–solvent interaction at a length of R. (c) This length is approximated as the sum of the solvent dipole radius and the effective radius of the ion's charge site (the atom(s) which have the highest charge density). The radial charge density, ϸ, is then calculated according to eqn (1). (d) Example ϸ values in C m−1 are shown for common Hofmeister anions. For SO42−, both the site-specific oxygen (O) and molecular (T) ϸ values are shown, and for SCN−, both the S and N values are given. Further details on this provided in the ESI Text and Fig. S13.† | ||
The formulation of the electrostatic parameter ϸ (“sho”) is depicted for anions in Fig. 1 and is based on the following logic: anions interact with neighbouring solvent molecules via the solvent's positive dipole(s). If the positive dipole of the solvent is located on an atom with radius δr+, then 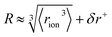 . Since the solvent's positive dipole will almost always reside on a hydrogen atom in a molecular solvent, δr+ will be effectively constant and small (despite dynamic behaviour, δr+ will ultimately average toward a constant value). The Coulombic interaction between the anion's active site and its immediate solvent environment is therefore simply proportional to its partial charge and effective radius, that is,
. Since the solvent's positive dipole will almost always reside on a hydrogen atom in a molecular solvent, δr+ will be effectively constant and small (despite dynamic behaviour, δr+ will ultimately average toward a constant value). The Coulombic interaction between the anion's active site and its immediate solvent environment is therefore simply proportional to its partial charge and effective radius, that is, 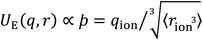 , (see Fig. S22† for a direct comparison). We calculate ϸ here via a first-principles charge decomposition scheme57,58 and list ϸ values for common atomic and polyatomic ions in Table S2.† For a molecular anion, ϸ quantifies our previous hypothesis that SIEs arise from site-specific interactions between the anion and its immediate solvent/solute environment.54§
, (see Fig. S22† for a direct comparison). We calculate ϸ here via a first-principles charge decomposition scheme57,58 and list ϸ values for common atomic and polyatomic ions in Table S2.† For a molecular anion, ϸ quantifies our previous hypothesis that SIEs arise from site-specific interactions between the anion and its immediate solvent/solute environment.54§
The value of our hypothesis and the ϸ parameter, outlined in Fig. 1, is demonstrated via the correlation between anion ϸ values and properties of aqueous electrolyte solutions, shown in Fig. 2. There is broad agreement between the descriptor ϸ for more than 15 anions and trends in wide-ranging SIE phenomena, including water specific interactions in the absence of co-solutes, viscosity B and diffusion coefficients, colloidal stability, chemical reaction rates and the relative activities of viruses and enzymes.¶
 | ||
| Fig. 2 SIE trends correlate widely with the anion–solvent coulombic interaction, as measured by the descriptor ϸ. (a) Specific ion–water interaction energies calculated from first principles. (b) Experimental enthalpies of hydration per coordinating water molecule59 (see also Fig. S14†). (c) Viscosity-B coefficients59 of electrolyte solutions per coordinating water molecule (see also Fig. S14†). (d) Diffusion coefficients of ions in water.59 (e) Gibbs energies of ion transfer from water to methanol.59 (f) ΔLCST of pNIPAM-coated silica particles in 1 M electrolyte solutions.60 (g) SN2 reaction rate of iodomethane and ionic nucleophiles in methanol.19 (h) Activity of a human rhinovirus.9 (i) Temperature dependence of the cloud point of lysozyme.10 Halide anions (○) include F−, Cl−, Br− and I−; isotropic polyatomic anions (×) include ClO4− and PF6−; anisotropic polyatomic anions include CH3COO−, SCN−, NO3−, N3−, H2PO4−, HSO4−, CN−, (purple ×), isotropic polyvalent anions include SO42−, PO43− (+), anisotropic polyvalent anions include S2O32−, CO32−, HPO42−, SO32− (grey +). Trendlines displayed are for all ions; R-squared values are for halides only. All data in (b–i) have a common counter-cation, quantum chemical data in (a) do not have a counter-cation. UE version in Fig. S30.† Datasets provided in ESI.† A database of ϸ values for anion is provided in Table S1.† | ||
For instance, the interaction energy between a hydrated ion and a solvating water molecule (Fig. 2a) and its enthalpy of hydration|| (Fig. 2b) both correlate remarkably well with ϸ, indicating that trends in anion interactions with water are dominated by electrostatics. The viscosity of a liquid is its resistance to applied shear, such as a foreign body pushing through the solution, and this resistance arises from the intermolecular forces within the liquid bulk. Viscosity generally increases upon the addition of a salt, indicated by positive viscosity B-coefficients (Fig. 2c), as the addition of ion–solvent interactions interspersed throughout the solution generally increases these average bulk intermolecular interactions. This change in the solution's viscosity B-coefficient¶ is strongly correlated to the descriptor ϸ. Ions' diffusion coefficients in water (Fig. 2d) have similar molecular origins to viscosity. Whereas viscosity B-coefficients are a measure of the strengthening or weakening of the average bulk solution intermolecular interactions to resist shear, diffusion coefficients measure how well the ions (and their complexed structures) can overcome these intermolecular interaction, deform the solvent structure and move through the solution. This results in a weaker correlation with ϸ, but the overall trend persists. Ions' Gibbs energies of transfer from water to methanol59 (Fig. 2e) are ion specific and quantitatively described by ϸ. Notably, ϸ reliably predicts the behaviour of anisotropic ions such as the acetate anion (CH3COO−), indicating that interactions between the solvent and ions are predominantly Coulombic and strongly site-specific. In the case of the acetate anion, weaker dispersion interactions between the hydrophobic methyl tail and the solvent are negligible by comparison. This trend is observed for many other nonaqueous solvents (Fig. S15–S17†). The stability of temperature-responsive polymers in solution can be controlled via the presence of dissolved salts. For instance, the LCST, or lower critical solution temperature (the temperature below which a polymer is miscible) of the polymer poly(N-isopropyl)acrylamide (pNIPAM) drops in concentrated aqueous electrolyte solutions.60Fig. 2f demonstrates that ϸ predicts the magnitude of this change for a range of different anions. Other temperature-responsive polymers exhibit similar correlations (Fig. S18†).
Fig. 2g–i show that the electrostatic nature of SIEs extends to chemical reactions in aqueous solution. This is shown for the archetypal Menshutkin SN2 reaction in Fig. 2g, for which the reaction rate is proportional to the nucleophile's ϸ value. This is attributed to the fact that, in order to react, a solvent/substrate exchange at the anion must take place, and this requires the momentary partial desolvation of the nucleophilic anion. There is a clear trend here for the monatomic nucleophiles Cl−, Br− and I−. Anisotropic anions (CH3COO−, N3−, SCN− and CN−) exhibit deviation from this clear trend, as anticipated on the basis of collision theory; anisotropic ions will only collide with the solvated reactant with the correct orientation a fraction of the time (see Fig. S19† for a more complete treatment of this point). Chemical reactivity in significantly more complex systems, such as virus and enzyme activity, also shows a strong correlation with ϸ, demonstrated here by the relative activities of human rhinovirus-14 (HRV-14) 3C protease9 (Fig. 2g) and lysozyme10 (Fig. 2h) respectively, (further examples are provided in Fig. S20†). This correlation demonstrates that these SIEs are principally determined by short-range Coulombic interactions associated with the dissolved anions present in solution, despite the mechanistic complexities of enzyme inhibition and/or activation, which can occur via direct competition for the binding site or changes in the virus/enzyme structure, due to allosteric binding.
Anion interactions in non-aqueous solvents
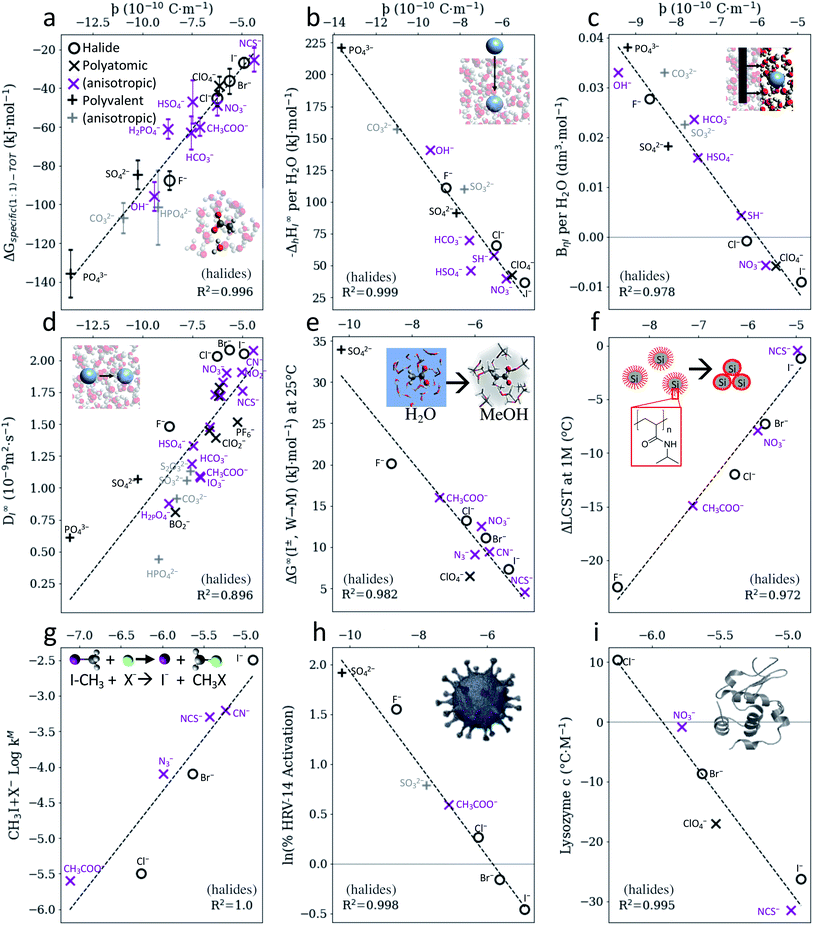
Fig. 2 indicates that, for anions, SIEs ultimately originate from specific electrostatic interactions between ions and their immediate environment. However, the parameter ϸ assumes these specific interactions to occur via positive dipoles on the solvent molecules, which are almost always located on a hydrogen atom. It follows then that similar correlations to those shown in Fig. 2 for water should also exist in non-aqueous solvents, as SIE have been shown to arise ubiquitously across a broad range of non-aqueous solvents.46,51,61 That is, correlations between anion SIEs and ϸ should be solvent independent, up to a scaling factor. Fig. 3 shows that this is indeed the case; the correlation between the anions' ϸ values and their Gibbs energies of transfer between water and methanol (Fig. 2b) is also observed in 18 other non-aqueous solvents (Fig. 3a and S15–S17†). Fig. 3b shows further that these correlations are themselves proportional to the solvent acceptor number (AN),62 which is an empirical measure of a solvent's ability to solvate anions (i.e., its Lewis acidity). This correlation persists even in an aprotic, non-aqueous solvent such as acetonitrile (Fig. S16g†), where the solvent dielectric has little meaning due to solvent ordering.63,64 The electrostatic origins of anion SIEs are therefore strong, quantified via the parameter ϸ, and general in nature. The magnitude of a SIE caused by a specific anion is, however, modulated via the solvent environment according to the solvent's Lewis acidity. In this respect, Fig. 3b shows that protic and aprotic solvents constitute two distinct solvent classes; for a given anion, aprotic solvents consistently yield larger Gibbs energies of transfer than protic solvents. For strong protic environments (i.e., gradients ∼0, Fig. 3b), competition between the two solvents for the anion largely mitigate its electrostatic preference for either solvent. In these cases, series variations and reversals may be more commonly observed; indeed, Fig. 3 shows that solvents with sufficiently high acceptor numbers (nearing 54.8, that of water) can induce a series reversal with respect to the radial charge density ϸ. Similar reversals are shown in Fig. S21† for bimolecular SN2 reaction rates.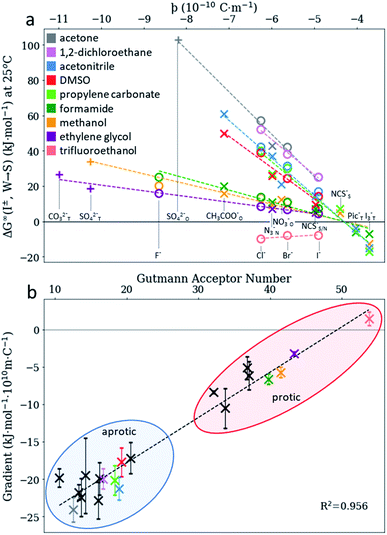 | ||
| Fig. 3 (a) Gibbs energies of transfer for anions59 between water and non-aqueous solvents can be quantified via the radial charge density parameter ϸ. (b) The magnitude of this specific anion effect (as measured by the gradients in (a)) is proportional to the solvent's Lewis acidity, as measured via the Gutmann acceptor number.62 SIE trends for anions therefore arise fundamentally from electrostatic interactions; the magnitude of the effect is modulated by the solvent's Lewis acidity. Note the Gutmann acceptor number of water is 54.8. | ||
Cation interactions
In a solvated environment, cations will interact with solvent molecules predominantly with the solvent's negative dipole, for example, water's oxygen atom. Quantum chemical calculations (Fig. S7, S9 and S10†) also indicate that cation–water interactions are primarily driven by electrostatics. The length of this Coulombic interaction can be approximated as above, i.e.,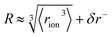 . The negative solvent dipole radius, δr−, will be larger than the positive solvent dipole radius, δr+, considered previously (considering the relative atomic radii of oxygen (or nitrogen) and hydrogen). Nonetheless, ϸ should reveal trends within a cationic family (Fig. S22†). This hypothesis is supported in Fig. 4a, which shows a strong correlation between ϸ and the interaction energy between a dissolved cation and its solvent, as well as in Fig. 4b and c, which shows the enthalpy of solvation and viscosity B-coefficients of cations, albeit each with distinct mono- and divalent cation trends. A more complete electrostatic analysis is necessary here (Fig. S31a–c and S32†).
. The negative solvent dipole radius, δr−, will be larger than the positive solvent dipole radius, δr+, considered previously (considering the relative atomic radii of oxygen (or nitrogen) and hydrogen). Nonetheless, ϸ should reveal trends within a cationic family (Fig. S22†). This hypothesis is supported in Fig. 4a, which shows a strong correlation between ϸ and the interaction energy between a dissolved cation and its solvent, as well as in Fig. 4b and c, which shows the enthalpy of solvation and viscosity B-coefficients of cations, albeit each with distinct mono- and divalent cation trends. A more complete electrostatic analysis is necessary here (Fig. S31a–c and S32†).
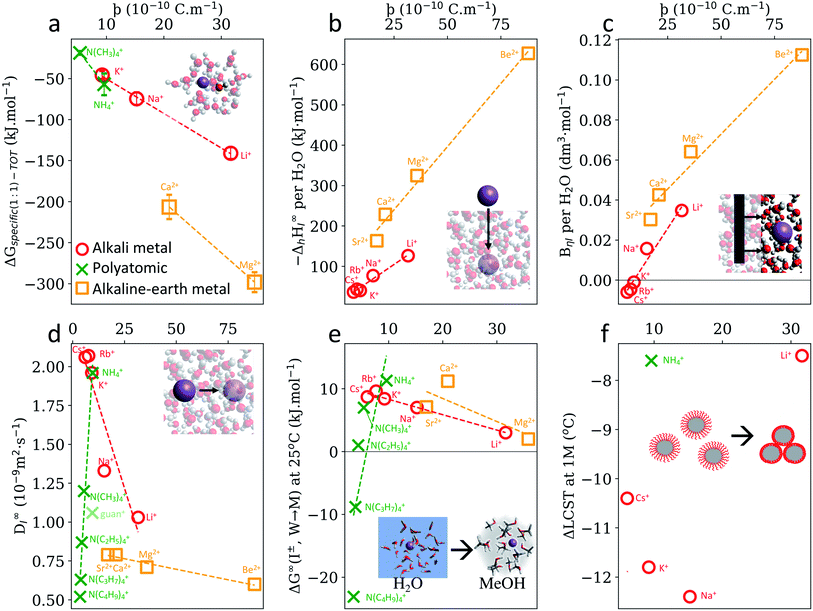 | ||
| Fig. 4 SIE trends for cations do not always arise from cation–solvent Coulombic interaction, as measured by the descriptor ϸ. (a) Specific ion–water interactions calculated from first-principles. (b) Experimental enthalpies of hydration per coordinating water molecule.59 (c) Viscosity B-coefficients59 of electrolyte solutions per coordinating water molecule (see also Fig. S11b†). (d) Diffusion coefficients of ions in water.59 Gibbs free energies of ion transfer from water to methanol.59 (f) ΔLCST of pNIPAM-coated silica particles in 1 M electrolyte solutions.60 Monovalent alkali metal cations (red circles) include Li+, Na+, K+, Rb+ and Cs+; polyatomic cations include NH4+, N(CH3)4+, N(C2H5)4+, N(C3H7)4+, N(C4H9)4+ (green cross) and guanidinium+ (light green cross); monatomic divalent alkaline earth metals include Be2+, Mg2+, Ca2+, Sr2+, Ba2+ (orange squares) and each set of data displayed has a common (or no) anion. UE version in Fig. S31.† A full list of cation ϸ values is provided in Table S31.† | ||
Perhaps more interesting, however, are the instances where SIE trends are not quantified by ϸ or UE, such as cation diffusion coefficients (Fig. 4d), Gibbs energies of transfer (Fig. 4e) and ΔLCST of pNIPAM-coated silica particles (Fig. 4f.) Each have distinct mono-, divalent and polyatomic trends with respect to ϸ. In these cases, specific ion phenomena cannot be attributed principally to Coulombic interactions, and this reveals a seemingly fundamental asymmetry between how anions and cations interact in solution. That is, SIE induced by anions can primarily be attributed to ion–solvent coulombic interactions, whereas SIE induced by cations cannot. Molecular cations such as ammonium, tert-alkyl ammonium and guanidinium, are notable in this respect. Guanidinium has previously been identified as having a unique behaviour due to its asymmetry, local hydration structure,65 cross-linking mechanisms66 and ability to utilise bidentate binding.67Fig. 4(d and e) show that both the dynamic and equilibrium behaviour of the isotropic ammonium cations in aqueous solution departs from the Coulombic behaviour established for other ions. Indeed, diffusion coefficients and Gibbs energies of transfer for these molecular cations are inversely proportional to the cation–solvent Coulombic interactions, as measured by ϸ, as the charge becomes increasingly shielded by bulky hydrophobic alkyl chains. Instead, dispersion interactions between these chains and their solvent environment are the predominant interactions causing these physicochemical phenomena (Fig. S11†). This is not surprising, considering the larger effective surface area and larger degree of configurational entropy afforded by the extended alkyl chains in these cations, and is also consistent with prior studies.40,68 Similar effects are observed in tetraphenylborate anions (Table S1†), and indeed, Gibbs free energies of transfer for hydrophobic cations and anions are highly correlated (Fig. S12† and accompanying discussion). Further to this point, previous studies40,68,69 and symmetry adapted perturbation theory calculations performed here (Fig. S10†) show a distinct difference between the dispersion dependence on the hydration energy for anions and cations, even for monatomic ions. More specifically, for anions, dispersion is proportional to the overall interaction energy and charge-independent, whilst it is inversely proportional for cations and distinctly dependent on the chemical structure and charge. In situations where a cation has comparable electrostatic interactions with two different species (e.g. water and methanol), dispersion could conceivably determine which species the ion preferentially interacts with. This competition potentially explains the non-linear trends observed in Fig. 4d–f and 3d–f, which consider only the electrostatic contribution. Induction, or polarisation, of the solvent and solute molecules in the vicinity of dissolved cations is also significant in this respect, particularly for non-aqueous solvents and solutes that are more polarisable than water. This also relates to the degree of covalency in these interactions. Direct energy decompositions of cation–solvent interactions (Fig. S9 and S10†), indicate that induction correlates well with the total interaction energy, and hence with ϸ (anions) and UE (cations). This is even evident in the interaction between ions and an isolated Kr atom – considered as an extreme limiting case in Fig. S26.† Induction for Kr appears to increase more rapidly with charge for cations than anions.
The contributions of each intermolecular force observed for cation–water and anion–water interactions (Fig. S10†) will be expected to vary for non-aqueous solvents. However, for anions the same overall trend is still observed across different solvents. For instance, Gibbs free energies of transfer of anions from water to non-aqueous solvents correlate linearly with ϸ irrespective of the solvent in question (Fig. 3a and S15–S17†). On the other hand, Gibbs free energies of transfer for cations exhibit non-linear correlations with ϸ that are distinct for each solvent (Fig. S23–S25†). It is conceivable that this arises from the fact that essentially any molecular solvent will interact with an anion via a hydrogen atom, whereas solvent–cation interactions potentially occur via a multitude of different elements (e.g. O (e.g. water, methanol etc.), N (e.g. acetonitrile), S (e.g. DMSO), Si, (e.g. tetramethylsilane), F, Cl (e.g. alkylhalides), P (phosphines), etc.). The relative Lewis acidity/basicity of a solvent, as measured by the Gutmann acceptor/donor number, is an additional factor here. For instance, water's Gutmann acceptor number is higher than any other solvent considered here (Fig. 3b). It is therefore reasonable to expect that, in general, the anion–water interaction dominates other interactions, leading to a singular anion series. On the other hand, water's Gutmann donor number is mid-range with respect to the solvents investigated here (see ESI†) and becomes less influential as cations become less charge dense (Fig. S27–S29†). Thus, it is more likely that cation–solvent Coulombic and induction interactions will respectively be similar in magnitude for different solvents, causing cation series to be more prone to reversals and deviations due to other factors such as dispersion. This idea of competing or preferential interactions is in line with our previous work,54 and whilst shown here with respect to different solvents in terms of Gibbs energies of transfer, the same rationale could be applied more generally regarding solute functional groups. It has been suggested that ion-pairing, which is concentration dependent (and ion specific70), is crucial to the net salt SIE, where the cations might mitigate some of the anionic salting out effects.71 Considering these complexities in cation interactions, perhaps it is unsurprising that SIEs, and trends in SIEs, for cations are more susceptible to nuance, are less predictable than their anion counterparts and more difficult to understand.
Conclusions
Despite the fundamental importance of specific ion effects (SIEs) across the sciences, consensus regarding their fundamental origins has proved elusive for more than a century. We have presented a meta-analysis of ion–solvent Coulomb interactions that shows SIEs on fundamental electrolyte properties, dynamic behaviour and chemical reactivity fundamentally arise from the specific Coulomb interactions between the anion and its surrounding environment, for both aqueous and non-aqueous solvents. For anions, this specific interaction can be quantified via a simple radial charge density descriptor ϸ, and its magnitude modulated via the solvent's Lewis acidity. When an anion is in the presence of a cosolute or cosolvent of similar Lewis acidity to the solvent, the electrostatic dominance is quenched sufficiently to supress the standard Hofmeister series of SIE trends. Furthermore, these competitive solvent/solute interactions for the ion account for observed reversal. On the other hand, specific ion phenomena caused by cations correlate more weakly with ϸ and UE (if at all). Instead, other fundamental interactions between cations and the solvent, notably dispersion, compete with Coulombic interactions. Consequently, cation SIEs are fundamentally less pronounced than anion SIEs, and far more susceptible to variation and reversal. This is particularly the case in aqueous solutions, where the Gutmann donor number of water makes it a moderate Lewis base compared with other common solvents (whereas it is a stronger Lewis acid than most in this respect). These results reveal a fundamental asymmetry in the manner by which cations and anions interact with their solvent environments and provide a new general basis for understanding and predicting SIE in aqueous and non-aqueous electrolyte solutions. They may indeed indicate the possibility for non-aqueous based abiogenesis.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Kasimir P. Gregory: conceptualisation, methodology, software, validation, formal analysis, investigation, data curation, manuscript preparation. Erica J. Wanless: conceptualisation, manuscript review & editing, supervision, project administration, funding acquisition. Grant B. Webber: conceptualisation, manuscript review & editing, supervision, project administration, funding acquisition. Vincent S. J. Craig: conceptualisation, manuscript review & editing, funding acquisition. Alister J. Page: conceptualisation, methodology, software, resources, manuscript review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. J. P., G. B. W., V. S. J. C. and E. J. W. acknowledge Australian Research Council funding (ARC DP190100788, LE170100032 (INTERSECT)). K. P. G. acknowledges an Australian Government Research Training Program (RTP) Scholarship. This research was undertaken with the assistance of resources provided at the NCI National Facility systems at the Australian National University, through the National Computational Merit Allocation Scheme supported by the Australian Government. The authors thank Gareth Elliot, Edwin Johnson, and Hayden Robertson (University of Newcastle) for useful discussions.Notes and references
- P. Lo Nostro and B. W. Ninham, Chem. Rev., 2012, 112, 2286 CrossRef CAS PubMed.
- Specific Ion Effects, ed. W. Kunz, World Scientific, 2010 Search PubMed.
- Q. Ye, G. L. Heck and J. A. DeSimone, Science, 1991, 254, 724–726 CrossRef CAS PubMed.
- M. Hayashi, T. Unemoto and M. Hayashi, Biochim. Biophys. Acta, Enzymol., 1973, 315, 83–93 CrossRef CAS.
- E. M. Wright and J. M. Diamond, Physiol. Rev., 1977, 57, 109–156 CrossRef CAS PubMed.
- A. Somasundar, S. Ghosh, F. Mohajerani, L. N. Massenburg, T. Yang, P. S. Cremer, D. Velegol and A. Sen, Nat. Nanotechnol., 2019, 14, 1129–1134 CrossRef CAS PubMed.
- J. C. Warren and S. G. Cheatum, Biochemistry, 1966, 5, 1702–1707 CrossRef CAS PubMed.
- M. G. Cacace, E. M. Landau and J. J. Ramsden, Q. Rev. Biophys., 1997, 30, 241 CrossRef CAS PubMed.
- Q. M. Wang and R. B. Johnson, Virology, 2001, 280, 80–86 CrossRef CAS PubMed.
- Y. Zhang and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15249–15253 CrossRef CAS PubMed.
- C. Carucci, F. Raccis, A. Salis and E. Magner, Phys. Chem. Chem. Phys., 2020, 22, 6749–6754 RSC.
- W. Kunz, J. Henle and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37 CrossRef CAS.
- R. L. Baldwin, Biophys. J., 1996, 71, 2056 CrossRef CAS PubMed.
- W. Yao, K. Wang, A. Wu, W. F. Reed and B. C. Gibb, Chem. Sci., 2021, 12, 320–330 RSC.
- B. C. Gibb, Nat. Chem., 2018, 10, 797–798 CrossRef CAS PubMed.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, in Molecular Biology of the Cell, Garland Science, 4th edn, 2002 Search PubMed.
- M. I. Chaudhari and S. B. Rempe, J. Chem. Phys., 2018, 148, 222831 CrossRef PubMed.
- P. A. Gurnev, T. C. Roark, H. I. Petrache, A. J. Sodt and S. M. Bezrukov, Angew. Chem., Int. Ed., 2017, 56, 3506–3509 CrossRef CAS PubMed.
- R. Alexander, E. C. F. Ko, A. J. Parker and T. J. Broxton, J. Am. Chem. Soc., 1968, 90, 5049–5069 CrossRef CAS.
- A. Blackman and L. R. Gahan, Aylward and Findlay's SI chemical data, John Wiley & Sons, 2014 Search PubMed.
- T. J. Murdoch, B. A. Humphreys, E. C. Johnson, G. B. Webber and E. J. Wanless, J. Colloid Interface Sci., 2018, 526, 429–450 CrossRef CAS PubMed.
- S. Z. Moghaddam and E. Thormann, J. Colloid Interface Sci., 2019, 555, 615–635 CrossRef CAS PubMed.
- M. Hua, S. Wu, Y. Ma, Y. Zhao, Z. Chen, I. Frenkel, J. Strzalka, H. Zhou, X. Zhu and X. He, Nature, 2021, 590, 594–599 CrossRef CAS PubMed.
- K. Li, J. Yang and J. Gu, Chem. Sci., 2019, 10, 5743–5748 RSC.
- K. Li, J. Yang, R. Huang, S. Lin and J. Gu, Angew. Chem., Int. Ed., 2020, 59, 14124–14128 CrossRef CAS PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- P. S. Cremer, A. H. Flood, B. C. Gibb and D. L. Mobley, Nat. Chem., 2018, 10, 8–16 CrossRef CAS PubMed.
- A. Läuchi and E. Epstein, Calif. Agric., 1984, 38, 18–20 Search PubMed.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC.
- A. Eftekhari, J. Power Sources, 2004, 126, 221–228 CrossRef CAS.
- W. Ding, X. Liu, F. Hu, H. Zhu, Y. Luo, S. Li and H. Li, J. Hydrol., 2019, 568, 492–500 CrossRef CAS.
- S. Li, H. Li, F. N. Hu, X. R. Huang, D. T. Xie and J. P. Ni, Eur. J. Soil Sci., 2015, 66, 921–929 CrossRef CAS.
- V. S. J. Craig, B. W. Ninham and R. M. Pashley, Nature, 1993, 364, 317–319 CrossRef CAS.
- S. Wu, C. Zhu, Z. He, H. Xue, Q. Fan, Y. Song, J. S. Francisco, X. C. Zeng and J. Wang, Nat. Commun., 2017, 8, 15154 CrossRef PubMed.
- A. A. Zavitsas, Chem.–Eur. J., 2010, 16, 5942–5960 CrossRef CAS PubMed.
- T. Zemb, L. Belloni, M. Dubois, A. Aroti and E. Leontidis, Curr. Opin. Colloid Interface Sci., 2004, 9, 74–80 CrossRef CAS.
- B. W. Ninham, T. T. Duignan and D. F. Parsons, Curr. Opin. Colloid Interface Sci., 2011, 16, 612–617 CrossRef CAS.
- A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC.
- R. Tian, G. Yang, H. Li, X. Gao, X. Liu, H. Zhu and Y. Tang, Phys. Chem. Chem. Phys., 2014, 16, 8828–8836 RSC.
- T. P. Pollard and T. L. Beck, Curr. Opin. Colloid Interface Sci., 2016, 23, 110–118 CrossRef CAS.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS PubMed.
- B. Kang, H. Tang, Z. Zhao and S. Song, Hofmeister Series: Insights of Ion Specificity from Amphiphilic Assembly and Interface Property, American Chemical Society, 2020, vol. 5 Search PubMed.
- M. Peng, T. T. Duignan and A. V. Nguyen, Langmuir, 2020, 36, 13012–13022 CrossRef CAS PubMed.
- T. T. Duignan, S. M. Kathmann, G. K. Schenter and C. J. Mundy, Acc. Chem. Res., 2021, 54, 2833–2843 CrossRef CAS PubMed.
- N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2010, 26, 7370 CrossRef CAS PubMed.
- V. Mazzini, G. Liu and V. S. J. Craig, J. Chem. Phys., 2018, 148, 222805 CrossRef PubMed.
- M. Boström, F. W. Tavares, S. Finet, F. Skouri-Panet, A. Tardieu and B. W. Ninham, Biophys. Chem., 2005, 117, 217–224 CrossRef PubMed.
- M. Senske, D. Constantinescu-Aruxandei, M. Havenith, C. Herrmann, H. Weingärtner and S. Ebbinghaus, Phys. Chem. Chem. Phys., 2016, 18, 29698–29708 RSC.
- W. J. Xie and Y. Q. Gao, J. Phys. Chem. Lett., 2013, 4, 4247 CrossRef CAS PubMed.
- M. Boström, D. F. Parsons, A. Salis, B. W. Ninham and M. Monduzzi, Langmuir, 2011, 27, 9504–9511 CrossRef PubMed.
- V. Mazzini and V. S. J. Craig, Chem. Sci., 2017, 8, 7052–7065 RSC.
- K. D. Collins and M. W. Washabaugh, Q. Rev. Biophys., 1985, 18, 323 CrossRef CAS PubMed.
- K. Garajová, A. Balogová, E. Dušeková, D. Sedláková, E. Sedlák and R. Varhač, Biochim. Biophys. Acta, Proteins Proteomics, 2017, 1865, 281–288 CrossRef PubMed.
- K. P. Gregory, G. B. Webber, E. J. Wanless and A. J. Page, J. Phys. Chem. A, 2019, 123, 6420–6429 CrossRef CAS PubMed.
- J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 153–163 CAS.
- O. A. Stasyuk, R. Sedlak, C. Fonseca Guerra and P. Hobza, J. Chem. Theory Comput., 2018, 14, 3440–3450 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC.
- Y. Marcus, Ions in Solution and their Solvation, John Wiley & Sons, 2015 Search PubMed.
- B. A. Humphreys, E. J. Wanless and G. B. Webber, J. Colloid Interface Sci., 2018, 516, 153–161 CrossRef CAS PubMed.
- V. Mazzini and V. S. J. Craig, ACS Cent. Sci., 2018, 4, 1056–1064 CrossRef CAS PubMed.
- U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257 CrossRef CAS.
- A. Stoppa, A. Nazet, R. Buchner, A. Thoman and M. Walther, J. Mol. Liq., 2015, 212, 963–968 CrossRef CAS.
- V. A. Koverga, O. M. Korsun, O. N. Kalugin, B. A. Marekha and A. Idrissi, J. Mol. Liq., 2017, 233, 251–261 CrossRef CAS.
- S. Heiles, R. J. Cooper, M. J. DiTucci and E. R. Williams, Chem. Sci., 2015, 6, 3420–3429 RSC.
- J. Heyda, H. I. Okur, J. Hladilkova, K. B. Rembert, W. Hunn, J. Dzubiella, P. Jungwirth, P. S. Cremer and T. Yang, J. Am. Chem. Soc., 2017, 139, 863 CrossRef CAS PubMed.
- V. Balos, B. Marekha, C. Malm, M. Wagner, Y. Nagata, M. Bonn and J. Hunger, Angew. Chem., Int. Ed., 2019, 58, 332–337 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, J. Phys. Chem. B, 2013, 117, 9412–9420 CrossRef CAS PubMed.
- T. T. Duignan, D. F. Parsons and B. W. Ninham, Chem. Phys. Lett., 2014, 608, 55–59 CrossRef CAS.
- S. J. Hawkes, J. Chem. Educ., 1996, 73, 421 CrossRef CAS.
- E. E. Bruce, H. I. Okur, S. Stegmaier, C. I. Drexler, B. A. Rogers, N. F. A. van der Vegt, S. Roke and P. S. Cremer, J. Am. Chem. Soc., 2020, 142, 19094–19100 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Methods, shielded ions, ϸ vs. polarisability for lysozyme, ion parameters vs. pNIPAM and Gibbs energy of transfer SIE series, GKS-EDA partitioning specific ion–solvent interactions from a cluster model, ion–water GKS-EDA comparison with Lewis strength index, Lewis strength index comparison with the radial charge density (ϸ), SAPT energy analysis, dispersion analysis, visualisation of ϸ, Coordination number adjustment analysis, anion Gibbs energy of transfer from water to non-aqueous solvents, thermoresponsive polymeric systems, SN2 reactions and effective surface area, biological SIEs, bimolecular SN2 reactions in aqueous and non-aqueous solvents, ϸ and electrostatic potential energy relationship, cation Gibbs energy of transfer from water to non-aqueous solvents, induced dipole on inert gas, donor number analysis for cation Gibbs energy of transfer from water to non-aqueous solvents, electrostatic potential energy analysis, DDEC6 theory analysis, anion parameters, cation parameters (PDF), data for ϸ values for many common Hofmeister anions and cations, data contained in figures, example computational input and output files (zip). See DOI: 10.1039/d1sc03568a |
‡ We approximate the radius of the ion's active site atom here as 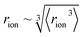 . rion is thus similar to the radial moment 〈rion〉 of a spherical electron density centred on the active site atom's nucleus (see ESI†). However, . rion is thus similar to the radial moment 〈rion〉 of a spherical electron density centred on the active site atom's nucleus (see ESI†). However, 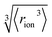 weights the density arising from valence shell electrons to give a more reliable description of the radius compared to rion itself and is not excessively skewed by Rydberg-like electrons that may occur for higher order radial moments. weights the density arising from valence shell electrons to give a more reliable description of the radius compared to rion itself and is not excessively skewed by Rydberg-like electrons that may occur for higher order radial moments. |
| § Complete details of this method, including computational details, are provided in ESI,† as are additional considerations for polyatomic ions, such as the use of atom-centred or molecular ϸ values (i.e., for SO42− the molecular value is higher), asymmetry (i.e., SCN− has a higher charge density at N, but higher charge at S according to DDEC6 calculations, so the sulfur end has stronger long range interactions) or when the charge centre is shielded (i.e., tetraphenyl salts (Fig. S11†) and tertiary-alkyl ammonium cations correlate with dispersion (Fig. S12†) or polarizability (Fig. S23–S25†)). |
| ¶ Experimental data in Fig. 2 and 4 generally used a Na+ or K+ counter-cation (Fig. 2) and a Cl− counter-anion (Fig. 4) to ensure for strong and approximately constant dissociation for each electrolyte, or have been made independent of the counterion through quantum chemical calculations, or extra-thermodynamic assumptions. Measurements were chosen at a constant concentration, or are terms that are reported per unit concentration (i.e., mol−1), and use water or methanol as the solvent. Except for the correlations that involve a temperature change, experimental data is at room temperature. |
|| These values are adjusted based on the ion's coordination number of water molecules (Fig. S14†), such that it is effectively a measure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ion–water interaction. 1 ion–water interaction. |
| This journal is © The Royal Society of Chemistry 2021 |
