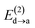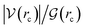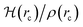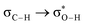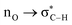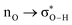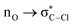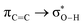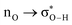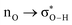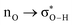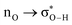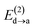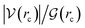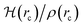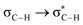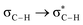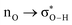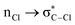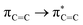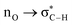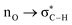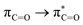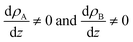Open Access Article
Open Access ArticleA molecular twist on hydrophobicity†
Sara
Gómez
 *a,
Natalia
Rojas-Valencia
*a,
Natalia
Rojas-Valencia
 bc,
Santiago A.
Gómez
bc,
Santiago A.
Gómez
 b,
Chiara
Cappelli
b,
Chiara
Cappelli
 a,
Gabriel
Merino
a,
Gabriel
Merino
 *d and
Albeiro
Restrepo
*d and
Albeiro
Restrepo
 *b
*b
aScuola Normale Superiore, Classe di Scienze, Piazza dei Cavalieri 7, 56126, Pisa, Italy. E-mail: sara.gomezmaya@sns.it
bInstituto de Química, Universidad de Antioquia UdeA, Calle 70 No. 52-21, Medellín, Colombia. E-mail: albeiro.restrepo@udea.edu.co
cEscuela de Ciencias y Humanidades, Departamento de Ciencias Básicas, Universidad Eafit, AA 3300, Medellín, Colombia
dDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados, Unidad Mérida. Km 6 Antigua Carretera a Progreso. Apdo. Postal 73, Cordemex, 97310, Mérida, Yucatan, Mexico. E-mail: gmerino@cinvestav.mx
First published on 15th June 2021
Abstract
A thorough exploration of the molecular basis for hydrophobicity with a comprehensive set of theoretical tools and an extensive set of organic solvent S/water binary systems is discussed in this work. Without a single exception, regardless of the nature or structure of S, all quantum descriptors of bonding yield stabilizing S⋯water interactions, therefore, there is no evidence of repulsion and thus no reason for etymological hydrophobicity at the molecular level. Our results provide molecular insight behind the exclusion of S molecules by water, customarily invoked to explain phase separation and the formation of interfaces, in favor of a complex interplay between entropic, enthalpic, and dynamic factors. S⋯water interfaces are not just thin films separating the two phases; instead, they are non-isotropic regions with density gradients for each component whose macroscopic stability is provided by a large number of very weak dihydrogen contacts. We offer a definition of interface as the region in which the density of the components in the A/B binary system is not constant. At a fundamental level, our results contribute to better current understanding of hydrophobicity.
1 Introduction
Hydrophobicity, a key concept in chemistry, is defined by IUPAC1 as “the association of non-polar groups or molecules in an aqueous environment which arises from the tendency of water to exclude non-polar molecules”. IUPAC also defines hydrophobic interactions as “The tendency of hydrocarbons (or of lipophilic hydrocarbon-like groups in solutes) to form intermolecular aggregates in an aqueous medium, and analogous intramolecular interactions. The name arises from the attribution of the phenomenon to the apparent repulsion between water and hydrocarbons. However, the phenomenon ought to be attributed to the effect of the hydrocarbon-like groups on the water–water interaction”. Except for the “apparent repulsion between water and hydrocarbons”, in situ discarded as the source of hydrophobicity, both definitions depart from the etymological meaning of the word, literally the fear of water, focusing instead on water⋯water, water⋯hydrophobe, and hydrophobe⋯hydrophobe interactions. This seems a sensible approach since substances that are entirely insoluble in water cannot be found in any source. To our knowledge, the lowest solubility is 0.28 μmol Hg per liter of water2 (clearly not zero); thus, the very concept of etymological hydrophobicity is questionable.The implications of hydrophobicity (as defined by IUPAC) on structural chemistry and biology are well understood. Since most biomolecules are ambiphilic, there is a complex interplay between hydrophobicity and hydrophilicity in determining protein structure and function.3 It is thought, for example, that despite the very weak nature of water⋯hydrophobe contacts, their vast numbers outweigh contributions from stronger interactions in the final overall structure of biomolecules in physiological environments.4,5 Furthermore, a popular view of the microscopic structure of water/hydrophobe mixtures calls for the formation of water cavities enclosing non-polar molecules3,6,7 even though a high entropy investment, which is compensated by a net entropy gain produced by the liberation of solvating water molecules into the environment.8,9 In his seminal review, Chandler10 offers a more thoughtful perspective for larger hydrophobes: “But the extreme view that pictures hydrophobic solvation in terms of rigid clathrate structures, like those surrounding hydrophobic particles in gas hydrates, is clearly incorrect: intermolecular correlations in liquid matter are insufficiently strong to be consistent with this crystalline picture. And while remnants of clathrate structure persist in the liquid near a small hydrophobic particle,11 a surrounding clathrate structure is geometrically implausible in the case of extended hydrophobic surfaces”.
It has long been recognized that hydrophobicity is an extremely hard theoretical problem,12 which has originated a number of sound statistical models with little attention to explicit quantum interactions, that have evolved over time into the current view,10,13–23 cemented in the Lum–Chandler–Weeks theory.24 In this view, hydrophobicity is a complex multicausal phenomenon, which is best explained based on the effects that a particular hydrophobe has on the surrounding hydrogen bonding network among water molecules, as envisioned by Stillinger half a century ago.25 These effects are dictated mostly by molecular size and shape of the hydrophobes,26–29 temperature and external conditions, and the nature of intermolecular interactions. In this context, molecular size, shape, and the length scale of interactions are directly related to hydrophobicity and phase separation because it is argued that unlike small solutes, large molecules have a chaotropic effect in the local hydrogen bonding network of the surrounding liquid by breaking the weak water⋯water contacts, inducing the freed water molecules to migrate to the bulk of the liquid, where those interactions are restored, effectively forming an interface around the hydrophobe. Intermolecular interactions are also quite relevant because in the current view, not repulsion, but only tiny stabilization energies are at play when hydrophobes interact with water at the molecular level.3,4,7,25,30,31 Appropriately, in this context, statements of this sort “Of all factors driving intermolecular interactions, the hydrophobic effect is the most often cited. At the same time, it is the least understood”,6 or “In spite of the enormous experimental and modeling efforts, many microscopic aspects related to the nature of forces and action mechanism are still not well understood”3 are a commonplace in the scientific literature. Finally, temperature and pressure confer a highly dynamic character to binary S/water mixtures, thus, energetic interfacial costs decrease while hydrophobic forces increase with increasing temperatures.
Despite all that is known about hydrophobicity and the hydrophobic effect, much remains obscure in the crucial problem of understanding, at a fundamental level, the nature of the intermolecular forces involved in the very weak structure determining water⋯hydrophobe and hydrophobe⋯hydrophobe interactions. For example, it has been pointed out that “water interactions with aliphatic chains are puzzling due to their inability to form hydrogen bonding or favorable electrostatic interaction”.7 This argument ignores the contributions from secondary hydrogen interactions (those where the proton in the HB comes from a C–H bond),32–41 and more specifically, it overlooks stabilizing orbital interactions.42–45 Recognizing present limitations, the same authors stated in a recent work3 “there have been no significant efforts in using modern quantum chemical methods to derive plausible forces from a true ab initio procedure”. Herein, we address this specific issue and offer an in-depth study of the nature of the delicate stabilizing interactions using Natural Bond Orbitals (NBO46–49), the Quantum Theory of Atoms in Molecules (QTAIM50–53), and Non-Covalent Interactions (NCI54–56) methods, analysis tools firmly rooted in the formalism of quantum mechanics. Our aim is to better our fundamental understanding of hydrophobicity and its questionable etymological origin by uncovering the molecular reasons driving this phenomenon.
2 Methods
How can hydrophobicity be quantified? Strictly speaking, etymological hydrophobicity should mean solubility = 0 and miscibility = 0, but, as stated above, this is never the case. An indirect measure of hydrophobicity is the partition coefficient, which measures relative affinity of a given substance towards two solvents, usually water and 1-octanol. Aldrich lists an extensive table of miscibilities for binary organic solvent/water mixtures.57 Within this list, a total of 20 solvents are marked (by an unspecified criterion) as water-immiscible. We selected those 20 solvents (Table 1), added 1-octanol (the organic solvent used to derive partition coefficients), address them collectively as solvents, or individually simply as S, and proceeded with the two separate approaches5,9,58–68 described in Section 1 of the ESI†. Because of space restrictions, in what follows, we will show explicit results for the S = heptane (HPT), benzene (BZN), cyclohexane (CYH), methyl ethyl ketone (MEK), diisopropylether (DPE), butyl acetate (BAC), carbon tetrachloride (CTC), 1-octanol (OTN) cases. This selection includes all kinds of functional groups as well as a representative sample of all polarities and solubilities within the systems studied in this work. Results for the extended list of solvents are listed in additional Tables available in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow),67 are also included. nS, nw are the numbers of organic solvent (S) and water molecules used during the MD runs. Temperatures in °C for the experimental densities are provided inside parentheses. It is the thickness of the interface (see Fig. 1). See text for the three letter code assigned to each S
Kow),67 are also included. nS, nw are the numbers of organic solvent (S) and water molecules used during the MD runs. Temperatures in °C for the experimental densities are provided inside parentheses. It is the thickness of the interface (see Fig. 1). See text for the three letter code assigned to each S
| S | MD conditions | Solubility (mg L−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow Kow |
Density (g cm−3) | I t (nm) | Minima | BEDLPNO-CCSD(T) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n S | n w | Experimental67 | MD | S⋯S | S⋯W | S⋯S | S⋯W | ||||
| HPT | 930 | 6916 | 3.40 | 4.66 | 0.67 (25) | 0.65 | 1.20 | 4 | 7 | 4.79 | 1.94 |
| CYH | 1000 | 8058 | 5.50 × 101 | 3.44 | 0.78 (20) | 0.76 | 1.48 | 2 | 4 | 2.93 | 1.68 |
| OTN | 819 | 6733 | 5.40 × 102 | 3.00 | 0.83 (25) | 0.82 | 1.40 | 2 | 7 | 9.05 | 1.94 |
| CTC | 1000 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 061 |
7.93 × 102 | 2.83 | 1.59 (20) | 1.56 | 1.44 | 1 | 3 | 4.73 | 2.39 |
| BZN | 1000 | 9244 | 1.79 × 103 | 2.13 | 0.88 (20) | 0.83 | 1.51 | 5 | 2 | 5.33 | 3.95 |
| BAC | 967 | 7124 | 8.33 × 103 | 1.78 | 0.88 (20) | 0.88 | 1.87 | 1 | 7 | 4.89 | 6.69 |
| DPE | 984 | 7217 | 8.80 × 103 | 1.52 | 0.72 (20) | 0.73 | 1.82 | 3 | 2 | 6.34 | 8.03 |
| MEK | 1000 | 9071 | 2.11 × 105 | 0.29 | 0.81 (20) | 0.67 | 3.60 | 7 | 3 | 7.62 | 6.50 |
3 Results and discussion
Table S1† lists the entire set of binary systems studied in this work in increasing order of solubility in water. Table 1 summarizes the chosen representative subset. The number of local minima in the PES for each dimer and the corresponding DLPNO-CCSD(T) binding energy are included. The number of water molecules (nw) and the number of molecules of the hydrophobe (nS) used in the MD runs are also included.3.1 MD simulations
Without exception, MD simulations for all binary systems considered here show equilibrated systems well before the 30 ns are consumed (see the videos of the corresponding trajectories provided in the ESI†). Fittingly, the solubility of S seems to correlate with the time needed for equilibration, thus, the higher the solubility, the longer equilibration time required. This observation is fully consistent with high diffusion rates for the least water-miscible organic solvent molecules which leads to earlier aggregation, a process that is considerably more difficult for stronger S⋯water explicit interactions. In fact, as a general rule, for low solubility cases, phase separation initiates as early as in the equilibration steps.A clear sign of the reliability of our results is the accurate reproduction of experimental densities for all S phases as shown in Table 1, Fig. 1, and the ESI† (Table S1 and Fig. S1), thus, it is evident that 30 ns MD simulations correctly describe bulk properties of the mixtures. The derivatives of the densities along the arbitrarily chosen z-axis are quite revealing and provide a formal way of defining the interface as that region where the derivatives of the densities along the reference axis are non-zero (solid vertical bars in Fig. 1). First, we point out that the crossing of density curves occurs at the corresponding inflexion points, that is, the crossing points mark the approximate coordinates for the maximum change in the densities. Second, it is clearly seen that S⋯water interfaces are not just thin films separating the two phases, instead, they appear to be complex, non-isotropic regions with density gradients in which the densities of the two components progressively approach the values for the isolated substances at their respective phases. Moreover, for the three most soluble solvents (n-butanol, ethyl acetate and methyl ethyl ketone), the density of S in the aqueous phase does not vanish, and the density of water in the organic phase does not vanish either (see for example the tails of the MEK plot in Fig. 1), clearly showing binary phases. Third, as seen in Fig. S2 of the ESI,† the thickness of the interface region (It, Tables 1 and S1†) is exponentially related to the solubility of S in water, with the most incompatible pairs showing narrower separations and larger deviations from the trend.
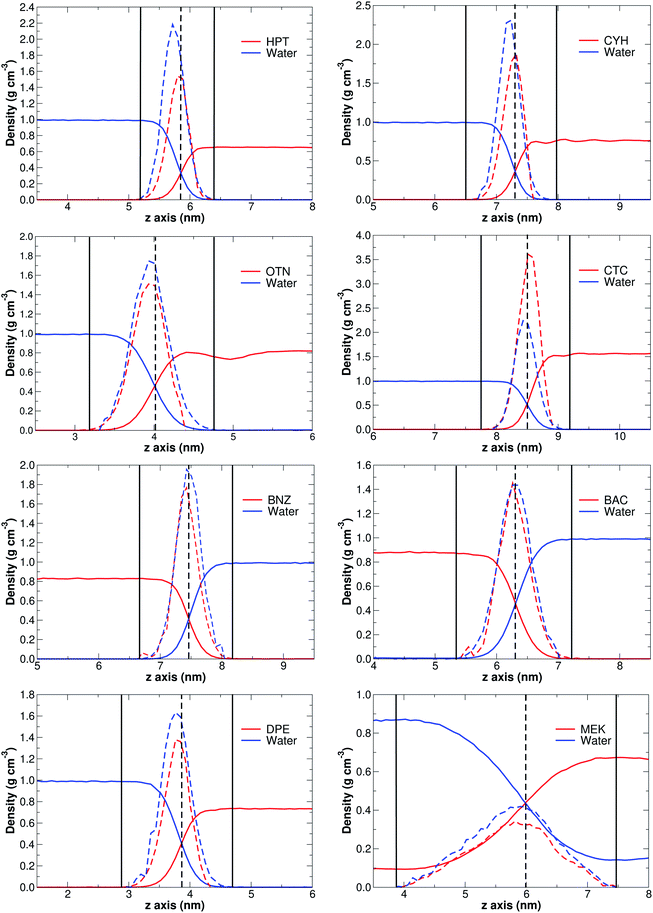 | ||
| Fig. 1 Densities (continuous lines) and derivatives of the densities (discontinuous lines) along the normal direction to the interface for the representative set of S. Vertical solid lines mark the boundaries of the interface. The complete set of plots is provided in Fig. S1 of the ESI.† | ||
The above discussed definition and structure of interfaces is also fully consistent with Gibbs' adsorption equation. A few reassuring points of our work are worth mentioning in the context of Gibbs' equation:
(1) The adsorption equation is an isotherm, thus, during its derivation the entropy −SdT term is eliminated from the free energy. Therefore, under this model, adsorption, or interface formation in our case, exclusively arise from the relative strength of intermolecular interactions and from chemical potentials.
(2) The density profiles in Fig. 1 and S1† provide essentially the same information as the density profiles in Fig. 5.2, page 139 of Rowlinson and Widom's book,69 which are traditionally obtained via numerical methods (finite differences) treatment of their eqn (5.35).
(3) We are providing in this work a straight forward method for obtaining these profiles from standard MD calculations once the system has reached equilibrium, but more importantly, we provide a method to obtain the derivatives of the densities, which are readily available, include the entropy contributions, and explicitly define the interfaces, which are only implicitly defined in the adsorption equation.
Heptane serves as a model for the study of hydrophobic interactions as currently defined by IUPAC.1 In fact, as discussed above, heptane/water phase separation is almost completed during the equilibration steps. Thus, in order to investigate the formation of intermolecular aggregates in the aqueous phase, we ran additional MD simulations under the same conditions as for all other systems using very dilute samples of heptane. For this purpose, we placed two heptane molecules at each corner and two more at the center of water-filled boxes and proceeded with the corresponding calculations (video available in the ESI†).
Even under this unfavorable dilute and long separation conditions, there seems to be little obstacle for the aggregation of the few heptane molecules. We rationalize this observation as follows: binding energies are (Tables 1 and 2) 5.60, 4.79, 1.94 kcal mol−1 for the W⋯W, HPT⋯HPT, and HPT⋯W dimers, respectively, thus, intermolecular interactions are highly favored for homomolecular dimers in this series. It is exciting to notice that the collective action of a number of very weak dispersive interactions (see NBO, QTAIM, NCI analysis below) lead to a strongly bound heptane dimer, which is as strongly bound as the water dimer. This result is consistent with increasing binding energies as a function of the number of carbon atoms in alkane chains, as reported by Tsuzuki and coworkers for the methane to decane series of dimers.70,71 These binding energies reveal that the collection of tiny interactions in the molecular regime is responsible for the boiling point of heptane (98.4 °C), which is quite close to the 100 °C boiling point of water at room conditions. The comparatively lower heteromolecular affinity confers heptane molecules a high diffusion coefficient in aqueous media, thus the short times needed for HPT⋯HPT encounters and aggregation, and for the ensuing phase separation.
The above results are significant in the interpretation of the hydrophobic effect: it appears that not much of “exclusion” (if literally taken as water ↔ S repulsions) of non-polar molecules from the aqueous phase is actually going on, rather, the hydrophobic effect results from a complex interplay between several factors: in a highly dynamic situation, aggregation of strongly interacting S molecules on one side and of water molecules on the other, play major roles. This role played on hydrophobicity by the attractive forces among solute molecules has been recognized before72 and is consistent with similar findings in MD simulations of aqueous Ar and methane interacting via Lennard-Jones potentials.21 In view of these observation, for the set of organic solvents studied here, enthalpic contributions to hydrophobicity (quantified below) should not be overlooked in favor of only entropic contributions (quantified in Section 2.1 of the ESI†). Furthermore, our results show that the diffusion of heptane molecules through the water-filled box is favored by the dissociation of the initial heptane dimers (which are not necessarily in an optimal configuration for the aqueous environment) and by internal rearrangement of HPT monomers, and is mediated by the formation of transient clathrates-like structures, that is, by the fast rearrangement of water molecules surrounding the heptane molecules as they diffuse on their way to finding other heptane molecules and forming larger aggregates. For more concentrated samples, this nucleation process continues until the aggregates reach critical sizes that confer the newly formed phases macroscopic stability.10
3.2 Non-covalent interactions at the interface
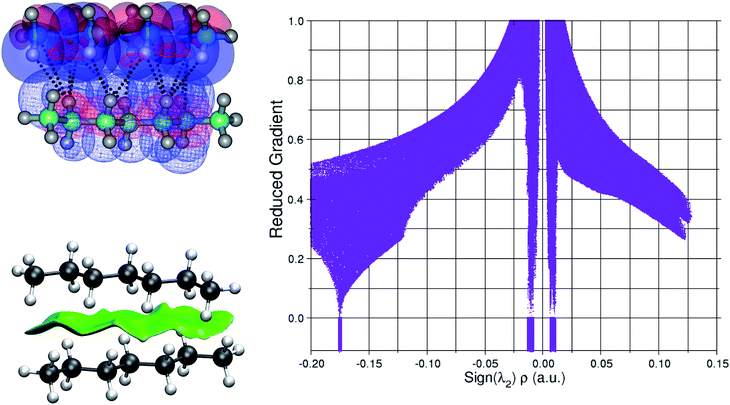
Our MD calculations correctly describe bulk properties of the mixtures, and, since quantum mechanics postulates that macroscopic properties are the statistical averages of microstates, it is appropriate to take snapshots of the MDs to analyze quantum interactions.5,63 Accordingly, Fig. 2 shows well defined large surfaces of attractive S⋯water non-covalent interactions for the representative subset (water⋯water and S⋯S interactions are not shown). NCI plots for the remaining pairs are available in Fig. S5 in the ESI.†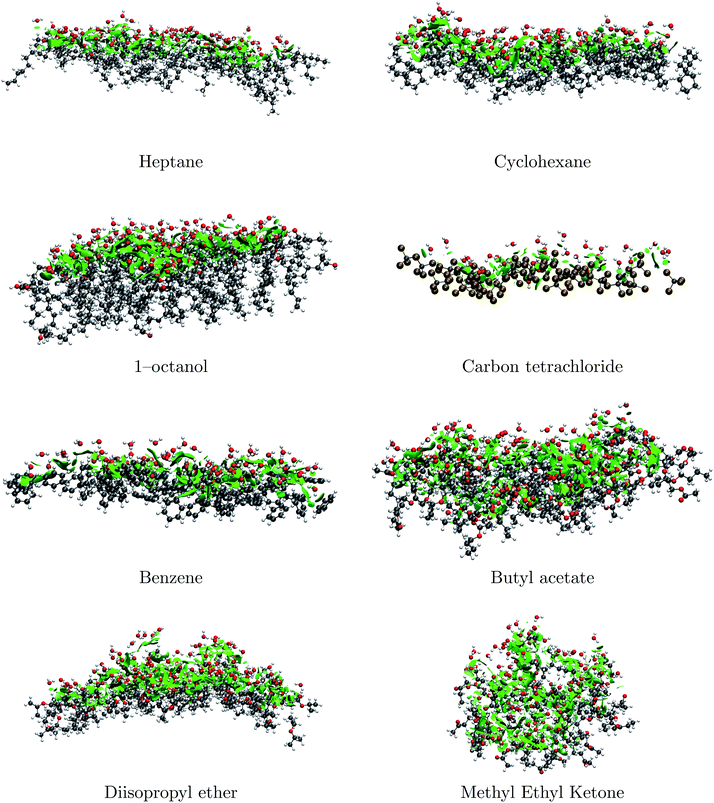 | ||
| Fig. 2 NCI surfaces at the S⋯water interfaces for the chosen subset. The complete set of plots is provided in Fig. S5 of the ESI.† | ||
The most important conclusion from these plots is that there are no hydrophobic repulsive interactions, thus, the enthalpic contribution to phase separation and the formation of the interfaces is always stabilizing. For pure hydrocarbons, the positioning of water molecules contrasts the tangential preference observed in the formation of clathrates,73 instead, O–H bonds seem to mostly be explicitly directed towards S molecules leading to the following interesting structural and energetic consequences: (i) for water molecules at the interface, water to water hydrogen bonding either to other water molecules at the interface or to water molecules at the bulk is energetically preferred over S⋯water interactions (ii) extremely weak dihydrogen contacts of the O–H⋯H–C type (not the expected O⋯H–C secondary hydrogen bonds) are the most common type of interaction at the interface! (iii) notwithstanding the very weak nature of individual dihydrogen contacts,74 it is the cumulative effect of a large number of interactions (precisely what is shown in Fig. 2) which provides macroscopic stability to the interfaces (iv) as expected, the interfaces for the least miscible S are better defined.
3.3 Dimers
The following analysis of S⋯S and S⋯water interactions is not an attempt to oversimplify the problem by reducing hydrophobicity to intermolecular interactions between isolated pairs of molecules. Rather, in an effort to understand the nature of intermolecular interactions and to offer a molecular perspective of hydrophobicity, we use the dimer approach, based in the following observation by Gao and coworkers21 referring to the Pratts and Chandler model:72 “The observed sensitivity of the hydrophobic interactions was attributed to a competition between the strengths of the solute–water and solute–solute attractive forces”. In this context, we point out that we make no inferences regarding macroscopic observations from isolated molecular pairs, instead, we emphasize that it is the collection of these interactions, as shown in the QTAIM, NBO, and (very clearly) in the NCI analysis, which leads to the observed exclusion of water molecules by the solute.As seen in Tables 1 and S1,† the potential energy surfaces for isolated S⋯S and S⋯water dimers are populated by large numbers of isomers. However, since the complexity of the PESs is not the focus of this work, due to a large number of structures, we only analyze the most representative interaction in the lowest energy structures for each case.
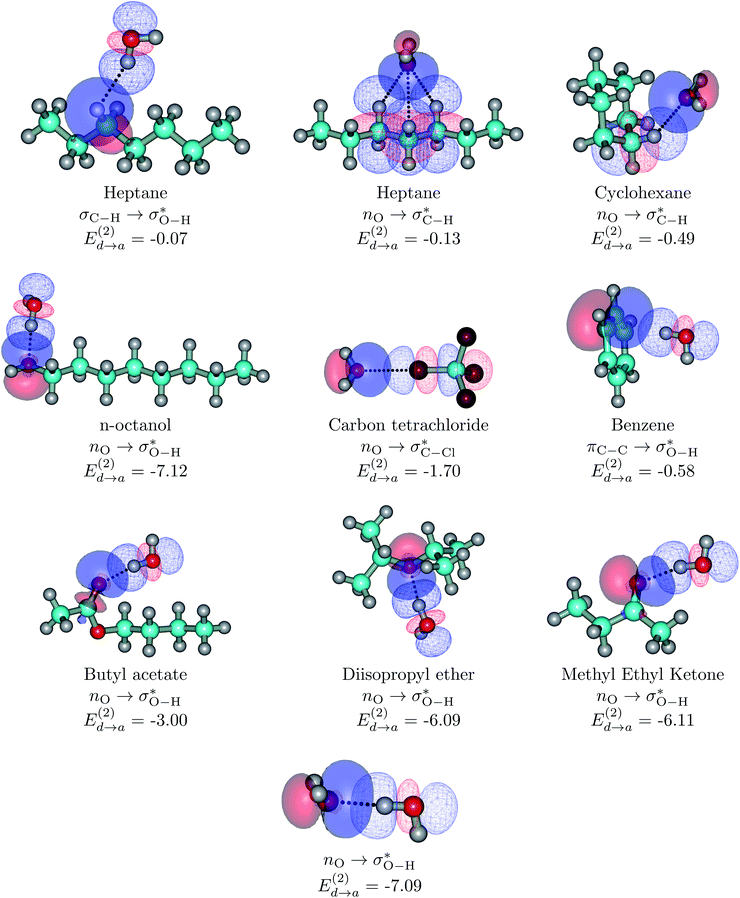 | ||
| Fig. 3 Dimers for the representative set of S⋯water pairs (orbital interactions for the entire set considered in this work are available in Fig. S6 of the ESI†). Explicit orbital interactions leading to the largest orbital interaction energies in kcal mol−1 are shown. Two configurations for HTP⋯water are shown: the configuration at the interface (top left) and the configuration of the minimum for the isolated dimer (second structure at the top row). The water dimer is included as a reference. Donor orbitals are shown as solid surfaces, acceptor orbitals are shown as line surfaces. All calculations are done on the MP2/6-311++G(d,p) minima. | ||
Without exception, all bonding descriptors reveal stabilizing interactions (Tables 2 and S2†), thus, even pure hydrocarbons are attracted to water and there are no reasons to think of molecular repulsion. All interactions are consistent with long-range stabilizing contacts in the form of primary (X–H⋯Y) and secondary (C–H⋯Y) hydrogen bonds, as well as dihydrogen (C–H⋯H–O) contacts, and interactions involving π clouds. From the NBO perspective, each orbital interaction fits one of the following donor → acceptor categories: n → σ*, n → π*, σ → σ*, π → π*, π → σ*. Note that in S⋯water dimers with the proper functional groups, despite QTAIM and NBO descriptors of bonding for X–H⋯Y primary hydrogen bonds revealing strong interactions, of the same order as in the water dimer, this molecular affinity does not necessarily translate into high miscibility because other aspects of the microscopic interactions, such as the size and shape of the non-polar regions, play significant roles in the properties of the bulk. The range of intermolecular interactions in the S⋯water dimers includes an interesting case of an antielectrostatic contact in the line of antielectrostatic hydrogen bonds:75 in H2O⋯Cl–CCl3, the two negative ends of the molecules are in direct contact via a 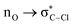 orbital interaction.
orbital interaction.
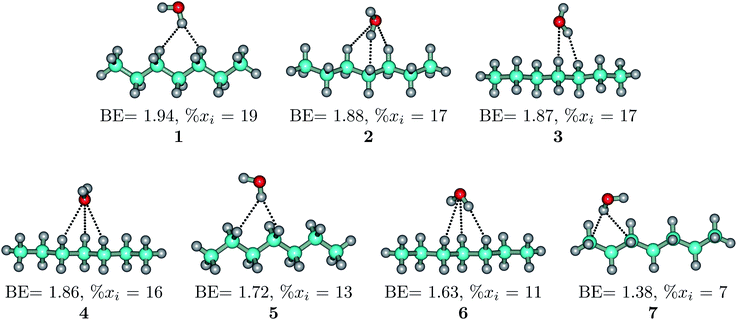
The heptane⋯water dimer may be taken as the archetypal system to study what a priori seems like an extreme case of hydrophobic (in the etymological sense) interaction. Indeed, the 1.20 nm thickness of the interface (Table 1) suggests one of the poorest interacting binary systems. Nonetheless, our stochastic search located seven well-defined minima with high populations shown in Fig. 4 with DLPNO-CCSD(T) binding energies ranging from 1.94 to 1.38 kcal mol−1. The donor → acceptor orbital interactions leading to the interface vs. isolated configurations of the heptane⋯water dimers are shown in Fig. 3. Orbital interaction energies in conjunction with QTAIM descriptors (Table 2) for all heptane⋯water contacts suggest long-range stabilizing interactions. Interestingly, these interactions are so small that the lowest energy minimum seems stabilized by two exotic bifurcated O–H⋯H–C dihydrogen contacts rather than by the still rare but more common H–O⋯H–C secondary hydrogen bonds present for example in dimer 2 (also notice how structurally close dimers 1 and 5 are). The richness of the heptane⋯water configurational space, the variety of explicit contacts, and the non-negligible stabilizing energies provide a picture far removed from the primitive electrostatic description of intermolecular interactions that plague general chemistry books.75
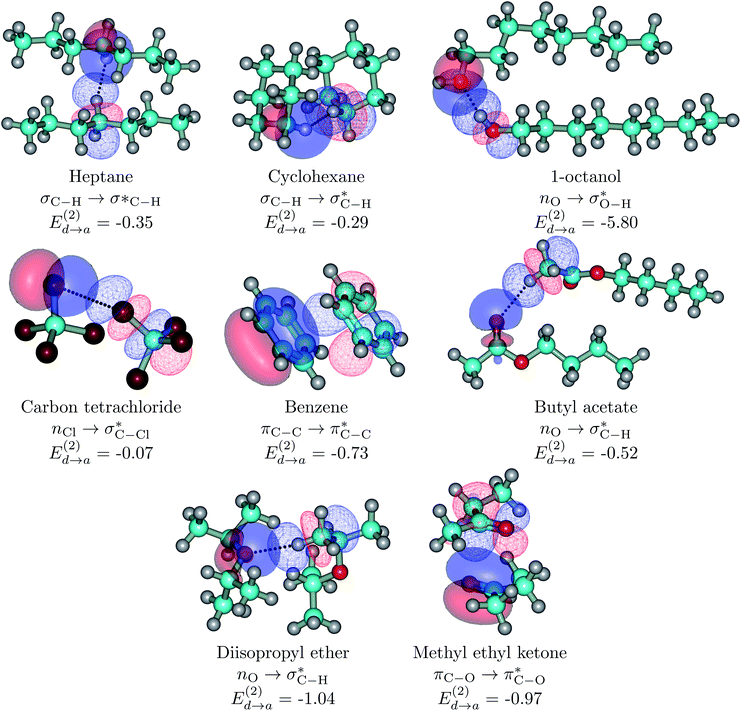 | ||
| Fig. 5 Dimers for the representative set of S⋯S pairs in this study (orbital interactions for the entire set listed in Tables 1 and S1† are available in Fig. S7 of the ESI†). Explicit orbital interactions leading to the largest orbital interaction energies (there are many more) in kcal mol−1 are shown. Donor orbitals are shown as solid surfaces, acceptor orbitals are shown as line surfaces. All calculations on the MP2/6-311++G(d,p) optimized global minima. | ||
As a general rule (except for the primary HBs in alcohols), orbital interaction energies and ρ(rc) at the BCPs associated to intermolecular interactions in the S⋯S dimers are sensibly smaller than in the S⋯water dimers. However, binding energies are of comparable magnitudes for both sets of dimers. This is a consequence of the cumulative effect of a large number of weak individual contacts in the non-polar regions which add up to yield large stabilization energies. This picture of a collective action of a multitude of individually weak intermolecular contacts provides a rationalization for the enthalpic contribution to solvent exclusion, phase separation, interface formation, and hydrophobicity: pure hydrocarbons and large S molecules have larger affinities towards each other than towards water molecules, water molecules also have larger affinities towards each other than towards S molecules (except for the ethers and butyl acetate), as a result S and water molecules aggregate separately rather than with each other. The only cases in which S⋯water binding energies are larger than for S⋯S are the three ethers, which cannot form the highly stabilizing ether⋯ether primary hydrogen bonds seen in ether⋯water.
Fig. 6 beautifully illustrates the cumulative stabilizing effect of a large number of weak interactions for the lowest energy heptane dimer (our stochastic search located four well-defined dimers, Table 1). According to NBO, there are 14 donor → acceptor interactions from molecule 1 to molecule 2, which duplicate from molecule 2 to molecule 1, thus, a total of 28 orbital interactions in (C7H16)2 are accounted for within the NBO threshold. The strongest intermolecular interaction is a C–H⋯H–C dihydrogen contact, affording E(2)d→a = −0.35 kcal mol−1 for the 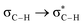 charge transfer, which is very small compared to the −7.09 kcal mol−1 associated to the
charge transfer, which is very small compared to the −7.09 kcal mol−1 associated to the 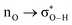 orbital interaction in the primary H2O⋯H–OH hydrogen bond in the water dimer. All other orbital interactions in the heptane dimer are considerably weaker, nonetheless, they add up to −3.57 kcal mol−1. This effect of a number of orbital interactions adding up to a large stabilization energy has also been reported for example in the microsolvation of monoatomic cations.76 The NCI surface of attractive non-covalent interactions provided in Fig. 6 is a consequence of all these orbital interactions and is responsible for the large binding energy of the heptane dimer (4.79 kcal mol−1, Tables 1 and 2) and of related alkanes.
orbital interaction in the primary H2O⋯H–OH hydrogen bond in the water dimer. All other orbital interactions in the heptane dimer are considerably weaker, nonetheless, they add up to −3.57 kcal mol−1. This effect of a number of orbital interactions adding up to a large stabilization energy has also been reported for example in the microsolvation of monoatomic cations.76 The NCI surface of attractive non-covalent interactions provided in Fig. 6 is a consequence of all these orbital interactions and is responsible for the large binding energy of the heptane dimer (4.79 kcal mol−1, Tables 1 and 2) and of related alkanes.
4 Summary and conclusions
A comprehensive set of theoretical tools including Molecular Dynamics simulations, stochastic (simulated annealing) explorations of complex energy landscapes, analytical optimization and characterization of molecular geometries, natural bond orbitals, quantum theory of atoms in molecules, and non-covalent interaction indices were used in this work to investigate hydrophobicity at the molecular level. Our subjects of study comprise binary systems between water and each one of 21 organic solvents (S) listed by Aldrich as immiscible with water. At a fundamental level, our results contribute to better current understanding of the questionable concept of etymological hydrophobicity.Our main findings may be summarized as follows:
(1) MD simulations accurately reproduce available experimental data for the bulk mixtures; thus, the quantum interactions are adequately treated.
(2) Without a single exception, all quantum descriptors of bonding yield stabilizing S⋯water interactions, so, there is no molecular reason for etymological hydrophobicity.
(3) IUPAC suggested exclusion of S molecules by water as the source of hydrophobicity, phase separation and the formation of interfaces results from a complex interplay between entropic (molecular organization, quantified in Section 2.1 of the ESI†), enthalpic (relative interaction strengths, quantified via NBO, QTAIM and NCIs plots), and dynamic (room conditions) factors.
(4) Extremely weak dihydrogen contacts of the O–H⋯H–C type, not the expected O⋯H–C secondary hydrogen bonds, are the most common type of interaction at the S⋯water interface.
(5) Notwithstanding the very weak nature of individual dihydrogen contacts, it is the cumulative effect of a large number of interactions which provides macroscopic stability to the interfaces.
(6) S⋯water interfaces are not just thin films separating the two phases, instead, they are complex, non-isotropic regions with density gradients for each component.
(7) We offer a rigorous definition of interface as the region in which the density of the components in the A, B binary system is not constant, or equivalently, in the region for which
(8) Pure hydrocarbon and large S molecules have larger affinities towards each other than towards water molecules. Water molecules also have larger affinities towards each other than towards S molecules (except for the ethers and for butyl acetate). Consequently, S and water molecules aggregate separately rather than with each other. These intermolecular interactions constitute a significant part of the enthalpic contribution to phase separation, which expose the relevance of solute⋯solute interactions to hydrophobicity.
Data availability
All our computational data is already included in the ESI and in the videos for the MD runs.Author contributions
Sara Gomez: conceptualization, methodology, data acquisition, curation and formal analysis, simulations, investigation. Natalia Rojas-Valencia: methodology, data acquisition, curation and formal analysis, simulations, investigation. Santiago A. Gomez: methodology, data acquisition, curation and formal analysis, simulations, investigation. Chiara Cappelli: conceptualization, formal analysis, funding acquisition, project administration, investigation. Gabriel Merino: conceptualization, formal analysis, project administration, investigation. Albeiro Restrepo: conceptualization, methodology, general supervision, funding acquisition, project administration, formal analysis. All authors equally contributed to the writing, review and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Partial financial support for this project from Universidad de Antioquia via “Estrategia para la sostenibilidad” is acknowledged. Partial funding for this project from H2020-MSCA-ITN-2017 European Training Network “Computational Spectroscopy In Natural sciences and Engineering” (COSINE), grant number 765739 is also acknowledged.References
- Compendium of Chemical Terminology, accessed: 2020-05-12, DOI: 10.1351/goldbook.
- S. Budavari, M. O'Neil, A. Smith, P. Heckelman and J. Kinneary, The Merck Index, An encyclopedia of chemicals, drugs and biologicals, Merck Research Laboratories Division of Merck & Co; Inc. Monograph, Whitehouse Station, NJ, 1996, vol. 4175 Search PubMed.
- G. Lanza and M. A. Chiacchio, The water molecule arrangement over the side chain of some aliphatic amino acids: A quantum chemical and bottom-up investigation, Int. J. Quantum Chem., 2020, 120, e26161 Search PubMed.
- V. Duarte Alaniz, T. Rocha-Rinza and G. Cuevas, Assessment of hydrophobic interactions and their contributions through the analysis of the methane dimer, J. Comput. Chem., 2015, 36, 361–375 Search PubMed.
- N. Rojas-Valencia, S. Gómez, S. Montillo, M. Manrique-Moreno, C. Cappelli, C. Hadad and A. Restrepo, Evolution of Bonding during the Insertion of Anionic Ibuprofen into Model Cell Membranes, J. Phys. Chem. B, 2020, 124, 79–90 Search PubMed.
- F. Biedermann, W. M. Nau and H.-J. Schneider, The Hydrophobic Effect Revisited–Studies with Supramolecular Complexes Imply High-Energy Water as a Noncovalent Driving Force, Angew. Chem., Int. Ed., 2014, 53, 11158–11171 Search PubMed.
- G. Lanza and M. A. Chiacchio, Quantum Mechanics Study on Hydrophilic and Hydrophobic Interactions in the Trivaline–Water System, J. Phys. Chem. B, 2018, 122, 4289–4298 Search PubMed , PMID: 29584432.
- C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, J. Wiley, 2nd edn, 1980 Search PubMed.
- N. Rojas-Valencia, I. Lans, M. Manrique-Moreno, C. Z. Hadad and A. Restrepo, Entropy drives the insertion of ibuprofen into model membranes, Phys. Chem. Chem. Phys., 2018, 20, 24869–24876 Search PubMed.
- D. Chandler, Interfaces and the driving force of hydrophobic assembly, Nature, 2005, 437, 640–647 Search PubMed.
- D. T. Bowron, A. Filipponi, M. A. Roberts and J. L. Finney, Hydrophobic Hydration and the Formation of a Clathrate Hydrate, Phys. Rev. Lett., 1998, 81, 4164–4167 Search PubMed.
- L. R. Pratt, Molecular Theory Of Hydrophobic Effects: She is too mean to have her name repeated, Annu. Rev. Phys. Chem., 2002, 53, 409–436 Search PubMed , PMID: 11972014.
- S. Garde and A. J. Patel, Unraveling the hydrophobic effect, one molecule at a time, Proc. Natl. Acad. Sci., 2011, 108, 16491–16492 Search PubMed.
- S. Vembanur, A. J. Patel, S. Sarupria and S. Garde, On the Thermodynamics and Kinetics of Hydrophobic Interactions at Interfaces, J. Phys. Chem. B, 2013, 117, 10261–10270 Search PubMed , PMID: 23906438.
- R. C. Remsing, E. Xi, S. Vembanur, S. Sharma, P. G. Debenedetti, S. Garde and A. J. Patel, Pathways to dewetting in hydrophobic confinement, Proc. Natl. Acad. Sci., 2015, 112, 8181–8186 Search PubMed.
- S. Vaikuntanathan, G. Rotskoff, A. Hudson and P. L. Geissler, Necessity of capillary modes in a minimal model of nanoscale hydrophobic solvation, Proc. Natl. Acad. Sci., 2016, 113, E2224–E2230 Search PubMed.
- D. M. Huang, P. L. Geissler and D. Chandler, Scaling of Hydrophobic Solvation Free Energies, J. Phys. Chem. B, 2001, 105, 6704–6709 Search PubMed.
- R. C. Remsing and J. D. Weeks, Dissecting Hydrophobic Hydration and Association, J. Phys. Chem. B, 2013, 117, 15479–15491 Search PubMed , PMID: 23944226.
- A. Gao, R. C. Remsing and J. D. Weeks, Short solvent model for ion correlations and hydrophobic association, Proc. Natl. Acad. Sci., 2020, 117, 1293–1302 Search PubMed.
- R. C. Remsing, S. Liu and J. D. Weeks, Long-ranged contributions to solvation free energies from theory and short-ranged models, Proc. Natl. Acad. Sci., 2016, 113, 2819–2826 Search PubMed.
- A. Gao, L. Tan, M. I. Chaudhari, D. Asthagiri, L. R. Pratt, S. B. Rempe and J. D. Weeks, Role of Solute Attractive Forces in the Atomic-Scale Theory of Hydrophobic Effects, J. Phys. Chem. B, 2018, 122, 6272–6276 Search PubMed , PMID: 29767526.
- J. D. Weeks, CONNECTING LOCAL STRUCTURE TO INTERFACE FORMATION: A Molecular Scale van der Waals Theory of Nonuniform Liquids, Annu. Rev. Phys. Chem., 2002, 53, 533–562 Search PubMed , PMID: 11972018.
- B. J. Berne, J. D. Weeks and R. Zhou, Dewetting and Hydrophobic Interaction in Physical and Biological Systems, Annu. Rev. Phys. Chem., 2009, 60, 85–103 Search PubMed , PMID: 18928403.
- K. Lum, D. Chandler and J. D. Weeks, Hydrophobicity at Small and Large Length Scales, J. Phys. Chem. B, 1999, 103, 4570–4577 Search PubMed.
- F. H. Stillinger, Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled-particle theory, J. Solution Chem., 1973, 2, 141–158 Search PubMed.
- L. R. Pratt and D. Chandler, Theory of the hydrophobic effect, J. Chem. Phys., 1977, 67, 3683–3704 Search PubMed.
- L. R. Pratt and D. Chandler, Hydrophobic solvation of nonspherical solutes, J. Chem. Phys., 1980, 73, 3430–3433 Search PubMed.
- L. R. Pratt and D. Chandler, Hydrophobic interactions and osmotic second virial coefficients for methanol in water, J. Solution Chem., 1980, 9, 1–17 Search PubMed.
- D. Chandler, Introduction to modern statistical mechanics, Oxford University Press, Oxford, UK, 1987; vol. 40, ch. 3, 5–7 Search PubMed.
- A. Stone, The Theory of Intermolecular Forces, Oxford University Press, New York, 1997 Search PubMed.
- I. G. Kaplan, The Theory of Intermolecular Forces, Wiley, West Sussex, 2006 Search PubMed.
- G. Gilli and P. Gilli, The nature of the hydrogen bond: outline of a comprehensive hydrogen bond theory, Oxford University Press, 2009, vol. 23 Search PubMed.
- S. M. Mejía, J. F. Espinal, A. Restrepo and F. Mondragón, Molecular Interaction of (Ethanol)2–Water Heterotrimers, J. Phys. Chem. A, 2007, 111, 8250–8256 Search PubMed , PMID: 17665885.
- C. Hadad, A. Restrepo, S. Jenkins, F. Ramírez and J. David, Hydrophobic meddling in small water clusters, Theor. Chem. Acc., 2013, 132, 1376 Search PubMed.
- J.-R. Salazar-Cano, A. Guevara-García, R. Vargas, A. Restrepo and J. Garza, Hydrogen bonds in methane–water clusters, Phys. Chem. Chem. Phys., 2016, 18, 23508–23515 Search PubMed.
- J. David, D. Guerra and A. Restrepo, Structural Characterization of the (Methanol)4 Potential Energy Surface, J. Phys. Chem. A, 2009, 113, 10167–10173 Search PubMed , PMID: 19711934.
- S. Gómez, D. Guerra, J. David and A. Restrepo, Structural characterization of the (MeSH) 4 potential energy surface, J. Mol. Model., 2013, 19, 2173–2181 Search PubMed.
- S. Gómez, A. Restrepo and C. Z. Hadad, Theoretical tools to distinguish O-ylides from O-ylidic complexes in carbene–solvent interactions, Phys. Chem. Chem. Phys., 2015, 17, 31917–31930 Search PubMed.
- N. Rojas-Valencia, C. Ibargüen and A. Restrepo, Molecular interactions in the microsolvation of dimethylphosphate, Chem. Phys. Lett., 2015, 635, 301–305 Search PubMed.
- P. Farfán, A. Echeverri, E. Diaz, J. D. Tapia, S. Gómez and A. Restrepo, Dimers of formic acid: Structures, stability, and double proton transfer, J. Chem. Phys., 2017, 147, 044312 Search PubMed.
- D. Guerra, L. A. Gómez, A. Restrepo and J. David, New stable phases of glycine crystals, Chem. Phys., 2020, 530, 110645 Search PubMed.
- A. E. Reed and F. Weinhold, Natural bond orbital analysis of near-Hartree–Fock water dimer, J. Chem. Phys., 1983, 78, 4066–4073 Search PubMed.
- E. Flórez, N. Acelas, F. Ramírez, C. Hadad and A. Restrepo, Microsolvation of F−, Phys. Chem. Chem. Phys., 2018, 20, 8909–8916 Search PubMed.
- E. Flórez, N. Acelas, C. Ibargüen, S. Mondal, J. L. Cabellos, G. Merino and A. Restrepo, Microsolvation of NO3−: structural exploration and bonding analysis, RSC Adv., 2016, 6, 71913–71923 Search PubMed.
- S. Gómez, J. Nafziger, A. Restrepo and A. Wasserman, Partition-DFT on the water dimer, J. Chem. Phys., 2017, 146, 074106 Search PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2018 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: New vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241 Search PubMed.
- F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, Wiley-VCH, Hoboken NJ, 2012, p. 319 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 Search PubMed.
- T. Keith, AIMALL (version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019, aim.tkgristmill.com Search PubMed.
- R. Bader, Atoms in Molecules: A Quantum Theory, Oxford Univ. press, Oxford, 1990 Search PubMed.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 Search PubMed.
- P. L. Popelier, Atoms in Molecules: An Introduction, Prentice Hall, London, 2000 Search PubMed.
- G. A. DiLabio and A. Otero-de-la Roza, Reviews in Computational Chemistry, John Wiley & Sons, Ltd, 2016, ch. 1, pp. 1–97 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, 2010, 132, 6498–6506.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, NCIPLOT: A Program for Plotting Noncovalent Interaction Regions, J. Chem. Theory Comput., 2011, 7, 625–632 Search PubMed.
- Merck KGaA, Darmstadt, Germany, accessed: 2020-04-30, https://www.sigmaaldrich.com/chemistry/solvents/solvent-miscibility-table.html.
- J. Pérez and A. Restrepo, ASCEC V02:Annealing Simulado con Energía Cuántica; Property, development, and implementation: Grupo de Química–Física Teórica, Instituto de Química, Universidad de Antioquia, Medellín, Colombia, 2008 Search PubMed.
- J. F. Pérez, C. Z. Hadad and A. Restrepo, Structural studies of the water tetramer, Int. J. Quantum Chem., 2008, 108, 1653–1659 Search PubMed.
- J. F. Pérez, E. Florez, C. Z. Hadad, P. Fuentealba and A. Restrepo, Stochastic Search of the Quantum Conformational Space of Small Lithium and Bimetallic Lithium–Sodium Clusters, J. Phys. Chem. A, 2008, 112, 5749–5755 Search PubMed.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 Search PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139, 134101 Search PubMed.
- S. A. Gomez, N. Rojas-Valencia, S. Gómez, F. Egidi, C. Cappelli and A. Restrepo, Binding of SARS-CoV-2 to cell receptors: a tale of molecular evolution, ChemBioChem, 2021, 22, 724–732 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25 Search PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- National Library of Medicine - National Institutes of Health, National Center for Biotechnology Information, Accessed: 2020-04-30, https://pubchem.ncbi.nlm.nih.gov/.
- S. Menon and N. Sengupta, Perturbations in inter-domain associations may trigger the onset of pathogenic transformations in PrPC: insights from atomistic simulations, Mol. BioSyst., 2015, 11, 1443–1453 Search PubMed.
- J. S. Rowlinson and B. Widom, Molecular theory of capillarity, Courier Corporation, 2013 Search PubMed.
- S. Tsuzuki, K. Honda, T. Uchimaru and M. Mikami, Magnitude of Interaction between n-Alkane Chains and Its Anisotropy: High-Level ab initio Calculations of n-Butane, n-Pentane, and n-Hexane Dimers, J. Phys. Chem. A, 2004, 108, 10311–10316 Search PubMed.
- S. Tsuzuki, K. Honda, T. Uchimaru and M. Mikami, Estimated MP2 and CCSD(T) interaction energies of n-alkane dimers at the basis set limit: Comparison of the methods of Helgaker et al. and Feller, J. Chem. Phys., 2006, 124, 114304 Search PubMed.
- L. R. Pratt and D. Chandler, Effects of solute-solvent attractive forces on hydrophobic correlations, J. Chem. Phys., 1980, 73, 3434–3441 Search PubMed.
- N. Acelas, E. Flórez, C. Hadad, G. Merino and A. Restrepo, A Comprehensive Picture of the Structures, Energies, and Bonding in [SO4(H2O)n]2−, n = 1–6, J. Phys. Chem. A, 2019, 123, 8650–8656 Search PubMed.
- D. Guerra, J. David and A. Restrepo, (H3N-BH3)4: the ammonia borane tetramer, Phys. Chem. Chem. Phys., 2012, 14, 14892–14897 Search PubMed.
- F. Weinhold and R. A. Klein, Anti-Electrostatic Hydrogen Bonds, Angew. Chem., Int. Ed., 2014, 53, 11214–11217 Search PubMed.
- N. Rojas-Valencia, S. Gómez, D. Guerra and A. Restrepo, A detailed look at the bonding interactions in the microsolvation of monoatomic cations, Phys. Chem. Chem. Phys., 2020, 22, 13049–13061 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized geometries for all S⋯S, S⋯water dimers. Cartesian coordinates for all interfaces. Plots for the variations of the densities along the normal direction to the interface, for the NCI surfaces, for the structures for all dimers in this work. A plot of the variation of the thickness of the interface as a function of the solubility of S. Videos for all MD runs. See DOI: 10.1039/d1sc02673a |
| This journal is © The Royal Society of Chemistry 2021 |