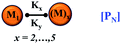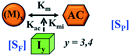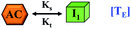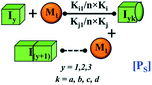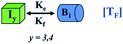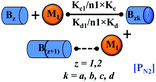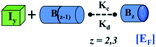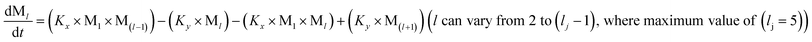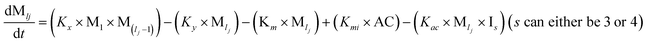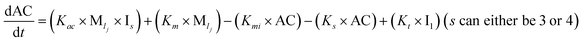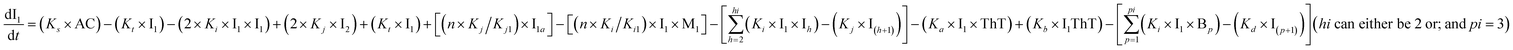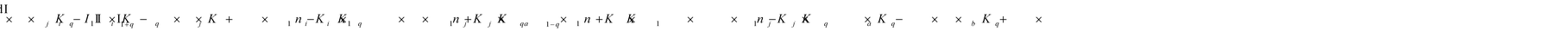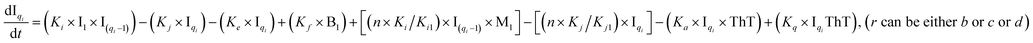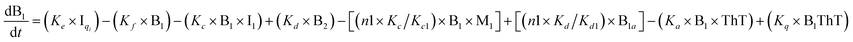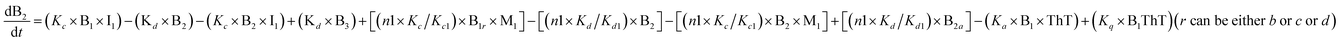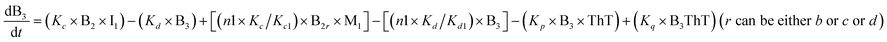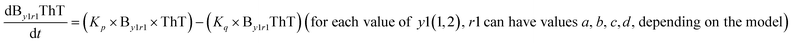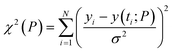Open Access Article
Open Access ArticleA generic approach to decipher the mechanistic pathway of heterogeneous protein aggregation kinetics†
Baishakhi
Tikader
a,
Samir K.
Maji
*b and
Sandip
Kar
 *a
*a
aDepartment of Chemistry, IIT Bombay, Powai, Mumbai – 400076, India. E-mail: sandipkar@iitb.ac.in
bDepartment of Biosciences and Bioengineering, IIT Bombay, Powai, Mumbai – 400076, India
First published on 3rd September 2021
Abstract
Amyloid formation is a generic property of many protein/polypeptide chains. A broad spectrum of proteins, despite having diversity in the inherent precursor sequence and heterogeneity present in the mechanism of aggregation produces a common cross β-spine structure that is often associated with several human diseases. However, a general modeling framework to interpret amyloid formation remains elusive. Herein, we propose a data-driven mathematical modeling approach that elucidates the most probable interaction network for the aggregation of a group of proteins (α-synuclein, Aβ42, Myb, and TTR proteins) by considering an ensemble set of network models, which include most of the mechanistic complexities and heterogeneities related to amyloidogenesis. The best-fitting model efficiently quantifies various timescales involved in the process of amyloidogenesis and explains the mechanistic basis of the monomer concentration dependency of amyloid-forming kinetics. Moreover, the present model reconciles several mutant studies and inhibitor experiments for the respective proteins, making experimentally feasible non-intuitive predictions, and provides further insights about how to fine-tune the various microscopic events related to amyloid formation kinetics. This might have an application to formulate better therapeutic measures in the future to counter unwanted amyloidogenesis. Importantly, the theoretical method used here is quite general and can be extended for any amyloid-forming protein.
Introduction
The existence of life is perfectly organized and controlled by the accurate functional efficiency of different types of proteins present within an organism.1,2 However, several peptides or proteins often fail to remain in their native functional state.3–5 This particular class of proteins under certain conditions produces thermodynamically stable aggregates, which are known as amyloid.6,7 Though some of these “amyloid” are called “functional amyloid” and are utilized to fabricate novel biomaterials for various application purposes,8,9 unfortunately, most of them are associated with a broad range of human diseases known as amyloidosis.10–19 Consequently, recent interest has been developed in this direction to find remedial measures to prevent these protein aggregation-related disorders by designing and developing novel drugs.11,20–22 However, designing a rational and effective therapeutic strategy to perfectly cure these diseases remains to be an open challenge in the field as these amyloid formation procedures are extremely complex, non-linear, heterogeneous, and in most cases experimentally intractable due to the transient nature of the intermediate structures.23 Therefore, a comprehensive and quantitative understanding of amyloidogenesis requires a general modelling approach, which can be further fine-tuned to control the dynamics of amyloid formation in a context-dependent manner.To analyse the aggregation mechanism successfully, one needs to identify all possible conformational states adopted by the polypeptide chain and the corresponding kinetic rates of the transitions among such states that eventually govern the temporal dynamics of the overall transformation.10 Experimentally, the characterizations of these transient oligomers are essential since some of these conformations are often found to be highly toxic, insoluble, and causative agent for deadly diseases.24,25 Thus, precise knowledge about the distribution of the population of these oligomeric species and identifying their interconversion rates during the aggregation process can be a crucial step forward to understand the pathogenesis of the protein deposition diseases holistically. In this regard, the mathematical modelling approach has emerged as an interesting tool to shed light on the different microscopic events happening at different time scales and dynamic features that are significant and insightful during the accumulation of amyloid.26–33
Previously, several experimental and theoretical studies have been put forward to disentangle various aspects of amyloid, but none of these studies have focused extensively on the internal kinetic progression of various oligomeric states, including structural reorganization-transition rate.34–36 Moreover, connecting these kinetic rates with each particular reaction event and an extension of this idea as a generic approach for a diverse range of proteins remains elusive in the literature. Additionally, in most of these models, the number of probable oligomers and the highest degree of the polymeric structure of any particular state, which is best compatible with the experimental data have mostly been assumed.28,37 An ODE-based mathematical model proposed by Pallitto & Murphy was extremely successful in delineating the different aspects of aggregation kinetics of Aβ42 protein along with estimating information about the filament/fibril length, which quantitatively corroborated with the experimental findings.30 However, the applicability of the proposed model was never examined for other proteins. Thus, it highlights the need for constructing a general modelling framework to elucidate the detailed mechanism of aggregation for various amyloid-forming proteins, which forms aggregates in diverse time scales.
Experimentally, it is a difficult task to track the entire kinetics of all molecular species that emerge during the process of fibrillation.24,38 Although the filamentous growth process varies from protein to protein, we must emphasize that most of these proteins pass through discrete elementary steps and ultimately reproduce a common structure by forming a linear, extended, unbranched filaments with a common cross-β backbone.39–41 Therefore, it can be speculated that a broad spectrum of proteins, despite having diversity in the interconversion mechanism may follow a common framework to produce amyloid fibril. Thus, it is imperative to develop a generic modelling strategy to understand the aggregation mechanism for a diverse range of proteins in a holistic manner.
A generic approach to model the self-assembly process of the protein by performing ensemble modelling
In this study, we intend to model the kinetics of the amyloid fibrillation mechanism in a general and simple way to understand the underlying mechanism of aggregation at the molecular level from a theoretical perspective. The structure of various proteins at the initial state (Fig. S1a†) and their corresponding three-dimensional structure of amyloid suggest that irrespective of having different structures and sequences, all these proteins form a cross-β spine (Fig. S1b†) sharing almost similar morphological characteristics.40 We have further schematically depicted how the disordered protein conformation converts to fibrillar state by passing the lag and growth phases (Fig. S1c†). A closer look into this observation reveals that various amino acid residues of a polypeptide chain can vary substantially for forming amyloid. However, in an amyloid state, the spacing, motif, and orientation may differ from one protein to another based on their sequence, side-chain orientation, and interactions with the solvent. The final structure of the amyloid state adopted by the polypeptide chain will be the most thermodynamically stable and accessible structure.23,42 Herein, we have employed a generic approach where we have included a combination of various possible intermediate structures and their subsequent conversion in the amyloid formation pathway by framing them into different probable canonical models (Fig. S2a–f†). The proposed model's (Fig. S2a–f†) have the common structural format as depicted in (Fig. 1), including the frequent presence of different states (such as random coil state, intermediate or fibril like aggregated states), which give rise to an almost identical canonical skeleton by systematically adding the conformational steps one by one for different states of the protein. Thereafter, each canonical set of models has been globally fitted with the available experimental kinetic data set for a specific protein by implementing specific statistical criteria to obtain the best-fitted model and the respective set of optimized kinetic parameters.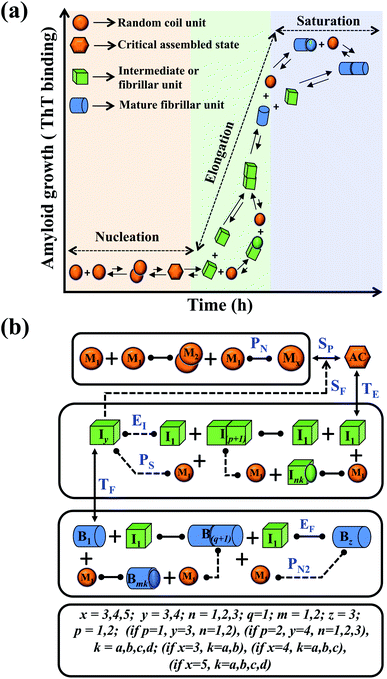 | ||
| Fig. 1 Principal steps of the protein aggregation that are involved in the proposed ensemble models for amyloid formation. (a) Schematic representation of various microscopic molecular mechanisms that are principally involved in different phases of the aggregation process of any amyloid-forming protein. (b) The proposed core interaction network consists of a different probable configurational variation of the intermediate species, which can be depleted in the amyloid formation process. The heterogeneity in different probable configurational states has been summarized here. Each distinct set of particular structures has been characterized by giving a different model name (Fig. S2a–f†). The various molecular entities involved in the generic model and all the molecular events associated with amyloid formation are described in (Table 1) for two different kinds of amyloid-forming proteins (for more details see ESI Section-3†). | ||
The model
We began constructing our model (Fig. 1) by simply considering the nucleation-dependent polymerization phenomena, which generally have three distinct phases (Fig. 1a): (1) the lag phase, where the protein gradually self-assembles to form aggregation competent nuclei for fibril growth, (2) elongation phase and (3) stationary phase.32,43–45For simplicity, in our model, we mostly consider the primary nucleation event in the lag phase and secondary nucleation in the growth phase following many previous studies, though recent studies have suggested that the lag phase is also composed of a significant contribution from the secondary nucleation process.43,46 At the beginning of the aggregation process, we have assumed that the protein in solution exists in its native structural state.47,48 The initial state of (M1) represents unstructured or structured monomer, which is the aggregation competent unit in our model. The first important key mechanism in the fibrillation process is the formation of the nucleus, where the monomer (M1) can self-assemble to form a dimer (M2), this dimer can further assemble with the monomer to form a trimer (M3) and the process can extend up to tetramer or pentamer (Mx, x = 1 to 5) in a highly reversible manner (Table 1).
Here, it is important to mention that in our model, the dimer/trimer/tetramer means the formation of any differently sized higher-order oligomer from monomer in the process of aggregation. We further assumed that depending on the nature of the aggregating protein, one of these oligomeric forms (i.e., either trimer, tetramer, or pentamer) can transform into a critical assembled state,49,50 either directly or facilitated by higher-order structure (Table 1). It has been shown that the self-association process of monomeric protein not only promotes aggregation to form oligomers but also induce the assembly-dependent structural transition (either unfolding for natively structured protein or partially folding for natively unstructured protein) to form partially folded intermediates [(Iy, y = 1 to 4)], for example, in the case of α-synuclein (α-Syn) protein (Table 1).51,52
However, there are instances where such partially folded intermediates were not observed or identified during the experiment, as a result, suitable experimental data for such intermediate are not available. Under such circumstances, we defined these species as the minimum fibrillar unit (as we have not provided kinetic data for partially folded intermediates) for proteins such as Aβ(1–42) protein (Aβ42), cMyb TAD (transactivation domain) peptide (Myb), and transthyretin (TTR) protein (case-2, Table 1).53–55 Thus, we have classified the amyloid-forming proteins either belonging to (case-1) or (case-2) based on the available experimental data to study the aggregation kinetics for the respective proteins (for details see Table S1†). However, it is important to emphasize that the model structurally remains the same (Fig. 1b) but the interpretation of the species involved in the aggregation process gets modified depending on the kind of amyloid-forming proteins (Table 1). The partially folded intermediate themselves can further aggregate individually with the monomers (M1), or they self-assemble to give rise to higher-order partially folded intermediate (case-1, Table 1). In the same way, we can hypothesize that the minimum fibrillar units can produce higher-order fibrillar units for the case-2 (Table 1) proteins, respectively.
Furthermore, we have inferred that higher-order partially folded intermediates can conformationally transit to the minimum fibrillar unit to further elongate into a mature fibril (case-1, Table 1). Additionally, for (case-2) proteins, we hypothesize that the minimal fibrillar units eventually convert to higher-ordered fibrillar units to form mature fibrils (Table 1). Finally, the mature fibrillar state [(Bz, z = 1 to 3)] can be formed by following two different paths, either via consecutive association with the respective minimum fibrillar units or through the secondary nucleation process56–58 by sequentially binding with the monomers of the aggregating proteins (Table 1). Thus, in our proposed generic model (Fig. 1), we have introduced most of the mechanistic details of the aggregation process that can account for various aspects of amyloidogenesis. Herein, we have considered an ensemble of models (Fig. S2a–f†) based on the different probable degrees of aggregation of the monomeric units (M3, M4, M5) and elongation units (I3, I4). For example, in the case of Model-1A, we have considered that the monomeric unit can aggregate up to a trimeric unit (M3) and the highest order elongation unit can form (I3). Whereas, in Model-2F, we assumed that the monomeric unit could extend till pentamer (M5) and the elongation unit could form a tetrameric unit (I4) as the highest structural degree. In this way, all the ensemble models are generated systematically (for more details see Fig. S2a–f, ESI Sections-2 and 3†).
To identify the optimum interaction network for a representative protein, each distinct network (Fig. S2a–f†) has been translated into sets of ordinary differential equations (ODE) (ESI Section-4†) based on simple mass-action kinetics. A generalised common framework (Table 2) of the ODEs has been summarised by considering the ODEs of all the proposed model variants (see ESI Section-4†) to succinctly depict our proposed approach. Each model variable and kinetic parameters involved in the generic model are described in Tables S2 and S3, ESI Section-1,† respectively. We have given a detailed account of the interactions in ESI Section-3,† where we have even described how different aggregated forms of the proteins interact with the thioflavin T (ThT) as designated in Fig. S3.†
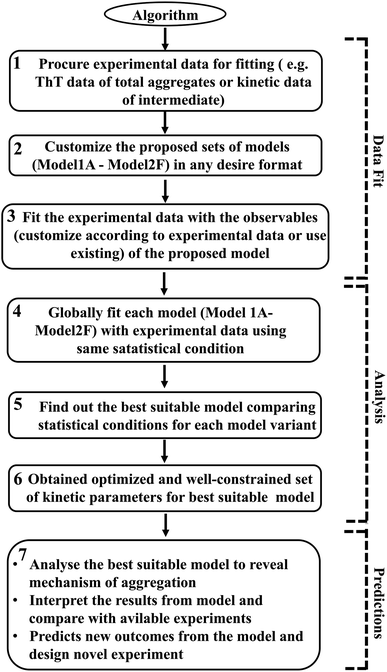
However, it is extremely important to get a reasonable estimate of the kinetic parameters involved in the proposed model to elucidate and investigate the inherent mechanism behind this heterogeneous aggregation process. Thus, each specific model has been optimized with the available experimental data set for a particular protein. The statistical parameter (χ2 and AIC (Akaike information criteria) value) obtained after data fitting for each model variant have been analysed and compared to distinguish the best-fitted model (Tables S5–S8†). We have used sophisticated parameter optimization software “Potterswheel”59 to fit and optimize our models with relevant experimental data using stringent statistical criteria (see Method section). To optimize our models, we have selected a series of experimental inputs for a group of amyloidogenic proteins/peptides (α-Syn, Aβ42, Myb, and TTR protein). The experimental inputs varied for different proteins, such as for α-Syn protein, we have focused on the normalized kinetic data of intermediate helix-rich oligomers combined with time-dependent thioflavin-T data of total aggregates reported by Ghosh et al.51 For Aβ42 and TTR protein, we have utilized only ThT fluorescence kinetic assay time-resolved data of amyloid formation.54,60 In the case of Myb protein, information about the amount of the initial and final secondary structures (α-helix and β-sheet) during the amyloid formation process, and the time profile of ThT fluorescence data of the overall kinetics as reported by the Gadhave et al.55 have been used. Selecting simultaneous experimental inputs for different proteins and attaining the desire interaction networks established the fact that our proposed canonical models can fit a diverse set of kinetic experimental data. Thus, our methodology to calibrate the proposed model with experimental data is quite advanced and it determines the kinetic parameters efficiently. The link for the core model network structure is available in sbml format in GitHub repository for the (https://github.com/baichandra05/Genericmodel_protein_aggregation) users to customize and fit any type of kinetic data set according to their preferences. A flowchart of the algorithm (Scheme 1) has also been included and detailed schematics have been provided in the ESI (Fig. S17†) to make the approach easy and understandable for the general readers. Thus, we have provided a general modelling framework to obtain a comprehensive understanding of the kinetics of amyloid formation that corroborates with various experimental observations for a diverse range of amyloid-forming proteins to dissect the underlying dynamical nature of amyloidogenesis.
Results and discussion
Identifying appropriate aggregation model variant for a diverse set of proteins by employing a generic modelling approach
We began investigating the acceptability of our generic modelling approach by challenging different model variants with the experimental data corresponding to a range of amyloid-forming proteins. To begin with, we have considered the α-Syn protein, which is an intrinsically disordered protein known to aggregate via nucleation-dependent polymerization reaction.61 The various model variants (Fig. S2a–f†) are globally optimized with the experimental data quantified for α-Syn by Ghosh et al.51 The optimization analysis unravels that model variant Model-1F could significantly represent the protein aggregation time profile (Fig. S4a and b†) by reproducing the experimentally observed kinetics of the partially folded intermediate of α-Syn than the other variants (Table S5†). Herein, we speculate that the aggregation ensemble model can be applied for a diverse set of proteins, hence we challenged our generic model variants (Fig. S2a–f†) with experimental data corresponding to other amyloid-forming proteins such as Aβ42 and Myb, which generally have a defined lag time.53,55 While for Aβ42 protein, Model-2C fits the data optimally (Fig. S4c and Table S6†) for Myb protein; Model-1C turns out to be the most preferred model variant (Fig. S4d†) among the different models (Table S7†). This was indicated by the appropriate χ2 and (AIC) (Tables S5–S7†), which found the most probable model by weighing the number of associated rate constants with the goodness of fits, thereby preventing overfitting.We further evaluated the ability of these aggregation ensemble models to improve the identifiability of the estimated parameters. To test this, we have plotted the maximum and minimum variability (bounded area shown as a spring green cloud in Fig. 2) at each time point from the best 2% fitted model trajectories and analysed the parameter identifiability by visualizing the corresponding box-plot (Fig. S5–S7†). In the case of α-Syn protein, though simultaneously two diverse kinds of data sets (the kinetics of amyloidogenesis by performing experiments with thioflavin T, and the kinetic evolution of the total partially folded intermediate (Itotal) during the amyloid formation) have been introduced to calibrate the model, still, the bounded area from the best-fitted trajectories remains well constrained along with all the experimental data (Fig. 2a and b) by reproducing a set of identifiable parameters (Fig. S5†). This observation significantly reveals that any particular parameter set belonging to the best 2% fits for Model-1F can capture the experimental data adequately. Hence, any kind of predictions made by these best-fitted kinetic rate constants (Table S4†) using Model-1 will be highly robust.
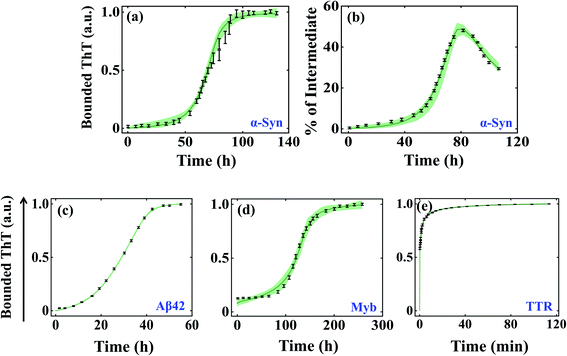 | ||
| Fig. 2 Self-aggregation kinetics of different amyloid-forming proteins emerge from the global fitting of experimental data using the best-optimized model variants. The bounded area (the maximum and minimum variability corresponding to each time point) of best 2% fits of the total ThT bounded aggregates (a) and % of total partially folded intermediate aggregates (b) obtained for α-Syn protein (300 μM) by fitting both the respective dataset simultaneously.51 The bounded area of 2% best-fits the total ThT bounded aggregates of (c) Aβ42 protein (10 μM), (d) Myb protein (20 μM), and (e) TTR protein (64 μM).53–55 In each case, the thick solid line represents the average of best 2% fitted trajectories taken out of ∼3000 fit sequences by fitting the experimental data with the best-fitted model. The black lines indicate the experimental data sets with error bars (the error bars designate standard deviation calculated with a standard error model in build within “Potterswheel” software).59 | ||
For the Aβ42 protein, as only one experimental data input has been utilized during the global fitting procedure, the bounded area from the 2% best-fitted trajectories is comparatively more constrained (Fig. 2c), which essentially makes most of the parameters highly identifiable (Fig. S6†). However, for Myb protein, the presence of some amount of secondary structure at the beginning of aggregation has been incorporated during the fitting. This created a greater deviation in the best 2% fitted trajectories (Fig. 2d) for some initial time points of the ThT experimental data leading to a greater number of non-identifiable kinetic rate constants (Fig. S7†). This indicates that the best-fitted parameter set for Myb protein will have lesser predictive power. As we are claiming that our approach can be globally applicable to a diverse set of proteins, next we chose a protein, TTR, which aggregates at a faster time scale and does not have any distinct lag phase.54 We found that Model-1D (Fig. S4e†) reproduces a set of highly robust and identifiable parameters (Fig. S8†), which is supported by the smaller variability among the 2% best-fitted trajectories (Fig. 2e).
Importantly, we have obtained additional insights about the most probable underlying network structure (Table 3) that eventually leads to such kind of kinetics. It suggests that for α-Syn protein, a pentameric random coil state (M5), forth-ordered partially folded intermediate (I4), and the higher-order fibrillar unit (B3) will be necessary to attain such kinetics of aggregation. The primary nucleation step involves a pentameric random coil state (M5) for Aβ42 and Myb proteins as well but preferred the (I3) state as the lower order fibrillar unit to aggregate. However, for TTR protein, the global fitting method automatically chooses the lowest possible configuration (M3) during the primary nucleation process, probably aligned with faster kinetics in the absence of the lag phase.
In summary, we have established that the particular model variants present in Table 3 are the optimal models for the respective proteins, which are consistent with the corresponding aggregation kinetics data. We found that the selected best model could not be further enhanced or reduced, but all the involved interactions are required to explain the complementary experimental data set. Thus, our study indicates that fitting the experimental data for any specific protein with one particular network model will not be sufficient to determine the best-fitted global model variant, as it ignores the configurational heterogeneity. Instead, fitting the experimental data to a set of aggregation ensemble models is extremely helpful to distinguish the appropriate aggregation network model and it improves the identifiability of the corresponding estimated kinetic parameters. Analysing the identifiability of the kinetic parameters for respective optimal models for any particular protein was necessary to decipher the important features and mechanistic insights of amyloid growth kinetics.
Model analysis reveals the initial monomer concentration dependency of the dynamics of the aggregation process
Previous analysis sorts out the precise model and an optimal set of kinetic parameters for each corresponding protein, which explicitly corroborates with the experimental data. If we want to check the predictive power of these models, first we need to analyse some robust model predictions with the acquired parameter set and compare the results with experimental observations. An important factor that has played a key role in the field of amyloidogenesis is the study of the kinetics of aggregation as a function of initial monomeric protein concentration.32,43,62 To investigate this aspect, we have taken the best-fitted parameter set (Table S4†) for a particular protein and then vary the initial monomeric protein concentration for a wide range by keeping the other kinetic parameters constant. It is worth mentioning that our model predictions can capture the essential features of the fibrillation process of different proteins in a concentration-dependent manner.For example, in the case of α-Syn, we have obtained a constrained set of best-fitted parameters (Table S4 and Fig. S5†) for the corresponding model (Table 3) for 300 μM protein concentration. Our model predicts that the decrease or increase of monomeric concentration of α-Syn will significantly modify the lag time threshold by altering the slope of the sigmoidal growth kinetics (Fig. 3a). However, for α-Syn, the model reconciles the difference between the time courses of fibrillation in the high, medium, and low concentration regimes following experimental data.51 The model simulation performed at a very low total protein concentration reestablishes the fact that a minimum concentration is required to maintain the nature of the amyloid formation kinetics (Fig. S9†). In the case of Aβ42 protein, our model perceives the similar observation that altering the initial monomeric protein concentration will change the lag time as well as the slope of the sigmoidal curve (Fig. 3b). However, for Myb protein, the model simulation performed under varied total protein concentrations does not help much to predict the dynamics directly, since we considered the presence of secondary structure content only at the beginning of the aggregation process according to the experimental data.55 This observation suggests that there is no perceptible change in the slope of the growth kinetics, however, the associated lag time changes moderately (Fig. 3c).
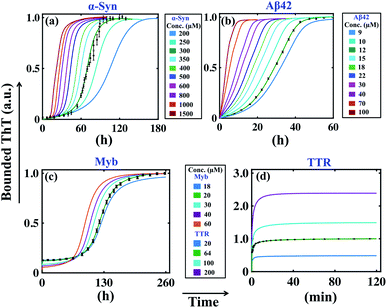 | ||
| Fig. 3 Model reconciles the concentration dependency of amyloid formation dynamics for different proteins. The best-fitted model (Table 3) predicted time courses of total ThT bound aggregates are shown for (a) α-syn, (b) Aβ42, (c) Myb, and (d) TTR proteins by varying the total protein concentrations, and keeping all other parameters same as given in (Table S4†). In each case, the green solid line indicates the best-fitted trajectory and the black dots represent the experimental data points with error bars. | ||
For TTR protein, though there is no existence of lag time, still, we performed the variation in the total monomeric concentration and found that the bounded ThT response was considerably higher or lower depending on the increase or decrease in the total TTR concentration (Fig. 3d). All these predictions from the model simulations substantiate the experimental observation to a greater extent.51,53–55 Overall, it can be concluded that the simulation analysis based on the best-fitted parameters disentangle the monomeric concentration dependence of the overall assembly process for the corresponding protein. Importantly, our model generates the qualitative dynamics of the aggregation kinetics at different concentration regimes even though we have fitted the most favourable model for a fixed total protein concentration in each case. At this point, we can speculate that the best-fitted models could capture the critical time scales associated with the aggregation kinetics efficiently.
Model disentangle various emerging time scales associated with the kinetics of amyloid formation
It was evident from the previous analysis that under current parametric conditions, our proposed model reproduces the concentration dependency of the aggregation kinetics satisfactorily, especially for α-Syn and Aβ42 proteins. To provide a structural interpretation of this result, we investigated further by quantifying some fundamental timescales, which coordinate the time evolution of growth kinetics such as (τlag) (time required to form nuclei) and (τ50) (time required to half complete the overall process) (Fig. 4a). Initially, we focused on α-Syn protein and found that both the time scales (τlag) and (τ50) decrease steeply with the increase in total protein concentration (Fig. 4b and c). However, beyond a higher total monomeric concentration (>1000 μM), the relative change in both (τlag) and (τ50) becomes marginal. It turns out that the parameter set (Table S4†) estimated by our optimization method, is capable of quantifying both these time scales with reasonable precision and they are almost linearly dependent on each other (Fig. 4c, inset).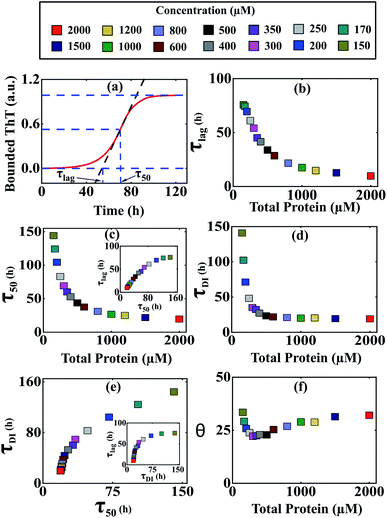 | ||
Fig. 4 Different time scales segregate the kinetics of amyloid formation of α-Syn protein. Time scales for the different conditions have been calculated by simulating Model-1F by varying total protein concentration Ptotal keeping the parameters fixed provided in Table S4.† (a) Schematic of the estimation of the duration of the lag phase (τlag) and the duration of the time taken to reach half of the saturation level of the bounded ThT response (τ50) at any given total protein concentration. (b) A plot of the variation of (τlag) as a function of total protein concentration calculated from the model predicted simulated time-courses. (c) The model-predicted variation of (τ50) as a function of total protein concentration showed similar behaviour as observed with (τlag). A correlation plot (inset) of (τlag) vs. (τ50) shows a higher degree of linear correlation up to a certain total protein concentration. (d) A plot of duration of partially folded intermediate (τDI) as a function of the total protein concentration obtained by simulating the Model-1F reproduces similar observation (τlag) as and (τ50). (e) The scatter plot represents the correlation of (τDI) with (τ50) and (τlag) (inset) under various total protein concentrations. (f) A plot of θ [in %, mathematically expressed as 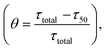 where (τtotal = τlag + τDI) against total protein, concentration illustrates the effect of intermediate in shaping up the amyloid-forming kinetics for α-Syn. where (τtotal = τlag + τDI) against total protein, concentration illustrates the effect of intermediate in shaping up the amyloid-forming kinetics for α-Syn. | ||
Intriguingly, it has been speculated experimentally that intermediate aggregates (defined as a partially folded intermediate in our model) may be a remarkable kinetic controller (say for α-Syn protein) of the fibrillation process.51 Herein, we want to interrogate whether or not these intermediates play an important role in influencing the kinetics of amyloidogenesis during the transitions from either lag phase to the elongation phase or elongation phase to the plateau phase. To inspect this, we define and quantify (τDI) (duration of partially folded intermediate, Fig. S10†) from our model predicted time profiles for different total protein levels. Our analysis reveals that (τDI) varies with the total protein concentration (Fig. 4d) in a similar fashion like (τlag) and (τ50). Moreover, there is a higher degree of correlation existing between (τDI) with (τ50) (Fig. 4e) and (τlag) (Fig. 4e, inset), where the respective profiles eventually saturate, once the total protein concentration crosses a certain threshold level.
To decipher the role of these time scales (τlag, τ50) and (τDI) precisely, we further defined a relative time scale, θ (Fig. 4f) in the context of α-Syn, which delineates the influence of partially folded intermediate aggregates in the transition from elongation to the plateau phase progressively with the variation in the total protein concentration. In the lower concentration regime (<400 μM), the abrupt decrease in θ (Fig. 4f) with a total protein concentration indicates the comparative steeper decrease in (τDI) over (τlag and τ50) and thereafter creating a smaller difference between (τtotal − τ50). This observation suggests that under low to moderate total protein concentrations, partially folded intermediate aggregates do influence the amyloid-forming kinetics in a significant manner. However, once the (τDI) value gets saturated beyond a threshold level of total protein concentration (Fig. 4d), the sharper decrease in (τ50) compared to (τlag) governs the relative increase in θ dynamics (Fig. 4f). This depicts that at a higher concentration regime, both primary nucleation events and partially folded aggregated intermediate synergistically control the temporal transition of aggregates.
Additionally, we have observed the dynamical evolution of different states of the α-Syn protein, which helps to dissect the aggregation kinetics from a microscopic viewpoint. Our analysis demonstrates that for α-Syn protein, the time-scale of the transformation of the unstructured monomeric unit to mature stable fibrils depends on temporal timing equilibrium existing between the conversions of random coil (RC) to intermediate (I) to mature fibril (B), which is protein concentration-dependent (Fig. S11†). At low concentrations (up to 250 μM), monomeric state decay very steadily and the relative accumulation of the intermediate is slow resulting in very slow kinetics. Whereas for higher total protein concentration, the random coil structure converts rapidly and the appearance and disappearance of intermediate aggregates are relatively fast, which leads to rapid advancement in the kinetic procession (Fig. S11†). Thus, the diverse nature of variation of all these time scales (Fig. 4) highlights the distinct effect of the evolution of different states (RC, I and B) that govern the dynamics of aggregation under different concentration domains.
Moreover, (τlag) and (τ50) associated with Aβ42 protein aggregation demonstrate a similar trend (Fig. S12†) with increasing initial monomeric protein concentration, as observed in the case of α-Syn. Interestingly, for Aβ42 protein, the dynamics of aggregation are found to be governed predominantly by the monomer-mediated fibril generation process (Fig. S13†) for any given concentration of the protein. The Myb protein kinetics remains almost independent of the initial monomer protein concentration and TTR protein does not have any lag phase, so the analysis based on these time scales is not applicable in the case of these two proteins. In conclusion, the time scale analysis reveals that (τlag) and (τ50) are significant parameters to characterize the kinetics of polymerization for an aggregating protein. However, for proteins, which have intermediate structures, two additional parameters (in the form of (τDI) and θ) described in this work and the analysis of timing equilibria between different states, provide a basis to dissect the kinetics of amyloidogenesis in a better way.
The model illustrates the specific signature in the reaction time courses for different proteins through the use of the pre-seeded assay
The analysis performed in the previous section demonstrates the influential role of different time scales in modulating aggregation kinetics. Reconciling the commonly available experimental results using a theoretical approach is one of the significant challenges in investigating the aggregation dynamics. In this context, we have performed numerical seeding experiments with our best-fitted models for different proteins to replicate the in vitro experimental observations.51,53–55 Experimentally, for α-Syn protein, it has been found that an active partially folded intermediate can eliminate the characteristic lag time.51 Herein, we performed similar numerical seeding experiments and found that when the preformed seed (intermediate aggregates) are added at the beginning of the reaction, it leads to the rapid creation of new aggregates through secondary nucleation pathways. Thus, the protein aggregates in a faster way compared to the non-seeded case (WT) (Fig. 5a). Additionally, the simulation study further displays that the presence of isolated partially folded intermediate alone can directly produce mature amyloid fibrils even without going through any lag phase (Fig. 5b), which corroborates with the experimental observations.51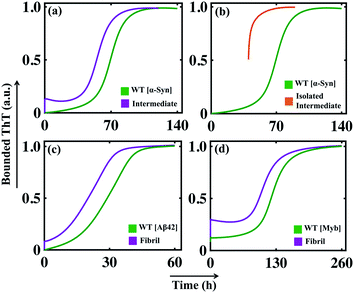 | ||
| Fig. 5 Analysis of the effect of seeding on the aggregation kinetics for different proteins. (a) Enhanced rate of the formation of the amyloid fibril in the presence of initial seed added in the form of basic intermediate like aggregates (I1 = 1.0, I2 = 0.5, I3 = 0.5, I4 = 0.5) in comparison to the control simulation performed for the WT (300 μM) α-Syn without any added seed. (b) Model simulation with only isolated partially folded intermediate predicts that the kinetics of amyloid fibril formation of these aggregates will have no lag time in comparison with monomeric protein (WT). The numerical simulation is performed (qualitatively similar to the experiment carried out to isolate the basic intermediate by Ghosh et al.51) by taking the initial conditions as (I4 = 10, AC = 10, M5 = 10), which set up the total protein concentration as [(10 × 20) + (10 × 5) + (10 × 5) = 300 μM]. (c) The model-predicted dynamics of Aβ42 protein for WT (10 μM) and in the presence of seed (I1 = 0.1). (d) Comparison of the model-predicted trajectory of Myb protein for WT (20 μM) and seeded dynamics (I1 = 0.2). Here, the numerical simulation has been performed with the parameter set provided in (Table S4†) for the respective protein using the best-optimized model (Table 3). | ||
Intriguingly, our model predicts that even for Aβ42 protein, the addition of the preformed fibril can evade the slow rate-determining nucleation step during aggregation in comparison to the WT situation (Fig. 5c). Similarly, for Myb protein, adding the seed material at the beginning of the aggregation process speeds up the growth process (Fig. 5d). According to our numerical simulation, even the seeding operation performed for TTR protein remarkably changes the kinetic profile of aggregation (Fig. S14†), which is commensurate with the experimental observation.
Model reconciles the intrinsic effect of specific mutation by rationally altering the rates of aggregation
In the previous section, we tested our model's predictive power and found that our model efficiently reproduces the aggregation kinetics for the seeded experiment. Recent studies reveal that the mutation can affect amyloid formation mechanism of the particular protein, and a range of amyloid diseases are found to be associated with specific point-mutation.63–68 Although the ability to form the amyloid appears to be a generic property of protein/peptides,40,69 we want to further explore the generic approach that can explain the varied aggregation kinetics in the case of single-point mutation of an amyloid-forming protein (for example, α-Syn protein).To begin with, this seems extremely difficult to achieve in our modelling framework, as our kinetic model does not contain any amino acid sequence information for a protein. Generally, the propensity of different amino acids to form different structures, such as partially folded intermediate or β-sheet rich fibril, under a given condition varies significantly. Now, if we know the relative tendencies to form different states (random coil, intermediate, or fibril) by the mutated sequences, it is possible to adjust the corresponding kinetic rate constant and get qualitative features of the kinetics of the mutant protein compared to the WT protein. To establish this hypothesis, we have chosen some mutants for α-Syn protein, which show faster kinetics than WT [A53T (fast mutant-1), A53V (fast mutant-2)] and some mutants known to behave oppositely by elongating the amyloid formation kinetics [A53K (slow artificial mutant-1), A53E (slow mutant-2), A30P (slow mutant-3)] compared to the WT α-Syn protein.63,64
The mutants such as A53V and A53T show a greater aggregation tendency to form fibril-like aggregates but have a reduced propensity to form the helical intermediate due to structural changes induced by the respective point mutations.63 On the contrary, the other set of mutants (A53K, A53E, and A30P) demonstrates a reduced propensity to form intermediate as well as fibril-like aggregates.64 In our modelling framework, we deal with such kinds of structural information's from a dynamical perspective by relatively altering the corresponding reaction rates associated with such different individual reaction mechanisms compared to the WT protein.
By comparing the relative tendencies of the particular mutant and fine-tuning the specific reaction rate constants, the model reproduces the kinetic behaviour in the case of both faster (Fig. 6a) and slower mutants (Fig. 6b), which qualitatively agrees with the experimental observations.63,64 This investigation summarizes an important inspection that if the relative inclination of any particular amino acid at different stages of fibrillization is known a priori, then it is possible to predict the aggregation propensity qualitatively for the respective mutant from our proposed model. Thus, our study can be very helpful in the context of monitoring the kinetics of mutants from a modelling perspective, as, experimentally following the dynamics of the mutant protein is a challenging and time-consuming task.
 | ||
| Fig. 6 The simulated dynamics of different mutants obtained for α-Syn protein. (a) The model (Model-1F) predicted relative time courses for the fast mutants [A53T (fast mutant-1, where Ks = 1.5, Ke = 0.6) or A53V (fast mutant-2, where Ks = 2.0, Ke = 0.6)] of α-Syn protein concerning the WT. (b) The model predicted relative trajectories of the slow mutants [A53K (slow mutant-1, where Ks = 0.9, Kc = 150), A53E (slow mutant-2, where Ks = 0.75, Kc = 130), and A30P (slow mutant-3, where Ks = 0.62, Kc = 110)] of α-Syn protein in comparison to the WT. For both (a) and (b), all other parameters are the same as provided in Table S4.† | ||
The model elucidates the inhibition of specific molecular events during fibrillation and hypothesizes experimentally testable intuitive predictions
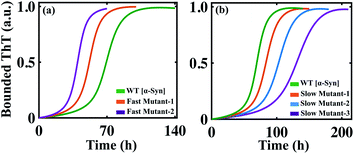
The success of any mathematical modelling approach relies on its predictive ability. Our modelling strategy provides a good estimate of the kinetic parameters that eventually organize the overall kinetics of aggregation. Recent kinetics studies have shown that a wide range of molecules can inhibit the aggregation process. Depending on the nature of the amyloid-forming proteins, the inhibitors generate a variety of dynamical responses, where the detailed molecular mechanism of actions is hard to track and interpret. In this context, with the help of our mathematical model, we tried to elucidate the principle microscopic mechanism affected by the inhibitors. Perni et al. have shown that a small molecule, squalamine, which has pharmacological activity, retards the initial event of the self-assembly process of α-Syn.70 We introduced the effect of the inhibitor (squalamine) in our best-fitted Model-1F for α-Syn protein (ESI Section-4†) and found that simultaneously inhibiting the primary nucleation process (PN) and conversion rate to the partially folded intermediate (TE), the effect of increasing concentration of squalamine on aggregation kinetics can be explained (Fig. 7a). On the other hand, by employing the computational method, we re-established the fact that the molecular chaperon belonging to the BRICHOS family suppresses both the primary nucleation process (PN) and monomer-mediated elongation events (PS) (Fig. S15a†) to prevent the aggregation process of Aβ42 protein, while the molecular chaperon DNAJB6 affects only a single specific step, i.e., the monomer based secondary nucleation event (Fig. S15b†) to inhibit the amyloidogenesis.71,72 | ||
| Fig. 7 The model reproduces different dynamical features of amyloid formation kinetics. (a) The model (where, Kx1 = 0.1, Ks1 = 0.1) qualitatively mimics the dynamics of α-Syn aggregation in the presence of an inhibitor such as squalamine70 in a concentration-dependent manner (see ESI Section-4†). (b) The model simulated trajectory of Aβ42 protein by increasing the primary nucleation (PN) rate by (Kx) 2 times [1], 10 times [2]. (c) Alteration in the amyloid formation kinetics of α-Syn protein by simulating the model with increasing the primary nucleation (PN) rate (Kx) by 5 times [1] and 10 times [2]. (d) The model-predicted dynamics of α-Syn protein by enhancing the effect of positive feedback (SF) mediated through the intermediate structure by increasing the rate (Kac) by 2 times [1] and 10 times [2]. (e) Acceleration of the dynamics of Aβ42 protein when the best-fitted model simulated with increasing rate (Kac, 1000 times, [1]). (f) Increasing the monomer mediated growth process (PS) of intermediate oligomers of α-Syn leads to elevated ThT response. Here, (PS) is stimulated by increasing the association rate of the elongation process (Ki), 50 times [1] in comparison to the WT case. In each case, the solid line represents the fitted trajectory and the dotted line represents the model-predicted dynamics, the simulation has been performed by keeping all other parameters the same as given in Table S4.† | ||
Finally, it can be concluded that by investigating a series of dynamical features of amyloidogenesis, we have established the best-possible interaction network for aggregation mechanism for a range of proteins by applying our generic modelling strategy. Therefore, this model may be used as a basis for making new predictions, which can be further verified experimentally. Our study reveals that facilitating the primary nucleation process can essentially lead to two distinct scenarios for α-Syn and Aβ42 proteins. For Aβ42 protein, a little increment in the rate of primary nucleation stimulates the aggregation process in a faster way (Fig. 7b) by reducing the lag time. In contrast, our model predicts that accelerating the primary nucleation process will slow down the aggregation kinetics in the case of α-Syn protein (Fig. 7c), as it causes rapid monomer depletion, which disrupts the monomer dependent elongation and secondary nucleation process. This implies that for α-Syn (case-1) protein, the monomer-dependent elongation and secondary nucleation processes predominantly drive the fibrillation mechanism. The rapid accumulation of the nucleus caused by the enhancement of the primary nucleation rate fails to compensate for the depletion of the monomer. Whereas for Aβ42 (case-2) protein, primary nucleation event majorly contributes to shaping the kinetics of aggregation. However, these are our model predictions, which need to be validated via experiments.
Importantly, our model analysis unravelled that the positive feedback facilitated through the higher-ordered structure (highest-ordered intermediate (case-1) structure or the highest degree of lower-order fibril (case-2)) in our proposed model either effectively (for α-Syn protein (Fig. 7d) or moderately (for Aβ42 protein (Fig. 7e) influences the kinetics of aggregation. Increasing the effect of the positive feedback accelerates the kinetics for both α-Syn and Aβ42 proteins, suggesting that positive feedback via intermediate structures has a critical contribution to the fibril growth process. This further explains why the monomer-dependent elongation and secondary nucleation processes appreciably affect the α-Syn protein aggregation. The higher degree of positive feedback regulation further supports the total monomer concentration-dependent aggregation pattern of α-Syn protein, as observed in Fig. 4.
We have considered that the aggregation process is reversible process, where equilibria exist between different states of the protein (random coil, intermediate, or fibril), and the proportion of various aggregated states changes with the advancement of the reaction. Intriguingly, our proposed model indicates that if the equilibrium is somehow shifted towards the intermediate structures (partially folded intermediate for α-Syn (case-1) protein or lower-order fibrillar structure for Aβ42 (case-2) protein) by fine-tuning the corresponding reaction rates, then one can obtain an even higher bounded ThT response (Fig. 7f and S16†). Though this prediction seems quite counter-intuitive, however, it can be rationalized, as this process may promote the formation of active seeds (intermediate (case-1) or lower order fibril (case-2)) for these two proteins. This predicted kinetics made from our modelling setup can be verified experimentally if the partially folded intermediate associated with the α-Syn or lower-order fibril for Aβ42 protein can be stabilized during the fibrillation process.73 However, this observation is only our model speculation, which demands further experimental verification.
Model-driven in silico inhibition of microscopic processes predicts rational therapeutic strategies to prevent amyloidogenesis
We aim to comprehend the aggregation process by understanding the influence of various molecular events involved in amyloidogenesis so that a fruitful therapeutic strategy can be achieved to prevent amyloid formation. The advantage of our modelling approach in comparison to other existing models in the literature lies in its detailed nature of delineating the aggregation phenomena as an assembly of discrete microscopic processes. Herein, we numerically investigate the effectiveness of inhibiting the microscopic processes depicted in Table 1 and Fig. 1b for either case-1 or case-2 categories of proteins by taking α-Syn and Aβ42 proteins as a representative example. To understand the efficacy of the individual step and contributions of discrete processes to the entire mechanism, first, we numerically inhibited the microscopic events, which significantly affected the mechanism and compared the two important time scales (τlag) and (τ50) corresponding to this situation with the WT case. Further, we hindered multiple molecular events together, and similarly quantified the changes in (τlag) and (τ50) in comparison to the WT. We envisaged that this systematic analysis using our model could provide mechanistic insights into how to reduce aggregation by substantially affecting (τlag) and (τ50). Fig. 8a depicts the duration of lag-time in comparison to the WT; if various microscopic events (one single event or multiple events together) have been inhibited in multiple folds and illustrates qualitative features of the corresponding duration of (τ50) as well (Fig. 8b).Indeed, we observe, for α-Syn protein that if the transition to critical assembled state (SP) and conversion rate to an intermediate structure (TE) are inhibited together, then it lengthens (τlag) and (τ50) effectively than inhibiting any other microscopic processes. Thus, our model essentially provides a qualitative rationale about how to design a drug for preventing amyloid formation in the case of α-Syn protein and predicts that the drug will be highly efficient if it can affect early microscopic events (SP, TE) individually or collectively. Intriguingly, a similar analysis for Aβ42 protein unravels that fibril growth is mostly contributed by primary nucleation (PN) and monomer-mediated elongation process (PS), and inhibiting these two processes together will affect the lag-time (τlag) and the (τ50) to almost the same extent (Fig. 8c and d). It depicts that the monomer should be targeted to prevent the aggregation process in the case of Aβ42 protein. We displayed that this investigation with the help of our modelling framework would provide mechanistic insights into how to reduce aggregation by substantially affecting (τlag) and (τ50). The present systematic analysis unveils the relative contributions of various microscopic events that are controlling (τlag) and (τ50) in the case of α-Syn and Aβ42 protein (Fig. 8), which can be extended for different proteins. Moreover, it figures out the important microscopic processes that can be targeted therapeutically by synthesizing novel drugs to prevent amyloidogenesis.
Conclusion
The protein aggregation process that leads to amyloid formation is undoubtedly a complex phenomenon. The mechanistic details via which monomeric proteins transform into amyloid-like fibril states and inflicts several disease phenotypes can only be understood by taking an appropriate system biology approach. In this work, we have developed a generic approach comprising most of the mechanistic complexities (Fig. 1) that represent the heterogeneities of protein aggregation by considering an ensemble set of models (Fig. S2a–f†). Our method globally fits the experimental data and successfully estimates the kinetic parameters by choosing the best suitable aggregation model (Table 3) for specific protein by elucidating how fibril formation depends on the fundamental molecular mechanisms.Our model provides kinetics interpretations, which help to qualitatively describe the concentration dependency of the aggregation kinetics (Fig. 3) and seeding experiments (Fig. 5). The significant role of the intermediates has been established by quantifying the duration of intermediates and correlating that with τlag and τ50 at different total protein concentrations (Fig. 4). The best-fitting model obtained for the WT proteins was able to explain the kinetics of mutant proteins in a qualitative manner, which adds a new dimension to the kinetic modelling approach (Fig. 6). In the case of most of the previous theoretical models (e.g. Pallitto & Murphy),30 very few approaches have been taken where the different states introduced in the model have been characterized by various microscopic kinetic parameters. In the present work, one of the primary goals is to analyse and dissect the kinetics of aggregation describing each emerging state and connecting these states to distinct microscopic rates. Thus, the model provides the emerging kinetic information, which helps to estimate the principal microscopic state affected by several inhibitors (Fig. 7). These intriguing investigations lead to several novel predictions (Fig. 7) and help to sort out important microscopic steps (Fig. 8) that have to be targeted for design drugs.
However, further modifications in the current method can make it even more useful and robust. For example, the aggregation phenomena can happen irreversibly, but all the reaction steps in the proposed model have been considered reversible. Moreover, protein aggregation can happen through a more complex set of molecular events than considered in our case (Fig. 1). The variation in model configurations for protein aggregation can vary up to any extent. Considering bigger models will lead to more kinetic parameters. Therefore, we need to develop a better computational modelling setup as well as accurate experimental data to make the model parameters indefinable. Additionally, the proposed generic modelling approach has not been explored to study molecular crowding effects. However, our model can be extrapolated by fine-tuning the rates associated with the primary nucleation and related to other molecular events to accommodate the effect of crowding environment. Currently, the entire method and model have been built assuming that protein aggregates in a homogenous medium. Our investigation can be further modified to include the effect of a heterogeneous environment on aggregation. In summary, it can be concluded that our modelling approach effectively decodes various mechanistic details that are crucially governing the amyloidogenesis for various proteins. We believe that our computational method and the results described in this work will provide important insights to develop precise therapeutic strategies by targeting different microscopic events during the fibrillation process and will find wide applicability.
Method
The regulatory network (Fig. 1b or S2†) was constructed in terms of ordinary differential equations (ODE). The kinetic parameters of the model were estimated using the PottersWheel software (version 4.1.1).59 The parameters were fitted globally in logarithm parameter space employing a genetic algorithm method, where the CVODE method was used for integrating the ODEs. Each model system was optimized (∼3000 times) by taking several random initial starting values of the kinetic parameters, and several parameter sets were obtained after the optimization process, which fit the experimental data adequately. A wide range (lower bound = 0.0001 and upper bound = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, see Table S4†) has been provided for estimating the kinetic parameters and the model has been optimized with ∼3000 fit sequence so that a reasonable number of parameter sets (here we choose best 2%. i.e. ∼60 parameter sets) can be available to perform identifiability analysis (Fig. S5–S8†). We have only shown the best-fitted results in each case for different models that are considered in Table S4.† Each parameter estimation round was started with parameter values that were disturbed with a strength of ε = 0.2, so that Pnew = Pcurrent × 10(ε×ϕ) with ϕ being normally distributed with mean 0 and variance 1. A detailed description of the development of entire models and their relative χ2 value and Akaike information criterion (AIC) have been provided in (ESI Section-2 and Section-3†). The χ2 value was calculated according to the following equation
000, see Table S4†) has been provided for estimating the kinetic parameters and the model has been optimized with ∼3000 fit sequence so that a reasonable number of parameter sets (here we choose best 2%. i.e. ∼60 parameter sets) can be available to perform identifiability analysis (Fig. S5–S8†). We have only shown the best-fitted results in each case for different models that are considered in Table S4.† Each parameter estimation round was started with parameter values that were disturbed with a strength of ε = 0.2, so that Pnew = Pcurrent × 10(ε×ϕ) with ϕ being normally distributed with mean 0 and variance 1. A detailed description of the development of entire models and their relative χ2 value and Akaike information criterion (AIC) have been provided in (ESI Section-2 and Section-3†). The χ2 value was calculated according to the following equationwhere, yi being the experimental data points and y(ti; P) is the simulated value at time point i for parameter value P, σ is the standard deviation of the experimental data set. The AIC (Akaike information criterion) is defined as-
| AIC = (−2 × LL) + (2 × p) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) likelihood) = (−0.5 × (N/2)log(2π), p designates the number of fitted parameters and N represents the number of fitted data points. Once the best-fitted parameter set for any model is obtained after optimization, the rest of the simulation and analysis was done using freely available software XPPAUT by considering corresponding ODE files for the respective best-fitted model. (http://www.math.pitt.edu/%7Ebard/xpp/xpp.html)
likelihood) = (−0.5 × (N/2)log(2π), p designates the number of fitted parameters and N represents the number of fitted data points. Once the best-fitted parameter set for any model is obtained after optimization, the rest of the simulation and analysis was done using freely available software XPPAUT by considering corresponding ODE files for the respective best-fitted model. (http://www.math.pitt.edu/%7Ebard/xpp/xpp.html)
Data availability
The datasets supporting this article have been uploaded as part of the ESI†. This includes the network figures, equations of the models, supplementary figures, additional model descriptions. The models are readily available in sbml format (https://github.com/baichandra05/Genericmodel_protein_aggregation) in GitHub repository.Author contributions
B. T., S. K. M, and S. K. designed the research problem. B. T. developed the mathematical model together with S. K. B. T. performed the parameter optimization and modelling studies with inputs from S. K. M. and S. K. B. T., S. K. M., and S. K. analysed the modelling outputs and wrote the paper together.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
Thanks are due to IIT Bombay for providing fellowship to BT. We want to acknowledge the help provided by Mr Pradeep Kadu, Ms. Debalina Datta and Dr Atanu Maity for the graphical representation of the ESI (Fig. S1†). This work is supported by the funding agency SERB, India (Grant no. CRG/2019/002640 and Grant no. MTR/2020/000261).References
- C. M. Dobson, Nature, 2003, 426, 884–890 CrossRef CAS PubMed.
- C. Soto, Nat. Rev. Neurosci., 2003, 4, 49–60 CrossRef CAS PubMed.
- K. A. Dill and J. L. MacCallum, Science, 2012, 338, 1042–1046 CrossRef CAS PubMed.
- R. Lumry and H. Eyring, J. Phys. Chem., 1954, 58, 110–120 CrossRef CAS.
- C. F. Wright, S. A. Teichmann, J. Clarke and C. M. Dobson, Nature, 2005, 438, 878–881 CrossRef CAS PubMed.
- F. Chiti and C. M. Dobson, Annu. Rev. Biochem., 2006, 75, 333–366 CrossRef CAS PubMed.
- J. Hardy and D. J. Selkoe, Science, 2002, 297, 353–356 CrossRef CAS PubMed.
- S. K. Maji, M. H. Perrin, M. R. Sawaya, S. Jessberger, K. Vadodaria, R. A. Rissman, P. S. Singru, K. P. R. Nilsson, R. Simon, D. Schubert and others, Science, 2009, 325, 328–332 CrossRef CAS PubMed.
- D. Otzen and R. Riek, Cold Spring Harbor Perspect. Biol., 2019, 11, a033860 CrossRef CAS PubMed.
- C. Soto and S. Pritzkow, Nat. Neurosci., 2018, 21, 1332–1340 CrossRef CAS PubMed.
- S. Mehra, S. Sahay and S. K. Maji, Biochim. Biophys. Acta, Proteins Proteomics, 2019, 1867, 890–908 CrossRef CAS PubMed.
- M. Goedert, Science, 2015, 349, 6248 CrossRef PubMed.
- M. G. Iadanza, M. P. Jackson, E. W. Hewitt, N. A. Ranson and S. E. Radford, Nat. Rev. Mol. Cell Biol., 2018, 19, 755–773 CrossRef CAS PubMed.
- E. Muchtar, A. Dispenzieri, H. Magen, M. Grogan, M. Mauermann, E. D. McPhail, P. J. Kurtin, N. Leung, F. K. Buadi, D. Dingli and others, J. Intern. Med., 2021, 289, 268–292 CrossRef CAS PubMed.
- M. A. Liz, T. Coelho, V. Bellotti, M. I. Fernandez-Arias, P. Mallaina and L. Obici, Neurology and Therapy, 2020, 1–8 Search PubMed.
- E. A. Fry and K. Inoue, Cancer Invest., 2019, 37, 46–65 CrossRef CAS PubMed.
- K. Tsukita, H. Sakamaki-Tsukita, K. Tanaka, T. Suenaga and R. Takahashi, Mov. Disord., 2019, 34, 1452–1463 CrossRef CAS PubMed.
- J.-C. Park, S.-H. Han and I. Mook-Jung, BMB Rep., 2020, 53, 10 CrossRef CAS PubMed.
- A. Bougea, L. Stefanis, G. P. Paraskevas, E. Emmanouilidou, K. Vekrelis and E. Kapaki, Neurol. Sci., 2019, 40, 929–938 CrossRef PubMed.
- A. Aguzzi and T. O'connor, Nat. Rev. Drug Discovery, 2010, 9, 237–248 CrossRef CAS PubMed.
- M. M. Picken, Acta Haematol., 2020, 143, 322–334 CrossRef CAS PubMed.
- J. Gottwald and C. Röcken, Crit. Rev. Biochem. Mol. Biol., 2021, 1–17 Search PubMed.
- L. Breydo and V. N. Uversky, FEBS Lett., 2015, 589, 2640–2648 CrossRef CAS PubMed.
- B. Winner, R. Jappelli, S. K. Maji, P. A. Desplats, L. Boyer, S. Aigner, C. Hetzer, T. Loher, M. Vilar, S. Campioni and others, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4194–4199 CrossRef CAS PubMed.
- T. P. J. Knowles, M. Vendruscolo and C. M. Dobson, Nat. Rev. Mol. Cell Biol., 2014, 15, 384–396 CrossRef CAS PubMed.
- S. I. A. Cohen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 08B611 Search PubMed.
- T. P. J. Knowles, C. A. Waudby, G. L. Devlin, S. I. A. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, Science, 2009, 326, 1533–1537 CrossRef CAS PubMed.
- C. C. Lee, A. Nayak, A. Sethuraman, G. Belfort and G. J. McRae, Biophys. J., 2007, 92, 3448–3458 CrossRef CAS PubMed.
- A. Lomakin, D. B. Teplow, D. A. Kirschner and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 7942–7947 CrossRef CAS PubMed.
- M. M. Pallitto and R. M. Murphy, Biophys. J., 2001, 81, 1805–1822 CrossRef CAS PubMed.
- G. Meisl, J. B. Kirkegaard, P. Arosio, T. C. T. Michaels, M. Vendruscolo, C. M. Dobson, S. Linse and T. P. J. Knowles, Nat. Protoc., 2016, 11, 252–272 CrossRef CAS PubMed.
- E. T. Powers and D. L. Powers, Biophys. J., 2006, 91, 122–132 CrossRef CAS PubMed.
- S. Ranganathan, D. Ghosh, S. K. Maji and R. Padinhateeri, Sci. Rep., 2016, 6, 1–14 CrossRef PubMed.
- R. Crespo, F. A. Rocha, A. M. Damas and P. M. Martins, J. Biol. Chem., 2012, 287, 30585–30594 CrossRef CAS PubMed.
- A. Lomakin, D. B. Teplow, D. A. Kirschner and G. B. Benedeki, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 7942–7947 CrossRef CAS PubMed.
- A. Lomakin, D. S. Chung, G. B. Benedek, D. A. Kirschner and D. B. Teplow, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 1125–1129 CrossRef CAS PubMed.
- J. D. Schmit, K. Ghosh and K. Dill, Biophys. J., 2011, 100, 450–458 CrossRef CAS PubMed.
- A. J. Dear, T. C. T. Michaels, G. Meisl, D. Klenerman, S. Wu, S. Perrett, S. Linse, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12087–12094 CrossRef CAS PubMed.
- M. Bucciantini, E. Giannoni, F. Chiti, F. Baroni, L. Formigli, J. Zurdo, N. Taddei, G. Ramponi, C. M. Dobson and M. Stefani, Nature, 2002, 416, 507–511 CrossRef CAS PubMed.
- R. Nelson, M. R. Sawaya, M. Balbirnie, A. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778 CrossRef CAS PubMed.
- S. Kumar and J. B. Udgaonkar, Curr. Sci., 2010, 639–656 CAS.
- R. Wetzel, Acc. Chem. Res., 2006, 39, 671–679 CrossRef CAS PubMed.
- J. E. Gillam and C. E. Macphee, J. Phys.: Condens. Matter, 2013, 25, 37 CrossRef PubMed.
- W. F. Xue, S. W. Homans and S. E. Radford, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8926–8931 CrossRef CAS PubMed.
- T. R. Serio, A. G. Cashikar, A. S. Kowal, G. J. Sawicki, J. J. Moslehi, L. Serpell, M. F. Arnsdorf and S. L. Lindquist, Science, 2000, 289, 1317–1321 CrossRef CAS PubMed.
- P. Arosio, T. P. J. Knowles and S. Linse, Phys. Chem. Chem. Phys., 2015, 17, 7606–7618 RSC.
- V. N. Uversky, Curr. Alzheimer Res., 2008, 5, 260–287 CrossRef CAS PubMed.
- A. K. Dunker, M. M. Babu, E. Barbar, M. Blackledge, S. E. Bondos, Z. Dosztányi, H. J. Dyson, J. Forman-Kay, M. Fuxreiter, J. Gsponer and others, Intrinsically Disord. Proteins, 2013, 1, e24157 CrossRef PubMed.
- K. Kuwajima, Proteins: Struct., Funct., Bioinf., 1989, 6, 87–103 CrossRef CAS PubMed.
- G. V. Semisotnov, N. A. Rodionova, O. I. Razgulyaev, V. N. Uversky, A. F. Gripas' and R. I. Gilmanshin, Biopolym. Orig. Res. Biomol., 1991, 31, 119–128 CAS.
- D. Ghosh, P. K. Singh, S. Sahay, N. N. Jha, R. S. Jacob, S. Sen, A. Kumar, R. Riek and S. K. Maji, Sci. Rep., 2015, 5, 1–15 Search PubMed.
- V. L. Anderson, T. F. Ramlall, C. C. Rospigliosi, W. W. Webb and D. Eliezer, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18850–18855 CrossRef CAS PubMed.
- C. Dammers, M. Schwarten, A. K. Buell and D. Willbold, Chem. Sci., 2017, 8, 4996–5004 RSC.
- T. Q. Faria, Z. L. Almeida, P. F. Cruz, C. S. H. Jesus, P. Castanheira and R. M. M. Brito, Phys. Chem. Chem. Phys., 2015, 17, 7255–7263 RSC.
- K. Gadhave and R. Giri, Biochem. Biophys. Res. Commun., 2020, 524, 446–452 CrossRef CAS PubMed.
- M. Törnquist, T. C. T. Michaels, K. Sanagavarapu, X. Yang, G. Meisl, S. I. A. Cohen, T. P. J. Knowles and S. Linse, Chem. Commun., 2018, 54, 8667–8684 RSC.
- T. C. T. Michaels, A. Šarić, S. Curk, K. Bernfur, P. Arosio, G. Meisl, A. J. Dear, S. I. A. Cohen, C. M. Dobson, M. Vendruscolo, S. Linse and T. P. J. Knowles, Nat. Chem., 2020, 12, 445–451 CrossRef CAS PubMed.
- S. I. A. Cohen, S. Linse, L. M. Luheshi, E. Hellstrand, D. A. White, L. Rajah, D. E. Otzen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9758–9763 CrossRef CAS PubMed.
- T. Maiwald and J. Timmer, Bioinformatics, 2008, 24, 2037–2043 CrossRef CAS PubMed.
- C. Dammers, M. Schwarten, A. K. Buell and D. Willbold, Chem. Sci., 2017, 8, 4996–5004 RSC.
- S. J. Wood, J. Wypych, S. Steavenson, J.-C. Louis, M. Citron and A. L. Biere, J. Biol. Chem., 1999, 274, 19509–19512 CrossRef CAS PubMed.
- M. Kodaka, Biophys. Chem., 2004, 109, 325–332 CrossRef CAS PubMed.
- G. M. Mohite, R. Kumar, R. Panigrahi, A. Navalkar, N. Singh, D. Datta, S. Mehra, S. Ray, L. G. Gadhe, S. Das and others, Biochemistry, 2018, 57, 5183–5187 CrossRef CAS PubMed.
- D. Ghosh, S. Sahay, P. Ranjan, S. Salot, G. M. Mohite, P. K. Singh, S. Dwivedi, E. Carvalho, R. Banerjee, A. Kumar and S. K. Maji, Biochemistry, 2014, 53, 6419–6421 CrossRef CAS PubMed.
- V. N. Uversky, J. Li, P. Souillac, I. S. Millett, S. Doniach, R. Jakes, M. Goedert and A. L. Fink, J. Biol. Chem., 2002, 277, 11970–11978 CrossRef CAS PubMed.
- F. Chiti, M. Stefani, N. Taddei, G. Ramponi and C. M. Dobson, Nature, 2003, 424, 805–808 CrossRef CAS PubMed.
- D. Ghosh, M. Mondal, G. M. Mohite, P. K. Singh, P. Ranjan, A. Anoop, S. Ghosh, N. N. Jha, A. Kumar and S. K. Maji, Biochemistry, 2013, 52, 6925–6927 CrossRef CAS PubMed.
- S. B. Nielsen, F. Macchi, S. Raccosta, A. E. Langkilde, L. Giehm, A. Kyrsting, A. S. P. Svane, M. Manno, G. Christiansen, N. C. Nielsen, L. Oddershede, B. Vestergaard and D. E. Otzen, PLoS One, 2013, 8, 1–13 CrossRef.
- S. Xu, J. Phys. Chem. B, 2009, 113, 12447–12455 CrossRef CAS PubMed.
- M. Perni, C. Galvagnion, A. Maltsev, G. Meisl, M. B. D. Müller, P. K. Challa, J. B. Kirkegaard, P. Flagmeier, S. I. A. Cohen, R. Cascella, S. W. Chen, R. Limboker, P. Sormanni, G. T. Heller, F. A. Aprile, N. Cremades, C. Cecchi, F. Chiti, E. A. A. Nollen, T. P. J. Knowles, M. Vendruscolo, A. Bax, M. Zasloff and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1009–E1017 CrossRef CAS PubMed.
- C. Månsson, P. Arosio, R. Hussein, H. H. Kampinga, R. M. Hashem, W. C. Boelens, C. M. Dobson, T. P. J. Knowles, S. Linse and C. Emanuelsson, J. Biol. Chem., 2014, 289, 31066–31076 CrossRef PubMed.
- S. I. A. Cohen, P. Arosio, J. Presto, F. R. Kurudenkandy, H. Biverstål, L. Dolfe, C. Dunning, X. Yang, B. Frohm, M. Vendruscolo and others, Nat. Struct. Mol. Biol., 2015, 22, 207 CrossRef CAS PubMed.
- A. Mukhopadhyay, S. Mehra, R. Kumar, S. K. Maji, G. Krishnamoorthy and K. P. Sharma, ChemPhysChem, 2019, 20, 2783–2790 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03190b |
| This journal is © The Royal Society of Chemistry 2021 |