Open Access Article
Open Access ArticleFiltering and continuously separating microplastics from water using electric field gradients formed electrochemically in the absence of buffer†
Jonathan R.
Thompson
 ,
Logan M.
Wilder
,
Logan M.
Wilder
 and
Richard M.
Crooks
and
Richard M.
Crooks
 *
*
Department of Chemistry, Texas Materials Institute, The University of Texas at Austin, 105 E. 24th St., Stop A5300, Austin, Texas 78712-1224, USA. E-mail: crooks@cm.utexas.edu; Tel: +1-512-475-8674
First published on 29th September 2021
Abstract
Here we use experiments and finite element simulations to investigate the electrokinetics within straight microchannels that contain a bipolar electrode and an unbuffered electrolyte solution. Our findings indicate that in the presence of a sufficiently high electric field, water electrolysis proceeds at the bipolar electrode and leads to variations in both solution conductivity and ionic current density along the length of the microchannel. The significance of this finding is twofold. First, the results indicate that both solution conductivity and ionic current density variations significantly contribute to yield sharp electric field gradients near the bipolar electrode poles. The key point is that ionic current density variations constitute a fundamentally new mechanism for forming electric field gradients in solution. Second, we show that the electric field gradients that form near the bipolar electrode poles in unbuffered solution are useful for continuously separating microplastics from water in a bifurcated microchannel. This result expands the potential scope of membrane-free separations using bipolar electrodes.
Introduction
In this report, we present detailed experimental results and finite element simulations aimed at understanding electrokinetics within microchannels that contain a bipolar electrode (BPE) and unbuffered electrolyte solution. This study is in contrast to earlier, related results from our group1,2 and others3–5 that relied on buffered solutions to modulate the local electric field in microchannels. Our new findings reveal that faradaic water hydrolysis at a BPE modulates both the ionic conductivity and the ionic current passing through an unbuffered solution. This result is significant because ionic conductivity gradients and the variations in the ionic current yield sharp, local electric field gradients by a fundamentally new mechanism. That is, unlike previously reported methods, this approach does not rely on ion depletion zones or geometric factors6,7 to form electric field gradients. Finally, we show that electric field gradients formed in unbuffered solutions are useful for both filtering and continuously separating microplastics from water. As we will discuss later, these results broaden the potential scope of membrane-free separations using BPEs.Microplastics are usually defined as plastic particles having a diameter smaller than 5.0 mm. Over the past decade such particles have been detected in various media, including seawater,8 drinking water,9,10 air,11 and soil.12 As a result, there is a growing effort to understand the potential environmental and human health impacts of microplastics.13–15 As microplastic exposure and hazard studies are being performed, however, it is becoming clear that there are not appropriate analytical tools for sampling, separating, and detecting microplastics.16 In light of this, the development of appropriate analytical techniques is critical for the field.
Charge-based separation processes are promising candidates for studying microplastics, because common plastics are often charged or develop a charge upon interacting with natural organic matter when in solution.17–20 One interesting charge-based technique that is useful for manipulating ion motion involves the use of electric field gradients. Indeed, the first report utilizing electric field gradients was published by Koegler and Ivory in 1996.6 In this article, an electrochromatography column having a variable cross-sectional area was used. Under constant electrolyte conditions, cross-sectional area is inversely related to the electric field. Thus, the variable cross-sectional area resulted in an electric field gradient along the length of the column, which was shown to be useful for isolating and focusing charged proteins.
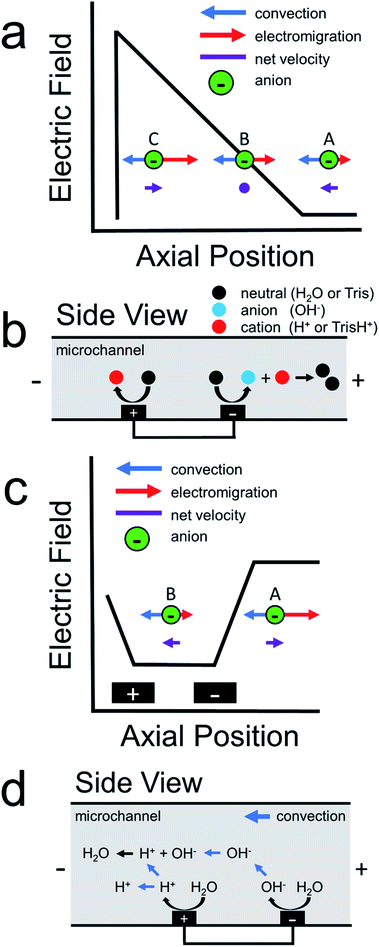
Scheme 1a illustrates how an electric field gradient can be used to focus charged analytes such as proteins. In this scheme, consider the motion of anions within a variable electric field. We assume uniform convection and uniform electrophoretic mobility of the charged analyte. At position A, convection dominates electromigration and anions move from right-to-left. In contrast, at position B, convection and migration are equal and opposite, and therefore anions experience no net force at this location. Lastly, anions that diffuse downstream to position C encounter a high electric field. This enhanced electric field acts as a restorative force, redirecting anions back to position B. The net effect is continuous focusing of the anionic species along the electric field gradient. Sensibly, this method was termed electric field gradient focusing.21
Following the initial report of electric field gradient focusing, many different approaches for forming electric field gradients were developed. These include temperature gradient focusing,22,23 digital field gradient focusing,24,25 conductivity gradient focusing,26 and ion concentration polarization.27,28 More recently, our group introduced an electrochemical method for forming electric field gradients, which we called faradaic ion concentration polarization (fICP).1,2Scheme 1b illustrates the fICP process. Here, a BPE is patterned on the floor of a microfluidic channel containing a buffered electrolyte solution. When a sufficiently high voltage is applied across the length of the microfluidic channel, water electrolysis occurs at the ends of the BPE.5,29,30 For example, water reduction occurs at the BPE cathode to form OH− (eqn (1)). If Tris buffer is present in solution, then OH− reacts with TrisH+ to yield neutral Tris (eqn (2)). To maintain charge neutrality across the BPE, water oxidation at the BPE anode produces H+ (eqn (3)).
BPE cathode:
| 2H2O + 2e− → 2OH− + H2 | (1) |
| TrisH+ + OH− → Tris + H2O | (2) |
BPE anode:
| 2H2O → 4H+ + 4e− + O2 | (3) |
During fICP, buffer neutralization (eqn (2)) in solution near the BPE cathode is important because it results in a lower local concentration of ions relative to the bulk solution. Accordingly, this region is termed an ion depletion zone (IDZ), and it is characterized by a relatively high solution resistance compared to the bulk. In the presence of an applied electric field, the solution conductivity gradient between the bulk solution and the IDZ forms a co-located electric field gradient.
We have shown that the electric field gradient formed during fICP is useful for enriching,31,32 separating,33–36 and controlling analyte motion in solution.37 One key limitation associated with the use of fICP for technological applications, however, is that fICP relies on the presence of a buffer in solution to facilitate the formation of the IDZ and concomitant electric field gradient.5 Therefore, it is desirable to consider methods that operate on the same principle as fICP but that do not require a buffer for practical uses like separating microplastics in seawater or fresh water.
In 2011, our group described an electrokinetic technique related to fICP that utilized BPEs in unbuffered solution to filter anions in microchannels.38 Due to the absence of a buffer in solution, we proposed that water electrolysis at the BPE locally increased solution conductivity between the BPE poles. As a result, the electric field between the BPE poles decreased relative to the electric field outside of the BPE poles. Scheme 1c is a schematic illustration for the proposed shape of the electric field during this experiment.38 As shown in this scheme, the elevated electric field upstream (to the right, at position A) of the BPE cathode results in increased electromigration. Under this set of conditions, electromigration of anions dominates convection (due to electroosmotic flow, EOF) and redirects anions upstream. Downstream of the BPE cathode (to the left, at position B), anions experience a decreased electric field. Here, anions flow downstream because convection dominates electromigration. The net effect is that low mobility anions are filtered from the vicinity of the BPE. Finally, it is important to note that, unlike fICP, this technique does not rely on the formation of an IDZ to alter the electric field. Rather, the increase in ion concentration between the BPE poles, relative to the bulk solution, accounts for the changes in the local electric field.
The present study uses both experiments and finite element simulations to develop an understanding of how ion filtering works in unbuffered electrolyte solutions. The results indicate that sharp electric field gradients form in solution near the BPE poles for two reasons. First, ionic conductivity gradients form and alter the electric field as discussed above in the context of Scheme 1c. Second, the BPE provides an alternative pathway for current to flow through the system. As a result, the BPE shunts electrical current away from the microchannel, which leads to less ionic current flowing in solution between the BPE poles relative to outside of the BPE poles.39–41 These variations in ionic current contribute to the electric field gradients that form in solution. This latter point is important because, while it is widely understood that BPEs shunt current away from solution, the consequences on the local electric field have previously been overlooked.
Finally, we show that by using a bifurcated microchannel, this new method for forming electric field gradients facilitates the continuous separation of microplastics in unbuffered electrolyte solutions. There are two main points arising from this result. First, continuous separations provide many benefits compared to the previously reported filtration experiment,38 including the ability to integrate downstream functionalities (e.g., detection) and the capability of separating multiple analytes simultaneously.34,42 Second, electrokinetic separations using BPEs are no longer limited to buffered solutions, which will greatly increase the range of membrane-free separations using BPEs.
Experimental section
Chemicals
Reagent grade KCl and HCl were obtained from Fisher Scientific. Carboxyl-functionalized polystyrene microbeads were purchased from Bangs Laboratories (diameter = 0.99 μm, electrophoretic mobility = −2.0 ± 0.5 μm cm V−1 s−1,34 Fishers, IN). The m-cresol purple pH indicator was obtained from Sigma-Aldrich. All solutions were prepared using deionized water (DI water, >18.0 MΩ cm, MilliQ Gradient System, Millipore, Burlington, MA). Polydimethylsiloxane (PDMS) was prepared using an elastomer kit (Sylgard 184, Dow Silicones Corp, Midland, MI). All reagents were used as received without additional purification.Microfluidic device fabrication
The hybrid glass/PDMS microfluidic device was fabricated using standard photolithographic procedures described in previous reports.34,43 Briefly, glass slides were placed in freshly prepared piranha solution (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2SO4
1 H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2, caution: piranha reacts violently with organic materials and solvents) for 15 min and then rinsed with DI water and dried with N2. Following this, Micro Prime HP Primer adhesion promoter (Shin-Etsu MicroSi, Phoenix, AZ) and AZ 1518 photoresist (AZ Electronic Materials, Somerville, NH) were spincoated onto the glass slides, which were then exposed to UV light through a mask. Next, the photoresist design was developed using AZ 400K developer (AZ Electronic Materials). Electron beam physical vapor deposition was then used to deposit 10 nm of Ti and 100 nm of Pt onto the resist-coated slide (Kurt J. Lesker Company, Jefferson Hills, PA). Finally, standard lift-off procedures were performed which resulted in Pt circuits on the glass slide.
H2O2, caution: piranha reacts violently with organic materials and solvents) for 15 min and then rinsed with DI water and dried with N2. Following this, Micro Prime HP Primer adhesion promoter (Shin-Etsu MicroSi, Phoenix, AZ) and AZ 1518 photoresist (AZ Electronic Materials, Somerville, NH) were spincoated onto the glass slides, which were then exposed to UV light through a mask. Next, the photoresist design was developed using AZ 400K developer (AZ Electronic Materials). Electron beam physical vapor deposition was then used to deposit 10 nm of Ti and 100 nm of Pt onto the resist-coated slide (Kurt J. Lesker Company, Jefferson Hills, PA). Finally, standard lift-off procedures were performed which resulted in Pt circuits on the glass slide.
The PDMS microchannel was formed using an elastomer kit and microchannel mold patterned using SU-8 photoresist (MicroChem, Westborough, MA) on a Si wafer. Inlet and outlet reservoirs were punched into the PDMS block using a 4 mm biopsy punch. The glass slide and PDMS were then rinsed with ethanol, dried with N2, and exposed to an O2 plasma for 45 s (medium power, 60 W, model PDC-32G, Harrick Scientific, Ithaca, NY). Finally, the PDMS and glass were brought into contact and baked at 65 °C for 5 min to promote irreversible bonding.
Filtration experiments
The filtration experiments were similar to those we have reported previously.38 Specifically, a 15.0 μm tall, 100.0 μm wide, and 6.0 mm long straight microchannel was used. 20.0 μL of a solution containing 1.0 mM KCl and 30 fM polystyrene microbeads (microplastics) were placed into the inlet reservoir of the device. The solution was allowed to flow through the device for 1 min. Because the density of polystyrene is about the same as water, the microplastics can be used as a proxy to track pressure-driven flow (PDF) in the absence of an applied voltage. With this in mind, the solution volume in the outlet reservoir was then adjusted so that there was approximately no PDF. Next, an electric field was established in solution by using a power supply (PWS 4721, Tektronix, Beaverton, OR) to apply 30.0 V to electrodes patterned on the floor of the inlet and outlet reservoirs. Two microband electrodes patterned on the floor of the microchannel were then connected externally using a jumper wire to form a 3.0 mm BPE. Note that two microband electrodes connected externally are equivalent to a single, continuous BPE of the same length.29,44 Finally, upon completion of the experiment, the two poles of the BPE were disconnected and the power supply was turned off.Filtration of microplastics was observed using an inverted microscope (Eclipse TE 2000-U, Nikon, Japan) and a CCD camera (Cascade 512, Photometrics, Tucson, AZ). Images were collected and analyzed using V++ (Digital Optics, New Zealand) and ImageJ (NIH, Bethesda, MD) software.
During the filtration process, the total current (iTOT) flowing through the microchannel was measured by placing an electrometer (6517B Electrometer, Keithley, Cleveland, OH) in series with the driving electrodes. Simultaneously, the current through the BPE (iBPE) was detected using a handheld multimeter (AM-1118, Aktakom, Russia) placed in series with the microband electrodes.
Conductivity measurements
Conductivity measurements were collected during the filtration experiments using a previously reported, homebuilt conductivity meter.45,46 Briefly, two microbands with a center-to-center spacing of 60.0 μm were used for the measurements. An AC sine wave (amplitude ± 0.30 V, 120 kHz) was applied to the first microband using a function generator (Model 182A, Wavetek, San Diego, CA). Current passed through solution to the second microband where it was amplified and converted back to a voltage using a transimpedance amplifier. The level of current attenuation was then correlated to solution conductivity using a calibration curve (ESI, Fig. S1†). Replicate experiments were performed on the same microfluidic device using different pairs of microband electrodes to obtain conductivity data at several locations along the length of the microchannel.pH indicator experiments
The pH indicator experiments were performed exactly as the foregoing filtration experiments but, in this case, the solution that flowed through the device contained 5.0 mM m-cresol purple (titrated to pH 7.0 using 1.0 M HCl) and 30 fM polystyrene microbeads. The color of the solution was observed using an inverted microscope (Eclipse Ti2, Nikon) and a color CMOS camera (DS-Fi3, Nikon). Images were acquired using NIS Elements software (Version 5.11, Nikon).Continuous separation experiments
Continuous separation experiments were similar to the filtration experiments, but with the following two differences. First, instead of a straight microchannel, a bifurcated microchannel (main channel: 15.0 μm tall, 200.0 μm wide, and 3.0 mm long; outlet channels: 15.0 μm tall, 100.0 μm wide, and 3.0 mm long) was used. Second, the solution that was flowed through the device during the experiment contained 5.0 mM KCl, instead of 1.0 mM KCl, and 30 fM polystyrene microbeads. Current data (iTOT, iBPE) and images of the continuous separation were collected in the same manner as for the filtration experiments.Numerical simulations
Finite element simulations were performed using COMSOL Multiphysics software (version 5.5) on a Dell Precision workstation (Model T7500) equipped with 108 GB RAM and two Intel Xeon processors (2.40 GHz). All simulations were run at steady state. Complete details regarding the simulations are provided in the ESI.†Results and discussion
Filtering microplastics in unbuffered solutions
The goal of this study is to understand the electrokinetic filtration of charged species in unbuffered solution. Microplastics were used in this case, rather than a molecular fluorophore,38 because microplastics can be tracked optically. As we will show, this provides certain benefits that improve our understanding of the filtration mechanism.Details of how the filtration experiments were performed are included in the Experimental section. Briefly, a solution containing 1.0 mM KCl and 30 fM of negatively charged, ∼1 μm polystyrene microbeads (microplastics) was placed into the reservoirs of a straight-microchannel device. The solution volumes in the inlet and outlet were then adjusted so that there was negligible PDF. Lastly, 30.0 V was applied across the length of the microchannel and the two poles of the BPE were connected externally using a jumper wire. Note that the BPE is considered “active” when the two poles are connected.
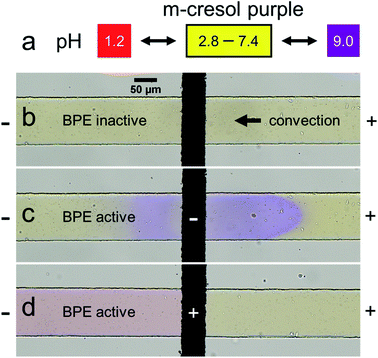
Fig. 1a is a schematic illustration of the straight microchannel device used during filtration experiments. Fig. 1b–d are a series of optical micrographs from a representative microplastic filtration experiment which display the region of the microchannel that contains the BPE cathode (Fig. 1a, dashed red box). The full video from which these frames are extracted is provided in the ESI (Video S1†). Fig. 1b was obtained after applying the driving voltage but before connecting the BPE poles. Here, the microplastics are moving from right-to-left by EOF, and they are evenly distributed throughout the microchannel. This is the expected result when the BPE is inactive because the electric field throughout the length of the microchannel, and thus microplastic transport, is uniform.
Fig. 1c shows the device 30 s after connecting the BPE poles. The most important result from this frame is that there are no microplastics present downstream (to the left) of the BPE cathode. This finding confirms that it is possible to filter microplastics from a microchannel that contains unbuffered solution. The mechanism of this electrokinetic filtration will be discussed later.
Finally, Fig. 1d shows the device ∼5 s after disconnecting the BPE poles. In this frame, there are more microplastics present in solution than before the filtration process (Fig. 1b). This is because filtering concentrates the microplastics near the right-most reservoir of the microchannel. Therefore, when the BPE poles are disconnected, the solution plug containing the enriched microplastics flows downstream. Note that this same type of analyte enrichment has been observed previously47–50 and was attributed to electric field gradients that formed as a consequence of non-uniform geometry at the channel entrance.
In the previous filtration report from our group,38 we hypothesized that the mechanism illustrated in Scheme 1d was responsible for analyte filtering. Here, water electrolysis occurs at the poles of the BPE. Specifically, OH− electrogenerated at the BPE cathode flows downstream by convection, which significantly increases solution conductivity between the BPE poles. The OH− flowing downstream also neutralizes the majority of H+ produced at the BPE anode. Unreacted H+ moves downstream, due to electromigration and convection, which slightly increases solution conductivity downstream of the BPE. Increased solution conductivity between the BPE poles and downstream of the BPE anode lowers the local electric field in these regions of the microchannel. Consequently, the electric field upstream of the BPE cathode is elevated relative to the downstream side (Scheme 1c). This redistribution of the electric field redirects anions away from the BPE cathode.
To explore the validity of the foregoing proposed mechanism, the microplastic filtration experiment discussed earlier was repeated, but in this case the solution contained 5.0 mM m-cresol purple in place of 1.0 mM KCl. The m-cresol purple is a pH indicator, and therefore it provides a simple means to investigate local pH variations in the microchannel. The mechanism embodied by Scheme 1d indicates that such position-dependent pH changes should be observed.
Fig. 2 shows the results of the pH indicator experiment. Fig. 2a represents the pH-dependent color of m-cresol purple. At low pH it is red, at intermediate pH yellow, and at high pH purple. Fig. 2b shows the region of the microchannel containing the BPE cathode before connecting the BPE poles. In this case, the solution color is yellow because the pH is neutral everywhere.
Fig. 2c shows the microfluidic device at the same location, but ∼1 s after connecting the BPE poles. Here, the solution color is in the process of changing from yellow to purple both upstream and downstream of the BPE cathode, indicating that the solution is basic (Fig. 2a, pH > 9.0). The observation of a basic pH upstream of the BPE cathode is significant, because it represents a deviation from the previously proposed filtration mechanism.38 Specifically, all OH− generated at the BPE cathode was hypothesized to move downstream (Scheme 1d) in the earlier analysis. In contrast, Fig. 2c reveals that a fraction of the OH− produced at the BPE cathode electromigrates upstream, against convection, toward the anode of the driving electrodes. The remainder of the OH− flows downstream due to solution convection (in accordance with Scheme 1d).
Fig. 2d shows the region of the channel near the BPE anode ∼5 s after connecting the BPE poles. The solution color is red downstream of the BPE anode, indicating that the solution is acidic (Fig. 2a, pH < 1.2). The solution upstream of the BPE anode remains yellow, however, showing the solution is less acidic. These findings are logical, because faradaic water oxidation produces H+ at the BPE anode, which is transported downstream due to both electromigration and solution convection. Accordingly, the pH upstream of the BPE anode should remain unchanged. Full videos of replicate pH indicator experiments are included in the ESI (Videos S2 and S3†).
Finally, Table 1 qualitatively summarizes the pH variations from both the previously proposed filtration mechanism38 and those observed during the pH indicator experiment. Most importantly, the pH variations predicted by our original hypothesis are not fully consistent with the experimentally observed pH changes, which indicate that the proposed filtration mechanism is not entirely correct. Therefore, in the next section, numerical simulations were performed to explore the ionic distributions and the electric field during the filtration process.
| Downstream of BPE | Between BPE poles | Upstream of BPE | |
|---|---|---|---|
| Proposed pH | Acidic | Basic | Neutral |
| Experimental pH | Acidic | Basic | Basic |
Numerical simulations
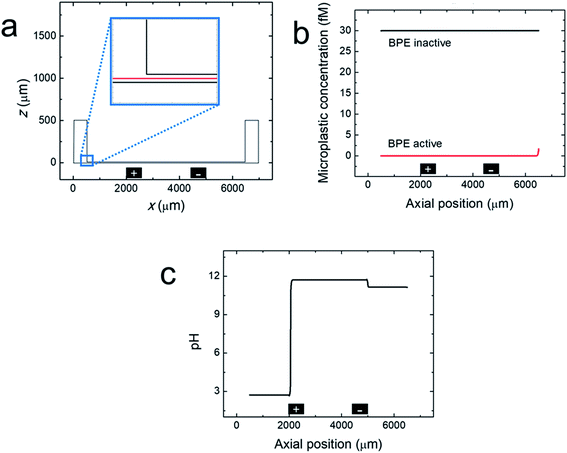
Finite element simulations were performed using a two-dimensional model of the xz plane of the straight-microchannel device. Fig. 3a shows the modeled domain, which contains the whole microchannel as well as a portion of the inlet and outlet reservoirs. The inset magnifies the portion of the domain where the microchannel meets the outlet reservoir. The red cutline shown in the inset is located at the mid-height of the microchannel (z = 7.5 μm).Complete details regarding the theory and methods used to perform the simulations are provided in the ESI. Briefly, solution convection was resolved using the Navier–Stokes equation, and mass transport and the electric potential were modeled using the Nernst–Planck and Poisson equations. EOF was approximated using the Helmholtz–Smoluchowski slip velocity boundary condition. Note that any dynamics associated with a variable zeta potential51,52 were not accounted for in the model. Products electrogenerated at the driving electrodes were not considered in the model (ESI, Fig. S2†). The BPE poles were modeled as boundaries on the floor of the microchannel; their locations are indicated by the black rectangles shown in Fig. 3a. The experimental steady-state current (iBPE) was used to calculate and fix the current through the BPE by setting a uniform ionic flux through the BPE surface. Here, all current through the BPE was assumed to go towards water reduction (eqn (1)) and water oxidation (eqn (3)) at the BPE cathode and BPE anode, respectively. Finally, the microplastics were modelled as point charges.
Fig. 3b, c and 4 show line plots of simulated parameters within the microchannel (from x = 500 μm to 6500 μm) as a function of axial position along the red cutline shown in the Fig. 3a inset. Fig. 3b shows the simulated microplastic concentration in the microchannel before and after activating the BPE. When the BPE is inactive, the microplastics are uniformly distributed throughout the microchannel at the initial concentration (30 fM). After activating the BPE, however, the concentration of the microplastics throughout the channel is 0. The slight increase in microplastic concentration observed near the microchannel entrance (x = 6500 μm) is due to a concentration gradient from the reservoir boundary to the microchannel entrance (ESI, Fig. S3†). These results confirm that the microplastics are filtered from the microchannel in the simulations, which corresponds well to the experimental results (Fig. 1b and c).
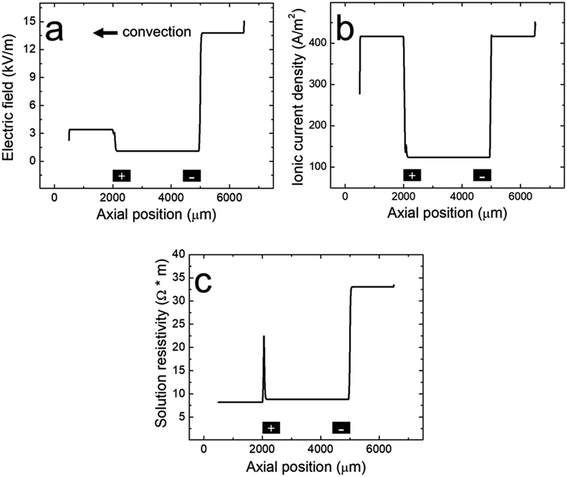 | ||
| Fig. 4 Line plots of the simulated (a) electric field, (b) ionic current density, and (c) solution resistivity within the microchannel along the red cutline shown in the Fig. 3a inset when the BPE is active during a filtration experiment. The black rectangles are not to scale, but represent the distal edges of the BPE poles. | ||
Fig. 3c presents the simulated pH when the BPE is active. This plot reveals that the solution upstream of the BPE cathode (x > 5000 μm) and between the BPE poles (2000 μm < x < 5000 μm) is basic. As discussed earlier, the solution upstream of the BPE cathode is basic because a fraction of the electrogenerated OH− migrates towards the driving anode. The remaining OH− flows downstream by convection, resulting in basic solution between the BPE poles. This OH− continues to the BPE anode where it partially neutralizes electrogenerated H+. Note that because a portion of the electrogenerated OH− migrates upstream, a corresponding fraction of H+ formed at the BPE anode is not neutralized and flows downstream, acidifying the solution at x < 2000 μm. The key point is that the numerical simulations shown in Fig. 3b and c are in qualitative agreement with the experimental results in Fig. 1 and 2.
To understand how microplastics are filtered from the microchannel, Fig. 4a shows the simulated electric field within the microchannel when the BPE is active (a corresponding plot showing the electric field when the BPE is inactive is provided in the ESI, Fig. S4a†). The significance of the simulated electric field is twofold. First, the asymmetric character of the electric field qualitatively agrees with the shape we previously proposed (Scheme 1c).38 Thus, while the ionic distributions were not predicted correctly, the proposed redistribution of the electric field and corresponding filtration mechanism are consistent with the simulations. Second, and most interesting, are the sharp electric field gradients that form in solution above the BPE poles.
To better understand the asymmetric shape of the electric field and the origin of the electric field gradients in solution, the simulated ionic current density and simulated solution resistivity are plotted separately in Fig. 4b and c (corresponding plots showing the simulated ionic current density and simulated solution resistivity when the BPE is inactive are provided in the ESI, Fig. S4b and c†). Specifically, Fig. 4b is a plot of the simulated ionic current density when the BPE is active. The ionic current density is lower between the BPE poles (2000 μm < x < 5000 μm) relative to outside of the poles because the BPE provides an alternative pathway for current, in the form of electrical current, to flow through the system. Additionally, a sharp increase and decrease in the ionic current density is observed near the microchannel entrance (x = 6500 μm) and exit (x = 500 μm), respectively. The increase in ionic current density at the microchannel entrance is related to the electric field and how the ionic current density was calculated (ESI†). The decrease in ionic current density at the microchannel exit results from the increase in cross-sectional area of the device as the microchannel expands into the solution reservoir.
Fig. 4c displays the simulated solution resistivity when the BPE is active. The key result here is that solution resistivity upstream of the BPE cathode (x > 5000 μm) is much higher than the downstream resistivity (x < 5000 μm). This difference in solution resistivity along the length of the microchannel primarily arises from variations in pH (Fig. 3c) and the difference in mobility of H+ (3.625 × 10−3 cm2 s−1 V−1) and OH− (2.05 × 10−3 cm2 s−1 V−1).53 Moreover, given the symmetric nature of the simulated ionic current density (Fig. 4b), it is clear that the variations in solution resistivity throughout the microchannel account for the observed asymmetry of the simulated electric field shown in Fig. 4a. One last point, the spike observed in the solution resistivity near x = 2000 μm results from a slight ion depletion zone where OH− neutralizes H+ (see pH gradient, Fig. 3c).
Finally, Fig. 4b and c indicate that there are ionic current density and solution resistivity gradients near the BPE poles (x = 2000 μm and 5000 μm), which are directly responsible for the simulated electric field gradients shown in Fig. 4a. Of particular interest is the electric field gradient that forms above the BPE cathode (Fig. 4a, x = 5000 μm), because the augmented electric field upstream of the BPE cathode is responsible for the experimentally observed microplastic filtration. Therefore, to quantify relative contributions of ionic current density and solution resistivity to the electric field gradient near the BPE cathode, the top half of Table 2 lists normalized values of the simulated ionic current density and simulated solution resistivity between the BPE poles and also upstream of the BPE cathode. These data reveal that variations in ionic current density and solution resistivity contribute approximately equally (i.e., a ∼3.5-fold change for both parameters) to the electric field gradient at the BPE cathode. This is a significant finding because, while electric field gradients have previously been formed using solution resistivity (conductivity) gradients, ionic current density gradients represent a new approach for forming electric field gradients in solution.
| Between BPE poles | Upstream of BPE cathode | |
|---|---|---|
| Simulated data | ||
| Normalized ionic current density | 1.00 | 3.37 |
| Normalized solution resistivity | 1.00 | 3.75 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Experimental data | ||
| Normalized ionic current density | 1.00 | 3.58 |
| Normalized solution resistivity | 1.00 | 2.88 |
Experimental ionic current density and solution resistivity measurements
The preceding numerical simulations suggest that variations in both ionic current density and solution resistivity contribute to the electric field gradients near the BPE poles. To corroborate the simulated results, experimental ionic current density and solution resistivity data were collected at multiple locations throughout a straight-microchannel device during a filtration experiment. These data were collected as described in the Experimental section. Briefly, total current through the microchannel (iTOT) and current through the BPE (iBPE) were monitored while the BPE poles were connected. Ionic current between the BPE poles was calculated by subtracting iBPE from iTOT. Experimental ionic current densities were then computed using the ionic current values and the microchannel dimensions. Solution conductivity measurements were made upstream of the BPE cathode, between the BPE poles, and downstream of the BPE anode using microband electrodes patterned on the floor of the channel and a home-built conductivity meter. Note that the measurement electrodes were placed sufficiently far away from the BPE poles to account for solution mixing. Solution conductivity values were then converted to solution resistivity.Table 3 compares the experimental ionic current density and solution resistivity values to the corresponding simulated results for different locations throughout the straight microchannel. The main point is that the experimental data are in near-quantitative agreement with the numerical simulations (corresponding experimental and simulated values are within a factor of 1.6). Additionally, the experimental data indicate that there are ionic current density and solution resistivity gradients in solution. This result is important because it experimentally supports the presence of electric field gradients, as simulated in Fig. 4a.
| Downstream of BPE | Between BPE poles | Upstream of BPE | |
|---|---|---|---|
| Ionic current density (A m −2 ) | |||
| Simulated | 420 | 120 | 420 |
| Experimental | 410 ± 30 | 110 ± 40 | 410 ± 30 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Solution resistivity (Ω m) | |||
| Simulated | 8.2 | 8.80 | 33 |
| Experimental | 13 ± 1 | 12.5 ± 0.4 | 36 ± 3 |
Finally, as discussed in the previous section, the electric field gradient near the BPE cathode is particularly interesting because the augmented electric field upstream of the BPE cathode is responsible for the experimentally observed microplastic filtration. Therefore, to quantify the relative contributions of the ionic current density and the solution resistivity to the electric field gradient near the BPE cathode, the bottom half of Table 2 lists normalized experimental values for the ionic current density and solution resistivity in the region between the BPE poles and upstream of the BPE. Importantly, the experimental data indicate that variations in ionic current density and solution resistivity contribute almost equally (i.e., a ∼3 to 3.5-fold change for each parameter) to the electric field gradient near the BPE cathode. This experimental result is in agreement with the simulated results (top half of Table 2).
Continuous separations
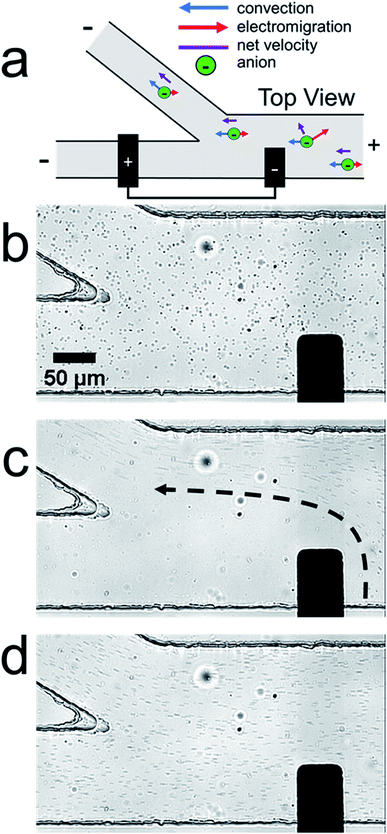
After investigating the electrokinetic filtration process in a straight microchannel, we hypothesized that the electric field gradient near the BPE cathode could facilitate the continuous separation of microplastics in a bifurcated microchannel. Fig. 5a is a schematic illustration of the experimental design. Here, because the BPE cathode only partially extends across the width of the main microchannel, we anticipated that the electric field gradient associated with the BPE cathode would be confined to the bottom half of the microchannel and therefore would redirect and continuously separate microplastics into the top outlet channel.Continuous separation experiments were performed in the same manner as the previously discussed filtration experiments, but in this case the solution contained 5.0 mM KCl instead of 1.0 mM KCl. Empirical observation indicated that this change improved the continuous separation of microplastics in the bifurcated microchannel in the absence of PDF. Fig. 5b–d are optical micrographs from a representative continuous separation experiment. The micrographs show the region of the microchannel near the channel bifurcation and the BPE cathode. Fig. 5b shows the device after applying the driving voltage but before connecting the BPE poles. In this image, the microplastics are evenly distributed throughout the microchannel because the electric field is uniform.
Fig. 5c shows the device ∼30 s after connecting the BPE poles. The trajectory of the microplastics is indicated by the dashed black arrow. The important point is that the microplastics are redirected away from the BPE cathode and into the top outlet channel. Consequently, the solution in the bottom outlet channel no longer contains a significant amount of microplastics (separation efficiency > 99%, ESI†). Note that, in this micrograph, the microplastics appear as streaks instead of circles. This occurs because the microplastics are moving fast relative to the image capture rate of the camera. It is also important to note that we have previously demonstrated this type of microplastic separation, but only in buffer-containing solutions.33,34 This continuous separation in the absence of buffer is the key outcome of this study.
Fig. 5d shows the device ∼20 s after disconnecting the BPE poles. Now the microplastics are redistributed throughout the entire channel because the BPE no longer perturbs the electric field. Note that the microplastics appear as streaks here because their velocity remains higher than in Fig. 5b. This likely occurs because pH variations throughout the system have not equilibrated to their initial state. The gradual return to steady state, and the associated slowing of the microplastics, can be seen in the video from which these frames were extracted (ESI, Video S4†).
To further investigate the continuous separation mechanism, finite element simulations were performed. Complete details regarding the simulations are provided in the ESI.† Briefly, the simulated domain was a two-dimensional model of the xy plane containing a fraction of the bifurcated microchannel (ESI, Fig. S5†). Due to the top-down orientation of these simulations, the BPE poles were modeled as boundaries placed on the wall of the microchannel, rather than extending into the microchannel. This approach is consistent with previous modeling from our group.34 Note that placing the electrode surface on the wall of the simulated domain is an approximation of the experimental system, which we use to simplify the numerical simulations. The important point, however, is that the model qualitatively captures trends in the simulated electric field and microplastic transport. Finally, the Navier–Stokes equation and Nernst–Planck equation with the electroneutrality condition were used to model solution convection, mass transport, and the electric field.
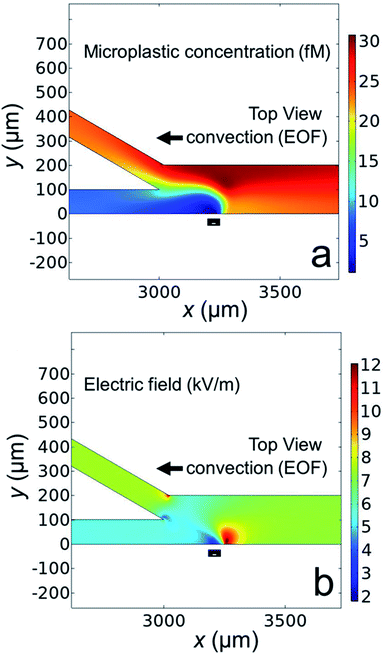
Fig. 6a shows the simulated microplastic concentration near the channel bifurcation when the BPE is active. The black rectangle along the microchannel wall indicates the location of the boundary representing the BPE cathode. The key finding is that the microplastics are redirected away from the BPE cathode near x = 3250 μm (a simulated plot of the microplastic flux near the BPE cathode is provided in the ESI, Fig. S6†), which is consistent with the results shown in Fig. 5.
Finally, in order to understand why the microplastics are redirected, Fig. 6b displays the simulated electric field near the microchannel bifurcation when the BPE is active. This plot indicates that the electric field is quite complex near the BPE cathode in the bifurcated microchannel. The main point, however, is the presence of a sharp electric field gradient (red lobe, corresponding line plots of the electric field in the x- and y-directions are provided in the ESI, Fig. S7†) just to the right of the BPE cathode. This perturbation to the electric field is responsible for the redirection of microplastics into the top outlet channel. This finding confirms our hypothesis that the electric field gradient associated with the BPE cathode can be used for microplastic redirection. Additionally, and most importantly, the results shown in Fig. 5 and 6 confirm buffer-free, continuous separations are possible using BPEs.
Summary and conclusions
Here, we investigated electrokinetics in microfluidic devices containing a BPE and an unbuffered electrolyte solution. Our results show that water electrolysis at a BPE in the absence of buffer produces sufficient variations in solution resistivity and ionic current density along the length of the microchannel to yield sharp electric field gradients near the BPE poles. This finding is significant because ionic current density gradients represent a fundamentally new paradigm for forming electric field gradients in solution. Additionally, by judiciously altering the experimental design, we leveraged the electric field gradient near the BPE cathode to redirect and continuously separate microplastics from water in the absence of buffer. The key point is that electrokinetic separations using BPEs are no longer restricted to buffered solutions. This result broadens the scope of using electric-field enabled, membrane-free separations.The filtration and continuous separation of microplastics from water, as demonstrated here, highlight the utility of using BPEs for modulating local electric fields and performing electrokinetic separations. Future work is aimed at developing a better understanding of the experimental parameters critical to forming optimal electric field gradients in the absence of buffer. Specifically, we are interested in exploring the effects of the device configuration, electrode dimensions, electrolyte concentration, and driving voltage. Additionally, due to the experimental flexibility afforded by BPEs, we intend to investigate more complex, continuous separations of multiple analytes or objects. Finally, other applications that require the use of electric field gradients, such as analyte enrichment and purification, may also benefit from buffer-free conditions. The results from these experiments will be reported in due course.
Data availability
Experimental videos and complete details regarding the COMSOL simulations are provided in the ESI.† Current and conductivity data from the microplastic filtration experiments are available at the Texas Data Repository, https://doi.org/10.18738/T8/4FBJ4Y.Author contributions
JRT, LMW, and RMC conceptualized experiments. JRT and LMW performed experiments. JRT performed simulations, analyzed results, and wrote the manuscript. JRT and RMC edited the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We gratefully acknowledge support from the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy (Grant: DE-FG02-06ER15758). We thank the Robert A. Welch Foundation (Grant F-0032) for sustained support of our research program. We gratefully acknowledge the Center for Electrochemistry at The University of Texas at Austin for access to modeling software and computational resources. JRT acknowledges support from the Provost's Graduate Excellence Fellowship.References
- R. Dhopeshwarkar, D. Hlushkou, M. Nguyen, U. Tallarek and R. M. Crooks, J. Am. Chem. Soc., 2008, 130, 10480–10481 CrossRef CAS PubMed
.
- R. K. Anand, E. Sheridan, K. N. Knust and R. M. Crooks, Anal. Chem., 2011, 83, 2351–2358 CrossRef CAS PubMed
.
- H. Song, Y. Wang, C. Garson and K. Pant, Anal. Methods, 2015, 7, 1273–1279 RSC
.
- R. K. Anand, E. S. Johnson and D. T. Chiu, J. Am. Chem. Soc., 2015, 137, 776–783 CrossRef CAS PubMed
.
- K. L. Rahn and R. K. Anand, Anal. Chem., 2021, 93, 103–123 CrossRef CAS PubMed
.
- W. S. Koegler and C. F. Ivory, J. Chromatogr. A, 1996, 229, 229–236 CrossRef
.
- W. S. Koegler and C. F. Ivory, Biotechnol. Prog., 1996, 12, 822–836 CrossRef CAS
.
- L. Cutroneo, A. Reboa, G. Besio, F. Borgogno, L. Canesi, S. Canuto, M. Dara, F. Enrile, I. Forioso, G. Greco, V. Lenoble, A. Malatesta, S. Mounier, M. Petrillo, R. Rovetta, A. Stocchino, J. Tesan, G. Vagge and M. Capello, Environ. Sci. Pollut. Res., 2020, 27, 8938–8952 CrossRef CAS PubMed
.
-
P. Marsden, B. Koelmans, J. Bourdon-Lacombe, T. Gouin, L. D'Anglada, D. Cunliffe, P. Jarvis, J. Fawell and J. De France, Microplastics in drinking-water, Geneva, 2019 Search PubMed
.
- A. A. Koelmans, N. H. Mohamed Nor, E. Hermsen, M. Kooi, S. M. Mintenig and J. De France, Water Res., 2019, 155, 410–422 CrossRef CAS PubMed
.
- Q. Zhang, E. G. Xu, J. Li, Q. Chen, L. Ma, E. Y. Zeng and H. Shi, Environ. Sci. Technol., 2020, 54, 3740–3751 CrossRef CAS PubMed
.
- B. Xu, F. Liu, Z. Cryder, D. Huang, Z. Lu, Y. He, H. Wang, Z. Lu, P. C. Brookes, C. Tang, J. Gan and J. Xu, Crit. Rev. Environ. Sci. Technol., 2020, 50, 2175–2222 CrossRef CAS
.
- S. Sharma and S. Chatterjee, Environ. Sci. Pollut. Res., 2017, 24, 21530–21547 CrossRef PubMed
.
- Z. Akdogan and B. Guven, Environ. Pollut., 2019, 254, 113011 CrossRef CAS PubMed
.
- C. Campanale, C. Massarelli, I. Savino, V. Locaputo and V. F. Uricchio, Environ. Res. Public Health, 2020, 17, 1212 CrossRef CAS PubMed
.
- A. D. Vethaak and J. Legler, Science, 2021, 371, 672–674 CrossRef CAS PubMed
.
- A. Amirbahman and T. M. Olson, Colloids Surf., A, 1995, 95, 249–259 CrossRef CAS
.
- S. R. Deshiikan, E. Eschenazi and K. D. Papadopoulos, Colloids Surf., A, 1998, 145, 93–100 CrossRef CAS
.
- K. N. Fotopoulou and H. K. Karapanagioti, Environ. Sci. Pollut. Res., 2015, 22, 11022–11032 CrossRef CAS PubMed
.
- O. Oriekhova and S. Stoll, Environ. Sci.: Nano, 2018, 5, 792–799 RSC
.
- R. T. Kelly and A. T. Woolley, J. Sep. Sci., 2005, 28, 1985–1993 CrossRef CAS PubMed
.
- D. Ross and L. E. Locascio, Anal. Chem., 2002, 74, 2556–2564 CrossRef CAS PubMed
.
- K. M. Balss, D. Ross, H. C. Begley, K. G. Olsen and M. J. Tarlov, J. Am. Chem. Soc., 2004, 126, 13474–13479 CrossRef CAS PubMed
.
- Z. Huang and C. F. Ivory, Anal. Chem., 1999, 71, 1628–1632 CrossRef CAS
.
- P. Myers and K. D. Bartle, J. Chromatogr. A, 2004, 1044, 253–258 CrossRef CAS PubMed
.
- R. D. Greenlee and C. F. Ivory, Biotechnol. Prog., 1998, 14, 300–309 CrossRef CAS PubMed
.
- S. J. Kim, Y.-A. Song and J. Han, Chem. Soc. Rev., 2010, 39, 912–922 RSC
.
- M. Li and R. K. Anand, Analyst, 2016, 141, 3496–3510 RSC
.
- S. E. Fosdick, K. N. Knust, K. Scida and R. M. Crooks, Angew. Chem., Int. Ed., 2013, 52, 10438–10456 CrossRef CAS PubMed
.
- G. Loget, D. Zigah, L. Bouffier, N. Sojic and A. Kuhn, Acc. Chem. Res., 2013, 46, 2513–2523 CrossRef CAS PubMed
.
- R. K. Anand, E. Sheridan, D. Hlushkou, U. Tallarek and R. M. Crooks, Lab Chip, 2011, 11, 518–527 RSC
.
- E. Sheridan, D. Hlushkou, K. N. Knust, U. Tallarek and R. M. Crooks, Anal. Chem., 2012, 84, 7393–7399 CrossRef CAS PubMed
.
- C. D. Davies, E. Yoon and R. M. Crooks, ChemElectroChem, 2018, 5, 877–884 CrossRef CAS
.
- C. D. Davies and R. M. Crooks, Chem. Sci., 2020, 11, 5547–5558 RSC
.
- D. R. Laws, D. Hlushkou, R. K. Perdue, U. Tallarek and R. M. Crooks, Anal. Chem., 2009, 81, 8923–8929 CrossRef CAS PubMed
.
- K. N. Knust, E. Sheridan, R. K. Anand and R. M. Crooks, Lab Chip, 2012, 12, 4107–4114 RSC
.
- K. Scida, E. Sheridan and R. M. Crooks, Lab Chip, 2013, 13, 2292–2299 RSC
.
- E. Sheridan, K. N. Knust and R. M. Crooks, Analyst, 2011, 136, 4134–4137 RSC
.
- F. Mavré, R. K. Anand, D. R. Laws, K.-F. Chow, B.-Y. Chang, J. A. Crooks and R. M. Crooks, Anal. Chem., 2010, 82, 8766–8774 CrossRef PubMed
.
- X. Zhang, Q. Zhai, H. Xing, J. Li and E. Wang, ACS Sens., 2017, 2, 320–326 CrossRef CAS PubMed
.
- J. P. Guerrette, S. M. Oja and B. Zhang, Anal. Chem., 2012, 84, 1609–1616 CrossRef CAS PubMed
.
- M. Kersaudy-Kerhoas, R. Dhariwal and M. P. Y. Desmulliez, IET Nanobiotechnol., 2008, 2, 1–13 CrossRef CAS PubMed
.
- D. C. Duffy, J. C. Mcdonald, O. J. A. Schueller and G. M. Whitesides, Anal. Chem., 1998, 70, 4974–4984 CrossRef CAS PubMed
.
- R. K. Perdue, D. R. Laws, D. Hlushkou, U. Tallarek and R. M. Crooks, Anal. Chem., 2009, 81, 10149–10155 CrossRef CAS PubMed
.
- M. Galloway, W. Stryjewski, A. Henry, S. M. Ford, S. Llopis, R. L. Mccarley and S. A. Soper, Anal. Chem., 2002, 74, 2407–2415 CrossRef CAS PubMed
.
- E. Yoon, C. D. Davies, T. A. Hooper and R. M. Crooks, Lab Chip, 2017, 17, 2491–2499 RSC
.
- M. M. Meighan, M. W. Keebaugh, A. M. Quihuis, S. M. Kenyon and M. A. Hayes, Electrophoresis, 2009, 30, 3786–3792 CrossRef CAS PubMed
.
- M. M. Meighan, J. Vasquez, L. Dziubcynski, S. Hews and M. A. Hayes, Anal. Chem., 2011, 83, 368–373 CrossRef CAS PubMed
.
- F. Zhu, B. L. Nannenga and M. A. Hayes, Biomicrofluidics, 2019, 13, 054112 CrossRef PubMed
.
- S. M. Kenyon, N. G. Weiss and M. A. Hayes, Electrophoresis, 2012, 33, 1227–1235 CrossRef CAS PubMed
.
- A. Sze, D. Erickson, L. Ren and D. Li, J. Colloid Interface Sci., 2003, 261, 402–410 CrossRef CAS PubMed
.
- W.-J. Lan, M. A. Edwards, L. Luo, R. T. Perera, X. Wu, C. R. Martin and H. S. White, Acc. Chem. Res., 2016, 49, 2605–2613 CrossRef CAS PubMed
.
-
A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, Hoboken, NJ, 2nd edn, 2001 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Solution conductivity calibration curve; numerical simulations of filtration experiment; micrograph showing the anodic reservoir during a pH indicator experiment; parametric sweep settings for filtration simulations; line plot of the simulated microplastic concentration along the whole domain during a filtration experiment; line plots showing the simulated electric field, ionic current density, and solution resistivity when the BPE is inactive during a filtration experiment; separation efficiency, numerical simulations of continuous separation experiment; simulated domain for continuous separations; parametric sweep settings for continuous separation simulations; simulated microplastic flux during a continuous separation; line plots showing the simulated electric field during a continuous separation; a video showing the filtration of microplastics in a straight microchannel; a video showing the bipolar electrode cathode during a pH indicator experiment; a video showing the bipolar electrode anode during a pH indicator experiment; a video showing the continuous separation of microplastics in a bifurcated microchannel. See DOI: 10.1039/d1sc03192a |
| This journal is © The Royal Society of Chemistry 2021 |