Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Activation by oxidation and ligand exchange in a molecular manganese vanadium oxide water oxidation catalyst†
Gustavo
Cárdenas
ab,
Ivan
Trentin
c,
Ludwig
Schwiedrzik
 a,
David
Hernández-Castillo
a,
David
Hernández-Castillo
 a,
Grace A.
Lowe
c,
Julian
Kund
d,
Christine
Kranz
a,
Grace A.
Lowe
c,
Julian
Kund
d,
Christine
Kranz
 d,
Sarah
Klingler
d,
Sarah
Klingler
 d,
Robert
Stach
d,
Boris
Mizaikoff
d,
Robert
Stach
d,
Boris
Mizaikoff
 d,
Philipp
Marquetand
d,
Philipp
Marquetand
 af,
Juan J.
Nogueira
af,
Juan J.
Nogueira
 bf,
Carsten
Streb
bf,
Carsten
Streb
 *c and
Leticia
González
*c and
Leticia
González
 *ae
*ae
aInstitute of Theoretical Chemistry, University of Vienna, Währinger Str. 17, 1090 Vienna, Austria. E-mail: leticia.gonzalez@univie.ac.at
bChemistry Department, Universidad Autónoma de Madrid, Calle Francisco Tomás y Valiente, 7, 28049 Madrid, Spain
cInstitute of Inorganic Chemistry I, Ulm University, Albert-Einstein-Allee 11, 89081, Ulm, Germany. E-mail: carsten.streb@uni-ulm.de
dInstitute of Analytical and Bioanalytical Chemistry, Ulm University, Albert-Einstein-Allee 11, 89081 Ulm, Germany
eVienna Research Platform on Accelerating Reaction Discovery, University of Vienna, Währinger Str. 17, 1090 Vienna, Austria
fIADCHEM, Institute for Advanced Research in Chemistry, Universidad Autónoma de Madrid, Madrid, Spain
First published on 30th August 2021
Abstract
Despite their technological importance for water splitting, the reaction mechanisms of most water oxidation catalysts (WOCs) are poorly understood. This paper combines theoretical and experimental methods to reveal mechanistic insights into the reactivity of the highly active molecular manganese vanadium oxide WOC [Mn4V4O17(OAc)3]3− in aqueous acetonitrile solutions. Using density functional theory together with electrochemistry and IR-spectroscopy, we propose a sequential three-step activation mechanism including a one-electron oxidation of the catalyst from [Mn23+Mn24+] to [Mn3+Mn34+], acetate-to-water ligand exchange, and a second one-electron oxidation from [Mn3+Mn34+] to [Mn44+]. Analysis of several plausible ligand exchange pathways shows that nucleophilic attack of water molecules along the Jahn–Teller axis of the Mn3+ centers leads to significantly lower activation barriers compared with attack at Mn4+ centers. Deprotonation of one water ligand by the leaving acetate group leads to the formation of the activated species [Mn4V4O17(OAc)2(H2O)(OH)]− featuring one H2O and one OH ligand. Redox potentials based on the computed intermediates are in excellent agreement with electrochemical measurements at various solvent compositions. This intricate interplay between redox chemistry and ligand exchange controls the formation of the catalytically active species. These results provide key reactivity information essential to further study bio-inspired molecular WOCs and solid-state manganese oxide catalysts.
Introduction
The development of noble metal-free water oxidation catalysts1,2 (WOCs) is often inspired by natural photosynthesis, where a calcium manganese oxide cubane (the oxygen evolving complex, OEC) oxidizes water near the thermodynamic potential.3,4 Molecular model complexes are often used in mechanistic studies of the catalytic cycle.5–8 Meanwhile, the design of solid-state metal oxide WOCs comes with its own set of challenges: structural complexity, typically mixed metal sites, and scarce information on the nature of their active sites.9 On the quest to surmount these challenges, molecular mixed metal oxides – so-called polyoxometalates (POMs) – have emerged as prototypes useful for homogeneous water oxidation catalysis and as models to correlate molecular reactivity with heterogeneous solid-state catalysts.10 Typically, POM-WOCs are engineered by functionalizing chemically robust POMs (mainly tungstates) with redox-active transition metals11–13 such as Ru,14,15 Co16,17 or Mn.18,19 Much research on POM-WOCs has focused on stabilizing bio-inspired polynuclear metal-oxo-aggregates [MxOy] using POM ligands, as this approach limits the oxidation state changes required per metal site during water oxidation.11–13,20While the last decade has seen tremendous progress in POM-WOC synthesis and catalysis, mechanistic studies are rare, in part due to challenges related to POM-WOC stability.21,22 Early studies by Musaev and colleagues explored the electronic structure and accessible oxidation states of ruthenium tungstate POM-WOCs.23 Later, pioneering studies by Poblet and colleagues provided a water oxidation mechanism for cobalt tungstate POM-WOCs using density functional theory (DFT).17,24 Also, Llobet, Bo, Bonchio and colleagues combined spectroscopic and spectro-electrochemical studies with DFT calculations to investigate the redox chemistry during water oxidation by ruthenium-containing POM-WOCs.25 However, for many POM-WOCs11,12,21 mechanistic understanding of their mode of action in water oxidation catalysis is lacking.
To date, most POM-WOC research is focused on metal-functionalized lacunary polyoxotungstates.11–13,21 In contrast, the use of vanadates to stabilize metal-oxo ligands is limited, possibly due to their more complex reactivity.26 Recently, some of us reported19 the embedding of OEC-inspired manganese oxo reaction centers3 into a molecular vanadium oxide WOC, [Mn4V4O17(OAc)3]3− (={Mn4V4}), see Fig. 1. This compound is capable of electrochemical and photochemical water oxidation when operated under homogeneous conditions in aqueous acetonitrile solutions with turnover numbers > 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and turnover frequencies > 200 min−1,19,27 but any knowledge related to its catalytic activity remains elusive. This insight is urgently required not only because this catalyst is one of the best-performing POM-WOCs reported, but also because it can be considered a model for the OEC and for technologically important manganese oxide water oxidation catalysts.
000 and turnover frequencies > 200 min−1,19,27 but any knowledge related to its catalytic activity remains elusive. This insight is urgently required not only because this catalyst is one of the best-performing POM-WOCs reported, but also because it can be considered a model for the OEC and for technologically important manganese oxide water oxidation catalysts.
Herein, we report the activation mechanism of the POM-WOC [Mn4V4O17(OAc)3]3− as a fundamental step towards understanding speciation in solution under catalytic conditions and elucidating the complete water oxidation cycle. Combining electrochemical measurements and theoretical calculations we unravel a three-step activation mechanism consisting of a one-electron oxidation of the catalyst, acetate-to-water ligand exchange, and a second one-electron oxidation. The calculations of the ligand exchange pathways and redox potentials allow us to precisely determine the nature of the experimentally observed redox transitions. Further, the complex interplay of proton-coupled redox processes is of general importance for understanding water oxidation catalysis and advancing the design of other efficient POM-WOCs.
Experimental
Electrochemistry
Voltammograms were recorded using a Gamry 1010B potentiostat and a three-electrode setup. A 3 mm diameter glassy carbon disk working electrode (CH Instruments, USA), Pt wire counter-electrode and a leakless miniature Ag/AgCl reference electrode were used. The reference electrode potential was measured against a standard calomel reference electrode (CH Instruments, USA) in pure electrolyte solution before and after each measurement. As pre-treatment, the glassy carbon (GC) electrode was cycled 10 times in 0.2 M aqueous H2SO4 between −0.5 V and 0.5 V to remove impurities. Between each square wave voltammetry (SWV) experiment, the electrode was polished with an alumina slurry. The counter-electrode Pt wire was polished with a 0.05 μm alumina slurry prior to use. Samples with varying water content were prepared by mixing the required amounts of water and acetonitrile with nBu4NPF6 (0.1 M) and background SWV were collected for each solvent mixture in the absence of {Mn4V4}. Successively, (nBu4N)3[Mn4V4O17(AcO)3] (32 mg, 2 mM) was added to the solution and stirred until dissolved (ca. 1 min).19 After ca. 5 min equilibration, the SWV was performed. Each experiment was performed at least in triplicate to ensure reproducibility. Between each experiment, the working electrode was polished to avoid interferences from possible electrode fouling (e.g. adsorption of intermediate species). SWV parameters were as follows: Frequency f = 25 Hz, pulse amplitude ESW = 25 mV, potential step Estep = 2 mV in a range between 0.2 and 1.7 V vs. Ag/AgCl (3.5 M KCl) at room temperature.Infrared spectroscopy
IR spectra were recorded using a Fourier-transform infrared (FT-IR) spectrometer (Alpha I, Bruker Optik GmbH, Ettlingen, Germany) equipped with a zinc selenide multi-bounce attenuated total reflection (ATR) accessory (Multi ATR, Bruker Optik GmbH, Ettlingen, Germany). The spectra were collected at a spectral resolution of 4 cm−1 averaging 42 spectra per measurement. For each measurement, an aliquot of 0.6 ml of the sample solution (4 mM) was deposited onto the ATR crystal inside a closed sampling cell to prevent evaporation of the solvent during the measurement.Computational
Ligand exchange mechanistic calculations
As in Siegbahn's studies of the OEC in photosystem II,28,29 calculations were carried out using the high-spin configuration and assuming that antiferromagnetic effects do not significantly affect either the reaction barriers or the geometry of the complex.30 Geometries were optimized using DFT and the B3LYP functional31,32 – as widely used in other studies of OEC model systems33–37 and polyoxometalate WOCs24,38–45—combined with the def2-SVP basis set.46 Local minima were confirmed by the absence of imaginary frequencies. Solvation effects were considered using the SMD implicit solvation model47 with a dielectric constant of 40.98. We use Grimme's D3 empirical dispersion correction48 and the zeroth-order DKH relativistic Hamiltonian.49 Electronic energies were refined using B3LYP with def2-TZVP46 for Mn, V, O atoms, and def2-SVP for C and H atoms. All these calculations were performed with the Gaussian 16 software package.50Redox potentials calculations
The geometries employed for the redox potential calculations were also optimized at the B3LYP/def2-SVP level of theory. Dielectric constants between 36.60 (0% water) and 38.79 (5% water) account for the variation of the solvent composition, as dictated by the experiment. The value of the dielectric constant of the mixture is calculated as:| εmixture = φwaterεwater + φacetonitrileεacetonitrile | (1) |
The standard reduction potentials 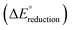 were calculated relative to the Ag/AgCl electrode as:
were calculated relative to the Ag/AgCl electrode as:
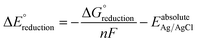 | (2) |
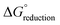 is the change in Gibbs free energy in the reduction reaction, n and F are the number of electrons transferred and the Faraday constant, respectively, and EabsoluteAg/AgCl is the absolute reduction potential of the Ag/AgCl electrode. The value of EabsoluteAg/AgCl was obtained considering an absolute reduction potential for the Standard Hydrogen Electrode (SHE) of 4.28 V (ref. 55) and a reduction potential of 0.22 V (ref. 56) for the Ag/AgCl electrode relative to the SHE. The Gibbs free energy of reduction was computed here by the so-called direct approach,57 in which the solution phase reaction energy is computed as the difference between the Gibbs free energy of the product and the reactant, each obtained from an optimization-frequency calculation in a continuum solvation model. Alternatively, thermodynamic cycles can be used to compute solution phase reaction energies, as they are parametrized to obtain accurate solvation free energies.55,57 When computing the Gibbs free energy of solvation in a thermodynamic cycle using implicit solvation models to obtain the solution phase reaction energy, explicit vibrational corrections are not included,58 although there are cases in which solvation can induce changes in vibrational frequencies. Therefore, it is advisable to consider these vibrational corrections,57,59 as we have done here using the direct approach. We note that the direct approach has also been applied in the computation of the redox potentials of POMs analogous to the one presented in this work.60,61
is the change in Gibbs free energy in the reduction reaction, n and F are the number of electrons transferred and the Faraday constant, respectively, and EabsoluteAg/AgCl is the absolute reduction potential of the Ag/AgCl electrode. The value of EabsoluteAg/AgCl was obtained considering an absolute reduction potential for the Standard Hydrogen Electrode (SHE) of 4.28 V (ref. 55) and a reduction potential of 0.22 V (ref. 56) for the Ag/AgCl electrode relative to the SHE. The Gibbs free energy of reduction was computed here by the so-called direct approach,57 in which the solution phase reaction energy is computed as the difference between the Gibbs free energy of the product and the reactant, each obtained from an optimization-frequency calculation in a continuum solvation model. Alternatively, thermodynamic cycles can be used to compute solution phase reaction energies, as they are parametrized to obtain accurate solvation free energies.55,57 When computing the Gibbs free energy of solvation in a thermodynamic cycle using implicit solvation models to obtain the solution phase reaction energy, explicit vibrational corrections are not included,58 although there are cases in which solvation can induce changes in vibrational frequencies. Therefore, it is advisable to consider these vibrational corrections,57,59 as we have done here using the direct approach. We note that the direct approach has also been applied in the computation of the redox potentials of POMs analogous to the one presented in this work.60,61
Results and discussion
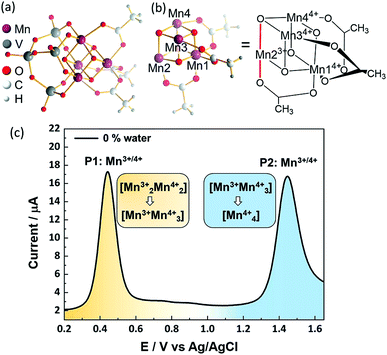
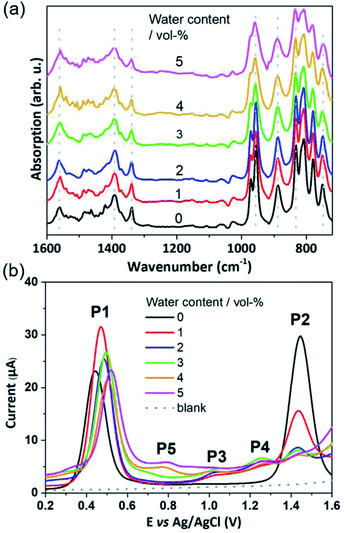
The POM-WOC [Mn4V4O17(OAc)3]3− is based on a tripodal tetravanadate ligand that coordinates to a [Mn4O4] cubane (abbreviated as [Mnx3+Mn4−x4+]); the manganese centers are further stabilized by three bridging acetate ligands, see Fig. 1a and b. Square wave voltammograms and cyclic voltammograms recorded in water-free acetonitrile show that the catalyst undergoes two quasi-reversible Mn-based oxidation reactions, [Mn23+Mn24+] → [Mn3+Mn34+] and [Mn3+Mn34+] → [Mn44+] (labelled P1 and P2, respectively, in Fig. 1c, see also Fig. S1 and Table S1 of the ESI†).19 Previous studies have shown that water oxidation occurs at potentials more positive than P2, suggesting that [Mn44+] is the species that enters the water oxidation cycle.19 Note that no protonation of the cluster is observed by crystallography, spectroscopy or mass spectrometry,19 unlike other POM-WOCs discussed in the literature.62In order to study the full catalytic cycle, first it is essential to understand how the catalyst reaches its active state. To this end, here, we investigate the P1 and P2 oxidation processes to elucidate the electronic and structural changes required to access the catalytically active species. We propose that the first step in the cluster activation is the [Mn23+Mn24+] → [Mn3+Mn34+] oxidation (rather than ligand exchange). This is based on in situ IR-spectroscopic data, which was recorded at conditions identical to the experimental electrochemistry discussed below (i.e., acetonitrile solutions containing up to 5 vol% water). The analysis of the characteristic metal oxide and acetate vibrations of [Mn4V4O17(OAc)3]3− in the 700–1600 cm−1 spectral range shows no significant changes during the experimental electrochemical timescale (i.e., sample preparation and experiment approx. 20 min; see Fig. 2a). Only the vanadate signature appears less well resolved at high water content, yet, no significant peak shift or change in intensity was observed.63,64 This suggests that the structural integrity of the cluster is maintained, and that no acetate-to-water ligand exchange is observed during this period. Consequently, we focus on mechanisms starting by oxidation of the native [Mn4V4O17(OAc)3]3− species. Particular focus is put on exploring (i) the formation of the highly oxidized [Mn44+] state through the [Mn3+Mn34+] → [Mn44+] redox reaction and (ii) the acetate ligand exchange reaction with water to generate the water-binding species required for subsequent O–O bond formation and oxygen evolution. Note that more complex reaction paths (including protonation or partial/full metal oxo framework hydrolysis) are principally possible but are not considered here, based on the stability studies discussed above.
To determine which redox pathways dominate at different water concentrations, the experimental redox potentials of the oxidation reaction P1 and P2 were determined at different MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratios as a basis for subsequent theoretical calculations. To this end, we employed SWV that eliminates the capacitive current component and thus is by a few orders of magnitude more sensitive than cyclic voltammetry (CV). By varying pulse frequency and pulse amplitude and recording the forward and backward scan, information on reaction mechanism and kinetics can be obtained.64 In the context of this study, plotting the difference of the forward and reverse current against potential gives well-defined SWV peaks (Fig. 1c, 2b and ESI Fig. S2–S5†). These mark the experimental oxidation potentials, which can subsequently be used to compare with the calculated values derived from theory.65 Square wave voltammograms were recorded for the native cluster (oxidation state [Mn23+Mn24+]) in MeCN
H2O ratios as a basis for subsequent theoretical calculations. To this end, we employed SWV that eliminates the capacitive current component and thus is by a few orders of magnitude more sensitive than cyclic voltammetry (CV). By varying pulse frequency and pulse amplitude and recording the forward and backward scan, information on reaction mechanism and kinetics can be obtained.64 In the context of this study, plotting the difference of the forward and reverse current against potential gives well-defined SWV peaks (Fig. 1c, 2b and ESI Fig. S2–S5†). These mark the experimental oxidation potentials, which can subsequently be used to compare with the calculated values derived from theory.65 Square wave voltammograms were recorded for the native cluster (oxidation state [Mn23+Mn24+]) in MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O solutions (containing 0.1 M nBu4NPF6 as electrolyte) with the water content varied from 0–5 vol%. Each electrochemical experiment (i.e., each MeCN
H2O solutions (containing 0.1 M nBu4NPF6 as electrolyte) with the water content varied from 0–5 vol%. Each electrochemical experiment (i.e., each MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratio) was performed using a freshly prepared catalyst solution and freshly cleaned electrodes to ensure maximum reliability and reproducibility. Each measurement was performed in triplicate. All data given are referenced against a Ag/AgCl (3.5 M) reference electrode.
H2O ratio) was performed using a freshly prepared catalyst solution and freshly cleaned electrodes to ensure maximum reliability and reproducibility. Each measurement was performed in triplicate. All data given are referenced against a Ag/AgCl (3.5 M) reference electrode.
In water-free, MeCN, the SWV results (Fig. 1c and 2b) correspond to the CV signals originally observed (ESI, Fig. S1†), showing an oxidative wave for the [Mn23+Mn24+] → [Mn3+Mn34+] transition at 0.45 V (labeled P1 in Fig. 2b), and the [Mn3+Mn24+] → [Mn44+] transition at 1.45 V (P2 in Fig. 2b). When increasing the water content to 5 vol%, we observed a positive potential shift of 80 mV. In addition, the current associated with P1 initially increases when going from 0% to 1% water content. At higher water content, the P1 current decreases again as shown in Fig. 2b. With increasing water content, P2 shows a significant decrease in current, while simultaneously three new signals at less positive potentials appear. The signals are labelled in their order of appearance: P3 (1.05 V), P4 (1.25 V), and P5 (0.70 V), see Fig. 2b and ESI Fig. S2.† Initial data interpretation suggests, that the [Mn3+Mn34+] → [Mn44+] transition is strongly influenced by the presence of water, leading us to suggest that for the one-electron oxidized species [Mn3+Mn34+], there may be two competing reaction pathways, i.e., further oxidation (to give [Mn44+]) or acetate-to-water ligand exchange.
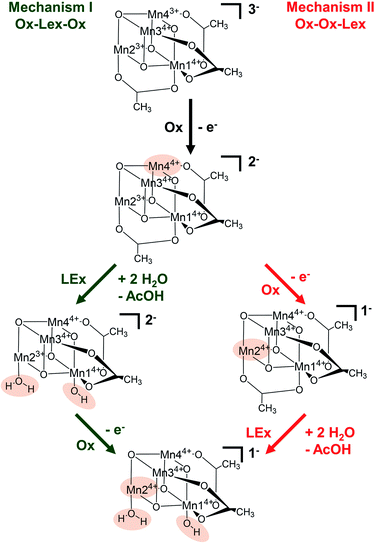
Based on these experimental data, we now use theory to calculate reaction energies and activation barriers to unravel which of the two plausible mechanisms—proposed in Scheme 1— follows the first [Mn23+Mn24+] → [Mn3+Mn34+] oxidation (Ox) step. In mechanism I (green in Scheme 1), the first oxidation is followed by the acetate ligand exchange (LEx) with water, after which the second [Mn3+Mn24+] → [Mn44+] oxidation step (Ox) takes place (globally summarized as Ox–LEx–Ox). In mechanism II (red), the first and second oxidations occur before the acetate ligand exchange (summarized as Ox–Ox–LEx). As the highest reactivity (based on turnover frequencies and electrochemical current densities) was observed in a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeCN
1 MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (v/v) mixture,19 these calculations were carried out considering the same solvent composition.
H2O (v/v) mixture,19 these calculations were carried out considering the same solvent composition.
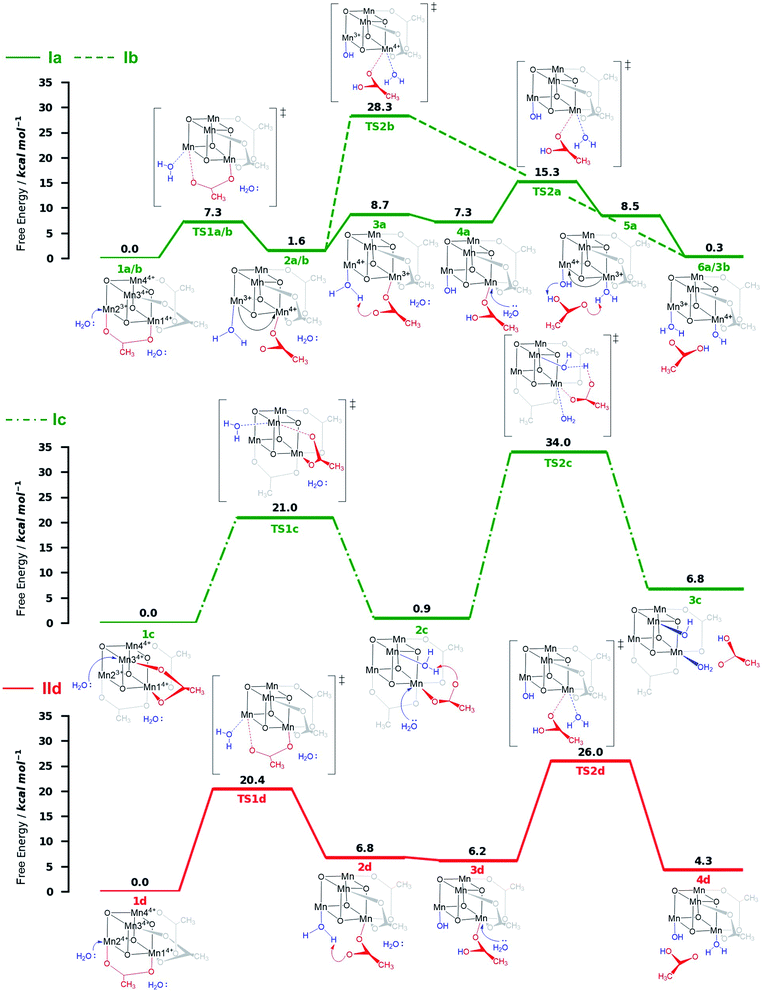
The X-ray structrure of the native catalyst19 has an idealized C3v symmetry (due to the appearence of delocalized electrons on the Mn-centres), so that in the [Mn4O4] cubane (Fig. 1b), Mn1 is located on the C3 axis, while the three manganese centers Mn2, Mn3 and Mn4 are symmetry equivalent. However, when considering the electronic structure of the one-electron-oxidized species [Mn3+Mn34+], the crystallographic C3v symmetry19 is lowered due to the presence of three Mn4+ centers and one Mn3+ center (which could correspond to any of the four Mn positions). Furthermore, Mn3+ (d4) ions in an octahedral environment show Jahn–Teller (JT) distortions, with one of the axes – the JT axis – elongated and the other two shortened. Such JT distortions have previously been identified in the analogous S2 oxidation state of the OEC,66,67 and in other related model complexes.28,61,68 The JT distortion implies that for each possible position of the Mn3+ ion, there are three possible JT axes, giving rise to three different structures. Due to the symmetry equivalence of Mn2, Mn3 and Mn4, we only have to consider localization of the Mn3+ ion at the positions Mn1 or Mn2, resulting in six possible structures (Fig. S6†). Accordingly, we performed geometry optimizations based on the six possible locations of the JT axes. In all cases, the geometries converged towards a minimum where the Mn3+ was localized at the Mn2 position, and the JT axis pointed along the Mn–acetate bond (red axis in Fig. 1b). This minimum energy structure was used hereafter. However, identifying the preferred JT axis localization does not yield any information on the acetate-to-water ligand exchange step, which could still occur at any of the Mn centers. Accordingly, in both mechanisms I and II, several ligand exchange pathways need to be considered (depicted in Fig. 3 and labelled (a)–(e)). The resulting intermediates and transition states (TS), together with their associated Gibbs free energies (Table S2†) and spin assignments (Tables S3 and S4†), are shown in Fig. 4.
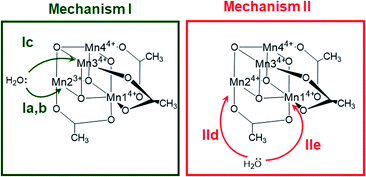 | ||
| Fig. 3 Possible water attack sites for the proposed ligand exchange pathways in mechanism I (Ox–LEx–Ox) and mechanism II (Ox–Ox–LEx), labelled (a)–(e). | ||
Both ligand exchange pathways Ia and Ib involve the nucleophilic attack of the first water molecule at the Mn2 center, and the second water molecule at the Mn1 center. The first step of pathway Ia (Fig. 4, green solid line) is the ligand exchange of one oxygen donor of the acetate group by a water molecule at Mn23+ (step 1a → 2a) with an activation barrier of 7.3 kcal mol−1 (TS1a/b). A sequential intramolecular electron transfer (ET) from Mn2 to Mn1 takes place (2a → 3a), followed by a proton transfer (PT) from the coordinated water molecule to the acetate ligand (3a → 4a), resulting in the formation of a Mn–OH group. This PT reaction is not water mediated (unlike analogous PT reactions reported by Maksimchuk et al.69) as the second water molecule does not actively participate in it. The second acetate ligand exchange at Mn13+ (4a → 5a) represents the rate determining step of this path, with an activation Gibbs free energy of 8.0 kcal mol−1 (TS2a). Finally, an intramolecular concerted electron-proton transfer (5a → 6a) gives rise to a more stable product featuring one Mn–OH2 and one Mn–OH group, where the JT axis is again localized on the Mn2 atom.
The initial step of pathway Ib (Fig. 4, green dashed line) is identical to pathway Ia (1b → 2b). However, the second ligand exchange occurs at Mn14+ (2b → 3b) via TS2b to give 3b, which is identical to 6a. Although thermodynamically possible, this pathway is kinetically unfavorable with an activation barrier of 26.7 kcal mol−1 and is therefore disregarded.
Pathway Ic (Fig. 4, green dashed-dotted line) starts with the nucleophilic attack of a water molecule at a Mn4+ atom (either the symmetry equivalent Mn3/Mn4 or Mn1). The attack on Mn3/4 gives an activation barrier of 21 kcal mol−1 (1c → TS1c → 2c). During the second ligand exchange, a proton is transferred from a Mn-coordinated water molecule to the departing acetate ligand, forming a Mn4+–OH moiety. This step (2c → 3c) presents a prohibitively high activation barrier of 33.1 kcal mol−1 (TS2c). An additional ligand exchange pathway initiated by water attacking the Mn1 center has not been explored further as no transition states for this pathway were found.
Pathways IId and IIe describe the ligand exchange within mechanism II, i.e., after the oxidation to [Mn44+] has taken place. The first ligand exchange can either occur at Mn24+ (pathway IId, Mn3 and Mn4 are symmetry equivalent to Mn2) or at Mn14+ (pathway IIe). The first ligand exchange in pathway IId (1d → 2d) has a barrier of 20.3 kcal mol−1 (TS1d) and is thus the rate limiting step. This step is followed by PT from the coordinated water to the acetate ligand (2d → 3d), generating again an OH group coordinated to Mn2. The second ligand exchange occurs at Mn1 with an activation barrier of 19.8 kcal mol−1 (TS2d). The structures and energetics of pathway IIe are very similar to those of pathway IId and thus are only shown in the ESI (Fig. S7†).
Pathways Ia and Ib are the most thermodynamically favorable ones with a total reaction free energy of 0.3 kcal mol−1. However, pathway Ib presents a very large energy barrier of 26.7 kcal mol−1 in the process 2b→3b via TS2b, in contrast to the 8 kcal mol−1 of pathway Ia in the step 4a → 5a via TS2a. The low barriers found only in pathway Ia appear to result from both acetate ligand exchange steps taking place at the Mn3+ centers, mirroring behavior observed in the OEC.28 Furthermore, all substitutions at Mn3+ centers occur along their JT axis, so that it is plausible to infer that the lower energy barriers evidenced for these ligand substitutions are associated with the elongated Mn3+–O bond being easier to cleave, with respect to its shorter Mn4+–O counterpart (see also Table S5†).
The calculations thus suggest that ligand exchange in mechanism I (Ox–LEx–Ox) is most likely to occur via pathway Ia. Concerning mechanism II (Ox–Ox–LEx), pathways IId and IIe have reaction free energies of 4.3 and 3.9 kcal mol−1, respectively, and are less favorable than pathways Ia and Ib, albeit still thermodynamically feasible. However, their large activation barriers (>20 kcal mol−1) make them both kinetically unfavorable. Interestingly, all pathways investigated end in a species with a water and an OH group as ligands.
Next, we used this detailed theoretical assessment to gain further insight into the catalyst activation by correlating theoretically calculated redox potentials with the experimental SWV data measured at different solvent water contents (Fig. 5, Table S6†). Since P1 can be unambiguously assigned to the [Mn23+Mn24+] → [Mn3+Mn34+] oxidation, the value of the redox potential obtained theoretically provides an estimate of the errors involved. Based on three calculated MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratios, the mean error in P1 is 0.09 V, which shows good agreement between theory and experiment and is in line with the literature.70–72 In addition, the shift of the experimental redox-potential to more positive values (80 mV when going from 0 vol% to 5 vol% water content, Fig. 5, black dots) is qualitatively reproduced by theory, where a shift of 20 mV (between 0 vol% and 5 vol% water content) is calculated (Fig. 5, gray dashed line).
H2O ratios, the mean error in P1 is 0.09 V, which shows good agreement between theory and experiment and is in line with the literature.70–72 In addition, the shift of the experimental redox-potential to more positive values (80 mV when going from 0 vol% to 5 vol% water content, Fig. 5, black dots) is qualitatively reproduced by theory, where a shift of 20 mV (between 0 vol% and 5 vol% water content) is calculated (Fig. 5, gray dashed line).
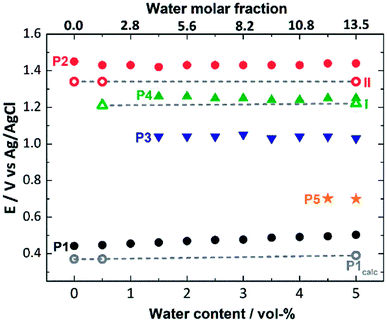 | ||
| Fig. 5 Comparison of experimental (full symbols) and theoretical (empty symbols, linked by gray dashed lines) oxidation potentials for the processes P1 to P5 (also see Fig. 2), depending on the water content (0–5 vol%) of the SWV electrolyte. | ||
The experimental P2 signal (1.45 V at 0 vol% water content) can then be assigned to the [Mn3+Mn34+] → [Mn44+] transition, as acetate-to-water ligand exchange cannot occur under water-free conditions. Comparison with the theoretical potential calculated in mechanism II (Ox–Ox–LEx, 1.34 V) gives a good agreement (mean error: 0.1 V). In the presence of water, the Ox–LEx–Ox mechanism I becomes possible, and our redox calculations predict that the [Mn3+Mn34+] → [Mn34+] oxidation following the most favorable pathway Ia in mechanism I (Scheme 1) will occur at a potential of 1.22 V. This is in line with the appearance of the new oxidation peak P4 (1.25 V, mean error 0.03 V) in the presence of water (Fig. 5). To gain further insights into the correlation between peaks P2 and P4, variable-frequency SWV analyses were used. This method (in analogy to scan rate variation in CV) allows frequency-dependent study of the kinetics of electron transfer processes, while retaining the advantages of SWV over CV. Variation of the SWV frequency between 5 and 50 Hz showed that with increasing frequency (analogous to higher scan rate in CV), process P2 is partially recovered (ESI, Fig. S4†). This is in line with the interpretation that at higher SWV frequencies, the oxidation step to [Mn44+] (ESI, Fig. S3,† step 2a) can now compete with the acetate-to-water ligand exchange (ESI, Fig. S3,† step 2b). Note that this suggestion is also in agreement with our initial hypothesis that under the given electrochemical conditions, ligand exchange occurs only after the [Mn23+Mn24+] → [Mn3+Mn34+] oxidation. This is also supported by IR-spectroscopic data described earlier (Fig. 2a) and will in the future be studied by in situ spectro-electrochemistry. Finally, the experimentally observed redox peaks P3 and P5 are at this point assigned to intermediate, electrode-surface-adsorbed species (ESI, Fig. S5†), which will be analyzed in more detail in a follow-up study.
In summary, these data support the hypothesis that mechanism I is most favorable at the given experimental conditions following these steps: (i) [Mn23+Mn24+] → [Mn3+Mn34+] oxidation, (ii) acetate for water ligand exchange and deprotonation of one water ligand, according to pathway Ia, and (iii) [Mn3+Mn34+] → [Mn44+] oxidation, i.e. Ox–LEx–Ox.
Conclusions
This work presents theoretical and experimental insights into the redox and ligand exchange processes of the initial activation steps of the molecular manganese vanadium oxide water oxidation catalyst [Mn4V4O17(AcO3)]3−. Extensive DFT calculations were used to model redox properties and the ligand exchange pathways of the catalyst prior to entering the water oxidation cycle. We demonstrate that the currently most plausible activation mechanism involves a one-electron oxidation of the catalyst [Mn23+Mn24+] → [Mn3+Mn34+], followed by acetate-to-water ligand exchange and a second one-electron oxidation from [Mn3+Mn34+] to [Mn44+]. The ligand exchange pathways investigated show that the kinetically most favorable pathway is characterized by two nucleophilic attacks of water molecules along the Jahn–Teller axis of Mn3+ centers. Theory predicts that the oxidized species [Mn4V4O17(OAc)2(H2O)(OH)]− features one H2O and one OH ligand, as a result of deprotonation of one water ligand and proton transfer to the leaving acetate group during the ligand exchange. The final products derived from the proposed mechanism allowed us to calculate redox potentials that are in excellent agreement with electrochemical measurements carried out at various solvent compositions, supporting our speciation assignment. This study therefore offers a comprehensive understanding of the complex interplay between electronic structure, redox chemistry, and acid–base ligand exchange in molecular metal-oxide water oxidation catalysts. Further, we provide a blueprint for how experimental electrochemistry and IR spectroscopy together with theoretical calculations can be utilized to explore complex mechanisms in multi-electron catalytic systems. We expect similar studies to guide the design of advanced mixed metal oxide water oxidation catalysts. Future work will focus on studying the speciation of the catalyst at higher oxidation states as a starting point for the water oxidation cycle.Data availability
Inputs/outputs as well as experimental results are available upon reasonable request.Author contributions
LG and CS designed the study. GC, DHC, and LS performed and analyzed the calculations. JJN, PM and LG supervised the theoretical work. IT synthesised the compound. JK, RS, SK and BM provided IR-spectroscopic analyses. IT, GL, CK and CS provided electrochemical analyses. GC, DHC and IT wrote the original draft. CS and LG reviewed and edited the manuscript. All authors discussed and commented on the manuscript. LG, CS, BM and CK acquired funding.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by the Deutsche Forschungsgemeinschaft DFG (TRR234 “CataLight”, project ID 364549901 (projects B3, C2, C3 and C4) and project STR1164/4), the Austrian Science Fund FWF (project no. I3987-N28) and the Comunidad de Madrid through the Attraction of Talent Program 2018 (Grant Ref. 2018-T1/BMD-10261). The Vienna Scientific Cluster is thanked for generous computational resources. Prof. Vera Krewald (TU Darmstadt) is acknowledged for initial fruitful discussions about the catalyst computations.References
- R. Matheu, P. Garrido-Barros, M. Gil-Sepulcre, M. Z. Ertem, X. Sala, C. Gimbert-Suriñach and A. Llobet, Nat. Rev. Chem., 2019, 3, 331–341 CrossRef CAS.
- M. D. Kärkäs, O. Verho, E. V. Johnston and B. Åkermark, Chem. Rev., 2014, 114, 11863–12001 CrossRef PubMed.
- J. Kern, R. Chatterjee, I. D. Young, F. D. Fuller, L. Lassalle, M. Ibrahim, S. Gul, T. Fransson, A. S. Brewster, R. Alonso-Mori, R. Hussein, M. Zhang, L. Douthit, C. de Lichtenberg, M. H. Cheah, D. Shevela, J. Wersig, I. Seuffert, D. Sokaras, E. Pastor, C. Weninger, T. Kroll, R. G. Sierra, P. Aller, A. Butryn, A. M. Orville, M. Liang, A. Batyuk, J. E. Koglin, S. Carbajo, S. Boutet, N. W. Moriarty, J. M. Holton, H. Dobbek, P. D. Adams, U. Bergmann, N. K. Sauter, A. Zouni, J. Messinger, J. Yano and V. K. Yachandra, Nature, 2018, 563, 421–425 CrossRef CAS PubMed.
- Y. Umena, K. Kawakami, J.-R. R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS.
- G. C. Dismukes, R. Brimblecombe, G. A. N. Felton, R. S. Pryadun, J. E. Sheats, L. Spiccia and G. F. Swiegers, Acc. Chem. Res., 2009, 42, 1935–1943 CrossRef CAS PubMed.
- X. Liu and F. Wang, Coord. Chem. Rev., 2012, 256, 1115–1136 CrossRef CAS.
- H. B. Lee, A. A. Shiau, P. H. Oyala, D. A. Marchiori, S. Gul, R. Chatterjee, J. Yano, R. D. Britt and T. Agapie, J. Am. Chem. Soc., 2018, 140, 17175–17187 CrossRef CAS PubMed.
- J. S. Kanady, P.-H. Lin, K. M. Carsch, R. J. Nielsen, M. K. Takase, W. A. Goddard and T. Agapie, J. Am. Chem. Soc., 2014, 136, 14373–14376 CrossRef CAS.
- B. M. Hunter, H. B. Gray and A. M. Müller, Chem. Rev., 2016, 116, 14120–14136 CrossRef CAS PubMed.
- L. Cronin and A. Müller, Chem. Soc. Rev., 2012, 41, 7325–7648 RSC.
- H. Lv, Y. V. Geletii, C. Zhao, J. W. Vickers, G. Zhu, Z. Luo, J. Song, T. Lian, D. G. Musaev and C. L. Hill, Chem. Soc. Rev., 2012, 41, 7572–7589 RSC.
- A. Sartorel, M. Carraro, F. M. Toma, M. Prato and M. Bonchio, Energy Environ. Sci., 2012, 5, 5592–5603 RSC.
- H. Dau, C. Limberg, T. Reier, M. Risch, S. Roggan and P. Strasser, ChemCatChem, 2010, 2, 724–761 CrossRef CAS.
- A. Sartorel, M. Carraro, G. Scorrano, R. De Zorzi, S. Geremia, N. D. McDaniel, S. Bernhard and M. Bonchio, J. Am. Chem. Soc., 2008, 130, 5006–5007 CrossRef CAS.
- Y. V. Geletii, B. Botar, P. Kögerler, D. a. Hillesheim, D. G. Musaev and C. L. Hill, Angew. Chem., Int. Ed., 2008, 47, 3896–3899 CrossRef CAS.
- Q. Yin, J. M. Tan, C. Besson, Y. V. Geletii, D. G. Musaev, A. E. Kuznetsov, Z. Luo, K. I. Hardcastle and C. L. Hill, Science, 2010, 328, 342–345 CrossRef CAS.
- M. Blasco-Ahicart, J. Soriano-Lopez, J. J. Carbo, J. M. Poblet and J. R. Galan-Mascaros, Nat. Chem., 2018, 10, 24–30 CrossRef CAS.
- R. Al-Oweini, A. Sartorel, B. S. Bassil, M. Natali, S. Berardi, F. Scandola, U. Kortz and M. Bonchio, Angew. Chem., Int. Ed., 2014, 11182–11185 CrossRef CAS PubMed.
- B. Schwarz, J. Forster, M. K. Goetz, D. Yücel, C. Berger, T. Jacob and C. Streb, Angew. Chem., Int. Ed., 2016, 55, 6329–6333 CrossRef CAS PubMed.
- J. J. Stracke and R. G. Finke, ACS Catal., 2014, 4, 909–933 CrossRef CAS.
- D. Gao, I. Trentin, L. Schwiedrzik, L. González and C. Streb, Molecules, 2020, 25, 157 CrossRef CAS PubMed.
- J. W. Vickers, H. Lv, J. M. Sumliner, G. Zhu, Z. Luo, D. G. Musaev, Y. V. Geletii and C. L. Hill, J. Am. Chem. Soc., 2013, 135, 14110–14118 CrossRef CAS PubMed.
- D. Quiñonero, A. L. Kaledin, A. E. Kuznetsov, Y. V. Geletii, C. Besson, C. L. Hill and D. G. Musaev, J. Phys. Chem. A, 2010, 114, 535–542 CrossRef.
- J. Soriano-López, D. G. Musaev, C. L. Hill, J. R. Galán-Mascarós, J. J. Carbó and J. M. Poblet, J. Catal., 2017, 350, 56–63 CrossRef.
- A. Sartorel, P. Miró, E. Salvadori, S. Romain, M. Carraro, G. Scorrano, M. Di Valentin, A. Llobet, C. Bo and M. Bonchio, J. Am. Chem. Soc., 2009, 131, 16051–16053 CrossRef CAS PubMed.
- C. Streb, Structure and Bonding in Molecular Vanadium Oxides: From Templates via Host–Guest Chemistry to Applications, in Polyoxometalate-Based Assemblies and Functional Materials, ed. Y.-F Song, Springer, Cham, 2018, vol. 176, DOI:10.1007/430_2017_2.
- F. L. Huber, S. Amthor, B. Schwarz, B. Mizaikoff, C. Streb and S. Rau, Sustainable Energy Fuels, 2018, 2, 1974–1978 RSC.
- P. E. M. Siegbahn, J. Am. Chem. Soc., 2013, 135, 9442–9449 CrossRef CAS.
- P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2018, 20, 22926–22931 RSC.
- P. E. M. Siegbahn, Chem.–Eur. J., 2006, 12, 9217–9227 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- E. M. Sproviero, J. Inorg. Biochem., 2017, 171, 52–66 CrossRef CAS.
- T. Wang, G. Brudvig and V. S. Batista, J. Chem. Theory Comput., 2010, 6, 755–760 CrossRef CAS PubMed.
- M. Shoji, H. Isobe, T. Nakajima and K. Yamaguchi, Chem. Phys. Lett., 2015, 640, 23–30 CrossRef CAS.
- M. Shoji, H. Isobe, S. Yamanaka, M. Suga, F. Akita, J.-R. Shen and K. Yamaguchi, Chem. Phys. Lett., 2015, 623, 1–7 CrossRef CAS.
- H. Isobe, M. Shoji, S. Yamanaka, Y. Umena, K. Kawakami, N. Kamiya, J.-R. Shen and K. Yamaguchi, Dalton Trans., 2012, 41, 13727–13740 RSC.
- K. Nishiki, N. Umehara, Y. Kadota, X. López, J. M. Poblet, C. A. Mezui, A. L. Teillout, I. M. Mbomekalle, P. De Oliveira, M. Miyamoto, T. Sano and M. Sadakane, Dalton Trans., 2016, 45, 3715–3726 RSC.
- Z. L. Lang, G. C. Yang, N. N. Ma, S. Z. Wen, L. K. Yan, W. Guan and Z. M. Su, Dalton Trans., 2013, 42, 10617–10625 RSC.
- A. E. Kuznetsov, Y. V. Geletii, C. L. Hill, K. Morokuma and D. G. Musaev, J. Am. Chem. Soc., 2009, 131, 6844–6854 CrossRef CAS PubMed.
- S. Piccinin and S. Fabris, Phys. Chem. Chem. Phys., 2011, 13, 7666–7674 RSC.
- S. Piccinin, A. Sartorel, G. Aquilanti, A. Goldoni, M. Bonchio and S. Fabris, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4917–4922 CrossRef CAS.
- S. Piccinin and S. Fabris, Inorganics, 2015, 3, 374–387 CrossRef CAS.
- X.-F. Su, W. Guan, L.-K. Yan, Z.-L. Lang and Z.-M. Su, J. Catal., 2019, 376, 146–149 CrossRef CAS.
- X.-F. Su, L.-K. Yan and Z.-M. Su, Inorg. Chem., 2019, 58, 15751–15757 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e3127 Search PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- E. Van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- R. G. Bates and J. B. Macaskill, Pure Appl. Chem., 1978, 50, 1701–1706 Search PubMed.
- J. Ho, Phys. Chem. Chem. Phys., 2015, 17, 2859–2868 RSC.
- J. Ho, A. Klamt and M. L. Coote, J. Phys. Chem. A, 2010, 114, 13442–13444 CrossRef CAS.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- V. Krewald, F. Neese and D. A. Pantazis, Phys. Chem. Chem. Phys., 2016, 18, 10739–10750 RSC.
- V. Krewald and D. A. Pantazis, Dalton Trans., 2016, 45, 18900–18908 RSC.
- C. A. Ohlin and M. Pascual-Borràs, Dalton Trans., 2018, 47, 13602–13607 RSC.
- C. M. Julien, M. Massot and C. Poinsignon, Spectrochim. Acta, Part A, 2004, 60, 689–700 CrossRef CAS.
- A. Chen and B. Shah, Anal. Methods, 2013, 5, 2158–2173 RSC.
- A. Molina, J. González, E. Laborda, Y. Wang and R. G. Compton, Phys. Chem. Chem. Phys., 2011, 13, 16748–16755 RSC.
- N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808 CrossRef CAS PubMed.
- V. Krewald, M. Retegan, N. Cox, J. Messinger, W. Lubitz, S. DeBeer, F. Neese and D. A. Pantazis, Chem. Sci., 2015, 6, 1676–1695 RSC.
- V. Krewald, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2013, 135, 5726–5739 CrossRef CAS PubMed.
- N. V. Maksimchuk, I. D. Ivanchikova, G. M. Maksimov, I. V. Eltsov, V. Y. Evtushok, O. A. Kholdeeva, D. Lebbie, R. J. Errington, A. Solé-Daura, J. M. Poblet and J. J. Carbó, ACS Catal., 2019, 9, 6262–6275 CrossRef CAS.
- S. Schönweiz, M. Heiland, M. Anjass, T. Jacob, S. Rau and C. Streb, Chem.–Eur. J., 2017, 23, 15370–15376 CrossRef PubMed.
- M. H. Anjass, K. Kastner, F. Nägele, M. Ringenberg, J. F. Boas, J. Zhang, A. M. Bond, T. Jacob and C. Streb, Angew. Chem., Int. Ed., 2017, 56, 14749–14752 CrossRef CAS PubMed.
- E. Falbo and T. J. Penfold, J. Phys. Chem. C, 2020, 124, 15045–15056 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Electrochemical, spectroscopic and theoretical data. See DOI: 10.1039/d1sc03239a |
| This journal is © The Royal Society of Chemistry 2021 |