Open Access Article
Open Access ArticleDirect metal–carbon bonding in symmetric bis(C–H) agostic nickel(I) complexes†
Weiying
He
 ab,
D. Dawson
Beattie
b,
Hao
Zhou
ab,
D. Dawson
Beattie
b,
Hao
Zhou
 ab,
Eric G.
Bowes
ab,
Eric G.
Bowes
 b,
Laurel L.
Schafer
b,
Laurel L.
Schafer
 b,
Jennifer A.
Love
b,
Jennifer A.
Love
 ab and
Pierre
Kennepohl
ab and
Pierre
Kennepohl
 *ab
*ab
aDepartment of Chemistry, University of Calgary, 2500 University Drive NW, Calgary, Alberta T2N 1N4, Canada. E-mail: pierre.kennepohl@ucalgary.ca
bDepartment of Chemistry, The University of British Columbia, 2036 Main Mall, Vancouver, BC V6T 1Z1, Canada
First published on 5th November 2021
Abstract
Agostic interactions are examples of σ-type interactions, typically resulting from interactions between C–H σ-bonds with empty transition metal d orbitals. Such interactions often reflect the first step in transition metal-catalysed C–H activation processes and thus are of critical importance in understanding and controlling σ bond activation chemistries. Herein, we report on the unusual electronic structure of linear electron-rich d9 Ni(I) complexes with symmetric bis(C–H) agostic interactions. A combination of Ni K edge and L edge XAS with supporting TD-DFT/DFT calculations reveals an unconventional covalent agostic interaction with limited contributions from the valence Ni 3d orbitals. The agostic interaction is driven via the empty Ni 4p orbitals. The surprisingly strong Ni 4p-derived agostic interaction is dominated by σ contributions with minor π contributions. The resulting ligand–metal donation occurs directly along the C–Ni bond axis, reflecting a novel mode of bis-agostic bonding.
Introduction
Metal-mediated activation and functionalisation of C–H bonds is one of the most influential strategies for the efficient synthesis of high-value products and materials.1,2 In many instances, C–H bond activation proceeds through the initial formation of a direct interaction between the metal ion and the C–H functionality. The formation of a σ complex, where a CH moiety acts as a donor towards a metal, is thus often a prerequisite for bond activation and functionalisation.3,4 Intramolecular σ interactions of this type are often termed agostic interactions, which are more commonly observed due to the significantly lower entropic penalty for bond formation (i.e., the chelate effect5). Studies of agostic complexes have dramatically increased our understanding of σ complexes even though most untethered σ complexes are transient species that are very difficult to trap and investigate.6,7Our understanding of the fundamental nature of M⋯H–C interactions continues to evolve, but it has become clear that the degree and directionality of charge redistribution upon bond formation plays a critical role in defining their reactivity.8 For example, if the CH moiety acts as a donor towards an electron-deficient metal centre (acting as a σ donor), the interaction is defined as a σCH interaction.9–12 Such a bond is often formally described as Md ← σCH donation, reflecting the fact that metal d orbitals act as acceptors.10 Charge transfer leads to weakening of the σCH bond, which is a requisite first step in a wide range of σ-bond activation methodologies, including ambiphilic ligand–metal activation13/cyclometallation deprotonation14 (AMLA/CMD), oxidative addition (OA),15 σ bond metathesis (SBM),16 and 2 + 1 addition.17,18 A better understanding of different modes of σ-bond activation may serve to further boost the development of C–H functionalisation chemistry.19–22 Other modes of (M⋯H–C) binding are also known. For example, electron-rich metal centres may form 3c–4e hydrogen bonds with an electron-deficient CH moiety.23 One must also consider potential anagostic interactions where Pauli repulsion between the metal centre and the σCH is overcome by steric factors.24,25 These different interactions are often classified based on geometric parameters as they have different geometric preferences (Fig. 1a): the M–H–C angle is more acute for σ complexes than for hydrogen bonds.26 Such interactions have also been observed with other E–H moieties, such as boranes and silanes.27–29
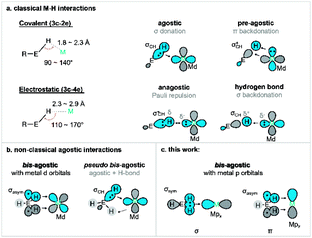 | ||
| Fig. 1 (a) Geometrical definition of various transition metal–hydrogen interactions: agostic, pre-agostic, anagostic and hydrogen bond (E = C);26 (b) summary of orbital interaction scheme for previous bis M⋯H–E interaction (E = C, Si, B). (c) New p orbital type bis-agostic interaction modes found in this work (E = C). | ||
Certain agostic complexes include more unusual bonding motifs – these are sometimes termed nonclassical agostic complexes. A prime example is that of “bis-agostic” interactions, where steric constraints enforce a geometry where two adjacent E–H bonds are near the metal centre (Fig. 1b). Symmetric bis-agostic complexes have been described as resulting from a single 4c–2e interaction between a delocalised H–E–H (E = B, Si, C) fragment orbital and a single empty metal d orbital.30–32 Cases of asymmetric binding of the H–E–H moiety (termed pseudo-bis-agostic bonds) often result from a dominant classical agostic interaction and a secondary hydrogen bond.30,33 We previously reported the linear nickel(I) complexes with pairs of nearly symmetric δ-bis(C–H) contacts from pendant methyl groups that were tentatively assigned as pseudo-bis-agostic complexes based on existing norms for the assignment of such species.34,35 Herein, we report additional spectroscopic data that correct our original assignment and identify a previously unrecognised mode of bis-agostic interaction that results from direct C–Ni bonding dominated by Ni 4p acceptor character with only minimal Ni 3d contributions. As a result, we consider these linear Ni(I) agostic complexes as the first examples of a new class of agostic complexes in organometallic chemistry.
Results and discussion
Synthesis and structure of complexes
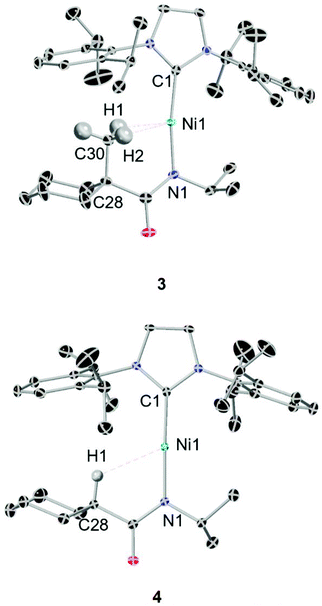
A series of four linear Ni(I) complexes 1–4 were investigated (Fig. 3a). The synthetic methodology, solid-state molecular structure and characterization of complexes 1 and 2 have been reported previously.34 Complexes 3 and 4 were synthesized and investigated to evaluate steric influences on the bis-agostic contact. These complexes were prepared via the same salt metathesis method using Na[amide] salt and 0.5 equiv. of Sigman's dimer as for 1 and 2 (see ESI Section 1†). X-band EPR spectra collected at 7 K (see ESI Section 1†) confirm the S = 1/2 spin state of the formal Ni(I) complexes. Evans measurements (3, μeff = 2.17μB. C6D6 at 27 °C; 4, μeff = 2.12μB. C6D6 at 25 °C) further support the preparation of the metalloradical Ni(I) species at ambient temperatures. Paramagnetic yellow crystals (Fig. 2) of 3 and 4 were obtained overnight at −35 °C in dry toluene layered with pentane.Compared with the less sterically-hindered agostic complex 1, the torsional angle ∠Ni1–N1–C28–C30 of complex 3 is twisted by 3.18°, necessarily leading to a more unsymmetric Ni–H interaction (details in ESI Section 4†). The C1–Ni1–N1 bond angle of complex 3 (∼171.09°) indicates a larger deviation from linearly, as compared to 4 (∼177.62°). Both 1 and 3 are best described as near-linear 2-coordinate Ni(I) complexes with bis-agostic interactions orthogonal to the amidate N–Ni bond. The non-agostic complex 4 exhibits a much longer Ni1–H1 distance (∼2.53 Å) than that observed in the agostic complex 3 (Ni1–H1 ∼ 1.93 Å; Ni1–H2 ∼ 2.15 Å) and has a large Ni1–H1–C28 bond angle (119.78°), which implies a weak electrostatic interaction in that case.
Ni K edge XAS studies
The first indication that these complexes were unusual came from the comparison of the experimental nickel K-edge X-ray absorption near edge structure (XANES) spectra for complexes 1–4 (Fig. 3a).34,35Fig. 3b shows the Ni K-edge pre-edge region for analogous complexes both with (1, 3) and without (2, 4) bis-agostic interactions: the spectra are strikingly different in this region. The edge spectra for 1–4 are consistent with previously reported Ni K-edge spectra of Ni(I) complexes,36–39 with an extremely weak electric-quadrupole allowed Ni 3d ← 1s transition A at 8330–8332 eV, and an intense dipole-allowed Ni 4p ← 1s feature at ∼8337 eV. However, the Ni 4p ← 1s feature40 exhibits substantial differences depending on the presence/absence of the agostic interaction. The non-agostic complexes 2 and 4 exhibit broad overlapping features with three observable components B, C, D in the second derivative of the data, see insets in Fig. 3b and c; these features collapse into two components B and C + D (for complexes 1 and 3) in the presence of the tethered methyl group adjacent to the metal centre. Based on the 2nd derivatives and relative intensities of these features, the simplest interpretation is that the two higher energy features C and D merge when the agostic interactions are present (ESI Fig. 3†). Such large effects in the 4p features in K-edge spectroscopy have previously been observed in Cu(I) complexes, where these features are highly sensitive to the coordination environment around the metal centre.41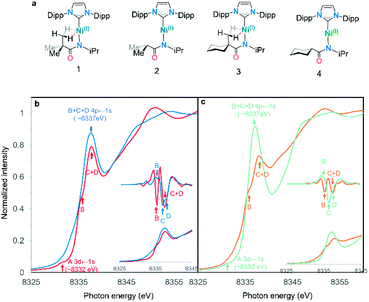 | ||
| Fig. 3 (a) Complexes 1–4 studied in this work. (b) Normalized Ni K-edge PFY XANES edge spectra for agostic complex (1) and its non-agostic analog (2). (c) Normalized Ni K-edge PFY XANES edge spectra for agostic complex (3) and its non-agostic analog (4). Pre-edges are shown in the inset with their second derivative.42 Features identified via the second derivative are marked with arrows in the same colour as their corresponding spectra. | ||
TD-DFT calculations & simulation of Ni K edge XAS
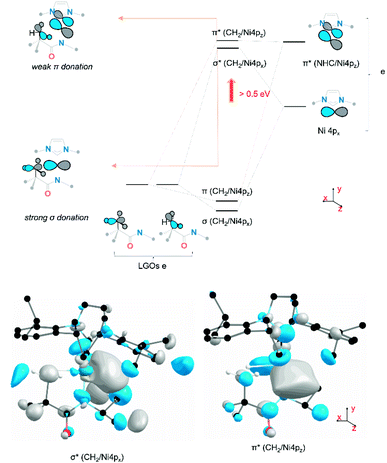
To understand the origins of the observed differences in the Ni K-edge spectra, we employed time-dependent density functional theory (TD-DFT) calculations to simulate the experimental XAS spectra. DFT-optimized structures for each of the complexes at the PBE0/Def2-TZVP level of theory are in good agreement with experimental solid-state molecular structures34 (ESI Section 4.1†). Furthermore, the calculated Ni K edge XANES spectra (Fig. 4) reproduce differences observed in the experimental data. The calculated spectra exhibit four distinct features in the pre-edge region (Fig. 4, features A–D). The lowest-lying and weakest feature (A, ∼8330 eV) corresponds to the electric-dipole forbidden Ni 3d ← 1s transition expected for a 3d9 Ni(I) metal ion. Any differences in this low energy feature would be difficult to observe given their weak intensity; the feature reflects the electric dipole forbidden excitation of a Ni 1s core electron into the half-occupied SOMO, which is assigned as the Ni 3dx2−y2 orbital. A more intense energy feature at higher energy (B, ∼8335 eV) is assigned as a transition to a ligand-based final state that reflects metal-mediated π-delocalization across the amido and NHC ligands (ESI Section 3.1†). This feature remains essentially invariant across the series but gains electric dipole intensity from symmetry-allowed Ni 3d/4p mixing. This π interaction is responsible for the fixed relative orientation of the two ligands and is perpendicular to the H3C–Ni axis. Together, the lower energy features A & B in the Ni K-edge spectra thus reflect the nature of bonding along the primary axis of these linear Ni(I) complexes; contributions to these features due to agostic interactions are relatively subtle. As anticipated, the agostic interactions do not dramatically influence of inherent nature of the bonding in these metal complexes.
final state that reflects metal-mediated π-delocalization across the amido and NHC ligands (ESI Section 3.1†). This feature remains essentially invariant across the series but gains electric dipole intensity from symmetry-allowed Ni 3d/4p mixing. This π interaction is responsible for the fixed relative orientation of the two ligands and is perpendicular to the H3C–Ni axis. Together, the lower energy features A & B in the Ni K-edge spectra thus reflect the nature of bonding along the primary axis of these linear Ni(I) complexes; contributions to these features due to agostic interactions are relatively subtle. As anticipated, the agostic interactions do not dramatically influence of inherent nature of the bonding in these metal complexes.
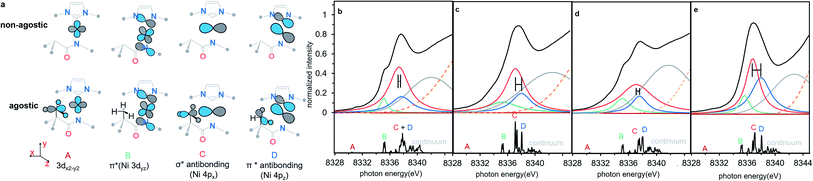 | ||
| Fig. 4 (a) Schematic molecular orbital acceptors contributed to the calculated transition features, all alkyl substitutes are omitted for clarity. (b–e) The experimental spectrum simulated with four Lorentzian function curves and one Gaussian curve (top), and the TD-DFT calculated Ni K-edge XAS spectra (bottom) of complexes 1–4, 1 (b), 2 (c), 3 (d), 4 (e). The difference of 4px ← 1s transition (feature C) and 4pz ← 1s transition (feature D) between agostic complexes and non-agostic complexes in the simulating features are highlighted a horizontal error bar. Four isolated pre-edge features are labelled with A–D, each label is highlighted in the same colour as the assigned simulating curve. The continuum is the group of high lying densely packed empty orbitals which do not contribute to the frontier valence interaction and simulated with a broad Gaussian curve (grey). The edge jump of XAS background is shown as an orange dotted line. All the TD-DFT calculated transition energy was shifted by 180.19 eV for a better comparison with experimental data. See details of calculated energy in ESI Section 2.2 and simulated energy in ESI Section 2.3.† | ||
By contrast, agostic contributions are much more significant in the higher energy region of the spectrum. Most notably, the splitting of features C and D decreases substantially in the presence of the agostic methyl group in 1/3 as compared to 2/4. More specifically, the energy of feature C is much higher in the agostic complexes (by ∼0.6 eV). This feature corresponds to transitions with large Ni 4px character; this acceptor orbital is thus strongly affected by the presence of the agostic interaction. Feature D, on the other hand, is much less affected by the agostic interaction. Qualitatively, the effect is the same in both pairs of complexes, albeit the decrease in C/D splitting is more pronounced in 1 than in 3. Simulated spectra based on the TD-DFT calculations reasonably reproduce the experimentally observed pre-edge data using these four main features (see Fig. 4 and Table 1), indicating that differences in the Ni K-edge spectra are well described by the electronic structure calculations.
| Exp | TD-DFT | Exp | TD-DFT | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | |||||||
| Peak | E (eV) | E (eV) | Ni 3d | Ni 4p | E (eV) | E (eV) | Ni 3d | Ni 4p |
| A | 8331.04 | 8330.48 | 91.45% | 8.55% | 8323.11 | 8330.19 | 90.2% | 9.4% |
| B | 8335.13 | 8335.27 | 35.12% | 64.06% | 8335.20 | 8335.34 | 34.8% | 64.8% |
| C | 8337.34 | 8337.84 | 7.34% | 89.84% | 8337.10 | 8337.12 | 19.0% | 75.4% |
| D | 8337.72 | 8338.11 | 11.33% | 83.83% | 8337.97 | 8338.07 | 5.7% | 91.5% |
| ΔE (C/D) | 0.38 | 0.27 | 0.87 | 0.95 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| 3 | 4 | |||||||
| Peak | Energy | Energy | Ni 3d | Ni 4p | Energy | Energy | Ni 3d | Ni 4p |
| A | 8331.57 | 8330.43 | 77.5% | 7.1% | 8327.81 | 8330.13 | 78.1% | 0.00% |
| B | 8335.27 | 8335.21 | 48.7% | 47.2% | 8335.72 | 8335.25 | 34.9% | 64.7% |
| C | 8337.32 | 8337.38 | 11.9% | 78.5% | 8336.90 | 8337.1 | 5.9% | 92.8% |
| D | 8337.78 | 8337.92 | 5.9% | 85.5% | 8338.10 | 8338.07 | 1.2% | 97.8% |
| ΔE (C/D) | 0.46 | 0.54 | 1.20 | 0.97 | ||||
The observed changes in the 4px,z final states can be explained, as shown in Fig. 5. The Ni 3d orbitals cannot contribute significantly to interactions with the agostic methyl group. However, the empty 4px,z orbitals have the correct symmetry to interact with appropriate donor orbitals on methyl group. The agostic methyl group has the correct orientation to interact with the empty Ni 4px,z orbitals and thus generate donor–acceptor interactions between the methyl group and the metal centre. The dominant σ-type interaction reflects a (C2p + H1s) → Ni4px donor interaction which yields an increase in the energy of the Ni 4px orbitals by >0.5 eV. The symmetry-allowed π interaction is extremely weak, due to both poor overlap and the existing involvement of the 4pz orbital in π bonding with the NHC and amido ligands.
A more detailed evaluation of the DFT results allows us to estimate the importance and relevance of the agostic interaction in these complexes. The influence of the agostic interaction can be (broadly) estimated via the increase in energy of feature C relative to the non-agostic analogue. From this, we estimate that the orbital contribution to the agostic σ donation is surprisingly large in both systems43 yet is somewhat larger in 1 (∼65 kJ mol−1) than in 3 (∼50 kJ mol−1). These differences are consistent with observed differences in steric repulsion between the two systems. The cyclohexyl substituent exhibits a larger steric clash with the NHC ligand substituent (Fig. 6a), which causes a distortion of the CH2⋯Ni agostic interaction (Fig. 6a) and thus weakens the carbon–nickel interaction. To probe the sensitivity of the Ni 4px,z final states to details of the agostic interaction, a relaxed surface scan was performed on 2 (Fig. 6b) starting from its ground state geometry and scanning about the Ni1–N2–C3–H4 dihedral angle (dNiNCH). Energetically, the formation of the agostic interaction (100° < dNiNCH < 120°) is not favourable due to steric repulsion by forcing the methyl group towards the metal centre (ΔΔE = 10 kJ mol−1, see ESI Section 3.4†). Electronically, the effect of the agostic interaction has a large impact on the Ni 4px final states. There is little change across a large dihedral range (0° < dNiNCH < 60°), where the agostic interaction does not form. Yet, once direct C → Ni orbital overlap is feasible (90° < dNiNCH < 119°), the Ni 4px,z splitting decreases (from 0.69 eV to 0.26 eV) due to the increase in energy of feature C (Fig. 6b) The Ni 4p final states are therefore highly sensitive to the location and orientation of the methyl group and thus reports directly on the presence of the bis-agostic interaction.
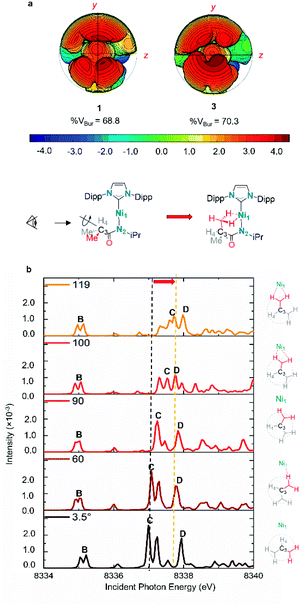 | ||
| Fig. 6 (a) Topographic steric maps of agostic complexes 1 and 3. Steric maps based on the density functional theory (DFT)-optimised structures of agostic Ni(I) complexes 1, 3. The steric maps are viewed down the x-axis from the pendant –CH3 side (shown in yz plane), showing the protrusion of bulk into the metal coordination sphere (defined with a radius of 4.5 Å); the isocontour scheme, in Å, is shown at the bottom. The red and blue zones indicate the more- and less-hindered zones, respectively. % VBur, percentage of buried volume. (b) Rotational relaxed scan of 2 along dihedral angle Ni1–N2–C3–H4 between two optimized geometry (3.5° non-agostic configuration to 119° agostic configuration, the black dash line and yellow dash line are highlighting the change of feature C along rotational scan). See ESI Section 3.4† for the energy profile of the rotational scan. TD-DFT calculated Ni K-edge XAS spectra of important structures were calculated. | ||
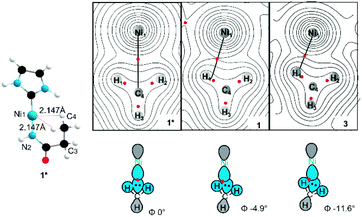
As noted previously, the specific geometry of the agostic interaction is very sensitive to the steric constraints imposed by the pendant substituents of the NHC. To explore this even further, a simplified model was constructed to focus exclusively on the electronic factors controlling the formation of the σCH → Ni4p agostic interaction. In this simplified model (1*), electron density analysis using the Atoms in Molecules formalism (AIM)44 reveals a single bond critical point (Fig. 7) connecting the carbon atom from the methyl group and the metal ion. The electron density value ρ(r) (0.0299 a.u) and the Laplacian of the energy density (∇2ρ(r) 0.117 a.u) are in good agreement with a previous AIM analysis on agostic interaction.45 However, the orientation of the methyl group in the full complex is slightly twisted (at a small energy cost of ∼0.08 kJ mol−1), which leads to a deviation of the agostic bcp (Fig. 7). The AIM calculation on both 1 and more twisted 3 reveals an offset single BCP (1ρ(r) = 0.038, ∇2ρ(r) = 0.159; 2ρ(r) = 0.038, ∇2ρ(r) = 0.152). The constrained adjustment of the dihedral angle Ni1–N2–C3–C4 of simplified model 1* illustrated that the BCP position is extremely sensitive to the relative position of the pendant methyl group (see ESI Section 3.2†). Both cases, the results differ markedly from that of other bis-agostic complexes, where two distinct bcp are observed.46,47 The presence of a single bond critical point connecting the methyl group to the metal highlights the unique character of these electron-rich Ni(I) species, which cannot make use of 3d states to accept electron density in forming the agostic bond. The direct C → Ni bonding energy can be estimated by the single BCP's potential energy density (60.4 kJ mol−1 for 1; 57.8 kJ mol−1 for 3),48 which aligns the energy shift of feature C (65 kJ mol−1 for 1, ∼50 kJ mol−1 for 3). The AIM calculation was also performed on non-agostic complexes 2 to reveal a BCP (2ρ(r) = 0.022, ∇2ρ(r) = 0.070), correlating to a weak hydrogen bond,49 a similar bcp was not found in complex 4 due to its longer Ni–H bond distance (see ESI Section 3.3†).
A second-order perturbation analysis using the natural bond orbital (NBO) formalism was also performed at an optimised higher level of theory (B3LYP/def2-TZVPP) to explore the nature of the Ni 4p interactions. Given that NBO calculations localize interactions (by design), it is not surprising that the second-order perturbation analysis identifies two distinct unsymmetrical C–H⋯Ni interactions from localised σCH to Ni 4p donation ([E(2)(H1): 103.1 kJ mol−1, E(2)(H2): 115.4 kJ mol−1] for 1 and [E(2)(H1): 124.5 kJ mol−1, E(2)(H2):75.5 kJ mol−1] for 3). The molecular orbital perspective, which is more consistent with the AIM results, describes these as resulting from a strong direct σ interaction and a weaker π interaction as shown in Fig. 5. Importantly, however, the sum of the NBO second-order perturbation energy shows the overall energy contribution of the agostic interaction and reflects a much stronger agostic interactions compared to the typical versions.9,12,43,50 (See comparisons of different theory level of second-order perturbation analysis and the orbital character of donation in ESI Section 3.3†).
The strong agostic interaction helps to prevent (or at least discourage) disproportionation,35 and contributes to C–H bond pre-activation and even a complete cleavage. We calculated the energy cost for cleavage of the agostic C–H bond in both 3 and 4 (see ESI Section 5†), allowing us to estimate that C–H bond cleavage is ∼100 kJ mol−1 lower in energy in the agostic complex. The activated C–H bond via the agostic contact allows a proton coupled electron transfer (PCET) mechanism to abstract a formal H atom from one of the agostic C–H interactions by a bulky radical reagent to afford the cyclometallated Ni(II) species (see ESI Section 5†) analogous to the Ni(II) reactive intermediate for C(sp3)–H bond functionalisation.51
Ni L2,3-edge XAS spectra
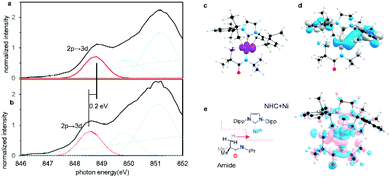
To confirm that these agostic interactions are dominated by Ni 4p and not strongly affected by Ni 3d contributions, Ni L2,3-edge XAS spectra were obtained for complexes 1, 2. In these spectra, Ni 2p–3d transitions are electric dipole allowed, thus permitting a more detailed look at Ni 3d contributions.Fits to the Ni L3 edges required inclusion of four features for the spectra of both 1 and 2 (See the assignment of each Gaussian curve in ESI Section 2.6†). The lowest energy feature in the spectrum correlates directly with feature A from the Ni K-edge spectra, but with significantly greater intensity. This 3d ← 2p feature differs by ∼0.2 eV between the two complexes (from 2 848.6 eV to 1 848.8 eV). TD-DFT calculations were also performed and predicted a small increase of ∼0.3 eV for this feature both from 1 to 2 and from 3 to 4 (ESI Section 2.6†). This feature correlates with a transition to the previously identified Ni 3dx2−y2-like SOMO and reflects minimal differences in the absence/presence of the agostic interaction. Although orbital interactions between the half-occupied Ni 3dx2−y2 orbital are possible with the agostic methyl group, these effects are mitigated by Pauli repulsion (Fig. 8c and d). The energy shift is consistent with a slight increase in electron density at the metal centre in the agostic complex as observed in electron density difference map (Fig. 8e). Electron donation from the methyl group into the valence Ni 4px causes a slight increase in the energy of the metal valence orbitals.50,52 We note that Pauli repulsion with the agostic methyl group is also expected to raise the energy of the 3d ← 2p feature. Notably, however, the observed effects are much smaller than those observed in the Ni 4p valence states, thus confirming the predominance of the Ni 4p contributions to the strong bis-agostic interaction in these complexes.
Conclusions
Herein, we report a fundamentally new form of bis-agostic interaction where the higher energy metal 4p orbitals are critical in the creation of a strong carbon–metal interaction. The metal 3d orbitals are essentially unavailable and thus alternative pathways are required. The specific nature of the parent linear Ni(I) complexes allows for a novel mode of bis-agostic bonding. This agostic interaction has a major impact on the X-ray spectroscopy allowing for both experimental and computational estimates of the strength of the different contributions. The bonding is dominated by the direct C 2p–N 4p σ donation, with minor contributions from σCH to Ni 4p π donation. This novel mode of binding is a particularly unexpected example of the importance of transition metal p orbitals in defining the nature of agostic interaction and σ complexes. We are now actively seeking to exploit this new binding mode to uncover unique reactivity in such systems.Methods
Synthetic methods
All experiments were carried out employing standard Schlenk techniques under an atmosphere of dry nitrogen employing degassed, dried solvents. Complex 1–2 used in this study are prepared according to literature procedures. Complex 3–4 are referred to Dr D. Dawson Beattie's thesis. Celite® was set in an oven at 180 °C for at least 24 hours, then brought into a glovebox overnight following standard procedures. Pyridine and acetonitrile were purchased from Sigma-Aldrich, dried over CaH2, and degassed by three freeze–pump–thaw cycles. d6-Benzene was purchased from Cambridge Isotope Laboratories Inc., dried over sodium metal, and degassed by three freeze–pump–thaw cycles. THF and Et2O were dried over sodium metal and degassed by three freeze–pump–thaw cycles. Hexanes and toluene were either dried over sodium metal or passed over activated alumina columns into Teflon sealed Schlenk flasks and degassed by three freeze–pump–thaw cycles. NMR spectra were recorded on Bruker Avance 300, 400, or 600 MHz spectrometers. 1H NMR spectra are reported in parts per million (ppm) and were referenced.53 to residual solvent: 1H(C6D6): δ 7.16; 13C(C6D6): δ 128.06; coupling constants are reported in Hz. 13C NMR spectra were performed as proton-decoupled experiments and are reported in ppm. The multiplicities are abbreviated as follows: s = singlet, d = doublet, dd = doublet of doublets, t = triplet, sept = septet. NMR spectra are shown using MestReNova 6.0.2 NMR processing software. Integrations of paramagnetic compounds 1–4 were not possible. EI-MS data were obtained using a Kratos MS-50 spectrometer (70 eV source). Elemental analyses were recorded on a Carlo Erba EA 1108 elemental analyser.Crystallographic methods
All measurements of complex 3 and 4 were made on a Bruker APEX DUO diffractometer with a TRIUMPH curved-crystal monochromator with Mo-Kα radiation. The data were collected at a temperature of −183.0 ± 0.1 °C. Data were collected in an of ϕ and ω 0.5° oscillations using 20.0 seconds exposures. The crystal-to-detector distance was 40.14 mm. Data were collected and integrated using the Bruker SAINT software package. Data were corrected for absorption effects using the multi-scan technique (SADABS). The data were corrected for Lorentz and polarisation effects. All non-hydrogen atoms were refined anisotropically. All hydrogen atoms were placed in calculated positions. The weighting scheme was based on counting statistics. Neutral atom scattering factors were taken from Cromer and Waber. Anomalous dispersion effects were included in Fcalc; the values for f′ and f′′ were those of Creagh and McAuley. The values for the mass attenuation coefficients are those of Creagh and Hubbell. All refinements were performed using the SHELXL-2013 via the OLEX2 interface. Additional EADP (2) and SADI (1) restraints were used in the refinement process of complex 4. All restraints led to improved model statistics. More crystallographic details are given in ESI.†Computational methods
Density functional theory calculations initial geometries for all molecules were obtained from crystallographic coordinates (where available) or constructed from standard models. Geometry optimisations and numerical frequency calculations were performed using version 4.21 of the ORCA computational chemistry package.54 Molecular geometries were optimised using the PBE0 functional34 and all-electron basis sets (def2-TZVP)55 for Ni centre and def2-SVP for all the rest atoms. Statistical mechanics calculations of entropic and thermal effects were performed using the rigid rotor and harmonic oscillator approximations at 298.15 K and 1 atm. Computational efficiency was improved by applying the RI approximation (RIJCOSX) for the hybrid functional.56 All calculations were performed with integration grid (ORCA Grid4). XAS TD-DFT (X-ray absorption time-dependent DFT) calculations were performed with a dense integration grid (Gird6) for better implementing scalar relativistic effects by using ZORA8 corrections and reduced by using MOanlayzer software. NBO57 calculations were calculated with Gaussian 09 program package,13 AIM44 calculations were performed in Multiwfn58 software by using NBO outputs using D3LYP40/def2-TZVPP level. All calculations were run on the UBC Chemistry Abacus cluster and on the Cedar of Compute Canada cluster.X-ray absorption spectroscopy
All the samples used in XAS Ni K edge and L edge experiments were analysed as solids under anaerobic conditions and diluted in boron nitride (20–50% by weight). Samples used in XAS Ni K-edge quickly frozen under liquid nitrogen environment. XAS Ni K-edges were acquired at the SSRL beamline 7-3, which is equipped with a Si(220) ϕ = 90° double crystal monochromator, a 9 keV cut-off mirror, and a He cryostat (at 20 K). Data were collected using a Canberra 30-element Ge solid-state detector with a 3 mm Co filter. Data averaging and energy calibration were performed using SixPack and the AUTOBK algorithm available in the Athena software package was employed for data reduction and normalisation.XAS L edge spectra were recorded at beamline 10-1 at the Stanford Synchrotron Radiation Lightsource (SSRL). An array of transition-edge-sensor (TES) detectors were used to obtain high energy resolution partial fluorescence yield (PFY) data. The TES array consists of 220 operational detectors spanning a total active area of 1.9 mm2. While the monochromator was scanned across the intended energy region (e.g., 840–960 eV), the total electron yield from the samples was measured using a Channeltron electron multiplier. The incident beam intensity was monitored via a gold grid and used as I0 to normalise the total electron yield signal I1. For comparison, the normalised (I1/I0) spectra were renormalised to each other's maximum. The scans were recorded with a step size of 0.3 eV and an integration time of 1 s per pt. The energy resolution of the incident radiation is ∼0.3 eV. Each final spectrum was the sum of five scans from different sample spots. Energy calibration was performed using NiF2, with an L3-edge feature at 852.7 eV.59 To minimise self-absorption in the fluorescence data, the incident angle was set at 55° with respect to the sample surface. All samples were measured at room temperature. To minimise radiation damage, a defocused beam (about 1 × 1 mm2) was used.
Data availability
All computational and spectroscopic data from this manuscript can be requested directly from the corresponding author if additional detail is required in addition to the ESI.†Author contributions
WH and PK conceived the study. PK, JAL, LLS supervised the study. WH performed the spectroscopic and TD-DFT/DFT computational studies. DDB performed the synthesis and collected X-ray diffraction data. DDB and WH collected and analysed the EPR data. DDB performed the PCET test. EB helped perform the NBO calculation and provided computational suggestions. HZ performed the EXAFS analysis. PK and WH wrote the paper. All authors discussed the results and participated in revising and finalising the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors thank The University of British Columbia (4YF to D. D. B., Laird to D. D. B., W. H., E. G. B.), the Government of Canada (Vanier Canada Graduate Scholarship to E. G. B.), and the Globalink Graduate Fellowship from Mitacs Canada to W. H. NSERC (Discovery Grant to P. K.). NSERC (Discovery, CREATE, and Instrumentation Grants to J. A. L. and L. L. S.), this work was undertaken, in part, thanks to funding from the Canada Research Chairs program (L. L. S.). Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH. We appreciate some very helpful discussions with Kris Altus on C–H activation. We also thank Dr Brian O Patrick for providing a final check on all crystallographic data.Notes and references
- P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2019, 119, 2192–2452 CrossRef CAS PubMed.
- Organotransition Metal Chemistry: From Bonding to Catalysis, https://hartwig.cchem.berkeley.edu/book/, accessed 11 June 2021 Search PubMed.
- J. Calleja, D. Pla, T. W. Gorman, V. Domingo, B. Haffemayer and M. J. Gaunt, A steric tethering approach enables palladium-catalysed C-H activation of primary amino alcohols, Nat. Chem., 2015, 7, 1009–1016 CrossRef CAS PubMed.
- S. D. Friis, M. J. Johansson and L. Ackermann, Cobalt-catalysed C–H methylation for late-stage drug diversification, Nat. Chem., 2020, 12, 511–519 CrossRef CAS PubMed.
- M. Etienne and A. S. Weller, Chem. Soc. Rev., 2014, 43, 242–259 RSC.
- W. H. Bernskoetter, C. K. Schauer, K. I. Goldberg and M. Brookhart, Characterization of a Rhodium(I) σ-Methane Complex in Solution, Science, 2009, 326, 553–556 CrossRef CAS PubMed.
- S. D. Pike, F. M. Chadwick, N. H. Rees, M. P. Scott, A. S. Weller, T. Krämer and S. A. Macgregor, Solid-state synthesis and characterization of σ-alkane complexes, [Rh(L2)(η2,η2-C7H12)][BArF4] (L2 = bidentate chelating phosphine), J. Am. Chem. Soc., 2015, 137, 820–833 CrossRef CAS PubMed.
- J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514 CrossRef CAS PubMed.
- W. Scherer and G. S. McGrady, Angew. Chem., Int. Ed., 2004, 43, 1782–1806 CrossRef CAS PubMed.
- M. Lein, Coord. Chem. Rev., 2009, 253, 625–634 CrossRef CAS.
- X. Lin, W. Wu and Y. Mo, Agostic Interactions in Early Transition-Metal Complexes: Roles of Hyperconjugation, Dispersion, and Steric Effect, Chem.–Eur. J., 2019, 25, 6591–6599 CrossRef CAS PubMed.
- W. Scherer, V. Herz, A. Brück, C. Hauf, F. Reiner, S. Altmannshofer, D. Leusser and D. Stalke, The Nature of β-Agostic Bonding in Late-Transition-Metal Alkyl Complexes, Angew. Chem., Int. Ed., 2011, 50, 2845–2849 CrossRef CAS PubMed.
- Y. Boutadla, D. L. Davies, S. A. Macgregor and A. I. Poblador-Bahamonde, J. Chem. Soc., Dalton Trans., 2009, 5820–5831 RSC.
- S. I. Gorelsky, D. Lapointe and K. Fagnou, Analysis of the concerted metalation-deprotonation mechanism in palladium-catalyzed direct arylation across a broad range of aromatic substrates, J. Am. Chem. Soc., 2008, 130, 10848–10849 CrossRef CAS PubMed.
- M. P. Jensen, D. D. Wick, S. Reinartz, P. S. White, J. L. Templeton and K. I. Goldberg, Reductive elimination/oxidative addition of carbon-hydrogen bonds at Pt(IV)/Pt(II) centers: Mechanistic studies of the solution thermolyses of TpMe2Pt(CH3)2H, J. Am. Chem. Soc., 2003, 125, 8614–8624 CrossRef CAS PubMed.
- J. F. Hartwig, K. S. Cook, M. Hapke, C. D. Incarvito, Y. Fan, C. E. Webster and M. B. Hall, Rhodium Boryl Complexes in the Catalytic, Terminal Functionalization of Alkanes, J. Am. Chem. Soc., 2005, 127, 2538–2552 CrossRef CAS PubMed.
- J. A. Flores, V. N. Cavaliere, D. Buck, B. Pintér, G. Chen, M. G. Crestani, M.-H. Baik and D. J. Mindiola, Methane activation and exchange by titanium-carbon multiple bonds, Chem. Sci., 2011, 2, 1457 RSC.
- V. N. Cavaliere, M. G. Crestani, B. Pinter, M. Pink, C.-H. Chen, M.-H. Baik and D. J. Mindiola, Room Temperature Dehydrogenation of Ethane to Ethylene, J. Am. Chem. Soc., 2011, 133, 10700–10703 CrossRef CAS PubMed.
- K. M. Waltz and J. F. Hartwig, Selective functionalization of alkanes by transition-metal boryl complexes, Science, 1997, 277, 211–213 CrossRef CAS.
- K. M. Waltz, X. He, C. Muhoro and J. F. Hartwig, Hydrocarbon Functionalization by Transition Metal Boryls, J. Am. Chem. Soc., 1995, 117, 11357–11358 CrossRef CAS.
- H. Chen, S. Schlecht, T. C. Semple and J. F. Hartwig, Thermal, catalytic, regiospecific functionalization of alkanes, Science, 2000, 287, 1995–1997 CrossRef CAS PubMed.
- J. F. Hartwig, S. Bhandari and P. R. Rabien, Addition of Catecholborane to a Ruthenium-Alkyl: Evidence for σ Bond Metathesis with a Low-Valent, Late Transition Metal, J. Am. Chem. Soc., 1994, 116, 1839–1844 CrossRef CAS.
- L. Brammer, J. M. Charnock, P. L. Goggin, R. J. Goodfellow, T. F. Koetzle and A. G. Orpen, Hydrogen bonding by cisplatin derivative: Evidence for the formation of N-H ⋯ Cl and N-H ⋯ Pt bonds in [NPrn4] 2{[PtCl4]·cis-[PtCl2(NH 2Me)2]}, J. Chem. Soc., Chem. Commun., 1987, 443–445 RSC.
- W. Scherer, A. C. Dunbar, J. E. Barquera-Lozada, D. Schmitz, G. Eickerling, D. Kratzert, D. Stalke, A. Lanza, P. Macchi, N. P. M. Casati, J. Ebad-Allah and C. Kuntscher, Anagostic Interactions under Pressure: Attractive or Repulsive?, Angew. Chem., Int. Ed., 2015, 54, 2505–2509 CrossRef CAS PubMed.
- H. V. Huynh, L. R. Wong and P. S. Ng, Anagostic interactions and catalytic activities of sterically bulky benzannulated N-heterocyclic carbene complexes of nickel(II), Organometallics, 2008, 27, 2231–2237 CrossRef CAS.
- M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914 CrossRef CAS PubMed.
- M. Kandiah, G. S. McGrady, A. Decken and P. Sirsch, [(Triphos)Ni(η2-BH4)]: an unusual nickel(I) borohydride complex, Inorg. Chem., 2005, 44, 8650–8652 CrossRef CAS PubMed.
- Y. Gloaguen, G. Alcaraz, A.-F. Pécharman, E. Clot, L. Vendier and S. Sabo-Etienne, Phosphinoborane and Sulfidoborohydride as Chelating Ligands in Polyhydride Ruthenium Complexes: Agostic σ-Borane versus Dihydroborate Coordination, Angew. Chem., Int. Ed., 2009, 48, 2964–2968 CrossRef CAS PubMed.
- R. Beck and S. A. Johnson, Structural similarities in dinuclear, tetranuclear, and pentanuclear nickel silyl and silylene complexes obtained via Si-H and Si-C activation, Organometallics, 2012, 31, 3599–3609 CrossRef CAS.
- W. Baratta, C. Mealli, E. Herdtweck, A. Ienco, S. A. Mason and P. Rigo, Nonclassical vs. Classical Metal⋯H3C-C Interactions: Accurate Characterization of a 14-Electron Ruthenium(II) System by Neutron Diffraction, Database Analysis, Solution Dynamics, and DFT Studies, J. Am. Chem. Soc., 2004, 126, 5549–5562 CrossRef CAS PubMed.
- L. Maria, A. Paulo, I. C. Santos, I. Santos, P. Kurz, B. Spingler and R. Alberto, Very small and soft scorpionates: water stable technetium tricarbonyl complexes combining a bis-agostic (k3-H, H, S) binding motif with pendant and integrated bioactive molecules, J. Am. Chem. Soc., 2006, 128, 14590–14598 CrossRef CAS PubMed.
- S. H. Crosby, G. J. Clarkson and J. P. Rourke, A delicate balance between sp2 and sp3 C-H bond activation: a Pt(II) complex with a dual agostic interaction, J. Am. Chem. Soc., 2009, 131, 14142–14143 CrossRef CAS PubMed.
- I. M. Riddlestone, D. Mckay, M. J. Gutmann, S. A. Macgregor, M. F. Mahon, H. A. Sparkes and M. K. Whittlesey, Isolation of [Ru(IPr) 2 (CO)H] + (IPr = 1,3-Bis(2,6-diisopropylphenyl)imidazol-2-ylidene) and Reactivity toward E–H (E = H, B) Bondsboranes H 3 B·NR 2 H (R = Me, H) gave [Ru(IPr) 2 (CO) 3 H]BAr 4 F (3), [Ru(IPr) 2 (CO)(η 2-H 2 )H]BAr 4 F (4), and [Ru(IPr) 2 (CO)(κ 2-H 2 BH·NR 2 H)H]BAr 4 F Chart 1, Organometallics, 2016, 35, 1301–1312 CrossRef CAS.
- D. D. Beattie, E. G. Bowes, M. W. Drover, J. A. Love and L. L. Schafer, Oxidation State Dependent Coordination Modes: Accessing an Amidate-Supported Nickel(I) δ-bis(C–H) Agostic Complex, Angew. Chem., Int. Ed., 2016, 55, 13290–13295 CrossRef CAS PubMed.
- D. D. Beattie, G. Lascoumettes, P. Kennepohl, J. A. Love and L. L. Schafer, Disproportionation Reactions of an Organometallic Ni(I) Amidate Complex: Scope and Mechanistic Investigations, Organometallics, 2018, 37, 1392–1399 CrossRef CAS.
- L. R. Furenlid, M. W. Renner and E. Fujita, XAS studies of Ni(I), Ni(II), and Ni(III) complexes, Phys. B, 1995, 208–209, 739–742 CrossRef.
- C. Uyeda and J. C. Peters, Access to formally Ni(i) states in a heterobimetallic NiZn system, Chem. Sci., 2013, 4, 157–163 RSC.
- N. Schuth, H. Gehring, B. Horn, P. Holze, R. Kositzki, P. Schrapers, C. Limberg and M. Haumann, Biomimetic mono- and dinuclear Ni(I) and Ni(II) complexes studied by X-ray absorption and emission spectroscopy and quantum chemical calculations, J. Phys.: Conf. Ser., 2016, 712, 012134 CrossRef.
- N. C. Tomson, K. D. Williams, X. Dai, S. Sproules, S. DeBeer, T. H. Warren and K. Wieghardt, Re-evaluating the Cu K pre-edge XAS transition in complexes with covalent metal–ligand interactions, Chem. Sci., 2015, 6, 2474–2487 RSC.
- L. shan Kau, D. J. Spira-solomon, J. E. Spira-solomon-penner-hahn, K. O. Hodgson and E. I. Solomon, X-ray Absorption Edge Determination of the Oxidation State and Coordination Number of Copper: Application to the Type 3 Site in Rhus vernicifera Laccase and Its Reaction with Oxygen, J. Am. Chem. Soc., 1987, 109, 6433–6442 CrossRef.
- C. J. Titus, M. L. Baker, S. J. Lee, H. M. Cho, W. B. Doriese, J. W. Fowler, K. Gaffney, J. D. Gard, G. C. Hilton, C. Kenney, J. Knight, D. Li, R. Marks, M. P. Minitti, K. M. Morgan, G. C. O'Neil, C. D. Reintsema, D. R. Schmidt, D. Sokaras, D. S. Swetz, J. N. Ullom, T. C. Weng, C. Williams, B. A. Young, K. D. Irwin, E. I. Solomon and D. Nordlund, L-edge spectroscopy of dilute, radiation-sensitive systems using a transition-edge-sensor array, J. Chem. Phys., 2017, 147, 214201 CrossRef PubMed.
- G. Von Frantzius, R. Streubel, K. Brandhorst and J. Grunenberg, How strong is an agostic bond? Direct assessment of agostic interactions using the generalized compliance matrix, Organometallics, 2006, 25, 118–121 CrossRef CAS.
- R. F. W. Bader, A Quantum Theory of Molecular Structure and Its Applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- V. Tognetti, L. Joubert, R. Raucoules, T. De Bruin and C. Adamo, Characterizing Agosticity Using the Quantum Theory of Atoms in Molecules: Bond Critical Points and Their Local Properties, J. Phys. Chem. A, 2012, 116, 5472–5479 CrossRef CAS PubMed.
- I. M. Riddlestone, D. McKay, M. J. Gutmann, S. A. Macgregor, M. F. Mahon, H. A. Sparkes and M. K. Whittlesey, Isolation of [Ru(IPr)2(CO)H]+ (IPr = 1,3-Bis(2,6-diisopropylphenyl)imidazol-2-ylidene) and reactivity toward E-H (E = H, B) Bonds, Organometallics, 2016, 35, 1301–1312 CrossRef CAS.
- K. Saha, R. Ramalakshmi, S. Gomosta, K. Pathak, V. Dorcet, T. Roisnel, J. F. Halet and S. Ghosh, Design, Synthesis, and Chemistry of Bis(σ)borate and Agostic Complexes of Group 7 Metals, Chem.–Eur. J., 2017, 23, 9812–9820 CrossRef CAS PubMed.
- S. Emamian, T. Lu, H. Kruse and H. Emamian, Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis Between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory, J. Comput. Chem., 2019, 40, 2868–2881 CrossRef CAS PubMed.
- U. Koch and P. L. A. Popelier, Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density, J. Phys. Chem., 2002, 99, 9747–9754 CrossRef.
- W. He and P. Kennepohl, Direct experimental evaluation of ligand-induced backbonding in nickel metallacyclic complexes, Faraday Discuss., 2019, 220, 133–143 RSC.
- D. D. Beattie, A. C. Grunwald, T. Perse, L. L. Schafer and J. A. Love, Understanding Ni(II)-Mediated C(sp3)–H Activation: Tertiary Ureas as Model Substrates, J. Am. Chem. Soc., 2018, 140, 12602–12610 CrossRef CAS PubMed.
- A. Desnoyer, W. He, P. Kennepohl, S. Behyan, W. Chiu, J. A. Love and A. Desnoyer, The importance of ligand-induced backdonation in the stabilization of square planar d10 nickel π-complexes, Chem.–Eur. J., 2019, 25, 5259–5268 CrossRef CAS PubMed.
- G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, NMR chemical shifts of trace impurities: Common laboratory solvents, organics, and gases in deuterated solvents relevant to the organometallic chemist, Organometallics, 2010, 29, 2176–2179 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree-Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: natural bond orbital analysis program, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. Olalde-Velasco, J. Jiménez-Mier, J. Denlinger and W.-L. Yang, Atomic multiplets at the L 2, 3 edge of 3 d transition metals and the ligand K edge in x-ray absorption spectroscopy of ionic systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245136 CrossRef.
- P. Olalde-Velasco, J. Jiménez-Mier, J. Denlinger and W.-L. Wang, Atomic multiplets at the L2,3 edge of 3d transition metals and the ligand K edge in X-ray absorption spectroscopy of ionic systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245136 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2114520 and 2114521. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc03578a |
| This journal is © The Royal Society of Chemistry 2021 |