A rare earth metallocene containing a 2,2′-azopyridyl radical anion

Abstract

Introducing spin onto organic ligands that are coordinated to rare earth metal ions allows direct exchange with metal spin centres. This is particularly relevant for the deeply buried 4f-orbitals of the lanthanide ions that can give rise to unparalleled magnetic properties. For efficacy of exchange coupling, the donor atoms of the radical ligand require high-spin density. Such molecules are extremely rare owing to their reactive nature that renders isolation and purification difficult. Here, we demonstrate that a 2,2′-azopyridyl (abpy) radical (S = 1/2) bound to the rare earth metal yttrium can be realized. This molecule represents the first rare earth metal complex containing an abpy radical and is unambigously characterized by X-ray crystallography, NMR, UV-Vis-NIR, and IR spectroscopy. In addition, the most stable isotope ⁸⁹Y with a natural abundance of 100% and a nuclear spin of ½ allows an in-depth analysis of the yttrium–radical complex via EPR and HYSCORE spectroscopy. Further insight into the electronic ground state of the radical azobispyridine-coordinated metal complex was realized through unrestricted DFT calculations, which suggests that the unpaired spin density of the SOMO is heavily localized on the azo and pyridyl nitrogen atoms. The experimental results are supported by NBO calculations and give a comprehensive picture of the spin density of the azopyridyl ancillary ligand. This unexplored azopyridyl radical anion in heavy element chemistry bears crucial implications for the design of molecule-based magnets particularly comprising anisotropic lanthanide ions.

---

Introduction

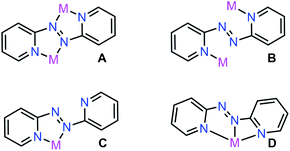
Azoaromatic ligands possess intriguing geometrical and electronic properties rendering them well-suited for the implementation in photo-responsive polymers and supramolecular assemblies.¹ Notably, the non-rigidity of this ligand class allows photoinduced cis–trans isomerization upon exposure to high-energy light (λ = 365 nm).² In particular, 2,2′-azobispyridine (abpy) has largely been employed in the realm of transition-metal (TM) chemistry owing to the energetic match between the π* orbitals of the ligand and the dπ of the metal.³ Azoaromatic compounds comprising rare earth metals are far less common and involved primarily the azobenzene ligand which bears the disadvantage of low coordinating ability often resulting in low yields and many side products.^4–6 Notably, structurally characterized abpy-containing rare earth metal complexes remain elusive.⁵

Abpy features two pyridyl rings bridged by a central azo-group (N=N), allowing for multiple coordination modes which the ligand can adopt for the generation of mono- and multi-metallic systems, respectively (Fig. 1). In bimetallic compounds, abpy is typically isolated in an ‘S-frame’ bonding motif where two metal centres are bridged by the abpy ligand through coordination to one pyridyl group and one nitrogen of the azo group (Fig. 1A), producing two five-membered chelate rings sharing the azo group.⁷ An alternative binding mode of abpy in bimetallic systems involves the coordination of only the pyridyl rings (Fig. 1B).⁸ Monometallic abpy complexes commonly exhibit a bidentate conformation of the ligand through both pyridyl and azo nitrogen coordination forming a five-membered chelate ring akin to that observed for the metal complexes of the ‘S-frame’ nature referring to one of the chelates therein (Fig. 1C).⁹ An alternative, but scarce, binding motif of abpy is a tridentate coordination environment arising from the rotation of the N_azo–C bond and coordination to the metal centre through three nitrogen donors of one azo-nitrogen and two pyridyl rings, Fig. 1D.^10,11

Fig. 1 Coordination modes of 2,2′-azobispyridine (abpy), where M = transition metal.

Abpy is redox-active and known to exist in neutral, radical anionic, and dianionic forms. Sequential addition of electrons to the azo-centred π* molecular orbital results in an elongation of the central N–N bond, ranging from ∼1.24 Å for the neutral ligand to ∼1.35 Å for the radical anionic and ∼1.40 Å for the dianionic ligand (Scheme 1).¹² The electron-accepting ability of abpy resulted in mixed-valent TM systems with ambiguous oxidation state of the metal.¹³ EPR spectroscopy could constitute a powerful method to shine light on the radical nature of the abpy ligand in such metal complexes. However, the recorded spectra are often poorly resolved which is attributed to pronounced anisotropic line broadening caused by the large concentration of spin density at the two central ¹⁴N nuclei of the azo group.¹⁴

Scheme 1 Oxidation states of 2,2′-azobispyridine with N–N distances (Å) of the azo unit.

We are particularly intrigued by the accessibility of the open shell abpy ligand and the possibility to successfully combine it synthetically with a rare earth metal which not only is a synthetically fascinating target but also has huge ramifications for molecular magnet design.^15,16 Of particular interest is a molecule class coined as single-molecule magnets (SMMs)^15,17,18 that exhibit slow magnetic relaxation and magnetic hysteresis in the wake of an energy barrier to spin inversion, and thus, show bulk magnetic properties on the molecular scale. Their property of preserving the spin direction for a long time at low temperatures renders such molecules highly intriguing for high-density information storage and spin-based computing.^19–22 The chase of SMMs with substantially high magnetic blocking temperatures involves deliberate molecular design, where in particular the lanthanides have reigned supreme owing to their innate high magnetic anisotropy stemming from large unquenched orbital momentum and strong spin orbit coupling.^23,24 Albeit various strategies have been exploited to achieve this goal, two approaches centred around increasing the single-ion anisotropy of the metal centre in mononuclear SMMs,^25–29 and introducing strong magnetic exchange coupling between metal centres in multinuclear SMMs,^16,30–32 have been overwhelmingly fruitful. The latter methodology profited from implementing an open-shell ligand to strongly couple paramagnetic metal centres and thus, increasing the energy separation between spin ground state and excited states, which ultimately afforded the highest coercive field of H_c = 7.9 T (at 10 K) observed for a molecular system to date in [(Cp^Me4H₂Tb)₂(μ-N₂˙)]⁻ (Cp^Me4H = tetramethylcyclopentadienyl).³⁰ Although a highly lucrative strategy, the number of radical ligands that have been proven to promote strong direct exchange is limited.¹⁶ Thus, the hunt for bridging redox-active ligands with adequate coordination geometry, orbital symmetry, and spin density is imperative for the generation of multinuclear SMMs that operate at significantly higher temperatures. To the best of our knowledge, the radical state of azobispyridine is unknown in molecular magnet design which together with its possible use in the realm of rare earth metal ions with a potential to pre-/postmodify the pyridine rings, has sparked our interest.

The tripositive yttrium ion among all rare earth metal ions bears the advantage of being diamagnetic and comparable in terms of ionic size to late lanthanide ions such as dysprosium and holmium (1.019 Å, 1.027 Å, and 1.015 Å for Y, Dy, and Ho respectively, coordination number (CN) = 8).³³ Hence, the isolation of an yttrium radical complex enables in-depth analysis of the electron spin distribution within the ligand and across the molecule, being conducive to assess metal–radical coupling strengths in respective congeners composed of heavier lanthanides. Here, we report the first unambiguously characterized rare earth metal complex containing a 2,2′-azobispyridine ligand, (Cp^Me4H)₂Y(abpy˙) (where Cp^Me4H = tetramethylcyclopentadienyl; abpy = 2,2-azobispyridine), 1, which has been fully analysed by X-ray crystallography, NMR-, UV-Vis-NIR- and IR spectroscopy. Structural analysis hinted at a monoanionic abpy unit and indeed, the radical nature of the ligand was unequivocally proven by EPR and ¹⁴N-HYSCORE spectroscopy. Notably, the collected and simulated HYSCORE data represent the first for any yttrium radical complex. In addition, DFT calculations support also our experimental findings and in particular the existence of the paramagnetic ligand in the yttrium complex.

Experimental methods

General information

All manipulations described below were performed under an inert atmosphere with rigorous exclusion of oxygen and moisture using Schlenk and glovebox techniques. House nitrogen was purified through a MBraun HP-500-MO-OX gas purifier prior to use. Toluene and THF were dried by refluxing over potassium using benzophenone as an indicator and distilled prior to use. n-Hexane was dried by refluxing over calcium hydride and distilled prior to use. 1,2,3,4-Tetramethylcyclopentadiene (Cp^Me4HH) was purchased from Sigma-Aldrich and dried over 4 Å sieves prior to use. Allylmagnesium chloride (2.0 M in THF), 6% sodium hypochlorite solution, and anhydrous YCl₃ were purchased from Sigma-Aldrich and used without further purification. 2-Aminopyridine was purchased from Alfa Aesar and used as received. Potassium bis(trimethylsilyl)amide, KN[Si(CH₃)₃]₂, was purchased from Sigma-Aldrich, dissolved in toluene, filtered through a Celite plug, and recrystallized from toluene at −35 °C. The compounds KCp^Me4H,³⁴ [HNEt₃][BPh₄],³⁵ KC₈,³⁶ 2,2-azobispyridine (abpy),³⁷ and (Cp^Me4H)₂Y(BPh₄)³⁸ were prepared according to literature procedures. A PerkinElmer 2400 Series II CHNS/O analyser was used for CHN elemental analyses. IR spectra were obtained through use of a Cary 630 diamond ATR-IR spectrometer in an argon-filled glovebox. UV-Vis-NIR data were collected on a PerkinElmer Lambda 1050 spectrometer in 1 cm sealed quartz cuvettes in THF. ¹H-NMR spectrum was collected with a 500 MHz Agilent DirectDrive2 500 and calibrated to the residual solvent signals (benzene-d₆: δ_H = 7.16 ppm). The sample was prepared in a nitrogen-filled glovebox using a standard NMR tube sealed air-tight.

Synthesis of (Cp^Me4H)₂Y(abpy˙), 1

A 1 mL THF solution of 33.7 mg (0.18 mmol) abpy was added dropwise to a stirring 3 mL THF solution of 117.3 mg (0.18 mmol) (Cp^Me4H)₂Y(BPh₄) to yield a deep blue solution. After five mins, 24.4 mg (0.18 mmol) KC₈ were added to the reaction mixture to afford a deep purple solution. The reaction was allowed to proceed for 40 min at 25 °C. The resulting purple solution was subsequently filtered through a Celite plug and dried under vacuum. The resulting purple tacky-solid was extracted with ten 1 mL portions of hexane. The combined purple-hexane fractions were subsequently filtered through a Celite-plug and evaporated to dryness under reduced pressure. Purple crystals of (Cp^Me4H)₂Y(abpy˙), 1, suitable for X-ray analysis were grown from a concentrated hexane solution at −35 °C in 47% yield (42.3 mg, 0.08 mmol) over the course of 48 h. IR (neat) 3056w, 2901s, 2854s, 2724w, 2505vw, 2322vw, 2285vw, 2083vw, 1579s, 1457s, 1431vs, 1379s, 1303s, 1257m, 1214w, 1142s, 1109w, 1023w, 989s, 937m, 865w, 772s, 737s, 690m cm⁻¹. Anal. Calcd for C₂₈H₃₄N₄Y: C, 65.24; H, 6.65; N, 10.87. Found C, 65.56; H, 7.17; N, 11.0. The paramagnetic nature of (Cp^Me4H)₂Y(abpy˙) results in significant peak broadening in the ¹H-NMR spectrum (Fig. S3†), thus signals were not integrated or assigned. ¹H-NMR (C₆D₆): δ 8.71, 4.98, 3.74, 2.95, 2.02, 1.71 ppm.

X-ray crystallography

A dark violet plate-shaped crystal with dimensions 0.16 × 0.15 × 0.09 mm³ was mounted. Data were collected using a XtaLAB Synergy, Dualflex, HyPix diffractometer equipped with an Oxford Cryosystems low-temperature device, operating at T = 100.01(10) K.

Data were measured using ω scans of 0.5° per frame for 0.1/0.5 s using Cu K_α radiation (micro-focus sealed X-ray tube, 50 kV, 1 mA). The total number of runs and images was based on the strategy calculation from the program CrysAlisPro (Rigaku, V1.171.41.90a, 2020). The achieved resolution was Θ = 77.278.

Cell parameters were retrieved using the CrysAlisPro (Rigaku, V1.171.41.90a, 2020) software and refined using CrysAlisPro (Rigaku, V1.171.41.90a, 2020) on 20 399 reflections, 61% of the observed reflections. Data reduction was performed using the CrysAlisPro (Rigaku, V1.171.41.90a, 2020) software which corrects for Lorentz polarization. The final completeness is 99.80 out to 77.278 in Θ CrysAlisPro 1.171.41.90a (Rigaku Oxford Diffraction, 2020) Numerical absorption correction based on Gaussian integration over a multifaceted crystal model empirical absorption correction using spherical harmonics, implemented in SCALE3 ABSPACK scaling algorithm.

The structure was solved in the space group P1̄ by using dual methods using the ShelXT structure solution program.³⁹ The structure was refined by least-squares using version 2018/2 of XL⁴⁰ incorporated in Olex2.⁴¹ All non-hydrogen atoms were refined anisotropically. Hydrogen atom positions were calculated geometrically and refined using the riding model, except for the hydrogen atom on the non-carbon atom(s) which were found by different Fourier methods and refined isotropically when data permits.

Evans method

Solution state magnetic studies were carried out using the Evans method.⁴² Data were collected using a Varian 600 MHz superconducting NMR-Spectrometer operating at 599.892 MHz from 250 to 300 K. A J. Young tube was charged with 15 mM toluene-d₈ solution of 1, along with a sealed capillary containing a 21 mM hexamethyldisiloxane reference. Diamagnetic contributions were accounted for through use of Pascal's constants. No approximation was included for the temperature dependence of toluene-d₈ density.

Computational methods

All DFT calculations were performed with the Gaussian'16 software package.⁴³ To determine a suitable method for the characterization of 1, six functionals were tested by comparing the bond metrics of the optimized geometries against the experimental crystallographic data. Calculations were performed with the unrestricted hybrid functionals TPSSh,⁴⁴ B3LYP,⁴⁵ PBE0,⁴⁶ and M06,⁴⁷ the range-separated hybrid functional, CAM-B3LYP,⁴⁸ as well as the pure DFT functional, TPSS,⁴⁹ and included the Grimmes D3 dispersion correction to account for dispersion effects.⁵⁰

1 was initially optimized with the 3-21G^51,52 basis set on all atoms and subsequently reoptimized using a mixed basis set approach. The polarization basis set, def2-TZVP,^53,54 was applied for Y, which includes a 28 in-core electrons ECP, and the atomic orbitals of N, C, and H atoms were described with the def2-SV(P) basis set,⁵⁴ which features polarization functions on non-hydrogen atoms. After all geometry optimizations were complete, an analysis of the bond metrics in 1 across the six unrestricted functionals with the def2-SV(P)&def2-TZVP basis set combination was performed, considering the mean deviation (MD), mean square error (MSE), root mean square error (RMSE), and mean absolute percent error (MAPE). The analysis suggested that the B3LYP functional was the most accurate method for the characterization of 1, Table S3.† Therefore, a final geometry optimization was performed using the unrestricted B3LYP functional and a valence triple-zeta polarization basis set description of the atomic orbitals on all atoms (def2-TZVP⁵⁴), with the fully relativistic effective core potential (ECP28MDF⁵⁵), Table S4.† An analytical frequency calculation confirmed that the stationary points were indeed local minima, and the Natural Bond Orbital analysis was computed from the final optimized geometry through the NBO 6 program.⁵⁶

EPR spectroscopy

Continuous-wave (cw) and pulsed EPR measurements were conducted by using a Bruker E-680X spectrometer operating at X-band frequencies. Cw-EPR measurements were taken at ambient temperature employing a Bruker 4102-ST cavity. Pulse-EPR experiments were performed using a Bruker ER 4118X-MD-X5-W1 (MD5) probe and were carried out at 40 K using an Oxford CF-935 cryostat and ITC-503 temperature controller. Hyperfine Sublevel Correlation (HYSCORE) measurements were done using the standard, 90°–τ–90°–t₁–180°–t₂–90°–τ-echo, 4-pulse sequence with all pulse widths set to 16 ns (FWHM). Two pulse channels were used so that the peak power of the 90° pulses could be attenuated by 6 dB from that used for the 180° degree pulse (approximately 800 W).⁵⁷ The four-step phase cycle designated for non-ideal pulses was used.⁵⁸ Data collection made use of 20 ns time increments for both t₁ and t₂ dimensions with a 128 × 128 grid of time points collected. Data were processed using a second order polynomial to remove background decays followed by application of a Hamming window, zero filling to 256 points in each dimension and 2D-FFT. Absolute value spectra are displayed as contour plots with the plotting threshold set at 5% of the maximum peak amplitude for the frequency window displayed.

Cw-EPR and HYSCORE simulations were done with EasySpin 5.2.28 running in the MATLAB 2020a environment.^59,60 For analysis of solution spectra, a combination of genetic, Monte-Carlo and Nelder-Mead Simplex algorithms were used to fit the data. HYSCORE simulations were judged by visual comparison of predicted contour peak patterns with experimental spectra.

Cyclic voltammetry

Cyclic voltammetry was performed using a Metrohm Autolab PGSTAT204 potentiostat with a glassy carbon working electrode, platinum wire pseudo-reference electrode, and platinum wire as the counter electrode. All electrochemistry experiments were performed within the confines of an MBraun glovebox under an atmosphere of argon with an atmosphere of <0.1 ppm of O₂ and H₂O. (Cp^Me4H)₂Y(abpy˙) (3 mM) was dissolved in 3 mL of a 250 mM solution of [NⁿBu₄][PF₆] in THF. The voltammogram was referenced externally to a 3 mM solution of ferrocene. Cyclic voltammetry of the ferrocene reference solution was performed five times to afford standard deviations in the potential shift, and the resulting Fc/Fc⁺ redox couple was found to be 1.1 ± 0.2 V. Subsequent experiments were referenced to this value.

Results and discussion

Synthesis and spectroscopic characterization

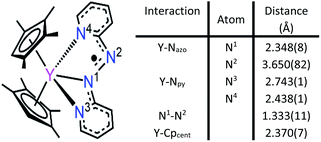
2,2′-Azobispyridine can be readily synthesized by the oxidative coupling of 2-aminopyridine in water at 0 °C.⁶¹ Treatment of (Cp^Me4H)₂Y(BPh₄) with abpy, followed by reduction with potassium graphite in THF yielded (Cp^Me4H)₂Y(abpy˙), 1, (Fig. 2). Mononuclear alkyl-substituted cyclopentadienyl tetraphenylborate synthons have been employed in salt-metathesis reactions to access radicals of bipyrimidine,⁶² diazafluorenylidene-substituted phosphaalkene,⁶³ dinitrogen,³⁰ tetrapyridylpyrazine,⁶⁴ hexaazatrinaphthylene,⁶⁵ and phenazine.⁴ An alternative approach exploited lanthanide allyl synthons to afford indigo radical-bridged metal complexes by alkene elimination.⁶⁶ Concentrated, purple-coloured hexane solution of 1 at −35 °C afforded crystals in 47% yield suitable for X-ray analysis. Compound 1 crystallizes in the space group P1̄ and constitutes a rare crystallographically characterized yttrium–radical complex. In fact, to the best of our knowledge, this is the second example of a mononuclear yttrium metallocene that bears a radical ligand.⁴ The structure of 1 exhibits two molecules in the unit cell where each features a nine-coordinate, trivalent yttrium ion ligated by two η⁵-(Cp^Me4H)⁻ ligands and one abpy ligand. Specifically, the abpy ligand adopts a cis-geometry to bind in a tridentate fashion to the metal ion. The bond order of the azo unit is assigned as 1.5 as the N–N distance of 1.333(11) Å compared to the N=N double bond of 1.245(1) Å in free abpy is significantly elongated and to the sp³-sp³ single bond of 1.416(4) Å in hydrazine is substantially shortened.^67,68 Hence, the structural parameters suggest that the main charge density is located on the azo moiety of the nitrogen ligand. The Y–N distances vary by up to 0.3 Å stemming from an asymmetrically coordinated abpy ligand to the yttrium centre. The distances of the pyridine entities to the Y^III ion are with 2.743(1) and 2.438(1) Å considerably longer than the 2.348(8) Å Y–N_azo distance, further attesting a larger charge distribution on the azo unit. The distance of Y to the non-coordinating N of the azo group is longest with a value of 3.650(82) Å. Select metrical distances of the various Y–N interactions are shown in Fig. 3. An in-depth analysis of distances across both molecules is given in Table S2.†

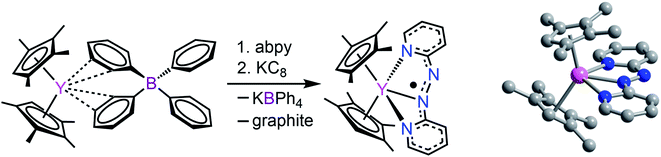Fig. 2 Left: Synthetic scheme for (Cp^Me4H)₂Y(abpy˙), 1. Right: Structure of 1. Pink, blue, and gray spheres represent Y, N, and C atoms, respectively; H atoms are omitted for clarity.

Fig. 3 Left: Labeling of nitrogen atoms. Right: Distances of relevant Y–N interactions.

The UV-Vis-NIR electronic absorption spectrum of 1 exhibits multiple transitions in the visible region centred at 385 and 551 nm (Fig. S4†). These transitions coincide well with predicted intraligand (IL) bands of an abpy radical from CNDO/S calculations, assigned to the π₇→π₈ and π₈→π₉ transitions, respectively. The π₈→π₁₁ band is not resolved in the experimental spectrum owing to its weak oscillator strength.⁶⁹ These transitions correspond well with observed electronic transitions for abpy˙, as previously measured through spectroelectrochemical methods on ruthenium complexes.⁷⁰

The monoanionic nature of the abpy ligand was further probed by IR spectroscopy on crystalline material of 1 (Fig. S5†). The N=N stretching mode of the abpy ligand is forbidden in the trans geometry but allowed in the cis.⁷¹1 exhibits a ν(N=N) at 1431 cm⁻¹, slightly higher in energy than that observed by the free ligand (1424 cm⁻¹),⁷² attributed to the reduction in bond order through population of the azo-centred π* molecular orbital. The high energy region of the infrared spectrum corresponds well to the stretching frequencies of other yttrium-based metallocenes, such as (Cp^Me4H)₂Y(BPh₄),³⁸ whereas the lower energy vibrations are dominated by abpy-like features.

Upon coordination of the abpy ligand an increase of energy of ν(C=C) and ν(C=N) (1430–1610 cm⁻¹) has been indicative of the coordination of the pyridyl residue to a metal centre.⁹ A comparison of the IR spectra of 1 with the free abpy ligand, Fig. S6,† highlights this phenomenon.

The solution state magnetic properties of 1 were investigated through the Evans method.⁴² Measurements were performed from 250 to 300 K in d₈-toluene with hexamethyldisiloxane as a reference. At room temperature, the value of the effective magnetic moment, μ_eff, of 1 is 1.53, which decreases steadily to 1.45 at 249 K, confirming the presence of one unpaired electron (Fig. S7†).

Computational study

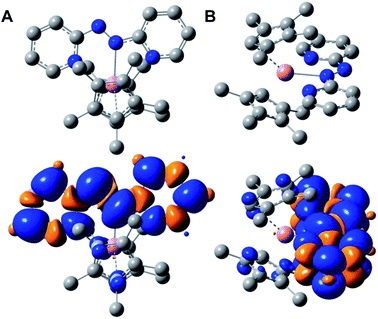
The diamagnetic nature of the trivalent yttrium ion allows for accurate determination of the localization of the electron spin density stemming from the monoanionic abpy radical. Thus, computational methods were employed to further elucidate the electronic structure, and among six different functionals, the unrestricted hybrid B3LYP⁴⁵ functional and mixed basis set description, def2-TZVP&def2-SV(P), for Y, and C, H, and N atoms, respectively, was determined to be the most accurate method for the characterization of 1 (Table S4†). Thus, a final geometry optimization was performed using the larger def2-TZVP basis set on all atoms, as well as a 28 in-core electrons pseudopotential (ECP28MDF⁵⁵). 1 was optimized as a neutral doublet and the resulting Mulliken spin density was found to be predominantly localized to the azo unit of the coordinated abpy ligand, with minor contributions from the ancillary (Cp^Me4H)⁻ ligands and metal centre, Fig. 4. Here, the unpaired spin density is asymmetrically distributed between the azo-nitrogen atoms, with a spin density of 0.216 and 0.330 for the coordinated (N¹) and non-coordinated (N²) nitrogen atoms, respectively. The pyridyl nitrogen atoms, N³ and N⁴, carry significantly lower spin densities of 0.092 and 0.115, respectively. In addition, the calculated LUMO+1 and LUMO largely reside along the pyridyl rings of the abpy ligand, which is similar to the computed SOMO that also resides principally along the abpy ligand. Conversely, the HOMO and HOMO−1 are largely localized to the metallocene fragment of 1, Fig. S9.†

Fig. 4 (A) Arial perspective of the optimized structure (top) and computed Mulliken spin density (bottom) of (Cp^Me4H)₂Y(abpy˙), 1. (B) Side perspective of the optimized structure (top) and computed Mulliken spin density (bottom) of 1. Pink, blue, and gray spheres represent Y, N, and C atoms, respectively; H atoms are omitted for clarity.

A Natural Bond Orbital (NBO) analysis of 1, confirms the ionic bonding picture between the trivalent yttrium ion and the anionic (abpy˙)⁻ and (Cp^Me4H)⁻ ligands. The Y–N interactions were heavily polarized towards the nitrogen atoms, exceeding 95% nitrogen-character in the case of both pyridyl nitrogen atoms, and 99% nitrogen-character between the coordinating azo-nitrogen, N¹, and the metal centre. Furthermore, the 1.5 bond order ascribed to the azo unit is supported by the NBO analysis, which describes a σ-bond between two singly occupied sp²-hybridized α and β spin orbitals (SOs), where the σ-bond is partially polarized towards the N¹ atom (52% N¹, 48% N²). In addition, the NBO description places an unpaired electron in each of the non-bonding alpha SOs of the azo nitrogen atoms, as well as an unpaired electron in the π-bonding beta SOs. Here, the unpaired electrons in each non-bonding alpha SO may interact with the unpaired beta electron, resulting in a singly unpaired and delocalized electron, as evidenced by the significant spin density on the azo nitrogen atoms.

A second-order perturbation theory analysis of 1, suggests that the four inequivalent Y–N interactions range in their degree of stabilization. Each of the Y–N bonds originate from nitrogen-centred lone pairs, donating into empty d- and sd-hybridized orbitals – most significantly between the lone pairs of the N¹ and N³ atoms at 36.4 kcal mol⁻¹ and 26.9 kcal mol⁻¹, respectively. In contrast, weaker donations were resolved from the second pyridyl nitrogen, N⁴, of 13.1 and 10.5 kcal mol⁻¹ into vacant sd⁴ -and sd²-hybrid orbitals on yttrium. From the non-coordinating azo-nitrogen atom, N², a significantly weaker interaction of 5.7 kcal mol⁻¹ could be determined. Furthermore, the calculated Wiberg Bond Indexes (WBI) for 1 are consistent with both the crystallographic Y–N distances and degree of stabilization from the second-order perturbation theory description of the Y–N interactions. The greatest WBI is the Y–N¹ value of 0.203 in contrast to 0.052 for Y–N². For comparison, the average Y–C_Cp bond index is 0.110. Additionally, the asymmetry of the pyridyl nitrogen atoms' interaction with the metal centre is also consistent with the computed WBI values of 0.164 and 0.173 for N³ and N⁴, respectively.

Electron paramagnetic resonance spectroscopy

The radical nature of the coordinating abpy ligand was unambiguously confirmed by EPR spectroscopy. The cw-EPR spectrum of 1 in a toluene solution is depicted in Fig. 5 (black trace). The signal is centred near g = 2.006 and shows more than 40 peaks, spread over a magnetic field range of about 4 mT, that arise from a combination of ¹⁴N, ¹H and possibly, ⁸⁹Y hyperfine couplings. The number of coupled nuclei and particularly the asymmetric coordination mode of the abpy radical ligand to Y renders an accurate interpretation of this intricate spectrum difficult without independent knowledge of some of the hyperfine couplings. To gain this information, we undertook a HYSCORE study of the radical at 40 K. HYSCORE is a two-dimensional electron spin echo envelope modulation method that is particularly well-suited for separating the contributions of ¹⁴N and ¹H hyperfine couplings to an EPR spectrum.⁵⁷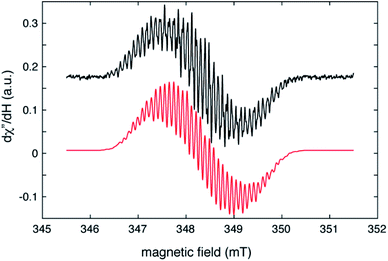

Fig. 5 Cw–EPR spectrum of (Cp^Me4H)₂Y(abpy˙), 1 (black trace), collected under the following conditions: microwave frequency, 9.7788 GHz; microwave power, 80 μW; modulation amplitude, 0.02 mT, modulation frequency, 100 KHz; sample temperature, 295 K. The red trace is a simulation produced by using the isotropic hyperfine couplings and model described in the text and summarized in Table 1.

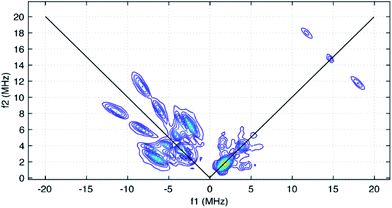
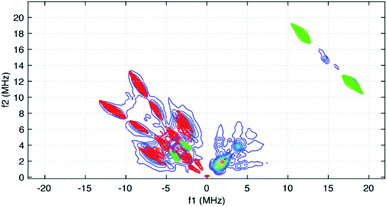
The HYSCORE spectrum collected near g = 2.006 using a τ-value of 204 ns is shown in Fig. 6. Because the hyperfine couplings for the four ¹⁴N atoms of the abpy ligand radical are expected to be greater than the ¹⁴N Larmor frequency of 1.07 MHz at 347.0 mT, their HYSCORE response is found in the (−,+) quadrant of the spectrum. The combined contributions of the cross peaks at (−8.2, 11.3 MHz), (−6.3,8.2 MHz), (−4.1, 5.3 MHz) and (−3.5, 3.7 MHz) with their partner cross peaks on the opposite side of the frequency diagonal form a V-shaped pattern in this quadrant. Herein, cross peak pairs will be referred to by the peak with the higher f2 value. This V-shaped pattern can arise from a ¹⁴N hyperfine coupling that features comparable isotropic and anisotropic (dipolar) contributions. Under these conditions, a 1-dimensional ESEEM or ENDOR spectrum would be expected to show overlapped powder pattern line shapes from α and β electron spin manifolds. ¹⁴N hyperfine couplings of this type have been reported in 1-dimensional ESEEM experiments.⁷³ We predicted that much of the HYSCORE response resolved in the (−,+) quadrant originated from the weaker-coupled, pyridine nitrogen atoms of the abpy ligand. Since the crystal structure of 1 indicates that the bonding from these heteroatoms to the central yttrium is relatively weak (the distances are greater than 2.4 Å), their ¹⁴N nuclear quadrupole coupling constants, e²qQ/h, could be restricted to the 3.0–4.5 MHz range based on results from previous NQR studies of pyridine coordinated to Zn^II and Cd^II in simple model compounds.⁷⁴

Fig. 6 HYSCORE spectrum of Cp^Me4H₂Y(abpy˙), 1, taken under the following conditions: microwave frequency, 9.7405 GHz; magnetic field, 347.0 mT; τ-value, 204 ns; sample temperature, 40 K. Data are displayed using a threshold of 5% of the maximum peak amplitude.

Taking the ¹⁴N hyperfine tensor to be axial with its principal axis aligned with the p^π orbital, and the principal axis the nuclear quadrupole interaction (nqi) to be directed along the N–Y bond, a reasonable simulation for the HYSCORE response detected in the (−,+) quadrant was obtained. One simulation is shown in Fig. 7 as the red contours superimposed on the data in the (−,+) quadrant. This simulation was obtained using isotropic hyperfine couplings of 4.4 MHz and dipolar couplings of 4.0 MHz for both coupled pyridine nitrogen atoms. The values of e²qQ/h and η (asymmetry parameter) that describe the nqi for each nitrogen were important for determining the positions of the cross peaks at (−2.3, 6.4 MHz) and (−3.5, 7.0 MHz) in our simulations. For one of the heteroatoms, values of e²qQ/h = 4.0 MHz and η = 0.1 were used, while values of e²qQ/h = 3.6 MHz and η = 0.3 were used for the second nitrogen. For both nitrogen atoms, the orientation of nqi principal axis system (PAS) was considered to be along their respective N–Y bonds giving rise to orientation angles of (0°, 90°, 0°) and (60°, 90°, 0°) for the “QFrame” function used by EasySpin to orient the nqi PAS within the framework of the hyperfine PAS (see Fig. S10†).

Fig. 7 HYSCORE simulations for the two pyridyl ¹⁴N atoms (red contours) added to simulations for the stronger-coupled abpy ligand protons (green) and the predicted coupling for the central ⁸⁹Y atom (green cross peaks in the (−,+) quadrant). For the ¹⁴N couplings, identical axial hyperfine couplings with A_iso = 4.4 and T = 4.0 MHz were taken into account. The nqi parameters employed for these nuclei were slightly different and are given in the text. The hyperfine coupling used for the ⁸⁹Y simulation considered an isotropic contribution of 7.6 MHz and a dipolar contribution of 2.0 MHz.

The cross peaks resolved at (11.7, 18.0 MHz) in Fig. 6 are due to coupled protons. Because this cross peak pair is close to the proton antidiagonal, the anisotropic portion of the coupling is modest and simulations show that this set of cross peaks is well described by a hyperfine tensor with principal values of (−5.6, −3.6, −10.6 MHz) and an isotropic coupling of −6.6 MHz. Simulations showing the contributions of this coupling, and a predicted coupling for ⁸⁹Y,⁷⁵ (see below) are shown as green contours added to the simulation plot of Fig. 7.

The isotropic hyperfine couplings from these two simulations can be used to estimate the unpaired electron spin density in the p^π orbitals of the abpy pyridyl nitrogen atoms and associated carbon atoms. Based on a Q-value of 22.5 G for ¹⁴N,⁷⁶ an isotropic hyperfine coupling of 4.4 MHz translates to an unpaired spin density of 0.07 for the pyridine nitrogens. The DFT calculations reported here show unpaired spin populations for the p^π orbitals of 0.09 and 0.10 for these nitrogen atoms in reasonable agreement with our experimental findings. These calculations also show that the abpy ligand retains much of the odd-alternate distribution of unpaired electron spin that characterizes a typical π-radical. As a result, the eight ligand protons should divide into two sets of couplings. If the −6.6 MHz coupling is translated into a p^π carbon spin density using a McConnell Q-factor −22.5 G, a spin density of 0.10 is determined. This value is close to the 0.11 average unpaired spin density calculated for the four corresponding carbon atoms of the abpy ligand by DFT. Given this agreement, a minimal model for simulating the cw-EPR spectrum of Fig. 5 was constructed where the hyperfine couplings for the two pyridyl nitrogens were set to 4.5 ± 0.5 MHz, and the couplings for the four stronger-coupled ligand protons were set to −6.6 ± 0.5 MHz. The two azo-nitrogens were allowed to vary independently and given starting couplings of 12 ± 5 MHz and 18 ± 5 MHz in accordance with the difference in their unpaired spin densities predicted by DFT. Given the extent of the hyperfine structure observed in the cw-EPR spectrum, and the size of the smallest observed line splitting in the spectrum, we added contributions from the four weaker-coupled protons of the abpy ligand, the central ⁸⁹Y atom and the two ring protons of the (Cp^Me4H)⁻ ligands. The best fit simulation for the cw-EPR spectrum is shown in Fig. 5 (red trace) and was obtained using the hyperfine couplings listed in Table 1. Our fitting approach made use of the genetic and Monte–Carlo algorithms available in EasySpin to identify parameter combinations with lower RMSD values. The Nelder–Mead Simplex algorithm was then used to refine the fits. With the symmetric coupling model described above, the best fit gave a RMSD value of 0.07. The hyperfine couplings determined from these calculations are summarized in Table 1. To improve on this error, a model that allowed for a less symmetric hyperfine coupling scheme would be required.

Table 1 Isotropic hyperfine couplings determined for (Cp^Me4H)₂Y(abpy˙)

Nucleus	Number	A iso (MHz)
^14Npy	2	4.4
^14Nazo	1	15.2
^14Nazo	1	11.4
^1Habpy	4	−6.5
^1Habpy	4	2.3
^89Y	1	7.6
^1H–Cp^Me4H	2	1.1

---

Among the isotropic hyperfine couplings determined from simulation of the cw-EPR spectrum is a (−)7.6 MHz coupling attributed to ⁸⁹Y. This value is consistent with a weak cross peak pair resolved at (−2.9, 4.7 MHz) in the HYSCORE spectrum (Fig. 5 and 7). When compared to the hyperfine coupling reported for atomic ⁸⁹Y in the gas phase, −1250 MHz, the unpaired electron spin density on the metal ion can be estimated to be 0.006.⁷⁷ The 7.6 MHz isotropic hyperfine coupling reported here is comparable to that observed for a N₂³⁻˙ radical-bridged yttrium complex, (8.1 MHz),⁷⁸ but substantially lower than the value of ∼100 MHz reported for organometallic Y(II) complexes in condensed phase.⁷⁹ Notably, the 7.6 MHz isotropic hyperfine coupling is greater than the 1.3 MHz value measured for ⁸⁹Y encapsulated in C₈₂.⁸⁰

Electrochemical study

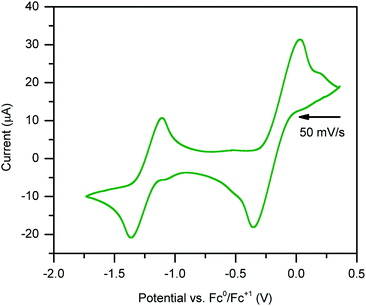
Stable, heterobimetallic transition metal complexes have been isolated from mononuclear synthons bearing the dianionic abpy ligand.⁸¹ To date, cyclic voltammetric analysis of even Cp-based transition metal complexes containing an azobispyridine ligand remain elusive. The closest study represents conducted electrochemistry on a ruthenium chloride arene complex, [(abpy)Ru^II(p-cymene)Cl][PF₆].⁸²

In order to assess the redox-activity of 1, cyclic voltammetry was performed in THF using [NⁿBu₄][PF₆] as a supporting electrolyte (Fig. 8). The measurement revealed two independent quasi-reversible processes, with one feature centred at E_1/2 = −1.2 ± 0.244 V versus [Fc]/[Fc⁺] and the other at −0.2 ± 0.244 mV. The quasi-reversible redox event at −1.2 ± 0.244 V can be attributed to the abpy²⁻/abpy¹⁻ redox couple, indicating that mononuclear rare earth metal complexes bearing a dianionic abpy ligand should be accessible under these conditions. The redox event located at more positive potentials can be tentatively assigned to the abpy¹⁻/abpy⁰ redox couple. Notably, the redox behaviour of 1 changed rapidly upon subsequent scans (Fig. S11†). Indeed, the redox event at more negative potentials featured a decline in both the reductive and oxidative waves upon iterative scans, indicating the onset of an irreversible chemical process coupled to the electron transfer. By contrast, the redox couple positioned at more positive potentials exhibited after several scans a stark disparity in the oxidative wave relative to the first scan. Taken together, we hypothesize that a one-electron oxidation initiates a chemical change of 1.

Fig. 8 Cyclic voltammogram of (Cp^Me4H)₂Y(abpy˙) vs. Fc. 250 mM [NⁿBu₄][PF₆] in THF and 3 mM analyte. Voltammogram features two quasi-reversible redox events: one process at E_1/2 = −1.2 ± 0.244 V, and one irreversible process at approximately −0.2 ± 0.244 mV.

The irreversible nature of the two observed redox events may be linked to the large difference in electronic structure when considering abpy⁰, abpy¹⁻, and abpy²⁻. Drastic alterations in the Lewis basicity of the chelating nitrogens may result in a conformational change of the organometallic complex. In addition, the low-energy barrier to rotation of the azo group, and high Lewis acidity of the yttrium^III ion could also contribute to a conformational change.

Conclusions

The first unambiguously characterized rare earth metal complex, (Cp^Me4H)₂Y(abpy˙), 1, containing an abpy radical ligand, was synthesized through stoichiometric addition of the abpy ligand to the (Cp^Me4H)₂Y(BPh₄) complex, followed by a one-electron reduction employing the strong reducing agent KC₈. Importantly, this discovery additionally constitutes the first molecular rare earth compound bearing any 2,2-/3,3-/4,4 azobispyridine ligand regardless of its oxidation state. The ramifications of this finding are huge and will pave the way to not only devise synthetic protocols that allow the isolation of lanthanide analogues but also may provide access to actinide congeners. Notably, actinide complexes comprising any azobispyridine are hitherto unknown, possibly due to the difficulty of taming the ligand in one isomer in conjunction with the enhanced challenge of a redox-active metal centre referring to early actinides. The structure of 1 reveals a rare tridentate coordination geometry for abpy, where binding to the metal centres occurs through both pyridyl rings and one nitrogen of the azo unit. NBO and Mulliken spin density calculations suggest an inequivalent coordination of the nitrogen atoms to the central Y^III ion. The radical nature of the abpy ligand was confirmed by both cw- and HYSCORE EPR spectroscopy. Through use of both techniques, the ¹⁴N hyperfine couplings were elucidated, confirming the large spin density located on both the azo- and pyridyl-nitrogen atoms. Noteworthy, this present intertwined EPR and HYSCORE spectroscopic investigation is the first of its kind on any yttrium radical complex. The results derived from the advanced spectroscopic, and computational analysis are in excellent agreement. Furthermore, the redox activity of 1 was probed via cyclic voltammetry and led to the discovery of a quasi-reversible redox event ascribed to a ligand-centred phenomenon. Taken together, the various coordination modes, multiple accessible oxidation states, and valuable possibility to functionalize the abpy ligand, positions it to be a paramount molecular building block in the realm of rare earth chemistry. These results offer a unique platform to pursue azopyridyl radical complexes comprising paramagnetic metals, whether it be lanthanides or actinides, since the radical character on the nitrogen donors should lead to strong magnetic exchange coupling. In fact, the combination of highly magnetic anisotropy and strong magnetic coupling results in single-molecule magnets with high blocking temperatures. In particular, radical-bridged homo- and heterobimetallic complexes featuring the magnetically anisotropic rare earth metals, dysprosium and terbium, are of great interest and will be pursued.⁸³

Data availability

All computational data, spectroscopic data, supplementary figures and tables, and detailed crystallographic information can be found in the ESI.† Crystallographic data are available via the Cambridge Crystallographic Data Centre (CCDC): 2101167.

Author contributions

F. D. prepared and characterized the compounds. F. D. collected, solved, and refined the X-ray diffraction data. E. C. carried out all computations and analyzed with S. D. the resulting data. F. D. and J. M. performed EPR and HYSCORE spectroscopy and studied with S. D. the obtained data. S. D. assisted with data analysis, formulated, and directed the research, and wrote the manuscript with input from all the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. D. is grateful to the Department of Chemistry at Michigan State University (MSU) for generous start-up funds. We are grateful to Dr Richard J. Staples at MSU for his assistance with the interpretation of the collected X-ray diffraction data and to the group of Prof. James K. McCusker (MSU) for providing access to the UV-Vis-NIR spectrometer. This work was supported in part through computational resources and services provided by the Institute for Cyber-Enabled Research at MSU. Funding for the Single Crystal X-ray diffractometer was provided by the MRI program by the National Science Foundation under Grant No. 1919565.

References

1. H. Ren, P. Yang and F. M. Winnik, Polym. Chem., 2020, 11, 5955–5961.
2. E. V. Brown and G. R. Granneman, J. Am. Chem. Soc., 1975, 97, 621–627.
3. S. I. Gorelsky, E. S. Dodsworth, A. B. P. Lever and A. A. Vlcek, Coord. Chem. Rev., 1998, 174, 469–494.
4. M. R. MacDonald, J. W. Ziller and W. J. Evans, Inorg. Chem., 2011, 50, 4092–4106.
5. D. J. Berg, J. M. Boncella and R. A. Andersen, Organometallics, 2002, 21, 4622–4631.
6. W. J. Evans, D. K. Drummond, L. R. Chamberlain, R. J. Doedens, S. G. Bott, H. Zhang and J. L. Atwood, J. Am. Chem. Soc., 1988, 110, 4983–4994.
7. W. Kaim, Coord. Chem. Rev., 2001, 219–221, 463–488.
8. M. Bardají, M. Barrio and P. Espinet, Dalton Trans., 2011, 40, 2570–2577.
9. D. A. Baldwin, A. B. P. Lever and R. V Parish, Inorg. Chem., 1969, 8, 107–115.
10. M. Camalli, F. Caruso, G. Mattogno and E. Rivarola, Inorg. Chim. Acta, 1990, 170, 225–231.
11. H. Tsurugi, H. Tanahashi, H. Nishiyama, W. Fegler, T. Saito, A. Sauer, J. Okuda and K. Mashima, J. Am. Chem. Soc., 2013, 135, 5986–5989.
12. R. Jana, F. Lissner, B. Schwederski, J. Fiedler and W. Kaim, Organometallics, 2013, 32, 5879–5886.
13. B. Sarkar, S. Patra, J. Fiedler, R. B. Sunoj, D. Janardanan, G. K. Lahiri and W. Kaim, J. Am. Chem. Soc., 2008, 130, 3532–3542.
14. S. Frantz, J. Fiedler, I. Hartenbach, T. Schleid and W. Kaim, J. Organomet. Chem., 2004, 689, 3031–3039.
15. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
16. S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176.
17. J. Gatteschi, D. Sessoli and R. Villain, Molecular Magnetism, Oxford University Press on Demand, Oxford, 2007.
18. R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816.
19. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197.
20. R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360.
21. S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138.
22. H. B. Heersche, Z. de Groot, J. A. Folk, H. S. J. van der Zant, C. Romeike, M. R. Wegewijs, L. Zobbi, D. Barreca, E. Tondello and A. Cornia, Phys. Rev. Lett., 2006, 96, 206801.
23. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
24. J. Lu, M. Guo and J. Tang, Chem.–Asian J., 2017, 12, 2772–2779.
25. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
26. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
27. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2020, 59, 18844.
28. K. Randall McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503.
29. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
30. S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144.
31. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542.
32. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239.
33. R. D. Shannon, Acta Crystallogr., Sect. A., 1976, 32, 751–767.
34. W. J. Evans, D. S. Lee, M. A. Johnston and J. W. Ziller, Organometallics, 2005, 24, 6393–6397.
35. B. J. Barker and P. G. Sears, J. Phys. Chem., 1974, 78, 2687–2688.
36. D. E. Bergbreiter and J. M. Killough, J. Am. Chem. Soc., 1978, 100, 2126–2134.
37. W. Fang, X. Liu, Z. Lu and T. Tu, Chem. Commun., 2014, 50, 3313–3316.
38. S. E. Lorenz, B. M. Schmiege, D. S. Lee, J. W. Ziller and W. J. Evans, Inorg. Chem., 2010, 49, 6655–6663.
39. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
40. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
41. O. V Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
42. D. F. Evans, J. Chem. Soc., 1959, 2003–2005.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennuci, H. P. Hrachian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Oligaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, revision B.01, Gaussian, Inc., Wallingford, CT, 2016.
44. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
45. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
46. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
47. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
48. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
49. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
50. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
51. J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947.
52. K. D. Dobbs and W. J. Hehre, J. Comput. Chem., 1987, 8, 880–893.
53. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141.
54. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
55. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
56. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
57. A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press on Demand, 2001.
58. C. Gemperle, G. Aebli, A. Schweiger and R. R. Ernst, J. Magn. Reson., 1990, 88, 241–256.
59. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
60. S. Stoll and R. D. Britt, Phys. Chem. Chem. Phys., 2009, 11, 6614–6625.
61. Y. S. Panova, A. V Sheyanova, N. V Zolotareva, V. V Sushev, A. V Arapova, A. S. Novikov, E. V Baranov, G. K. Fukin and A. N. Kornev, Eur. J. Inorg. Chem., 2018, 2018, 4245–4254.
62. S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549.
63. C. Chen, Z. Hu, J. Li, H. Ruan, Y. Zhao, G. Tan, Y. Song and X. Wang, Inorg. Chem., 2020, 59, 2111–2115.
64. S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701–4711.
65. C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, Angew. Chem., Int. Ed., 2017, 56, 10103–10107.
66. F.-S. Guo and R. A. Layfield, Chem. Commun., 2017, 53, 3130–3133.
67. H. Bock, R. Dienelt, H. Schödel and T. T. H. Van, Struct. Chem., 1998, 9, 279–288.
68. S. Patai, Chemistry of the Hydrazo, Azo, and Azoxy groups, Wiley, 1975.
69. M. Krejcik, S. Zalis, J. Klima, D. Sykora, W. Matheis, A. Klein and W. Kaim, Inorg. Chem., 1993, 32, 3362–3368.
70. S. Frantz, M. Sieger, I. Hartenbach, F. Lissner, T. Schleid, J. Fiedler, C. Duboc and W. Kaim, J. Organomet. Chem., 2009, 694, 1122–1133.
71. H. Hacker, Spectrochim. Acta, 1965, 21, 1989–2004.
72. J. W. Le Fevre, M. F. O'Dwyer and R. L. Werner, Aust. J. Chem., 1953, 6, 341–359.
73. J. McCracken, J. Peisach, C. E. Cote, M. A. McGuirl and D. M. Dooley, J. Am. Chem. Soc., 1992, 114, 3715–3720.
74. Y.-N. Hsieh, G. V Rubenacker, C. P. Cheng and T. L. Brown, J. Am. Chem. Soc., 1977, 99, 1384–1389.
75. J. R. Persson, Zeitschrift für Physik D Atoms, Molecules and Clusters, 1997, 42, 259–262.
76. J. K. Dohrmann and W. Kieslich, J. Magn. Reson., 1978, 32, 353–366.
77. W. Weltner, Magnetic Atoms and Molecules, Courier Corporation, 1989.
78. M. Fang, J. E. Bates, S. E. Lorenz, D. S. Lee, D. B. Rego, J. W. Ziller, F. Furche and W. J. Evans, Inorg. Chem., 2011, 50, 1459–1469.
79. J. F. Corbey, D. H. Woen, C. T. Palumbo, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, Organometallics, 2015, 34, 3909–3921.
80. S. Knorr, A. Grupp, M. Mehring, U. Kirbach, A. Bartl and L. Dunsch, Appl. Phys. A, 1998, 66, 257–264.
81. S. Frantz, M. Weber, T. Scheiring, J. Fiedler, C. Duboc and W. Kaim, Inorg. Chim. Acta, 2004, 357, 2905–2914.
82. A. Das, T. M. Scherer, A. D. Chowdhury, S. M. Mobin, W. Kaim and G. K. Lahiri, Inorg. Chem., 2012, 51, 1675–1684.
83. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2101167. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc04285h

---