Open Access Article
Open Access ArticlePlanar hexacoordinate gallium†
Meng-hui
Wang
a,
Chen
Chen
a,
Sudip
Pan
 *bc and
Zhong-hua
Cui
*bc and
Zhong-hua
Cui
 *ad
*ad
aInstitute of Atomic and Molecular Physics, Key Laboratory of Physics and Technology for Advanced Batteries (Ministry of Education), Jilin University, Changchun, China. E-mail: zcui@jlu.edu.cn
bInstitute of Advanced Synthesis, School of Chemistry and Molecular Engineering, Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing Tech University, Nanjing, China
cFachbereich Chemie, Philipps-Universität Marburg, Hans-Meerwein-Strasse 4, 35032 Marburg, Germany. E-mail: pans@chemie.uni-marburg.de
dBeijing National Laboratory for Molecular Sciences, China
First published on 26th October 2021
Abstract
We report the first planar hexacoordinate gallium (phGa) center in the global minimum of the GaBe6Au6+ cluster which has a star-like D6h geometry with 1A1g electronic state, possessing a central gallium atom encompassed by a Be6 hexagon and each Be–Be edge is further capped by an Au atom. The electronic delocalization resulting in double aromaticity (both σ and π) provides electronic stability in the planar form of the GaBe6Au6+ cluster. The high kinetic stability of the title cluster is also understood by Born–Oppenheimer molecular dynamics simulations. The energy decomposition analysis in combination with the ‘natural orbitals for chemical valence’ theory reveals that the bonding in the GaBe6Au6+ cluster is best expressed as the doublet Ga atom with 4s24p⊥1 electronic configuration forming an electron-sharing π bond with the doublet Be6Au6+ moiety followed by Ga(s)→[Be6Au6+] σ-backdonation and two sets of Ga(p‖)←[Be6Au6+] σ-donations.
Introduction
The creative mind is always fascinated in breaking the usual established rules, supported by the traditional knowledge, to set a new limit to break. That is the way science is progressing. In chemistry, the realization of planar tetracoordination for carbon, in contrast to the usual tetrahedral arrangement, was one of such events that arose much curiosity in the scientific community in the late twentieth century when Hoffmann et al.,1 in their hallmark paper published in 1970, put forward the effective electronic stabilization strategy for planar tetracoordinate carbon (ptC). Over the past half century, persistent research and great efforts were made by several groups in this area, which led to the detection or synthesis and/or theoretical prediction of a variety of planar hypercoordinate carbon and other elements.2–27 Amongst them, there are numerous successful examples (global structure) in the literature for the planar tetracoordinate (pt) species4–6,28–45 and even some of them (CAl4−, CAl42−, CAl3Si−, CAl3Ge− and CAl4H−)46–50 were detected in the gas-phase. Research is not only restricted to carbon, but anionic ptAl15 and neutral ptSi16–18 were also synthesized which could show astonishing reactivities as well. If achievement of planar tetracoordinate centers is elegant, the designing of planar hypercoordinate species beyond tetracoordination is no less than an artist's imagination in an excellent mood. Focusing on groups 13 and 14 elements, such hypercoordination violates both the usual coordination number and geometry (tricoordinates and trigonal geometry for the former and tetracoordinates and tetrahedral geometry for the latter case).The achievement of planar hypercoordinate species essentially benefits from the electronic or steric stabilization strategy, or a combination of both.1 In other words, the electronic and structural match between the planar center and ligand ring is a key factor for designing planar hypercoordinate species, especially the prerequisites become much more crucial with the increasing coordination number since they clearly violate both conventional bonding constraints simultaneously. Indeed, in contrast to numerous planar tetracoordinate species, only a few higher coordinated species have been reported so far, and mostly for planar pentacoordinate (pp) motifs.2,3,23,24,51–60 CAl5+ is the first masterpiece which possesses ppC in its global minimum.19 Readers can further refer to a recent review to know the present status of ppC systems.2
The realization of a planar hexacoordinate (ph) bonding motif, that is both thermodynamically and kinetically stable, is extremely rare.23,24 The research in that direction was triggered by the theoretical report of CB62− containing a phC25 which later turned out to be a high-lying isomer.60 The first true global minimum phC was found in the D3h symmetric CO3Li3+ cluster,24 although there is some doubt whether the C–Li linkage can be called a true coordination because of electrostatic repulsion originating from the positively charged phC and Li centers. Recently Tiznado and co-workers reported a series of global minimum for CE3M3+ (E = S, Se, Te; M = Li–Cs) having phC where the phC center carries a negative charge, and therefore, it induces electrostatic attraction between phC and alkali atoms.23 In these clusters, phC is multiply bonded to three chalcogens and ionically connected to the three alkali metals. Planar hypercoordinate boron in all-boron clusters is common because of the remarkable ability of boron to form planar structures even for much larger clusters and to form multicentered delocalized bonds owing to its inherent electron deficient nature.61 The planar hexacoordinate boron that is relevant to the present study is the most stable isomer of BBe6H6+ with a phB center and having dual (σ + π) aromaticity.26,27 A cluster containing a phAl in the global minimum form of the Al4C6 cluster was also reported.62 Apart from these, planar hexacoordination in an isolated cluster was not found. Note that the planar hexacoordinate motifs can be embedded in a two-dimensional (2D) nanosheet,63–65 which can provide both electronic stabilization and electronic-stabilization-induced steric force supports.65 But that is a different story as compared to the isolated clusters, which basically only rely on the electronic stabilization strategy, making their design extremely challengeable.
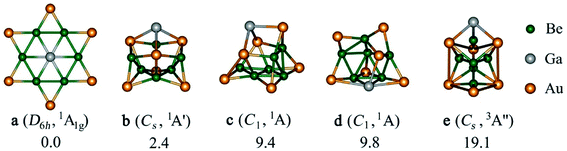
Herein, we report a thermodynamically and kinetically stable phGa cluster. To locate the planar hexacoordinate motifs, the appropriate peripheral ligand is a key factor, for example, the good π-acceptor/σ-donor capability (electronic factor) and strong ligand–ligand bond for the self-stability of the peripheral ligand ring (mechanical factor) could be the best target. In the light of the great superiority (real minimum) and clear limit (high-lying structure) of a boron monocyclic ring in the formation of planar hypercoordinate species, we systematically tested the possibility of using a beryllium ring (Ben), decorated by bridging s-block atoms (being isoelectronic to the boron monocyclic ring), in the planar hexacoordinate bonding. The global minimum of the GaBe6Au6+ cluster has a star-like D6h geometry with a 1A1g electronic state, possessing a central gallium atom encompassed by a Be6 hexagon and each Be–Be edge is further capped by an Au atom. The other group 13 elements do not lead to a planar hexacoordinate moiety as the most stable isomer.
Computational details
The structure search was performed using the CALYPSO (Crystal Structure Analysis by Particle Swarm Optimization) code, where the particle swarm optimization algorithm is implemented.66,67 PBE0/def2-SVP68,69 was used to optimize the initial structure of EBe6Au6+ (E = Al, Ga, In, Tl) with singlet and triplet spin states, and for the low-lying (within 40 kcal mol−1 relative energy window with respect to the global minimum) isomers we employed a bigger def2-TZVP basis set for better geometrical and frequency prediction. The single-point calculations for the low-lying energy isomers were performed at the CCSD(T)/def2-TZVP//PBE0/def2-TZVP level.69,70 Total energies were corrected using the zero-point energies (ZPEs) obtained at the PBE0/def2-TZVP level. Note that since we are comparing relative energies between two isomers, the relative error introduced in the results for adding ZPEs at the DFT level to the CCSD(T) energies will also be minimized. All these calculations were carried out with the Gaussian 09 program package.71 The natural bond orbital analysis for phGa was performed by using the NBO 7.0 program.72–74 The electron localization function (ELF) and the quantum theory of atoms in molecules (QTAIM)75,76 analyses were done using the Multiwfn program.77The Born–Oppenheimer molecular dynamics (BO-MD) simulation78 was carried out at temperatures of 300 and 400 K at the PBE0/def2-SVP level. Each simulation ran for 10 ps with a step size of 0.5 fs from the equilibrium global minimum structure with random velocities assigned to the atoms according to a Maxwell–Boltzmann distribution for both temperatures, and then normalized so that the net angular momentum for the whole system is zero. BO-MD simulations were performed using Gaussian 09 software.71
The energy decomposition analysis (EDA)79 in combination with the natural orbitals for chemical valence (NOCV)80 method was performed at the PBE0/TZ2P-ZORA//PBE0/def2-TZVP level using the ADF (2018.105) program package.81,82 In the EDA method, the interaction energy (ΔEint) between two prepared fragments is divided into three energy terms, viz., the electrostatic interaction energy (ΔEelstat), which represents the quasiclassical electrostatic interaction between the unperturbed charge distributions of the prepared atoms, the Pauli repulsion (ΔEPauli), which is the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments into the wavefunction that properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the product wavefunction, and the orbital interaction energy (ΔEorb), which originates from the mixing of orbitals, charge transfer and polarization between the isolated fragments. Therefore, the interaction energy (ΔEint) between two fragments can be defined as:
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb | (1) |
The orbital term may be further divided into contributions from each irreducible representation of the point group of the interacting system as follows:
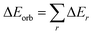 | (2) |
The EDA–NOCV combination allows the partition of ΔEorb into pairwise contributions of the orbital interactions, which gives important information about bonding. The charge deformation Δρk(r) which originates from the mixing of the orbital pairs Ψk(r) and Ψ−k(r) of the interacting fragments gives the size and the shape of the charge flow because of the orbital interactions (eqn (3)), and the corresponding ΔEorb reflects the amount of orbital interaction energy coming from such interaction (eqn (4)).
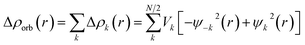 | (3) |
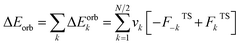 | (4) |
More information about the method and its applicability can be found in a recent review.83
Structures and stability
Firstly, we have checked the optimized geometries and nature of the stationary points for EBe6Au6+ (E = Al, Ga, In, Tl) clusters having a phE center enclosed by a Be6 ring with the latter being further decorated by bridging Au atoms. The resulting arrangement has a D6h symmetry and 1A1g electronic state. It turns out that the (BeAu)6 ring could indeed be a suitable peripheral ring to stabilize a phE, where the phE isomer of EBe6Au6+ turns out to be a real minimum for E = Ga and Tl, but a transition state with one imaginary frequency of 90.2i and 22.0i cm−1 for E = Al and In, respectively. The mode of the imaginary frequency corresponds to the out-of-plane movement of E which leads to a quasi-planar C6v symmetric structure where E is located 0.90 Å for Al and 0.98 Å for In above the Be6 basal plane. Similar results are also obtained taking different levels, B3LYP/def2-TZVP and TPSS/def2-TZVP (see Fig. S1 in the ESI†) which confirms that this observation is not an artefact of a particular level. Note that Be6Au6q (q = −1, 0, 1) clusters without any group 13 dopant have a three-dimensional unsymmetric geometry as the most stable isomer, whereas the planar isomer having a Be6 ring capped with Au at the bridging positions is a higher order saddle point (see Fig. S2†). Therefore, it indicates that the bonding between E and Be6Au6 unit is crucial to facilitate the planarization of the latter cluster.Next, a detailed potential energy surface (PES) search for the EBe6Au6+ (E = Al, Ga, In, Tl) clusters is performed and some low-lying isomers are provided in Fig. S3–S6.† Except for E = Ga, for others the most stable isomer is a three-dimensional cluster having a Be5 ring with Be at the center of the ring and E located at one side of the ring. Au atoms are at the bridging position of Be–Be bonds. It is interesting to note that although for E = Tl, phTl is a minimum, it lies significantly high (by 27.0 kcal mol−1) above the global minimum (see Fig. S7†). Only for GaBe6Au6+, the D6h symmetric phGa isomer turns out as the most stable isomer (see Fig. 1). It is also important to check the reliability of the single-reference based method. The T1 diagnostic values from the converged CCSD wavefunction are reasonably small to confirm the reliability of the results (see Fig. S4†). The second and third lowest-energy ones (isomer b and c) lie 2.4 and 9.4 kcal mol−1 higher in energy than phGa, respectively, at the CCSD(T)/def2-TZVP//PBE0/def2-TZVP level with zero-point energy correction of the PBE0/def2-TZVP level. The nearest triplet structure (isomer e) has a very high relative energy (19.1 kcal mol−1) as compared to the global phGa. Therefore, the present results indicate that only for E = Ga, the interaction between Ga and Be6Au6 unit is strong enough to afford the large energy needed to reorient the shape of the Be6Au6 unit. This needs two factors to satisfy. First, the size of E atoms should be suitable to place at the center of the ring without causing significant steric repulsion, and second, E forms a sufficiently strong bond with the ring to make it energetically the most stable isomer. Note that both Al and Ga have almost similar covalent radius, but still the phAl isomer, which is a transition state, is 11.8 kcal mol−1 higher in energy than the three-dimensional global minimum, while the energy minimum of the C6v isomer is 6.7 kcal mol−1 higher in energy than the most stable form (see Fig. S7†). Therefore, the bonding between Al and the outer ring must be weaker in phAl than that in phGa which can be better understood from the EDA–NOCV results (vide infra). It is also interesting to notice that the global minimum structure of EBe6Au6+ for E = Al, In, Tl may be considered as the interaction of E with the most stable structure of Be6Au6. Only a slight alteration in structural integration occurs, E replaces Au in the axial position of Be6Au6 and Au is shifted to the bridging position of the Be–Be bond. In other words, only Ga has the capability to induce the drastic change in the Be6Au6 structure.
Another somewhat surprising observation is that although In and Tl have similar covalent radius, the D6h isomer for the former case is not even a minimum, while for the latter one phTl is a true minimum, albeit significantly higher energy isomer than the global minimum. We rechecked the results with three different levels of theory and obtained similar results. The heaviest element sometimes shows anomalous behavior because of the relativistic effect. For the present cases, we attempted to shed light on the reason through the EDA–NOCV results of D6h and C6v isomers (vide infra).
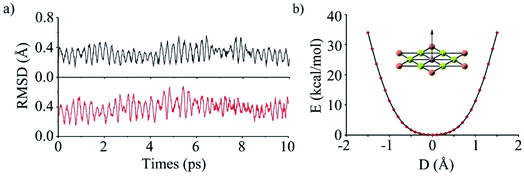
To evaluate the kinetic stability of phGa, the BO-MD78 simulations were carried out at the PBE0/def2-SVP level at 300 and 400 K. Throughout the simulation time scale, the structural integrity and planarity is well maintained, and no isomerization or other structural alterations occur as shown by the small RMSD (root mean square deviation) values in Fig. 2a (see the movies in the ESI†). The non-planar fluctuation in the BO-MD simulations correlates with the lowest vibrational mode (8.0 cm−1), which is out-of-plane vibration of the phGa center. We plotted the calculated potential energy curve (PES) as a function of out-of-plane displacement of the central Ga atom as shown in Fig. 2b. It shows that the smooth PES occurs within 0.3 Å but after that it sharply goes up, indicating a perfectly planar structure of phGa to be energetically more favorable than the non-planar one. Overall, the present results reveal that phGa possesses considerable thermodynamic and kinetic stability to be suitable for experiment detection.
Bonding
Structural and electronic properties can help us to understand the reason behind the thermodynamic and kinetic stability of phGa species. Molecules with a D6h symmetric planar hexacoordinate center require bond distances between two ligand centers in the hexagonal ring being equal to bond distances between the central atom and ligands, and, thus, this intriguing shape makes the design of such species not trivial. phGa GaBe6Au6+ possesses a Ga–Be bond distance of 2.229 Å with a WBI of 0.35, suggesting the typical single bonding characteristic according to the self-consistent covalent radii of Pyykkö (2.26 Å).84 The Be–Be and Be–Au peripheral ligand–ligand contacts have a similar bond distance in the range of 2.20–2.23 Å, yet the pronounced WBI for Be–Au (0.42) but ignorable Be–Be (0.09) suggests that strong bonding interaction between Be and bridging Au exists in the peripheral ligand ring.For the systems containing Be atoms, the natural charges should be discussed with caution since NBO algorithm only considers the 2s orbital of Be as valence space whereas it treats 2p orbitals as Rydberg orbitals, and then it gives different weightages to the valence and Rydberg spaces, putting more priority to the former ones. However, in the present case since the cluster possesses a delocalized π orbital involving the pz orbitals of Be (considering z axis perpendicular to the molecular plane), the natural atomic charges will not be reliable. Fig. 3 displays the partial atomic natural charges and Hirshfeld charges. Clearly, the values differ significantly. The charges computed using some other different methods are also given in Table S1.† The extent to which the values vary depending on the method is remarkable. But no other methods give such a high negative charge on Ga as NBO.
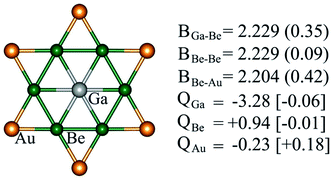 | ||
| Fig. 3 Bond properties (B, bond distances (Å), WBIs (in parentheses)), NPA and Hirshfeld (in square brackets) charges (Q, in |e|) of GaBe6Au6+ computed at the PBE0/def2-TZVP level. | ||
EDA–NOCV calculations were performed to understand the nature of bonding between phGa and the outer hexagonal ring. Particularly, this method gives quantitative information about the strength of each bonding component. It also allows us to assign the correct oxidation state of the phGa center. However, the choice of charge and electronic states of the interacting fragments are not trivial. The best fragmentation scheme to reflect the bonding situation in the molecule is understood by using the size of the orbital interaction (ΔEorb) as a probe.85–89 The fragments which give the lowest ΔEorb value best reflect the actual bonding situation in the molecule since it requires the least change in the electronic charge of the fragments to obtain the electronic structure of the final molecule. Table S2† provides the numerical results of EDA considering Ga and Be6Au6 in different charges and electronic states as interacting fragments. An inspection of the relative size of the ΔEorb value reveals that the most reasonable fragmentation scheme is Ga in the doublet state with the 4s24p⊥1 electronic configuration forming an electron-sharing π bond with the doublet Be6Au6+ moiety. The detailed EDA–NOCV results of this most favorable scheme are tabulated in Table 1. The results show that one third of attractive interaction comes from the electrostatic interaction (ΔEelstat), whereas two thirds of attraction originates from the covalent interaction. In fact, the repulsive interaction coming from the exchange term (Pauli repulsion, ΔEPauli) completely cancels the coulombic attraction.
| Energy | Interaction | Ga (D, 4s24p⊥1) + Be6Au6+ (D) |
|---|---|---|
| a The percentage contribution with respect to total attraction is given in parentheses. b The percentage contribution in parentheses is given with respect to total orbital interaction. | ||
| ΔEint | — | −261.6 |
| ΔEPauli | — | 137.1 |
| ΔEelstata | — | −137.5 (34.5%) |
| ΔEorba | — | −261.1 (65.5%) |
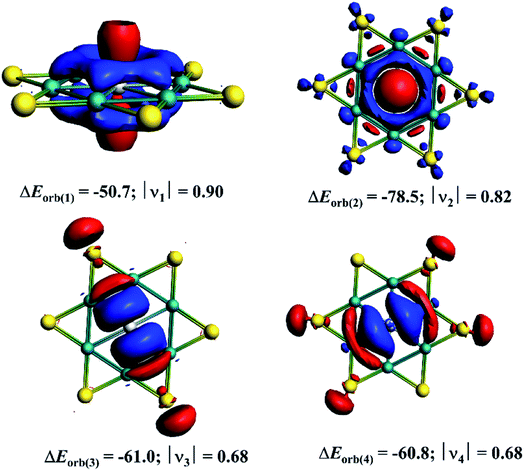
| ΔEorb(1)b | Ga(p⊥)–[Be6Au6+] electron-sharing π-bond | −50.7 (19.4%) |
| ΔEorb(2)b | Ga(s)→[Be6Au6+] σ-backdonation | −78.5 (30.1%) |
| ΔEorb(3)b | Ga(p‖)←[Be6Au6+] σ-donation | −61.0 (23.4%) |
| ΔEorb(4)b | Ga(p‖)←[Be6Au6+] σ-donation | −60.8 (23.3%) |
| ΔEorb(rest)b | — | −10.1 (3.9%) |
The decomposition of ΔEorb value into pairwise orbital interaction, ΔEorb(1)−(4) in the EDA–NOCV method gives the most valuable information about bonding. The corresponding deformation densities are given in Fig. 4 which helps to assign the nature of bonds and involved orbitals. The results show that the Ga(p⊥)–[Be6Au6+] electron-sharing π-bond is responsible for 19.4% of total covalent interaction. This interaction involves the largest amount of electron as revealed by the charge eigenvalue, |ν| given in Fig. 4. Note that there is no correlation between electron involvement and stabilization energy as it will depend on the nature and orientation of the orbitals. The strongest orbital contribution (30.1%) comes from the Ga(s)→[Be6Au6+] σ-backdonation. There are also two sets of Ga(p‖)←[Be6Au6+] σ-donations which together account for 46.7% of total orbital interaction. Therefore, in the GaBe6Au6+ cluster the Ga center is involved in one electron-sharing bond and three dative bonds, and this bonding arrangement makes the actual oxidation state of Ga center as +1.
Now, why does only Ga enable the formation of phGa? To get an answer to this question we performed EDA–NOCV analysis for the whole set of EBe6Au6+ cluster considering the phE isomer (see Table S3†). It is remarkable that the intrinsic interaction between E and Be6Au6+ fragments is maximum for E = Ga, and the size of the ΔEorb value also follows the same order. In Table S2,† we have also provided the steric interaction,90 ΔESteric which is the sum of ΔEPauli and ΔEelstat. ΔESteric values indicate that the coulombic attraction completely cancels the Pauli repulsion for E = Al and Ga but for E = In and Tl, because of their larger size, ΔESteric values are positive. Therefore, for the latter two cases, both steric interaction and smaller covalent interaction disfavor the phE isomer, while in the case of E = Al, the smaller ΔEorb value is the reason for this. This indicates that the size of the spatial distribution of p orbitals of E is also crucial for the strength of the bonding, and 4p orbitals seem to be in the right size to form bonds with the Be6 ring. Also, the larger electronegativity of Ga compared to Al might be another reason for stronger E(p‖)←[Be6Au6+] σ-donation in the former than in the latter.
The remaining question: why is the C6v isomer more stable than the D6h one for the InBe6Au6+ cluster while it is vice versa for the TlBe6Au6+ cluster. To get the factors behind this, we performed EDA taking both the isomers (see Table S4†).91 For the InBe6Au6+ cluster, although the C6v isomer possesses larger steric repulsion than the D6h isomer, the larger ΔEorb value of the former overcompensates that making it more stable than the latter one. In contrast, in the case of the TlBe6Au6+ cluster, smaller steric repulsion in the D6h isomer is responsible for making it slightly more stable than the C6v isomer, although the latter has larger covalent interaction.
Electron delocalization
The adaptive natural density partitioning (AdNDP)92 analysis was carried out for understanding the chemical bonding and electronic structure of global phGa. All the orbitals except for the d orbitals of Au are given in Fig. 5, and they basically can be divided into three categories. Six 3c–2e (three center-two electrons) σ bonds of the Be–Au–Be ring with occupation numbers (ONs) of 1.95|e| are responsible for the planarity and stability of the peripheral ring. The remaining orbitals are all associated with the central phGa atom, including three 7c−2e σ bonds with ONs of 1.97–1.98|e| and one 7c−2e π bond with ONs of 1.78|e|. Therefore, the valence shell of the central phGa atom has eight electrons, fulfilling the octet rule (3σ + 1π bonds). Meanwhile, phGa involves six delocalized σ electrons and two delocalized π electrons, both satisfying the Hückel's (4n + 2) rule for 6σ + 2π double aromaticity,93 especially the latter (delocalization of the perpendicular pz orbital of the central atom) can be viewed as the key factor of planarity.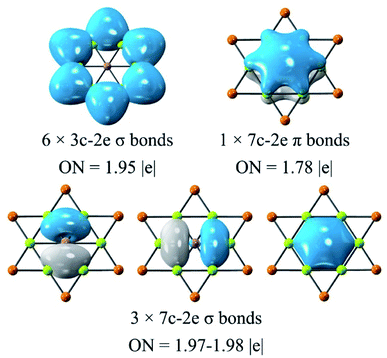 | ||
| Fig. 5 AdNDP analysis of phGa GaBe6Au6+ computed at the PBE0/def2-TZVP level. Occupation number (ON) values are shown in |e|. | ||
The electron density distribution picture is further analyzed in the following tests. The diagram of electron localization function (ELF)94 is shown in Fig. 6a, where the electron density is strongly localized in the GaBe6 core, consistent with three σ and one π orbitals in this region. The contour plot of Laplacian distribution of the charge density ∇2ρ(r) of GaBe6Au6+ along with the bond critical points and ring critical points is shown in Fig. 6b. Note that the Ga–Be and peripheral Be–Au bonds possess clear bond critical points (blue dots), and the region with negative values of ∇2ρ(r) located at the GaBe6 core vividly confirm the covalent bonding picture.
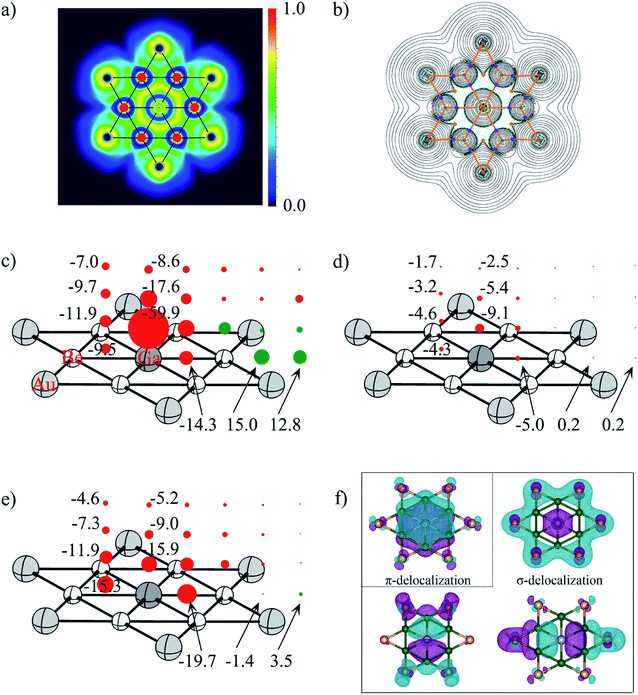 | ||
| Fig. 6 (a) Electron localization function (ELF) and (b) the contour plot of the Laplacian distribution of electron density, ∇2ρ(r) including bond critical points and bond paths of phGa, where cyan dashed lines indicate areas of charge concentration (∇2ρ(r) < 0) and solid black lines show areas of charge depletion (∇2ρ(r) > 0). The solid orange lines connecting the atomic nuclei are the bond paths. Blue dots are bond critical points (BCPs), and orange dots are ring critical points (RCPs); (c) NICSzz, (d) NICSπzz, (e) NICSσzz (σ-delocalization) and (f) the shape of π-delocalized CMO and three σ-delocalized CMOs of the D6h GaBe6Au6+ at the PBE0/def2-TZVP level (the values in the left column refer to the center of the Be–Ge–Be triangle). Diatropic and paratropic tensors are shown in red and green, respectively. NICS values are in ppm. | ||
To quantitatively evaluate the aromatic character in the phGa GaBe6Au6+, the out-of-plane tensor components of the nucleus-independent chemical shift (NICSzz)95 were considered as displayed in Fig. 6. In the picture, the diatropic NICS tensors on and above the plane of phGa in 1 Å interval up to 3 Å are given as red spheres, whereas the paratropic tensors are depicted by the green spheres. Inside the hexagon, at three points, viz., at the center of the Be–Be–Ga triangle, at the middle pint of the Be–Ga bond, and at the phGa center, the shielding tensors are computed. As reflected from Fig. 6c, the full hexagon is located in a moderate diatropic region, whereas the outside region of the hexagonal ring has a paratropic response. Focusing on the Be–Be–Ga triangle, NICSzz(0) is −9.5 ppm and NICSzz(1) is −11.9 ppm. The NICSzz values decrease along with the increasing distances from the molecular plane. But even at 3 Å above the triangular plane, it still has considerable diatropic response. Note that the phGa center is itself located at a very strong diatropic region as indicated by the very negative NICSzz values. An inspection of results of canonical molecular orbital (CMO)-NICSzz originating from the one π and three σ delocalized orbitals indicate that the diatropic contribution from the delocalized π orbital is rather small with an NICSπzz(1) value of −9.1 ppm above the phGa center and −4.6 ppm above the Be–Be–Ga triangle (see Fig. 6d). Note that similar analysis was used to elucidate the aromaticity in the CAl5+ cluster with ppC by Schleyer and Zeng and co-workers.19 The results of CMO-NICSzz in the CAl5+ cluster are very similar to the present one where the diatropic contribution developed from the delocalized π orbital is rather small (NICSπzz(1): −11.5 ppm above ppC and −4.3 ppm above the center of the C–Al–Al triangle). In fact, the comparison of the NICSπzz profile between these two systems shows that the magnetic response at 2 Å and 3 Å above the present phGa center is more diatropic in nature than those above the ppC center. This is presumably because in the former cluster the 4pz orbital is involved while in the latter case the smaller 2pz orbital is engaged. Note that both phGa and ppC clusters are significantly less π aromatic than the prototype aromatic system, benzene (see Fig. S8†). The tensor contribution from the delocalized σ-orbitals is more diatropic in nature (see Fig. 6e). This highlights the greater importance of σ-delocalization than the π-delocalization for the stabilization of the planar form. The shape of delocalized σ and π CMOs is also displayed in Fig. 6f. Therefore, the magnetic response of the cluster corroborates with the number of delocalized σ and π electrons. It is interesting to note that the much higher energy phTl isomer is also doubly aromatic (see Fig. S9†) which implies that the aromaticity is not solely a predetermining factor to stabilize the planar form, rather the delicate balance between the size of the atom and its ability to form strong bonds with the outer ring are important.
Conclusions
We herein report the first phGa center in the most stable isomer of the GaBe6Au6+ cluster by systematically exploring the potential energy surface of the full set of the EBe6Au6+ (E = Al, Ga, In, Tl) cluster. The global minimum of the GaBe6Au6+ cluster has a star-like D6h geometry with 1A1g electronic state, possessing a centered Ga atom encompassed by a Be6 hexagon and each Be–Be edge is further capped by an Au atom. The present results also show that among group 13 elements, Ga can form the strongest bonds with the hexagonal ring in the D6h symmetric isomer, and, thus it facilitates the drastic reorientation of the Be6Au6 cluster which has a three-dimensional geometry as the lowest energy isomer. The planarization of the GaBe6Au6+ cluster is well supported by the three delocalized σ bonds and one delocalized π bond which individually satisfy Hückel's rule of aromaticity. Furthermore, the CMO-NICSzz values corroborate with the double aromaticity assignment. The large barrier against isomerization is also reflected from the BO-MD simulations performed at 300 and 400 K. The energy decomposition analysis in combination with the natural orbitals for chemical valence theory reveals that the bonding in the GaBe6Au6+ cluster is best expressed as the doublet Ga atom with 4s24p⊥1 electronic configuration forming an electron-sharing π bond with the doublet Be6Au6+ moiety followed by Ga(s)→[Be6Au6+] σ-backdonation and two sets of Ga(p‖)←[Be6Au6+] σ-donations. We hope that the current findings will provide useful information for obtaining the rule-breaking planar hypercoordinate clusters.Data availability
All our computational data is already included in the ESI† and in the videos for the BO-MD runs.Author contributions
M.-h. W. and C. C. performed the computations. S. P. and Z.-h. C. analyzed the results and wrote the draft.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was funded by the National Natural Science Foundation of China (No. 11874178, 11922405, 91961204). This work was supported by the Beijing National Laboratory for Molecular Sciences (BNLMS201910). The partial calculations in this work were supported by the High Performance Computing Center of Jilin University, China.References
- R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4492–4493 CrossRef.
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 1–10 CrossRef.
- L. M. Yang, E. Ganz, Z. F. Chen, Z. X. Wang and P. V. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501 CrossRef CAS PubMed.
- G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372 CrossRef CAS PubMed.
- R. Keese, Chem. Rev., 2006, 106, 4787–4808 CrossRef CAS PubMed.
- W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371 RSC.
- G. Erker, Chem. Soc. Rev., 1999, 28, 307–314 RSC.
- J. J. Sui, J. Xu and Y. H. Ding, Dalton T, 2016, 45, 56–60 RSC.
- A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed., 2000, 39, 3307–3310 CrossRef CAS PubMed.
- E.-U. Würthwein and P. V. R. Schleyer, Angew. Chem., Int. Ed., 1979, 18, 553–554 CrossRef.
- H. Y. Wang and F. L. Liu, Acs Omega, 2020, 5, 24513–24519 CrossRef CAS PubMed.
- Z. C. Liu, J. Y. Lei, M. Frasconi, X. H. Li, D. Cao, Z. X. Zhu, S. T. Schneebeli, G. C. Schatz and J. F. Stoddart, Angew. Chem., Int. Ed., 2014, 53, 9193–9197 CrossRef CAS PubMed.
- G. Castillo-Toraya, M. Orozco-Ic, E. Dzib, X. Zarate, F. Ortiz-Chi, Z. H. Cui, J. Barroso and G. Merino, Chem. Sci., 2021, 12, 6699–6704 RSC.
- W. Feng, C. Y. Zhu, X. M. Liu, M. Zhang, Y. Geng, L. Zhao and Z. M. Su, New J. Chem., 2020, 44, 767–772 RSC.
- F. Ebner, H. Wadepohl and L. Greb, J. Am. Chem. Soc., 2019, 141, 18009–18012 CrossRef CAS PubMed.
- P. Ghana, J. Rump, G. Schnakenburg, M. I. Arz and A. C. Filippou, J. Am. Chem. Soc., 2021, 143, 420–432 CrossRef CAS PubMed.
- F. Ebner and L. Greb, Chem, 2021, 7, 2151–2159 CAS.
- F. Ebner and L. Greb, J. Am. Chem. Soc., 2018, 140, 17409–17412 CrossRef CAS PubMed.
- Y. Pei, W. An, K. Ito, P. V. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400 CrossRef CAS PubMed.
- Z. X. Wang and P. V. Schleyer, Science, 2001, 292, 2465–2469 CrossRef CAS PubMed.
- M. H. Wang, X. Dong, Z. H. Cui, M. Orozco-Ic, Y. H. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775 RSC.
- A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah, I. Baruah and A. K. Guha, Inorg. Chem., 2020, 59, 17880–17883 CrossRef CAS PubMed.
- L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2020, 133, 8782–8786 CrossRef.
- Y. B. Wu, Y. Duan, G. Lu, H. G. Lu, P. Yang, P. V. Schleyer, G. Merino, R. Islas and Z. X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 14760–14763 RSC.
- K. Exner and P. V. Schleyer, Science, 2000, 290, 1937–1940 CrossRef CAS PubMed.
- A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah and A. K. Guha, Chem. Commun., 2020, 56, 12597–12599 RSC.
- X. F. Zhao, J. J. Li, H. R. Li, C. X. Yuan, X. X. Tian, S. D. Li, Y. B. Wu, J. C. Guo and Z. X. Wang, Phys. Chem. Chem. Phys., 2018, 20, 7217–7222 RSC.
- A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972 CrossRef CAS.
- P. v. R. Schleyer and A. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 21, 1536–1538 RSC.
- H. F. Zheng, J. Xu and Y. H. Ding, Phys. Chem. Chem. Phys., 2020, 22, 3975–3982 RSC.
- J. C. Guo, L. Y. Feng and H. J. Zhai, New J. Chem., 2020, 44, 18293–18302 RSC.
- E. Ravell, S. Jalife, J. Barroso, M. Orozco-Ic, G. Hernandez-Juarez, F. Ortiz-Chi, S. Pan, J. L. Cabellos and G. Merino, Chem.-Asian. J., 2018, 13, 1467–1473 CrossRef CAS PubMed.
- J. C. Guo, L. Y. Feng and H. J. Zhai, Phys. Chem. Chem. Phys., 2018, 20, 6299–6306 RSC.
- O. Yanez, A. Vasquez-Espinal, R. Pino-Rios, F. Ferraro, S. Pan, E. Osorio, G. Merino and W. Tiznado, Chem. Commun., 2017, 53, 12112–12115 RSC.
- M. Contreras, S. Pan, M. Orozco-Ic, J. L. Cabellos and G. Merino, Chem.–Eur. J., 2017, 23, 11430–11436 CrossRef CAS PubMed.
- Y. B. Wu, Z. X. Li, X. H. Pu and Z. X. Wang, Comput. Theor. Chem., 2012, 992, 78–83 CrossRef CAS.
- A. C. Castro, M. Audiffred, J. M. Mercero, J. M. Ugalde, M. A. Mendez-Rojas and G. Merino, Chem. Phys. Lett., 2012, 519, 29–33 CrossRef.
- Y. B. Wu, Z. X. Li, X. H. Pu and Z. X. Wang, J. Phys. Chem. C, 2011, 115, 13187–13192 CrossRef CAS.
- Y. B. Wu, J. L. Jiang, H. G. Lu, Z. X. Wang, N. Perez-Peralta, R. Islas, M. Contreras, G. Merino, J. I. C. Wu and P. V. Schleyer, Chem.–Eur. J., 2011, 17, 714–719 CrossRef CAS PubMed.
- Z. H. Cui, M. Contreras, Y. H. Ding and G. Merino, J. Am. Chem. Soc., 2011, 133, 13228–13231 CrossRef CAS PubMed.
- P. D. Pancharatna, M. A. Mendez-Rojas, G. Merino, A. Vela and R. Hoffmann, J. Am. Chem. Soc., 2004, 126, 15309–15315 CrossRef CAS PubMed.
- G. Merino, M. A. Mendez-Rojas, H. I. Beltraan, C. Corminboeuf, T. Heine and A. Vela, J. Am. Chem. Soc., 2004, 126, 16160–16169 CrossRef CAS PubMed.
- S.-D. Li, G.-M. Ren, C.-Q. Miao and H.-J. Zhai, Angew. Chem., Int. Ed., 2004, 43, 1371–1373 CrossRef CAS PubMed.
- Y. Sahin, C. Prasang, M. Hofmann, G. Subramanian, G. Geiseler, W. Massa and A. Berndt, Angew. Chem., Int. Ed., 2003, 42, 671–674 CrossRef CAS PubMed.
- G. Merino, M. A. Mendez-Rojas and A. Vela, J. Am. Chem. Soc., 2003, 125, 6026–6027 CrossRef CAS PubMed.
- J. Xu, X. Zhang, S. Yu, Y. H. Ding and K. H. Bowen, J. Phys. Chem. Lett., 2017, 8, 2263–2267 CrossRef CAS PubMed.
- X. Li, H. J. Zhai and L. S. Wang, Chem. Phys. Lett., 2002, 357, 415–419 CrossRef CAS.
- X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 39, 3630–3633 CrossRef CAS PubMed.
- A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed., 2000, 39, 3445–3448 CrossRef.
- X. Li, L. S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038 CrossRef CAS.
- O. Yanez, R. Baez-Grez, J. Garza, S. Pan, J. Barroso, A. Vasquez-Espinal, G. Merino and W. Tiznado, Chemphyschem, 2020, 21, 145–148 CrossRef CAS PubMed.
- M. H. Wang, X. Dong, Y. H. Ding and Z. H. Cui, Chem. Commun., 2020, 56, 7285–7288 RSC.
- J. C. Guo, L. Y. Feng, J. Barroso, G. Merino and H. J. Zhai, Chem. Commun., 2020, 56, 8305–8308 RSC.
- S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350–12355 RSC.
- J. C. Guo, L. Y. Feng, X. Y. Zhang and H. J. Zhai, J. Phys. Chem. A, 2018, 122, 1138–1145 CrossRef CAS PubMed.
- Z. H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y. H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141 RSC.
- J. C. Guo, G. M. Ren, C. Q. Miao, W. J. Tian, Y. B. Wu and X. T. Wang, J. Phys. Chem. A, 2015, 119, 13101–13106 CrossRef CAS PubMed.
- Y. B. Wu, Y. Duan, H. G. Lu and S. D. Li, J. Phys. Chem. A, 2012, 116, 3290–3294 CrossRef CAS PubMed.
- J. O. C. Jimenez-Halla, Y. B. Wu, Z. X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778 RSC.
- B. B. Averkiev, D. Y. Zubarev, L. M. Wang, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2008, 130, 9248–9250 CrossRef CAS PubMed.
- H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008 CrossRef CAS PubMed.
- C. J. Zhang, H. G. Xu, X. L. Xu and W. J. Zheng, J. Phys. Chem. A, 2021, 125, 302–307 CrossRef CAS PubMed.
- B. J. Feng, B. T. Fu, S. Kasamatsu, S. Ito, P. Cheng, C. C. Liu, Y. Feng, S. L. Wu, S. K. Mahatha, P. Sheverdyaeva, P. Moras, M. Arita, O. Sugino, T. C. Chiang, K. Shimada, K. Miyamoto, T. Okuda, K. H. Wu, L. Chen, Y. G. Yao and I. Matsuda, Nat. Commun., 2017, 8, 1–6 CrossRef CAS PubMed.
- L. M. Yang, V. Bačić, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762 CrossRef CAS PubMed.
- Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895 CrossRef CAS PubMed.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc, Wallingford CT, 2009 Search PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- F. Corts-Guzman and R. F. W. Bader, Coord. Chem. Rev., 2005, 249, 633–662 CrossRef.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, J. Chem. Phys., 1999, 111, 3800–3805 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- ADF2018, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- L. L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chem. Rev., 2019, 119, 8781–8845 CrossRef CAS PubMed.
- P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337 CrossRef PubMed.
- W. L. Yang, K. E. Krantz, L. A. Freeman, D. A. Dickie, A. Molino, G. Frenking, S. D. Pan, D. J. D. Wilson and R. J. Gilliard, Angew. Chem., Int. Ed., 2020, 59, 3850–3854 CrossRef CAS PubMed.
- R. Saha, S. Pan, P. K. Chattaraj and G. Merino, Dalton Trans., 2020, 49, 1056–1064 RSC.
- S. M. N. V. T. Gorantla, S. Pan, K. C. Mondal and G. Frenking, Chem.–Eur. J., 2020, 26, 14211–14220 CrossRef CAS PubMed.
- L. Pecher, S. Pan and G. Frenking, Theor. Chem. Acc., 2019, 138, 47 Search PubMed.
- C. X. Chi, S. Pan, L. Y. Meng, M. B. Luo, L. L. Zhao, M. F. Zhou and G. Frenking, Angew. Chem., Int. Ed., 2019, 58, 1732–1738 CrossRef CAS PubMed.
- For more information the readers are referred to F. M. Bickelhaupt and E. J. Baerends, Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, in: Rev. Comput. Chem, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- Note that for TlBe6Au6+ cluster, the imposed C6v isomer is automatically converged to planar D6h isomer during optimization. Although the job with transition state optimization is not fully converged, it was nearly converged. Only one parameter, maximum force (0.000544) does not fall under the threshold value (0.000450). We took that structure and performed frequency calculation and found that all are real. Since this structure is very close to stationary point, it does not alter the total electronic energy.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- J. Chandrasekhar, E. D. Jemmis and P. v. R. Schleyer, Tetrahedron Lett., 1979, 20, 3707–3710 CrossRef.
- A. Savin, R. Nesper, S. Wengert and T. F. Fassler, Angew. Chem., Int. Ed., 1997, 109, 1892–1918 CrossRef.
- Z. F. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05089c |
| This journal is © The Royal Society of Chemistry 2021 |