Topological engineering of two-dimensional ionic liquid islands for high structural stability and CO₂ adsorption selectivity

Abstract

Ionic liquids (ILs) as green solvents and catalysts are highly attractive in the field of chemistry and chemical engineering. Their interfacial assembly structure and function are still far less well understood. Herein, we use coupling first-principles and molecular dynamics simulations to resolve the structure, properties, and function of ILs deposited on the graphite surface. Four different subunits driven by hydrogen bonds are identified first, and can assemble into close-packed and sparsely arranged annular 2D IL islands (2DIIs). Meanwhile, we found that the formation energy and HOMO–LUMO gap decrease exponentially as the island size increases via simulating a series of 2DIIs with different topological features. However, once the size is beyond the critical value, both the structural stability and electrical structure converge. Furthermore, the island edges are found to be dominant adsorption sites for CO₂ and better than other pure metal surfaces, showing an ultrahigh adsorption selectivity (up to 99.7%) for CO₂ compared with CH₄, CO, or N₂. Such quantitative structure–function relations of 2DIIs are meaningful for engineering ILs to efficiently promote their applications, such as the capture and conversion of CO₂.

---

Introduction

Due to the green and environmentally-friendly nature,^1,2 ionic liquids (ILs) have been used in many cutting-edge fields, including green chemistry,^3–5 electrochemistry,^6,7 energy storage,^8,9 gas separation,^10,11 and catalysis.^12,13 In the real application environment, solid-surface supported IL (SSIL) films always exist and show several advantages compared with the bulk ones,^14,15 for example, higher stability, less usage of ILs, faster adsorption kinetics, etc. Consequently, SSIL films have attracted broad attention in the academy and industrial community.^16,17 The structure, property, and function of SSILs should be the result of the balance between hydrogen bonding, van der Waals (vdW), Coulomb, and interfacial interactions, which are far more complex than those of simple systems such as water, CO, etc. Hence, quantitative understanding of the structure–function relationship of SSIL films has great significance in the rational design and management of IL-based chemistry.

Recently, plenty of experiments and simulations have been conducted to clarify the correlation between the structure and performance of SSIL films.^18–20Via using the physical vapor deposition (PVD) technique,¹⁸ Cremer et al.¹⁹ demonstrated that an ultrathin IL film consisting of a closed monolayer structure could be produced, which is stable under ambient conditions and should be the sub-structure of SSILs. Moreover, through scanning tunneling microscopy (STM) and theoretical simulations, previous pioneering studies^21–24 identified that ILs could form the so-called ordered checkerboard or disordered glass structure of the monolayer ILs on the metal surface. Considering that the ordered monolayer IL structure should be grown from subunits, Meusel et al.²⁵ studied the subunits within the monolayer ILs on the Au(111) substrate via atomic force microscopy (AFM) and STM, discovering that the striped and hexagonal subunits were composed of two and three cation–anion pairs. Meanwhile, subunits can assemble into different two-dimensional IL islands (2DIIs), for instance, IL islands with branched or quasi-dendritic shapes on the Cu(111) surface.²⁶ Hence, the 2DIIs can indeed be prepared, and their structure depends greatly on the substrate surface, temperature (T), and other external conditions.

Originating from the designable microenvironments and functions, thin IL films or islands have broad application prospects, especially in CO₂ capture and fixation. For example, Su et al.²⁷ improved the catalytic activity of ILs in converting CO₂ into cyclic carbonates via confining the ILs in the mesoporous silica nanopore, in addition, Xie et al.^28,29 and Tang et al.³⁰ substantially strengthened CO₂ adsorption capacity and selectivity by just decreasing the thickness of IL films. These excellent performances of SSIL films suggest that the 2DII should be a preferred candidate in IL-based applications.³¹ However, up to now, beyond qualitative understanding of 2DIIs, the quantitative characterization is still a major challenge, for instance, the detailed subunit structure, electronic properties, and gas adsorption performance. Such limitations restrict the theoretical understanding, rational design, and applications of ILs in the field of highly efficient and low-cost gas separation and capture processes.

In the present work, the image charge augmented quantum mechanics/molecular mechanics (IC-QM/MM) and full-atomistic molecular dynamics (MD) simulations are performed to reveal the structure and properties of 2DIIs on graphite. We aimed at exploring the potential subunits of the ordered 2DIIs, gaining deeper insights into how the hydrogen bond (HB) network drives subunits and how the topological feature determines the thermodynamic stability, electronic properties, and even the gas adsorption mechanism of 2DIIs. Four different subunits are theoretically proposed, and the critical size (N_C) for various 2DIIs is demonstrated, where the thermodynamic stability converges once the size is beyond N_C. The mechanisms that the subunit and size jointly control the melting behavior and electronic structure of 2DIIs are further revealed, showing the easy-regulating feature of 2DIIs. Finally, the dynamic gas adsorption processes on 2DIIs are conducted, suggesting that the edges of 2DIIs are dominant adsorption sites for CO₂ and possess high selectivity for CO₂/CO, CO₂/CH₄, and CO₂/N₂.

Results and discussion

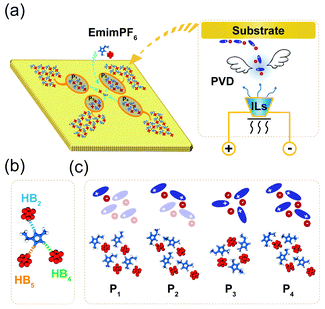
Hydrogen bonds driving subunits of 2DIIs

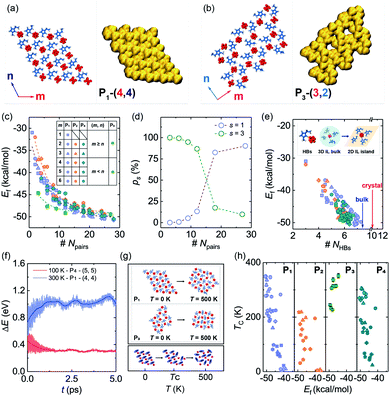
Due to the strong correlation originating from special HBs in ILs,³² the gaseous particles will be cation–anion pairs in the PVD process (Fig. 1a), which can be deposited on the solid surface and easily assembled into different island structures, especially when IL pairs are few. As illustrated in Fig. 1b, the HBs in 2DIIs mainly include three kinds, C₂–H₂⋯F, C₄–H₄⋯F, and C₅–H₅⋯F, namely HB₂, HB₄, and HB₅. Owing to the unique directional feature of HBs, the cation–anion pair can construct several subunit, as shown in Fig. 1c, namely P_N, where N = 1, 2, 3, and 4, representing the number of cation–anion pairs. For P₁, P₂, and P₄, the differences are mainly the combination styles of HBs and relative orientations within the neighboring cations. However, for P₃, the subunit is composed of three pairs of ILs and is an annular structure. The unique structure of subunits can further dominate the permutation structures of 2DIIs and meanwhile form feature edges.

Fig. 1 (a) A schematic diagram of 2DIIs on the graphite surface via PVD, where red, blue, yellow, white, and silver colors represent [PF₆]⁻, [Emim]⁺, C atoms in graphite, H_2/4/5 atoms, and H atoms in the alkyl chain, respectively. (b) Three main HBs in the ILs, where HB_2,4,5 represents the HB between F and H in different sites of the imidazole ring. (c) The illustrated diagrams and atomic structures of the P₁-based 2DII with four subunits, the P₂-based 2DII with two subunits, the P₃-based 2DII with one subunit, and the P₄-based 2DII with one subunit, respectively.

Based on the formation mechanism of various graphene polycrystals grown on the surface of liquid copper reported by Dong et al.,³³ taking subunits as an origin, they can grow into different 2DIIs in the form of parallelograms (m,n), where m and n are the number of cation–anion pairs (P_1/2/4-based 2DIIs) or subunits (P₃-based 2DIIs) along two edges (ESI Movie M1†). The size of 2DIIs, N_pairs, is defined as the total number of cation–anion pairs. To represent the structural feature of 2DIIs, the simulated STM images of P_1/2/3/4-based 2DIIs with typical combinations of (m,n) are displayed in Fig. 2a and b and S4.† For P_1/2/4-based 2DIIs, two different feature edges exist, namely Z₄ and Z₅, where Z₄ comprises HB₂ and HB₄ while Z₅ includes HB₂ and HB₅. Similarly, edges of P₃-based 2DIIs are defined as E₁ and E₂ (Fig. S5†), where the types of HBs in E₁ are almost the same as E₂. Moreover, the thermodynamic stability of 2DIIs can be measured by the formation energy (E_f, see ESI Note†). Comparing E_f of 2DIIs with the same size but different combinations of (m,n), it can be found that P_1/2/4-based 2DIIs with longer Z₅ are more stable than those with longer Z₄. For instance, E_f of P₁-based 2DIIs with (4,2) and (2,4) is −44.97 and −46.32 kcal mol⁻¹, respectively. However, there is no obvious difference between E₁ and E₂. The anisotropic nature of P_1/2/4-based 2DIIs and the isotropic nature of P₃-based 2DIIs coincide well with the styles of HBs in the feature edges, indicating the feasibility of structure and property regulation via controlling the HBs within 2DIIs.

Fig. 2 (a and b) Atomic structures and simulated STM images of the P₁-based 2DIIs with (4,4) and the P₃-based 2DIIs with (3,2), respectively. The bias energy for the generation of all STM images is 20 eV, and the iso-contour value of all STM images is 5.0 × 10⁻⁵ Hartree. (c) E_f as a function of N_pairs, where the dashed lines represent exponential decay fitting. (d) p_s for different 2DIIs changes with N_pairs. (e) The correlation between E_f and N_HBs, where the inset shows the atomic structures of HBs in the bulk and a 2DII. (f) ΔE of two typical 2DIIs from the AIMD simulations. (g and h) T_C in the melting process of various 2DIIs as a function of E_f.

Size-dependent thermodynamic stability and melting process of 2DIIs

To further quantify the influence of size on the structural stability, E_f for 2DIIs with different N_pairs is summarized in Fig. 2c, authenticating that E_f will decline with growing N_pairs for all 2DIIs. When N_pairs exceeds the critical value (N_C = 18), E_f for various 2DIIs will only fluctuate in a small range, that means as N_pairs increases, the thermodynamic stability of 2DIIs will keep increasing until convergence. Interestingly, E_f for P_1/2/4-based 2DIIs is almost the same, implying that relative orientations within the neighboring cations only have little effect on the thermodynamic stability. Moreover, the tendencies of E_f–N_pairs for P_1/2/4-based 2DIIs are fully different from those for P₃-based 2DIIs: when the size of 2DIIs is small (N_pairs < N_C), the E_f of P₃-based 2DIIs is the most negative; in contrast, the E_f of P_1/2/4-based 2DIIs will be the lowest once the size is beyond N_C.

Assuming that N_pairs is fixed, the Boltzmann factor can be used to describe the distribution of P_1/3-based 2DIIs, that is, 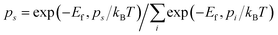, where s = 1 and 3, i = 1 versus 3, k_B is the Boltzmann constant, and T is set as 300 K.³⁴ As displayed in Fig. 2d, there exist two stages in p_s–N_pairs. For instance, when N_pairs = 12, p₁ and p₃ are respectively 13.18 and 86.82%, while when N_pairs = 18, p₁ and p₃ are 82.51 and 17.49%, respectively. Hence, P₃ will be the likeliest subunit if N_pairs < 18, which is the opposite when N_pairs ≥ 18. The turnover of p_s implies that the structural transition from P₃ to P₁ may occur during the assembly process. Furthermore, the detailed internal arrangements of many large-sized monolayer IL films from experiments^20,21,25 are almost like those in P_1/2/4-based 2DIIs rather than those in P₃-based 2DIIs, reflecting the rationality of the simulated results herein.

The HBs are further analyzed, as shown in Fig. S6,† to understand the correlation between the structure and thermodynamic stability. The angle and energy of HBs in 2DIIs are respectively larger and lower than those in the bulk and crystal ILs, showing that graphite strengthens HBs in 2DIIs and further enhances the structural stability of 2DIIs. As displayed in Fig. 2e, E_f almost decreases linearly with the number of HBs per cation–anion pair (N_HBs), indicating the dominant role of HBs in constructing 2DIIs. When N_pairs > N_C, N_HBs will catch up with the bulk value, agreeing well with convergent E_f. Furthermore, the 5 ps long ab initio MD (AIMD) simulations of representative 2DIIs at T = 300 and 100 K were performed. The energy difference per cation–anion pair (ΔE, see ESI Note†) with N_pairs = 16 and 25 is only 0.28 and −0.15 eV, respectively (Fig. 2f), and the structures at different simulation times are almost unchanged (Fig. S7†). Hence, the AIMD simulations verify the structural stability of the corresponding 2DIIs.

To further confirm the dynamic stability of 2DIIs, the melting processes are elucidated via classical MD simulations. As T increases, 2DIIs first maintain initial structures and then the in-plane transition at the critical temperature (T_C) occurs, along with losing the ordered internal arrangements (Fig. 2g). Fig. 2h shows the evolution of T_Cversus E_f, demonstrating that a negative relation exists in P_1/2/4-based 2DIIs while a positive relation exists in P₃-based 2DIIs. For instance, E_f of P₁-based 2DIIs (N_pairs = 28) and P₃-based 2DIIs (N_pairs = 3) is respectively −50.77 and −44.64 kcal mol⁻¹, and T_C for them is 349.14 and 351.73 K (Fig. S8†), respectively. Hence, for some small P₃-based 2DIIs and large P_1/2/4-based 2DIIs, T_C is above room temperature, indicating their excellent dynamic stability. The different relationships between P_1/2/4-based and P₃-based 2DIIs coincide well with two stages of p_s–N_pairs (Fig. 2d). Combining E_f–N_pairs, E_f–N_HBs, T_C–E_f, and T_C–N_pairs, it can be concluded that HB networks can determine the stability of 2DIIs.

The arrangement-size binary control mechanism of the electronic structure in 2DIIs

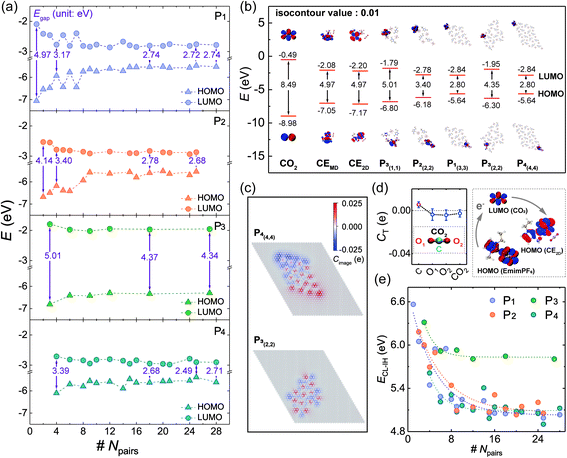
Considering the SSILs widely used in electrochemistry and energy storage, where the electronic properties of 2DIIs can play a dominant role, the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO), and energy gap (E_gap) are summarized in Fig. 3a, displaying that the overall trend of the HOMO and the LUMO respectively increases and declines as N_pairs expands, leading to the reduction of E_gap. For example, when N_pairs goes up from 1 to 18, E_gap of P_1,2,4-based 2DIIs will drop by 44.87%, 44.06%, and 46.08%, respectively. However, E_gap of P₃-based 2DIIs only drops by 12.07%. Meanwhile, E_gap of P_1/2/3/4-based 2DIIs with N_pairs > 24 is 2.74, 2.68, 4.34, and 2.71 eV, respectively, demonstrating that P₃-based 2DIIs always possess the largest E_gap, no matter how big the 2DII is.

Fig. 3 (a) The HOMO, the LUMO, and E_gap of 2DIIs change with N_pairs. (b) Electron distributions of the HOMO and the LUMO in different IL systems. (c) The image charge distributions of first-layer graphite in P₄-based and P₃-based 2DIIs. (d) The charge transfer quantity of the CO₂ molecule before and after adsorption on the 2DII, where the schematic diagram shows electron transfer from ILs to CO₂. (e) The energy gap between HOMO_IL and LUMO_CO2 changes with N_pairs, where the dotted lines represent exponential decay fitting.

Furthermore, the electron distributions of the HOMO and LUMO in 2DIIs are calculated, as shown in Fig. 3b. Interestingly, the electron of the HOMO and LUMO in P_1/2/4-based 2DIIs is localized in two different corners, far different from the overlapping distribution of that in P₃-based 2DIIs. The localized electron distribution should originate from the anisotropic image charge (C_image) distribution of graphite. Taking the P₄-based 2DII with (4,4) as an example, the C atoms at the upper left corner have negative C_image while those at the lower right corner have positive C_image, that means graphite will help decouple the electron in the HOMO and LUMO, especially in the ions at the edges of P_1/2/4-based 2DIIs. Thus, for P_1/2/4-based 2DIIs, with more ions at the edge comes more obvious decoupling, enhancing the electrical insulation feature of central ions and the electron transferability between edge ions and the substrate, leading to the plunge of E_gap–N_pairs. However, for P₃-based 2DIIs, the C_image distribution of graphite differs from P_1/2/4-based 2DIIs, and the decoupling effect is extremely weak, producing the largest E_gap. Thus, the subunit and size can jointly regulate the electronic properties of 2DIIs, the longer edges of P_1/2/4-based 2DIIs, and the stronger electron transferability of 2DIIs.

The SSIL films have been widely used in the process of gas capture and conversion, where the interaction between gas and 2DIIs plays a dominant role. Taking CO₂ as an example, the charge transfer quantity (C_T) between a CO₂ molecule and the typical 2DII is displayed in Fig. 3d, by statistical averaging from 9 independent adsorption sites. This shows that the C_T of CO₂ is negative, demonstrating that CO₂ will get electrons from the 2DII in the typical chemical process.^35,36 This means electrons may transfer from the HOMO of 2DIIs (HOMO_IL) to the LUMO of CO₂ (LUMO_CO2). The difficulty of the electronic transfer process can be quantitatively described by the energy difference: E_CL-IH = LUMO_CO2 − HOMO_IL, as shown in Fig. 3e. Excitingly, E_CL-IH will decline exponentially as N_pairs increases for various 2DIIs, especially for P_1/2/4-based 2DIIs, representing that larger 2DIIs can transfer electrons to CO₂ more quickly and be effective in the capture and fixation process of CO₂.

Edge selective adsorption of 2DIIs in the CO₂ capture process

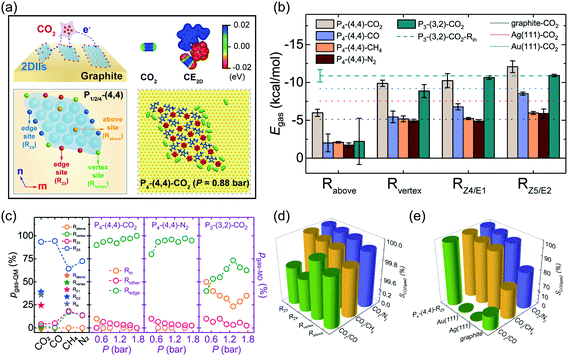
During the practical reactive application of gas capture and conversion, the gas adsorption process, especially for CO₂, is meaningful for the rational design of the corresponding catalyst. To evaluate the gas adsorption stability, we defined four different adsorption sites of 2DIIs (vertex site – R_vertex, edge sites – R_Z4/R_Z5/R_E1/R_E2, above site – R_above, and inside site – R_in), as shown in Fig. 4a and S9.† The adsorption energy (E_gas, see ESI Note†) of different sites is also calculated, as shown in Fig. 4b. For instance, E_gas of CO₂ at R_vertex, R_Z4, R_Z5, and R_above in the P₄-based 2DII with (4,4) is −9.88, −10.24, −12.08, and −5.99 kcal mol⁻¹, respectively, reflecting that the edge site (R_Z5) provides the strongest adsorption ability (ESI Movie M2 and M3†). The lower E_gas should originate from the anisotropic C_image distribution of graphite in Fig. 3c, providing the additional adsorption force to the target gas molecules. However, for the P₃-based 2DII, E_gas of CO₂ at R_in, R_E1, and R_E2 is close, agreeing well with the isotropic C_image distribution. In addition, since the position of the CO₂ molecule at R_above is so far away from the graphite substrate, this leads to weaker substrate contribution, further resulting in a higher E_gas compared with that of other sites. Besides, E_gas of CO, CH₄, and N₂ at various sites of the P₄-based 2DII also shows the same order as that of CO₂.

Fig. 4 (a) Schematic diagrams of CO₂ molecules adsorbed on different sites of 2DIIs, electrostatic potential (ESP) mapped to the van der Waals surface (electron-density isosurface = 0.01 e Bohr⁻³) of a CO₂ molecule before (left) and after (right) adsorption on the P₁-based 2DII with (1,1), and the illustration in the dotted box shows the atomic structures of CO₂ molecules adsorbed on the 2DII at P = 0.88 bar. (b) E_gas for different gases adsorbed on 2DIIs and pure solid surfaces. (c) The p_gas-QM and p_gas-MD for gases adsorbed on different sites. (d and e) The CO₂ adsorption selectivity to other gases on the 2DII and pure solid surfaces.

To quantitatively explore the dynamic stability of gases adsorbed on 2DIIs, MD simulations of the adsorption process were further performed at T = 300 K (Fig. 4a and S10†). As the partial pressure of gases (P) ranges from 0.44 to 1.76 bar, almost all gas molecules adsorb on the edges of the P₄-based 2DII, while some adsorb on the sites inside the P₃-based 2DII (ESI Movie M4†). Excitedly, as shown in Fig. 4c, the Boltzmann factor of E_gas (p_gas-QM, see ESI Note†) is well consistent with the proportion of gases adsorbed on different sites (p_gas-MD, see ESI Note†), verifying that the edges of 2DIIs are dominant adsorption sites for different gases.

Furthermore, compared with many pure solids, E_gas of different gases on edge sites of 2DIIs is even stronger (Fig. 4b and S11†). Taking CO₂ as an example, E_gas of R_Z5 in the P₄-based 2DII with (4,4), Au(111), Ag(111), and graphite is −12.08, −9.20, −7.54, and −5.13 kcal mol⁻¹, respectively. Considering that E_gas of CO₂ is always lower than that of CO, CH₄, and N₂ when they adsorb on the P₄-based 2DII, we further calculated the CO₂ adsorption selectivity to other gases (S_CO2/gas2, see ESI Note†) on different solid surfaces. Fantastically, S_CO2/gas2 for the P₄-based 2DII is bigger than 99.70% (Fig. 4d and e), indicating that all adsorption sites of 2DIIs show extremely high CO₂ selectivity.

Meanwhile, S_CO2/CH4, S_CO2/CO, and S_CO2/N2 of the P₄-based 2DII can be up to 1.31, 1.52, and 1.23 times higher than those of the pure graphite surface. Moreover, S_CO2/CH4, S_CO2/CO, and S_CO2/N2 for Au (111) are 98.59, 1.26, and 98.91%, respectively, lower than those for 2DIIs. The high CO₂ adsorption selectivity suggests that the 2DII can be viewed as a promising adsorbent or reaction promoter in the process of carbon capture and utilization, which agrees well with recent experiments on the IL-stabilized single-atom catalysts.³⁷ Considering that some 2DIIs can maintain stable structures above room temperature, it should be feasible to achieve higher gas adsorption and selectivity by extending the edges of 2DIIs or modulating the ionic microenvironment around the catalyst.

Additional discussion

Physically, the selective edge adsorption for different gases should originate from the unique C_image distribution of the graphite supporting P_1/2/4-based 2DIIs, where the structure, thermodynamic stability, electronic properties, and gas adsorption can also be further enhanced by selecting species of ILs and solid substrates. Moreover, the length of edges can measure the potential effectiveness of 2DIIs adsorbing the gas reactants. The longer side length of the 2DIIs is more conducive to playing the function of 2DIIs in the application of gas adsorption and selectivity. However, the bigger 2DII will lead to the large usage of ILs, which will be a challenge, especially considering the high synthesis cost of ILs.

Excitingly, the optimal size of a P_1/2/4-based 2DII can be determined from the size-dependent E_f and E_gap (Fig. 2c and 4a). A too-small P_1/2/4-based 2DII (N_pairs < N_C) will be thermodynamically unstable and possess a large E_gap. Meanwhile, a too-large P_1/2/4-based 2DII (N_pairs > N_C) will have almost the same thermodynamic stability and E_gap as the 2DII of N_C. Hence, the suitable size of P_1/2/4-based 2DIIs should exist in practical applications, for instance, highly efficient and low-cost CO₂ capture and conversion. Hence, multiple P_1/2/4-based 2DIIs with an optimal size rather than a single large 2DII can provide the best performance, including high electrical conductivity and efficient CO₂ adsorption and selectivity, and minimize the usage of ILs to the greatest extent, which is valuable to overcome the economic barrier of the high-price of ILs in real applications.

Conclusions

In brief, this study set out to better understand the structure, thermodynamic stability, electronic properties, and gas adsorption performance of 2DIIs via combined IC-QM/MM calculations and classical MD simulations. We proposed four kinds of subunits, which can assemble into various 2DIIs supported by graphite. Both the formation energy and HOMO–LUMO energy gap decrease as the size of the 2DIIs grow, and they converge once the size is beyond the critical value; some 2DIIs can also maintain their stable structures even above room temperature. Meanwhile, the HOMO–LUMO gap of the sparsely arranged (Table S2†) annular 2DII (P₃) is far larger than that of close-packed ones (P_1/2/4). Furthermore, the edges of 2DIIs are dominant adsorption sites for CO₂, CO, CH₄, and N₂, and also show high CO₂/CH₄, CO₂/CO, and CO₂/N₂ selectivity, which is up to 1.31, 1.52, and 1.23 times higher than that of the pure graphite surface. The adsorption stability and selectivity are even better than those of some pure metal surfaces. The quantitative structure–function relationship of 2DIIs proves that it is feasible to achieve a higher electronic or gas adsorption performance just by adopting an optimal size of 2DIIs, which is meaningful for the rational design and management of IL-based green chemical engineering applications.

Computational details

Atomic structures

The IL considered herein is 1-ethyl-3-methylimidazolium hexafluoro-phosphate, namely EmimPF₆, widely used as the electrolyte in supercapacitors and other applications.^38–41 Considering the applications of the EmimPF₆–graphite interface in the field of batteries, electrochemical reactions, and other chemical engineering processes,^42,43 graphite was adopted as the solid surface. A three-layer slab models the graphite substrates, and a periodic boundary condition (PBC) was applied in all three dimensions, as shown in Fig. S1.† To properly accommodate the adsorbates on the surface, avoiding spurious interactions with the periodic images, at least 13 × 13 replicas of the unit cell in graphite are used in the lateral dimensions. To decouple the periodic images in the dimension perpendicular to the surface, a vacuum of at least ∼1.7 nm is added along the z-direction.

An IC-QM/MM approach

The optimization of the hybrid IL-graphite system was performed using the CP2K/QUICKSTEP program.^44,45 In order to expand the number of atoms in the hybrid IL-graphite system as much as possible, we employed the IC method⁴⁶ within a QM/MM^47,48 framework, where the QM part is treated at the Kohn–Sham (KS) density functional theory (DFT) level within a mixed Gaussian and plane wave⁴⁹ (GPW) formalism. The accuracy of the IC-QM/MM approach is evaluated by comparing the structural and energetic properties to the full DFT results, as shown in Fig. S2.† “Full DFT” in this context means that graphite and the adsorbate are both treated at the DFT level. For QM calculations, double-ζ valence plus polarization (DZVP) basis sets of the Molopt-type⁵⁰ are used to represent the valence electrons. The interactions between valence and core electrons are described by norm-conserving Goedecker, Teter, and Hutter pseudopotentials.^51–53 The Becke–Lee–Yang–Parr (BLYP) functional^54,55 models the exchange and correlation potential. The van der Waals interactions are accounted for by employing the DFT-D3 dispersion correction. The energy cutoff for the auxiliary plane wave expansion of the density is set to 400 Ry. Moreover, The MM-based interactions between EmimPF₆ and graphite are modeled with the parameters from the MD simulations.

MD simulations

The parameters of the bond, angle, dihedral, van der Waals interactions, and electrostatic interactions of EmimPF₆ were described by the all-atom optimized potentials for the liquid simulations (OPLS-AA) force field,^56–58 which has been used to successfully obtain the structures and liquid properties of ILs.^59,60 Previously, Tang et al. found that the non-polarizable force field could prophesy a rational interfacial structure at the IL-graphite interface via the AIMD simulation.^61,62 Therefore, the non-polarizable OPLS-AA force field employed here commendably described the structure and properties of 2DIIs on graphite. The interactions between EmimPF₆ and graphite can be divided into electrostatic and van der Waals interactions. The former one, the long-range coulombic interaction, was computed using the particle–particle–particle–mesh (PPPM) algorithm with an accuracy of 0.0001.⁶³ The latter one was represented by using the 12-6 Lennard-Jones (LJ) potential, which was truncated at 1.2 nm. The Lorentz–Berthelot mixing rules were used to calculate the van der Waals interactions between different atomic species. The SHAKE algorithm⁶⁴ was applied to the C–H bonds to reduce high-frequency vibrations. All MD simulations in this work were carried out using a large-scale atomic/molecular massively parallel simulator (LAMMPS).⁶⁵ The time step for integrating the Newtonian equations of motion was set as 2.0 fs, which was demonstrated to ensure energy conservation. The in-plane (x–y) size of the graphite surface was set as 3.20 × 3.20 nm² at least, and the height of the PBC box along the z-direction is 20 nm. The atoms of the graphite substrate were fixed during the MD simulations to maintain the planar structure. P₁, P₂, P₃, and P₄ were chosen from the equilibrium configuration of monolayer EmimPF₆ in Fig. S1.† Then, P_1/2/3/4-based 2DIIs with different N_pairs were placed about 0.3 nm above the graphite substrate, which was relaxed in the NVT ensemble at T = 0.01 K, controlled by using the Berendsen thermostat.⁶⁶ After a 10 ns long MD simulation, the initial structure of the hybrid IL–graphite system can be obtained.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

H. H., Y. W., and S. Z. designed this research; C. W. performed the simulations; Z. G., Y. L., C. Q., and F. H. discussed the results; C. W., Y. W., H. H., and S. Z. contributed to preparing the final manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research was funded by the National Natural Science Foundation of China (21922813, 22078322, 22178344, and 21890762), the Youth Innovation Promotion Association of CAS (2021046), the Fund of State Key Laboratory of Multiphase Complex Systems (MPCS-2021-A-10), DNL Cooperation Fund, CAS (DNL180202), and the Innovation Academy for Green Manufacture, Chinese Academy of Sciences (IAGM2020C16).

References

1. K. Dong, X. Liu, H. Dong, X. Zhang and S. Zhang, Chem. Rev., 2017, 117, 6636–6695.
2. R. Rogers and K. Seddon, Science, 2003, 302, 792–793.
3. J. Avila, L. Lepre, C. Santini, M. Tiano, S. Denis-Quanquin, K. Chung Szeto, A. Padua and M. Costa Gomes, Angew. Chem., Int. Ed., 2021, 60, 12876–12882.
4. B. Li, C. Wang, Y. Zhang and Y. Wang, Green Energy Environ., 2021, 6, 253–260.
5. Z. Wu, W. Ding, Y. Zhang, Y. Wang and H. He, Acta Phys.-Chim. Sin., 2021, 37, 2002021.
6. M. Hope, K. Griffith, B. Cui, F. Gao, S. Dutton, S. Parkin and C. Grey, J. Am. Chem. Soc., 2018, 140, 16685–16696.
7. J. Feng, H. Gao, L. Zheng, Z. Chen, S. Zeng, C. Jiang, H. Dong, L. Liu, S. Zhang and X. Zhang, Nat. Commun., 2020, 11, 4341.
8. H. Sun, P. Liang, G. Zhu, W. Hung, Y. Li, H. Tai, C. Huang, J. Li, Y. Meng, M. Angell, C. Wang and H. Dai, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27847–27853.
9. S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng, T. Chen, M. Dincă, A. Kornyshev and G. Feng, Nat. Mater., 2020, 19, 552–558.
10. H. Dou, B. Jiang, M. Xu, Z. Zhang, G. Wen, F. Peng, A. Yu, Z. Bai, Y. Sun, L. Zhang, Z. Jiang and Z. Chen, Angew. Chem., Int. Ed., 2019, 58, 13969–13975.
11. S. Budhathoki, J. Shah and E. Maginn, Ind. Eng. Chem. Res., 2017, 56, 6775–6784.
12. M. Babucci, C. Fang, A. Hoffman, S. Bare, B. Gates and A. Uzun, ACS Catal., 2017, 7, 6969–6972.
13. W. Sun, M. Wang, Y. Zhang, W. Ding, F. Huo, L. Wei and H. He, Green Energy Environ., 2020, 5, 183–194.
14. B. Xin and J. Hao, Chem. Soc. Rev., 2014, 43, 7171–7187.
15. B. Polesso, F. Bernard, H. Ferrari, E. Duarte, F. Vecchia and S. Einloft, Heliyon, 2019, 5, e02183.
16. L. Offner-Marko, A. Bordet, G. Moos, S. Tricard, S. Rengshausen, B. Chaudret, K. Luska and W. Leitner, Angew. Chem., Int. Ed., 2018, 57, 12721–12726.
17. S. El Sayed, A. Bordet, C. Weidenthaler, W. Hetaba, K. Luska and W. Leitner, ACS Catal., 2020, 10, 2124–2130.
18. J. Armstrong, C. Hurst, R. Jones, P. Licence, K. Lovelock, C. Satterley and I. Villar-Garcia, Phys. Chem. Chem. Phys., 2007, 9, 982.
19. T. Cremer, M. Killian, J. Gottfried, N. Paape, P. Wasserscheid, F. Maier and H. Steinrück, ChemPhysChem, 2008, 9, 2185–2190.
20. B. Uhl, F. Buchner, D. Alwast, N. Wagner and R. Behm, Beilstein J. Nanotechnol., 2013, 4, 903–918.
21. T. Cremer, M. Stark, A. Deyko, H. Steinrück and F. Maier, Langmuir, 2011, 27, 3662–3671.
22. C. Wang, C. Qian, Z. Li, N. Wei, N. Zhang, Y. Wang and H. He, Ind. Eng. Chem. Res., 2020, 59, 8028–8036.
23. S. Zhang, Y. Lu, C. Peng, H. Liu and D. Jiang, J. Phys. Chem. C, 2019, 123, 618–624.
24. B. Uhl, H. Huang, D. Alwast, F. Buchner and R. Jürgen-Behm, Phys. Chem. Chem. Phys., 2015, 17, 23816–23832.
25. M. Meusel, M. Lexow, A. Gezmis, S. Schötz, M. Wagner, A. Bayer, F. Maier and H. Steinrück, ACS Nano, 2020, 14, 9000–9010.
26. B. Uhl, F. Buchner, S. Gabler, M. Bozorgchenani and R. Jürgen-Behm, Chem. Commun., 2014, 50, 8601–8604.
27. Q. Su, Y. Qi, X. Yao, W. Cheng, L. Dong, S. Chen and S. Zhang, Green Chem., 2018, 20, 3232–3241.
28. W. Xie, X. Ji, X. Feng and X. Lu, AIChE J., 2015, 61, 4437–4444.
29. W. Xie, X. Ji, X. Feng and X. Lu, Ind. Eng. Chem. Res., 2016, 55, 366–372.
30. Z. Tang, L. Lu, Z. Dai, W. Xie, L. Shi and X. Lu, Langmuir, 2017, 33, 11658–11669.
31. S. Zhang, Y. Wang, H. He, F. Huo, Y. Lu, X. Zhang and K. Dong, Green Energy Environ., 2017, 2, 329–330.
32. K. Dong, S. Zhang and J. Wang, Chem. Commun., 2016, 52, 6744–6764.
33. J. Dong, D. Geng, F. Liu and F. Ding, Angew. Chem., Int. Ed., 2019, 131, 7805–7809.
34. X. Zhou, H. Shu, Q. Li, P. Liang, D. Cao and X. Chen, J. Mater. Chem. C, 2020, 8, 4432–4440.
35. M. Asadi, K. Kim, C. Liu, A. Addepalli, P. Abbasi, P. Yasaei, P. Phillips, A. Behranginia, J. Cerrato, R. Haasch, P. Zapol, B. Kumar, R. Klie, J. Abiade, L. Curtiss and A. Salehi-Khojin, Science, 2016, 353, 467–470.
36. Y. Oh and X. Hu, Chem. Commun., 2015, 51, 13698–13701.
37. S. Ding, Y. Guo, M. Hülsey, B. Zhang, H. Asakura, L. Liu, Y. Han, M. Gao, J. Hasegawa, B. Qiao, T. Zhang and N. Yan, Chem, 2019, 5, 3207–3219.
38. F. Huo, Z. Liu and W. Wang, J. Phys. Chem. B, 2013, 117, 11780–11792.
39. X. Liu, D. Wu, H. Wang and Q. Wang, Adv. Mater., 2014, 26, 4370–4375.
40. T. Zhao, J. Liang, Y. Zhang, Y. Wu and X. Hu, Chem. Commun., 2018, 54, 8964–8967.
41. B. Moghadam, M. Razmkhah, M. Mosavian and F. Moosavi, Phys. Chem. Chem. Phys., 2016, 18, 33053–33067.
42. X. Shi, W. Zhang, J. Wang, W. Zheng, K. Huang, H. Zhang, S. Feng and H. Chen, Adv. Energy Mater., 2016, 6, 1601378.
43. Q. Dou, M. Sha, H. Fu and G. Wu, J. Phys.: Condens. Matter, 2011, 23, 175001.
44. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
45. J. Vandevondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
46. D. Golze, M. Iannuzzi, M. Nguyen, D. Passerone and J. Hutter, J. Chem. Theory Comput., 2013, 9, 5086–5097.
47. T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2005, 1, 1176–1184.
48. T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2006, 2, 1370–1378.
49. B. Lippert and J. Parrinello, Mol. Phys., 1997, 92, 477–488.
50. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
51. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
52. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
53. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
54. A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
55. C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
56. J. Canongia Lopes, J. Deschamps and A. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047.
57. J. Canongia Lopes, J. Deschamps and A. Pádua, J. Phys. Chem. B, 2004, 108, 11250.
58. J. Canongia Lopes and A. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898.
59. C. Qian, B. Ding, Z. Wu, W. Ding, F. Huo, H. He, N. Wei, Y. Wang and X. Zhang, Ind. Eng. Chem. Res., 2019, 58, 20109–20115.
60. Y. Wang, C. Wang, Y. Zhang, F. Huo, H. He and S. Zhang, Small, 2019, 15, 1804508.
61. F. Tang, T. Ohto, T. Hasegawa, M. Bonn and Y. Nagata, Phys. Chem. Chem. Phys., 2017, 19, 2850–2856.
62. S. Kim, S. Zhou, Y. Hu, M. Acik, Y. Chabal, C. Berger, W. De Heer, A. Bongiorno and E. Riedo, Nat. Mater., 2012, 11, 544–549.
63. R. Hockney and J. Eastwood, Computer simulation using particles, Taylor & Francis, Inc., 1988.
64. J. Ryckaert, G. Ciccotti and H. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
65. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
66. H. Berendsen, J. Postma, W. Van Gunsteren, A. Dinola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05431g

---