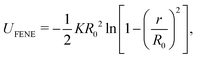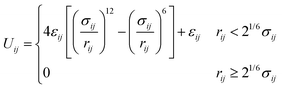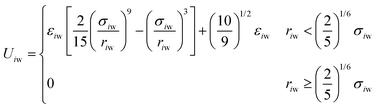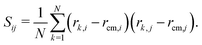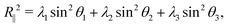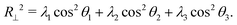Crowding-induced interactions of ring polymers

Abstract

Macromolecular crowding and the presence of surfaces can significantly impact the spatial organization of biopolymers. While the importance of crowding-induced depletion interactions in biology has been recognized, much remains to be understood about the effect of crowding on biopolymers such as DNA plasmids. A fundamental problem highlighted by recent experiments is to characterize the impact of crowding on polymer–polymer and polymer–surface interactions. Motivated by the need for quantitative insight, we studied flexible ring polymers in crowded environments using Langevin dynamics simulations. The simulations demonstrated that crowding can lead to compaction of isolated ring polymers and enhanced interactions between two otherwise repulsive polymers. Using umbrella sampling, we determined the potential of mean force (PMF) between two ring polymers as a function of their separation distance at different volume fractions of crowding particles, ϕ. An effective attraction emerged at ϕ ≈ 0.4, which is similar to the degree of crowding in cells. Analogous simulations showed that crowding can lead to strong adsorption of a ring polymer to a wall, with an effective attraction to the wall emerging at a smaller volume fraction of crowders (ϕ ≈ 0.2). Our results reveal the magnitude of depletion interactions in a biologically-inspired model and highlight how crowding can be used to tune interactions in both cellular and cell-free systems.

---

1 Introduction

Macromolecules within cells can occupy up to 40% of the total cellular volume and crowd the intracellular environment.^1,2 The presence of macromolecular crowders can induce attractive depletion interactions between larger objects, an entropically-driven phenomenon first described by Asakura and Oosawa.³ Crowding-induced depletion interactions have been shown to impact protein stability⁴ and biochemical reaction equilibria,^5,6 and there is a growing realization that they play an important role in cellular organization.^7,8 For example, macromolecular crowding impacts the organization of bacterial chromosomes^9–13 and can lead to phase separation in the cytoplasm.^8,14

Crowding-induced depletion interactions have been shown to impact biopolymers like DNA in a number of experimental studies. Polymeric crowders can lead to the compaction of both linear DNA and circular DNA plasmids.^15,16 While linear DNA chains collapse with an increase in crowding in bulk conditions, in nanochannels, they can exhibit depletion-induced elongation.¹⁷ Crowding can also lead to aggregation of DNA plasmids,¹⁸ and polynucleosomes that are soluble in uncrowded solutions form large assemblies and sediment in the presence of crowders.¹⁹

Computer simulations have been an important tool for understanding the effects of crowding on conformations of biopolymers. Shendruk et al.²⁰ showed that crowding-induced depletion interactions can lead to the collapse of a model chromosome polymer, causing a coil-to-globule transition. Kang et al.²¹ carried out simulations of a linear polymer for different sizes of crowding particles. They found that crowding decreased the radius of gyration of the polymer and that smaller crowding particles resulted in a larger decrease at the same volume fraction of crowders. Additionally, polydispersity in the size of crowding particles has been shown to swell sufficiently stiff polymer chains,²² and flexible polymeric crowders result in larger compaction of a polymer chain than hard spheres at the same crowding fraction.²³

The presence of surfaces such as cell membranes can be of consequence to biopolymers because crowders can induce depletion attractions between a polymer and a surface. Simulations have shown that crowding can induce adsorption of a polymer chain onto a cylindrical wall,²⁴ that a model DNA chain in spherical confinement preferentially resides near the boundary at high levels of crowding,²⁵ and that depletion interactions are responsible for separation of two arms of a model chromosome or two ring polymers under strong cylindrical confinement.^11,26 However, these studies did not quantify the magnitude of the effective interactions, which is important for understanding the relative importance of interactions in the bulk versus at the surface.

In parallel with the previous studies, there has been a growing body of work on gene expression in synthetic, cell-free platforms.²⁷ Recent studies have used synthetic, monodisperse crowding molecules to study the impact of crowding on expression from DNA plasmids.^28–30 Interestingly, crowding can lead to spatially heterogeneous regions of gene expression,^28,29 and confining the crowded systems to cell-sized vesicles caused DNA to localize near the inner surfaces.^30,31 The physical reasons for the spatial organization remain unclear.

Taken together, a variety of experimental and simulation studies highlight the importance of crowding-induced depletion interactions between biopolymers in cellular and cell-free systems. However, in most instances, a detailed quantitative understanding of the depletion interactions is lacking. In this work, we help to address this gap by using computer simulations to characterize effective interactions in a model that captures key physical features of DNA plasmids and crowding particles. We focus particularly on characterizing depletion interactions in the context of cell-free gene expression platforms, but our results are relevant in other biological and non-biological contexts as well.

2 Methods

We employed Langevin dynamics computer simulations to explore the behavior of flexible ring polymers in crowded environments. We used the simulations to study the effects of crowding on isolated ring polymers, pairs of ring polymers, and systems in which a ring polymer is near a surface. We characterized effective interactions by using umbrella sampling to obtain potentials of mean force (PMFs) for various levels of crowding.

The ring polymer was modeled as a self-avoiding flexible chain consisting of 50 beads. The adjacent beads of the polymer were connected by the finitely extensible nonlinear elastic (FENE) bond potential,³² given by

where r is the center-to-center distance between two adjacent beads. The maximum distance between two beads connected via a FENE bond (R₀) was chosen to be 2σ with spring constant K = 15ε/σ². In this work, σ and ε set the length and energy units respectively.

Crowder particles were modeled as purely repulsive particles of radius R_c. All particles (polymer beads and crowders) interacted via the short-ranged and purely repulsive Weeks–Chandler–Andersen (WCA) potential,³³

where r_ij is the center-to-center distance between particles i and j. The strength parameter was the same for all pairs, ε_ij = ε = k_BT. Further, σ_ij = R_i + R_j, where R_i and R_j denote the radii of particles i and j, respectively. The sizes (σ_ii) of polymer beads and crowder particles were chosen to be 1.5σ and 0.6σ, respectively, because the Kuhn length of DNA is larger than the size of typical crowding molecules. The level of crowding was controlled by the number of crowding particles (N_c), with the volume occupied defined as V_c = N_c4πR_c³/3. We refer to the volume fraction of the crowding particles (ϕ = V_c/V) as the crowding fraction.

The size of the system without walls was 30σ × 30σ × 30σ, with periodic boundaries in all dimensions. For the system with walls, we imposed repulsive walls in one dimension (z) and periodic boundaries in the other dimensions (x and y). This system was 30σ in the z direction and 25σ in the x and y directions. Particles interacted with the walls via the 9-3 Lennard-Jones wall potential at the lower and upper boundaries in the z direction,³⁴

where r_iw is the distance between the particle and the wall surface. The strength factor for wall-particle interactions was the same for all particles, ε_iw = ε = k_BT. The length parameter σ_iw was specified by the relation (2/5)^1/6σ_iw = σ_ii/2. With this condition, a particle experienced a repulsive force when the distance between the wall and the particle was less than the particle radius.

The Langevin equation was integrated forward in time using the velocity-Verlet algorithm in the LAMMPS simulation package.^35,36 The timestep for integration was 0.005τ, where τ is the natural unit of time. The friction coefficient for component k was chosen to be 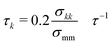with σ_mm and σ_kk being the diameter for polymer beads and component k respectively. Resulting trajectories were visualized using OVITO.³⁷

Umbrella sampling

We employed umbrella sampling and the weighted Histogram analysis method (WHAM) to determine the potential of mean force (PMF) as a function of the distance between the centers of mass of two polymers (r₁₂). We sampled along the coordinate r₁₂via a harmonic bias potential using the COLVARS module in LAMMPS.³⁸ Distances and the strength of the biasing potential were chosen to obtain good overlap of histograms generated in adjacent windows (see ESI†). WHAM was then used to determine an unbiased potential.^39,40 Because the reaction coordinate r₁₂ is a nonlinear function of the Cartesian coordinates defining the state of the system, an additional term (2k_BT ln r₁₂) was added to the potential obtained using WHAM to give the PMF, U(r₁₂). The additional term accounts for the r₁₂-dependent size of configuration space.⁴¹

We also calculated the PMF as a function of the distance in the z direction between a wall and the center of mass of the ring polymer (z_pw) using same procedure as above. Because the size of accessible configuration space remains constant with increasing z_pw, no correction term was required in this case. Details of the umbrella sampling can be found in ESI.†

The statistical errors in the PMFs were calculated using a Monte Carlo bootstrap analysis method.⁴⁰ For each time series corresponding to a different umbrella potential, we first calculated the correlation time (τ_c) by determining the time it took for the autocorrelation function to decay by a factor of e. Each original time series consisted of t_f data points. 50 new bootstrapped distributions, with a total of t_f/τ_c data points, were generated at random (with replacement) from the probability distribution of the simulated trajectory at each distance. 50 PMFs were calculated from the bootstrapped data sets, which were then used to calculate the mean and standard deviation of the PMF.

3 Results

Crowding causes compaction of an isolated ring polymer

We first considered a single ring polymer in a simulation box with periodic boundaries in all dimensions. No walls were present, and the volume fraction occupied by crowding particles (ϕ) ranged from no crowding (ϕ = 0) to highly crowded (ϕ = 0.42). Fig. 1A shows the radius of gyration (R_g) of the polymer as a function of the crowding fraction. The average radius of gyration decreased with an increase in crowding, with a pronounced decrease seen at the largest crowding fractions (ϕ = 0.4 and 0.42). Fig. 1B shows the full distributions of R_g for each crowding fraction. The distributions shift to smaller values with increasing ϕ and have a qualitatively different shape at ϕ = 0.4 and 0.42, where they are less symmetric. Fig. S1 (ESI†) shows that at these crowding levels, the mode of the distribution shifts to the left of the mean.

Fig. 1 (A) Radius of gyration of an isolated polymer at different crowding fractions (ϕ). Error bars denote the standard deviation. (B) Probability density of the radius of gyration scaled by 〈R_g(0)〉, the average radius of gyration in uncrowded conditions. Distributions are shown for different crowding fractions. (C) Asphericity of the polymer. (D) Snapshots of the ring polymer for the most probable value of R_g at different crowding fractions.

We also calculated the asphericity (b) of the polymer, 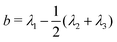, where λ₁ ≥ λ₂ ≥ λ₃ are the eigenvalues of the gyration tensor,^42,43

Here, N = 50 is the number of beads in the polymer, r_k,i is the ith coordinate of the position of the kth particle, and r_cm,i is the corresponding component of the center of mass. The asphericity is zero for a sphere and non-zero for non-spherical shapes, with larger values indicating larger deviations from sphericity. Fig. 1C shows that the average asphericity also decreases with an increase in crowding.

Fig. 1D shows snapshots of the ring polymer at various crowding fractions. For each case, a representative snapshot was chosen from the most probable bin in Fig. 1B. By inspection, the snapshots illustrate the decreasing size and asphericity at higher crowding fractions.

Taken together, these results show that increased crowding causes a decrease in the characteristic size (〈R_g〉) and in the asphericity (〈b〉) of a ring polymer. Fig. 1B and Fig. S1 (ESI†) further demonstrate a qualitative change in the distribution of R_g at large values of ϕ. These results indicate that the ring polymer adopts conformations that are more compact and globule-like as crowding increases. This effect arises due to crowding-induced depletion interactions between beads of the polymer and is consistent with previous work on linear polymers.²¹

Crowding promotes interactions between two polymers

In the absence of crowding particles, two ring polymers are expected to experience an effective repulsion when they approach one another due to the entropic penalty arising from reduced conformational degrees of freedom.⁴⁴ In Fig. 1, we characterized changes in the size and shape of a single ring polymer due to crowding-induced depletion interactions between its segments. Based on this, we hypothesized that crowding could also induce attraction between two otherwise purely repulsive polymers.

We simulated two polymers in a box with periodic boundaries and characterized N₁₂, the number of beads of polymer 1 within the WCA cutoff distance (2^1/6σ_mm) of any bead of polymer 2. Fig. 2 shows N₁₂ as a function of time. When the two polymers were in contact, larger crowding fractions resulted in a longer duration of contact and an increase in the number of beads in contact (N₁₂). The larger values of N₁₂ are not attributable to an effect of slower diffusion alone, suggesting that there was a crowding-induced reduction in the effective repulsion between the two polymers. The effect was most pronounced at large crowding fractions (ϕ = 0.4 and 0.42). Inset snapshots show the conformations of the two polymers at the maximum value of N₁₂ in each figure. At low levels of crowding, the polymers stayed relatively expanded with small numbers of beads in contact. At higher levels of crowding, the polymers made more extensive contacts and were closer together in more compact conformations.

Fig. 2 Number of beads of polymer 1 in contact with any bead of polymer 2 (N₁₂) as a function of time for different crowding fractions (ϕ). Inset: Snapshot corresponding to the configuration with the largest value of N₁₂ for each crowding fraction.

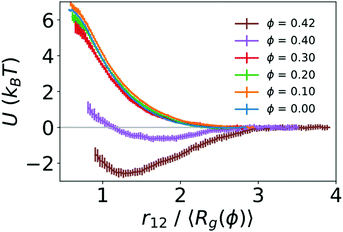
To quantify the strength of the effective interaction between the two polymers, we used umbrella sampling to calculate the potential of mean force (PMF) as a function of the distance between the centers of mass of the two polymers (r₁₂). Fig. 3 shows the resulting PMFs at different crowding fractions. As expected, the PMFs are flat at large distances, indicating that the polymers did not interact when sufficiently far away from one another. For reference, we set the PMFs to zero at the largest value of r₁₂ considered (15σ for ϕ = 0.0 and 0.1, and 13σ for larger crowding fractions). This was in the regime in which the two polymers did not interact. When not in contact, the two polymers were more compact at higher crowding fractions, which was analogous to the single-polymer results in Fig. 1B. In Fig. 3, we present the PMFs in terms of the characteristic polymer size by scaling the distance (r₁₂) by the average radius of gyration for each crowding fraction.

Fig. 3 Potentials of mean force (U) between two polymers as a function of the distance between their centers of mass. For each crowding fraction (ϕ), the distance (r₁₂) is scaled by the average radius of gyration of an isolated polymer (〈R_g(ϕ)〉). Error bars indicate the standard deviation determined using the bootstrapping procedure described in Methods.

For the uncrowded system (ϕ = 0) in Fig. 3, the PMF indicates a purely repulsive interaction, with the repulsive part of the potential (dU/dr₁₂ < 0) emerging when the centers of mass of the polymers are slightly farther apart than 2〈R_g〉. The PMFs associated with crowding fractions ϕ = 0.1, 0.2, and 0.3 exhibit similar monotonic behavior, indicating purely repulsive interactions. However, the magnitude of the PMF is modestly smaller for ϕ = 0.3. This indicates a smaller energetic penalty to bring two polymers into contact at higher crowding fractions, which is consistent with the larger number of beads in contact (N₁₂) observed in Fig. 2. For ϕ = 0.4, in contrast with smaller values of ϕ, the PMF exhibits a small attractive minimum (U_min = −0.64k_BT) at r₁₂ = 1.65〈R_g〉 = 6.10σ. The behavior at smaller values of r₁₂ is repulsive. For ϕ = 0.42, the PMF exhibits a deeper minimum (U_min = −2.59k_BT) at r₁₂ = 1.27〈R_g〉 = 4.20σ.

These results highlight the role of depletion interactions in shaping the effective interactions of two ring polymers. In the absence of crowding, there is an effective repulsion between the two polymers at short distances due to the decreased conformational entropy of the polymers. Depletion interactions due to crowding can offset the loss of conformational entropy. This leads to enhanced contact between the polymers due to a smaller effective repulsive potential (ϕ ≤ 0.3) that becomes attractive at large crowding fractions (ϕ = 0.4 and 0.42).

Crowding leads to polymer adsorption at a wall

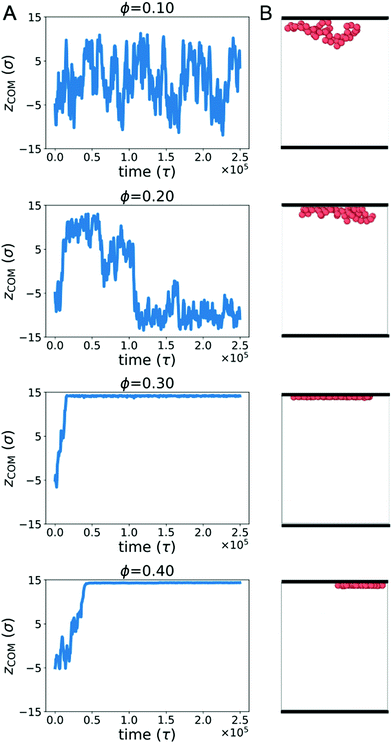
Biopolymers commonly encounter extended surfaces in both cellular and cell-free environments. Crowding-induced depletion interactions can influence the effective interaction between a polymer and a surface. To characterize this effect, we simulated a single ring polymer in the presence of repulsive walls.

We first simulated a ring polymer in a simulation box with walls located at z = ±15σ. Fig. 4A shows the time-dependent position of the center of mass of the polymer in the z direction when the polymer started near the center. At ϕ = 0.1, the polymer remained within the bulk of the simulation box, with the center of mass remaining separated from the wall. This is consistent with an effective repulsion that the polymer is expected to experience near the wall due to reduced conformational entropy.

Fig. 4 (A) Center of mass of a polymer in the z direction (z_COM) as a function of time in unbiased simulations. A single trajectory with a polymer starting away from the walls is shown for each crowding fraction (ϕ). (B) Snapshot from each trajectory, with walls denoted by the thick black lines at the upper and lower bounds of the box (z = ±15σ). To facilitate comparison between different crowding fractions, each snapshot corresponds to the frame in which the polymer was closest to the wall.

However, at ϕ = 0.2, qualitatively different behavior emerged. Here, the center of mass of the polymer was more likely to reside close to a wall for an extended period of time. At larger crowding fractions (ϕ = 0.3 and 0.4), the polymer became strongly associated with one of the walls for the duration of the simulation. The behavior for ϕ ≥ 0.2 is consistent with the polymer experiencing an effective attraction to the wall, with the strength of the attraction increasing with larger crowding fractions.

Fig. 4B shows snapshots of the polymer in the presence of walls at different crowding fractions (viewed from the side). To facilitate comparison, each snapshot corresponds to the polymer configuration that was closest to the wall in Fig. 4A. At ϕ = 0.2, the polymer appears to be partially adsorbed to the surface. In conjunction with the time-dependence of the center of mass, this suggests that the polymer was transiently adsorbed with parts of the polymer in contact with the wall. Because only part of the polymer was in contact, the center of mass remained farther from the wall than the polymer configurations seen at ϕ = 0.3 and 0.4. At these crowding fractions, the polymer is strongly adsorbed, with almost all of the polymer beads in contact with the wall.

To further characterize the conformations of the polymer, Fig. 5A and B show the radius of gyration (R_g) and asphericity (b) of the polymer. With a wall present, both quantities increased for ϕ ≥ 0.25. This is in contrast with the behavior of an isolated polymer in the bulk (Fig. 1), which became more compacted and spherical at these crowding fractions.

Fig. 5 (A) Radius of gyration of a polymer in the presence of walls at different crowding fractions. (B) Asphericity of the polymer. (C) Extension of the polymer in the directions parallel to (R_‖) and perpendicular to (R_⊥) the wall. (D) Snapshots of the polymer for the most probable value of R_g at different crowding fractions. The polymer is viewed along the z direction (toward a wall).

Snapshots from Fig. 4B suggested a flattening of the polymer against the wall at higher crowding fractions, so we investigated a measure of the extension of the polymer in the directions parallel to and perpendicular to the wall:⁴⁵

Here, θ_i is the angle between the eigenvector corresponding to eigenvalue λ_i of the gyration tensor and the z axis, which is normal to the wall. Fig. 5C shows that for ϕ ≥ 0.25, the polymer became extended in the directions parallel to the wall and contracted in the direction perpendicular to the wall.

In this regime, the presence of a wall leads to a flattening of the polymer against the wall, resulting in conformations that are extended in the x and y dimensions relative to the z dimension (Fig. 5C and D). This leads to the increase in the average radius of gyration and asphericity and the decrease in the average value of R_⊥. This demonstrates that crowding can lead to markedly different conformations of the polymer in the presence and absence of a confining wall.

We also observed modest decreases in the average radius of gyration and the average value of R_‖ between ϕ = 0.3 and 0.4. However, the average asphericity was relatively constant in this range. This was due to the polymer remaining flattened against the wall but becoming more compact in two dimensions due to depletion interactions between different parts of the polymer. Thus, at large crowding fractions, the degree of crowding can impact the quasi-two-dimensional conformations of the strongly adsorbed polymer.

To quantify the strength of the effective interaction between the ring polymer and the wall, we determined the PMF as a function of the distance between the center of mass of the polymer and the position of the wall in the z direction (z_pw). Fig. 6 shows the PMFs for various crowding fractions. We considered crowding fractions ϕ ≤ 0.25 because of challenges associated with obtaining adequate, equilibrated sampling at larger values of ϕ, where the polymer strongly adsorbs to the wall. For ϕ = 0 and 0.1, the PMFs are strictly repulsive at small distances. For ϕ = 0.2, there is a shallow attractive well (U_min = −1.21k_BT) with a minimum at z_min = 4.3σ. This is consistent with the typical location of the center of mass of the polymer being close to the wall, as observed in Fig. 4. The effective repulsion at small values of z_pw indicates that depletion interactions do not offset further loss of conformational entropy associated with more monomers being in contact with the wall.

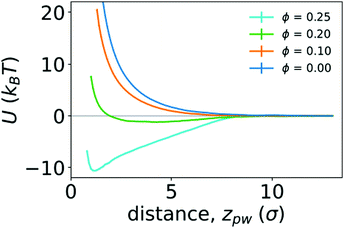Fig. 6 Potentials of mean force (U) between a polymer and a wall as function of the distance between them (z_pw), for different crowding fractions.

Increasing the crowding fraction further resulted in stronger attraction to the wall. For ϕ = 0.25, the well depth is −10.59k_BT. This is notably larger than the depth of the attractive well between two polymers in the bulk at the largest crowding fraction considered (ϕ = 0.42). The location of the minimum for ϕ = 0.25 is z_min = 1.2σ, which is closer to the wall than the minimum for ϕ = 0.2. This is consistent with increased crowding driving the polymer from a partially adsorbed state at intermediate crowding fractions to a strongly adsorbed state at larger crowding fractions. When strongly adsorbed, the polymer nearly completely flattens against the wall, as shown in Fig. 5. We anticipate that larger crowding fractions would result in PMFs with even deeper attractive wells.

4 Discussion

Crowding-induced depletion interactions have been long studied in the context of soft matter systems, especially those comprised of colloids and polymers. The impacts of depletion interactions in cellular environments, which are crowded with macromolecules, have been increasingly appreciated.^7,8,14 Additionally, cell-free experiments incorporating biological components and synthetic crowders have become a new way to study the impact of crowding on biological systems.^28,29

In this work, we studied a simple model of a ring polymer, monodisperse crowding particles, and a static wall. All components of the system interacted only via short-ranged repulsive interactions. We neglected specific energetic interactions that can play important roles in the organization of biomolecules, and the static wall provided an approximation of dynamic membrane surfaces in the cell. Instead, our focus was on characterizing the magnitude and consequences of depletion interactions as they would apply to a variety of biological systems. We focused on exploring the strength of polymer–polymer and polymer–wall attraction, which was motivated by recent experiments in cell-free systems.^28–30 While we studied a specific crowder size in this work, based on crowding-induced compaction of linear polymers,²¹ we expect that decreasing the crowder size would increase the magnitude of attractive interactions. However, it would not impact the qualitative features.

We first studied the conformations of isolated ring polymers without a wall present. We observed that crowding generated depletion interactions between segments of the same polymer, leading to compaction of the polymers (Fig. 1). Our results are consistent with studies that observed the effects of depletion interactions on the compaction of linear polymers^20,21 and penetrable ellipsoids.⁴⁶ The collapse of a polymer with crowding may have important consequences in biology. It has been attributed as a major factor in the condensation of chromosomes in prokaryotes.⁴⁷ Additionally, macromolecular crowding improves the encapsulation of polymers in lipid vesicles, which has been attributed to polymer condensation due to crowding.⁴⁸ This is of particular consequence to synthetic cell-free systems encapsulated in vesicles.

We further studied how crowding impacts the effective interactions between two polymers and between a polymer and a surface. We first showed that crowding can lead to enhanced interactions between two ring polymers, and that at sufficiently high crowding fractions (ϕ ≈ 0.4), an effective attraction between polymers emerged (Fig. 3). Attraction between polymers can result in aggregation and phase separation, and the impact of crowding-induced depletion interactions on phase separation in biological systems is a topic of intense current interest.⁴⁹ Our work helps to contextualize the magnitude of depletion interactions between ring polymers like DNA plasmids.

We also showed that crowding can induce adsorption of a ring polymer to a wall, with an effective attraction emerging at lower crowding fractions (ϕ ≈ 0.2). Between ϕ = 0.2 and 0.3, the polymer transitioned from partially adsorbed to fully adsorbed, with nearly all of the monomers in direct contact with the wall. In this regime, the polymer adopted a flattened conformation that was extended in the lateral dimensions. We characterized the strength of the attraction to the wall for ϕ = 0.2 and 0.25 by the depth of the minimum in the potential of mean force. The polymer–wall interactions for ϕ = 0.25 exhibited a deeper minimum than those observed for polymer–polymer interactions, indicating a significantly stronger interaction.

The markedly different conformations of ring polymers in the bulk versus adsorbed at the wall have the potential to influence the interactions of the polymer with other molecules. Transcriptional machinery is less likely to be able to access compacted conformations of DNA plasmids, potentially impacting the dynamics of gene expression. Tsuji and Yoshikawa⁵⁰ showed that different conformations of the widely studied bacteriophage T4 DNA lead to significantly different behavior of transcription. They observed that high concentrations of Mg²⁺ ions caused DNA to adsorb at the surface of cell-sized lipid vesicles, leading to extended conformations of the DNA. The extended conformations exhibited transcription similar to DNA coils in aqueous solutions. In contrast, collapsed DNA obtained via addition of the polycation spermine showed no transcriptional activity.

Our work suggests that crowding could be used in much the same way to influence the conformations of DNA, hence impacting gene expression. In a crowded environment, it is also possible that an effective polymer–polymer attraction could impact gene expression by causing aggregation of DNA. It highlights crowding as a potential variable with which to control the spatial organization and conformations of DNA, as well as dynamics of gene expression. This control is possible in both cellular and cell-free environments. Indeed, our results suggest a possible mechanism to explain recent cell-free experiments in which crowding modulated the spatial organization of biopolymers. In systems with large volumes, there was evidence of spatially localized transcription that emerged with increasing crowding,^28,29 which could potentially arise due to attractive depletion interactions. In systems confined in small vesicles, crowding induced localization at the walls,³⁰ which is consistent with the strong attraction we found for polymer–wall interactions.

Our results show that crowding can impact the conformations of individual ring polymers, enhance interactions between two polymers, and strongly promote interactions with surfaces. It has implications for understanding the role of entropic interactions in shaping the behavior of biopolymers in both cellular and cell-free systems. Interesting directions for future investigation include the effects of polydisperse crowders, flexible membrane surfaces, and additional species differentially impacted by depletion interactions.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research was conducted as part of the Interface Directed Assembly Theme at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. This research also made use of computational resources at the University of Tennessee Advanced Computing Facility.

References

1. R. J. Ellis, Curr. Opin. Struct. Biol., 2001, 11, 114–119.
2. H.-X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375–397.
3. S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192.
4. M. S. Cheung, D. Klimov and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4753–4758.
5. N. Kozer, Y. Y. Kuttner, G. Haran and G. Schreiber, Biophys. J., 2007, 92, 2139–2149.
6. Y.-L. Zhou, J.-M. Liao, J. Chen and Y. Liang, Int. J. Biochem. Cell Biol., 2006, 38, 1986–1994.
7. D. Marenduzzo, K. Finan and P. R. Cook, J. Cell Biol., 2006, 175, 681–686.
8. M. Delarue, G. P. Brittingham, S. Pfeffer, I. Surovtsev, S. Pinglay, K. Kennedy, M. Schaffer, J. Gutierrez, D. Sang and G. Poterewicz, et al. , Cell, 2018, 174, 338–349.
9. O. L. Kantidze and S. V. Razin, Nucleic Acids Res., 2020, 48, 4614–4626.
10. J. Pelletier, K. Halvorsen, B.-Y. Ha, R. Paparcone, S. J. Sandler, C. L. Woldringh, W. P. Wong and S. Jun, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E2649–E2656.
11. C. Jeon, Y. Jung and B.-Y. Ha, Sci. Rep., 2017, 7, 1–10.
12. P. Swain, B. M. Mulder and D. Chaudhuri, Soft Matter, 2019, 15, 2677–2687.
13. R. Hancock, PLoS One, 2012, 7, e36045.
14. T. Kaur, I. Alshareedah, W. Wang, J. Ngo, M. M. Moosa and P. R. Banerjee, Biomolecules, 2019, 9, 71.
15. L. Lerman, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 1886–1890.
16. A. N. Gupta and J. R. van der Maarel, Macromolecules, 2017, 50, 1666–1671.
17. C. Zhang, P. G. Shao, J. A. van Kan and J. R. van der Maarel, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16651–16656.
18. D. Pastré, L. Hamon, A. Mechulam, I. Sorel, S. Baconnais, P. A. Curmi, E. Le Cam and O. Piétrement, Biomacromolecules, 2007, 8, 3712–3717.
19. R. Hancock, Eur. Biophys. J., 2008, 37, 1059–1064.
20. T. N. Shendruk, M. Bertrand, H. W. de Haan, J. L. Harden and G. W. Slater, Biophys. J., 2015, 108, 810–820.
21. H. Kang, P. A. Pincus, C. Hyeon and D. Thirumalai, Phys. Rev. Lett., 2015, 114, 068303.
22. H. Kang, N. M. Toan, C. Hyeon and D. Thirumalai, J. Am. Chem. Soc., 2015, 137, 10970–10978.
23. A. Chen and N. Zhao, Phys. Chem. Chem. Phys., 2019, 21, 12335–12345.
24. J. Kim, C. Jeon, H. Jeong, Y. Jung and B.-Y. Ha, Soft Matter, 2015, 11, 1877–1888.
25. C.-Y. Shew and K. Yoshikawa, J. Phys.: Condens. Matter, 2015, 27, 064118.
26. J. Shin, A. G. Cherstvy and R. Metzler, New J. Phys., 2014, 16, 053047.
27. A. D. Silverman, A. S. Karim and M. C. Jewett, Nat. Rev. Genet., 2019, 1–20.
28. M. M. Hansen, L. H. Meijer, E. Spruijt, R. J. Maas, M. V. Rosquelles, J. Groen, H. A. Heus and W. T. Huck, Nat. Nanotechnol., 2016, 11, 191.
29. S. E. Norred, P. M. Caveney, G. Chauhan, L. K. Collier, C. P. Collier, S. M. Abel and M. L. Simpson, ACS Synth. Biol., 2018, 7, 1251–1258.
30. S. E. Norred, R. M. Dabbs, G. Chauhan, P. M. Caveney, C. P. Collier, S. M. Abel and M. L. Simpson, bioRxiv, 2018, 445544.
31. N. Biswas, M. Ichikawa, A. Datta, Y. T. Sato, M. Yanagisawa and K. Yoshikawa, Chem. Phys. Lett., 2012, 539, 157–162.
32. R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Fluid Mechanics, Wiley, 1987, vol. 1.
33. J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247.
34. W. A. Steele, The interaction of gases with solid surfaces, Pergamon, 1974, vol. 3.
35. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, Sandia National Labs., Albuquerque, NM (United States) technical report, 1993.
36. S. Plimpton, A. Thompson, P. Crozier and A. Kohlmeyer, http://lammps.sandia.gov, 2011.
37. A. Stukowski, Model. Simul. Mater. Sci. Eng., 2009, 18, 015012.
38. G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345–3362.
39. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339–1350.
40. A. Grossfield, “WHAM: an implementation of the weighted histogram analysis method”, http://membrane.urmc.rochester.edu/content/wham. Accessed July, 2020.
41. D. Trzesniak, A.-P. E. Kunz and W. F. van Gunsteren, ChemPhysChem, 2007, 8, 162–169.
42. H. Arkın and W. Janke, J. Chem. Phys., 2013, 138, 054904.
43. B. Li and S. M. Abel, Soft Matter, 2018, 14, 185–193.
44. A. Narros, A. J. Moreno and C. N. Likos, Soft Matter, 2010, 6, 2435–2441.
45. I. Chubak, E. Locatelli and C. N. Likos, Mol. Phys., 2018, 116, 2911–2926.
46. W. K. Lim and A. R. Denton, J. Chem. Phys., 2014, 141, 114909.
47. D. Yang, J. Männik, S. T. Retterer and J. Männik, Mol. Microbiol., 2020, 113, 1022–1037.
48. L. M. Dominak and C. D. Keating, Langmuir, 2008, 24, 13565–13571.
49. A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58.
50. A. Tsuji and K. Yoshikawa, J. Am. Chem. Soc., 2010, 132, 12464–12471.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01847c

---