Nanoscale mapping of wavelength-selective photovoltaic responses in H- and J-aggregates of azo dye-based solar cell films†
Shashank
Shekhar
 ,
Inkyoung
Park
,
Jeongsu
Kim
,
Myungjae
Yang
,
Duckhyung
Cho
and
Seunghun
Hong
*
,
Inkyoung
Park
,
Jeongsu
Kim
,
Myungjae
Yang
,
Duckhyung
Cho
and
Seunghun
Hong
*
Department of Physics and Astronomy, Institute of Applied Physics, Seoul National University, Seoul, 08826, Korea. E-mail: seunghun@snu.ac.kr
First published on 25th November 2020
Abstract
In the present study, nanoscale wavelength-selective photovoltaic activities in H- and J-aggregates of azo dye-based solar cell films were mapped by wavelength-dependent photoconductive noise microscopy. In this strategy, the local conductivities and charge traps in dye films were mapped by a conducting probe scanning the surface while illuminating the lights with selected wavelengths. We observed the formation of localized domains exhibiting wavelength-dependent photoconductivities. The individual domains could be identified as H- and J-aggregates, which showed dominant photoexcitations at wavelengths of 600 and 450 nm, respectively. Notably, the short-circuit currents Isc and photoconductivities ΔσPC of the film showed power-law dependencies with trap densities under illuminated conditions (NT_L) and the trap density change by the illumination (ΔNT), respectively, like ΔσPC ∝ |ΔNT|1/2 and Isc ∝ NT_L−3/4 for each wavelength illumination. These results revealed the carrier recombination process in cooperation with the traps which could be a major factor determining the performance of solar cells. Significantly, the J-aggregates showed lower trap densities than those of the H-aggregates, resulting in superior solar cell characteristics of the J-aggregates, such as a higher Isc and larger open circuit voltages. Since our method allows mapping the nanoscale photovoltaic activities of solar cell film aggregates, it can be a powerful tool for both basic research and in the application of photoelectronic devices.
1. Introduction
Dye-based solar cells can be a promising source of clean energy due to their high performance, easy processability and low cost.1–11 The outstanding characteristics of dyes, such as their high absorption coefficients, high luminescence efficiencies, wide range of absorption bands, and efficient generation of photocarriers in the solar spectra at low intensities, make them suitable for light-harvesting materials.3–7 In particular, metal-free azo dyes, such as methyl red (MR), have unique optoelectronic properties originating from their delocalized photoexcited carriers from a lone pair of electrons existing in them, and, thus, they have recently attracted significant interest for use in solar cell devices.3,12–15On the other hand, dye molecules usually form various aggregates in thin films due to π–π interactions, which may affect the structural and spectral properties of the films as well as the performance of dye-based photovoltaic devices.3,16–19 Previously, extensive efforts have been devoted to investigating the effects of aggregates on the optoelectronic properties of dye films using various spectroscopic and microscopic techniques.20,21 However, these studies usually showed only accumulative effects of all the aggregates on the film without elaborating the nanoscale effects of individual ones. In this regard, the mapping of localized aggregates in a film and understanding their photophysical properties in an operational solar cell device still remain challenging, though those are essential for the further improvement of dye-based optoelectronic device performances.
Herein, we report the nanoscale mapping of wavelength-dependent photoresponses in H- and J-aggregates of azo dye-based solar cell films using wavelength-selective photoconductive noise microscopy. In this strategy, we quantitatively mapped the localized variations of conductivities (σ) and electronic trap densities in an azo-dye film by a conducting probe scanning the surface while illuminating with lights of various wavelengths. The results showed localized individual domains exhibiting the wavelength-selective excitations of the carriers, allowing identification of the domains as H- or J-aggregates. Furthermore, we obtained wavelength-dependent maps of the short-circuit currents (Isc), photocurrents, and charge-trap densities in the aggregates of the dye film. Interestingly, the short-circuit currents Isc of the dye-based solar cells and photoconductivities ΔσPC of the dye film exhibited power-law dependencies with trap densities under illuminated conditions (NT_L) and trap density change by illumination (ΔNT), respectively, in both aggregates, like Isc ∝ NT_L−3/4 and ΔσPC ∝ |ΔNT|1/2. The results were attributed to the carrier recombination process enhanced by charge traps in the film, revealing that the charge traps are one of the major factors determining the performances of dye-based solar cell devices. Importantly, J-aggregates exhibited a lower trap density than H-aggregates, and, thus, they had higher short-circuit currents as well as larger open circuit voltages, indicating that the J-aggregates are more favourable structures for solar cell application. Our method allowed mapping the nanoscale optoelectronic properties of solar cell films in a wavelength-selective manner and provided an important guideline for improving the performance of solar cell devices based on films. Thus, it can be a powerful tool for both basic research and for the applications of optoelectronic devices based on dye molecules.
2 Results and discussion
2.1 Wavelength-selective photoconductive noise microscopy set-up in dye-based solar cells
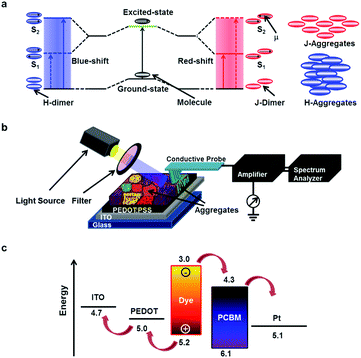
Fig. 1a shows an optical excitation diagram of different dye aggregates. When two molecules come close, they form a dimer to minimize their energy, and the overlap of the electronic wave functions results in a splitting of the energy levels, as shown in the diagram.21 It was previously reported that two dye molecules could align in a parallel (face-to-face stacking) or a head-to-tail arrangement (end-to-end stacking).21 A parallel or a head-to-tail stacking of two molecules is known as a H- or a J-dimer, which leads to the formation of H- or J-aggregates, respectively (Fig. 1a). The formation of H-aggregates may require a high density of molecules, because the effective overlaps between molecules are much larger in H-aggregates than those in J-aggregates. When light of a suitable wavelength is illuminated, electrons in the dye molecules can be excited to the higher energy levels of antibonding orbitals. The parallel transition dipoles (face-to-face) of H-aggregates produce a blue-shift in the transition spectrum as formulated by the molecular exciton theory.21 Conversely, the staggered (head-to-tail) transition dipoles of J-aggregates produce a red-shift in the transition spectrum. MR dye films have shown a rather large cluster size by molecular assembly due to strong intermolecular π–π interactions and substrate-MR interactions, resulting in a well-packed formation of stable J- and H-aggregates with different photo-excitation and noise properties.12,22–25 Due to being such stable aggregates with versatile properties, MR dye films can be an ideal sample for researchers to use to develop new analysis tools for mapping the wavelength-dependent photophysical properties of such microstructures in solar cell films and their effects on solar cell efficiency.Fig. 1b is a schematic illustration showing the experimental set-up for the mapping of wavelength-selective local photocurrents and charge-trap activities on the dye-based solar cell film. Details on the solar cell fabrication and photoconductive noise microscopy measurements are described in the Experimental and method section. In brief, a MR-phenyl-C61-butyric acid methyl ester (PCBM) film of ∼80 nm thickness was prepared on poly(3,4-ethylenedioxythiophene):polystyrene sulfonate (PEDOT:PSS)-coated indium tin oxide (ITO) glass via a solution process strategy.26–28 The dye-PCBM layer acted as a photoactive material, while the PEDOT:PSS-coated ITO layer worked as a hole-collecting layer.29 For the photoconductive noise microscopy measurements, a Pt-based conducting probe installed on a conducting atomic force microscopy system (AFM) (XE-70, Park Systems) made direct contact with the dye-PCBM film and was used to measure the electrical currents through it. Further, we integrated a wavelength controllable light source with the AFM set-up to enable wavelength-selective photoconductive noise measurements.28,30–32 Here, the local currents and current noises through the probe were measured while the film was illuminated by lights with different wavelengths. The measured current noises were analyzed by a home-built spectrum analyzer, a band pass filter, and a RMS-to-DC converter.33,34 By scanning the probe over the film, we were able to obtain maps of the local currents and electrical noises of the same area, simultaneously. The measured maps were analyzed to obtain the distribution maps of the conductivity and the charge-trap density. Here, photoconductive noise microscopy was used to provide a comprehensive picture of photo-induced charge transports and charge-trap activities in solar cell films.
Fig. 1c is an energy-level diagram of the MR-PCBM bulk heterojunction solar cell. The energy diagram shows the conduction band minimum (CBM) and the valence band maximum (VBM) of MR and PCBM along with the Fermi levels of the Pt tip and the ITO electrode. Upon light illumination, the electrons of the MR dye, a strong absorber of the visible spectrum, are excited from the valance band to the conduction band through the transitions from bonding orbitals to anti-bonding orbitals such as n–π* and π–π*,12,17 leaving holes in the valence band. The excited electrons at the CBM of MR (∼−3 eV) can be easily transferred to the CBM of PCBM, which is at a lower energy level (∼−4.3 eV). The electrons are finally collected at the metal electrode. The holes at the VBM of the MR dye (∼5 eV) are favourably collected by the PEDOT:PSS-coated ITO due to the lower Fermi level of the ITO (∼4.7 eV) as compared to the VBM of MR.
2.2 Optical characterization of methyl red dye and dye-based solar cell films
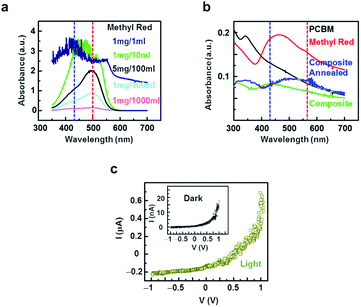
Fig. 2a shows UV-visible absorption spectra of the MR dye in a dichlorobenzene (DCB) solution at various MR concentrations. Here, MR (10 mg) was first dissolved in DCB (10 ml) by sonication for 90 minutes. Then, the UV-visible spectra were measured in the 350–700 nm range by an Agilent 8430 spectrophotometer. The UV-visible spectra of the dilute solutions (∼1 μg l−1) exhibited an absorption maximum peak (λmax) at ∼490 nm, which was close to the λmax (∼484 nm) of an individual strand of the MR dye.35 As the concentration of the MR was increased, another absorption peak with a relatively low intensity appeared at the wavelength of ∼430 nm. However, at high concentrations (∼1 mg ml−1), the peak at the 430 nm became prominent and blue-shifted. In previous reports, a very dilute solution or an individual strand of MR dye showed a peak near ∼500 nm, while the absorbance peak near ∼430 nm was reported to become prominent with a high concentration solution, possibly due to the formation of H-aggregates, which is consistent with our results.35–39 It should also be noted that the peak at a rather long wavelength of ∼490 nm showed the tendency of a red-shift, whereas the one with a rather shorter wavelength of ∼430 nm showed a blue-shift as the concentration of the MR was increased in the solution from ∼1 μg l−1 to ∼1 mg ml−1. Overall, the absorption spectra and peaks of the dye were strongly dependent on the concentration of the dye in the solution. The blue- and red-shifts in the respective peaks could be attributed to the formation of aggregates in the concentrated solution.1,17,19–21,35 When small molecules come close to each other, they interact through transition dipoles and form aggregates, resulting in an overlap of the molecular orbitals and electronic wave functions.20,21 These lead to two characteristic peaks in the absorption spectra of the dye molecules. One peak gets blue-shifted (hypsochromic), whereas another peak is red-shifted (bathochromic) when compared with the absorption peak of a monomer molecule. The molecular aggregates, depending on their side-wise or head-to-tail alignments, are commonly denoted as H-aggregates (or hypsochromic-aggregates) or J-aggregates (or bathochromic-aggregates), causing hypsochromic or bathochromic absorption peaks, respectively. It is worth mentioning that previous works reported the emission spectra of MR dye exhibited mirror-image characteristics of those of the absorption spectra.37,40,41 The emission spectra were reported to have two peaks at 450 nm and 600 nm, and the dominant peak showed a red-shift at an increased dye concentration, which is somewhat consistent with our optical measurement data.37,40,41 Our results showed that dye films include H- and J-aggregates, and that inter-molecular interactions play a decisive role in the photophysical properties of the film, as reported previously.21Fig. 2b shows the UV-visible absorption spectra of the thin films of MR, PCBM and MR-PCBM blends spun on glass substrates, which were plotted with red, black and green colours, respectively. The details of the film preparation method are described in the Experimental and method section. The UV-visible spectra were measured in the range of 300–700 nm by using an Agilent 8453 spectrophotometer. The MR (graph plotted with the red line) showed two absorption peaks at ∼450 and ∼550 nm, which were similar to the absorption peaks of the concentrated solution of MR shown in Fig. 2a. This implies that J- and H-aggregates were also formed in the solid state. Notably, the intensity of the absorption peak of the H-aggregate was higher than that of the J-aggregate, indicating the large fraction of H-aggregates. The PCBM film (graph plotted with the black coloured lines) showed an absorption peak in the UV region (∼350 nm) as reported previously.32 We could not observe the formation of any aggregates in the PCBM film spun from the 1 mg ml−1 solution in DCB, presumably due to the non-linear structure of the PCBM and a lack of π–π interactions as reported previously.42 The spun film from the mixture of dye-PCBM exhibited an intense peak at ∼450 nm, predominantly due to the formation of H-aggregates.35,41 The intensity of the peak due to J-aggregates was negligibly small, implicating a low fraction of J-aggregates in the film. However, after annealing the sample at 130 °C for 90 min, we observed the recovery of a bathochromic peak (graph plotted with the blue line) with a broad range of absorption in the visible regime. This implied that the annealing process enabled the rearrangement of molecules in the thin film, presumably due to the evaporation of the trapped solvent, leading to the reemergence of J-aggregates. These results indicate that the microstructures of our dye films could be tuned externally by providing physical or chemical treatment to the film.1,12
Fig. 2c shows the current–voltage (I–V) characteristics of a solar cell film measured with (olive coloured line) or without (inset graph) the illumination of a white light (intensity ∼100 mW cm−2). Here, the currents were measured through the MR-PCBM film between the Pt electrode and an electrically-grounded PEDOT:PSS-coated ITO substrate. In dark conditions, a typical asymmetric I–V curve of a junction behaviour was observed with a very low reverse bias current.28 When the film was illuminated with white light, the current increased significantly as compared to the current in the dark condition, implying the generation of photoexcited carriers. In addition, even at a zero external bias, we observed a nearly 100 nA short-circuit current, showing the proper operation as a solar cell. The open circuit voltage (VOC) measured at the zero current value was close to 500 mV. Presumably, the large band gap of the MR makes the dye suitable for solar cell applications with a large open circuit voltage.43
2.3 Mapping effects of charge-traps on the photoconductivity in aggregates of dye-based solar cell films in resonance and off-resonance cases
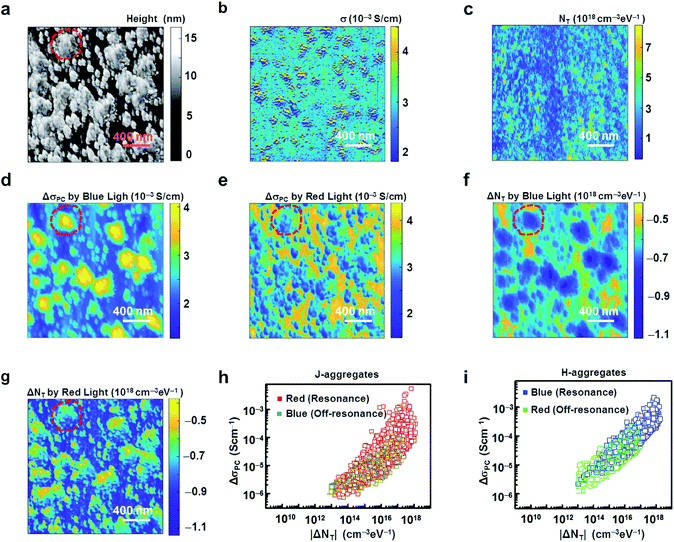
Fig. 3a shows an AFM topography image of an MR-PCBM film on the PEDOT:PSS-coated ITO substrate in a solar cell configuration. Here, 1 μN of contact force was maintained to provide a good contact between the probe and the film surface during imaging. The topography image shows a height variation in the film due to the formation of domains with ∼500 nm sizes, which is similar to previous results.18 We could repeatedly image the surface without any changes in the topography, indicating the stable formation of our films.15–17A local conductivity map measured in the dark condition in the same region as in Fig. 3a is shown in Fig. 3b. Here, we first measured a current map at a bias voltage of 0.1 V (Fig. S1, ESI†) and then used it to calculate the conductivity (σ) map using the method reported previously.26,27 The details of the calculation method are described in the Experimental and method sections. In brief, we assumed that charge carriers flowed mainly in a vertical direction from the ITO electrode to the conducting probe through the dye film, and the parasitic current in the lateral direction inside the film was limited due to the low conductivity of the dye film. In this case, the conductivity can be written as: σ = Id/(VA), where I, d, V and A represent the measured current, the thickness of the film, the applied voltage and the contact area of a conducting probe, respectively. The estimated local conductivity map indicated a stable electrical contact between the tip and the film regardless of the topological roughness of the dye film (MR-PCBM). The film showed a conductivity up to 10−3 S cm−1, which was similar to the previously values observed in PCBM films.44 Notably, we did not observe any correlation between the topography and the conductivity maps, indicating that the conductivity variation came from the electronic properties of the aggregates rather than the surface roughness.
Fig. 3c shows a distribution map of the charge-trap density under dark conditions (NT) obtained from the noise and current maps (Fig. S1 and S2, ESI†), which were measured simultaneously in the same region as in Fig. 3a. The details of the NT calculations are described in the Experimental and method section.26,27 Note that the NT showed a rather large value with some random variations as large as 1018 cm−3 eV−1.26,27 Presumably, in organic materials such as dyes, electrical noises can be generated by various localized traps, such as defects, impurities, entanglements, disorders and structural inhomogeneities, resulting in a high NT.26–28,45,46
Fig. 3d and e exhibit the photoconductivity maps in the same region as in Fig. 3a while illuminated by lights with the wavelengths of 450 and 600 nm, respectively. Here, we measured the current map at 0.1 V with a specific wavelength light filtered from the white light of the power of 100 mW cm−2. The measured current map was subtracted by the corresponding current map obtained in the dark condition to obtain the photocurrent map, from which we estimated the photoconductivity map as explained in the description of Fig. 3b. Note that the domains with relatively high heights (protruded regions marked by red dotted circles in the topography image Fig. 3a) exhibited high photoconductivities when illuminated with blue light at the wavelength of 450 nm. To the contrary, the complementary domains with relatively low heights showed high photoconductivities with the red light of the wavelength 600 nm. On the basis of the correlation between the topography and photoconductivity maps, we could envisage the formation of different kinds of aggregates with different resonance absorption wavelengths at the sub-micron level. More specifically, the domains showing high photoconductivities at an excitation wavelength of 450 nm or 600 nm could be attributed to the regions with H- or J-aggregates, respectively, as their carriers could be easily excited by the resonance wavelength.1,17 These results are in accordance with the absorption spectra (Fig. 2a and b), where we observed two different absorption peaks corresponding to H- and J-aggregates.35–37
Fig. 3f and g show the mapping of the charge-trap density change ΔNT measured in the same region as in Fig. 3a when illuminated with light of wavelengths 450 (blue) and 600 (red) nm, respectively. In the case of the blue light illumination to the dye film (Fig. 3f), the protruded regions (H-aggregates) showed a relatively large decrease in the trap density. Similarly, the trap density decrement was large in the lower height regions (J-aggregates) when the film was illuminated with the red light (Fig. 3g). Significantly, there was an overall decrease in the trap density by ∼5 × 1017 cm−3 eV−1 when the dye film was illuminated with blue or red light. These results show that the resonance absorption of light induced a larger decrease in the trap density than from the non-resonance absorption in both the H- and J-aggregates. Presumably, the excess resonant photocarriers could have filled the charge-traps, resulting in an overall decrease in the trap density.47
Fig. 3h and i are scattered plots showing the photoconductivity dependence on the trap density change by the illumination of light with the wavelengths of 450 and 600 nm, in J- and H-aggregates, respectively. The red (green) and dark yellow (blue) coloured plots in Fig. 3h and i showed the dependence for the red and blue lights, respectively, in the J- (H-)aggregates. Each data point showed a pair of photoconductivity and trap density changes by illumination at the same location in the maps of the dye film. Note that, regardless of the resonance and off-resonance cases in the J- and H-aggregates, the photoconductivity was found to be directly proportional to the 0.5 power of the modulus of the trap density change by the illumination of light like ΔσPC ∝ |ΔNT|1/2. Plausibly, the dependence can be explained by a trap-assisted recombination process model as reported previously.28,48 Briefly, the change in conductivity ΔσPC can be mathematically expressed as,
| ΔσPC = eμLnL − eμn = e(μ + Δμ)(n + Δn) − eμn = eμΔn + enΔμ +eΔμΔn, | (1) |
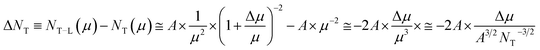 | (2) |
Thus, Δμ dependence on NT can be approximated as 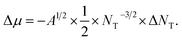 Substituting μ and Δμ values in eqn (1), we can obtain
Substituting μ and Δμ values in eqn (1), we can obtain
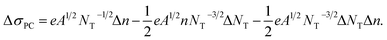 | (3) |
Let us assume that n′ and p′ are electron and hole densities in the material, respectively. Also NT is the total trap density, out of which NTp and NTe are traps occupied by holes and electrons, respectively. Then, the charge neutrality requires52,53
| (n′ − p′) + (NTe − NTp) = 0. | (4) |
Upon illumination, we have a change in the respective quantities by Δn′, Δp′, ΔNTe and ΔNTp.
| {(n′ + Δn′) − (p′ − Δp′)} + {(NTe + ΔNTe) − (NTp − ΔNTp)} = 0 | (5) |
| Δn′ + Δp′ + ΔNTe + ΔNTp = 0, or Δn + ΔNT = 0, Δn = −ΔNT, | (6) |
 | (7) |
Experimentally, we observed a dramatic reduction in the trap density under illumination. A plausible explanation for this can be the filling of traps by photocarriers. Analytically, a change in the trap density causes a shift in the Fermi level by the photocarriers.52,53 Thus, at a higher trap density location, screening in the trap density would be rather large due to the filling of the traps by the photocarriers, resulting in a larger trap density change at larger NT values.52,53 Therefore, |NT| ∝ |ΔNT|. Also, we observed a similar behaviour (ESI Fig. S3†). Thus, |NT| in eqn (7) can be substituted by C|ΔNT|. Then, eqn (7) can be modified as
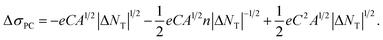 | (8) |
On average, ΔNT (1014 to 1018 cm−3 eV−1) is much larger than the initial carrier density n under dark conditions (≪1012 cm−3 eV−1) in a dye,54 which holds in our cases. Therefore, we can neglect the 2nd term in eqn (8), and (9) can be further simplified as
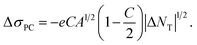 | (9) |
So,
| ΔσPC = D|ΔNT|1/2 | (10) |
2.4 Mapping of resonant and off-resonant short-circuit currents in H- and J-aggregates
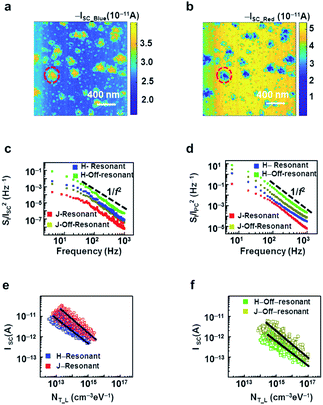
In our experimental set-up, the dye films with an underlying ITO electrode and a conducting AFM probe formed a solar cell structure. Thus, we could map the short-circuit currents on the different regions of the dye film to estimate the efficiency of the regions as a solar cell component. Fig. 4a and b are short-circuit current maps of the dye solar cell film while illuminated with blue (450 nm) and red (600 nm) light, respectively. In this work, we mapped the wavelength-dependent photocurrents with a zero bias voltage while illuminating with specific wavelength lights. The average levels of the short-circuit current were ∼2.5 and 3.5 pA (current density ∼1 mA cm−2) under blue and red lights, respectively. These currents are typical values for a MR dye-based heterojunction solar cell.15 Note that the domains showing a larger short-circuit currents with blue light (marked with a red dotted circle) exhibited smaller currents with red light and vice versa. These results indicated that the domains with high short-circuit currents upon illumination with blue or red light could be attributed to the formation of H- or J-aggregates, respectively. In the resonance cases, both types of domains showed currents in the order of ∼10 pA, whereas the off-resonant currents were less than ∼1 pA. Presumably, in a resonance absorption case, a high absorption cross-section and an efficient inter-molecular transfer of energy between the molecules allow for the efficient conversion of photons into photocurrents.26,55 Notably, with both on- and off-resonance cases, the short-circuit currents in the J-aggregates were higher than those in the H-aggregates. Previous works showed that J-aggregates have better efficiencies in converting photons to currents in comparison to H-aggregates.20 The strong vibronic interactions in H-aggregates due to the larger overlaps of the molecules can lead to a faster decay of the excited carriers, making J-aggregates better for short-circuit current generation. Importantly, our method allowed us to map the different efficiencies of the aggregates in the dye film, providing important insights into the photoconductive properties in aggregates.Fig. 4c shows the scattered plots for the normalized noise power spectral density (PSD) SI/I2 spectra of the short-circuit currents as a function of the frequency at a zero bias voltage. The SI/I2 was measured in J-aggregates (H-aggregates) of the dye film in resonance or off-resonance cases plotted with red or dark-yellow (blue or green) symbols, respectively. Here, the probe made stationary contact at a specific position on the dye solar cell film, and the electrical currents were measured and analyzed using a fast Fourier transform (FFT) signal analyzer (SR770, Stanford Research Systems). All the measurements were performed in the presence of blue or red light. The slopes of all the curves of the H- and J-aggregates (Fig. 4c) were close to ∼−2, indicating that noise PSD followed a 1/f2 behaviour. Previous works showed that the noise PSD of the traps of a single relaxation time can be expressed by a Lorentzian function like SI/I2 ∝ 1/[1 + (2πfτ)2], and the dependence approximates to 1/f2 at sufficiently high frequencies.14
Plausibly, in our film, the intermolecular electron–phonon (e–p) coupling in the aggregate of dye molecules could create the dominant trap states with an identical potential depth and relaxation time, resulting in a 1/f2 dependence.56,57 It also should be noted that the H-aggregates showed higher noise PSD values than the J-aggregates. Presumably, the e–p coupling strength varied from one type of aggregates to another due to the different intermolecular distances, resulting in different noise levels in the various aggregates, as reported previously.56,57 In the H-aggregates, the high packing densities of the molecules could produce strong e–p coupling due to the formation of a large number of junction potentials (traps), causing a high noise level.57,58 Interestingly, the SI/I2 was higher in the off-resonance cases in comparison to the resonance cases of the J- and H-aggregates (Fig. 4c), which could be due to the strong e–p coupling in the off-resonance cases. In off-resonance cases, there can be a spatial variation in the absorption cross-section of the dye and a large absorption linewidth of the light, which can lead to the photocarrier inhomogeneity and an enhanced e–p coupling, resulting in a large number of trapping potentials.55,58
Fig. 4d shows the SI/I2 plot, the measure of the photocurrent fluctuations with an applied bias of 0.1 V as a function of the frequency. The experimental procedure was similar as that described in Fig. 4c. The SI/I2 was measured in the J- (H-)aggregates in the resonance or off-resonance cases of the dye film at an applied bias of 0.1 V, plotted with red or dark-yellow (blue or green) symbols, respectively. Here, we also observed 1/f2 noise behaviours in different aggregates for both the resonance and off-resonance conditions. Notably, the resonance cases showed two orders of magnitude lower noise in comparison to the off-resonance cases. Moreover, the photocurrent noises were much higher (two orders) than the corresponding short-circuit noises. Presumably, an external bias could excite and inject additional carriers in the aggregates, creating a high lattice distortion and significantly increased e–p coupling, which would result in the enhanced electrical noises.59
Fig. 4e and f are scatter plots showing the dependence of the short-circuit current on the trap density in the resonance and off-resonance cases, respectively. The red and blue coloured symbols in Fig. 4e represent the resonance cases for the J- and H-aggregates, respectively. Similarly, the dark-yellow and green coloured symbols in Fig. 4f represent the off-resonance cases for the J- and H-aggregates, respectively. Each data point represents the short-circuit current and corresponding trap density values of a single type of aggregate at a specific position. The results show that the short-circuit currents Isc were inversely proportional to ∼3/4 power of the trap densities under the illuminated conditions NT_L in both type of aggregates, like Isc ∼ NT_L−0.75. This behaviour could also be explained by the trap-assisted recombination process. In the short-circuit condition with light, the photocarriers generated in a solar cell should diffuse to the electrodes to contribute to the current. Here, the Isc in the solar cell should be proportional to the multiplication of the generation rate of the photocarriers (G) and the photocarrier collection length (Lc) of the solar cell as,60
| Isc ∝ (G × Lc) | (11) |
In our case, G is proportional to the carrier density under illumination nL, which is inversely proportional to NT_L0.5, as shown in the previous report.28 On the other hand, Lc is approximately linearly proportional to the carrier diffusion length (LD) of the photoactive layer in the solar cell.28,61LD is known to be proportional to the square root of the carrier lifetime (τ) as,62
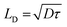 | (12) |
3 Experimental and methods
3.1 Materials and device fabrication
The methyl red dye (2-(4-dimethylaminophenylazo)benzoic acid, 4-dimethylaminoazobenzene-2-carboxylic acid) (Product ID 250198, Mw ∼ 270), PCBM (Product ID 684449), and PEDOT:PSS (Product ID 655201) were purchased from Sigma-Aldrich. The low sheet resistance (∼8 Ω □−1) ITO glass was also obtained from Sigma-Aldrich (Product ID 703192). Here, 10 mg of each of the methyl red and PCBM were separately dissolved in 10 ml of 1,2 dichlorobenzene. They were dissolved by sonication at 60 °C for 90 min. The prepared solutions were then mixed together and sonicated for another 1 h to obtain the blend in a solution form. The blend solution was spin coated on the PEDOT:PSS-coated ITO substrate at 4000 rpm for 60 s. The dye film was heated at 130 °C for 90 min.3.2 Wavelength-selective mapping of the photocurrents and electrical noises
A Pt-based conducting probe (25Pt300B, Park Systems) installed on an AFM instrument (XE-70, Park Systems) approached and contacted the surface of the dye solar cell film as described in Fig. 1b. Here, the contact force of the AFM probe to the film surface was maintained as 1 μN via the contact force feedback loop of the AFM system. A DC bias voltage was applied between the AFM probe and the PEDOT:PSS on the ITO substrate using a function generator (DS345, Stanford Research Systems), and the current signals through the probe were measured and amplified by a low-noise preamplifier (SR570, Stanford Research Systems) connected to the probe. The amplified current signals were filtered by a band-pass filter included in the preamplifier to obtain the electrical noise signal, which was the fluctuating component of the current signals. The RMS power of the noise signal could be obtained using a RMS-to-DC converter built using an AD737 chip (purchased from Analog Devices). Note that the obtained noise power is the integrated value of the noise PSDs over the frequency range of the pass band of the used band-pass filter. Finally, we obtained the noise PSD value at the central frequency of the pass band by dividing the measured noise power by the bandwidth of the band-pass filter. By scanning the AFM probe on the dye film surface, we could obtain the current and noise PSD maps simultaneously. Further, we measured a current map while illuminating a filtered (wavelength-selected) light using a light source (LS-F100HS) and compared the map with that obtained in a dark condition to estimate the photocurrent map. The optical filters (supplied by Edmund Optics, Product ID 88-700) of bandwidth 25 nm and optical density ∼4 (transmitted intensity attenuated by 104) were used for the wavelength selection.3.3 Calculation of the conductivities of the dye solar cell films
Since the conductivity of the dye solar cell film was rather low, we can assume that the charge carriers mainly flowed in a vertical direction from an underlying ITO substrate to a conducting probe through the film layer, and the parasitic currents in a lateral direction inside the layer were limited. Thus, we calculated the conductivity of the dye film assuming vertical charge transport. In this case, the conductivity σ can be calculated using σ = Id/(VA), where I, d, V and A represent the measured current, the thickness of the film, the applied voltage, and the contact area of the conducting probe, respectively. In our experiment, the thickness of the film was ∼80 nm. The contact area A of our conducting probe was estimated as ∼2000 nm2 from the effective contact radius.343.4 Calculation of the charge-trap density in dye solar cell films
In this measurement, electrical currents flowed vertically between a conducting AFM tip and an underlying ITO film. Thus, the majority of electrical noises should be generated by the charge-traps inside the small volume of the dye film between the ITO electrode and the conducting AFM tip. Then, the PSD of the mean-square fluctuation in the number of occupied charge-traps in the small segment of the dye film within the contact area A of the tip can be written as63,64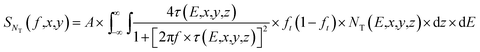 | (13) |
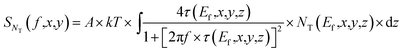 | (14) |
Assuming that charge-traps are distributed uniformly over the z direction, then eqn (14) can be approximated as
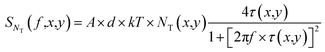 | (15) |
The noise PSD ΔSI can be written as
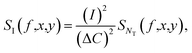 | (16) |
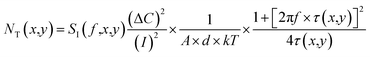 | (17) |
The average trapping time τ and the carrier density in the dye were reported as ∼10−5 s and ∼1012 cm−3 eV−1, respectively.54,65
3.5 Measurement of the UV-visible absorption spectra
The UV-visible absorption spectra of our films were measured using an Agilent 8453 spectrophotometer, where deuterium-discharge and tungsten filament lamps were used to get the UV and visible ranges of the lights, respectively. For the measurement, MR solution with a known concentration was poured inside a quartz cuvette, and the absorbance spectra were recorded in the transmittance mode. Here, the incident or reference light intensity (P0) through a solvent filled cuvette was first measured. Then, the intensity P of the light through the dye solution was measured. The transmittance (T) was measured as the ratio of the output intensity like P/P0. From the Beer–Lambert Law, the absorbance intensity A is estimated as −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T or log(P0/P).66 For a dye solution with a high concentration, the transmittance became very small, and the noise level of the photodetector began to affect the measured absorption signals. Thus, we observed a rather large noise level in the absorbance spectra, determining the detection limit of our absorption measurements.
T or log(P0/P).66 For a dye solution with a high concentration, the transmittance became very small, and the noise level of the photodetector began to affect the measured absorption signals. Thus, we observed a rather large noise level in the absorbance spectra, determining the detection limit of our absorption measurements.
4 Conclusions
We successfully performed the nanoscale mapping of the H- and J-aggregates and their photovoltaic activities in a dye solar cell film using wavelength-selective photoconductive noise microscopy. The H- and J-aggregates could be identified in photoconductive mapping by their characteristic excitations by selective-wavelength illumination. Interestingly, the H- or J-aggregates showed an enhanced formation of photocarriers at 450 nm or 600 nm wavelength, respectively, resulting in high photoconductivities and low charge-traps. Furthermore, we observed that the photoconductivity significantly depended on the charge-trap density change by the illumination of the aggregates in the film, and they showed a power-law relationship like ΔσPC ∝ |ΔNT|1/2 for each individual wavelength illumination. Further, we observed that the wavelength-dependent short-circuit current of the dye solar cell was inversely proportional to 3/4 the power of the trap density under illuminated conditions, which revealed that the photocarriers and their recombination by charge-traps can be the major factor governing the performance of dye solar cell films. Importantly, J-aggregates showed higher short-circuit currents and larger open circuit voltages due to the lower levels of trap density, making J-aggregates favourable structures for solar cell applications. Since our method allows mapping the nanoscale wavelength-dependent photovoltaic activities in various microstructures of a solar cell film, it can be a powerful tool for both basic research and in the applications of photoelectronic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by BioNano Health-Guard Research Center funded by the Ministry of Science, ICT (MSIT) of Korea as Global Frontier Project (No. 2013M3A6B2078961). S. H. also acknowledges the support from National Research Foundation Korea grant (No. 2020R1A2B5B02002152) and the European Research Council under the European Union's Horizon 2020 Research and Innovation Programme (grant agreement no. 682286).Notes and references
- A. Liess, A. Arjona-Esteban, A. Kudzus, J. Albert, A.-M. Krause, A. Lv, M. Stolte, K. Meerholz and F. Wurthner, Adv. Funct. Mater., 2018, 28, 201805058 Search PubMed.
- L. Gao, C. Ge, W. Li, C. Jia, K. Zeng, W. Pan, H. Wu, Y. Zhao, Y. He, J. He, Z. Zhao, G. Niu, X. Guo, F. P. G. De Arquer, E. H. Sargent and J. Tang, Adv. Funct. Mater., 2017, 27, 1702360 CrossRef.
- L. Zhang and J. M. Cole, J. Mater. Chem. A, 2017, 5, 19541 RSC.
- M. Freitag, J. Teucher, Y. Saigili, X. Zhang, F. Giordano, P. Liska, J. Hua, S. M. Zakeeruddin, J.-E. Moser, M. Gratzel and A. Hagfeldt, Nat. Photonics, 2017, 11, 372 CrossRef CAS.
- B. E. Hardin, E. T. Hoke, P. B. Armstrong, J.-H. Yum, P. Comte, T. Torres, J. M. J. Frechet, M. K. Nazeeruddin, M. Gratzel and M. D. McGehee, Nat. Photonics, 2009, 3, 406 CrossRef CAS.
- O. Brain and M. Gratzel, Nature, 1991, 353, 6346 Search PubMed.
- H.-C. Su, Y.-Y. Wu, J.-L. Hou, G.-L. Zhang, Q.-Y. Zhu and J. Dai, Chem. Commun., 2016, 54, 4072 RSC.
- L. Zhou, R. Wang, C. Yao, X. Li, C. Wang, X. Zhang, C. Xu, A. Zeng, D. Zhao and F. Zhang, Nat. Commun., 2015, 6, 6938 CrossRef CAS PubMed.
- X. Munoz-Berbel, R. Rodriguez-Rodriguez, N. Vigues, S. Demming, S. Buttgenbach, E. Verpoorte, P. Ortiz and A. Lloobera, Lab Chip, 2013, 13, 4239 RSC.
- J. Kim, H. Yoo, V. A. PhamBa, N. Shin and S. Hong, Sci. Rep., 2018, 8, 11958 CrossRef PubMed.
- K. Yamjala, M. S. Nainar and N. R. Ramisetti, Food Chem., 2016, 192, 813 CrossRef CAS PubMed.
- M. M. Makhlouf and A. El-Denglawey, Jpn. J. Appl. Phys., 2018, 57, 042401 CrossRef.
- E. N. Cho, D. Zhitomirsky, G. G. D. Han, Y. Liu and J. C. Grossman, ACS Appl. Mater. Interfaces, 2017, 9, 8679 CrossRef CAS PubMed.
- D. Cho, M. Yang, N. Shin and S. Hong, Nanotechnol, 2018, 29, 11958 Search PubMed.
- S. Saha and N. B. Manik, Thin Solid Films, 2012, 520, 6274 CrossRef CAS.
- H. Asanuma, K. Shriasuka, T. Takarada, H. Kashida and M. Komiyama, J. Am. Chem. Soc., 2003, 125, 2217 CrossRef CAS PubMed.
- E. Rivera, M. d. P. Carreon-Castro, I. Buendia and G. Cedillo, Dyes Pigm., 2006, 68, 217 CrossRef CAS.
- R. C. Advincula, E. Fells and M.-k. Park, Chem. Mater., 2001, 13, 2870 CrossRef CAS.
- K. K. Karukstis, L. A. Perelman and W. K. Wong, Langmuir, 2002, 18, 10363 CrossRef CAS.
- M. Mas-Montoya and R. A. J. Janssen, Adv. Funct. Mater., 2017, 27, 1605779 CrossRef.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069 CrossRef CAS.
- R. T. Buwalda, J. M. Jonker and J. B. F. N. Engberts, Langmuir, 1999, 15, 1083 CrossRef CAS.
- L. Zhang, X. Liu, W. Rao and J. Li, Sci. Rep., 2016, 6, 35893 CrossRef CAS PubMed.
- L. Zhang and J. M. Cole, ACS Appl. Mater. Interfaces, 2014, 6, 15760 CrossRef CAS PubMed.
- M. Wubs and J. Knoester, J. Lumin., 1998, 76–77, 359 CrossRef.
- S. Shekhar, D. Cho, D.-g. Cho, M. Yang and S. Hong, Nanotechnol, 2018, 29, 205204 CrossRef PubMed.
- M. Yang, D. Cho, J. Kim, N. Shin, S. Shekhar and S. Hong, Small, 2018, 14, 1800885 CrossRef PubMed.
- D. Cho, T. Hwang, D.-g. Cho, B. Park and S. Hong, Nano Energy, 2018, 43, 29 CrossRef CAS.
- M. D. Irwin, D. B. Buchholz, A. W. Hains, R. P. H. Chang and T. J. Marks, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2783 CrossRef CAS.
- X.-D. Dang, A. B. Tamayo, J. Seo, C. V. Hoven, B. Walker and T.-Q. Nguyen, Adv. Funct. Mater., 2010, 20, 3314 CrossRef CAS.
- D.-C. Coffey, O. G. Reid, D. B. Rodovsky, G. P. Bartholomew, B. Walker and D. S. Ginger, Nano Lett., 2007, 7, 238 CrossRef PubMed.
- J. L. Luria, N. Hoepker, R. Bruce, A. R. Jacobs, C. Groves and J. A. Marohn, ACS Nano, 2012, 11, 9392 CrossRef PubMed.
- M. Engelson, Modern Spectrum Analyzer Theory and Applications, Artech House, 1984 Search PubMed.
- S. Shekhar, D. Cho, H. Lee, D.-g. Cho and S. Hong, Nanoscale, 2016, 8, 835 RSC.
- H. Asanuma, K. Shirasuka, T. Takarada, H. Kasida and M. Komiyama, J. Am. Chem. Soc., 2003, 125, 2217 CrossRef CAS PubMed.
- R. T. Narayan and K. D. Veeranna, J. Appl. Chem., 2014, 76, 762 Search PubMed.
- G. J. Lee, D. Kim and M. Lee, Appl. Opt., 1995, 34, 138 CrossRef CAS PubMed.
- M.-C. Wu, M.-P. Lin, S. W. Chen, P. H. Lee, J.-H. Li and W.-F. Su, RSC Adv., 2014, 4, 10043 RSC.
- M. S. Masoud and H. H. Hammud, Spectrochim. Acta, Part A, 2001, 57, 977 CrossRef.
- C. On, E. K. Tanyi, E. Harrison and M. A. Noginov, Opt. Mater. Express, 2017, 7, 4286 CrossRef CAS.
- J. E. Selwyn and J. I. Steinfeld, J. Phys. Chem., 1972, 76, 762 CrossRef CAS.
- S. Cook, H. Ohkita, Y. Kim, J. J. Benson-Smith, D. D. C. Bradley and J. R. Durrant, Chem. Phys. Lett., 2007, 445, 276 CrossRef CAS.
- O. O. Ogunsolu, J. C. Wang and K. Hanson, Inorg. Chem., 2017, 56, 11168 CrossRef CAS.
- G. Zuo, Z. Li, H. Andersson, H. Abdalla, E. Wang and M. Kemerink, J. Phys. Chem. C, 2017, 121, 7767 CrossRef CAS.
- H. Suzuki and S. Hosino, J. Appl. Phys., 1996, 79, 8816 CrossRef CAS.
- H. Kang and V. Subramanian, Appl. Phys. Lett., 2014, 104, 023301 CrossRef.
- J. L. Bricks, Y. L. Solminskii, I. D. Panas and A. P. Demchenko, Methods Appl. Fluoresc., 2018, 6, 012001 CrossRef.
- M. Kuik, L. J. A. Koster, G. A. H. Wetzelaer and P. W. M. Blom, Phys. Rev. Lett., 2011, 107, 256805 CrossRef CAS PubMed.
- I. I. Fishchuk, A. K. Kadashchuk, A. Vakhnin, Y. Korosko, H. Bassler, B. Souharce and U. Scherf, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115210 CrossRef.
- C.-M. Li, T. Sjodin and H.-L. Dai, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15252 CrossRef CAS.
- R. H. Bube and H. E. MacDonald, Phys. Rev., 1961, 121, 473 CrossRef CAS.
- M. L. Tietze, L. Burtone, M. Riede, B. Lussem and K. Leo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035320 CrossRef.
- M. L. Tietze, P. Pahner, K. Schmidt, K. Leo and B. Lussem, Adv. Funct. Mater., 2015, 25, 2701 CrossRef CAS.
- J. N. Coleman, S. Curran, A. B. Dalton, A. P. Davey, B. Mc Carthy, W. Balu and R. C. Barklie, Synth. Met., 1999, 102, 1174 CrossRef CAS.
- M. A. Drobizhev, M. N. Sapozhnikov, I. G. Scheblykin, O. P. Varnavsky, M. V. der Auweraer and A. G. Vitukhnovsky, Chem. Phys., 1996, 211, 455 CrossRef CAS.
- A. V. Sorokin, N. V. Pereverzev, I. I. Grankina, S. L. Yefimova and Y. V. Malyukin, J. Phys. Chem. C, 2015, 119, 27865 CrossRef CAS.
- A. V. Sorokin, I. Y. Ropakova, S. Wolter, R. Lange, I. Barke, S. Speller, S. L. Yefimova, Y. R. Malyukin and S. Lochbrunner, J. Phys. Chem. C, 2019, 123, 9428 CrossRef CAS.
- M. Wubs and J. Knoester, Chem. Phys. Lett., 1998, 284, 63 CrossRef CAS.
- Y. Lan, B. J. Dringoli, D. A. Valverde-Chavez, C. S. Ponseca Jr, M. Sutton, Y. He, M. G. Kanatzidis and D. G. Cooke, Sci. Adv., 2019, 5, 5558 CrossRef PubMed.
- R. S. Crandall, J. Appl. Phys., 1983, 54, 7176 CrossRef CAS.
- Y. S. Lee, T. Gershon, O. Gunawan, T. K. Todorov, T. Gokman, Y. Virgus and S. Guha, Adv. Energy Mater., 2015, 5, 1401372 CrossRef.
- Z. Z. Bandic, P. M. Bridger, E. C. Piquette and T. C. McGill, Appl. Phys. Lett., 1998, 73, 3276 CrossRef CAS.
- R. Jayaraman and C. G. Sodini, IEEE Trans. Electron Devices, 1989, 36, 1773 CAS.
- Z. Celik-Butler and T. Y. Hsiang, IEEE Trans. Electron Devices, 1988, 35, 1651 CAS.
- J. Bisquert, F. Fabregat-Santiago, I. Mora-Sero, G. Garcia-Belmonte and S. Gimenez, J. Phys. Chem. C, 2009, 113, 17278 CrossRef CAS.
- D. F. Swinehart, J. Chem. Educ., 1962, 39, 333 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Current and noise maps of dye solar cell films. See DOI: 10.1039/d0ta07328h |
| This journal is © The Royal Society of Chemistry 2021 |