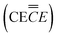Structure and chemistry of the solid electrolyte interphase (SEI) on a high capacity conversion-based anode: NiO†
Benjamin
Ng
 ,
Ehsan
Faegh
,
Saheed
Lateef
,
Stavros G.
Karakalos
,
Ehsan
Faegh
,
Saheed
Lateef
,
Stavros G.
Karakalos
 and
William E.
Mustain
and
William E.
Mustain
 *
*
Department of Chemical Engineering, University of South Carolina, Columbia, SC 29208, USA. E-mail: mustainw@mailbox.sc.edu
First published on 16th December 2020
Abstract
Electroanalytical techniques are specialized tools with high-sensitivity that when combined with electron transfer theory can shed light on the mechanisms of highly complex, heterogeneous, multi-step reactions. This study focuses on competitive reactions between the formation of the solid-electrolyte interphase (SEI) and the conversion reaction of a NiO Li-ion metal oxide anode as a function of state-of-charge (SOC). To our knowledge, this work is the first thorough analysis for the formation of the SEI on a conversion-based anode. NiO oxide was chosen because of recent reports in half cells and full cells showing good high-rate performance, though it is believed that NiO may act as a representative material for many of the conversion anodes. Galvanostatic intermittent titration technique (GITT) is applied to probe both the complex diffusional processes and the electrokinetic phenomena along the reaction pathway. Butler–Volmer (BV) and Marcus–Hush–Chidsey (MHC) models are used to investigate the reaction transfer coefficients and reorganizational energies at the inner/outer Helmholtz plane of the electrode/electrolyte interface. Next, the effective transfer coefficient is extracted and analyzed to provide new mechanistic insight into the rate determining step and the reaction pathway at different SOC.
1. Introduction
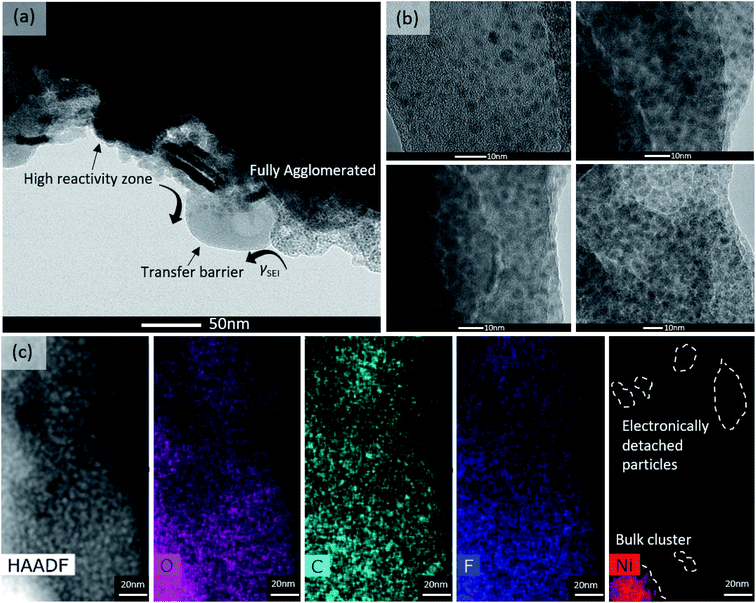
This past year, Li-ion batteries were again thrust to the forefront of our discussion on energy and energy mobility as the contributions of John B. Goodenough, M. Stanley Whittingham, and Akira Yoshino were recognized with the 2019 Nobel Prize in chemistry.1 Since their pioneering work, researchers around the world have worked together to better understand the chemistry and reactivity of Li-ion battery materials (e.g. lithium metal oxides, sulfur, graphite, silicon, Li-metal, etc.),2–6 studied their performance in multiple formats in real devices (e.g. coin cells, pouch cells, modules, etc.),7,8 and developed phenomenological/theoretical relationships (e.g. porous electrode theory)9–11 for their behavior in real batteries. However, there remains much ground to cover, more breakthroughs to develop, and hurdles to overcome before high-energy density, incredibly durable, and ultra-safe batteries are realized.As higher energy density materials are developed to enable such next-generation Li-ion batteries, their interfacial interaction with the electrolyte and reaction mechanism might be expected to be different than existing materials. This will be particularly important at the anode, where the formation of the solid electrolyte interphase (SEI) from electrolyte decomposition at low potentials is one of the most important phenomena that allows for conventional graphite anodes to be chemically stable over long-duration cycling and/or storage. The SEI and its formation is well-characterized for graphite, and even on some alternative materials such as Si.12–14Fig. 1a shows the electrode/electrolyte interface immediately after cell assembly, but before charge has been passed, where a non-faradaic electric double layer formation (via specific and non-specific adsorption/desorption) and faradaic electrochemical reactions (facilitated by the reversible transfer of electrons at open circuit) occur.15 The thermodynamic potential gap between the electrode and electrolyte (Fig. 1b) determines the initial specific adsorption behavior, solvation-shell near the interface, and the electrochemical reaction (e.g. intercalation/conversion/alloying, electrolyte decomposition, Li plating, etc.). The SEI is formed during initial charging where the anode potential is driven negative of its open-circuit value (Fig. 1c). Electrolyte instability at these potentials lead to electrolyte reduction to more stable compounds – both organic and inorganic. One of the most pervasive components of modern electrolytes is ethylene carbonate (EC), and it is known to play an important role in SEI formation. Aurbach et al.16,17 proposed a general reaction pathway for EC reduction on carbon-based anodes.
| EC + 2e− + Li+ → C2H4 + (CO3Li)− | (1) |
| (CO3Li)− + Li+ → Li2CO3 | (2) |
| (CO3Li)− + Li+ + EC → Li2EDC(PSEI) | (3) |
 | ||
| Fig. 1 Understanding the temporal evolution of the anode surface. (a) Illustration of the anode/electrolyte interface immediately after cell assembly; and (b) energy diagram of a Li-ion battery and how its changing electrode potentials during charge move the cell into potential regions where both the SEI and cathode electrolyte interphase (CEI) form. Also shown are illustrations of the anode structural evolution as the cell proceeds from the first cycle (c) and intermediate cycles (d) to its end-of-life (e) where extensive SEI formation has occured. The schematic is meant to capture the interfacial dynamics in the inner/outer Helmholtz plane (I/O-HP) and shows desolvated Li+ transport through the SEI. Adapted from ref. 24 and 25. | ||
Experimentally, it has been shown that EC reduction occurs at potentials around 0.8–1.4 V vs. Li/Li+, which is in reasonable agreement with theoretical calculations that fall between 0.48–0.96 V.16,17 EC undergoes a 2-electron reduction, though the reaction pathway can vary based on the EC concentration. At high EC concentrations, the 1st electron transfer destabilizes a Li+–EC moiety, causing the carbonate anion to attack a neighboring Li+–EC to form Li+(CO3)R(CO3)Li+ (where R can be methyl, ethyl, butyl, etc.). At low EC concentrations and potentials closer to the Li/Li+ redox couple, the carbonate anion will instead abstract Li+ to form Li2CO3.16 The more stable compounds become an electronically insulating shield (typically 10–40 nm for graphite-based electrodes,18 ∼0–50 nm for metal oxide based electrodes,19 and non-observable for titanate-based electrodes20) that naturally prevents the high energy electrode surface from further reaction, and enhancing long-term durability and capacity retention.21 Depending on the electrolyte, the SEI is considered to be fully formed after 1–5 cycles,22 however, different stress factors (e.g. volumetric expansion, gas formation, Li-plating, external impact) can expose reactive surfaces that allow additional SEI to grow during operation (Fig. 1d). The continual build-up and consumption of the electrolyte increases the internal resistance of the cell, leading to performance loss (Fig. 1e), which can eventually include battery failure. Though the SEI formation on carbon/graphite has been extensively studied, very little information exists in the literature regarding SEI formation on promising next-generation anode materials with high capacity, which are expected to be vital to device design and operation in the near future as the demand to increase the energy density of Li-ion batteries for commercial devices intensifies.23
By leveraging the breakage of bonds, both alloying materials (e.g. Si, capacity up to 4200 mA h g−1)26 and M–X conversion materials (capacity ∼700–1200 mA h g−1, where M = V, Cr, Mn, Fe, Co, Ni, Cu, W, Mo, Ru and X = H, N, O, F, P, or S),27 can store significantly more electrons per unit mass than intercalation compounds. Alloying materials undergo several crystallographic phase changes to accommodate the inclusion of Li, which results in a tradeoff between the desire for high energy density and need to avoid catastrophic volumetric expansion and material fracture. When the latter occurs, the original solid–solid interfaces (active material-binder-conductive carbon) break down and contact resistance increases, or, worse yet, delamination (electrode particles becoming fully detached from the current collector) occurs. The most common characteristic of alloying materials in Li-on batteries is rapid capacity loss (some <10 cycles).28 Conversion materials, on the other hand, operate under similar bond-breaking principle, but the reaction also involves the displacement of the counter-ion (X) from the parent host (M). This helps to limit volumetric expansion. Generically, conversion-based reactions follow the generalized reaction below27
| Mαμ+Xβπ− + βπ(Li+ + e−) ⇌ αM + βLiπX | (4) |
Also unlike Si, M–X conversion-based materials have a higher reversible redox potential than graphite (∼1 V vs. Li/Li+).29 Though at first this may seem like a negative, because it does slightly lower the operating voltage in practical batteries, it is actually an advantage because high potentials offer significantly increased protection from thermal runaway by avoiding Li plating and dendrite formation. Additionally, it should be noted that the much higher capacity for M–X materials more than compensates for the reduced operating voltage from an energy density perspective. Though M–X materials do show promise, they are still relatively understudied, particularly when it comes to their long-term stability and operation in LiBs. That being said, researchers30–34 have started to understand and control the in-cell M–X degradation pathways, including: (1) metal (charge) trapping, (2) transition of the MO to higher oxidation states, (3) exposed reactive sites for electrolyte decomposition, and (4) agglomeration-induced loss of electrochemically active sites, which causes capacity fade and oscillations/low coulombic efficiency. Various methodologies have been proposed in the literature to improve the cyclability of these M–X electrodes (encapsulation, nanoconfinement, etc.).35,36 One of the M–X materials that has particularly shown high performance recently is NiO. In fact, NiO-based anodes have boosted their cycle performance from <25 cycles37 a decade ago to >2000 deep cycles in 2020 at a 1C rate.38,39 These promising results have increased interest in this family of materials for commercial applications, which makes further studies regarding their reactivity and long-term stability an important endeavor, including developing a better understanding of the formation of the SEI on these materials.
Therefore, the overarching goal of this paper is to electroanalytically decouple the multi-step SEI reaction mechanism from the conversion reaction at the Ni–O/electrolyte interface. A multitude of electroanalytical techniques, such as galvanostatic intermittent titration technique (GITT) and transient voltammetry were performed. The resulting data was analyzed using kinetic relationships derived from electron transfer theory (Marcus–Hush–Chidsey, Butler–Volmer). Diffusivity (S2D) and apparent exchange current (i0S) measurements at different states of charge (SOC) were calculated to elucidate the complex mesostructural changes of the conversion reaction. The effective transfer coefficient (αeff) was used to provide a mechanistic understanding for EC activation at the NiO/electrolyte interface. The combined electroanalytical techniques and theory are combined to fundamentally deconvolute the complex growth mechanism of the SEI on conversion-based electrodes.
2. Experimental and theoretical framework
2.1 Reagents
Pluronic P123 triblock copolymer (poly(ethylene glycol)-block-poly(propylene glycol)-block-poly(ethylene glycol), Mn ∼ 5800, CAS #9003-11-6), tetraethyl orthosilicate (TEOS, >99.0%, CAS #78-10-4) and hydrochloric acid (HCl, ACS reagent grade 37%, CAS #7647-01-0) were purchased from Sigma Aldrich. Nickel(II) nitrate hexahydrate (Ni(NO3)2–6H2O, 99%, CAS #13478-00-7) and potassium hydroxide (NaOH, certified ACS, CAS #1310-58-3) were purchased from Fisher Scientific. Vulcan XC-72R was purchased from Cabot. All water used in the synthesis processes uses ultrapure deionized water (18.2 MΩ cm) from a lab-scale Millipore Milli-Q Integral system with E-POD. All chemicals were used as received with no further purification.2.2 Synthesis of highly ordered mesoporous nickel oxide (NiO)
Highly ordered mesoporous NiO was produced via a mesoporous silica (SBA-15) template-assisted synthesis. The SBA-15 template was synthesized in accordance to a similar procedure in our previous publications.33,40,41 Typically, 6 g of Pluronic P123 triblock copolymer and 13.6 mL tetraethylorthosilicate was dissolved in 180 mL of concentrated (2 M) HCl solution, heated to 45 °C for 20 hours, and then heated to 100 °C for an additional 24 hours. The product was washed with a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 vol% DI water/ethanol mixture, dried in a Fisherbrand Isotemp Model 281A vacuum oven (∼−30 in. Hg, 50 °C) for 12 hours and calcined at 500 °C for 3 hours in air.
50 vol% DI water/ethanol mixture, dried in a Fisherbrand Isotemp Model 281A vacuum oven (∼−30 in. Hg, 50 °C) for 12 hours and calcined at 500 °C for 3 hours in air.
Next, an aqueous 0.5 M Ni(NO3)2 solution was added dropwise to a beaker containing the synthesized SBA-15 until 6.3 mL gSBA-15−1 was achieved. The resulting gel was magnetically stirred under ambient conditions and then calcined at 400 °C for 3.5 h in air. After calcination, the template was removed by immersion in a 5 M KOH solution for 12 hours at 100 °C. Finally, the remaining solids were rinsed with three rounds of excess deionized water, centrifuged at 4500 rpm, and dried under vacuum at 70 °C for 8 hours.
2.3 Electrode fabrication and coin cell assembly
Anodes were created using either the highly ordered mesoporous NiO anodes or Vulcan XC-72R carbon. Vulcan XC-72R carbon black was chosen in this study as a control material since it does not store charge significantly via intercalation; this allows the reaction plateaus to be dominated from electrolyte decomposition and not muddled with intercalation-based phase changes. NiO-based anodes were prepared with a ratio of 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (by mass) active material to polyvinylidene fluoride binder (PVDF, Kynar Blend). Vulcan-based anodes were prepared with a 90
5 (by mass) active material to polyvinylidene fluoride binder (PVDF, Kynar Blend). Vulcan-based anodes were prepared with a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 carbon
10 carbon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVDF mass ratio. The change in the active material
PVDF mass ratio. The change in the active material![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVDF ratio between the two types of electrodes considers the differences in their surface area (conductive carbon > NiO) and the amount of binder required to maintain sufficient particle–particle contact. In a typical setup, 400 μL of N-methyl-pyrrolidone (NMP, Acros, 99.5% Extra Dry) solvent was micropipetted into a vial containing a total of 100 mg of total solids to obtain an ink with moderate viscosity. The ink was homogenized via 3 successive rounds of sonication (20 min) and magnetic stirring (8 h). The ink was sprayed onto a 50 μm thick Cu current collector (Alfa Aesar, catalog no. AA42972FI) with an Iwata-Medea Eclipse HP-CS. The electrodes were then dried at 75 °C for 24 hours under vacuum. Then, to minimize particle–particle contact resistance, the electrodes were hydraulically pressed at 1500 lbs (MTI 5T Max. Manual Mechanical Press) and calendared (MTI Electric Roller-MSK-MR100DC) to a specified gap of 60 μm. The final active loading target was 1 mg cm−1.
PVDF ratio between the two types of electrodes considers the differences in their surface area (conductive carbon > NiO) and the amount of binder required to maintain sufficient particle–particle contact. In a typical setup, 400 μL of N-methyl-pyrrolidone (NMP, Acros, 99.5% Extra Dry) solvent was micropipetted into a vial containing a total of 100 mg of total solids to obtain an ink with moderate viscosity. The ink was homogenized via 3 successive rounds of sonication (20 min) and magnetic stirring (8 h). The ink was sprayed onto a 50 μm thick Cu current collector (Alfa Aesar, catalog no. AA42972FI) with an Iwata-Medea Eclipse HP-CS. The electrodes were then dried at 75 °C for 24 hours under vacuum. Then, to minimize particle–particle contact resistance, the electrodes were hydraulically pressed at 1500 lbs (MTI 5T Max. Manual Mechanical Press) and calendared (MTI Electric Roller-MSK-MR100DC) to a specified gap of 60 μm. The final active loading target was 1 mg cm−1.
Coin cell assembly was done inside of an argon-filled (ultra-high purity 5.0 argon, Airgas) MBraun Labmaster SP glove box (O2 and H2O < 0.1 ppm). All coin cells were assembled in a half cell configuration using CR2032 coin cells (Hohsen Corp.). The counter/reference electrode was a 1.5 cm diameter lithium metal foil (99.9%, Alfa Aesar). In a typical procedure, the Li foil was polished, positioned at the center of the coin cell base, and then flattened to ensure minimal contact resistance. Then, 15 μL of electrolyte (1 M lithium hexafluorophosphate (LiPF6, Acros 98%) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volumetric mixture of ethylene carbonate (EC, Acros 99+%): dimethyl carbonate (DMC, Acros 98+%): diethyl carbonate (DEC, Acros 99+%)) was injected uniformly onto the Li-metal. A Celgard 2320 tri-layer PP/PE/PP separator was centered on top of the Li-metal/electrolyte surface. Next, an additional 15 μL of electrolyte was injected uniformly onto the separator. The gasket was placed along the outer diameter of the coin-cell base to ensure proper centering of the working electrode and sealing of the cell. A spacer disk and spring was used to ensure uniform distribution of pressure and electrical continuity in the cell. Finally, the cap of the coin cell was used to seal the cell with an MTI hydraulic press (MSK-110) at a pressure of 750 PSI.
1 volumetric mixture of ethylene carbonate (EC, Acros 99+%): dimethyl carbonate (DMC, Acros 98+%): diethyl carbonate (DEC, Acros 99+%)) was injected uniformly onto the Li-metal. A Celgard 2320 tri-layer PP/PE/PP separator was centered on top of the Li-metal/electrolyte surface. Next, an additional 15 μL of electrolyte was injected uniformly onto the separator. The gasket was placed along the outer diameter of the coin-cell base to ensure proper centering of the working electrode and sealing of the cell. A spacer disk and spring was used to ensure uniform distribution of pressure and electrical continuity in the cell. Finally, the cap of the coin cell was used to seal the cell with an MTI hydraulic press (MSK-110) at a pressure of 750 PSI.
2.4 Chemical and structural characterization
Pre-/post-cycled transmission electron microscopy (TEM) was performed on electrodes of interest by a similar procedure that was outlined in our previous publication.37 In order to preserve the region of interest during microscopy, a Cu TEM finder grid (3 mm diameter, 100 mesh, Ted Pella, Inc) was used. First, 1 μL of diluted active material slurry (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 dilution ratio) was deposited onto the grid and capillary drained via light application of a lint-free laboratory cloth (Kimwipes™). The procedure was repeated three times and fully-dried prior to TEM. After microscopy, the TEM grid, loaded with the active material, was mounted into a custom-designed electrode fixture between a Teflon shroud and a cylindrical Cu current collector. The assembly was electrochemically cycled (details in the following section) in a 3-electrode cell inside of an Ar-filled Mbraun glovebox. After the electrochemical experiments, the TEM grid with active material removed from the assembly, was submerged in excess DMC for 30 minutes and dried inside the glovebox for 24 hours prior to additional microscopy. All microscopy was performed using a FEI Talos scanning transmission electron microscope (S/TEM) and a Hitachi H8000 TEM with integrated energy dispersive X-ray spectroscopy (EDS). In addition, X-ray Photoelectron Spectroscopy (Kratos AXIS Ultra DLD XPS System) was used to determine the elemental composition on the surface, chemical state, and electronic structure of the active material.
10 dilution ratio) was deposited onto the grid and capillary drained via light application of a lint-free laboratory cloth (Kimwipes™). The procedure was repeated three times and fully-dried prior to TEM. After microscopy, the TEM grid, loaded with the active material, was mounted into a custom-designed electrode fixture between a Teflon shroud and a cylindrical Cu current collector. The assembly was electrochemically cycled (details in the following section) in a 3-electrode cell inside of an Ar-filled Mbraun glovebox. After the electrochemical experiments, the TEM grid with active material removed from the assembly, was submerged in excess DMC for 30 minutes and dried inside the glovebox for 24 hours prior to additional microscopy. All microscopy was performed using a FEI Talos scanning transmission electron microscope (S/TEM) and a Hitachi H8000 TEM with integrated energy dispersive X-ray spectroscopy (EDS). In addition, X-ray Photoelectron Spectroscopy (Kratos AXIS Ultra DLD XPS System) was used to determine the elemental composition on the surface, chemical state, and electronic structure of the active material.
2.5 Electrochemical testing
Three electrochemical methods were primarily used in this work. Current-pulse relaxation, via the galvanostatic intermittent titration technique (GITT), was done using an Arbin MSTAT battery cycler under pseudo-isothermal conditions inside a Tenney T6S-1 climate-control chamber at 25 °C. The method involves 100 intermittent current pulses at C/10 for a time that satisfies t ≪ L2/D, followed by a relaxation time (i.e. no current) to electrochemical equilibrium. In addition to a time constraint (i.e. satisfies t ≪ L2/D), the voltage window was specified to be 0.001–3.0 V. The GITT data allowed for the apparent diffusion coefficients and apparent exchange current densities to be extracted as a function of the state of charge (SOC). The other method used in this work was linear sweep voltammetry (LSV), which was done using the Arbin MSTAT battery cycler. LSV was used to determine the effective transfer coefficient as a function of the SOC during a parallel GITT test. The scan rate was 1 mV s−1 and the upper and lower cutoff voltages were ±100 mV vs. the open circuit voltage (OCV). A 30 minute relaxation time was given between the positive and negative scan. Finally, the samples deposited on the TEM grid for pre-post imaging were exposed to cyclic voltammetry (CV) at a 0.1 mV s−1 scan rate over the same potential window as the GITT measurements (0.001–3.0 V).2.6 Electrokinetic and mass transfer framework
The electrokinetics for complex heterogeneous reactions (combinations of multi-step electrochemical and/or chemical reactions) are developed to understand current–potential (i–E) relationships. The i–E relationship can be rigorously derived by applying Dirac's time-dependent perturbation theory to Schrodinger's wavefunction (Ψ) of an electron and integrating the density of states for the electrolyte (detailed proof can be found in Fletcher et al.42). For most reactions, the reaction rate is expressed in the Butler–Volmer (BV) formulation, given as eqn (5):43| i = i0[e−αefff(E−E0) − e(n−αeff)f(E−E0)] | (5) |
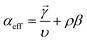 | (6) |
![[small gamma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c3.gif) is the number of electrons prior to the rate determining step, υ is the number of times the rate determining step occurs, ρ is either 0 (if the rate-determining step, RDS, is a chemical step) or 1 (if the RDS is an electrochemical step), and β is 0.5.
is the number of electrons prior to the rate determining step, υ is the number of times the rate determining step occurs, ρ is either 0 (if the rate-determining step, RDS, is a chemical step) or 1 (if the RDS is an electrochemical step), and β is 0.5.
The Butler–Volmer electrokinetic expression is typically valid in a very narrow regime where the free energy curves for oxidation and reduction are linear. However, the potential energy surface based on Marcus theory is represented by intersecting parabolas that account for the cumulative coordination energy between the initial and final states of the electrolyte. This model results in the Marcus–Hush–Chidsey (MHC) relationship between the current and overpotential, which is given below:45
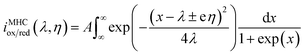 | (7) |
In eqn (7), λ is reorganizational energy normalized to the thermal voltage, and η = e(E − E0)/kBT. The Fermi distribution of the electronic energy upon an applied potential is accounted for in the MHC framework by integrating x = (εe1 − eE)/kBT. The pre-exponential factor (A) accounts for the strength of the electronic coupling and density of states. Previous studies46 found that the Fermi distribution in the MHC is negligible (x = (εe1 − eE)/kBT), resulting in the low overpotential approximation for the Marcus–Hush–Chidsey kinetic expression. Therefore, the MHC breaks down to a modified transfer coefficient to the Butler–Volmer expression and can be represented as a potential dependent property and as a function of the electrolyte reorganizational energy, (eqn (8)).46
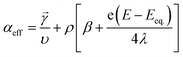 | (8) |
The effective diffusion coefficient of Li+ ions can be extracted when the system is perturbed by a constant current pulse (I) for a given pulse-time (τ) and then relaxed at open circuit. The relationship between the pulse and the potential response during the relaxation period gives the effective chemical diffusion coefficient, eqn (9), and is rigorously derived by Weppner and Huggins,47
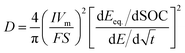 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.3 C mol−1 (Faraday's constant), Vm is the molar volume, S is the electrochemically active surface area, and SOC is the state of charge. The dEeq/dSOC or
485.3 C mol−1 (Faraday's constant), Vm is the molar volume, S is the electrochemically active surface area, and SOC is the state of charge. The dEeq/dSOC or 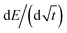 components of the equation are calculated based on the linear regression of the corresponding regions in each pulse.
components of the equation are calculated based on the linear regression of the corresponding regions in each pulse.
2.7 Mechanistic framework – known EC reactions on C-based anodes
The effective transfer coefficient can help researchers to elucidate the mechanistic pathway of the reaction and it is capable of decoupling multi-step reactions because it reveals the nature of the RDS. For a generalized multi-step reaction that follows the form of A + ne− ⇌ Z, the RDS plays an essential role in the rate of reaction. Therefore, a multi-step reaction can be broken down into number of electrons prior to the RDS and number of electrons after the RDS to give a cumulative number of electrons of n. By writing out every rate expression for every step of the pathway, the effective transfer coefficient can be derived and used for mechanistic insight (Table S1 in the ESI†).With the present theoretical framework for multi-step reactions, electroanalytical techniques can be applied to study the activation of EC on conversion electrodes. There are numerous studies that have applied high-level density functional theory (DFT) calculations for the reduction pathway of EC, which is the dominant reactant participating in the SEI formation step on carbon/graphite (eqn (10)–(18)).17,48,49 First, supermolecules of (EC)n and Li+ are formed during the electrolyte preparation step.
| nEC + Li+ → (EC)n − Li+ | (10) |
The supermolecules of Li+(EC)n then undergo a 2 electron decomposition reaction at the electrified surface. The 1st electron transfer step destabilizes the system to an ion-pair intermediate via homolytic C–O bond cleavage:
| (EC)n − Li+ + e− → [(EC)−] − Li+ − (EC)n−1 | (11) |
| (EC)n − Li+ + e− → (EC)n − Li | (12) |
| [(EC)−] − Li+ − (EC)n−1 → H2ĊCH2(CO3)−Li+ − (EC)n−1 | (13) |
From here, the EC can further decompose to a lithium organic (R) dicarbonate (ROCO2Li)2 where R can either be ethylene or butylene:
| 2H2ĊCH2(CO3)−Li+ − (EC)n−1 → (EC)n−1 − Li+(CO3)−(CH2)4(CO3)−Li+ − (EC)n−1 | (14) |
| 2H2ĊCH2(CO3)−Li+ − (EC)n−1 → (EC)n−1 − Li+(CO3)−(CH2)2(CO3)−Li+ − (EC)n−1 + C2H4 | (15) |
An alternative decomposition reaction can occur at low EC concentrations48–50via the formation of an unpaired carbonate nucleophile (LiCO3−), which can react after the 1st electron transfer to either Li2CO3 or (CH2OCO2Li)2:
| H2ĊCH2(CO3)−Li+ − (EC)n−1 + e− → (CO3)2−Li+ − (EC)n−1 + C2H4 | (16) |
| (EC)n − Li+ + (CO3)2−Li+ − (EC)n−1 → (EC)n − Li+(CO3)2−Li+ − (EC)n−1 | (17) |
| (EC)n − Li+ + (CO3)2−Li+ − (EC)n−1 → (EC)n−1 − Li+(CO3)−(CH2)2(CO3)−Li+ − (EC)n−1 + C2H4 | (18) |
Despite the plethora of experimental data that corroborates the EC reaction mechanism above for carbon (a detailed DFT study can be found in Wang et al.51), there is a demand to generalize the reaction mechanism on developmental-stage electrodes with higher energy densities or phenomenal reversibility. Therefore, this paper attempts to bridge this gap by providing a systematic approach to deconvoluting the SEI reaction mechanism on an M–X conversion anode (NiO). First, SEI formation is summarized on Vulcan XC-72R carbon. Vulcan XC-72R provides a control case for SEI formation that is well-studied (i.e. carbon) where the result is well known – without interference from intercalation. This is meant to validate the overall methodology, which can then be extended to NiO (and other M–X materials). To our knowledge this study contains the most comprehensive dataset and analysis for the SEI formation on a conversion based anode, which has resulted in a much more complete understanding of the reaction mechanism as a function of SOC on this family of materials as well as a framework for others to apply to similar systems in the future.
3. Results and discussion
3.1 Solid electrolyte interphase on carbon
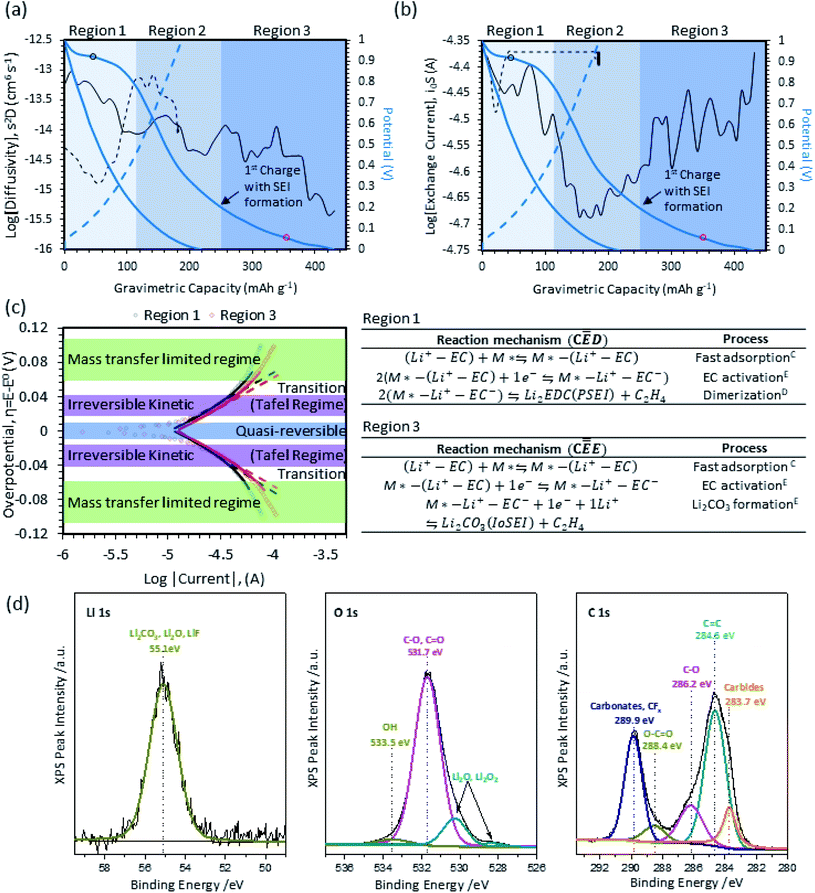
The SEI reaction mechanism and location of the electrolyte decomposition (inner or outer-sphere reaction) primarily occurs during the first charge. The curve for the first charge of Vulcan XC-72R (carbon control) is shown in Fig. 2a. It can be split into 3 regions (Arabic numerals: 1, 2, 3). In Region 1, charge is primarily stored via electric double layer (EDL) capacitance, though some of the current passed also contributes to electrolyte decomposition/SEI formation. In Region 2, the behavior is dominated by charging the EDL. Finally, Region 3 shows both EDL charge storage as well as extended capacity from electrolyte reduction. The diffusional transport properties extracted from galvanostatic intermittent titration technique shows a stepwise decrease in the apparent diffusion coefficient (S2D) and is represented as the solid/dashed black lines in Fig. 2a. Region 1 shows a gradual decrease in the apparent diffusion coefficient from 10−13 to 10−14 cm6 s−1. The electrolyte reduction process and formation of the SEI impedes Li+ diffusion, resulting in an average diffusion coefficient that decreases as a function of the SEI film growth. The transition from Region 1 to Region 2 is reflected by a stabilization of the apparent diffusion coefficient, which corresponds well with the inflection point of the OCP (i.e. transition from an electrochemical reaction (EC) that forms the SEI to a purely capacitive behavior). The transition between Region 2 to Region 3 is marked by a comparative extension in the capacity in the low potential range and the increase in the diffusional barrier. The stage-wise decrease in the diffusion coefficient captures a two-stage SEI formation process and this phenomena elucidates some of the previous SEI-related literatures (i.e. a porous SEI near the electrolyte interface and a densification near the electrode surface).18 The apparent exchange current in Fig. 2b captures the kinetics at different SOC. The V-shape curve for i0S is consistent with the potential response and delineation of Region 1–3. Region 1, which shows tendencies that are consistent with an electrochemical reaction with EDL charge storage. The delineation is reflected in the form of a higher exchange current in-comparison to Region 2, which comparatively shows similarities to subsequent cycles. The steep drop in the apparent exchange current in the transition from Region 1 to Region 2 marks the near completion of the first SEI formation process. At low potentials vs. Li/Li+ the apparent exchange current increases significantly, which is a corollary to a secondary plateau or more specifically a secondary reaction.Linear sweep voltammograms taken in Region 1 and Region 3 during the first charge are plotted in Fig. 2c. In Fig. 2c, experimental data is represented by semi-transparent dots, while Tafel curves are indicated by straight dashed lines and the low overpotential approximated MHC analysis are indicated by solid lines. The highlighted colors and labels in Fig. 2c also show the constituent physical and/or chemical processes that primarily contribute to the LSV behavior in various potential regimes. At low overpotentials, the quasi-reversible regime near the equilibrium potential is highlighted in blue. In this regime, reversible interfacial charge transfer occurs. At moderate overpotentials, highlighted in purple, linear Tafel behavior can be observed. At high overpotentials, highlighted in green, mass transfer limitations take over as the log(i) response deviates significantly from linearity.45,46,52 Calculations of αeff and low overpotential MHC calculations of the reorganization energy (λ) for Vulcan XC-72R carbon black are provided in Table 1. First, the reorganizational energy for Region 1 and Region 3 were found to be λ = 0.33 eV ± 0.01 and 0.37 eV ± 0.01, respectively. The small reorganizational energy suggests that electrolyte reduction is controlled by electron transfer and not solvation/desolvation ion transport mechanisms that typically exhibit reorganizational energies above 0.5 eV. The good agreement of the experimental data to the MHC model, combined with low reorganization energies, indicates that the SEI formation on carbon in this region is an outer-sphere electron transfer process.53
| Region 1 | Region 3 | |
|---|---|---|
| α eff | 0.43 ± 0.01 | 0.47 ± 0.01 |
| λ | 0.33 eV ± 0.01 | 0.37 eV ± 0.01 |
As shown in Table 1, kinetic deconvolution of the LSV data yielded an αeff of 0.43 in Region 1. From this value, it can be surmised that ![[small gamma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c3.gif) = 0 and ρ = 1, meaning that the rate determining step is the first electron transfer step. To ascertain the number of times the RDS occurs, additional information is needed. Wang et al.51 proposed the reaction mechanism in Fig. 2c for Region 1, which indicates a fast adsorption step followed by an activation step and a dimerization reaction to form organic Li2EDC and ethylene (translates to a υ = 2). From their DFT calculations, they also proposed the 1st electron transfer step to be the rate determining step. In this region, the SEI formation is dominated by organic species formation because the bulk EC concentration (∼7 M) makes it highly available, with high surface coverage as well. Even though surface mobility of activated EC is low due to steric hindrance, there is a boundless supply of EC in Region 1 prior to SEI formation. In this region, the simultaneous ethylene evolution and Li2EDC formation enables the formation of the porous, organic portion of the SEI. The mechanistic information is consistent with other studies that used XPS at various potentials to study the transient chemistry,54,55 simultaneous EQCM-D/CV to calculate the mass per electron for the generation of heavier vs. lighter molecules along the reaction pathway, and DFT calculations of the reaction mechanism.17,56
= 0 and ρ = 1, meaning that the rate determining step is the first electron transfer step. To ascertain the number of times the RDS occurs, additional information is needed. Wang et al.51 proposed the reaction mechanism in Fig. 2c for Region 1, which indicates a fast adsorption step followed by an activation step and a dimerization reaction to form organic Li2EDC and ethylene (translates to a υ = 2). From their DFT calculations, they also proposed the 1st electron transfer step to be the rate determining step. In this region, the SEI formation is dominated by organic species formation because the bulk EC concentration (∼7 M) makes it highly available, with high surface coverage as well. Even though surface mobility of activated EC is low due to steric hindrance, there is a boundless supply of EC in Region 1 prior to SEI formation. In this region, the simultaneous ethylene evolution and Li2EDC formation enables the formation of the porous, organic portion of the SEI. The mechanistic information is consistent with other studies that used XPS at various potentials to study the transient chemistry,54,55 simultaneous EQCM-D/CV to calculate the mass per electron for the generation of heavier vs. lighter molecules along the reaction pathway, and DFT calculations of the reaction mechanism.17,56
During the first charge, Region 3 has an αeff of 0.47, which again suggests that ![[small gamma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c3.gif) = 0 and ρ = 1. However, by the time that the charge has reached Region 3, the surface is much different than it was in Region 1 since a significant portion of the porous, organic SEI (Li2EDC) has already been formed as discussed above. The existence of this porous layer, as opposed to a flat, open surface, also means that the reaction likely becomes EC mass transport limited.48 Because the surface mobility of activated EC is low, the lower concentration of EC results in severely hindered dimerization due to lack of proximity between active species.48 Also, in Region 3, the anode potential is lower than it was in Region 1. The combination of a high driving force and low EC concentration16 results in nucleophilic attack of neighboring Li-species, as shown in Fig. 2c, which changes the formed reduction products from organic species to inorganic compounds such as Li2CO3.
= 0 and ρ = 1. However, by the time that the charge has reached Region 3, the surface is much different than it was in Region 1 since a significant portion of the porous, organic SEI (Li2EDC) has already been formed as discussed above. The existence of this porous layer, as opposed to a flat, open surface, also means that the reaction likely becomes EC mass transport limited.48 Because the surface mobility of activated EC is low, the lower concentration of EC results in severely hindered dimerization due to lack of proximity between active species.48 Also, in Region 3, the anode potential is lower than it was in Region 1. The combination of a high driving force and low EC concentration16 results in nucleophilic attack of neighboring Li-species, as shown in Fig. 2c, which changes the formed reduction products from organic species to inorganic compounds such as Li2CO3.
In addition to the electroanalytical analysis, XPS was used to corroborate the reaction mechanism for SEI formation on carbon. High resolution Li 1s, O 1s, and C 1s for post-SEI formation on carbon are presented in Fig. 2d. The Li 1s high resolution spectrum captures one broad peak at 55.1 eV, which is difficult to deconvolute but characteristic of Li2CO3 (Eb ∼ 55.2 eV), Li2O (Eb ∼ 53.8 eV), LiF (Eb ∼ 55.6 eV), and ROCO2Li (Eb ∼ 54.7 eV).57–59 A deconvolution of the O 1s high resolution spectrum indicates the presence of C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functionalities (Eb ∼ 531.7 eV), and possible O–H (Eb ∼ 533.5 eV). In addition, a shoulder corresponding to the formation of Li2O is observed at 528.5 eV. The C 1s spectrum contains a convoluted set of peaks that are consistent with carbonate/CFx (Eb ∼ 289.9 eV), O–C
O functionalities (Eb ∼ 531.7 eV), and possible O–H (Eb ∼ 533.5 eV). In addition, a shoulder corresponding to the formation of Li2O is observed at 528.5 eV. The C 1s spectrum contains a convoluted set of peaks that are consistent with carbonate/CFx (Eb ∼ 289.9 eV), O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Eb ∼ 288.4 eV), C–O (Eb ∼ 284.6 eV), and carbide-related species (Eb ∼ 283.7 eV). The observed CFx binding energies are expected and related to the PVDF binder. The remaining peaks correspond to compounds in the SEI and conductive carbon and are consistent with the known products for SEI formation on carbon, including lithium alkyl carbonates (e.g. ROCO2Li) in Region 1 and Li2CO3 in Region III.
O (Eb ∼ 288.4 eV), C–O (Eb ∼ 284.6 eV), and carbide-related species (Eb ∼ 283.7 eV). The observed CFx binding energies are expected and related to the PVDF binder. The remaining peaks correspond to compounds in the SEI and conductive carbon and are consistent with the known products for SEI formation on carbon, including lithium alkyl carbonates (e.g. ROCO2Li) in Region 1 and Li2CO3 in Region III.
The potential and concentration dependence of the SEI formation process can therefore be broken down into three primary regions on the carbon control. In Region 1, the extended reaction plateau at 0.93 V and the non-existent reaction plateau in the subsequent cycles, can be used to decouple the two charge storage mechanisms, EDL charging and SEI formation. The SEI formation process can then be further deconvoluted via electron transfer theory to yield an effective transfer coefficient (αeff = 0.43) that corroborates the reaction pathway of highly concentrated EC to the organic-phase SEI (either (CH2CH2OCO2Li)2 or (CH2OCO2Li)2). In Region 2, the potential profile resembles characteristics of subsequent cycles and indicates a charge storage that is consistent with EDL storage (i.e. no definitive reaction plateau). As the charging reaches Region 3, an extended reaction plateau at <0.3 V is observed and corroborates the widely accepted 2nd reaction pathway of the SEI. A further deconvolution of Region 3 reveals an effective transfer coefficient of 0.47, which leads to the observation that the 1st electron transfer step is the rate determining step. These findings agree with the widely-accepted literature pathway for SEI formation, where EC reduction leads to the formation of Li2CO3.16,17,48 Though this first section is a validation of already-published work, it is included here to provide a baseline for comparison with the true system of interest in this work: NiO specifically, and M–X compounds generally. The results above show that the mechanistic framework shown here is fully capable of deconvoluting the complex multi-step reaction pathway of the primary active electrolyte species (EC) – meaning that it can be extended to M–X species like NiO with a high chance for success.
3.2 Solid electrolyte interphase on conversion metal oxide
After confirming the plausibility for the DFT-proposed reaction mechanisms by Wang et al.60,61 and the experimental observations by Aurbach et al.48 for SEI formation on the control-carbon electrodes in this study, the methodology was extended to NiO. Fig. 3a shows the galvanostatic intermittent titration technique (GITT) results for the open circuit potential (OCP) and diffusivity (S2D) for NiO as a function of the state of charge (SOC) during the initial charge (solid lines) and discharge (dashed lines). The apparent exchange current as a function of SOC during the initial charge (solid line) and discharge (dashed line), also from GITT, is shown in Fig. 3b. Because SEI formation occurs during the 1st charge, that will be the focus of the discussion. From the trends in the data, four regions (denoted by Roman numerals: I, II, III, IV) could be identified.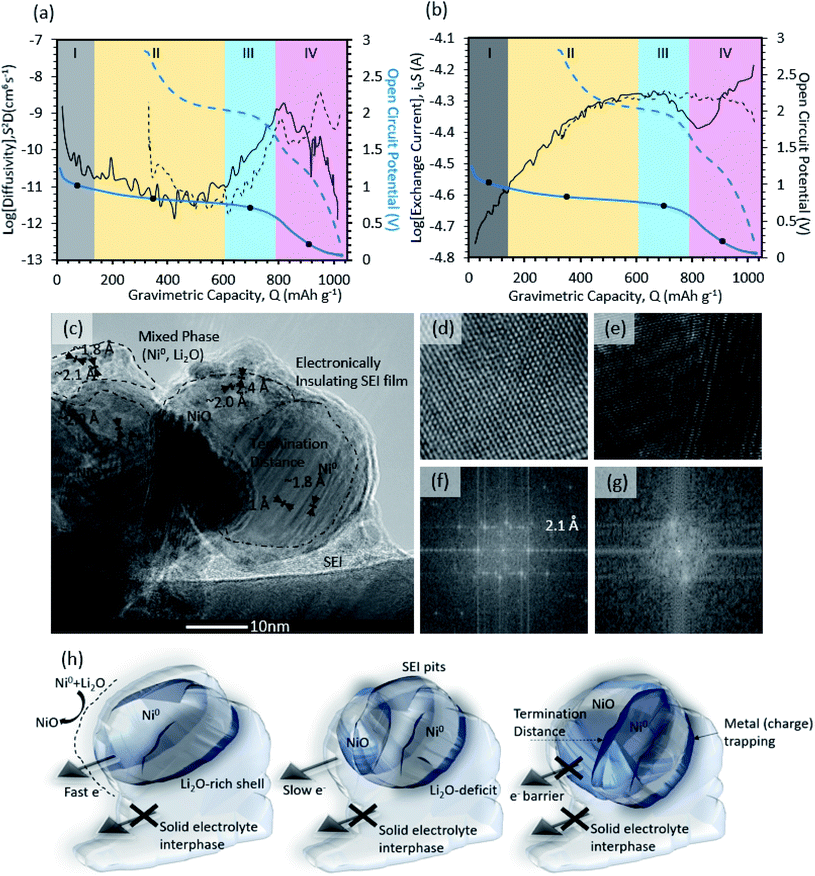 | ||
| Fig. 3 Galvanostatic intermittent titration technique for the parameter extraction of (a) apparent diffusion coefficient and (b) the apparent exchange current. Both plots contain the open circuit potential of NiO marked in (blue). Each section contains a dot which indicates locations where linear sweep voltammetry is done. Four sections are broken down (I, II, II, IV) to delineate the dominant mechanisms. In addition, high resolution transmission electron microscopy of post-cycled NiO is shown (c) along with atomic resolution HRTEM images of a Ni-dominated domain (panel d, ∼2.1 Å [111], ∼1.8 Å [200]) and a NiO-dominated domain (panel e, 2.4 Å [111], 2.0 Å [200]). The Fast Fourier Transform (FFT) analysis of the HRTEM images for Ni (f) and NiO (g) domains. Schematic for NiO particle transformation (h), showing the conversion reaction front propagation for the particle-level HRTEM image in Fig. 3c where lithiation propagates from the bulk electrode until the reaction front stops due to high local polarization (i.e. the electrical losses generate a termination distance) – resulting in trapped charge. | ||
In Region I (OCP > 1 V), the initial reaction occurs at the solid/liquid interface, which is indicated by a high apparent diffusion coefficient (10−8 to 10−9 cm6 s−1) and the lowest exchange current, ca. 2 × 10−5 A. By the end of Region 1, the apparent diffusion coefficient decreased to 10−10 cm6 s−1, while the apparent exchange current increased slightly to ca. 2.5 × 10−5 A. In Region II (0.7 < OCP < 1 V vs. Li/Li+, 72 < Q < 610 mA h g−1), the apparent diffusion coefficient was fairly stable (∼10−11 cm6 s−1) and its magnitude is characteristic of solid-state diffusion, most likely lithium ions through the porous SEI and active metal oxide particles. Concurrently, the apparent exchange current continuously increased to ca. 5.0 × 10−5 A. In Region III (0.5 < OCP < 0.7 V vs. Li/Li+, 610 < Q < 790 mA h g−1), there was an increase in the apparent diffusion coefficient from ∼10−11 to ∼10−9, which indicates a possible transition in the diffusion mechanism from purely solid-state diffusion back to a combination of solid-state + liquid-state phase diffusion. The most likely reason for this phenomenon can be attributed to slight volumetric expansion as well as the phase segregation of Ni-metal + Li2O domains, which exposes additional active material surface to the electrolyte (visual evidence will be discussed later along with Fig. 3c). However, the exchange current was not changed in this region. In Region IV (0 < OCP < 0.5 V vs. Li/Li+, Q > 790 mA h g−1), there was a rapid drop in the apparent diffusion coefficient from (10−9 to 10−12), suggesting a transition from a mixed solid-state/liquid-state diffusion back to a purely solid-state mechanism. The rapid drop in the diffusion coefficient in combination with an overpotential in-proximity to Li/Li+ is consistent with the 2nd stage of SEI formation in carbon electrodes, which included densification and a transition from organic to inorganic electrolyte decomposition products.
A HRTEM image of a partially charged NiO particle is shown in Fig. 3c. The image captures a moving phase boundary between the charged state and the discharged-state that does not begin homogenously at the surface and move inward, a so-called shrinking core model, as might be initially expected. Instead, evidenced by a distinct lateral phase boundary in the particle, the particles begin their charge from the side of the particle closest to the current collector/substrate and the reaction plane moves from that side of the particle to the other. By zooming in at higher magnification, atomic resolution images are captured for both the charged Ni (Fig. 3d) and discharged NiO (Fig. 3e) domains within the particle. The corresponding fast Fourier transform (FFT) is also shown below the HRTEM images for both phases. The FFT deconvolution shows two distinct lattice fringes neighboring the phase boundary with lattice constants of 2.0 Å [200] and 2.4 Å [111] corresponding to planes of NiO in Fig. 3f, and 2.1 Å [111] and 1.8 Å [200] corresponding to Ni-metal in Fig. 3g. The anisotropic lithiation/delithiation behavior of the conversion reaction suggests that the reaction front is controlled by electronic conductance (the charge does result in the formation of metallic Ni particles, which have high conductivity). This seems to confirm previous work showing that the charge/discharge efficacy of metal oxide anode materials is strongly dependent on the intra-particle and inter-particle conductivity.5,34
Fig. 4 applies Tafel and MHC electrokinetic models to LSV data taken in each region during the first charge, as was done for carbon in the previous sections, to better understand the reaction mechanism during SEI formation. In all regions, the Tafel and MHC descriptions capture the near linear log(i) response with reasonable agreement and the resulting effective transfer coefficients and reorganizational energies are shown in Table 2. Even with the simplification of the MHC used here, the model is in good agreement with the data, suggesting that the Fermi distribution and EDL have a negligible contribution to the kinetic behavior in this system. In addition, symmetry in the data indicates that an electron transfer step is rate-limiting, and not ion transport through the EDL or the prematurely formed SEI, even though some studies have suggested that desolvation of Li+ from the electrolyte into the SEI may be rate limiting.62 Typically, desolvation requires reorganizational energies greater than 0.5 eV. Since Marcus theory53 was originally derived for outer sphere electron transfer reactions, the reorganizational energy indicates reduction of EC at the outer Helmholtz plane.
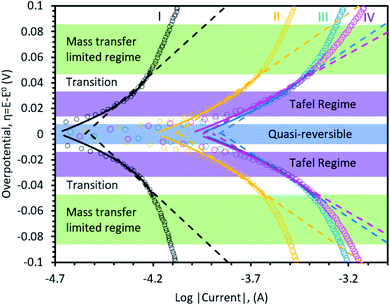 | ||
| Fig. 4 Represents Tafel-like plots for Butler–Volmer (solid line) and Marcus–Hush–Chidsey (dashed lines) models on-top of experimental data (dots). | ||
| I | II | III | IV | |
|---|---|---|---|---|
| α eff | 0.41 ± 0.01 | 0.55 ± 0.02 | 0.58 ± 0.01 | 0.67 ± 0.02 |
| λ | 0.23 eV ± 0.01 | 0.28 eV ± 0.01 | 0.30 eV ± 0.01 | 0.38 eV ± 0.01 |
The interfacial interaction of the electrolyte and the electrode can be deconvoluted from the reorganization energy in the MHC model, and studied at different SOC to provide a temporal view of the electrode/electrolyte interaction across the entire reaction coordinate. From the beginning to the end of the first charge, Region I → II → III → IV, λ continuously increased from 0.23 to 0.38. Since λ is an indicator for the energy required to reorganize the electrolyte, differences in this value can elucidate surface interactions. The fact that electrolyte reorganization energy increased from low SOC to high SOC suggests that the interface is altered by the SEI formation and it is likely that the ion-pairing between Li+ and solvent dipoles or PF6− anions become stronger at higher SOC (i.e. the coordination level increases or ion-pairing changes). In comparison, the reorganizational energy on carbon is higher than on NiO at low SOC (λC = 0.33 eV ± 0.01 in Region 1 vs. λNiO = 0.23 eV ± 0.01 for Region I), which means the transfer of charge on an oxide surface is initially more facile on NiO. This could be due to a catalytic effect, since the surface area of C (250 m2 g−1) vs. NiO (80.4 m2 g−1) is drastically different, though this needs to be probed more deeply in the future. However, as the electrolyte decomposition proceeds to a more mature stage, the reorganization energies (and hence the electrolyte-SEI interaction) become statistically identical (λC = 0.37 eV ± 0.01 in Region 3 vs. λNiO = 0.38 eV ± 0.01 for Region IV), which suggests that the advanced SEI/electrolyte interfaces are likely similar.
Because two processes are occurring simultaneously during the first charge, both the conversion reaction and SEI formation, isolating the process of interest can be difficult and requires several pieces of experimental data to be systematically combined to generate a full understanding. Based on the effective transfer coefficient in Region I, and the consistency to Region 1 in carbon, the analysis strongly suggests that the reaction pathway for the reduction of EC to (ROCO2Li)2 also occurs on NiO. The effective transfer coefficient results are also fully consistent, with value of the αeff indicating that the reaction is again rate-limited by the 1st electron transfer (![[small gamma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c3.gif) = 0, ρ = 1). Here, Li+(EC)n supermolecules are rapidly adsorbed onto the active material, followed by activation and dimerization to Li2EDC and ethylene. Again, the lower reorganization energy for this initial process does suggest possible catalytic decomposition in the early stages of SEI formation on the NiO surface, which requires future study.
= 0, ρ = 1). Here, Li+(EC)n supermolecules are rapidly adsorbed onto the active material, followed by activation and dimerization to Li2EDC and ethylene. Again, the lower reorganization energy for this initial process does suggest possible catalytic decomposition in the early stages of SEI formation on the NiO surface, which requires future study.
The effective transfer coefficient in Regions II and III were very similar (αeff = 0.55 for Region II and αeff = 0.58 for Region III). In-combination with the behavior of the apparent diffusion coefficient as discussed above and the apparent exchange current density, the behavior in these two regions appears to correspond primarily to the conversion reaction (Ni2+O2− + Li+ → Ni0 + Li2O), not SEI formation. Palmieri et al. proposed a reaction mechanism based on thermodynamic arguments and on behaviors consistent with our observations here.34 Because it is not expected that significant SEI formation occurs in Regions II and III, they will not be extensively discussed here as their dynamics fall outside of the focus of this work.
XPS was performed to guide the mechanistic deconvolution of Region IV, which also is comprised of responses from multiple reactions. Fig. 5a shows a high resolution XPS spectrum for pre-cycled NiO in the Ni 2p spectra, which shows characteristic (872.5 eV) 2p1/2 and (854.3 eV) 2p3/2 with a 18.2 eV displacement from the split spin–orbit of nickel oxide (NiO). Satellite peaks for Ni 2p1/2 at 872 eV and Ni 2p3/2 at 862 eV can be observed as well. After being cycled (100×), the Ni 2p spectra (Fig. 5b) indicates the presence of mixed oxidation states between Ni2+ and Ni3+ that is characteristic of Ni2O3, NiF2, and Ni carbide species at Ni 2p3/2 at binding energies of 858 eV, 855.5 eV, and 849.7 eV, respectively.
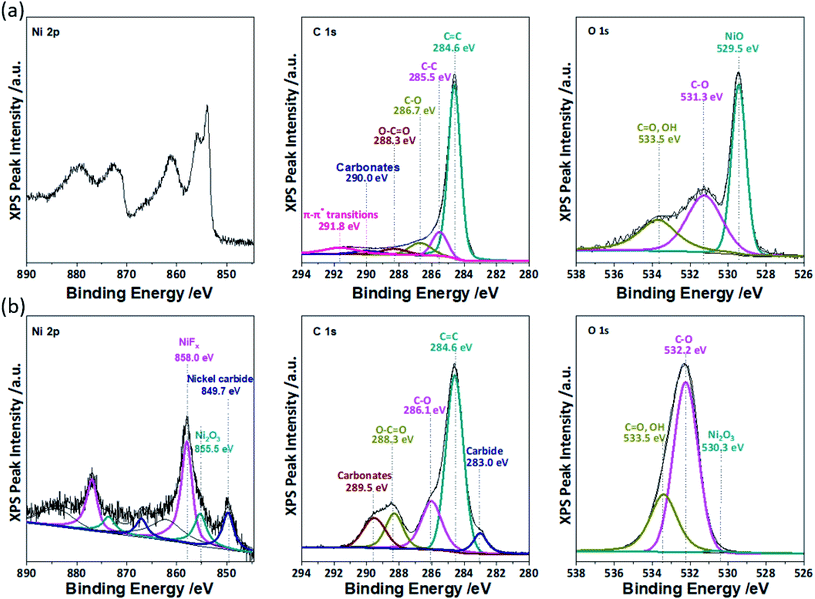 | ||
| Fig. 5 High resolution XPS spectra of (a) pre-cycled and (b) post-cycled NiO electrodes in the Ni 2p, C 1s, and O 1s spectra. | ||
In the pre-cycled C 1s spectrum, responses were observed from C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (Eb ∼ 284.6 eV), C–C/C–H (Eb ∼ 285.5 eV), C–O (Eb = 286.7 eV), O–C
C (Eb ∼ 284.6 eV), C–C/C–H (Eb ∼ 285.5 eV), C–O (Eb = 286.7 eV), O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Eb ∼ 288.3 eV), and –CO3– (or PVDF at Eb ∼ 290.0 eV) species. In addition, π–π* shakeup satellites were observed at Eb ∼ 291.8 eV. The high resolution pre-cycled C 1s spectrum shows functionalities for PVDF and carbon black. The post-cycled C 1s spectrum reveals a significant increase in –CO3– functionalities at Eb ∼ 289.5 eV. O–C
O (Eb ∼ 288.3 eV), and –CO3– (or PVDF at Eb ∼ 290.0 eV) species. In addition, π–π* shakeup satellites were observed at Eb ∼ 291.8 eV. The high resolution pre-cycled C 1s spectrum shows functionalities for PVDF and carbon black. The post-cycled C 1s spectrum reveals a significant increase in –CO3– functionalities at Eb ∼ 289.5 eV. O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Eb ∼ 283.3 eV), C–O (Eb ∼ 286.1 eV), and C
O (Eb ∼ 283.3 eV), C–O (Eb ∼ 286.1 eV), and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (Eb ∼ 284.6 eV) were also observed, which correspond to the typical SEI components discussed for carbon, including Li2CO3 and Li(CO3)–R–(CO3)Li. Finally, a noticeable shoulder peak was observed at Eb ∼ 283.0 eV, which corresponds to the formation of carbides and corroborates the Ni 2p peak at 849.7 eV.
C (Eb ∼ 284.6 eV) were also observed, which correspond to the typical SEI components discussed for carbon, including Li2CO3 and Li(CO3)–R–(CO3)Li. Finally, a noticeable shoulder peak was observed at Eb ∼ 283.0 eV, which corresponds to the formation of carbides and corroborates the Ni 2p peak at 849.7 eV.
The pre- and post-cycled high resolution XPS spectra for O 1s are also shown in Fig. 5. The O 1s XPS spectrum for the post-cycled electrode shows the presence of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Eb ∼ 533.5 eV) and C–O bonds (Eb ∼ 532.2 eV), which corroborates the C 1s spectrum for the formation of Li2CO3. Additional lithium alkyl carbonate species R–CH2
O (Eb ∼ 533.5 eV) and C–O bonds (Eb ∼ 532.2 eV), which corroborates the C 1s spectrum for the formation of Li2CO3. Additional lithium alkyl carbonate species R–CH2![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (C
(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OLi (Eb ∼ 532.2 eV) and R–CH2O(C
O)OLi (Eb ∼ 532.2 eV) and R–CH2O(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif)
![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) )OLi (Eb ∼ 533.5 eV) were also identified during the deconvolution. A less pronounced peak for Ni2O3 (Eb ∼ 530.3) was observed from the peak shoulder at 530.3 eV.
)OLi (Eb ∼ 533.5 eV) were also identified during the deconvolution. A less pronounced peak for Ni2O3 (Eb ∼ 530.3) was observed from the peak shoulder at 530.3 eV.
By coupling the XPS results with electroanalytical analysis of the RDS, it is possible to decouple the controlling processes in the reaction mechanism. There is a discrepancy in the effective transfer coefficient when comparing Region I to Region II/III and to Region IV. Like SEI formation on the carbon black control, αeff was ∼0.4. For carbon, the transfer coefficient is almost independent of the SOC, but for NiO αeff increased with the SOC from 0.41 to 0.67, suggesting a deviation in the reaction mechanism. More specifically, in Region IV the observed effective transfer coefficient is an amalgam of the competition between the SEI formation and the conversion. From previous work,34 it is known that the transfer coefficient for the conversion reaction is around 0.5. This means that the large positive deviation in the measured αeff must come from a process whose transfer coefficient is >0.5 and the only other process occurring is the latter stages of SEI formation, which is discussed below.
As the conversion and SEI formation simultaneously occur, there is likely a depletion of Li+ reactants near the anode surface. This phenomena does not affect the conversion due to the fact that the Ni+ transition state formed during the RDS is unstable and all the subsequent steps are relatively facile (i.e. the dissociation step and formation of Li2O is highly thermodynamically favorable). However, electrolyte reduction in its latter stages, just like carbon, relies on the reaction of free electrolyte that is trapped inside of the pore space formed during reaction in Region I. When this happens, the reaction is not just limited by surface activated electrolyte species, it also encounters a deficiency in Li+ ions that may be abstracted to form Li2CO3. This abstraction is energetically uphill, and if it becomes controlling, this chemical step would be the RDS and the resulting transfer coefficient would be 1 (![[small gamma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c3.gif) = 1, υ = 1, ρ = 0) and fully consistent with all of the experimental observations in this work. The likely mechanisms for both the MO conversion reaction and EC decomposition are summarized in Table 3. Interestingly, though the early-stage mechanisms for SEI formation on C and NiO are very similar, there appears to be a deviation in the latter stages that result in the formation of the inorganic products.
= 1, υ = 1, ρ = 0) and fully consistent with all of the experimental observations in this work. The likely mechanisms for both the MO conversion reaction and EC decomposition are summarized in Table 3. Interestingly, though the early-stage mechanisms for SEI formation on C and NiO are very similar, there appears to be a deviation in the latter stages that result in the formation of the inorganic products.
Fig. 6a shows TEM images of the mesoscale–scale structure of the post-cycled NiO. Compared to pre-cycled NiO (Fig. S2 in the ESI†), significant structural changes were observed. Some were expected, such as particle agglomeration – leading to a loss of distinguishable boundaries between particles. Also observed was the non-uniform deposition of SEI components onto the surface of the active material. In fact, NiO and SEI components were found to preferentially cluster, leading to fully agglomerated regions and partial vacancies in the SEI that can be areas for high reactivity.
High resolution TEM images in Fig. 6b show two regions in the SEI with multiple particles embedded into the SEI matrix. HAADF and EDS elemental mapping in Fig. 6c suggest that the SEI's elemental composition consists of C, O, F, P and Ni, confirming constituents of Li2CO3, Li(CO3)R(CO3)Li, LiF, trapped-Ni, etc. Also, from elemental mapping, some Ni clusters appear to be enveloped inside of the electronically insulating SEI. This indicates a possible aging mechanism that involves metals becoming trapped and detached from the bulk electrode. This metal-trapping mechanism leads to the active material becoming stuck in the charged state, reducing the achievable capacity. It also can sacrifice the mechanical integrity of the SEI itself, which relates back to the GITT results, where the apparent diffusion coefficient increased near the end of Region III. What is likely occuring is that the volumetric changes from the conversion reaction, coupled with the formation of the SEI forcing some particles off the surface, temporarily increase the porosity of the newly-formed SEI, allowing a different mode of transport (fully solid-state to liquid phase diffusion) to be active.
In summary, characteristic regions were isolated for conversion-based MOs anodes based on the thermodynamic, kinetic, and transport properties at different SOC. The reaction mechanisms were isolated for each region, which revealed very similar characteristics to the SEI formation process in Region 1 on carbon and Region I on MO. Unlike carbon, where only SEI formation and EDL storage were observed, MOs store charge via bond-breakage, which dominated the response for Regions II and III. The conversion reaction mechanism also occurs extensively in Region IV; however, increased driving force for SEI formation (lower potential) leads to a competition between the two reaction that revolves around the Li+ dissociation from the SEI. This results in a shift in the Tafel slope and the RDS for SEI formation from an electrochemical step to a chemical step with an αeff = 1. Cumulatively, it can be surmised that the SEI formation on NiO appears to initiate identically to carbon, though some surface may show a catalytic effect that needs to be studied further. However, the final stages of SEI formation, though they result in very similar inorganic products, appear to diverge mechanistically. It will be interesting in future studies by our group and others to see if the behavior on NiO is representative of at least a subset of all of the possible M–X materials, or if each conversion-based anode has unique chemistry during the formation of the SEI.
4. Conclusions
In this study, the results of GITT-derived apparent diffusion coefficients and apparent exchange current densities were paired with electrokinetic analysis and physical characterization to understand and decouple the competitive multi-step reactions for SEI formation on NiO, where NiO is used as a model M–X compound (M = V, Cr, Mn, Fe, Co, Ni, Cu, W, Mo, Ru and X = H, N, O, F, P, or S). M–X compounds are important next-generation anodes for Li-ion batteries that use conversion reactions to store significantly more charge than is possible with intercalation materials, and have much less volumetric expansion than alloying materials.SEI formation on NiO was broken down into four regions. At the beginning of SEI formation on NiO in Region I, the results were very consistent to those observed during early-stage SEI formation on carbon, suggesting that SEI formation begins very similarly from a mechanistic perspective. After the early stages of SEI formation, behavior in Regions II and III were dominated by the conversion reaction itself with little contribution to the SEI formation. The conversion reaction did result in some volumetric expansion and some particle detachment from the surface, with those detached particles being embedded in the SEI. In Region IV, a densified SEI layer is formed, just like on carbon-based materials, but the mechanism for that formation is different. On carbon-based materials the formation of the dense SEI is limited by the electrochemical activation of low concentration EC-intermediates on the surface. For NiO, the nature of the RDS to form the dense SEI is consistent with Li+ abstraction from the SEI. In the future, these new insights can help battery manufacturers to engineering appropriate environments and pre-treatment protocols to build robust SEI layers on this family of materials, enabling long-life, stable, high capacity Li-ion batteries.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge state funds through the University of South Carolina for the financial support to execute this project.References
- E. S. Davide Castelvecchi, Nature, 2019, 574, 308 CrossRef PubMed.
- P. L. Taberna, S. Mitra, P. Poizot, P. Simon and J. M. Tarascon, Nat. Mater., 2006, 5, 567 CrossRef CAS PubMed.
- D. Kim, M. Park, S. M. Kim, H. C. Shim, S. Hyun and S. M. Han, ACS Nano, 2018, 12, 10903 CrossRef CAS PubMed.
- D. Lin, Y. Liu and Y. Cui, Nat. Nanotechnol., 2017, 12, 194 CrossRef CAS PubMed.
- A. Palmieri, S. Yazdani, R. Kashfi-Sadabad, S. G. Karakalos, B. Ng, A. Oliveira, X. Peng, M. T. Pettes and W. E. Mustain, Improved Capacity Retention of Metal Oxide Anodes in Li-Ion Batteries: Increasing Intraparticle Electronic Conductivity through Na Inclusion in Mn3O4, ChemElectroChem, 2018, 5, 2059–2063 CrossRef CAS.
- N. Zhu, S. Han, S. Gan, J. Ulstrup and Q. Chi, Adv. Funct. Mater., 2013, 23, 5297 CrossRef CAS.
- B. Ng, P. T. Coman, E. Faegh, X. Peng, S. G. Karakalos, X. Jin, W. E. Mustain and R. E. White, ACS Appl. Energy Mater., 2020, 3, 3653 CrossRef CAS.
- S. Gao, L. Lu, M. Ouyang, Y. Duan, X. Zhu, C. Xu, B. Ng, N. Kamyab, R. E. White and P. T. Coman, J. Electrochem. Soc., 2019, 166, A2065 CrossRef CAS.
- B. Ng, X. Duan, F. Liu, E. Agar, R. E. White, W. E. Mustain and X. Jin, J. Electrochem. Soc., 2020, 167, 020523 CrossRef CAS.
- B. Ng, P. T. Coman, W. E. Mustain and R. E. White, J. Power Sources, 2020, 445, 227296 CrossRef CAS.
- T. F. Fuller and J. Newman, J. Electrochem. Soc., 1994, 141, 855 Search PubMed.
- F. A. Soto, A. Marzouk, F. El-Mellouhi and P. B. Balbuena, Chem. Mater., 2018, 30, 3315 CrossRef CAS.
- M. Lanz and P. Novák, J. Power Sources, 2001, 102, 277 CrossRef CAS.
- M. Steinhauer, S. Risse, N. Wagner and K. A. Friedrich, Electrochim. Acta, 2017, 228, 652 CrossRef CAS.
- H. G. Steinrück, C. Cao, Y. Tsao, C. J. Takacs, O. Konovalov, J. Vatamanu, O. Borodin and M. F. Toney, Energy Environ. Sci., 2018, 11, 594 RSC.
- D. Aurbach, B. Markovsky, I. Weissman, E. Levi and Y. Ein-Eli, Electrochim. Acta, 1999, 45, 67 CrossRef CAS.
- T. Li and P. B. Balbuena, Chem. Phys. Lett., 2000, 317, 421 CrossRef CAS.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood, Carbon, 2016, 105, 52 CrossRef CAS.
- S. Wang, W. Zhang, Y. Chen, Z. Dai, C. Zhao, D. Wang and C. Shen, Appl. Surf. Sci., 2017, 426, 217 CrossRef CAS.
- S. Wang, K. Yang, F. Gao, D. Wang and C. Shen, RSC Adv., 2016, 6, 77105 RSC.
- Y. Sun, N. Liu and Y. Cui, Nat. Energy, 2016, 1, 16071 CrossRef CAS.
- C. Shen, S. Wang, Y. Jin and W. Q. Han, ACS Appl. Mater. Interfaces, 2015, 7, 25441 CrossRef CAS PubMed.
- X. Wang, R. Kerr, F. Chen, N. Goujon, J. M. Pringle, D. Mecerreyes, M. Forsyth and P. C. Howlett, Adv. Mater., 2020, 32, 1905219 CrossRef CAS PubMed.
- C. Yan, R. Xu, Y. Xiao, J. F. Ding, L. Xu, B. Q. Li and J. Q. Huang, Adv. Funct. Mater., 2020, 30, 1 Search PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS.
- P. Li, J. Y. Hwang and Y. K. Sun, ACS Nano, 2019, 13, 2624 CAS.
- B. Ng, X. Peng, E. Faegh and W. E. Mustain, J. Mater. Chem. A, 2020, 8, 2712 RSC.
- H. Wang, J. Fu, C. Wang, J. Wang, A. Yang, C. Li, Q. Sun, Y. Cui and H. Li, Energy Environ. Sci., 2020, 13, 848 RSC.
- O. Elishav, Y. Shener, V. Beilin, G. E. Shter, B. Ng, W. E. Mustain, M. V. Landau, M. Herskowitz and G. S. Grader, Nanoscale, 2020, 12, 12993 RSC.
- H. Liu, Q. Li, Z. Yao, L. Li, Y. Li, C. Wolverton, M. C. Hersam, J. Wu and V. P. Dravid, Adv. Mater., 2018, 30, 1 Search PubMed.
- J. Deng, X. Yu, X. Qin, D. Zhou, L. Zhang, H. Duan, F. Kang, B. Li and G. Wang, Adv. Energy Mater., 2019, 9, 1 Search PubMed.
- W. Ren, D. Liu, C. Sun, X. Yao, J. Tan, C. Wang, K. Zhao, X. Wang, Q. Li and L. Mai, Small, 2018, 14, 1 Search PubMed.
- N. S. Spinner, A. Palmieri, N. Beauregard, L. Zhang, J. Campanella and W. E. Mustain, J. Power Sources, 2015, 276, 46 CrossRef CAS.
- A. Palmieri, N. Spinner, S. Zhao and W. E. Mustain, Carbon, 2018, 130, 515 CrossRef CAS.
- S. Yan, H. Song, S. Lin, H. Wu, Y. Shi and J. Yao, Adv. Funct. Mater., 2019, 29, 1 Search PubMed.
- J. Hao, J. Zhang, G. Xia, Y. Liu, Y. Zheng, W. Zhang, Y. Tang, W. K. Pang and Z. Guo, ACS Nano, 2018, 12, 10430 CrossRef CAS PubMed.
- N. Spinner, L. Zhang and W. E. Mustain, J. Mater. Chem. A, 2014, 2, 1627 RSC.
- Y. Lu, J. Nai and X. W. D. Lou, Angew. Chem., Int. Ed., 2018, 57, 2899 CrossRef CAS PubMed.
- Z. Liu, X. Y. Yu and U. Paik, Adv. Energy Mater., 2016, 6, 3 Search PubMed.
- S. Shrestha and W. E. Mustain, J. Electrochem. Soc., 2010, 157, B1665 CrossRef CAS.
- D. Zhao, J. Feng, Q. Huo, N. Melosh, G. H. Fredrickson, B. F. Chmelka and G. D. Stucky, Science, 1998, 279, 548 CrossRef CAS PubMed.
- S. Fletcher, J. Solid State Electrochem., 2009, 13, 537 CrossRef CAS.
- M. Z. Bazant, Acc. Chem. Res., 2013, 46, 1144 CrossRef CAS PubMed.
- J. O. M. Bockris and Z. Nagy, J. Chem. Educ., 1973, 50, 839 CrossRef CAS.
- P. Bai and M. Z. Bazant, Nat. Commun., 2014, 5, 1 Search PubMed.
- D. T. Boyle, X. Kong, A. Pei, P. E. Rudnicki, F. Shi, W. Huang, Z. Bao, J. Qin and Y. Cui, ACS Energy Lett., 2020, 5, 701 CrossRef CAS.
- B. C. Han, A. Van Der Ven, D. Morgan and G. Ceder, Electrochim. Acta, 2004, 49, 4691 CrossRef CAS.
- D. Aurbach, M. Moshkovich, Y. Cohen and A. Schechter, Langmuir, 1999, 15, 2947 CrossRef CAS.
- D. Aurbach, M. D. Levi, E. Levi and A. Schechter, J. Phys. Chem. B, 1997, 101, 2195 CrossRef CAS.
- C. R. Yang, Y. Y. Wang and C. C. Wan, J. Power Sources, 1998, 72, 66 CrossRef CAS.
- Y. Wang, S. Nakamura, K. Tasaki and P. B. Balbuena, J. Am. Chem. Soc., 2002, 124, 4408 CrossRef CAS PubMed.
- S. Ahamad and A. Gupta, Electrochim. Acta, 2019, 297, 916 CrossRef CAS.
- R. A. Marcus, Angew. Chem., Int. Ed. Engl., 1993, 32, 1111 CrossRef.
- M. Lu, H. Cheng and Y. Yang, Electrochim. Acta, 2008, 53, 3539 CrossRef CAS.
- P. Lu, C. Li, E. W. Schneider and S. J. Harris, J. Phys. Chem. C, 2014, 118, 896 CrossRef CAS.
- Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708 CrossRef CAS PubMed.
- J. A. Gilbert, J. Bareño, T. Spila, S. E. Trask, D. J. Miller, B. J. Polzin, A. N. Jansen and D. P. Abraham, J. Electrochem. Soc., 2017, 164, A6054 CrossRef CAS.
- D. C. Bock, G. H. Waller, A. N. Mansour, A. C. Marschilok, K. J. Takeuchi and E. S. Takeuchi, J. Phys. Chem. C, 2018, 122, 14257 CrossRef CAS.
- S. Chattopadhyay, A. L. Lipson, H. J. Karmel, J. D. Emery, T. T. Fister, P. A. Fenter, M. C. Hersam and M. J. Bedzyk, Chem. Mater., 2012, 24, 3038 CrossRef CAS.
- Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708 CrossRef CAS PubMed.
- Y. Wang, S. Nakamura, K. Tasaki and P. B. Balbuena, J. Am. Chem. Soc., 2002, 124, 4408 CrossRef CAS PubMed.
- S. Y. Vassiliev, V. V. Sentyurin, E. E. Levin and V. A. Nikitina, Electrochim. Acta, 2019, 302, 316 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta09683k |
| This journal is © The Royal Society of Chemistry 2021 |

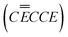
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) SEI + Li+
SEI + Li+