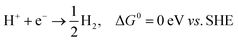Design of phosphorus-functionalized MXenes for highly efficient hydrogen evolution reaction†
Youchao
Kong‡
a,
Shanshan
Yan‡
a,
Jinxian
Feng
a,
Shuangpeng
Wang
 *ab and
Hui
Pan
*ab and
Hui
Pan
 *ab
*ab
aMOE Joint Key Laboratory, Institute of Applied Physics and Materials Engineering, University of Macau, Macao SAR, 999078, P. R. China. E-mail: huipan@um.edu.mo; spwang@um.edu.mo; Fax: 853-88222454; Tel: 853-88224427
bDepartment of Physics and Chemistry, Faculty of Science and Technology, University of Macau, Macao SAR, 999078, P. R. China
First published on 27th November 2020
Abstract
As an important family of 2D materials, MXenes show great potential in various applications due to their specific physical and chemical properties, such as high conductivity and surface activity. Here, we investigate 54 phosphorus-functionalized MXenes (P-MXenes) and screen out 10 stable structures by analyzing their dynamical, thermal, and mechanical stabilities based on first-principles calculations. We find that these stable P-MXenes remain metallic and show weak magnetism. We show that they are effective as electrocatalysts for the hydrogen evolution reaction (HER) with near-zero Gibbs free energies of hydrogen adsorption, which are comparable to that of Pt. To understand the microkinetic process in the HER, an explicit water model is used to examine the Volmer–Heyrovsky (V–H) and Volmer–Tafel (V–T) pathways. We find that P-MXenes show a high HER performance along the V–H process due to the low activation barrier. Our systematic study confirms the possibility for the phosphorus-functionalization of MXenes, guides the design of novel electrocatalysts for the HER via surface-modification, and provides deep understanding on the HER mechanism.
1 Introduction
Two-dimensional (2D) materials have been intensively studied from theoretical and experimental perspectives due to their excellent physical and chemical properties, such as semiconductivity, strong spin-orbital coupling, high conductivity, and chemical activity.1,2 2D materials, such as graphene, black phosphorus, transition metal dichalcogenides, and hexagonal boron nitride, have shown wide-range applications spanning from devices, optoelectronics, sensors, and catalysts, to medical science and technology.3–5 As a fast-growing family of 2D materials, MXenes have recently attracted increasing attention because of their unique combination of various properties, such as electrical conductivity, mechanical property, and chemical activity, which result especially in application for energy storage and harvesting, such as Li batteries, supercapacitors, and catalysis.6,7 MXenes are 2D transition metal carbides or nitrides with a general formula of Mn+1Xn (n = 1–3), where the metal atoms are exposed on their surfaces. MXenes have strong interaction with small molecules, such as O2 and H2O, and show high activity in the oxygen reduction reaction (ORR) and water splitting.8–10Normally, MXenes could be obtained by chemically etching their precursors, leading to a functionalized surface with various functional groups, such as O, F, Cl, OH, and N.11–16 Surface-functionalized MXenes exhibit different physical and chemical properties from their pristine counterparts. For example, Ti2CO2 is semiconducting, while Ti2C is metallic.17 Most importantly, surface functionalization benefits the catalytic performance of MXenes. For example, oxygen-functionalized Ti3C2 (Ti3C2O2) presented the best HER activity with a nearly perfect Gibbs free energy (∼0 eV) at a H coverage of 4/8, much better than that of bare Ti3C2 (∼−1.4 eV).18 Therefore, novel properties, such as improved catalytic activity and long-term stability, could be developed in MXenes by modifying their surface chemistry.19–21
Recently, phosphorized MoCTx was obtained by a simple phosphorization, and showed improved HER activity, indicating the potentially excellent properties of MXenes in combination with the P element.22 Moreover, as an earth-abundant element (∼0.1%), phosphorus plays a vital role in modern society; then how to fully use it is also a hot issue in scientific research.23 To the best of our knowledge, however, there is no systematic investigation of phosphorus-functionalized MXenes (P-MXenes) and their application in catalysis. In this work, we present a comprehensive study on 54 P-functionalized M2C (M = transition metals) monolayers in different symmetries (2H-CC, 2H-CH, 2H-HH, 1T-CC, 1T-CH, and 1T-HH) and evaluate their structural, mechanical, magnetic, electronic and catalytic properties based on density-functional theory (DFT) calculations. We find that 10 structures are dynamically, mechanically, and thermodynamically stable. We show that M2CP2 remains metallic and some of the monolayers exhibit weak or no magnetism due to the anti-magnetic moment of P or the hybridization between TM-d (TM-transition metal) and P-p orbitals. We further show that their phases could be transferred between 2H-CH and 2H-HH/-CC with a low energy barrier. P-MXenes demonstrate excellent HER performance because the Gibbs free energy of hydrogen adsorption is near zero at certain H coverages. Based on an explicit water model, we find that the H* reduction on P-MXenes via the V–H process experiences a relatively low energy barrier at the equilibrium electrode potential.
2 Computational methods
All the computations were performed based on density-functional theory (DFT), as implemented in the Vienna Ab initio Simulation Package (VASP).24,25 The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation was used for the exchange–correlation energy.26 The cutoff energy for the plane-wave basis was 500 eV. The coverage tolerances for energy and force were set to 10−5 eV and −0.02 eV Å−1, respectively. The Brillouin zone was sampled with a K-point of 4 × 4 × 1 for the supercell 3 × 3 × 1 in reciprocal space during geometry optimization.27 To avoid interaction between neighboring images, a vacuum space of >15 Å was adopted in the z direction. The standard hydrogen electrode (USHE) was theoretically defined in solution (pH = 0, p(H2) = 1 bar). The DFT-D3 method was adopted to include dispersion correction for the hydrogen bonding between water molecules.28 The climbing-image nudged elastic band (CI-NEB) method29 implemented in VASP was used to determine the diffusion energy barrier and the minimum energy pathways for H2 evolution on the P-MXene surface. The transition states were obtained by relaxing the force below 0.05 eV Å−1. Only one imaginary frequency exists in the transition state.In an acid solution, the overall HER pathway can be described as:30
Upon setting the reference potential to be that of the standard hydrogen electrode (SHE), the chemical potential (chemical potential per H) for the initial (H+ + e−) and final (1/2H2) states is equal.31 Hence, the Gibbs free energy of an intermediate adsorbed hydrogen (H*) is an important descriptor for the HER activity of the electrocatalyst, and the HER performance can be quantified using the reaction Gibbs free energy of hydrogen adsorption (ΔGH),
| ΔGH = ΔEH + EZPE − TΔS |
| ΔEH = E[nH] − E[(n − 1)H] − 1/2E[H2] |
3 Results and discussion
In this work, we focus on searching for new stable P-functionalized MXenes (M2CP2), which have a five-atom-thick layer in a sequence of P–M–C–M–P. Considering that there are two possible phases (2H and 1T) and three alignments (CC, CH, and HH) of the P atom on the surfaces of M2C, there are six structures for each M2CP2 (Fig. 1). Specifically, there are two possible sites for P to stay, top carbon (C) and the center of the honeycomb (H). If the P atoms at both sides occupy the C or H sites, these structures are named M2CP2-2H(1T)-CC or M2CP2-2H(1T)-HH. Otherwise, the structure is denoted as M2CP2-2H(1T)-CH, in which the P atoms align asymmetrically on both sides. In the family of 2D M2CP2, M is the transition metal (TM), including 3d (Ti, V, and Cr), 4d (Zr, Nb, and Mo), and 5d (Hf, Ta, and W) elements. To evaluate the structural stability and possible experimental realization, a series of calculations are carried out, including structure optimization, formation energy, phonon dispersion, mechanical property, and ab initio molecular dynamics (AIMD) simulation.33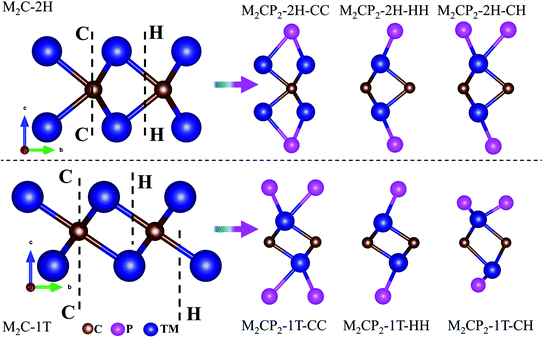 | ||
| Fig. 1 Side views of optimized 2D M2C and P-functionalized M2C (M2CP2) with different symmetries. Blue, brown and purple denote transition metals, carbon and phosphorus, respectively. | ||
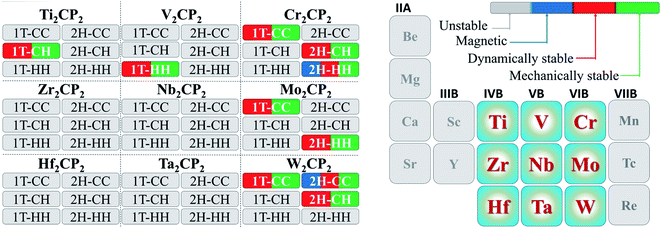
3.1 Structure optimization and stability
We first carried out calculations to confirm the dynamical stabilities of the designed structures. Our computations indicate that all structures of M2CP2 for M = Zr, Nb, Hf, and Ta are dynamically unstable because of the large imaginary frequencies in the Brillouin zone (Fig. S1–S6†). For M = Ti, V, Cr, Mo, and W, some M2CP2 structures show the perfect phonon dispersion spectra (Fig. S7†). Specifically, Cr2CP2 (W2CP2) is stable in 1T-CC, 2H-CH (2H-CC), and 2H-CH phases (Fig. S8†). Mo2CP2 has two possible stable structures, Mo2CP2-1T-CC/2H-HH (Fig. S9†). Ti2CP2 and V2CP2 exhibit only one stable structure, that is, Ti2CP2-1T-CH and V2CP2-1T-HH (Fig. S9†). We further screen out the stable structures by AIMD at 300 K for 2 ps with a time step of 1 fs. The results show that all the above predicted structures are stable at room temperature (Fig. S10†).Additionally, the mechanical stability is calculated. For 2D materials, the criteria for evaluating mechanical stability are based on the Born principle,34 by calculating four nonzero elastic constants c11, c22, c12, and c66 using the standard Voigt notation.35 Moreover, the hexagonal structure further reduces the complexity, since c11 = c22 and c66 = (c11 − c12)/2 according to the symmetry.34 Then the 2D membrane is stable if the in-plane planar Young's (Yx, Yy) and shear moduli (Gxy) are positive, which are calculated below:
| Yx = (c11c22 − c12c21)/c22 |
| Yy = (c11c22 − c12c21)/c11 |
| Gxy = c66 |
The strain–stress method is adopted to calculate Yx and Gxy,36 and graphene is taken as a reference. The calculated Young's and shear moduli of graphene are 341.42 and 144.82 N m−1 (Table 1), respectively, which are in good agreement with the previous study.35 Although the mechanical strengths of P-MXenes could not be compatible with that of graphene due to the much smaller values of Young's and shear moduli, their mechanical stabilities are promising because of the positive Yx and Gxy (Table 1).
| c 11 (N m−1) | Y x (N m−1) | Y y (N m−1) | G xy (N m−1) | |
|---|---|---|---|---|
| Graphene | 352.68 | 341.42 | 341.42 | 144.82 |
| W2CP2-1T-CC | 174.12 | 128.64 | 128.64 | 42.57 |
| W2CP2-2H-CC | 214.19 | 95.38 | 95.38 | 27.33 |
| W2CP2-2H-CH | 202.15 | 136.09 | 136.09 | 43.30 |
| Cr2CP2-1T-CC | 152.31 | 131.15 | 131.15 | 47.77 |
| Cr2CP2-2H-HH | 219.16 | 144.30 | 144.30 | 45.54 |
| Cr2CP2-2H-CH | 208.98 | 131.04 | 131.04 | 40.68 |
| Mo2CP2-2H-HH | 199.15 | 132.12 | 132.12 | 41.81 |
| Mo2CP2-1T-CC | 158.05 | 125.28 | 125.28 | 43.04 |
| Ti2CP2-1T-CH | 171.13 | 144.43 | 144.43 | 51.77 |
| V2CP2-1T-CH | 147.36 | 63.06 | 63.06 | 17.95 |
| V2CP2-1T-HH | 181.33 | 110.95 | 110.95 | 34.18 |
We further calculated the formation energy (Ef) to evaluate the possibility for the experimental realization of stable 2D P-MXenes using Ef = E(M2CP2) − E(M2C) − 2E(P), where E(M2CP2) and E(M2C) are the total energies of 2D M2CP2 and M2C, respectively, and E(P) is the chemical potential of the P atom obtained from the total energy of its unit cell divided by the number of atoms in the cell. The results show that most of the processes are exothermic due to the negative formation energy (Table S1†), indicating that they could be fabricated in experiments. However, Ti2CP2-1T-CH exhibits a large positive Ef of 11.64 eV, leading to less possibility for its experimental realization (endothermic process).
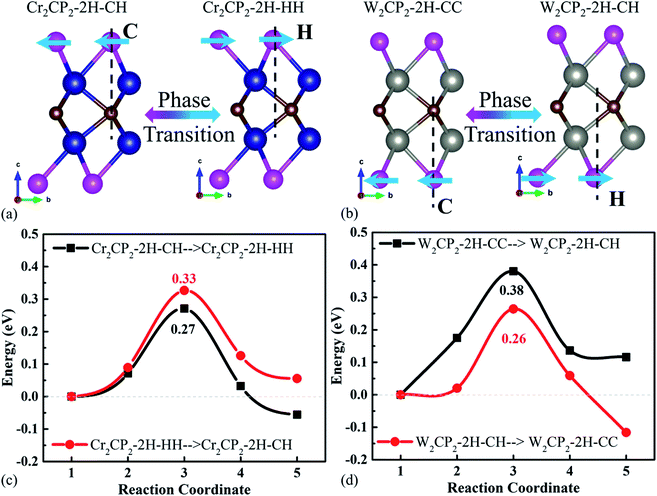
It was recently reported that the phase transition of MXenes could be resulting from oxygen coverage.37 Meanwhile, we see that the energies of the designed structures with the same formula are close to each other (Table S2†). For example, the energy difference between Cr2CP2-2H-CH (W2CP2-2H-CC) and Cr2CP2-2H-HH (W2CP2-2H-CH) is merely 0.05 (0.12) eV, indicating that the phase transition would happen between these two phases. To confirm this point, the CI-NEB method was adopted to investigate the kinetic transition barrier using Cr2CP2 and W2CP2 as examples (Fig. 2). The P atoms aligned to the C atoms move to the center of the honeycomb, leading to the phase transition from 2H-CC (2H-CH) to 2H-CH (2H-HH) (Fig. 2a and b). We find that the transition barriers are quite small, 0.27 and 0.26 eV for 2H-CH to 2H-HH and 2H-CH to 2H-CC, respectively (Fig. 2c and d). Reversely, the barriers are slightly higher, 0.33 and 0.38 eV for the transitions, respectively. Additionally, 1T-CC is believed to be the ground states of Cr2CP2 , Mo2CP2, and W2CP2, due to the more negative system energies (Table S2†). It is believed that the stable stacking of P-MXenes is important to their physical and chemical properties.37 Moreover, the low energy barrier for a phase transition is beneficial to volume stability when external ions or molecules are adsorbed on the surface of P-MXenes, leading to potential application in ion-batteries38 and catalysis.39
3.2 Electronic and magnetic properties
The above analysis shows that ten 2D M2CP2 structures are dynamically, thermally, and mechanically stable. Based on the optimized structures, we investigated their electronic and magnetic properties. We find that all the stable 2D M2CP2 structures are metallic, as indicated by their gapless band structures near the Fermi level (Fig. S11 and S12†). Herein, the surface covered with the P atoms cannot change its highly conductive properties, which should be beneficial to its catalytic applications.Different from the electronic properties, the magnetism of 2D M2CP2 becomes weak or even disappears compared with the magnetic M2C. The calculated results show that only Cr2CP2-2H-HH and W2CP2-2H-CC have non-zero magnetic moments, which are mainly contributed to Cr (0.28 μB) and W atoms (0.09 μB) (Fig. S12†). Specifically, a large magnetic moment in Cr2C is quenched by the P atom after the surface functionalization. To understand the change, the spin-polarized partial densities of states (PDOSs) of Cr and P were calculated for Cr2C and Cr2CP2-1T-CC. The 2D and 3D charge density differences were also calculated to find the charge transfer between P and Cr. We can see that the strong magnetism in Cr2C is contributed to the high asymmetry of spin-up and spin-down Cr-d states, especially the localized Cr-d orbitals near the Fermi level (dashed line at 0 eV, Fig. 3). However, the electrons between Cr and C redistribute and accumulate between Cr and P when the surfaces of Cr2C are covered with the P atoms, leading to a symmetric distribution of spin-up and spin-down PDOSs. Then, the system magnetic moment of Cr2CP2 disappears. The results confirm that the magnetic properties of MXenes depend on their terminal groups.40
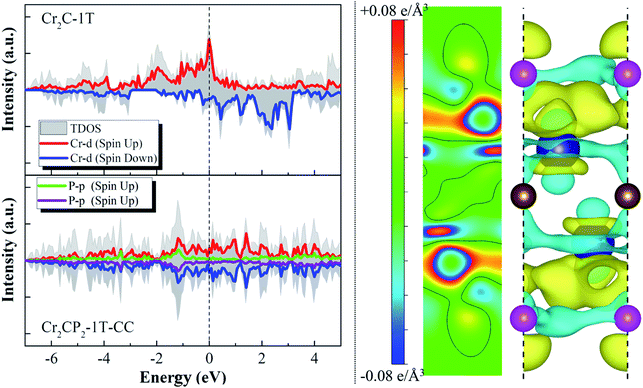 | ||
| Fig. 3 Spin-polarized densities of states (DOSs) of Cr2C-1T and Cr2CP2-1T-CC (left column); 2D and 3D charge density differences of Cr2CP2-1T-CC (right column). The isosurface is set to 0.06e Å−3. | ||
Based on the above analysis, the physical properties of the 54 designed M2CP2 monolayers are summarized (Fig. 4).
3.3 ΔGH on M2CP2 and the optimal coverage
Pure M2C with transition metals exposed on the surfaces has been proved to effectively split water molecules. However, the strong M–H bonding impedes the reaction rate, as indicated by the large Gibbs free energy (ΔGH) of *H (<−1.0 eV).41 The moderate strength of the P–H bond has been proved to facilitate the HER activity in phosphorus-based materials.31,42 Metallic M2CP2 also has high conductivity, which is a prerequisite for electrocatalysis (Fig. S11 and S12†). Hence, it is meaningful to study the HER performance of stable M2CP2 with high intrinsic conductivity and rich-P surfaces.In thermal equilibrium, ΔGH qualitatively evaluates the HER performance in an acid situation. ΔGH is more close to 0 eV, so the reaction is faster.30 We consider all possible adsorption sites of *H on one surface of M2CP2 (H1–H3, Fig. S13a†). The results indicate that H prefers the H1 site (top of the P atom), due to the lowest adsorption energy (Table S3†). It is noted that some predicted stable M2CP2 shows large surface distortion at a certain H coverage due to the relatively small Young's moduli (Table 1). For example, V2CP2 shows large surface distortion when only one H adsorbs on it because its Yx (63.06 N m−1) is the smallest among the 10 stable structures (Fig. S14†). W2CP2-2H-CC and Mo2CP2-2H-HH could remain stable until the second and third H atom anchors, due to the relatively large Yx (Fig. S14† and Table 1). The large surface distortion means that these M2CP2 structures may be unstable in the HER process, which will not be considered in the following discussion.
Then, we calculated ΔGH as a function of H coverage in the absence of a water layer (Fig. 5). The results suggest that a P-MXene is catalytically active for the HER, due to the overall low values for the adsorption energy (<|0.5 eV|). Compared with P-MXenes with M = 3d elements (e.g. Cr), 4d and 5d element (e.g. Mo and W) based P-MXenes have stronger H adsorption at low coverage, as indicated by the Barge charge analysis (Fig. S17†). For example, ΔGH is around −0.1 eV for Cr2CP2-2H-CH at a hydrogen coverage of 1/9 (Fig. 5a), while that of W2CP2-2H-CH is about −0.42 eV (Fig. 5b). We can see that free energy close to 0 eV happens at a hydrogen coverage from 1/9 to 3/9 for Cr2CP2, while 3/9–5/9 for Mo2CP2 and W2CP2. Hence, the HER is optimal at a H coverage of 2/9 for Cr2CP2 and 4/9 for W- or Mo-based P-MXenes, respectively.
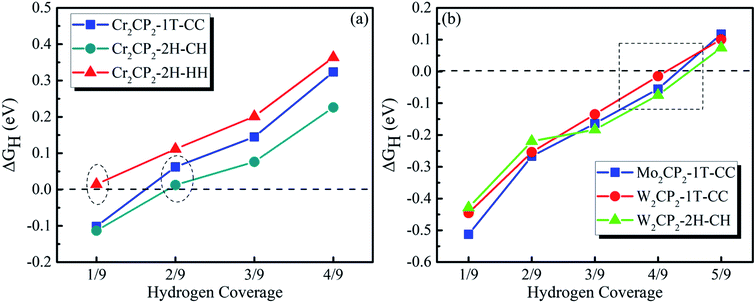 | ||
| Fig. 5 Calculated ΔGH as a function of hydrogen coverage on (a) Cr2CP2 and (b) Mo2/W2CP2, respectively. | ||
As reported, ΔGH is related not only to the binding energy between H and the slab, but also to the coverages (numbers and arrangement) of H atoms on the active surface.43 Therefore, we analyze the effect of these two factors on the HER in detail (ESI†). We find that the value of charge transfer in the previous step dramatically affects the HER performance in the next step and nearly all M2CP2 structures prefer the pathway of R4 (P1 → P13 → P124 → P1234) (Fig. S16 and S17†). Our result shows that the HER performance is sensitive to the H coverage and arrangement on the surface, which provides a guidance for the HER improvement by controlling the active sites and the distance between adsorbed H through space confinement.44
3.4 Water–catalyst interface
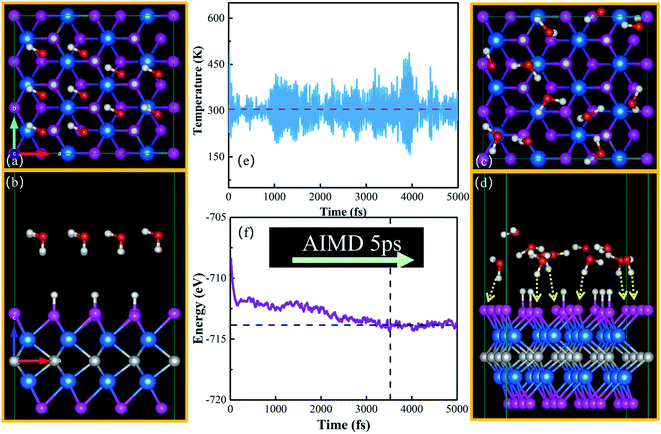
The above evaluation of the HER performance on M2CP2 is based on the thermoneutral electrode potential (ΔGH → 0 eV). Although most materials have a ΔGH quite close to that of Pt(111) (0.08 eV), their HER performances cannot be comparable to that of Pt(111), that is, the principle of G ∼ 0 eV for hydrogen evolution cannot explain the observed kinetics only.45 Recently, an explicit water model was proposed to evaluate the Volmer, Tafel, and Heyrovsky steps from microkinetic perspectives (Fig. S19†).Then, we examine the HER microkinetic activity around the H coverage for optimal HER (Fig. 6) using W2CP2-2H-CH (WCH) as an example. The water–catalyst interface is a crucial part in this simulation. We adopted the approach proposed by Lindgren et al., which was initially used to study the HER on Pt(111).45 The Helmholtz layer is often set to a 3 Å electrical double layer, which can be represented by one water layer. By tuning the number of H atoms, the electrostatic potential of the interface can be adjusted, which is deduced from the calculation of the work function.45
Here, we put one layer of water molecules on the surface of H-adsorbed WCH. A supercell with a size of 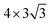 units and a H coverage of 6/12 was used. The initial setup of the water layer is that the H atoms of each H2O molecule point down toward the surface, as proposed by Tang Qi et al.46 (Fig. 6a and b). A stable water layer with 10H2O molecules is achieved by AIMD simulation at 300 K for 5 ps. The tiny variation of energy indicates that the water layer is stable after 3.5 ps (dashed line, Fig. 6f). We find that there has a weak bonding between P and H2O, as highlighted by the yellow dashed arrow (Fig. 6d). Since there is no experimental study on the exact structure of the water overlayer on WCH, we calculated the electrode potential corresponding to the model system at −0.28 V, in comparison with a NHE (4.4 V, Fig. S12†), which agrees well with a previous study.47
units and a H coverage of 6/12 was used. The initial setup of the water layer is that the H atoms of each H2O molecule point down toward the surface, as proposed by Tang Qi et al.46 (Fig. 6a and b). A stable water layer with 10H2O molecules is achieved by AIMD simulation at 300 K for 5 ps. The tiny variation of energy indicates that the water layer is stable after 3.5 ps (dashed line, Fig. 6f). We find that there has a weak bonding between P and H2O, as highlighted by the yellow dashed arrow (Fig. 6d). Since there is no experimental study on the exact structure of the water overlayer on WCH, we calculated the electrode potential corresponding to the model system at −0.28 V, in comparison with a NHE (4.4 V, Fig. S12†), which agrees well with a previous study.47
Then, a proton (H+) is added onto the water molecule to introduce a hydronium ion (H3O+),46 which is further optimized to obtain a stable structure (Fig. S20†). The possible pathways for HER include the Volmer–Heyrovsky (V–H) and Volmer–Tafel (V–T) reactions in acid media (Fig. S19†). It is believed that the Volmer process is very fast, in which initial adsorption of a proton from the acid solution takes place to form an adsorbed H*. Then, if a dissolved proton from the water layer reacts with H* on the surface of the catalyst, H2 is generated, which is called the V–H reaction (Fig. S20†). If two H*s evolve into one H2, the process is called the V–T mechanism (Fig. S20†). Since there are proton–electron transfers in a supercell with a periodic boundary, we will use the extrapolation method to counterbalance the changed electrode potential along this pathway.46 That is, the reaction energy (ΔE = E(FS) − E(IS)) and activation energy (Ea) at balanced electrode potential (ΔU = 0, work function difference between the IS (initial step) and FS (final step)) will be achieved by extrapolating the results to the balanced electrode potential (Fig. S21†).
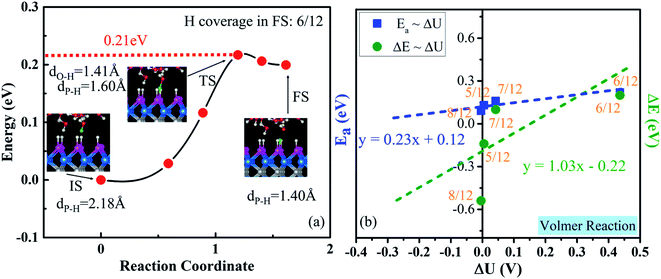
3.5 First step of the HER process: Volmer reaction
Now, we consider the very first step: the Volmer step, which is indicated by the minimum-energy path for the transfer of one proton to the WCH surface (Fig. 7a). It exhibits quite a small activation energy of 0.21 eV and a reaction energy of 0.20 eV. In the transition state, the transferred H is in the middle between O and P, dO–H = 1.41 Å and dP–H = 1.60 Å. To obtain the reaction energy (ΔE) and activation energy (Ea) at the balanced electrode potential, we extrapolate our results by studying the Volmer reaction around the optimal H coverage (Fig. 7b and S22†) and the change of ΔU between the IS and FS (Table S4†). The extrapolated Ea and ΔE are 0.12 and −0.22 eV, respectively, indicating that the Volmer step is exothermic (ΔE < 0) and has a small energy barrier at an electrode potential around −0.28 V vs. NHE on the WCH monolayer.3.6 Second step of the HER process: V–H reaction
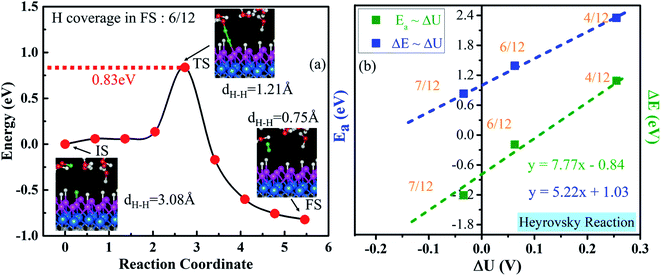
As illustrated in Section 3.4, the V–H reaction needs a proton–electron pair in the water layer to attack one surface H* (Heyrovsky step), where one H* is approached by a hydrogen ion of H3O+ in the water layer and breaks to form H2 (Fig. 8a). We find that a surface H* and a proton start to approach from a distance of 3.08 Å and break from the catalyst's surface and H3O+ when they are close to 1.21 Å. Then, they climb a barrier of 0.83 eV to overcome the transition step (TS). Lastly, they evolve into one weakly adsorbed H2 molecule with a dH–H of 0.75 Å above the catalyst. The corresponding activation energy and reaction energy are 0.83 eV and −0.82 eV at a H coverage of 6/12 (final state), respectively. We also calculate Ea and ΔE at different H coverages (Fig. S23†). Similar to those for the Volmer step, the extrapolated Ea and ΔE for the Heyrovsky reaction are 1.03 and −0.84 eV, respectively (Fig. 8b). Therefore, the H desorption is the rate-determining step in the V–H pathway, due to the much larger activation barrier, compared with that of the Volmer step (0.12 eV, Fig. 7).3.7 Second step of the HER process: V–T reaction
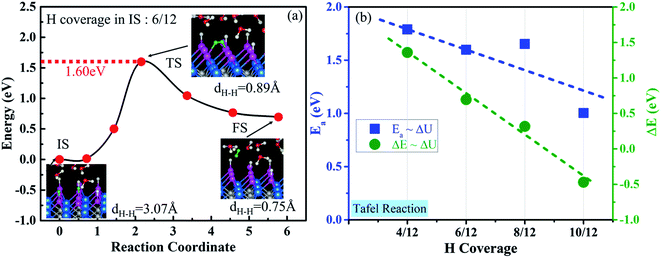
Two surface H atoms evolve into one H2 in the Tafel process, where there is no extra charge transfer between the water layer and catalyst (Fig. S20†). Therefore, the work function remains unchanged from the initial state to the final state, leading to an uncharged surface potential during the reaction (Fig. S21d†). To evaluate the formation of H2 from two H*s, the activation and reaction energies were calculated (Fig. S19†) on the WCH surface with a H coverage of 6/12. We find that two adjacent H atoms have a distance (H*–H*) of 3.07 Å in the IS. They approach each other and form a TS with a dH–H of 0.89 Å. In the final state, the evolved H2 molecule desorbs from the WCH surface with a H–H bond length of 0.75 Å. The activation energy (Ea) for this Tafel process is calculated to be 1.60 eV, and the reaction energy (ΔE) to be 0.69 eV (Fig. 9a). We also calculate Ea and ΔE at different H coverages (Fig. S24†). Both activation and reaction energies are sensitive to the H coverage (Fig. 9b), and decrease as the H coverage increases. But, we notice that the Tafel reaction is still sluggish even though Ea is down to 1.0 eV at a H coverage of 10/12, which is much larger than the Ea in the Heyrovsky reaction (≤1.0 eV) around an optimal coverage of 4/9.Overall, we study the Volmer, Heyrovsky, and Tafel reactions based on the 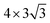 WCH supercell at an electrode potential of −0.28 V around a H coverage of 4/9 (∼44%). We find that both activation energies of Heyrovsky and Tafel processes decrease as the H coverage increases, due to the weak binding of P–H at high H coverage (Fig. S16†). By comparing the energy barriers of Heyrovsky and Tafel reactions, we see that Ea for the Heyrovsky pathway goes down faster than that of the Tafel one, and an intersection is observed at a H coverage of 14%. Hence, we conclude that the HER process on P-MXenes follows the V–T pathway with a considerably low reaction barrier at a low H coverage (Fig. 10). As the coverage increased (>14%), it turns to the V–H pathway, due to the low reaction barrier of the Heyrovsky step (Fig. 10). We believe that the V–H process is dominant at the mainly driven coverage (green band, Fig. 10). Besides, we also compare our work with other typical 2D catalyst studies on the HER performance (Table S5†). We find that P-functionalized MXenes show great potential as HER catalysts, due to the relatively low activation barrier and small reaction energy.
WCH supercell at an electrode potential of −0.28 V around a H coverage of 4/9 (∼44%). We find that both activation energies of Heyrovsky and Tafel processes decrease as the H coverage increases, due to the weak binding of P–H at high H coverage (Fig. S16†). By comparing the energy barriers of Heyrovsky and Tafel reactions, we see that Ea for the Heyrovsky pathway goes down faster than that of the Tafel one, and an intersection is observed at a H coverage of 14%. Hence, we conclude that the HER process on P-MXenes follows the V–T pathway with a considerably low reaction barrier at a low H coverage (Fig. 10). As the coverage increased (>14%), it turns to the V–H pathway, due to the low reaction barrier of the Heyrovsky step (Fig. 10). We believe that the V–H process is dominant at the mainly driven coverage (green band, Fig. 10). Besides, we also compare our work with other typical 2D catalyst studies on the HER performance (Table S5†). We find that P-functionalized MXenes show great potential as HER catalysts, due to the relatively low activation barrier and small reaction energy.
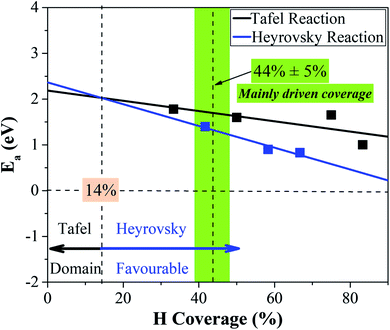 | ||
| Fig. 10 Competition between the Tafel and Heyrovsky reactions as a function of hydrogen coverage in the IS. | ||
4 Conculsions
In summary, we design a new family of MXenes by P-functionalization and systematically investigate their stability, electronic and magnetic properties, and HER performance based on DFT calculations. We find 10 stable structures out of 54 predefined structures. The band structures indicate that the stable structures are metallic with high conductivity, suggesting their potential applications in electrocatalysis. The magnetic moments of MXenes are reduced or disappear after their surfaces are covered with phosphorus atoms due to the hybridization between TM-d and P-p orbitals. Importantly, these stable P-MXenes demonstrate excellent HER performance, due to the Gibbs free energy of hydrogen adsorption near zero at a certain H coverage. We further show that P-MXenes show a potential high HER performance via the Volmer–Heyrovsky mechanism with a relatively low reaction barrier. We expect that our findings will provide insightful guidance on the design of functionalized MXenes and other 2D catalysts for the promotion of water splitting.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Science and Technology Development Fund from Macau SAR (FDCT-0102/2019/A2, FDCT-0035/2019/AGJ, FDCT-0154/2019/A3, FDCT-0081/2019/AMJ, FDCT-199/2017/A3, and FDCT-0125/2018/A3) and Multi-Year Research Grants (MYRG2017-00027-FST, MYRG2018-00003-IAPME, and MYRG2017-00149-FST) from the University of Macau. The DFT calculations were performed at High Performance Computing Cluster (HPCC) of Information and Communication Technology Office (ICTO) at University of Macau.References
- E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC.
- J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 1–15 Search PubMed.
- A. F. Khan, D. A. Brownson, E. P. Randviir, G. C. Smith and C. E. Banks, Anal. Chem., 2016, 88, 9729–9737 CrossRef CAS.
- K. Novoselov, A. Mishchenko, A. Carvalho and A. C. Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed.
- Y. Kong, H. Ai, W. Wang, X. Xie, K. H. Lo, S. Wang and H. Pan, ACS Appl. Nano Mater., 2020, 3, 2804–2812 CrossRef CAS.
- Z. W. Seh, K. D. Fredrickson, B. Anasori, J. Kibsgaard, A. L. Strickler, M. R. Lukatskaya, Y. Gogotsi, T. F. Jaramillo and A. Vojvodic, ACS Energy Lett., 2016, 1, 589–594 CrossRef CAS.
- X. Liang, A. Garsuch and L. F. Nazar, Angew. Chem., 2015, 127, 3979–3983 CrossRef.
- Z. Li, Z. Zhuang, F. Lv, H. Zhu, L. Zhou, M. Luo, J. Zhu, Z. Lang, S. Feng and W. Chen, Adv. Mater., 2018, 30, 1803220 CrossRef.
- C. F. Du, K. N. Dinh, Q. Liang, Y. Zheng, Y. Luo, J. Zhang and Q. Yan, Adv. Energy Mater., 2018, 8, 1801127 CrossRef.
- C. Ling, L. Shi, Y. Ouyang, Q. Chen and J. Wang, Adv. Sci., 2016, 3, 1600180 CrossRef PubMed.
- C. Ling, L. Shi, Y. Ouyang and J. Wang, Chem. Mater., 2016, 28, 9026–9032 CrossRef CAS.
- A. C. Rajan, A. Mishra, S. Satsangi, R. Vaish, H. Mizuseki, K.-R. Lee and A. K. Singh, Chem. Mater., 2018, 30, 4031–4038 CrossRef CAS.
- H. Weng, A. Ranjbar, Y. Liang, Z. Song, M. Khazaei, S. Yunoki, M. Arai, Y. Kawazoe, Z. Fang and X. Dai, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075436 CrossRef.
- S. Li, P. Tuo, J. Xie, X. Zhang, J. Xu, J. Bao, B. Pan and Y. Xie, Nano Energy, 2018, 47, 512–518 CrossRef CAS.
- D. Wang, Y. Gao, Y. Liu, Y. Gogotsi, X. Meng, G. Chen and Y. Wei, J. Mater. Chem. A, 2017, 5, 24720–24727 RSC.
- M. Khazaei, M. Arai, T. Sasaki, A. Ranjbar, Y. Liang and S. Yunoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075411 CrossRef.
- Y. Zhang, X.-H. Zha, K. Luo, N. Qiu, Y. Zhou, J. He, Z. Chai, Z. Huang, Q. Huang and Y. Liang, J. Phys. Chem. C, 2019, 123, 6802–6811 CrossRef CAS.
- J. Liu, W. Peng, Y. Li, F. Zhang and X. Fan, Trans. Tianjin Univ., 2020, 1–23 Search PubMed.
- Y. Li, X. Deng, J. Tian, Z. Liang and H. Cui, Appl. Mater. Today, 2018, 13, 217–227 CrossRef.
- H. Yu, Y. Wang, Y. Jing, J. Ma, C. F. Du and Q. Yan, Small, 2019, 15, 1901503 CrossRef PubMed.
- Z. Fu, C. Ling and J. Wang, J. Mater. Chem. A, 2020, 8, 7801–7807 RSC.
- G. Qu, Y. Zhou, T. Wu, G. Zhao, F. Li, Y. Kang and C. Xu, ACS Appl. Energy Mater., 2018, 1, 7206–7212 CrossRef CAS.
- K. Ruttenberg, TrGeo, 2003, vol. 8, p. 682 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdottir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 18182–18197 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- V. Wang, N. Xu, J. Liu, G. Tang and W. Geng, 2019, arXiv preprint arXiv:1908.08269.
- R. N. Barnett and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2081 CrossRef CAS PubMed.
- Y. Ding and Y. Wang, J. Phys. Chem. C, 2013, 117, 18266–18278 CrossRef CAS.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- A. Politano and G. Chiarello, Nano Res., 2015, 8, 1847–1856 CrossRef CAS.
- J. D. Gouveia, F. Viñes, F. Illas and J. R. Gomes, Phys. Rev. Mater., 2020, 4, 054003 CrossRef CAS.
- X. Li, M. Li, Q. Yang, H. Li, H. Xu, Z. Chai, K. Chen, Z. Liu, Z. Tang and L. Ma, ACS Nano, 2020, 14, 541–551 CrossRef CAS PubMed.
- H. Pan, Sci. Rep., 2016, 6, 32531 CrossRef CAS PubMed.
- N. C. Frey, A. Bandyopadhyay, H. Kumar, B. Anasori, Y. Gogotsi and V. B. Shenoy, ACS Nano, 2019, 13, 2831–2839 CrossRef CAS PubMed.
- L. R. Johnson, S. Sridhar, L. Zhang, K. D. Fredrickson, A. S. Raman, J. Jang, C. Leach, A. Padmanabhan, C. C. Price and N. C. Frey, ACS Catal., 2019, 10, 253–264 CrossRef.
- S. Lin, Y. Li, J. Qian and S. P. Lau, Mater. Today Energy, 2019, 12, 1–25 CrossRef.
- B. Conway and L. Bai, Electrochim. Acta, 1986, 31, 1013–1024 CrossRef CAS.
- Z. Chen, K. Leng, X. Zhao, S. Malkhandi, W. Tang, B. Tian, L. Dong, L. Zheng, M. Lin and B. S. Yeo, Nat. Commun., 2017, 8, 1–9 CrossRef.
- P. Lindgren, G. Kastlunger and A. A. Peterson, ACS Catal., 2019, 10, 121–128 CrossRef.
- Q. Tang and D.-e. Jiang, ACS Catal., 2016, 6, 4953–4961 CrossRef CAS.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta10136b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |