Two-dimensional vanadium tetrafluoride with antiferromagnetic ferroelasticity and bidirectional negative Poisson's ratio†
Lei
Zhang
ab,
Cheng
Tang
 ab and
Aijun
Du
ab and
Aijun
Du
 *ab
*ab
aSchool of Chemistry and Physics, Queensland University of Technology, Gardens Point Campus, Brisbane, QLD 4000, Australia. E-mail: aijun.du@qut.edu.au
bCentre for Materials Science, Queensland University of Technology, Gardens Point Campus, Brisbane, QLD 4000, Australia
First published on 12th November 2020
Abstract
Two-dimensional (2D) antiferromagnetic ferroelasticity and bidirectional auxeticity are highly sought for next-generation nanoelectronics, spintronics, or mechanical devices, but are rarely reported. Herein, using first-principles calculations, we report the coexistence of these intriguing properties in the vanadium tetrafluoride (VF4) monolayer. 2D VF4 is a direct wide-gap semiconductor with antiferromagnetic order stemming from the synergy between the direct exchange and superexchange of the dxy orbitals in adjacent V atoms. Notably, 2D VF4 features ferroelasticity with a moderate reversible strain and low transition barrier, enabling manipulation of the in-plane magnetic easy axis via external strain. Additionally, 2D VF4 simultaneously harbors an ultra-large negative Poisson's ratio (NPR) in both the in-plane and out-of-plane directions due to the hinged connection between the neighboring VF6 octahedra. Our work highlights a new material for the exploration of 2D multiferroic physics and the integration of antiferromagnetic ferroelasticity and large bidirectional auxeticity renders 2D VF4 a versatile candidate for the development of novel multifunctional devices.
Introduction
2D multiferroics, referring to the integration of two or more ferroic orders in a singular 2D material, offer the unique opportunity to control one ferroicity via using another and hold great promise for applications in next-generation electronic/spintronic devices.1–10 Among various ferroic properties, antiferromagnetism (AFM) has aroused great research interest due to the robustness against perturbation of magnetic fields, the absence of parasitic stray fields, ultrahigh resonance frequency, and large magnetotransport effects.11,12 However, AFM based multiferroics are rarely reported, partially due to the mutual exclusion between ferroelectricity and magnetism, known as the d0 rule.13,14 Ferroelasticity (FA), in contrast, shows better compatibility with other ferroic properties because neither breaking centrosymmetry nor partially filled d orbitals are required.15,16 The integration of AFM and FA in one material would be ideal for the exploration of AFM based multiferroics. So far, only the weakly-magnetic AgF2 monolayer is reported with the combination of AFM and FA,17 but there is no magnetoelastic (AFM–FA) coupling. Therefore, searching for new materials with strong AFM–FA coupling remains a great challenge in the 2D multiferroic world.Apart from multiferroic properties, materials with NPR, also known as auxetic materials, are another research focus in the 2D regime. When stretched/compressed in the longitudinal direction, auxetic materials will expand/shrink in the transverse direction, providing many novel mechanical properties including enhanced indentation/shear/fracture resistance,18–20 and acoustic/vibration absorption,21,22 and promising novel applications in biomedicine, sports equipment, and defense.21,23 Currently, most reported 2D auxetic materials only demonstrate unidirectional auxeticity along either the in-plane or out-of-plane direction.24 Only 2D X3M2 (X = S, Se; M = N, P, As) and Ag2S were reported with unusual bidirectional auxeticity,25,26 but none of them is layered in the bulk phase, suggesting a low possibility of experimental fabrication. Especially, the in-plane auxetic performance of X3M2 monolayers is poor due to the small NPR value (−0.026). Hence, it is highly desired to explore new 2D auxetic materials with both experimental accessibility and large bidirectional NPRs.
In this work, we predict a novel multifunctional 2D material, namely the VF4 monolayer. 2D VF4 with high dynamical, thermal, and mechanical stabilities could be easily exfoliated from the layered bulk counterpart, which is experimentally accessible. The synergy between the direct exchange in neighboring V atoms and superexchange mediated by the F atoms leads to a robust antiferromagnetic order. Notably, the two equally stable lattice variants with different orientations can transfer to each other with a low energy barrier, suggesting intrinsic ferroelasticity. More interestingly, 2D VF4 exhibits ultra-large bidirectional auxeticity due to the hinged connection between the neighboring VF6 octahedra.
Computational details
Our density functional theory (DFT) calculations were carried out using the Vienna Ab-initio Simulation Package (VASP).27–29 The generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) type functional30,31 was applied as it can provide an accurate description of the lattice parameters of bulk VF4 (see Table S1, ESI†). The projector augmented wave (PAW) method was applied to treat the electron–core interactions.32 The van der Waals (vdW) interaction was included by the DFT-D3 method.33 The cutoff energy for plane waves was set to 520 eV and the Brillouin zone was sampled by a 6 × 6 × 1 mesh. A vacuum space of 15 Å was introduced to avoid the interaction between neighboring images. The structure was fully relaxed until the residual forces and the energy were converged to 0.005 eV Å−1 and 1 × 10−7 eV, respectively. The electronic structure was calculated using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional34 and the finite displacement method was used to calculate the phonon spectrum as implemented in the PHONOPY code.35 The NEB method was applied to study the ferroelastic phase transition36 and 15 images were applied to give a refined transition path and an accurate transition barrier. The convergence of the transition barrier with the number of images is shown in Fig. S1 (ESI†). An ab initio molecular dynamics (AIMD) simulation was carried out for a total of 5 ps with a time step of 1.0 fs at 300 K and the Andersen thermostat was used to control the temperature.37Results and discussion
Bulk VF4 crystallizes in a monoclinic structure with the space group P21/c and was experimentally synthesized three decades ago.38 The lattice parameters are calculated to be a = 5.43 Å, b = 5.18 Å, c = 5.38 Å, and β = 59.4° at the PBE-D3 level, which are in good agreement with the experimental values (a = 5.38 Å, b = 5.17 Å, c = 5.34 Å, and β = 59.7°).38 As shown in Fig. 1a, bulk VF4 is a layered material with the VF4 layers stacked along the [101] direction. The weak van der Waals interlayer bonding suggests that monolayer VF4 could be exfoliated from the layered bulk counterpart.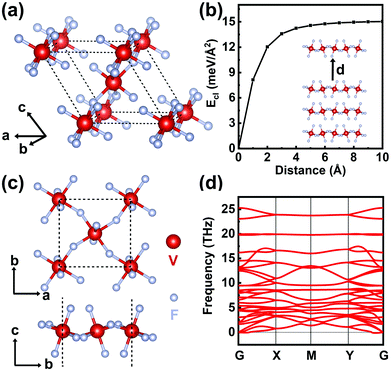 | ||
| Fig. 1 (a) and (c) present the atomic structure of bulk and monolayer VF4, respectively. (b) and (d) present the cleavage energy and phonon spectrum of the VF4 monolayer, respectively. | ||
To quantitively explore the possibility of exfoliating monolayer VF4 from the layered bulk phase, the cleavage energy (Ecl) is calculated, i.e. the energy that is required to overcome the weak interlayer van der Waals bonding.39 As shown in Fig. 1b, Ecl of monolayer VF4 is only 15 meV Å−2, which is smaller than that of graphene (21 meV Å−2), MoS2 (26 meV Å−2), and phosphorene (23 meV Å−2),39 indicating the high feasibility of obtaining a VF4 monolayer through mechanical exfoliation methods in experiments. As shown in Fig. 1c, the atomic structure of 2D VF4 consists of VF6 octahedra with their vertices joined and displays a buckled geometry along the b-direction. The lattice parameters are calculated to be a = 5.39 Å and b = 5.05 Å. To evaluate the stability of 2D VF4, the phonon spectrum is first calculated as shown in Fig. 1d. Only a tiny imaginary frequency (−0.14 THz) is found around the Gamma point for one of the acoustic modes, indicating the dynamical stability of 2D VF4.25,40,41 Furthermore, the total energy and structure of 2D VF4 only fluctuate slightly during the AIMD simulations for 5 ps as shown in Fig. S2 (ESI†), suggesting its thermal stability. Additionally, the calculated elastic constants for 2D VF4 are C11 = 34.81 N m−1, C22 = 18.90 N m−1, C12 = 14.84 N m−1, and C66 = 30.58 N m−1, respectively. As C11, C66 > 0 and C11 × C22 > C122, the Born mechanical stability criteria for 2D materials are fully fulfilled.42
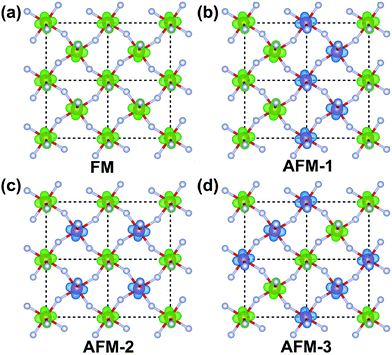
2D VF4 may possess magnetism due to the unpaired electron in the V4+ ions. To explore this effect, four magnetic configurations (denoted as FM, AFM-1, AFM-2, and AFM-3)13,43 in a larger supercell (2 × 2 × 1) are considered for 2D VF4 and the corresponding spin density distributions are presented in Fig. 2. AFM-2 ordering with the nearest magnetic moments antiferromagnetically aligned is the energetically most favorable magnetic configuration (see Table S2, ESI†). The spin density is localized around the V cations with a local magnetic moment of 1 μB per atom. The magnetic anisotropy energy (MAE) is further evaluated in the presence of spin–orbit coupling (SOC). Three in-plane directions (the [100], [010], and [110] directions) and four out-of-plane directions (the [111], [101], [011], and [001] directions) are considered and the calculated energies along these directions are summarized in Table S3 (ESI†). Clearly, the easy magnetization-axis of the VF4 monolayer lies along the longer lattice vector direction, i.e. the [100] direction, showing an in-plane magnetization feature. The largest MAE reaches up to 40 μeV per V atom, which is much larger than those of Fe (1 μeV per Fe atom) and Ni (3 μeV per Ni atom)44 and comparable to other 2D antiferromagnets like Mn2C (69 μeV per Mn atom)45 and VOCl2 (17 μeV per V atom).43
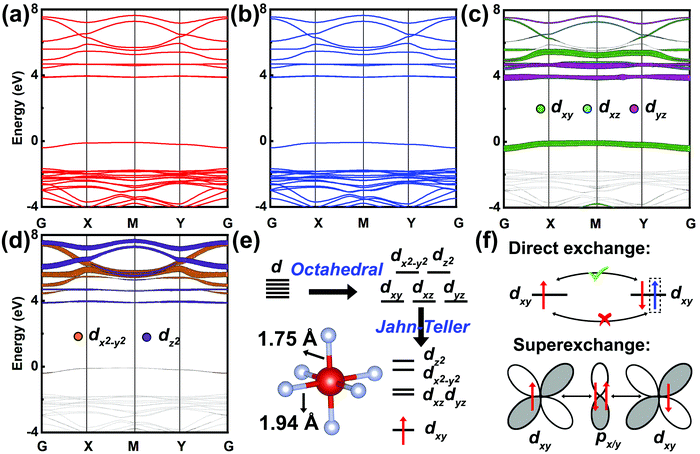
To understand the origin of the antiferromagnetic ordering, we first need to know the electronic structure of 2D VF4. Fig. 3 presents the spin-polarized and orbital-resolved band structures calculated using the HSE06 functional. 2D VF4 is a direct semiconductor with a wide bandgap of 3.96 eV. Crystal field theory indicates that the d orbitals in a perfect octahedral environment shall split into double-degenerate eg and triple-degenerate t2g orbitals.46 However, as shown in Fig. 3e, the V–F bonds within the xy-plane are significantly longer than those along the z-direction, suggesting the existence of Jahn–Teller distortion.47 Such a distortion further splits the d orbitals into four subgroups as revealed by the orbital-resolved band structures (see Fig. 3c and d): the dxy, dx2−y2, and dz2 singlets, and the dxz and dyz doublet, with the lowest dxy orbital occupied.
Based on the above orbital analysis, we can establish the magnetic exchange paths along the diagonal direction of V–F–V chains, as shown in Fig. 3f. One typical exchange interaction is antiferromagnetic direct exchange between adjacent dxy orbitals of V atoms, obeying the Pauli exclusion principle.48 Another one is the F-mediated superexchange interaction following the dxy–px/y–dxy linear paths, which also favors antiparallel spin alignments in terms of the Goodenough–Kanamori–Anderson rule.49–51 The superexchange interaction can be further revealed by the squared real-space wavefunction of the highest valence band at the gamma point (see Fig. S3, ESI†), which clearly shows the characteristics of V: dxy and F: px/y orbitals. The coexistence of the above two exchange interactions results in the AFM-2 ordering in the ground state.
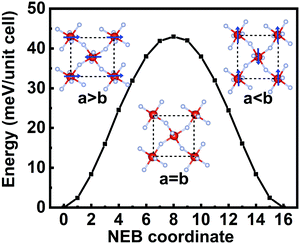
The unique atomic geometries in the VF4 monolayer also enable the ferroelastic transition between the two energy-equivalent states: the a > b state (S) and the a < b state (S′). The nudged elastic band (NEB) method is used to investigate the ferroelastic transformation pathway, where both the lattice and atomic positions are spontaneously optimized to obtain an accurate energy barrier. As shown in Fig. 4, the S and S′ states are connected by an intermediate paraelastic state (a = b = 5.28 Å). Using this state as a reference, the transformation strain matrix calculated within Green–Lagrange strain tensor theory52 indicates that there is a 2.1% tensile strain along the x/y-direction and a 4.3% compressive strain along the y/x-direction for the S/S′ state. The overall transition barrier is only 43 meV per unit cell and the reversible strain defined as (|b|/|a| − 1) × 100% is calculated to be 6.7%, which are comparable to those of phosphorene analogues such as SnS and SnSe.5 The low switching barrier suggests high feasibility of experimental realization and the moderate reversible strain can avoid structural failure before switching is achieved.53 Therefore, 2D VF4 is a multiferroic material with both antiferromagnetic order and intrinsic ferroelasticity. Moreover, the in-plane magnetic easy axis is strongly coupled to the lattice direction (along the longer lattice vector), making it possible to tune the spin orientation via strain. As shown in Fig. 4, the easy axis will rotate 90° when S is transferred to S′, and thus the spin orientation will also experience a 90° rotation during the ferroelastic transition. Such a feature is expected to offer new opportunity for the design of controllable spintronic devices.
Then the in-plane Poisson's ratio vin as a function of θ is calculated as shown in Fig. 5a using the following equation:54
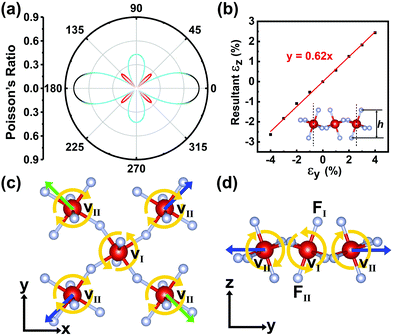
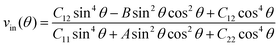 | (1) |
 | ||
| Fig. 5 (a) The in-plane Poisson's ratio as a function of θ for 2D VF4. θ = 0° represents the x-direction. The NPR region is highlighted in red. (b) Resultant out-of-plane strain as a function of applied strain along the y-direction. The response of εz to εx is plotted in Fig. S5a (ESI†), showing a positive Poisson's ratio. (c) and (d) The schematic diagram showing the atomic mechanism for in-plane and out-of-plane auxeticity, respectively. | ||
Our further analysis indicates that the bidirectional NPR in 2D VF4 is attributed to the hinged connection between adjacent VF6 octahedra. As shown in Fig. 5c, when stretched along one diagonal direction, the buckled –V–F–V– chain along that direction tends to align linearly, leading to the counterclockwise/clockwise rotation of the VIF6/VIIF6 octahedron. Such rotation pushes away the octahedra along the other diagonal direction, resulting in the in-plane auxeticity. Similarly, tensile strain along the y-direction would give rise to the counterclockwise/clockwise rotation of the VIF6/VIIF6 octahedron within the yz-plane (see Fig. 5d), leading to a decrease in the angle between FI–FII and the z-axis (θ). Meanwhile, the distance between FI and FII (l) barely changes (see Fig. S5b, ESI†) because the rotation of VF6 octahedra counteracts its structural variation in the presence of strain. Therefore, the thickness of 2D VF4 (h), defined as h = l × cos θ, would increase when stretching along the y-direction, resulting in the out-of-plane NPR.
Conclusions
In conclusion, we theoretically predicted the coexistence of antiferromagnetism, ferroelasticity, and bidirectional auxeticity in a stable VF4 monolayer. 2D VF4 could be easily exfoliated from the layered bulk phase due to the very low cleavage energy (15 meV Å−2). The Jahn–Teller distortion leads to a single-electron occupied dxy orbital, and the coexistence of direct exchange and superexchange between adjacent dxy orbitals results in long-range antiferromagnetic order. The magnetic easy axis lies along the x-direction, which can be switched to the y-direction through the ferroelastic phase transition, indicating robust magnetoelastic coupling. Besides, the hinged joints between adjacent VF6 octahedra enable bidirectional ultra-large NPRs (−0.26 and −0.62 along the in-plane and out-of-plane directions, respectively). The predicted VF4 monolayer can be an ideal platform to explore novel 2D multiferroics and holds great potential for the development of nanosized electronic, spintronic, and mechanic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge generous grants of high-performance computing resources provided by NCI National Facility and the Pawsey Supercomputing Centre through the National Computational Merit Allocation Scheme supported by the Australian Government and the Government of Western Australia. A. D. also greatly appreciates the financial support of the Australian Research Council under Discovery Project (DP170103598).References
- H. Wang, X. Li, J. Sun, Z. Liu and J. Yang, 2D Mater., 2017, 4, 045020 CrossRef.
- H. Wang and X. Qian, 2D Mater., 2017, 4, 015042 CrossRef.
- Q. Yang, W. Xiong, L. Zhu, G. Gao and M. Wu, J. Am. Chem. Soc., 2017, 139, 11506–11512 CrossRef CAS.
- J.-J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, J. Am. Chem. Soc., 2018, 140, 9768–9773 CrossRef CAS.
- M. Wu and X. C. Zeng, Nano Lett., 2016, 16, 3236–3241 CrossRef CAS.
- C. Gong, E. M. Kim, Y. Wang, G. Lee and X. Zhang, Nat. Commun., 2019, 10, 2657 CrossRef.
- Y. Zhao, L. Lin, Q. Zhou, Y. Li, S. Yuan, Q. Chen, S. Dong and J. Wang, Nano Lett., 2018, 18, 2943–2949 CrossRef CAS.
- Y. Gao, M. Wu and X. C. Zeng, Nanoscale Horiz., 2019, 4, 1106–1112 RSC.
- T. Hu and E. Kan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1409 Search PubMed.
- C. Huang, Y. Du, H. Wu, H. Xiang, K. Deng and E. Kan, Phys. Rev. Lett., 2018, 120, 147601 CrossRef.
- M. B. Jungfleisch, W. Zhang and A. Hoffmann, Phys. Lett. A, 2018, 382, 865–871 CrossRef CAS.
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- H. Tan, M. Li, H. Liu, Z. Liu, Y. Li and W. Duan, Phys. Rev. B, 2019, 99, 195434 CrossRef CAS.
- L. Weston, X. Y. Cui, S. P. Ringer and C. Stampfl, Phys. Rev. B, 2016, 93, 165210 CrossRef.
- N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694–6709 CrossRef CAS.
- N. A. Spaldin, S.-W. Cheong and R. Ramesh, Phys. Today, 2010, 63, 38–43 CrossRef.
- X. Xu, Y. Ma, T. Zhang, C. Lei, B. Huang and Y. Dai, Nanoscale Horiz., 2020, 5, 1386–1393 RSC.
- I. I. Argatov, R. Guinovart-Díaz and F. J. Sabina, Int. J. Eng. Sci., 2012, 54, 42–57 CrossRef.
- J. B. Choi and R. S. Lakes, J. Mater. Sci., 1992, 27, 5375–5381 CrossRef CAS.
- J. Choi and R. Lakes, Int. J. Fract., 1996, 80, 73–83 CrossRef.
- M. Mir, M. N. Ali, J. Sami and U. Ansari, Adv. Mater. Sci. Eng., 2014, 753496 Search PubMed.
- Y. Prawoto, Comput. Mater. Sci., 2012, 58, 140–153 CrossRef CAS.
- T. Allen, N. Martinello, D. Zampieri, T. Hewage, T. Senior, L. Foster and A. Alderson, Procedia Eng., 2015, 112, 104–109 CrossRef.
- R. Peng, Y. Ma, Q. Wu, B. Huang and Y. Dai, Nanoscale, 2019, 11, 11413–11428 RSC.
- R. Peng, Y. Ma, Z. He, B. Huang, L. Kou and Y. Dai, Nano Lett., 2019, 19, 1227–1233 CrossRef.
- Y. Chen, X. Liao, X. Shi, H. Xiao, Y. Liu and X. Chen, Phys. Chem. Chem. Phys., 2019, 21, 5916–5924 RSC.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- S. Becker and B. G. Müller, Angew. Chem., Int. Ed. Engl., 1990, 29, 406–407 CrossRef.
- J. H. Jung, C.-H. Park and J. Ihm, Nano Lett., 2018, 18, 2759–2765 CrossRef CAS.
- B. Zhang, L. Fan, J. Hu, J. Gu, B. Wang and Q. Zhang, Nanoscale, 2019, 11, 7857–7865 RSC.
- B. Zhang, G. Song, J. Sun, J. Leng, C. Zhang and J. Wang, Nanoscale, 2020, 12, 12490–12496 RSC.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- H. Ai, X. Song, S. Qi, W. Li and M. Zhao, Nanoscale, 2019, 11, 1103–1110 RSC.
- G. H. O. Daalderop, P. J. Kelly and M. F. H. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11919–11937 CrossRef CAS.
- L. Hu, X. Wu and J. Yang, Nanoscale, 2016, 8, 12939–12945 RSC.
- R. G. Burns and R. G. Burns, Mineralogical applications of crystal field theory, Cambridge university press, Cambridge, 2nd edn, 1993 Search PubMed.
- M. A. Halcrow, Chem. Soc. Rev., 2013, 42, 1784–1795 RSC.
- J. B. Goodenough and A. L. Loeb, Phys. Rev., 1955, 98, 391–408 CrossRef CAS.
- J. B. Goodenough, Magnetism and the Chemical Bond, John Wiley & Sons, Inc., New York, London, 1st edn, 1963 Search PubMed.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- F. Zhang, Y.-C. Kong, R. Pang, L. Hu, P.-L. Gong, X.-Q. Shi and Z.-K. Tang, New J. Phys., 2019, 21, 053033 CrossRef CAS.
- W. Li and J. Li, Nat. Commun., 2016, 7, 10843 CrossRef CAS.
- Z. Tu and M. Wu, Sci. Bull., 2020, 65, 147–152 CrossRef CAS.
- H. Wang, X. Li, P. Li and J. Yang, Nanoscale, 2017, 9, 850–855 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0tc04846a |
| This journal is © The Royal Society of Chemistry 2021 |