Distinctive exchange bias and unusual memory effects in magnetically compensated Pr_0.75Gd_0.25ScGe

Abstract

Tuning the chemistry of materials often leads to discoveries of interesting phenomena that expand basic science and support practical applications. Here we show how different spin–orbit coupling in light and heavy lanthanides can be exploited to create complex magnetic ground states and thereby unusual spontaneous exchange bias (SEB), conventional exchange bias (CEB), and magnetic memory effects in almost ideally magnetically compensated Pr_0.75Gd_0.25ScGe, which is a representative of the PrScGe–GdScGe solid solution. We report the synthesis and detailed characterization of Pr_0.75Gd_0.25ScGe by X-ray powder diffraction, scanning electron microscopy, and magnetization measurements in magnetic fields up to 140 kOe. Partial substitution of a light lanthanide, Pr, with a heavy lanthanide, Gd, results in a complex magnetic ground state, which includes large spontaneous and conventional exchange biases reaching magnitudes of ∼1.7 kOe and ∼3.5 kOe, respectively, at T = 2 K, as well as shape dependent magnetic compensation and bias phenomena occurring in small external fields.

---

Introduction

Rare earth based materials have found many uses: from champion permanent magnets for energy technologies^1,2 to innovative magnetocaloric materials bound to support emergent solid state refrigeration,^3,4 with many of them displaying interesting physical phenomena whose applications have yet to see fruition.⁵ Because of this, it comes as no surprise that rare earth compounds are also at the forefront of research on quantum materials with the likes of spin liquids^6,7 and high temperature superconductors,⁸ while showing potentially promising bulk behaviours typically found in two-dimensional (2D) materials.⁹ Despite substantial advances, work remains to better understand basic science of these materials so that the science can be turned into practice. As a family of closely related elements, the rare earths support the largest subset of variable chemistries and crystal structures in a broad class of intermetallic compounds when combined with other elements in the periodic table. Further, most of the lanthanides carry large localized magnetic moments. Hence, everything learned from chemistry-crystal structure interplay to magnetic interactions between different elements to the effects of impurities will aid in our ability to control desirable properties and induce both exotic and practical physical behaviours.

Ternary equiatomic RTX intermetallic compounds, where R = rare earth element, T = transition metal, and X = p-block element, exhibit a wide range of structures and physical properties,^9–20 including quantum mechanical effects such as Kondo behaviour²¹ and superconductivity,^22–24 which make them a perfect sandbox for exploring the basic science behind classical and quantum phenomena. One such example is the family of RScX compounds with X = Si or Ge crystallizing in the closely related CeScSi-type²⁵ (space group I4/mmm) or CeFeSi-type (P4/nmm) structures illustrated in Fig. 1. They exhibit unusually complex magnetism despite their relative crystallographic simplicity.^18,26–28 In both crystal structures, the R atoms form corrugated layers while the scandium atoms form flat sheets separating the rare earth layers. Loosely occupied, nearly flat sheets of X atoms are embedded in the space between the R and Sc layers, resulting in [Sc–X–R–X]₂ and [Sc–X–R–X] layering sequences for CeScSi- and CeFeSi-types, respectively.^29,30 The peculiarly layered crystallography should, in principle, allow for 2D physical property behaviours to emerge in these compounds and their derivatives, yet this area of research remains barely explored.

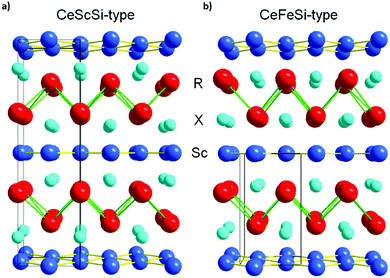Fig. 1 Layered tetragonal CeScSi-type (space group I4/mmm) (a) and CeFeSi-type (space group P4/nmm) (b) crystal structures.

Physical properties of RScX compounds are highly sensitive to chemical modifications, and the materials are clearly responsive to external stimuli, such as temperature and magnetic field. For example, Chevalier et al. showed that after hydrogenation, long range magnetism of RScSi and RScGe when R = Ce is strongly suppressed, and Kondo-type interactions when R = La and Ce develop.⁹ Similar phenomena have been observed by Tence et al.³¹ in NdScSi and NdScGe hydrides, Mahon et al.³² in NdScSi carbide, and Mahon et al.¹⁷ in GdScGe hydride. Guillou et al. demonstrated that metamagnetic behaviour emerges when a CeScSi-type (represented by the GdScGe parent) and CeFeSi-type (represented by the GdScSb parent) compounds are combined in a pseudobinary GdScGe_1−xSb_x by substituting one X-element for another.³³ Further, Ivanova et al. reported that by substituting Sc with Ti on the T site and creating the pseudobinary GdSc_1−xTi_xGe, one could enhance the already high T_C of GdScGe from 320 K for x = 0 to 377 K for x = 1.³⁴ Adding variable spin–orbit coupling into the mix may lead to additional electronic and magnetic complexities while maintaining crystallographic simplicity, and thus result in remarkable physics when light and heavy lanthanides are combined on the R site. The different signs of spin–orbit coupling (J = L − S in light and J = L + S in heavy lanthanides, where J, L, and S are the total angular momentum, orbital momentum, and spin quantum numbers, respectively) may result in antiparallel alignment of different lanthanide magnetic moments located on the same atomic site.³⁵ Therefore, it should be possible, for example, to design an RTX system with strong magnetic exchange interactions and long-range magnetic ordering occurring near room temperature, yet with nearly zero net magnetization due to complete compensation of the magnetic moments of the light and heavy lanthanides.

An excellent model system to both validate this assumption and study this effect in detail is pseudobinary (PrScGe)_1−x(GdScGe)_x, which is expected to form the continuous solid solution Pr_1−xGd_xScGe, and adopt the same CeScSi-type crystal structure regardless of x. The PrScGe compound is, probably, the most magnetically complex material among the known ternary RScGe compounds. According to neutron diffraction measurements, it exhibits a paramagnetic (PM) to antiferromagnetic (AFM) transition at a relatively high Néel temperature, T_N = 140 K, an AFM to ferrimagnetic (FiM-I) transition at Curie temperature, T_C = 82 K, and a spin reorientation transition from FiM-I to FiM-II at T_SR = 62 K.³⁰ GdScGe – which has been studied for its magnetocaloric properties and clear 2D character when hydrogenated – crystallizes in the same tetragonal CeScSi-type structure, with minor disorder on the R-site, where Sc may replace Gd in small concentrations.^18,26,36,37 The GdScGe compound undergoes a second-order PM to ferromagnetic (FM) transition at an unusually high T_C = 352 K, the temperature range suitable for potential near room temperature applications.³¹ The competition between J = L − S and J = L + S atoms, when Pr replaces Gd, in the presence of a 3d metal (Sc) may, on the other hand, facilitate strong exchange in a potentially 2D structure with a more subtle yet fundamentally interesting behaviour worthy of replicating in other materials.

While the entire series of Pr_1−xGd_xScGe compositions is expected to result in a range of interesting phenomena, the x = 0.25 compound, Pr_0.75Gd_0.25ScGe, is the focus of this work. First, the x = 0.25 seems to be the “magic composition” known to be unique in other admixed lanthanide systems, for example, solid solutions of rare earth dialuminides, where unexpected physics related to electronic instabilities is most prominent.^38–41 Further, Kulkarni et al. showed that Nd_0.75Gd_0.25ScGe is magnetically compensated and inferred that it is due to competition between the different magnetic constituents, i.e., Nd and Gd.⁴² Finally, they also noted a unique magnetic memory effect where the material “remembers” the field it was cooled in and hypothesize that Nd moments are “freezing” parallel or antiparallel to the applied field.⁴² With this in mind, here we report the structural and magnetic properties of the Pr_0.75Gd_0.25ScGe compound.

Methods

Two polycrystalline Pr_0.75Gd_0.25ScGe alloys, weighing 5 g each, were prepared by arc melting stoichiometric amounts of the constituent elements in a high-purity argon atmosphere. During the synthesis, the alloys were re-melted 5 times, flipping the as-solidified buttons upside down after each melting to ensure homogeneity. Weight losses after melting were less than or equal to 0.3%. Pr, Gd, and Sc were obtained from the Materials Preparation Center (MPC) of Ames Laboratory and were better than 99.9 wt% (99 at%) pure with respect to all other elements in the periodic table. Ge was purchased from Meldford Metals and was at least 99.99 wt% pure. The elements used for the sample preparation were from the same batch for each corresponding element, except for Gd, where one alloy was made with Gd that contained a rather high concentration of Al as an impurity (∼0.5 at%), while the other Gd source contained more oxygen (see the ESI,† Table S1 for more details). From here on, the Al rich sample will be referred to as sample 1 and the Al-poor, O-rich material as sample 2. Data presented here are for sample 1 unless otherwise specified. After the arc melting, both alloys were wrapped in a tantalum foil, sealed in a quartz tube under a low pressure (∼1/3 bar) helium atmosphere, and heat-treated using the following protocol: (i) the samples were quickly brought to 550 °C where they dwelled for one day, (ii) the temperature was then quickly ramped up to 950 °C where the samples dwelled for three weeks, and (iii) the furnace was turned off, and the samples were allowed to slowly cool to room temperature. Additionally, we prepared powdered samples, screened to particle size ≤45 μm, by hand grinding the arc melted and annealed buttons of both samples using an agate mortar and a pestle.

The crystal structures, as well as phase purities, were determined using X-ray powder diffraction (XRPD) carried out on a modified Rigaku TTRAX system equipped with Mo Kα radiation⁴³ and a PANalytical X’Pert Pro powder diffractometer with Cu Kα radiation. The diffractometers used a step size of 0.01° and 0.015°, respectively. Full-profile XRPD refinements were performed using LHPM Rietica.⁴⁴ The microstructure and energy dispersive spectroscopy (EDS) measurements were carried out on an FEI Teneo scanning electron microscope (SEM) equipped with an Oxford Instruments Aztec Energy Dispersive Spectroscopy (EDS) system. Magnetic properties were measured as functions of temperature and applied magnetic field using a Quantum Design, Inc. physical property measurement system (PPMS). Additional dc magnetization and ac magnetic susceptibility measurements were also carried out in a Quantum Design, Inc. superconducting quantum interference device (SQUID) magnetometer (MPMS XL-7).

Results and discussion

Crystallography and microstructure

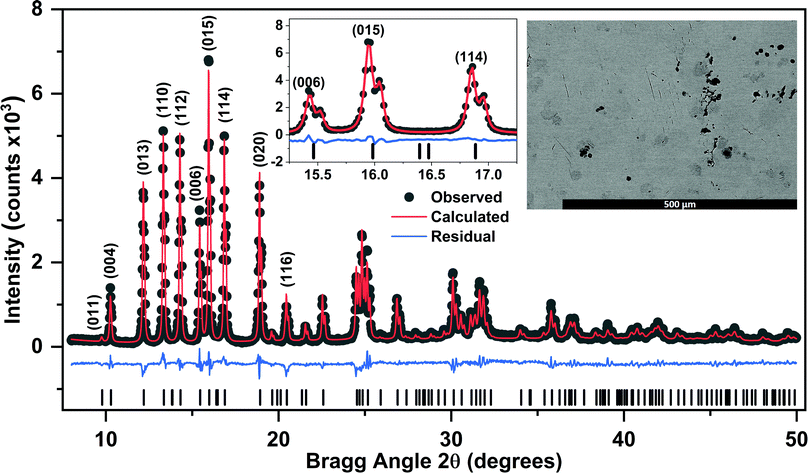
The XRPD patterns for both samples are practically identical, and that of sample 1 is shown in Fig. 2. Rietveld refinement, using crystallographic data for PrScGe reported in Bodak et al.²⁵ as a starting point, confirms that Pr_0.75Gd_0.25ScGe crystallizes in a CeScSi-type structure with space group I4/mmm. Refined atomic parameters listed in Table 1 are close to those of both parent compounds, and there were no discernible secondary phases. Rietveld refinements of both samples resulted in good fits (R_Bragg = 3.89 and 4.10% and R_P = 8.06 and 8.15%, including the backgrounds, for samples 1 and 2, respectively). Lattice parameters, along with basic magnetic properties, are listed in Table 2. Considering the tetragonal lattice parameters for PrScGe published by Singh et al.²⁹ and GdScGe reported by Guillou et al.,³³ and assuming that Vegard's law applies, the expected lattice parameters for Pr_0.75Gd_0.25ScGe are a = b = 4.313 Å and c = 15.817 Å. Both are slightly smaller than the experimentally obtained values. It is worth noting that the minor deviations from Vegard's law, seen here, are not uncommon in intra rare earth alloys.⁴⁵

Fig. 2 Rietveld-refined room temperature XRPD pattern of Pr_0.75Gd_0.25ScGe showing the experimental (symbols) and calculated (solid line drawn through the symbols) intensities with the residual (line beneath the pattern) and calculated positions of Bragg peaks (short vertical tick marks at the bottom). The insets show details in the 15–17.5° 2θ range to better illustrate the quality of the fit and an SEM image of the polished sample, respectively. The SEM image illustrates the nearly single phase nature of this material with minor surface oxidation (darker grey spots) and pitting (black spots).

Table 1 Experimentally determined coordinates of atoms in the tetragonal (space group I4/mmm) unit cell of Pr_0.75Gd_0.25ScGe, sample 1

Element	Wyckoff site	x/a	y/b	z/c
0.75Pr + 0.25Gd	4e	0	0	0.3233(1)
Sc	4c	0	0.5	0
Ge	4e	0	0	0.126(1)

---

Table 2 Experimentally determined values of the lattice parameters, a and c, and basic magnetic properties of Pr_0.75Gd_0.25ScGe: Weiss temperatures (θ_P) and effective magnetic moments (p_eff) determined from the Curie–Weiss law, maximum magnetizations (M_max) observed in 70 kOe field, and Curie temperatures (T_C), for both samples as well as for the parent ternaries. Values for GdScGe and PrScGe are from Guillou et al.³³ and Singh et al.,²⁹ respectively, unless indicated otherwise

Material	a (Å)	c (Å)	θ P (K)	T C (K)	M max (μB per f.u.)	p eff (μB per f.u.)
* Estimated from published data.
PrScGe^29	4.331(1)	15.890(2)	125	140	2.4*	2.88
Sample 1	4.31794(5)	15.8339(3)	127	190	0.21	4.7
Sample 2	4.3146(3)	15.8243(3)	131	183	0.26	4.7
GdScGe^33	4.2590(5)	15.598(1)	Not listed	352	7.1	7.8^18

---

To further analyse phase purity and microstructure, scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS) measurements were performed. Due to the extreme sample brittleness, surface polishing results in many micropores and microcracks, which makes analysis of the SEM and EDS data difficult. Furthermore, polishing with colloidal silica degrades and chemically etches the surface causing a clean SEM image to be practically unattainable. The darker areas seen in Fig. 2 inset are caused by extrinsic factors, such as surface reaction with air and water, cracks, and pitting, which occurred during sample preparation. SEM shows single-phase materials. EDS suggests a minor deviation (within error margin) from the nominal stoichiometry, averaging the Gd content slightly higher and Sc content slightly lower than stoichiometric. Therefore, this material may be similar to “GdScGe,” whose actual composition, as determined by X-ray single crystal diffraction, is Gd_1.02Sc_0.98Ge.³⁷ However, we were unable to find a good quality single crystal in either of the alloys and considering the large errors commonly associated with EDS measurements, we are unable to determine whether the actual composition is off-stoichiometric. Negligible weight losses during arc-melting and single phase nature indicate that both samples are practically stoichiometric.

Magnetic properties

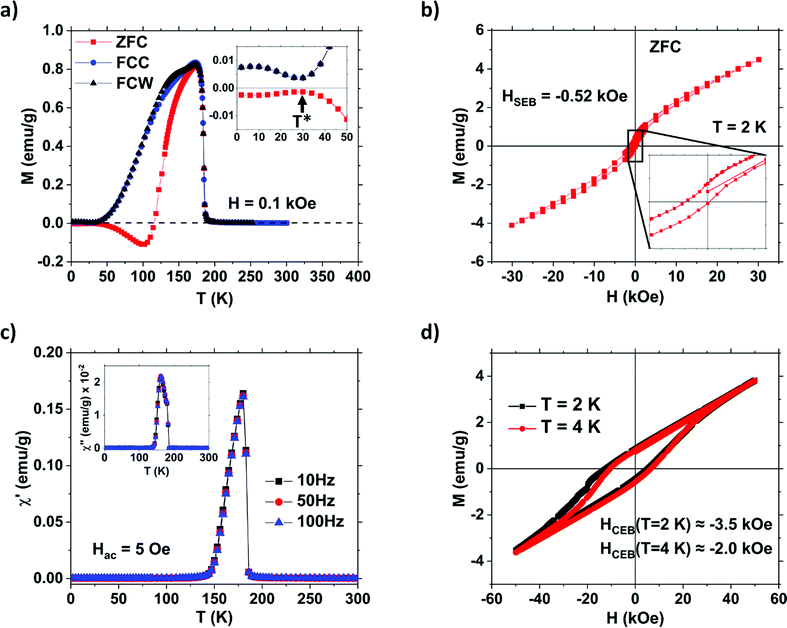
Fig. 3 illustrates the magnetic properties of bulk Pr_0.75Gd_0.25ScGe while Fig. 4 shows the same for the compound in the form of powder (likewise the corresponding Fig. S1 and S2 (ESI†) show the magnetic properties of the bulk and powder forms for sample 2, respectively). The magnetism of the Pr_0.75Gd_0.25ScGe compound is governed by the lanthanide (Gd and Pr) atoms (Ge is non-magnetic and Sc may have a small induced 3d magnetic moment due to hybridization of Sc 3d electrons with the 5d electrons of Gd and Pr), whose indirect magnetic exchange is mediated by a Ruderman–Kittel–Kasuya–Yosida (RKKY)-type interactions.^46–49 While Sc can enhance the RKKY exchange in gadolinium germanides,⁵⁰ one may assume that in the PrScGe–GdScGe system, the T_C will scale with de Gennes factor, as is typical for lanthanides. Using a linear relation between T_Cs of the parent compounds (Table 2) and de Genes factors of 0.8 and 15.75, for Pr and Gd, respectively, we estimate a T_C of 197 K, which is higher than but still close to the T_C = 190 K (183 K for sample 2) found experimentally. That being said, it is also possible that the observed minor deviations from the Vegard's law (see above) also affect the RKKY exchange and magnetism. It is worth noting that in this estimate we used the T_C = 352 K found in Guillou et al.,³³ which is on the higher end of reported T_C values for GdScGe: for example, Nikitin et al. report 320 K,¹⁸ Manfrinetti et al. report 350 K,³⁶ Couillaud et al. report 348 K,³⁷ and Ivanova et al. report 320 K.³⁴ The two of the lowest T_Cs of 320 K are likely the result of using commercial grade Gd with much higher concentrations of impurities compared to other reports.

Fig. 3 (a) ZFC, FCC, and FCW M(T) of Pr_0.75Gd_0.25ScGe measured at H = 0.1 kOe. Inset shows details around the maximal local compensation point (T*) in FCC and FCW data. (b) ZFC M(H) measured at T = 2 K with the inset highlighting spontaneous exchange bias. (c) AC magnetic susceptibility measured at different driving field frequencies with amplitude of 5 Oe and zero bias dc field. (d) M(H) measured at T = 2 and 4 K after cooling in dc magnetic field of 70 kOe.

Fig. 4 (a) M(T) behaviour of powdered sample 2 with the legend arranged in chronological order of the measurements. (b) M(H) of powdered sample 2 at T = 2 K with the inset highlighting the spontaneous exchange bias, SEB. (c) AC magnetic susceptibility of sample 1 measured in a 5 Oe driving field at different frequencies without a bias dc field. The inset shows the imaginary component of the ac susceptibility. (d) M(H) of sample 2 measured at T = 2 K after cooling in 70 kOe field. The inset highlights the dramatic decrease of CEB in the powdered samples.

Fitting of the paramagnetic region to the Curie–Weiss law indicates a Weiss temperature of 127 K (131 K for sample 2), far below the observed Curie temperature. This signals an antiparallel coupling between the Gd and Pr moments. Further evidence can be seen in the M(H) data, Fig. 3b and 4b, for the bulk and powder, respectively, where magnetization does not saturate in fields up to at least 30 kOe. In fact, after cooling in a large field, magnetization does not saturate in fields up to 140 kOe (Fig. S3, ESI†), indicating a very strong antiparallel coupling between the Pr and Gd moments. At high magnetic fields, the M(H) behaviour is not fully linear (exemplified in Fig. S3, ESI†), which points toward a rather complicated magnetic behaviour developing with field. The antiparallel coupling is far from classical ferrimagnetism as the Gd and Pr are randomly occupying the same crystallographic site and not unique sublattices. Furthermore, the magnetic structure gets even more complicated when considering the effects of Sc. The magnetic moments of the J = L − S Pr and J = S Gd (L = 0 for Gd) atoms are likely to align differently (parallel or antiparallel) with respect to the orientation of induced Sc 3d moments. Noting that Sc fully occupies its own sublattice, this creates a peculiar magnetic system that is both magnetically frustrated and magnetically ordered.

Using the saturation magnetization of GdScGe and PrScGe compounds found in Guillou et al.³³ and Singh et al.,²⁹ respectively (see Table 2), one can estimate the expected saturation magnetic moment of Pr_0.75Gd_0.25ScGe to be 0.03 μ_B per f.u. for a collinear FiM ordering. However, a nearly zero moment is not practically obtainable at finite temperatures even for a fully compensated antiferromagnet. With this in mind, the relatively low observed maximum magnetization of 0.51 μ_B per f.u. at 2 K in 140 kOe field supports the ferrimagnetic ordering postulated above.

Magnetic compensation is observed in both the powder (Fig. 4a) and bulk samples (Fig. 3a), stemming from interactions between the heavy and light lanthanide ions. Pr_0.75Gd_0.25ScGe is fully compensated with M = 0 for ZFC, at T_comp = 115 K (118 K and 76 K for sample 2, Fig. S1, more information given in ESI†). A nearly ideal magnetic compensation seen in Fig. 3a is observed around T* = 30 K (29 K for sample 2) in the FCC and FCW data where M(T) reach local minima. Interestingly, the ZFC data reach a local maximum at T* resulting in a local maximum in compensation (proximity to M = 0) seen in all sets of the data, i.e., ZFC, FCC, and FCW. This magnetic reversal (M close to being mirrored across M = 0) behaviour is most likely due to a spin reorientation of the R moments that are aligned parallel or antiparallel to the fields for ZFC or field cooled conditions, respectively.

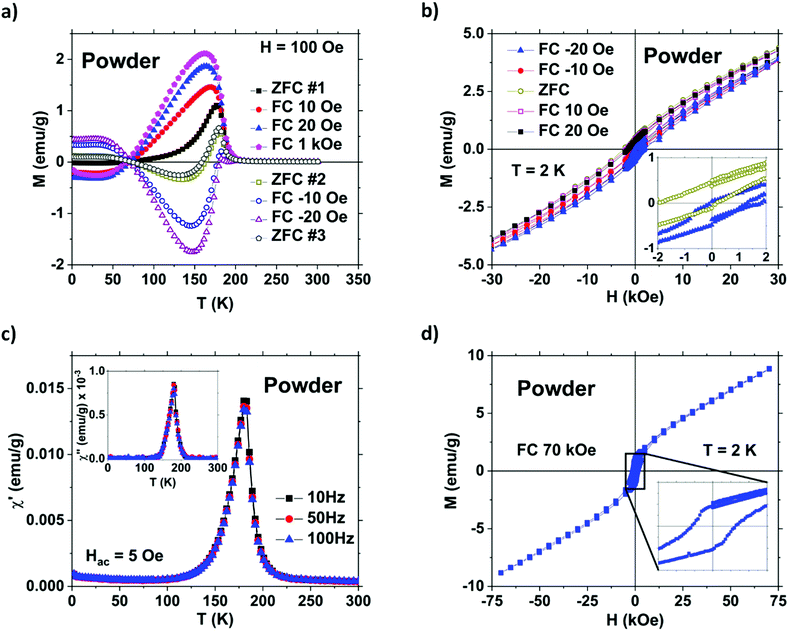
The powder shows a fundamental change in terms of compensation, Fig. 4a. Unlike bulk sample 1, the magnetization of the powder has two sign changes at approximately 180 K and 70 K for both field cooled and ZFC conditions. Even more interesting is the fact that magnetic reversal occurs between the positive and negative field cooled measurements, contrary to the bulk where it was seen between field cooled and ZFC conditions. This magnetic reversal has previously been explained in a similar system by kinetically arrested magnetic lattices.⁴² Furthermore, the magnitude of the field cooling determines the magnitude of the resulting magnetization during the measurement performed in the same 100 Oe fields. Together, these phenomena make up the full extent of the “magnetic memory effects” at work in Pr_0.75Gd_0.25ScGe. It is worth noting that the ZFC data do not represent true ZFC cooling, but rather cooling in a small trapped field of opposite direction than the previously set field of the superconducting magnet, which explains why they appear similar to negative field cooled behaviour.⁵¹ Surprisingly, these magnetic memory effects occur when cooled in very weak fields that are well below the coercivity, and yet their effects persist through fields orders of magnitudes larger and temperatures up to near T_C. While the appearance of compensation is likely a phenomena resulting from the interactions of heavy and light lanthanide ions sitting on the same lattice site, the difference in compensation between the bulk and the powder are likely a result of a convolution of a plethora of effects. These are: elimination of grain and magnetic domain boundaries, internal stress from pulverization (Fig. S3c and S4b, ESI†), surface oxidation, and anisotropy effects (Fig. S4a, ESI†). More work is needed to better understand the complexity of these phenomena.

The magnetization as a function of the magnetic field, M(H), measured at 2 K and illustrated in Fig. 3b and 4b, shows unidirectional anisotropy, also called exchange bias (EB), H_EB = (H₋ − H₊)/2, where H₋ and H₊ are H(M = 0) for the decreasing and increasing magnetic field directions, respectively. For sample 1, the exchange bias values tops out at −0.52 kOe (Fig. 3b) for ZFC spontaneous exchange bias (SEB), and −3.5 kOe for field cooled (FC) conventional exchange bias (CEB), Fig. 3d. Sample 2, on the other hand, has a SEB of −1.7 kOe (Fig. S2b, ESI†) and a CEB of −3.5 kOe (Fig. S2c, ESI†). The difference in SEB is likely a result of formation of minute quantities of magnetic Gd–Al intermetallics, also see ESI.† The SEB is larger than that of Pr_1−xGd_xAl₂,³⁸ and the CEB is comparable to some perovskite materials such as La_1−xPr_xCrO₃.⁵² The presence of magnetic compensation is likely responsible for these magnetic exchange bias phenomena^5,42,52–54 despite being usually reported near T_Comp. Large SEB, similar to what is seen here, is normally observed in oxide materials where super- or double-exchange interactions are dominant, but not often in materials with the indirect RKKY interactions, however, this is most likely due to the less extensive research of the rare earth based intermetallics as compared to oxides. In addition, large SEB is usually reported in single-phase materials as a result of super-spin-glass (SSG) behaviour,^53,55,56 which is not the case here – the ac magnetic susceptibility measured at different frequencies rules out any spin-glass behaviour (Fig. 3c and 4c). This suggests exchange bias behaviour similar to that reported in single phase Mn₂PtGa⁵⁷ and Pr_0.6Er_0.4Al₂,³⁵ where clustering due to atomic environment inhomogeneities leads to different signs of magnetic exchange interactions locally prevailing.

Additionally, the powder samples show a decrease in the magnitude of SEB and CEB to 0.5 kOe (Fig. 4b) and 0.25 kOe (Fig. 4d), respectively. This change in EB, induced by breaking a brittle solid into fine powders, points towards a shape dependent EB. Normally the magnitude of EB is dependent on the number of compensated and uncompensated spins in the magnetic interface supplied by the differing magnetic materials. However, by pulverizing the sample and thus substantially increasing the surface area, many of these domain interfaces have been removed. This is most likely the underlying cause of the shape dependent EB seen here. This also gives rise to a potential new variable for controlling exchange bias.

Conclusions

Pr_0.75Gd_0.25ScGe adopts the CeScSi-type structure with mixed Pr/Gd occupancy and displays interesting and novel physical properties due to nearly ideal magnetic compensation. The observed compensated ferrimagnetic ordering at low temperature is due to the antiparallel alignment of two different lanthanide moments, which results in magnetic compensation and spontaneous exchange bias magnitudes reaching as high as 1.7 kOe. Unusual for single-phase materials and in the absence of spin glass behaviour, the compound also exhibits a high magnitude of conventional exchange bias reaching 3.5 kOe that can be attributed to magnetic compensation. Conventional exchange bias is shape-dependent, i.e. its magnitude changes when the material is converted from bulk to powder, hence grain (particle) size can be used as a new variable in exchange bias control. Magnetic memory effects, including magnetic reversal, are observed in powder samples but not in bulk samples. While there is a clear competition in how Gd and Pr spins, statistically distributed across the same magnetic sublattice, align with respect to weak induced magnetic moments of Sc occupying its own sublattice, the title compound exhibits no signs of magnetic frustration nor spin glass behaviour. Based on the interesting magnetic phenomena observed, it is possible to predict that fine-tuning of the chemical compositions in other intra-lanthanide systems with RKKY interactions, would create full magnetic compensation, potentially leading to anomalous magnetism. Whereas not every crystal lattice will support such behaviour, it appears that layered structures, similar to the CeScSi- or CeFeSi-types, may be better suited for the creation of fully compensated, bulk magnetic systems.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was performed at Ames Laboratory and was supported by the Materials Sciences and Engineering Division of the Office of Basic Energy Sciences, Office of Science of U. S. Department of Energy (DOE). Ames Laboratory is operated for the U.S. DOE by Iowa State University of Science and Technology under Contract No. DE-AC02-07CH11358. Tyler Del Rose and Arjun K. Pathak wish to acknowledge the Science Undergraduate Laboratory Internships (SULI) program for summer support. Authors would like to acknowledge Matthew Lynn for performing SEM/EDS measurements and Kirk Rudolph for synthesizing some of the samples.

Notes and references

1. M. Sagawa, S. Fujimura, N. Togawa, H. Yamamoto and Y. Matsuura, J. Appl. Phys., 1984, 55, 2087.
2. O. Gutfleisch, M. A. Willard, E. Brück, C. H. Chen, S. G. Sankar and J. P. Liu, Adv. Mater., 2011, 23, 821–842.
3. V. K. Pecharsky and K. A. Gschneidner Jr., Phys. Rev. Lett., 1997, 78, 4494–4497.
4. C. Zimm, A. Boeder, J. Chell, A. Sternberg, A. Fujita, S. Fujieda and K. Fukamichi, Int. J. Refrig., 2006, 29, 1302–1306.
5. P. D. Kulkarni, V. Vaidya and S. K. Dhar, EPL, 2009, 86, 47003.
6. Y. Li, G. Chen, W. Tong, L. Pi, J. Liu, Z. Yang, X. Wang and Q. Zhang, Phys. Rev. Lett., 2015, 115, 167206.
7. Z. L. Dun, J. Trinh, K. Li, M. Lee, K. W. Chen, R. Baumbach, Y. F. Hu, Y. X. Wang, E. S. Choi, B. S. Shastry, A. P. Ramirez and H. D. Zhou, Phys. Rev. Lett., 2016, 116, 157201.
8. A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. F. Balakirev, D. E. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz and M. I. Eremets, Nature, 2019, 569, 528–531.
9. B. Chevalier, W. Hermes, B. Heying, U. C Rodewald, A. Hammerschmidt, S. F. Matar, E. Gaudin and R. Pottgen, Chem. Mater., 2010, 22, 5013–5021.
10. S. Gupta and K. G. Suresh, J. Alloys Compd., 2015, 618, 562–606.
11. H. Kumigashira, T. Sato, T. Yokoya, T. Takahashi, S. Yoshii and M. Kasaya, Phys. Rev. Lett., 1999, 82, 1943–1946.
12. R. Pottgen and D. Johrendt, Chem. Mater., 2000, 12, 875–897.
13. Y. Tokiwa, M. Garst, P. Gegenwart, S. L. Bud’ko and P. C. Canfield, Phys. Rev. Lett., 2013, 111, 116401.
14. D. J. García, V. Vildosola and P. S. Cornaglia, J. Phys.: Condens. Matter, 2020, 32, 285803.
15. K. Katoh, T. Takabatake, A. Minami, I. Oguro and H. Sawa, J. Alloys Compd., 1997, 261, 32–36.
16. Y. Öner, S. Senoussi, O. Sologub and P. Salamakha, Phys. B, 1999, 259–261, 887–889.
17. T. Mahon, E. Gaudin, A. Villesuzanne, R. Decourt, J.-L. Bobet, O. Isnard, B. Chevalier and S. Tencé, Inorg. Chem., 2018, 57, 14230–14239.
18. S. A. Nikitin, I. A. Ovtchenkova, Y. V. Skourski and A. V. Morozkin, J. Alloys Compd., 2002, 345, 50–53.
19. H. Zhang, Y. Li, E. Liu, Y. Ke, J. Jin, Y. Long and B. Shen, Sci. Rep., 2015, 5, 11929.
20. J. Fikáček, P. Javorský, J. Vejpravová, J. Prchal, J. Kaštil, G. Nénert and E. Šantavá, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 214410.
21. T. Takabatake, G. Nakamoto, H. Tanaka, Y. Bando, H. Fujii, S. Nishigori, H. Goshima, T. Suzuki, T. Fujita, I. Oguro, T. Hiraoka and S. K. Malik, Phys. B, 1994, 199–200, 457–462.
22. J. Goraus, A. Ślebarski and M. Fijałkowski, J. Phys.: Condens. Matter, 2013, 25, 176002.
23. Y. Pan, A. M. Nikitin, T. V. Bay, Y. K. Huang, C. Paulsen, B. H. Yan and A. de Visser, EPL, 2013, 104, 27001.
24. B. Chevalier, P. Lejay, A. Cole, M. Vlasse and J. Etourneau, Solid State Commun., 1982, 41, 801–804.
25. O. I. Bodak and Z. M. Kokhan, Inorg. Mater., 1983, 19, 987–989.
26. A. V. Morozkin, Y. D. Seropegin, V. K. Portnoy, A. V. Leonov and I. Sviridov, J. Alloys Compd., 1998, 278, L1–L5.
27. A. V. Morozkin and Y. D. Seropegin, J. Alloys Compd., 1996, 237, 124–138.
28. A. V. Morozkin, L. M. Viting, I. A. Sviridov and I. A. Tskhadadze, J. Alloys Compd., 2000, 297, 168–175.
29. S. Singh, S. K. Dhar, P. Manfrinetti, A. Palenzona and D. Mazzone, J. Magn. Magn. Mater., 2004, 269, 113–121.
30. P. Manfrinetti, A. V. Morozkin, O. Isnard, P. Henry and A. Palenzona, J. Alloys Compd., 2008, 450, 86–91.
31. S. Tencé, T. Mahon, E. Gaudin, B. Chevalier, J. L. Bobet, R. Flacau, B. Heying, U. C. Rodewald and R. Pöttgen, J. Solid State Chem., 2016, 242, 168–174.
32. T. Mahon, E. Gaudin, A. Villesuzanne, B. Chevalier and S. Tencé, Inorg. Chem., 2019, 58, 15255–15268.
33. F. Guillou, A. K. Pathak, T. A. Hackett, D. Paudyal, Y. Mudryk and V. K. Pecharsky, J. Phys.: Condens. Matter, 2017, 29, 485802.
34. T. I. Ivanova, M. V. Gavrilko, S. A. Nikitin, I. A. Ovchenkova, A. V. Morozkin, D. Badurski and K. P. Skokov, J. Magn. Magn. Mater., 2006, 300, e489–e932.
35. A. K. Pathak, D. Paudyal, W. T. Jayasekara, S. Calder, A. Kreyssig, A. I. Goldman, K. A. Gschneidner Jr. and V. K. Pecharsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 224411.
36. P. Manfrinetti, M. Pani, A. Palenzona, S. K. Dhar and S. Singh, J. Alloys Compd., 2002, 334, 9–13.
37. S. Couillaud, E. Gaudin, V. Franco, A. Conde, R. Pöttgen, B. Heying, U. C. Rodewald and B. Chevalier, Intermetallics, 2011, 19, 1573–1578.
38. P. D. Kulkarni, S. Venkatesh, A. Thamizhavel, V. C. Rakhecha, S. Ramakrishnan, A. K. Grover, V. C. Rakhecham, S. Ramakrishnan and A. K. Grover, IEEE Trans. Magn., 2009, 45, 2902–2906.
39. P. D. Kulkarni, A. K. Nigam, S. Ramakrishnan and A. K. Grover, Field induced changes across magnetic compensation in Pr1−xGdxAl2 alloys, ArXiv, 2010, 1008, 3872.
40. V. S. R. De Sousa, A. M. G. Carvalho, E. J. R. Plaza, B. P. Alho, J. C. G. Tedesco, A. A. Coelho, N. A. De Oliveira and P. J. Von Ranke, J. Magn. Magn. Mater., 2011, 323, 794–798.
41. A. L. Lima, K. A. Gschneidner Jr., V. K. Pecharsky and A. O. Pecharsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134409.
42. P. D. Kulkarni, U. V. Vaidya, S. K. Dhar, P. Manfrinetti and A. K. Grover, J. Phys. D: Appl. Phys., 2009, 42, 082001.
43. A. P. Holm, V. K. Pecharsky, K. A. Gschneidner Jr., R. Rink and M. N. Jirmanus, Rev. Sci. Instrum., 2004, 75, 1081–1088.
44. B. A. Hunter, Int. Union Crystallogr. Comm. Powder Diffr. Newsl.
45. K. A. Gschneidner Jr., J. Less-Common Met., 1985, 114, 29–42.
46. M. A. Ruderman and C. Kittel, Phys. Rev., 1954, 96, 99–102.
47. T. Kasuya, Prog. Theor. Phys., 1956, 16, 45–57.
48. K. Yosida, Phys. Rev., 1957, 106, 893–898.
49. P. G. De Gennes, J. Phys. Radium, 1962, 23, 510–521.
50. Y. Mudryk, D. Paudyal, J. Liu and V. K. Pecharsky, Chem. Mater., 2017, 29, 3962–3970.
51. M. Buchner, K. Höfler, B. Henne, V. Ney and A. Ney, J. Appl. Phys., 2018, 124, 161101.
52. K. Yoshii, Appl. Phys. Lett., 2011, 99, 142501.
53. X. X. Wang, S. Gao, X. Yan, Q. Li, J. C. Zhang, Y. Z. Long, K. Q. Ruan and X. G. Li, Phys. Chem. Chem. Phys., 2018, 20, 3687–3693.
54. R. P. Singh, C. V. Tomy and A. K. Grover, Appl. Phys. Lett., 2010, 97, 182505.
55. P. Liao, C. Jing, X. L. Wang, Y. J. Yang, D. Zheng, Z. Li, B. J. Kang, D. M. Deng, S. X. Cao, J. C. Zhang and B. Lu, Appl. Phys. Lett., 2014, 104, 092410.
56. S. Chatterjee, S. Giri, S. K. De and S. Majumdar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 092410.
57. A. K. Nayak, M. Nicklas, S. Chadov, C. Shekhar, Y. Skourski, J. Winterlik and C. Felser, Phys. Rev. Lett., 2013, 110, 127204.

---

Footnote

† Electronic supplementary information (ESI) available: Magnetization in higher fields, grain orientation and oxidation effects, and aluminium impurity effects. See DOI: 10.1039/d0tc05087c

---