An [Fe^III₃₀] molecular metal oxide

Abstract

Dissolution of FeBr₃ in a mixture of acetonitrile and 3,4-lutidine in the presence of an amine results in the formation of an [Fe₃₀] molecular metal oxide containing alternating layers of tetrahedral and octahedral Fe^III ions. Mass spectrometry suggests the cluster is formed quickly and remains stable in solution, while magnetic measurements and DFT calculations reveal competing antiferromagnetic exchange interactions.

---

The diverse chemistry of the earth abundant Fe ion remains at the forefront of a variety of transformative scientific disciplines, including biochemistry,¹ catalysis,² porous materials,³ nanoparticles,⁴ batteries,⁵ superconductivity,⁶ thermoelectrics,⁷ spintronics,⁸ and magnetism.⁹ In the latter area Fe remains ubiquitous in both solid-state¹⁰ and molecule-based chemistry.^11,12

The recent discoveries of three molecular iron oxide compounds, [Fe₁₃],^13,14 [Fe₁₇],¹⁵ and [Fe₃₄],¹⁶ with structures related to minerals such as ferrihydrite and magnetite, suggests that several other very large, high symmetry, molecular clusters exist en route to the formation of 3D oxide or oxyhydroxide mineral phases. In turn, this hints that (large) lacunary or diminished molecular oxyhydroxide [FeO(OH)] clusters not conforming to mineral structure types, including heterometallic species, must also exist. The plausibility of this concept is further supported by the existence of the iron storage protein ferritin which holds ∼4500 Fe^III ions in a molecular ferrihydrite cluster in the inner wall of its spherical shell.¹⁷

The synthetic procedures used to make [Fe₁₃], [Fe₁₇] and [Fe₃₄] are remarkably straightforward. For example, [Fe₁₇] is made by dissolving anhydrous FeBr₃ in wet pyridine (py) (or from a combination of pyridine with a second co-solvent).¹⁵ [Fe₃₄] comes from an analogous reaction to [Fe₁₇] but with a different solvent ratio and in the presence of an additional base/templating agent.¹⁶ The wet pyridine acts as a solvent, a source of H₂O (O²⁻, OH⁻), base, ligand, and cation (pyH⁺). Charge balancing anions originate from the salt employed. Interestingly, in the formation of the [Fe₁₇] cage the py can be replaced with a number of different analogues, including 4-ethylpyridine, β-picoline, 3,5-lutidine and isoquinoline, reflecting the relative stability of the compound.¹⁵

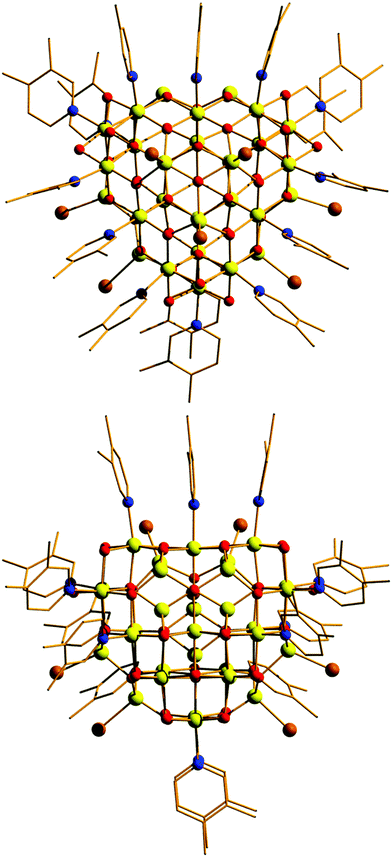
In order to explore this reaction space more efficiently we initially turned to an automated robotic crystallisation platform which methodically explored the combination of multiple reactants under a range of conditions. Initial results indicated the presence of crystalline species containing up to 36 Fe^III ions. Further manual examination revealed that the dissolution of FeBr₃ in a 3,4-lutidine (lut)/acetonitrile solution, in the presence of hexamethylenetetramine (HMTA) results in the formation of (lutH)[Fe^III₃₀(μ₄-O)₆(μ₃-O)₂₆(μ-OH)₁₅Br₉(lut)₁₅]Br₃ (1, Fig. 1 and Table S1, ESI†). A similar reaction replacing the 3,4-lutidine with 4-ethylpyridine (Et-py) affords the isostructural species (Et-pyH)[Fe^III₃₀(μ₄-O)₆(μ₃-O)₂₆(μ-OH)₁₅Br₉(Et-py)₁₅]Br₃ (1a). See the ESI† for details. For the sake of brevity, we restrict all further discussion to complex 1.

Fig. 1 Orthogonal views of the molecular structure of the cluster cation of 1. Colour code: Fe = yellow, O = red, N = blue, C = black, Br = brown. H atoms, lutH cations and Br anions omitted for clarity.

Compound 1 crystallises in the monoclinic space group Pn with two [Fe₃₀] complexes in the asymmetric unit. The metallic skeleton of the [Fe₃₀] cage (Fig. 2 and Fig. S1, ESI†) is constructed from alternate layers of tetrahedral and octahedral Fe^III ions. In the centre of the cage is a [Fe^III₃] triangle of tetrahedral Fe ions. This is surrounded by a partial [Fe^III₁₈] supertetrahedron of octahedral Fe ions – in which three of the corners are truncated into three-membered rings, and one corner is truncated into a six membered ring. The [Fe^III₁₈] cage is surrounded by a partial [Fe^III₉] cuboctahedron of tetrahedral Fe ions. Thus, in total, there are twelve tetrahedral Fe^III sites and eighteen octahedral Fe^III sites. The Fe ions in the inner [Fe^III₃O₉]⁹⁻ triangle are linked to each other and to the metal ions in the [Fe^III₁₈] unit through six μ₄- and three μ₃-O²⁻ ions. Twenty two μ₃-O²⁻ ions then link the octahedral Fe ions in the [Fe^III₁₈O₂₂]¹⁰⁺ unit to each other and to the tetrahedral Fe ions in the outer [Fe^III₉] partial cuboctahedron. The remaining μ₃-O²⁻ ions link three tetrahedral Fe ions in the [Fe^III₉] partial cuboctahedron.

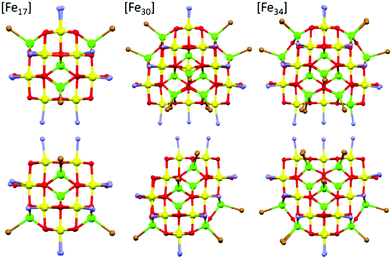Fig. 2 A comparison of the core structures of [Fe₁₇] (left), [Fe₃₀] (middle) and [Fe₃₄] (right). The bottom panel shows the same figures as the upper panel, but rotated 90°. The tetrahedral Fe ions are in green and the octahedral Fe ions are in yellow, highlighting the structural similarity and growth of the metal–oxygen cores. Figures not to scale. Remaining colour code as Fig. 1.

The fifteen hydroxide ions are all located in the [Fe^III₁₈] cage and are of two types: six are μ-bridging between Fe ions in the [Fe₆] ring and the remaining nine are μ-bridging between Fe ions in the [Fe₃] rings. The monodentate 3,4-lutidine ligands are all bonded to octahedral Fe ions in the [Fe^III₁₈] moiety, while the nine tetrahedral iron ions in the outer partial [Fe^III₉] cuboctahedron are each capped by a terminal Br ion. The Fe–O–Fe angles fall into two distinct categories: those connecting the tetrahedral metal ions to tetrahedral/octahedral metals ions are much larger (115.5(7)–134.9(6)°) than those connecting octahedral metal ions to other octahedral metal ions (90.1(5)–104.9(6)°). The [Fe₃₀] cage has an overall charge of 2+, balanced by the presence of three Br counter anions (H-bonded to the μ-OH ions associated with the truncated [Fe₃] rings (Fig. S2 and S3, ESI,†) OH⋯Br, ∼3.3 Å), and one lutH cation. The closest inter-cluster interactions occur between neighbouring Me (lut) groups (C⋯C, ∼3.2–3.6 Å) and between the terminal Br ions and Me(lut) groups (Br⋯C, ∼3.2–3.6 Å).

A structural comparison to the previously published molecular Fe oxides [Fe₁₇] and [Fe₃₄] (Fig. 2) and to the [Fe₁₃] Keggin ion, shows some striking similarities. In each case the cluster is built up from alternate layers of tetrahedral and octahedral Fe ions. In [Fe₁₃] and [Fe₁₇] there is a single tetrahedral Fe ion in the centre, surrounded by a truncated tetrahedron of octahedral metal ions. [Fe₁₇] has an additional outer shell of four tetrahedral metal ions arranged in a tetrahedron. [Fe₃₄] contains a central tetrahedron of tetrahedral metal ions, surrounded by a truncated tetrahedron of octahedral metals ions, surrounded by a truncated tetrahedron of tetrahedral metal ions. [Fe₃₀] has a central triangle of tetrahedral metal ions, rather than a tetrahedron, which clearly modifies the subsequent self-assembly process. The resultant changes in structure and symmetry have significant consequences for the magnetic behaviour (vide infra). The structural similarities across the [Fe₁₃], [Fe₁₇], [Fe₃₀] and [Fe₃₄] series, and to Fe mineral phases such as ferrihydrite and magnetite, do therefore hint that the growth of these complexes occurs layer by layer through addition of polynuclear building blocks.

Mass spectrometry (see the ESI† for full details) of the initial reaction solution indicates that the [Fe₃₀] species is formed quickly with the t = 0 spectrum showing peaks corresponding to the [[M₃₀]-(lut) + 2(MeCN)]²⁺ and [[M₃₀]-2(lut) + 2(MeCN)]²⁺ fragments. The cluster continues to be present throughout the reaction time with measurements at t = 2 hours and t = 4 hours also showing these peaks (Fig. S4, ESI†). Mass spectrometry of crystalline 1 redissolved in a 20/80 mix of lut/MeCN shows the [Fe₃₀] cage is present with one, two and three ligands removed, with measurements repeated over a period of 24 hours showing that the molecule is present in solution for at least 1 day (Fig. S5–S7, ESI†).

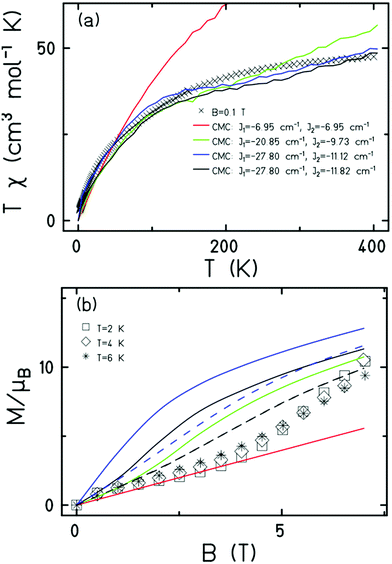
Magnetic measurements of 1 reveal relatively strong antiferromagnetic interactions between the Fe centres. The experimental dc susceptibility data (T = 2–400 K, B = 0.1 T) for 1 is plotted in Fig. 3 as the χT product versus T, where χ is the molar magnetic susceptibility, T is the temperature, and B the applied magnetic field. The value of χT at T = 300 K is ∼45 cm³ K mol⁻¹, significantly lower than that expected for the sum of the Curie constants for thirty Fe^III (S = 5/2) ions with g_Fe = 2.00 (131.25 cm³ K mol⁻¹). As the temperature decreases, the magnitude of χT decreases rapidly, reaching a value of ∼3.5 cm³ K mol⁻¹ at T = 2 K, suggestive of a small/diamagnetic spin ground state. At T > 300 K, the χT value increases slowly, with no sign of an inflection or jump in value. Magnetisation data (T = 2–7 K, B = 0.5–7 T) appear somewhat S-shaped, with the low field data appearing to saturate at ∼2 T before increasing rapidly up to ∼5 T, and then increasing more gradually up to 7 T. This is indicative of the presence of multiple low lying spin states, stabilised through increasing field strength.

Fig. 3 (a) Plot of the χT product versus T in the 400–2 K temperature range in an applied field, B = 0.1 T. (b) Plot of M versus B in the 2–6 K range for 0.5 ≤ B ≤ 7T. In the latter the solid curves are for T = 2 K, dashed curves for T = 6 K. The colour coded CMC simulation values in (b) are the same as those provided in (a).

It is computationally impossible to quantitatively analyse the magnetic data of a molecule containing 30 × S = 5/2 spins via conventional matrix diagonalisation techniques. Even the finite-temperature Lanczos method¹⁸ which can approximately solve problems in Hilbert spaces with dimensions up to 10¹¹ cannot be applied here. We thus turn to a classical spin model and classical Monte Carlo (CMC).¹⁹ This allows approximations of the magnetisation and the magnitude of the exchange interactions to be obtained. Note however that classical spin models constitute a high-temperature approximation and thus can be inaccurate at (low) temperatures smaller than the typical interaction strength. Although there are nine different exchange interactions present in 1, DFT calculations (vide infra) suggest they can be grouped into two categories: strongly antiferromagnetic and weakly ferro- or antiferromagnetic based on the larger Fe(tet)–O–Fe(tet/oct) angles and the smaller Fe(oct)–O–Fe(oct) angles, respectively. We therefore simplified the numerical simulations by employing a model with just two different J values representing these two different Fe–O–Fe exchange pathways. Simulations with one strong AF coupling of −20.85 ≤ J_s ≤ −27.80 cm⁻¹ and one weak AF coupling of −6.95 ≤ J_w ≤ −11.82 cm⁻¹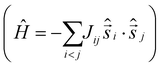 come closest to replicating the magnetic observables (Fig. 3), being superior to a model containing just one exchange interaction, J = −6.95 cm⁻¹.

To further support the relative sign and magnitude of the coupling constants obtained above, we have performed DFT calculations (see the ESI† for the computational details) on model complexes derived from complex 1 (Fig. S9, ESI†). These suggest that the nine independent exchange interactions (Scheme S1 and Fig. S10–S18 (ESI†) show the spin density plots) are in the range |J| ≈ 6–71 cm⁻¹ (Table S2, ESI†). All the computed exchange interactions are antiferromagnetic, with the exception of 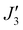where a weak ferromagnetic exchange of +14.3 cm⁻¹ has been estimated. The large antiferromagnetic interactions originate from multiple strong overlap integrals between the SOMOs of Fe^III centres bridged by μ₃/μ₄-O²⁻ ions (Tables S3–S11, ESI†). The overlap integral is much smaller for the 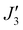exchange pathway where only one dominant d_z²|p_z|d_z² overlap integral is found (Table S7, ESI†). This results in a very small contribution to the antiferromagnetic part of the interaction (J_AF, where J = J_AF + J_F) resulting in a small ferromagnetic interaction overall (Table S2, ESI†). The results are in agreement with previous magneto-structural correlations developed for oxo-bridged Fe^III complexes in which the magnitude of J is dictated by the Fe–O–Fe angle and Fe–O/Fe distances, and with the results observed for [Fe₁₇] and [Fe₃₄] in which J(tet–oct) ≫ J(oct–oct).^14,15,20

The simplicity of the experimental procedure and the structural similarity of [Fe₃₀] to previously published molecules such as [Fe₁₃], [Fe₁₇] and [Fe₃₄], and to bulk oxides such as ferrihydrite and magnetite, which all possess structures composed of alternating layers of tetrahedral and octahedral Fe^III ions, suggests that many more molecular iron oxides must exist. The self-assembly process also suggests that multi-functional ‘core–shell’ species in which the Fe-oxo core is encapsulated within another (stabilising) material, e.g. a polyoxometalate, will be attractive targets for a diverse array of applications.

A. E. D., D. J. C., M. C., E. L., S. S. and H. W. L. F. all contributed to the synthetic methodologies; S. D. and G. R. performed the DFT calculations; G. S. N. collected and solved the XRD data; D. J. C. and M. C. measured the mass spectrometry and magnetic data; J. S. simulated the magnetic data. L. C. and E. K. B. conceived the idea. All authors contributed to the writing of the article.

E. K. B. thanks EPSRC for funding grants EP/P025986/1 and EP/N01331X/1. EKB/LC thank U21/EPSRC for studentships (E. L., D. J. C.).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. Cho, S. Jeon, S. A. Wilson, L. V. Liu, E. A. Kang, J. J. Braymer, M. H. Lim, B. Hedman, K. O. Hodgson, J. S. Valentine, E. I. Solomon and W. Nam, Nature, 2011, 478, 502–505.
2. J. H. Docherty, J. Peng, A. P. Dominey and S. P. Thomas, Nat. Chem., 2017, 9, 595–600.
3. Z. Chen, P. Li, R. Anderson, X. Wang, X. Zhang, L. Robison, L. R. Redfern, S. Moribe, T. Islamoglu, D. A. Gómez-Gualdrón, T. Yildirim, J. F. Stoddart and O. K. Farha, Science, 2020, 368, 297–303.
4. R. A. Revia and M. Zhang, Mater. Today, 2016, 19, 157–168.
5. C. Xie, Y. Duan, W. Xu, H. Zhang and X. Li, Angew. Chem., Int. Ed., 2017, 56, 14953–14957.
6. S. Zhu, L. Kong, L. Cao, H. Chen, M. Papaj, S. Du, Y. Xing, W. Liu, D. I. Wang, C. Shen, F. Yang, J. Schneeloch, R. Zhong, G. Gu, L. Fu, Y.-Y. Zhang, H. Ding and H.-J. Gao, Science, 2020, 367, 189–192.
7. A. Sakai, S. Minami, T. Koretsune, T. Chen, T. Higo, Y. Wang, T. Nomoto, M. Hirayama, S. Miwa, D. Nishio-Hamane, F. Ishii, R. Arita and S. Nakatsuji, Nature, 2020, 581, 53–57.
8. R. Lebrun, A. Ross, S. A. Bender, A. Qaiumzadeh, L. Baldrati, J. Cramer, A. Brataas, R. A. Duine and M. Kläui, Nature, 2018, 561, 222–225.
9. S. Loth, S. Baumann, C. P. Lutz, D. M. Eigler and A. J. Heinrich, Science, 2012, 335, 196–199.
10. L. Ye, M. Kang, J. Liu, F. von Cube, C. R. Wicker, T. Suzuki, C. Jozwiak, A. Bostwick, E. Rotenberg, D. C. Bell, L. Fu, R. Comin and J. G. Checkelsky, Nature, 2018, 555, 638–642.
11. S. Ohkoshi, K. Imoto, Y. Tsunobuchi, S. Takano and H. Tokoro, Nat. Chem., 2011, 3, 564–569.
12. (a) G. Serrano, L. Poggini, M. Briganti, A. L. Sorrentino, G. Cucinotta, L. Malavolti, B. Cortigiani, E. Otero, P. Sainctavit, S. Loth, F. Parenti, A.-L. Barra, A. Vindigni, A. Cornia, F. Totti, M. Mannini and R. Sessoli, Nat. Mater., 2020, 19, 546–551; (b) S. L. Heath and A. K. Powell, Angew. Chem., Int. Ed. Engl., 1992, 31, 191–192.
13. (a) O. Sadeghi, L. N. Zakharov and M. Nyman, Science, 2015, 347, 1359–1362; (b) O. Sadeghi, C. Falaise, P. I. Molina, R. Hufschmid, C. F. Campana, B. C. Noll, N. D. Browning and M. Nyman, Inorg. Chem., 2016, 55, 11078–11088; (c) N. A. G. Bandeira, O. Sadeghi, T. J. Woods, Y.-Z. Zhang, J. Schnack, K. R. Dunbar, M. Nyman and C. Bo, J. Phys. Chem. A, 2017, 121, 1310–1318.
14. (a) A. Bino, M. Ardon, D. Lee, B. Spingler and S. J. Lippard, J. Am. Chem. Soc., 2002, 124, 4578–4579; (b) J. van Slageren, P. Rosa, A. Caneschi, R. Sessoli, H. Casellas, Y. V. Rakitin, L. Cianchi, F. Del Giallo, G. Spina, A. Bino, A.-L. Barra, T. Guidi, S. Carretta and R. Caciuffo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 014422.
15. (a) G. W. Powell, H. N. Lancashire, E. K. Brechin, D. Collison, S. L. Heath, T. Mallah and W. Wernsdorfer, Angew. Chem., Int. Ed., 2004, 43, 5772–5775; (b) C. Vecchini, D. H. Ryan, L. M. D. Cranswick, M. Evangelisti, W. Kockelmann, P. G. Radaelli, A. Candini, M. Affronte, I. A. Gass, E. K. Brechin and O. Moze, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224403; (c) M. Evangelisti, A. Candini, A. Ghirri, M. Affronte, G. W. Powell, I. A. Gass, P. A. Wood, S. Parsons, E. K. Brechin, D. Collison and S. L. Heath, Phys. Rev. Lett., 2006, 97, 167202; (d) I. A. Gass, C. J. Milios, M. Evangelisti, S. L. Heath, D. Collison, S. Parsons and E. K. Brechin, Polyhedron, 2007, 26, 1835–1837; (e) I. A. Gass, E. K. Brechin and M. Evangelisti, Polyhedron, 2013, 52, 1177–1180.
16. A. E. Dearle, D. J. Cutler, H. W. L. Fraser, S. Sanz, E. Lee, S. Dey, I. F. Diaz-Ortega, G. S. Nichol, H. Nojiri, M. Evangelisti, G. Rajaraman, J. Schnack, L. Cronin and E. K. Brechin, Angew. Chem., Int. Ed., 2019, 58, 16903–16906.
17. F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, Science, 2007, 316, 1726–1729.
18. (a) J. Jaklič and P. Prelovšek, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5065–5068; (b) J. Schnack and O. Wendland, Eur. Phys. J. B, 2010, 78, 535–541; (c) J. Schnack, J. Richter and R. Steinigeweg, Phys. Rev. Res., 2020, 2, 013186.
19. C. Schröder, H. Nojiri, J. Schnack, P. Hage, M. Luban and P. Kögerler, Phys. Rev. Lett., 2005, 94, 017205.
20. (a) H. Weihe and H. U. Güdel, J. Am. Chem. Soc., 1998, 120, 2870–2879; (b) C. Cañada-Vilalta, T. A. O'Brien, E. K. Brechin, M. Pink, E. R. Davidson and G. Christou, Inorg. Chem., 2004, 43, 5505–5521.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic procedures, X-ray data, mass spectrometry, DFT methodology. CCDC 2105690 and 2105691. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1cc06224g

‡ Contributed equally to this work.

---