Translational dependence of the geometry of metallic mono- and bilayers optimized on semi-ionic supports: the cases of Pd on γ-Al2O3(110), monoclinic ZrO2(001), and rutile TiO2(001)†
A. A.
Rybakov
 a,
V. A.
Larin
b,
D. N.
Trubnikov
a,
S.
Todorova
a,
V. A.
Larin
b,
D. N.
Trubnikov
a,
S.
Todorova
 c and
A. V.
Larin
c and
A. V.
Larin
 *a
*a
aDepartment of Chemistry, Moscow State University, GSP-2, Leninskie Gory, Moscow 119992, Russia. E-mail: nasgo@yandex.ru
bTechnology Center Lantan, LTD, Rubtsovskaya naber., 2, korp.4, Moscow, 105082, Russia
cInstitute of Catalysis, Bulgarian Academy of Sciences, Acad. G. Bonchev St., Bldg 11, 1113 Sofia, Bulgaria
First published on 16th November 2021
Abstract
A simplified computational scheme for “deposition” of a metallic (Pd) monolayer on semi-ionic supports is considered. An arbitrary selection of the initial position of the deposited layer relative to the surface of the support cannot provide the best solution for an optimal atom–atom binding. The energy and/or geometry changes were checked relative to a slide of the mono- and bilayers in parallel to the support layer and re-optimization. Two types of possible consequences are shown at the slide length of 1–3 Å for γ-Al2O3(110), monoclinic ZrO2(001) (or m-ZrO2), and rutile TiO2(001) (or TiO2 below). First consequence option: either the Pd monolayer completely collapses after the shift/optimization, or it yields a new geometry (at γ-Al2O3(110) and m-ZrO2) at different steps. Second consequence option: the shift leads to a loss of the Pd stabilization while the ordered monolayer's geometry is retained (at TiO2 and m-ZrO2). The extent of such destabilization varies depending on the strength of the interaction with the support. It is thus recommended to verify Pd stabilization energy by sliding/optimizing the monolayer along one or two monolayer directions in order to avoid its energy underestimation. The activity of such monolayers for modelling catalysis is demonstrated using H2O dissociation in the Pd monolayer/rutile system.
1. Introduction
The formation of clusters, monolayers or/and multilayer slabs is conventionally defined by a combination of three mechanisms, i.e., Stranski–Krastanov, Volmer–Weber, and Frank–van der Merwe. Two of them (with the exception of the Volmer–Weber type) pass through the monolayer formation but the details of its formation remain poorly understood. Modern research effectively completes this domain. The explosion of interest in 2D systems covers different types of materials from semiconductors1,2 and dielectrics3,4 to semimetals5 and metals.6–13 The studies of atomically thin layers composed of under-coordinated metal atoms and named as “metallenes” are directed by their new possibilities in electrocatalysis14 and catalysis for oxygen reduction reactions.15 The main interest in “metallenes” is connected with multilayer slabs (3–5 layers15 and more16) because several methods to produce an atomic monolayer seem to be under study for different metals (Rh,12 Pt,17 Au18) to the best of our knowledge. The monolayer metallenes can acquire new properties when deposited onto semi-ionic supports. The most detailed studies of mono- and bilayer formation were realized on TiO2(110) (ref. 19–24) (please, see Discussion). A large fraction of small 2D Au clusters over Au/TiO2(110) showed a turnover-of-frequency (TOF) maximum for the CO oxidation reaction19 in parallel revealing a non-metallic type of electric conductivity.20 Such type of conductivity was also shown for small flat Pd clusters at the TiO2(110) plane.24 Their properties on other semi-ionic supports (such as carbides and nitrides) can be evaluated from numerous experimental and theoretical studies for flat square Mex clusters, Me = Pd, Pt,11 Cu,10,11 Ag,11 Au,10,11 Ni,9,10x = 4, 9, and 16. Continuous Pt monolayers, which can be considered as metallenes, were theoretically studied as catalysts for the water gas shift (WGS) reaction when deposited onto TiC(100) carbide.6–8 Recently, the catalytic capabilities of a Pd monolayer deposited on a γ-Al2O3(100) plane were theoretically shown for catalysis of CH4, H2O, and O2 dissociation.13 So, the problem of an accurate search for the most stable metallic monolayers on different supports becomes an important part of modeling.Earlier, the passivation of a defective Si(110) plane by a thin Al2O3 layer was realized as alternate O/Al/O deposition or a Si(110) reaction with the existing Al2O3 fragment.3,4 A reaction was admitted between the plane of regularly ordered Al or O atoms and the Si(110) support.3,4 Such a method looks to be better suited for deposition of metallic Me slabs because the monolayer precursor can be cut from a selected direction in the Me bulk13,25–27 being a good approximation for the final monolayer.13 It is possibly a consequence of the close Pd–Pd distances between the bulk and the deposited species, while the geometry of the latter can be different, for example, alternation of one parallel row of squares and four rows of triangles in the Pd monolayer deposited on γ-Al2O3(100).13 The layer was thus obtained with better Pd stabilization than single Pd atoms at favorable sites of the γ-Al2O3(100) plane.13 Closer Au–Au or Pt–Pt distances compared to respective values for bulk metals were illustrated in a new hybrid form of a flat Au9Pt9 monolayer without deposition on any support.28
However, such joining/optimization of a metallic monolayer precursor and support depends on a large number of parameters and cannot “immediately” guarantee an optimal atom–atom binding and hence the highest metal stabilization. Within periodic boundary conditions, some limited freedom remains for monolayer sliding in parallel to the support. This aspect also applies to other systems, for example, to atomic H coverage at the W(110) surface when a quantitative agreement with experimental data requires a model with translational 1D motion of H atoms on the W-surface.29 An additional problem arises due to the unclear density of the deposited Me atoms per selected unit cell (UC) to complete the monolayer. Some deviations from a totally flat shape of the Pd monolayers are partly a consequence of the non-flat surface of the support. This complicates an accurate assessment. A series of shifts of Pd monolayers over fixed γ-Al2O3(100), rutile TiO2(001), monoclinic ZrO2(001) supports are proposed to find their new optimal position. Below we characterized the qualitative changes of the geometry thus optimized and the order of values for possible errors. After the presentation of computational details (part 2), the structures of the Pd monolayers on γ-Al2O3(110) (part 3.1), rutile TiO2(001) (part 3.2), and monoclinic ZrO2(001) (part 3.3) are discussed. The example of H2O dissociation in the Pd monolayer/rutile system is presented to illustrate the catalytic perspectives of the Pd monolayers (part 3.2.2), while the case of Pt and Pd monolayers is analyzed on the TiC support where the Pt monolayer formation was confirmed experimentally (part 4).
2. Computational details
Plane wave computations with periodic boundary conditions using the PBE30 functional were performed within the projector augmented wave (PAW) method31,32 implemented in VASP.33,34 The GPU version of the VASP code35,36 was used for geometry optimization. Dispersive energy corrections were considered zero damping D3 (ref. 37 and 38) levels. The PBE-D3 accuracy was verified via testing for the Au8 cluster37 and later for periodic systems39 (molecular crystals and adsorbed molecules). The atomic charge density distribution was analyzed using Bader analysis.40 The scripts provided by the transition state tools for VASP were used to build the initial images for the climbing image nudged elastic band (cNEB) calculations.41,42 The energy cut-off was set to 500 eV. The Brillouin zone k-sampling was restricted to the Γ-point for the geometry optimization and transition state (TS) search via cNEB calculation. Spin polarized solution was considered for testing the basic Pd/γ-Al2O3(110) model. Vibrational frequencies were calculated using the finite difference method (0.015 Å atomic displacements) as implemented in VASP. For the selected reaction, the TS showed a single imaginary frequency corresponding to the reaction path. The figures of the 3D structure of the different models were drawn with MOLDRAW 2.0.43 Steps of the reaction simulations (see the ESI†) were realized using wxMacMolPlt.443. Results and discussion
3.1 Pd on γ-Al2O3(110)
One has to compare the respective Pd stabilization in each case (single Pd atom, cluster, slab) in order to roughly estimate the respective probabilities of such growth. The relative stabilization energy (eV per Pd) per Me atom is| UMe = (Utot − Uox)/N | (1) |
| System | N | −UPd | Fig. | |
|---|---|---|---|---|
| a For a smaller UC such as Al14O20 (see the text and ESI†). b After shift by 1 Å along the OY direction. c After shift by 2 Å along the OY direction. d After shift by 3 Å along the OY direction. e Shift by 1 Å along both the OX and OY directions. f Shift by 1 Å along the OX direction. g (111) model. h “band” type structure. i 1/1 model. j (100) model. k 4R–4R model. l “mix” model. m Thin Zr16O32 support model. n For Pt with UPt = −6.218 eV for bulk at the PBE level. | ||||
| Al2O3 | Atom | 1 | 5.314 | S1g† |
| 3.787 | — | |||
| 3.755 | — | |||
| 5.159a | 1b | |||
| 1-Layer | 24 | 4.852 | 2a and b | |
| 4.886b | 2c and d | |||
| 4.749c | 2e and f | |||
| 4.896d | 2g and h | |||
| 28 | 4.847 | 3f | ||
| 4.865e | — | |||
| 4.862f | 3h | |||
| 30 | 4.865 | 3i | ||
| 2-Layer(100) | 48 | 4.936g | 1c | |
| 4.941e,g | — | |||
| TiO2 | Atom | 1 | 3.318 | S1a† |
| 3.111 | S1b† | |||
| 2.726 | S1c† | |||
| Cluster | 24 | 4.278 | 1e | |
| 1-Layer (111) | 24 | 4.094 | S1d† | |
| 24f | 4.071 | S1e† | ||
| 24h | 4.190 | 4f | ||
| 27 | 4.263 | 4d and e | ||
| 28 | 4.305 | 6a | ||
| 30 | 4.710 | 4g and h | ||
| 30f | 4.362 | 4i and j | ||
| 32 | 4.353 | S3b† | ||
| 2-Layer (111) | 48 | 4.618 | S1f† | |
| 4-Layer (110) | 72 | 4.714 | 1f | |
| m-ZrO2 | Atom | 1 | 4.267 | S1h† |
| 1-Layer | 16 | 4.294i | 5a | |
| 4.243j | — | |||
| 4.325g | — | |||
| 4.336k | 5b and c | |||
| 4.336l | 5d | |||
| 2-Layer (111) | 32m | 4.920g | S2b† | |
| 4.836g | S2a† | |||
| TiC | 1-Layer | 16 | 5.086 | 7c |
| 18 | 5.153 | 7b | ||
| 5.895n | 7a | |||
| γ-Al2O3(110) | γ-Al2O3(100) | |||||
|---|---|---|---|---|---|---|
| No. | 0 | +1 Å | +2 Å | +3 Å | No. | 0 |
| a Optimized 2-layer Pd48 slab possesses −5.148 e at the same position. b PBE-D3. c Calculated bulk cohesion energy of −5.834 eV per Pd instead of −5.250 eV per Pd at the PBE level. | ||||||
| 137 | −0.592 | −0.597 | −0.285 | 0.028 | 117 | 0.113 |
| 138 | 0.108 | −0.06 | −0.198 | −0.047 | 118 | −0.196 |
| 139 | −0.004 | −0.027 | 0.076 | 0.011 | 119 | 0.333 |
| 140 | 0.116 | 0.014 | −0.406 | −0.592 | 120 | 0.114 |
| 141 | −0.613 | −0.597 | −0.285 | 0.028 | 121 | −0.248 |
| 142 | 0.050 | −0.060 | −0.198 | −0.047 | 122 | 0.104 |
| 143 | 0.038 | −0.027 | 0.076 | 0.011 | 123 | −0.155 |
| 144 | 0.008 | 0.014 | −0.406 | −0.592 | 124 | −0.258 |
| 145 | −0.658 | −0.622 | −0.546 | −0.622 | 125 | 0.109 |
| 146 | 0.143 | 0.019 | 0.039 | 0.018 | 126 | 0.090 |
| 147 | −0.533 | −0.304 | −0.294 | −0.314 | 127 | −0.260 |
| 148 | 0.158 | 0.003 | −0.475 | −0.591 | 128 | 0.325 |
| 149 | −0.691 | −0.622 | −0.546 | −0.622 | 129 | 0.119 |
| 150 | 0.098 | 0.019 | 0.039 | 0.018 | 130 | −0.259 |
| 151 | −0.478 | −0.304 | −0.294 | −0.314 | 131 | 0.107 |
| 152 | 0.041 | 0.003 | −0.475 | −0.591 | 132 | −0.146 |
| 153 | −0.627 | −0.609 | 0.144 | −0.052 | 133 | −0.171 |
| 154 | −0.627 | −0.622 | −0.163 | −0.307 | 134 | 0.085 |
| 155 | −0.049 | −0.014 | −0.337 | 0.001 | ||
| 156 | −0.358 | −0.297 | −0.572 | −0.626 | ||
| 157 | −0.602 | −0.609 | 0.144 | −0.052 | ||
| 158 | −0.671 | −0.622 | −0.163 | −0.307 | ||
| 159 | −0.036 | −0.014 | −0.337 | 0.001 | ||
| 160 | −0.347 | −0.297 | −0.572 | −0.626 | ||
| Q | −6.126a | −6.232 | −6.034 | −6.186 | — | −0.194 |
| −Uox | 953.797 | 952.894 | 953.652 | 952.844 | — | 782.358 |
| ΔUox | 5.430 | 6.243 | 5.485 | 6.156 | — | — |
| ΔUtot | 0.000 | −0.821 | 3.297 | −3.530 | — | — |
| −Utot | 1075.617 | 1076.438 | 1073.141 | 1076.671 | — | 858.330 |
| −UPd | 4.852 | 4.886 | 4.749 | 4.896 | — | 4.221 |
| −Utotb | 1099.454 | 1101.163 | 1097.848 | 1101.153 | — | — |
| −UPdb,c | 5.293 | 5.364 | 5.226 | 5.363 | — | — |
3.1.2.1 Decomposition of the total energy while shifting the Pd24 slab. Dividing the total energy variations (from Table 2) per number of Pd atoms (24) at these three steps gives −0.034 (0–1), 0.137 (1–2), and −0.147 (2–3) eV per Pd per every shift. Despite the disconnected parts, the layer after the “+1 Å” shift is slightly more stable than the initial distorted (111) model (Fig. 2a and b) or the one after the shift by 2 Å (Fig. 2e and f) (Tables 1 and 2). Perturbed naked (without the Pd layer) and frozen (without optimization) supports at the new Pd positions possess energies of −953.797, −952.894, −953.652, and −952.844 eV, respectively, instead of the initial −959.137 eV. The destabilization of the oxide support due to the interaction with Pd24 (5.430, 6.243, 5.485, and 6.156 eV, respectively) is rather large while changing in the opposite manner relative to the total energy at every 0–1, 1–2, 2–3 step. The higher the deformation, the higher the interaction energy in absolute value. It shows that respective changes of the total energy have important contribution from the chemical interaction between the monolayer and support.
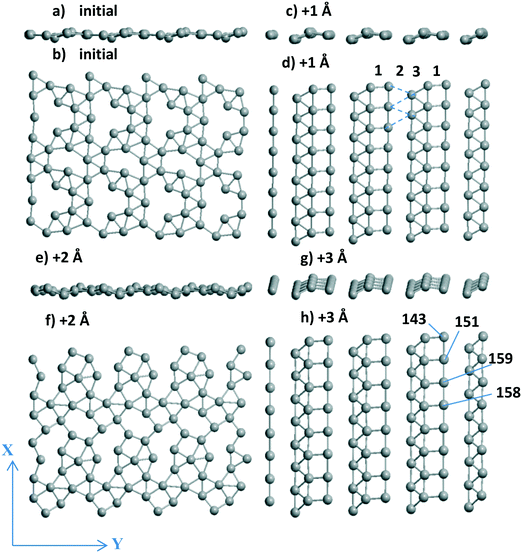
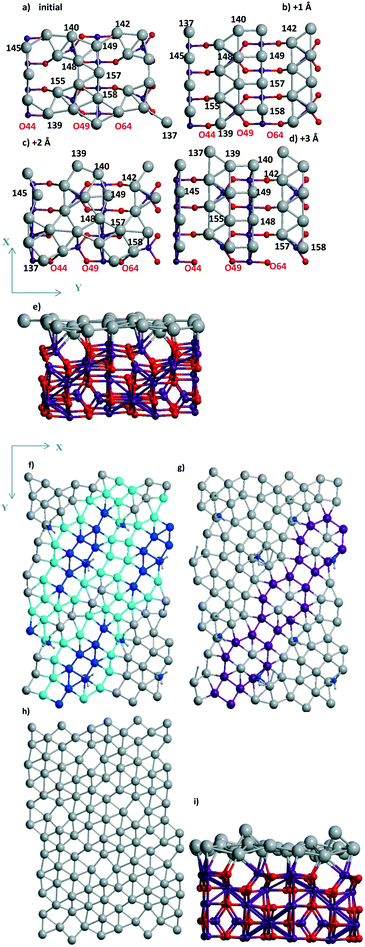
3.1.2.2 Visualization of the shift of the Pd layer relative to the support. Due to the presence of two 4-atom Al chains (shown in magenta from top to bottom in Fig. 3a–d) at the surface, the respective chains of Pd atoms coordinated to the Al-chain are held in the “disordered” (Fig. 3a and c) and “ordered” (Fig. 3b and d) Pd24 forms. The Pd atoms of these chains can relax after every shift, finally keeping or losing their favored bi-coordinated sites (Fig. S1g and 1b). In the second case, another Pd atom occupies the free bi-coordinated site. In order to demonstrate the slide of the Pd slab relative to the support with every +X Å step, the numbers of some O atoms of the upper oxide layers are shown together with the Pd numbers (using red and black notations for O and Pd, respectively, in color version of Fig. 3). The most convenient landmark to trace the monolayer motion relative to the oxide (from left to right) is the position of the Pd158 atom relative to that of O64. It can be easily seen that different atoms of the monolayer make different steps upon the imposed total shift. Only two atoms (Pd145 and Pd149) remain at their sites in all four models.
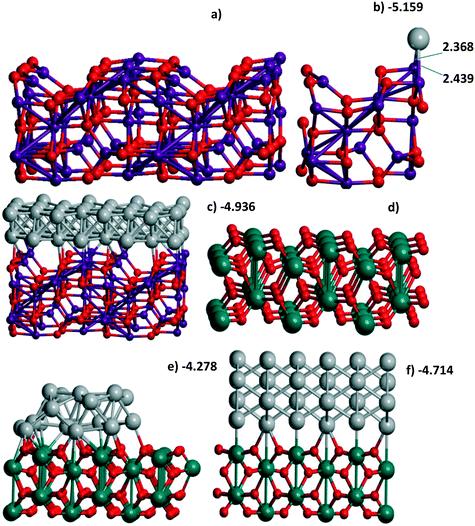 | ||
| Fig. 1 (a) Al56O80 and (b) Al14O20 model of γ-Al2O3(110) with one Pd atom or (c) Al56O80 with a Pd48 bilayer, (d) Ti36O72 model of the rutile TiO2(001) surface with (e) the Pd24 cluster and (f) 4-layer Pd72(110) slab all optimized at the PBE-D3 level. The UPd energies (in eV per Pd) correspond to Table 1 when Pd atoms are involved. The atomic colors are given in red, magenta, green, and gray for O, Al, Ti, and Pd, respectively. | ||
We selected a limited set of Pd atoms in order to show: 1) the changes of the geometries for the atoms with a drastic charge variation along with the 0–3 steps (Table 2), i.e., from −0.592 |e| to 0.028 |e| for Pd137‡ and inverse change from 0.116 |e| to −0.592 |e| for Pd140. These atoms perform the shifts in the opposite directions, i.e., Pd137 loses its position at a favorable site near Al atoms and Pd140 vice versa; 2) the neighboring Pd atoms with opposite charges, like the Pd140(−0.591 |e|)⋯Pd139(0.011 |e|)‡ pair, in the final model after the shift +3 Å (Table 2). This Pd140⋯Pd139 pair could be attractive sites for dissociation of small heteronuclear molecules (part 3.2.2). The charge selection was based on the Bader type charges because projected DOS (pDOS) analysis for Pd atoms also shows essential correlations with the Bader charges of the same atoms (for Pd/γ-Al2O3(100), will be shown elsewhere).
The most important result of the sliding and optimization is a highly ordered Pd24 slab after the steps +1 Å (side and upper views in Fig. 2c and d) and +3 Å (Fig. 2g and h) which stabilize the system. No plane of symmetry is preserved for the Pd atoms in one UC after the +2 Å step as it was in the initial model (Fig. 2a and b). Disjoined “bands” for these two configurations include the fragments (squares, triangles) of the (100) and (111) planes. One band of squares (band no. 1 in Fig. 2d) is combined with one band of triangles (band no. 3 in Fig. 2d). The dashed lines therein show the missing band 2 of triangles due to rather long Pd⋯Pd distances of 3.6–3.7 Å (Fig. 2d). The variation of the total Bader charge of the Pd slab between the steps varies rather slightly between −6.034 and −6.232 |e| even if some atomic charges can change their sign in the course of an optimization after a single translation (Pd137, Pd141 etc. in Table 2). The difference in the absolute Pd monolayer charges (−0.169 versus −6.034 |e| at γ-Al2O3(100) and γ-Al2O3(110), respectively) can be explained by different types of the favored Pd sites, i.e., O–Pd–O at γ-Al2O3(100) and Al–Pd–Al at γ-Al2O3(110). A similar Al–Pd–Al site (the shortest Pd–Al are 2.522 and 2.529 Å in γ-Al2O3(100)) is absent at the γ-Al2O3(100) surface because it allows two additional shorter bonds with two O atoms (2.251 and 2.344 Å) and an essentially worse UPd value of −2.751 eV per Pd. As soon as the favored site for O–Pd–O at the γ-Al2O3(100) surface possesses UPd = −4.375 eV per Pd for a single atom which is slightly smaller (in absolute value) than UPd = −4.392 eV per Pd for the Pd20 monolayer,13 the probability of Pd monolayer formation becomes higher at γ-Al2O3(100). Due to this deviation between γ-Al2O3(100) and γ-Al2O3(110), the Pd stabilization energies of the favorable site of a single atom and the Pdn monolayer obey the |UPd(Pd1/γ-Al2O3(100))| < |UPd(Pd20/γ-Al2O3(100))| relation for (100),13 which is inverse |UPd(Pd1/γ-Al2O3(110))| > |UPd(Pdn/γ-Al2O3(110))|, n = 24–28, for γ-Al2O3(110). This illustrates better conditions for monolayer growth at the γ-Al2O3(100) plane.
The importance of checking the shifts has also been shown for Pd28 stability. Even if a modest energy gain was found to be present (from −4.847 to −4.865 or −4.862 eV per Pd, Table 1), both structures obtained by the shifts (of +1 Å along OX or along OX and OY together) clearly demonstrate a distorted (111) geometry (Fig. 3h). Surprisingly, this does not enhance the respective Pd28 stability compared to the one for the most stable Pd24 models with vacancies (or “empty space” between the bands, Fig. 2d) despite the larger number of Pd atoms. One could propose that the absence of essential energy variations relative to the sliding can be one of the signs of a complete Pd monolayer.
3.1.3.1 Difference between mono- and multilayers relative to the shifts. An important observation about the weak influence of the shift on the Pd stabilization of bilayers is noted for γ-Al2O3(110). The first example demonstrated that the Pd48(100) bilayer can hardly be effectively stabilized upon the shift possibly due to a higher “rigidity” of the slab. The initial bilayer Pd48(100) slab at γ-Al2O3(110) was tested with respect to the shift by +1 Å but the optimized (100) geometry is retained with a small increase (0.1%) of the relative stability expressed via the energy UPd (1). The shift of the Pd48 bilayer at γ-Al2O3(110) (Table 1) was accompanied by switching from some bonds to others without a significant improvement of the stabilization (by only 0.005 eV per Pd) compared to the drastic change of the Pd24 monolayer of 2.9% (Table 1). An even higher energy of 7.4% was gained by shifting a complete Pd24 monolayer at the TiO2(001) surface (part 3.2.1) below. An opposite case of relatively stronger stabilization of the Pd bilayer upon a shift (1.7%) was found for Pd32(111) at m-ZrO2(001) (Table 1, see part 3.3).
3.2 Pd/rutile TiO2(001)
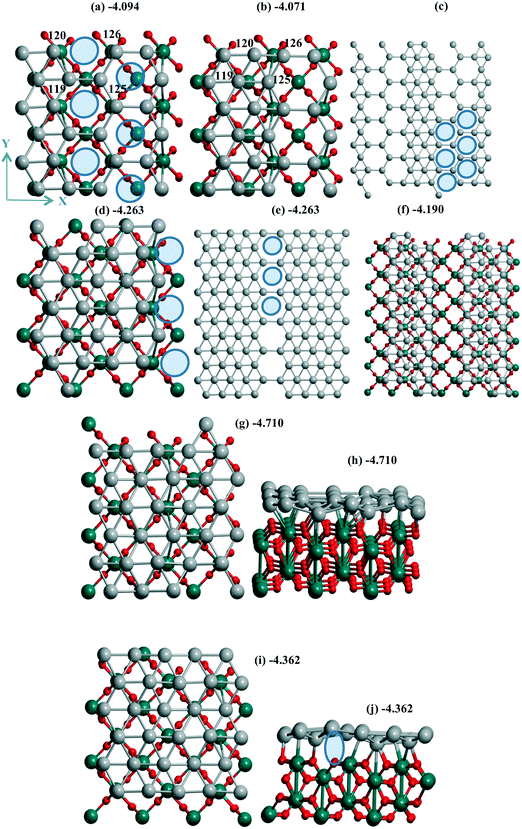 | ||
| Fig. 4 Pd30 monolayer with isolated (a–c) six, (d–f) three mono-vacancies, and (g–j) without vacancies including views of 2 × 2 cells (c, e and f). Atomic notations (a and b) are given before (a) and after (b) shift/optimization by 1 Å along OX. The case of “band” type Pd24 monolayer is in (f) with the inverted OX and OY axes relative to the common case. In (a and c–e) ellipses show the Pd vacancies. The lost bonds upon the slide are shown by ellipse in (j). The color agreement corresponds to Fig. 1. | ||
Two situations with the slide/optimization of the Pd24 and Pd30 monolayers at rutile TiO2(001) can illustrate the second variant of the influence of support heterogeneity on their final structure, i.e., a conservation of the geometry with a destabilization upon the monolayer's shift. For a Pd24 monolayer, both the initial (Fig. 4a) and shifted (Fig. 4b) models correspond to the same geometry with 6 monovacancies per UC (shown by 6 ellipses for one of the four UCs in Fig. 4c). These numerous mono-vacancies result in the lower stability of these Pd24 monolayers (−4.094 and −4.071 eV per Pd) relative to a Pd24 cluster (−4.278 eV per Pd, Fig. 1e). A reconstruction of the monolayer after its slide/optimization can be controlled regarding the Pd atomic numbers (Fig. 4a and b) and distances between the Pd atoms in (a) and (b). A saturation of three of them already stabilizes a Pd27 monolayer (−4.263 eV per Pd, Fig. 4d and e).
One can note the possible energy gain/loss upon the shift of a Pd24 monolayer (2.9%) and a Pd48 bilayer (0.1%) parallel to γ-Al2O3(110). The minor change for the bilayer was assigned to its rigidity. The shift of a Pd24 monolayer with 6 monovacancies relative to the TiO2(001) surface mentioned above (previous passage) is also accompanied by a small UPd destabilization of 0.5%. This weak influence can be explained by a poor interaction which is not strongly perturbed (Fig. S1d and e†). Opposite partial loss of the bonds during the shift of the Pd30 monolayer is evident from a comparison of the respective geometries before (Fig. 4g) and after the shift (Fig. 4i). The absent bonds are shown by an ellipse in the second case (side view in Fig. 4j). This lost binding led to the largest decrease of the Pd stabilization of 7.4% throughout all models on all three supports.
A similarity between the Pd24 monolayers at both supports is manifested, revealing a higher stabilization of the denser models in the form of bands. Such a band at the TiO2(001) surface possesses a Pd(111) geometry (Fig. 4i) while it forms a kind of hybrid structure including both squares and triangles (Fig. 2c, d, g and h) for Pd24/γ-Al2O3(110). On both supports the UPd decrease has one order of value, i.e., 2.3% and 0.9% (the difference between the maximal and minimal values between four Pd24 models at γ-Al2O3(110)), respectively. The importance of these values can be properly evaluated regarding analogous values for concurrent models of metallic species. In the case of TiO2(001) the best stabilization of −4.278 eV per Pd for 24 Pd atoms is achieved for a bilayer cluster (Fig. S1f†). However, a drastic UPd increase takes place for a Pd30 monolayer (−4.710 eV per Pd) so that it exceeds the stability of the Pd48 bilayer slab (−4.618 eV per Pd) and the Pd24 bilayer cluster. These intermediate UPd values for the Pd24 monolayer show a possible concurrence between the monolayer and the small clusters at intermediate coverage of TiO2(001).
| Pd | No H2O | H2O | ||
|---|---|---|---|---|
| REA | TS | PRO | ||
| 112 | 0.014 | 0.028 | 0.032 | 0.025 |
| 113 | 0.074 | 0.023 | 0.031 | 0.099 |
| 114 | −0.004 | −0.017 | −0.004 | 0.002 |
| 115 | −0.034 | −0.086 | −0.092 | −0.053 |
| 116 | −0.022 | −0.062 | 0.007 | 0.171 |
| 117 | −0.006 | −0.048 | −0.037 | −0.002 |
| 118 | −0.175 | −0.186 | −0.184 | −0.209 |
| 119 | 0.080 | 0.089 | 0.086 | 0.075 |
| 120 | 0.243 | 0.222 | 0.232 | 0.230 |
| 121 | −0.149 | −0.138 | −0.142 | −0.158 |
| 122 | 0.233 | 0.255 | 0.253 | 0.256 |
| 123 | −0.174 | −0.153 | −0.111 | −0.111 |
| 124 | 0.248 | 0.366 | 0.425 | 0.433 |
| 125 | −0.180 | −0.236 | −0.174 | −0.147 |
| 126 | 0.005 | 0.072 | 0.089 | 0.027 |
| 127 | −0.081 | −0.012 | −0.002 | −0.066 |
| 128 | −0.178 | −0.192 | −0.201 | −0.185 |
| 129 | 0.070 | 0.071 | 0.080 | 0.087 |
| 130 | −0.186 | −0.172 | −0.155 | −0.194 |
| 131 | 0.159 | 0.126 | 0.119 | 0.161 |
| 132 | 0.055 | 0.080 | −0.016 | 0.036 |
| 133 | −0.045 | −0.04 | −0.008 | −0.021 |
| 134 | 0.170 | 0.127 | 0.125 | 0.153 |
| 135 | −0.213 | −0.245 | −0.239 | −0.218 |
| 136 | 0.183 | 0.205 | 0.209 | 0.183 |
| 137 | −0.170 | −0.179 | −0.175 | −0.183 |
| 138 | 0.204 | 0.194 | 0.215 | 0.204 |
| 139 | −0.182 | −0.156 | −0.179 | −0.179 |
| Q | −0.061 | −0.064 | 0.184 | 0.416 |
The steps (Fig. 5) are shown for the reaction with a moderate barrier E# of 0.69 eV and exothermic heat ΔU of −0.08 eV to be compared with the E#/ΔU pairs of 1.05/0.46,48 1.09/0.59,49 and 1.12/0.01 (ref. 50) at Pd(111) using PW91/USPPs, PW91/PAW, and PBE/Troullier–Martines norm-conserving PPs, respectively. Regarding the different approaches applied in ref. 48–50 one could also mention the 1.06/0.36 pair at a 5-layer Pd90(100) but using the same PBE-D3/PAW level13 as considered herein.
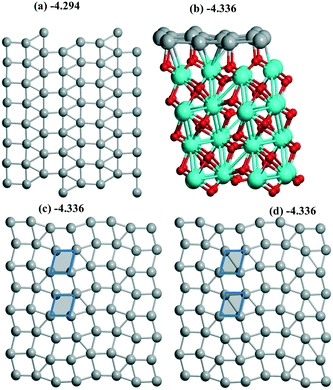 | ||
| Fig. 5 Pd16 monolayers of (a) 1/1, (b and c) 4R–4R, and (d) “mix” types include (a, c and d) the views of 2 × 2 supercells. Atoms of the support are shown in (b). Different rhomb elements between (d) “mix” and (c) 4R–4R geometries are given via shaded tetragons. The color agreement corresponds to Fig. 1. | ||
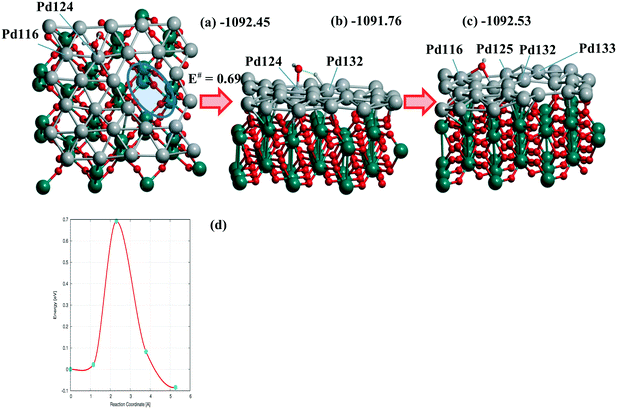 | ||
| Fig. 6 (a) Reagents, (b) transition state, (c) products, and (d) energy profile of H2O dissociation at the Pd28 monolayer with one di-vacancy (shown by ellipse in (a)) deposited over rutile-TiO2(001) optimized at the PBE-D3 level. (a) The activation energy E# and total energies are shown in eV. The atomic colors are given in gray (small spheres), red, green, and gray (large spheres) for H, O, Ti, and Pd, respectively. Respective (d) reaction profile is unified with the one for H2O dissociation at the 5-layer Pd90(100) slab.13 | ||
Similar or smaller barriers E# of 0.37 and 0.67 eV were calculated for H2O dissociation earlier at Pd18/γ-Al2O3(100) near two separate mono-vacancies and 0.40 eV at Pd20/γ-Al2O3(100) without vacancies in the deposited Pd20 monolayer.13 Exothermic heats ΔU were obtained in all cases (−0.31, −0.40, and −0.18 eV, respectively).13 It points to a comparable effect of the TiO2(001) support on the dissociation reaction.13 From Table 3 one can evaluate the charging of the Pd28 layer in the course of the reaction. While the reagents change the total charge of the monolayer (from −0.061 to −0.064 |e|) after adsorption very slightly, the dissociation raises it up to the final value of 0.416 |e| (Table 3). The maximum and minimum Pd charges are approximately the same, i.e., 0.248 to −0.213 |e| without H2O and 0.256 to −0.218 |e| after the reaction. The numbers of Pd atom-participants (116, 124 with the OH group, 125, 132, 133 with H) are shown in bold in Table 3. It illustrates the response of the Pd monolayer to the reaction.
3.3 Pd/ZrO2(001)
Both reconstruction and conservation were observed upon Pd sliding along the m-ZrO2 surface. Starting from an initial Pd(100) monolayer joined with a m-ZrO2 supercell (10.338 Å, 10.464 Å) the hybrid 1/1 model was optimized with a Pd density of 6.89 Å2 per Pd (Fig. 5a) being the largest throughout those studied above. After a shift of this 1/1 model by 1 Å in both OX and OY directions, the 4R–4R (4-atom rhomb – 4-atom rhomb) geometry (Fig. 5b and c) was obtained. The shift of the 1/1 model by 0.73 Å in the OX direction only resulted in the new (111) less stable geometry with an energy of −4.325 eV (Table 1). After a shift of this 4R–4R model by 1 Å in both OX and OY directions, nearly the same “mix” geometry (Fig. 5c) was conserved with an energy of −4.336 eV. The minor difference between the latter and the 4R–4R one is illustrated for the “mix” model showing a rhomb fragment (Fig. 5c and d) which transforms to square from the rhombohedral geometry in the 4R–4R (no short diagonal in the shaded rhomb in Fig. 5d) model. The shift of the 4R–4R model by 0.73 Å in the OX direction also resulted in the (111) geometry with an energy of −971.278 eV (Table 1). So, the iso-energetic conservation upon the shift is related to the close 4R–4R and “mix” models, while other cases correspond to a monolayer's reconstruction. Compared to Al2O3(110) all these slabs are more stable than respective single Pd atoms (Table 1) as well as at rutile (part 3.2) which increases the possibility of slab formation from separate atoms.For ZrO2 we obtained a series of different monolayer geometries for the same Pd coverage including conventional low index (111) and (100) planes. It is instructive to compare the respective surface energies γ for these analogues. γ can be expressed via UPd and Pd density (A):
| γ = ((UPd(slab) − UPd(bulk)) × N)/S = (UPd(slab) − UPd(bulk))/A | (2) |
Our result in favor of a weak influence of shifts on the Pd(100) bilayer at γ-Al2O3(110) (part 3.1.3.1) contradicts the opposite example of the (111) bilayer at ZrO2. Two similar Pd(111) models at a thinner ZrO2 oxide slab were constructed independently by us. But its upper view (Fig. S2†) clearly shows relative displacement between the Pd32(111) slabs relative the same support. An approximate estimation shows the shifts of −0.12 and 0.50 Å along the OX and OY axes, respectively. Regarding the Pd48(100) bilayer at γ-Al2O3(001) (part 3.1.3.1, Table 1), a relatively strong UPd stabilization of the Pd32(111) bilayer at the m-ZrO2(001) Pd bilayer upon a shift was found (Table 1) of 1.7% despite the close Pd–O distances in both the (111) slabs (Table S1†). It is important to note that this shift was realized at the smaller Zr16O32 support model. Moreover, the more rigid model was obtained by fixing 20 lowest Zr/O atoms in the lower part of the Zr16O32 support instead of 8 lowest O atoms only in the larger Zr32O64 model. Nevertheless, the more rigid support led to 1.7% variation of the UPd value compared to a 0.01% variation for the Pd48(111) bilayer at γ-Al2O3(001) (part 3.1.3.1). One may suggest that the additional “free” atoms can lead to the excess of this UPd growth of 1.7% (in absolute value). This example illustrates that the relaxation of a bilayer upon the shift depends on the type of support, thus achieving the value being comparable with the one for a non-complete monolayer at alumina (2.9% for Pd24). It confirms the necessity to verify possible stabilization of mono- or bilayers relative to an optimization in a new position after a shift parallel to the support.
4. Discussion
The Pd24 geometry changes drastically at different slide steps along the γ-Al2O3(110) support. It is important that a new ordered geometry of the monolayers appears. It signifies that the selection of the “best” support for Pd monolayer stabilization based on the best geometric coherence between the a priori known monolayer geometry (like Pd(111) or Pd(100)) and the geometry of the surface atoms of a support (Al, Ti, O) cannot predict that the combined model will have minimum energy. This is because a new Pd monolayer geometry can be formed instead of Pd(111) or Pd(100) after shifting and subsequent optimization. One example of new hybrid geometry of a Pt9–Au9 monolayer was theoretically proposed for the atoms with similar sizes.28The hybrid Pd24 examples at γ-Al2O3(110) (Fig. 2c, d, g and h) are related to the case of the monolayers with vacancies. It can create an impression that a proper choice of a larger number of atoms and a better slide direction will result in the well-known Pd(111) layers irrespective of a slide like for Pd30(111)/TiO2(001). New Pd28/γ-Al2O3(110) obtained by +4Pd addition and shift/optimization indeed resembles the (111) packing; however, it remains less stable than Pd24 hybrids obtained due to the shifts of +1 and +3 Å. The advantage of the hybrid was also demonstrated for the case of Me = Pd, Pt, Rh at γ-Al2O3(100).13 It was shown that their monolayers can adopt a stable hybrid Pd(1/4) form named so because of alternated bands of squares (1 band) and triangles (4 bands). Our late evaluations confirmed that their UMe stability exceeds the one of a single Me atom at γ-Al2O3(100) for Me = Pt and Rh also (it was demonstrated for Pd only13). This hybrid form is partly similar to the one obtained herein for Pd24 at γ-Al2O3(110) (Fig. 2c, d, g and h), i.e., alternation of the bands of triangles and squares. The Me–Me distances in the hybrids have reasonable values relative to those in the bulk. The search for such new models can be achieved via slide testing. Our examples above for slides by +1 or +3 Å confirm this because they led to very close monolayer geometries.
Similar problems of the vacancies arise in 2D vdW hetero-structures. Removing some atoms from a borophene 2D monolayer has recently been proposed as a way for stabilization of a nodal-line semimetal.5 The stabilization of the respective 2D monolayer with vacancies could be enforced by a search for a suitable support with the required geometry of the surface atoms. The search for the slide direction along the appropriate support could be a solution for a stable siting of a semi-metal with ordered defects.
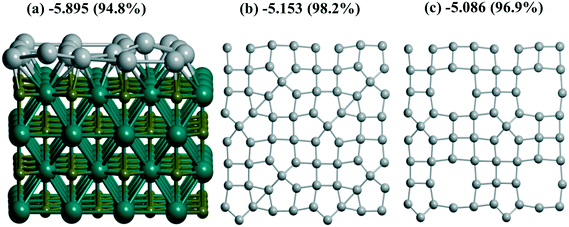
γ-Al2O3(110) (Fig. 1a), on the one hand, and rutile TiO2(001) (Fig. 1d) or monoclinic ZrO2(001) surfaces, on the other hand, reveal different trends for Pd monolayer formation. The dehydroxylated γ-Al2O3(110) surface possesses an attractive site for Pd which is bi-coordinated to a pair of Al atoms (Fig. S1g and 1b) where UPd = −5.314 eV per Pd exceeds the respective bulk value, i.e., −5.250 eV per Pd at the same PBE level or smaller (−5.637 eV per Pd) than the one of the bulk of −5.821 eV per Pd at the PBE-D3 level (Table S2†). This large energy was verified by using the Al14O20 model with a smaller UC for the γ-Al2O3(110) surface (Fig. 1b). The latter is sufficient to model the trapping of one Pd atom but is not convenient to simulate a slab. This model results in the smaller estimate of −5.159 eV per Pd (Table 1) but is in reasonable agreement with −5.314 eV per Pd obtained for the larger UC at the same PBE theory level. The other sites at the γ-Al2O3(110) surface result in a moderate stabilization (−3.787 and −3.755 eV per Pd). These sites together with the 8 favorable Pd positions (bi-coordinated to Al atoms) per UC form the upper and lower boundaries for the Pd24 monolayer stabilization at γ-Al2O3(110), i.e., −4.896 and −4.886 eV per Pd (Table 1). These intermediate UPd values between the most stable and the others for the Pd24 monolayer show a possible concurrence with the small clusters at intermediate coverage. As shown above (part 3.2), Pd stabilization in the Pd30(111) monolayer at the rutile TiO2(001) (Fig. 1d) surface exceeds the stabilization in any isolated atomic positions as we have observed for the hybrid Pd20(1/4) monolayer at γ-Al2O3(100).
Experimental evidence for monolayer formation at the oxides under study is known for TiO2(110).19–24 Long discussion of the strong metal–support interaction (SMSI) concept included the behavior of metallic particles (Pt, Pd, Os, Ir, Rh, Ru) on various oxide supports (also at a mixture of anatase and rutile TiO2 polymorphs) where the nearly equivalent CO or H2 adsorption relative to deposited Me metal (CO/Me ∼ 1 or H2/Me ∼ 1) in the reduced systems at 200 °C was not compatible with different hypotheses (collapse, poisoning) of the tentative nanoparticle/oxide structure.21 Electron micrographs of 2% Pd/TiO2 and 2% Ir/TiO2 gave no evidence for Pd or Ir crystallites greater than 1 nm.21 Later the authors22 proposed a flat structure of the Pt nanoparticle (up to monoatomic thickness) which correlated with the results of Baker et al. for Pt/TiO2.23 The last study demonstrated similar temperature intervals for the existence of metallic forms at oxides with SMSI, i.e., H2 reduction at 152 °C was sufficient for the SMSI type structure. The authors21 also admitted Pt interaction with both cations and anions of the oxide.22 Mono- and bilayers of Au (ref. 19) and Pd monolayers24 at TiO2(110) were characterized as non-metallic species with a small gap. Possibly, due to the dominant (110) plane at the γ-Al2O3 surface51,52 compared to the (100) plane, where the formation of Pd monolayers is more favorable, such observations were not fixed for γ-Al2O3. The nature of metal interactions with support atoms could be extended in the future using the QTAIM approach as realized for example in ref. 53 and 54.
A coherence between the experimental findings and stabilities predicted from theory can be achieved for Pt and Pd monolayers on the TiC(001) support where the formation of the Pt monolayer was electrochemically characterized.17 A stable Pt/Ti X-ray photoelectron spectroscopy signal ratio excludes the possibility of Pt agglomeration or detachment in the course of the hydrogen evolution reaction.17 Regarding the similarity between Pt and Pd monolayers shown earlier13 at γ-Al2O3(100), we also studied Pd monolayers at the Ti64C64(001) slab which is relatively easy to model. A measure of the stabilization of both PtN and PdN monolayers at TiC (12.242 × 12.242 Å), N = 16, 18, was done in the same way (Fig. 7). The Bader Pd charges vary between −0.106 and −0.318 |e| in agreement with the calculated Pt charge of −0.33 |e|.6 The high theoretical stabilization of the Pt monolayer is in agreement with experimental evidence of its formation.17 But the stabilization of the Pd monolayer is even higher than that of the Pt one which seems to be an argument in favor of similar stable Pd monolayers at TiC.
5. Conclusions
We showed that testing the shift of a Pd monolayer parallel to a support is a highly desirable subject after its initial deposition and relaxation. The number of possible variants for such sliding is limited by periodic boundary conditions so that the testing is not too time costly. Both the charge and energy depend on a proper choice of the monolayer position that can be important for both the reagent adsorption and reactivity of the monolayer. The greatest loss of the Pd stabilization of 7.4% was shown at rutile due to the corrupted Pd interaction with the support atoms. The evaluation of the required step could be given on the basis of the distance that provides the maximal number of the favored Al–Pd–Al contacts at γ-Al2O3(110). The drastic reconstruction upon a shift can be a sign of a non-complete monolayer. This possibility seems to be important for monolayers and bilayers. Due to the different O–Pd–O and Al–Pd–Al favorable sites at the γ-Al2O3(100) and γ-Al2O3(110) forms, respectively, a higher probability of Pd monolayer formation is predicted at γ-Al2O3(100) from our calculations with the smaller charge of the Pd monolayer (in absolute value). The surface Pd density spans a narrow interval from 6.45 (γ-Al2O3(110)) > 6.32 (rutile TiO2(001)) > 6.29 Å2 per Pd (γ-Al2O3(100)13) with slightly higher 6.89 Å2 per Pd for m-ZrO2(001) despite three different types of Pd packing in complete monolayers (without vacancies), i.e., (4R–4R), (111), (1/4) for ZrO2, γ-Al2O3(110) and TiO2, γ-Al2O3(100), respectively (the Pd(111) types at γ-Al2O3(110) and TiO2 rather coincide). Respective surface energies γ (2) obey the sequence 60 < 78 < 133 < 136 meV Å−2 for γ-Al2O3(110), TiO2, ZrO2, and γ-Al2O3(100). The activation barrier of 0.69 eV for water dissociation at the Pd28 monolayer/rutile is pretty close to the moderate 0.67 eV at Pd18/γ-Al2O3(100),13 which points to the catalytic capability of Pd monolayers on various supports. The high theoretical stabilization energies of Pt and Pd monolayers at TiC are in agreement with experimental evidence of monolayer formation (Pt).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for financial support from the Bulgarian Science Fund through contracts KΠ-06-RUSSIA-22 and the Russian Foundation of Basic Research within the grant 20-53-18001-Bolg_a. The research has been carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University.55 This research used resources of the “Plateforme Technologique de Calcul Intensif (PTCI)” (http://www.ptci.unamur.be) located at the University of Namur, Belgium, which is supported by the FNRS-FRFC, the Walloon Region, and the University of Namur (Conventions No. 117, GEQ U.G006.15, 1610468 et RW/GEQ2016). The PTCI is member of the “Consortium des Équipements de Calcul Intensif (CÉCI)” (http://www.ceci-hpc.be).References
- V. Zatko, S. M. M. Dubois, F. Godel, C. Carrétéro, A. Sander, S. Collin, M. Galbiati, J. Peiro, F. Panciera, G. Patriarche, P. Brus, B. Servet, J. C. Charlier, M. B. Martin, B. Dlubak and P. Seneor, ACS Nano, 2021, 15, 7279–7289 CrossRef CAS PubMed
.
- C. Tantardini, A. G. Kvashnin, C. Gatti, B. I. Yakobson and X. Gonze, ACS Nano, 2021, 15, 6861–6871 CrossRef CAS PubMed
.
- A. A. Rybakov, A. V. Larin, D. P. Vercauteren and G. M. Zhidomirov, Theor. Chem. Acc., 2016, 135, 152 Search PubMed
.
-
A. A. Rybakov, A. V. Larin, D. P. Vercauteren and G. M. Zhidomirov, in Practical Aspects of Computational Chemistry IV, ed. J. Leszczynski and M. K. Shukla, Springer, US, Boston, MA, 2016, pp. 303–351 Search PubMed
.
- F. Liu, F. Qu, I. Žutić, S. Xie, D. Liu, A. L. A. Fonseca and M. Malard, J. Phys. Chem. Lett., 2021, 12, 5710–5715 Search PubMed
.
- Y. Wang, X. Zhang, Z. Fu, Z. Lu and Z. Yang, J. Phys.: Condens. Matter, 2019, 31, 305201 CrossRef CAS
.
- Y. Wang and Z. Yang, J. Chem. Phys., 2018, 149, 054705 CrossRef
.
- X. Zhang, Z. Lu and Z. Yang, J. Power Sources, 2016, 321, 163–173 CrossRef CAS
.
- P. Lozano-Reis, H. Prats, R. Sayós, J. A. Rodriguez and F. Illas, J. Phys. Chem. C, 2021, 125, 12019–12027 CrossRef CAS
.
- J. A. Rodriguez, J. Evans, L. Feria, A. B. Vidal, P. Liu, K. Nakamura and F. Illas, J. Catal., 2013, 307, 162–169 CrossRef CAS
.
- T. Gomez, E. Florez, J. A. Rodriguez and F. Illas, J. Phys. Chem. C, 2011, 115, 11666–11672 CrossRef CAS
.
- H. Duan, N. Yan, R. Yu, C.-R. Chang, G. Zhou, H.-S. Hu, H. Rong, Z. Niu, J. Mao, H. Asakura, T. Tanaka, P. J. Dyson, J. Li and Y. Li, Nat. Commun., 2014, 5, 3093 CrossRef PubMed
.
- A. A. Rybakov, S. Todorova, D. N. Trubnikov and A. V. Larin, Dalton Trans., 2021, 50, 8863–8876 RSC
.
- P. Prabhu and J.-M. Lee, Chem. Soc. Rev., 2021, 50, 6700–6719 RSC
.
- H. Yu, T. Zhou, Z. Wang, Y. Xu, X. Li, L. Wang and H. Wang, Angew. Chem., Int. Ed., 2021, 60, 12027–12031 CrossRef CAS PubMed
.
- Y. Zheng, X. Wang, Y. Kong and Y. Ma, CrystEngComm, 2021, 23, 6454–6469 RSC
.
- Y. C. Kimmel, L. Yang, T. G. Kelly, S. A. Rykov and J. G. Chen, J. Catal., 2014, 312, 216–220 CrossRef CAS
.
- L. Wang, Y. Zhu, J.-Q. Wang, F. Liu, J. Huang, X. Meng, J.-M. Basset, Y. Han and F.-S. Xiao, Nat. Commun., 2015, 6, 6957 CrossRef CAS PubMed
.
- M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650 CrossRef CAS PubMed
.
- M. S. Chen and D. W. Goodman, Science, 2004, 306, 252–255 CrossRef CAS PubMed
.
- S. J. Tauster, S. C. Fung and R. L. Garten, J. Am. Chem. Soc., 1978, 100, 170–175 CrossRef CAS
.
- S. J. Tauster, S. C. Fung, R. T. K. Baker and J. A. Horsley, Science, 1981, 211, 1121–1125 CrossRef CAS
.
- R. Baker, J. Catal., 1979, 56, 390–406 CrossRef CAS
.
- C. Xu, X. Lai, G. W. Zajac and D. W. Goodman, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13464–13482 CrossRef CAS
.
- A. A. Rybakov, I. A. Bryukhanov, A. V. Larin, S. Todorova and G. M. Zhidomirov, Struct. Chem., 2019, 30, 489–500 CrossRef CAS
.
- A. A. Rybakov, I. A. Bryukhanov, S. Todorova, R. Velinova, A. Naydenov and A. V. Larin, J. Phys. Chem. C, 2020, 124, 605–615 CrossRef CAS
.
- A. A. Rybakov, I. A. Bryukhanov, A. V. Larin, S. Todorova, D. P. Vercauteren and G. M. Zhidomirov, Catal. Today, 2020, 357, 368–379 CrossRef CAS
.
- K. Takahashi, T. Hussain, L. Takahashi and J. D. Baran, Cryst. Growth Des., 2016, 16, 1746–1750 CrossRef CAS
.
- Z. A. Piazza, R. D. Kolasinski, M. Ajmalghan, E. A. Hodille and Y. Ferro, J. Phys. Chem. C, 2021, 125, 16086–16096 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- M. Hutchinson and M. Widom, Comput. Phys. Commun., 2012, 183, 1422–1426 CrossRef CAS
.
- M. Hacene, A. Anciaux-Sedrakian, X. Rozanska, D. Klahr, T. Guignon and P. Fleurat-Lessard, J. Comput. Chem., 2012, 33, 2581–2589 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS
.
- E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC
.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 CrossRef PubMed
.
- P. Ugliengo, D. Viterbo and G. Chiari, Z. Kristallogr., 1993, 207, 9–23 CAS
.
- B. M. Bode and M. S. Gordon, J. Mol. Graphics Modell., 1998, 16, 133–138 CrossRef CAS
.
- C.-M. Lin, T.-L. Hung, Y.-H. Huang, K.-T. Wu, M.-T. Tang, C.-H. Lee, C. T. Chen and Y. Y. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125426 CrossRef
.
- S. G. Wang, E. K. Tian and C. W. Lung, J. Phys. Chem. Solids, 2000, 61, 1295–1300 CrossRef CAS
.
- J.-M. Zhang, F. Ma and K.-W. Xu, Appl. Surf. Sci., 2004, 229, 34–42 CrossRef CAS
.
- A. A. Phatak, W. N. Delgass, F. H. Ribeiro and W. F. Schneider, J. Phys. Chem. C, 2009, 113, 7269–7276 CrossRef CAS
.
- G. Wang, S. Tao and X. Bu, J. Catal., 2006, 244, 10–16 CrossRef CAS
.
- Y. Cao and Z.-X. Chen, Surf. Sci., 2006, 600, 4572–4583 CrossRef CAS
.
- J.-P. Beaufils and Y. Barbaux, J. Chem. Phys., 1981, 78, 347–352 CAS
.
- P. Nortier, P. Fourre, A. B. M. Saad, O. Saur and J. C. Lavalley, Appl. Catal., 1990, 61, 141–160 CrossRef CAS
.
- A. N. Usoltsev, S. A. Adonin, A. S. Novikov, D. G. Samsonenko, M. N. Sokolov and V. P. Fedin, CrystEngComm, 2017, 19, 5934–5939 RSC
.
- A. N. Usoltsev, S. A. Adonin, A. S. Novikov, P. A. Abramov, M. N. Sokolov and V. P. Fedin, CrystEngComm, 2020, 22, 1985–1990 RSC
.
-
V. Sadovnichy, A. Tikhonravov, V. Voevodin and V. Opanasenko, in Contemporary High Performance Computing: From Petascale toward Exascale, ed. J. S. Vetter, CRC Press, Boca Raton, USA, 2013, pp. 283–307 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Pd–O bond lengths in the bilayer Pd32(111) slabs at m-ZrO2(001) (Table S1, Fig. S2), complete data about with total energies (Utot, Uox) and UPd values at the PBE and PBE-D3 levels (Table S2), the geometries of single Pd atoms (Fig. S1a–c, g and h), monolayers (Fig. S1d and e and S3a–c), and bilayers (Fig. S1f) at γ-Al2O3(110) (Fig. S1g), TiO2(001) (Fig. S1a–c and S3a–c), and m-ZrO2(001) (Fig. S1h). Simulation steps of water dissociation at rutile can be visualized using the “H2O_dissociation_rutile_TiO2.xyz” file and wxMacMolPlt software. See DOI: 10.1039/d1ce01365c |
| ‡ The atom changes its position (from top to bottom or from left to right) due to periodic boundary conditions (Fig. 3a–d). |
| This journal is © The Royal Society of Chemistry 2022 |