Understanding the thermal stability of apalutamide crystalline solvates through crystal structure analyses and computational studies†
Jupally
Prashanth
ab,
A.
Sivalakshmi Devi
c,
Artem O.
Surov
 *d,
Alexander P.
Voronin
*d,
Alexander P.
Voronin
 d,
Andrei V.
Churakov
d,
Andrei V.
Churakov
 e,
German L.
Perlovich
e,
German L.
Perlovich
 d and
Sridhar
Balasubramanian
d and
Sridhar
Balasubramanian
 *ab
*ab
aCentre for X-ray Crystallography, Department of Analytical & Structural Chemistry, CSIR-Indian Institute of Chemical Technology, Tarnaka, Uppal Road, Hyderabad-500007, Telangana, India. E-mail: bsridhar@iict.res.in
bAcademy of Scientific and Innovative Research (AcSIR), Uttar Pradesh-201 002, India
cLaurus Labs Ltd., DS-1, IKP Knowledge Park, Turkapally, Shameerpet, Hyderabad-500078, India
dG.A. Krestov Institute of Solution Chemistry RAS, 153045, Ivanovo, Russia
eInstitute of General and Inorganic Chemistry RAS, Leninsky Prosp. 31, 119991, Moscow, Russia
First published on 31st March 2022
Abstract
Apalutamide (APA) is a nonsteroidal antiandrogen (NSAA) drug used for prostate cancer treatment. The crystal structures of apalutamide–dimethylformamide (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 & 1
1 & 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), apalutamide–1,4-dioxane, apalutamide–N,N-dimethylacetamide, apalutamide–cyclohexanone, apalutamide–acetonitrile, apalutamide–acetone, apalutamide–2-butanol and apalutamide–ethanol were determined. Thermal analysis and lattice energy calculations were performed to understand the stability of the solvent molecules in the crystal structures. Characteristic amide catemer hydrogen bonding was observed in all structures except in the structure of the acetonitrile solvate, in which the amide N–H atom was bonded to the solvent molecule. In all the structures APA⋯APA and APA⋯solvent interactions were used to build a supramolecular hydrogen-bonded network in the crystal packing. The solvent molecules were involved in strong interactions with APA molecules and were seen to stabilize the crystal structures. Crystal packing similarity analysis revealed that the APA solvates show modest structural resemblance.
1), apalutamide–1,4-dioxane, apalutamide–N,N-dimethylacetamide, apalutamide–cyclohexanone, apalutamide–acetonitrile, apalutamide–acetone, apalutamide–2-butanol and apalutamide–ethanol were determined. Thermal analysis and lattice energy calculations were performed to understand the stability of the solvent molecules in the crystal structures. Characteristic amide catemer hydrogen bonding was observed in all structures except in the structure of the acetonitrile solvate, in which the amide N–H atom was bonded to the solvent molecule. In all the structures APA⋯APA and APA⋯solvent interactions were used to build a supramolecular hydrogen-bonded network in the crystal packing. The solvent molecules were involved in strong interactions with APA molecules and were seen to stabilize the crystal structures. Crystal packing similarity analysis revealed that the APA solvates show modest structural resemblance.
1. Introduction
Solution crystallization is not only an integral part of organic synthesis and purification stages in the processing pipeline of drug compounds1 but also a widely used screening technique for new solid forms of pharmaceutical materials.2–5 As a result of these operations, solvent molecules can be entrapped into the crystal lattice of an active pharmaceutical ingredient (API), forming a distinct multicomponent crystal known as a solvate.6 Although solvates with hazardous compounds are generally considered as an unwanted outcome of the solid form landscape of an API and, therefore, are rarely selected for further development due to toxicity and regulatory concerns, pharmaceutically acceptable solvents can be utilized to modify the crucial physicochemical properties of a compound, including solubility, dissolution rate, stability and particle morphology, which would further affect drug processing.6–12 Currently, several drugs formulated as solvates are available on the market.8,13 It is well known that desolvation of different solvates can be used as a potential route for the preparation of specific or unknown polymorphic forms of single- and multicomponent crystals, which are difficult to attain by conventional crystallization techniques.14–17 Desolvation has also been proved as an effective method for the purification of drug compounds (e.g. enzalutamide).18 Moreover, it has been suggested that a detailed crystallographic investigation of solvates for a particular API may shed some light on the nature and mechanism of nucleation and growth processes of a compound from solutions, as the local environment of the solvated structure is assumed to resemble the nucleation clusters of molecules in the crystallization medium.19–21 Thus, a systematic study of the solvated crystal structures and formation mechanism of different solvates is important not only in terms of practical application but also relevant for the fundamental understanding of the crystallization phenomenon.The growth in importance of pharmaceutical solvates has been recently highlighted in several Cambridge Structural Database (CSD22) surveys that sought to establish both structural and thermodynamic relationships that determine the likelihood of solvate formation.23–26 It has been generally accepted that the following two factors are mainly responsible for the solvent incorporation in the crystal lattice of organic compounds:27–29 (i) the introduction of the solvent molecules is likely to compensate for unsatisfactory intermolecular interactions of the host molecules and contribute to stronger intermolecular interaction; (ii) solvate formation is expected to reduce an excess void space providing more dense and efficient packing arrangements. In most cases, both these aspects contribute to the driving force of the process, decreasing the free energy of the resulting multicomponent system. A more quantitative approach towards solvate formation propensity has been developed by Cruz-Cabeza et al., who introduced a concept of the entropy cost that a system must spend to accommodate a liquid component in a crystalline environment.26 It has been shown that the occurrence of solvates in the CSD is inversely proportional to the calculated value of the entropy penalty, indicating that the formation of solvates associated with a high entropy penalty would require a larger lattice energy gain. This approach was further explored in the subsequent theoretical study by Iuzzolino,23 who showed that 79.5% of the solvates are thermodynamically more stable than their single-component constituents, while 20.5% of the solvates represent metastable systems and are likely to be kinetically favored.
The present study aims at constructing the solvent landscape for a novel and little-studied antiandrogenic compound apalutamide (APA)30,31 (Fig. 1). It has been reported that the aqueous solubility of APA in pharmaceutically relevant media does not exceed 8 × 10−6 mol l−1,32 and, according to the biopharmaceutical classification system (BCS), the drug belongs to class II of the BCS with low aqueous solubility and high membrane permeability.33 The solid-state landscape of the drug, however, is barely investigated. Even though several patents have claimed the existence of a range of APA solvates and two polymorphic forms of the compound, only a limited amount of structural information and a scarce description of the thermal properties of these solid forms are available.34–36 We have to note that in the course of drafting this manuscript, crystal structures of non-solvated APA (Form B; CSD Refcode: FAVYEK) and its cocrystal with methylparaben (CSD Ref code: FAVYAG) have been published, providing the first instance of crystallographic data in the academic literature as well as the CSD.37 The lack of structural information on this drug prompted us to undertake a comprehensive screening for different polymorphic modifications and solvates of APA to extend currently known set of the drug's solid forms and to gain deeper knowledge of its structural chemistry. In this work, anhydrous form of apalutamide (APA) and nine solvates namely, apalutamide–dimethylformamide (APA–DMF 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 & 1
1 & 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), apalutamide–1,4-dioxane (APA–DOX), apalutamide–N,N-dimethylacetamide (APA–DMA), apalutamide–cyclohexanone (APA–CYH), apalutamide–acetonitrile (APA–ACN), apalutamide–acetone (APA–ACE), apalutamide–2-butanol (APA–BUT) and apalutamide–ethanol (APA–EtOH) were obtained and characterized by single-crystal X-ray diffraction (SCXRD) and other analytical techniques, including hot-stage microscopy (HSM), differential scanning calorimetry (DSC) and thermogravimetric analysis (TG). A detailed investigation of molecular conformations, crystal packing and structure of the void framework enabled us to obtain valuable insights into structure-dependent stability and propose desolvation pathways of the solvates. In addition, the packing similarity and the intermolecular energies were calculated to rationalize the role of solvent molecules in packing arrangements and to elucidate the difference in thermal stability of the solid forms.
1), apalutamide–1,4-dioxane (APA–DOX), apalutamide–N,N-dimethylacetamide (APA–DMA), apalutamide–cyclohexanone (APA–CYH), apalutamide–acetonitrile (APA–ACN), apalutamide–acetone (APA–ACE), apalutamide–2-butanol (APA–BUT) and apalutamide–ethanol (APA–EtOH) were obtained and characterized by single-crystal X-ray diffraction (SCXRD) and other analytical techniques, including hot-stage microscopy (HSM), differential scanning calorimetry (DSC) and thermogravimetric analysis (TG). A detailed investigation of molecular conformations, crystal packing and structure of the void framework enabled us to obtain valuable insights into structure-dependent stability and propose desolvation pathways of the solvates. In addition, the packing similarity and the intermolecular energies were calculated to rationalize the role of solvent molecules in packing arrangements and to elucidate the difference in thermal stability of the solid forms.
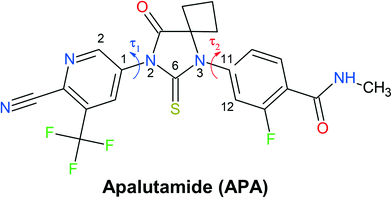 | ||
| Fig. 1 Molecular structure of apalutamide. Arrows indicate the most flexible torsion angles τ1 and τ2. | ||
2. Materials and methods
2.1. Compounds and solvents
Apalutamide was received as a gift sample from M/s Laurus Labs, Hyderabad. All solvents were available commercially and were used as received without further purification.2.2. Crystallization procedure
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DMF-2
1 (APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
APA (20 mg) was dissolved in 0.5 ml of DMF which was heated at 90 °C to obtain a clear solution. It was left for slow evaporation at room temperature covered with parafilm. Crystals formed after one month.
1).
APA (20 mg) was dissolved in 0.5 ml of DMF which was heated at 90 °C to obtain a clear solution. It was left for slow evaporation at room temperature covered with parafilm. Crystals formed after one month.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DMF-1
1 (APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
APA (20 mg) was dissolved in 0.5 ml of DMF under hot conditions at 90 °C and left for slow evaporation at room temperature without parafilm cover. Crystals formed within 4 days.
1).
APA (20 mg) was dissolved in 0.5 ml of DMF under hot conditions at 90 °C and left for slow evaporation at room temperature without parafilm cover. Crystals formed within 4 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DOX-2
1 (APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
20 mg of APA was placed in a small sample vial and the compound was dissolved using 0.5 ml of 1,4-dioxane. This small sample vial containing the 1,4-dioxane solution of the compound was carefully placed in a larger weighing bottle containing 3 ml of hexane and closed with a lid. Crystallization progressed by vapor diffusion of hexane into 1,4-dioxane solution. Crystals were obtained after 7 days.
1).
20 mg of APA was placed in a small sample vial and the compound was dissolved using 0.5 ml of 1,4-dioxane. This small sample vial containing the 1,4-dioxane solution of the compound was carefully placed in a larger weighing bottle containing 3 ml of hexane and closed with a lid. Crystallization progressed by vapor diffusion of hexane into 1,4-dioxane solution. Crystals were obtained after 7 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DMA-1
1 (APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
20 mg of APA was placed in a small sample vial and the compound was dissolved using 0.4 ml of N,N-DMA. This small sample vial containing the N,N-DMA solution of the compound was carefully placed in a larger weighing bottle containing 4 ml of cyclohexane and closed with a lid. Crystallization progressed by vapor diffusion of cyclohexane into N,N-DMA solution. Crystals were obtained after 7 days.
1).
20 mg of APA was placed in a small sample vial and the compound was dissolved using 0.4 ml of N,N-DMA. This small sample vial containing the N,N-DMA solution of the compound was carefully placed in a larger weighing bottle containing 4 ml of cyclohexane and closed with a lid. Crystallization progressed by vapor diffusion of cyclohexane into N,N-DMA solution. Crystals were obtained after 7 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–CYH-1
1 (APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
APA (50 mg) was dissolved in 2 ml of cyclohexanone under hot conditions at 90 °C to obtain a clear solution and left for slow evaporation under ambient conditions. Crystals were formed within 7 days.
1).
APA (50 mg) was dissolved in 2 ml of cyclohexanone under hot conditions at 90 °C to obtain a clear solution and left for slow evaporation under ambient conditions. Crystals were formed within 7 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–ACN-1
1 (APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
Apalutamide (50 mg) was dissolved in acetonitrile (0.5 ml) and then 2 ml of Millipore water (antisolvent) was added dropwise. A fine white precipitate started forming which was then stirred for 2 h at room temperature and later dissolved in 1 ml of acetonitrile. This solution was allowed to stand for slow evaporation at room temperature. Crystals were formed within 2 days.
1).
Apalutamide (50 mg) was dissolved in acetonitrile (0.5 ml) and then 2 ml of Millipore water (antisolvent) was added dropwise. A fine white precipitate started forming which was then stirred for 2 h at room temperature and later dissolved in 1 ml of acetonitrile. This solution was allowed to stand for slow evaporation at room temperature. Crystals were formed within 2 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–ACE-2
1 (APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
100 mg of APA was placed in a small sample vial and the compound was dissolved using 1 ml of acetone. This small sample vial containing the acetone solution of the compound was carefully placed in a larger weighing bottle containing 10 ml of diethyl ether and closed with a lid. Crystallization progressed by vapor diffusion of diethyl ether into the acetone solution. Crystals were obtained in a week.
1).
100 mg of APA was placed in a small sample vial and the compound was dissolved using 1 ml of acetone. This small sample vial containing the acetone solution of the compound was carefully placed in a larger weighing bottle containing 10 ml of diethyl ether and closed with a lid. Crystallization progressed by vapor diffusion of diethyl ether into the acetone solution. Crystals were obtained in a week.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 0.5 (APA–BUT-1
0.5 (APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 0.5).
APA (20 mg) was dissolved in 2 ml of 2-butanol which was heated at 90 °C to obtain a clear solution and left for slow evaporation under ambient conditions. Crystals were formed within 7 days.
0.5).
APA (20 mg) was dissolved in 2 ml of 2-butanol which was heated at 90 °C to obtain a clear solution and left for slow evaporation under ambient conditions. Crystals were formed within 7 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–EtOH-2
1 (APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
20 mg of APA was placed in a small sample vial and the compound was dissolved using 5 ml of ethanol. This small sample vial containing the ethanol solution of the compound was carefully placed in a larger weighing bottle containing 2 ml of n-pentane and closed with a lid. Crystallization progressed by vapor diffusion of n-pentane into the ethanol solution. Crystals were obtained in 7 days.
1).
20 mg of APA was placed in a small sample vial and the compound was dissolved using 5 ml of ethanol. This small sample vial containing the ethanol solution of the compound was carefully placed in a larger weighing bottle containing 2 ml of n-pentane and closed with a lid. Crystallization progressed by vapor diffusion of n-pentane into the ethanol solution. Crystals were obtained in 7 days.
2.3. X-Ray diffraction experiments
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (at 100 K), and APA–DMF-2
1 (at 100 K), and APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (at 150 K) were collected on a SMART APEX II diffractometer as well as for APA–DMF-1
1 (at 150 K) were collected on a SMART APEX II diffractometer as well as for APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (at 100 K) on a Bruker D8 Venture machine (Bruker AXS, Germany) with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å) at the Centre of Shared Equipment of IGIC RAS. Absorption corrections based on measuring equivalent reflections were applied.38 The X-ray diffraction data for APA–DMF-2
1 (at 100 K) on a Bruker D8 Venture machine (Bruker AXS, Germany) with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å) at the Centre of Shared Equipment of IGIC RAS. Absorption corrections based on measuring equivalent reflections were applied.38 The X-ray diffraction data for APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DOX-2
1, APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DMA-1
1, APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–CHY-1
1, APA–CHY-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–BUT-1
1, APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 and APA–EtOH-2
0.5 and APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were collected at 100 K at the Center for X-ray Crystallography, CSIR-Indian Institute of Chemical Technology, Hyderabad on a Bruker D8 QUEST instrument with an IμS Mo microsource (λ = 0.7107 Å) and a PHOTON-100 detector for all structures except APA–DOX and APA–DMA, which were collected at room temperature (294(2) K). These crystals were first attempted at low temperature, while the data quality was not good. Later, data were collected at room temperature for the same crystals. The raw data frames were reduced and corrected for absorption effects using the Bruker Apex 3 software suite programs39 The structure was solved using an intrinsic phasing method40 and further refined with the SHELXL41 program and expanded using Fourier techniques.
1 were collected at 100 K at the Center for X-ray Crystallography, CSIR-Indian Institute of Chemical Technology, Hyderabad on a Bruker D8 QUEST instrument with an IμS Mo microsource (λ = 0.7107 Å) and a PHOTON-100 detector for all structures except APA–DOX and APA–DMA, which were collected at room temperature (294(2) K). These crystals were first attempted at low temperature, while the data quality was not good. Later, data were collected at room temperature for the same crystals. The raw data frames were reduced and corrected for absorption effects using the Bruker Apex 3 software suite programs39 The structure was solved using an intrinsic phasing method40 and further refined with the SHELXL41 program and expanded using Fourier techniques.
The structures were solved by direct methods and refined by full matrix least-squares on F2 with anisotropic thermal parameters for all the non-hydrogen atoms.42 Out of nine structures, APA–ACN has no disorder. For the rest of the structures, either APA or solvate or both were disordered, which is described in the ESI.† All amino hydrogen atoms were located from difference Fourier maps and their positional parameters were freely refined. The hydrogen atom attached to the oxygen atom of the 2-butanol solvate was located in the difference density map and its position and isotropic displacement parameters were refined. The hydrogen atom attached to the O atom of the ethanol solvate was located in difference density maps, but was positioned geometrically and included as a riding atom with O–H = 0.82 Å and Uiso(H) = 1.5Ueq(O). C-bound H atoms were located in difference density maps but were positioned geometrically and included as riding atoms with C–H = 0.93–0.98 Å, and Uiso(H) = 1.5Ueq(C) for methyl H atoms and 1.2Ueq(C) for all other H atoms. Hydrogen bonding details are given in Tables S2–S11.† The ORTEP diagrams were drawn using DIAMOND software,43 and both molecular overlay and packing diagrams were depicted using MERCURY software.44
Detailed crystallographic and refinement data are listed in Table S1.† The crystallographic data were deposited with the Cambridge Crystallographic Data Centre as supplementary publications under the CCDC numbers 2151550–2151553 for APA, APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DMF-2
1, APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DMF-1
1, APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2152151–2152157 for APA–DMF-2
1 and 2152151–2152157 for APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DOX-2
1, APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DMA-1
1, APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–CHY-1
1, APA–CHY-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–BUT-1
1, APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, APA–ACN-1
0.5, APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–EtOH-2
1, APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
2.4. Hot stage microscopy (HSM)
A polarizing microscope (model LEICA S8APO) attached to a Linkam hot stage (model LTS420) was used to observe the melting patterns of the obtained cocrystals. A LEICA MC170HD camera with the help of Leica Application Suite software version 4.8 (LAS V4.8) and Captura 8.0 software was used for capturing images of thermal events. For connecting the temperature control device between the hot stage and the display, link connection software was used. APA and its solvated crystals were heated from 30 °C to 220 °C at a heating rate of 5 °C per minute.2.5. Differential scanning colorimetry (DSC)
The DSC studies were carried out on a TA Instrument Discovery DSC 250, and the data were plotted in TA Trios V4.5.1.42498 software. Typically, a sample of ∼3 mg was sealed in aluminium pans and was subjected to heating from room temperature to 300 °C at a heating rate of 5 °C per minute. The thermal analysis was also carried out using a Perkin Elmer DSC 4000 differential scanning calorimeter with a refrigerated cooling system (USA). The sample was heated in sealed aluminium sample holders at a rate of 5 °C min−1 in a nitrogen atmosphere. The unit was calibrated with indium and zinc standards. The accuracy of the weighing procedure was ±0.01 mg.2.6. Thermogravimetric (TG) analysis
TG analysis was performed in a nitrogen atmosphere using a TA Q600 instrument under the DSC-TGA module. The sample was placed in an aluminium sample pan and heated over the temperature range of 30–400 °C at a heating rate of 10 °C per minute. The TG experiments were also carried out using a TG 209 F1 Iris thermomicrobalance (Netzsch, Germany). Approximately 10 mg of the sample was added to a platinum crucible. The samples were heated at a constant heating rate of 10 °C min−1. The samples were purged with a stream of flowing dry Ar at 30 ml min−1 throughout the experiment.2.7. Computational studies
Periodic DFT computations were performed using CRYSTAL17 software45 at the B3LYP-D3(BJ,ABC)/6-31G(d,p) level of theory.46–49 It was demonstrated that this level of theory provided reliable and consistent results in studying the non-covalent interactions in organic crystals.50–52 Atomic positions from the SC-XRD experiments were used for SCF computations and quantum topology analysis of periodic electron density, with hydrogen atom positions normalized to the standard X–H distances from neutron diffraction data. The CRYSTAL parameters describing the level of accuracy in evaluating the Coulomb and Hartree–Fock exchange series were set to 7 7 7 7 15. Tolerance on energy controlling the self-consistent field convergence was set to 10−10 hartree. The mixing coefficient of Hartree–Fock/Kohn–Sham matrices was set to 25%. The shrinking factor of the reciprocal space net was set to 4.The crystal lattice energy (Elatt) of an n-component crystal was estimated as the difference between the sum of the total electronic energies of isolated molecules in their relaxed conformations Emol and the total energy of the optimized crystal Ecryst calculated per asymmetric unit with respect to basis set superposition error (BSSE):53
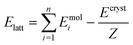 | (1) |
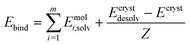 | (2) |
| Estab = Elatt − Ebind | (3) |
Quantum topology analysis of non-covalent interactions in considered solvates was performed in Topond software55 currently implemented into the CRYSTAL suit. The search for (3, −1) critical points was performed using a standard algorithm, and the following quantities were computed in the critical point: electron density, ρb, its Laplacian, ∇2ρb, and the positively defined local electronic kinetic energy Gb. The interaction energy of a particular hydrogen bond, Eint, was estimated using the correlation equation proposed by Mata et al.:56
| Eint (kJ mol−1) = 1124Gb (atomic units) | (4) |
3. Results and discussion
3.1. Crystal structure analysis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DMF-2
1 (APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–DMF-2
1).
The APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvate structure crystallizes in the triclinic P
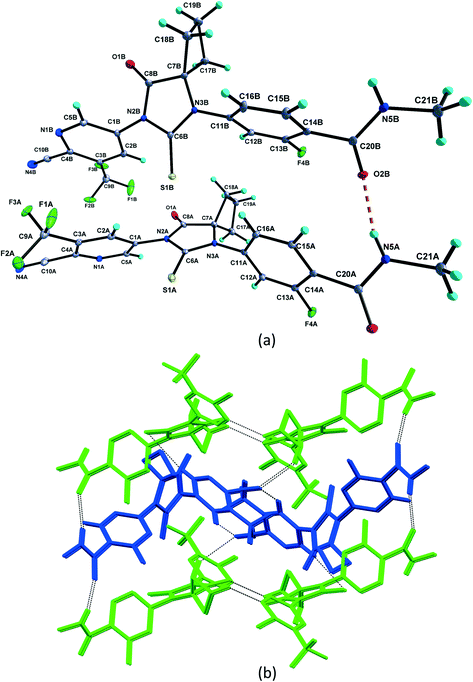
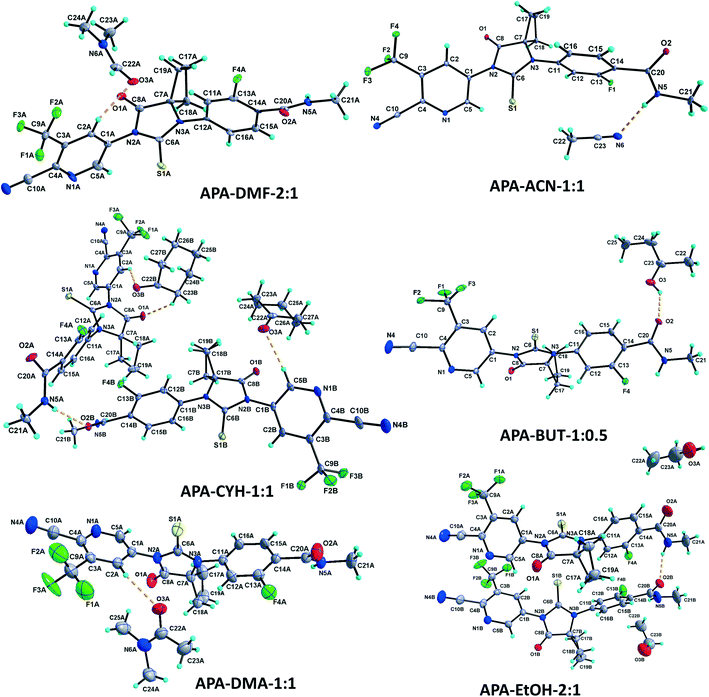
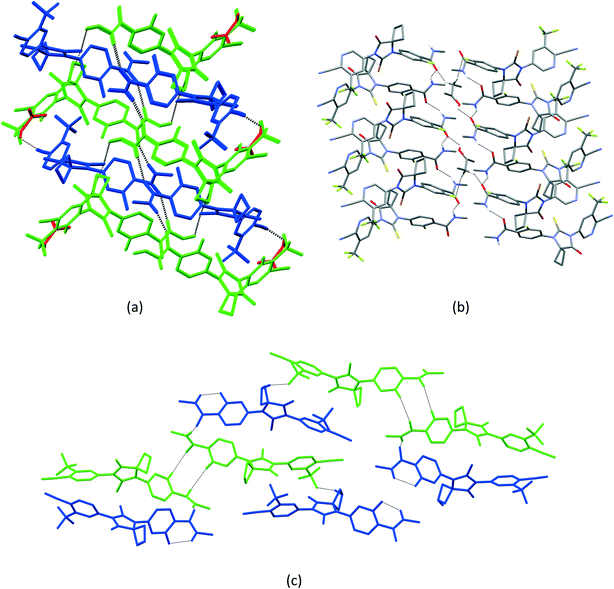
1 solvate structure crystallizes in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with four molecules of apalutamide molecules (suffix with labels A–D) and two DMF solvates (suffix with labels A and B) in the asymmetric unit (Fig. 3). APA molecule A links the adjacent molecule B through the N5A–H5NA⋯O2B hydrogen bond. The APA molecule B interacts with adjacent molecule B via C18B–H18D⋯O3B and APA molecule D through N5B–H5NB⋯O2D and C16B–H16B⋯S1D interactions along with the C17B–H17D⋯F3A (−x + 1, −y + 1, −z) interaction with symmetry-related APA molecule A. The molecule C links the adjacent molecule A via N5C–H5NC⋯O2A hydrogen bonds and symmetry-related molecule B through the C21C–H21I⋯S1B (−x, −y, −z + 1) interaction. The molecule D connects the trans-related molecule C through the N5D–H5ND⋯O2C (x, y + 1, z) hydrogen bond. The APA molecules A and D also interlink the DMF solvates A and B through C2A–H2A⋯O3A and C2D–H2D⋯O3B interactions. The DMF molecule A links APA molecule A through the C24A–H24B⋯N4A (x − 1, y + 1, z) hydrogen bond. The N–H⋯O hydrogen bonds interlink the four APA molecules and aggregate them into an infinite one-dimensional chain along the b-axis. In the crystal packing, the four apalutamide molecules are arranged like a column. In the column, the first row is accommodated by the pairs of inversion-related APA molecules D, while the second row is filled by trans-related APA molecules C and D. The third row has pairs of inversion-related APA molecules A. These rows are arranged alternately along the b-axis. The APA molecules in the row and its adjacent row were interlinked by N–H⋯O, C–H⋯F and C–H⋯S interactions, which leads to the formation of a two-dimensional hydrogen bonded network. The inversion-related DMF solvates crosslink the 2D network with the adjacent network through C–H⋯O and C–H⋯N interactions thereby generating a three-dimensional network of hydrogen bonds (Fig. 5a).
space group with four molecules of apalutamide molecules (suffix with labels A–D) and two DMF solvates (suffix with labels A and B) in the asymmetric unit (Fig. 3). APA molecule A links the adjacent molecule B through the N5A–H5NA⋯O2B hydrogen bond. The APA molecule B interacts with adjacent molecule B via C18B–H18D⋯O3B and APA molecule D through N5B–H5NB⋯O2D and C16B–H16B⋯S1D interactions along with the C17B–H17D⋯F3A (−x + 1, −y + 1, −z) interaction with symmetry-related APA molecule A. The molecule C links the adjacent molecule A via N5C–H5NC⋯O2A hydrogen bonds and symmetry-related molecule B through the C21C–H21I⋯S1B (−x, −y, −z + 1) interaction. The molecule D connects the trans-related molecule C through the N5D–H5ND⋯O2C (x, y + 1, z) hydrogen bond. The APA molecules A and D also interlink the DMF solvates A and B through C2A–H2A⋯O3A and C2D–H2D⋯O3B interactions. The DMF molecule A links APA molecule A through the C24A–H24B⋯N4A (x − 1, y + 1, z) hydrogen bond. The N–H⋯O hydrogen bonds interlink the four APA molecules and aggregate them into an infinite one-dimensional chain along the b-axis. In the crystal packing, the four apalutamide molecules are arranged like a column. In the column, the first row is accommodated by the pairs of inversion-related APA molecules D, while the second row is filled by trans-related APA molecules C and D. The third row has pairs of inversion-related APA molecules A. These rows are arranged alternately along the b-axis. The APA molecules in the row and its adjacent row were interlinked by N–H⋯O, C–H⋯F and C–H⋯S interactions, which leads to the formation of a two-dimensional hydrogen bonded network. The inversion-related DMF solvates crosslink the 2D network with the adjacent network through C–H⋯O and C–H⋯N interactions thereby generating a three-dimensional network of hydrogen bonds (Fig. 5a).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DMF-1
1 (APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–DMF-1
1).
The APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvate structure crystallizes in the orthorhombic Pca21 space group with four molecules of apalutamide (suffix with labels A–D) and four molecules of DMF solvates (suffix with labels A–D) in the asymmetric unit (Fig. S1†). Both molecules A and B are interlinked with each other through N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B and N5B–H5NB⋯O2A (x − 1/2, −y + 2, z)) and form an infinite chain along the a-axis. Similarly, molecules C and D are interlinked with each other via N–H⋯O hydrogen bonds (N5C– H5NC⋯O2D and N5D–H5ND⋯O2C (x + 1/2, −y + 1, z)) and form an infinite chain along the a-axis. The APA molecules D and C are further interlinked by C19D–H19H⋯F2C (1/2 + x, 2 − y, z) hydrogen bonds. The APA molecule A connects the DMF molecule A through the C5A–H5A⋯O3A hydrogen bond, in turn, the DMF molecule A links APA molecule B through the C23A–H23A⋯N4B (1/2 + x, 1 − y, z) hydrogen bond. The APA molecule B connects the DMF molecule D through C2B–H2B⋯O3D, while DMF molecule D links the APA molecules A and B via C24D–H24J⋯N4A (x, 1 + y, z) and C23D–H23J⋯O1B hydrogen bonds. The APA molecule C links the DMF molecule B by C5C–H5C⋯O3B, and DMF molecule B connects the APA molecule C by C24B–H24F⋯O1C hydrogen bonds. The APA molecule D links the DMF molecule C through the C2D–H2D⋯O3C hydrogen bond, while DMF molecule C links the APA molecule D by the C24C–H24H⋯O1D hydrogen bond. The APA molecules A and B are arranged alternately in the infinite chains which are further interconnected by DMF molecules A and D. The combination of N–H⋯O, C–H⋯O and C–H⋯N interactions generates a two-dimensional hydrogen-bonded network. In the crystal, the four APA molecules form two sets of columns. The first set of the column is accommodated by an alternate arrangement of APA molecules C and D, which are further interlinked by DMF solvates B and C. Meanwhile the second column is filled by APA molecules A and B alternately and further interlinked by DMF solvates A and D, respectively (Fig. 5b).
1 solvate structure crystallizes in the orthorhombic Pca21 space group with four molecules of apalutamide (suffix with labels A–D) and four molecules of DMF solvates (suffix with labels A–D) in the asymmetric unit (Fig. S1†). Both molecules A and B are interlinked with each other through N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B and N5B–H5NB⋯O2A (x − 1/2, −y + 2, z)) and form an infinite chain along the a-axis. Similarly, molecules C and D are interlinked with each other via N–H⋯O hydrogen bonds (N5C– H5NC⋯O2D and N5D–H5ND⋯O2C (x + 1/2, −y + 1, z)) and form an infinite chain along the a-axis. The APA molecules D and C are further interlinked by C19D–H19H⋯F2C (1/2 + x, 2 − y, z) hydrogen bonds. The APA molecule A connects the DMF molecule A through the C5A–H5A⋯O3A hydrogen bond, in turn, the DMF molecule A links APA molecule B through the C23A–H23A⋯N4B (1/2 + x, 1 − y, z) hydrogen bond. The APA molecule B connects the DMF molecule D through C2B–H2B⋯O3D, while DMF molecule D links the APA molecules A and B via C24D–H24J⋯N4A (x, 1 + y, z) and C23D–H23J⋯O1B hydrogen bonds. The APA molecule C links the DMF molecule B by C5C–H5C⋯O3B, and DMF molecule B connects the APA molecule C by C24B–H24F⋯O1C hydrogen bonds. The APA molecule D links the DMF molecule C through the C2D–H2D⋯O3C hydrogen bond, while DMF molecule C links the APA molecule D by the C24C–H24H⋯O1D hydrogen bond. The APA molecules A and B are arranged alternately in the infinite chains which are further interconnected by DMF molecules A and D. The combination of N–H⋯O, C–H⋯O and C–H⋯N interactions generates a two-dimensional hydrogen-bonded network. In the crystal, the four APA molecules form two sets of columns. The first set of the column is accommodated by an alternate arrangement of APA molecules C and D, which are further interlinked by DMF solvates B and C. Meanwhile the second column is filled by APA molecules A and B alternately and further interlinked by DMF solvates A and D, respectively (Fig. 5b).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DOX-2
1 (APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–DOX-2
1).
The APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structure crystallizes in the monoclinic C2/c space group with two molecules of APA (suffix with labels A and B) and one molecule of the DOX solvate in the asymmetric unit (Fig. 4). The amide N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B (x, −y + 2, z − 1/2) and N5B–H5NB⋯O2A) link the APA molecules A and B and form an infinite one-dimensional chain along the c-axis. The APA molecule A connects the two symmetry-related APA molecules B by C5A–H5A⋯S1B (x, −y + 1, z − 1/2) and C15A–H15A⋯S1B (3/2 − x, 3/2 − y, 1 − z), while the APA molecule B links the neighbor APA molecule A by the C5B–H5B⋯S1A hydrogen bond. These N–H⋯O and C–H⋯S interactions aggregate the APA molecules into a two-dimensional hydrogen-bonded network. In the crystal, the inversion-related APA molecules A and B are arranged alternately and form a column, which is interlinked with adjacent columns by the above-mentioned N–H⋯O and C–H⋯S interactions thereby forming a 2D network. The DOX solvate links the APA molecules A and B via C2A–H2A⋯O3 (x, y + 1, z) and C22–H22A⋯N4B interactions and generate a three-dimensional hydrogen-bonded network (Fig. 6a).
1 structure crystallizes in the monoclinic C2/c space group with two molecules of APA (suffix with labels A and B) and one molecule of the DOX solvate in the asymmetric unit (Fig. 4). The amide N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B (x, −y + 2, z − 1/2) and N5B–H5NB⋯O2A) link the APA molecules A and B and form an infinite one-dimensional chain along the c-axis. The APA molecule A connects the two symmetry-related APA molecules B by C5A–H5A⋯S1B (x, −y + 1, z − 1/2) and C15A–H15A⋯S1B (3/2 − x, 3/2 − y, 1 − z), while the APA molecule B links the neighbor APA molecule A by the C5B–H5B⋯S1A hydrogen bond. These N–H⋯O and C–H⋯S interactions aggregate the APA molecules into a two-dimensional hydrogen-bonded network. In the crystal, the inversion-related APA molecules A and B are arranged alternately and form a column, which is interlinked with adjacent columns by the above-mentioned N–H⋯O and C–H⋯S interactions thereby forming a 2D network. The DOX solvate links the APA molecules A and B via C2A–H2A⋯O3 (x, y + 1, z) and C22–H22A⋯N4B interactions and generate a three-dimensional hydrogen-bonded network (Fig. 6a).
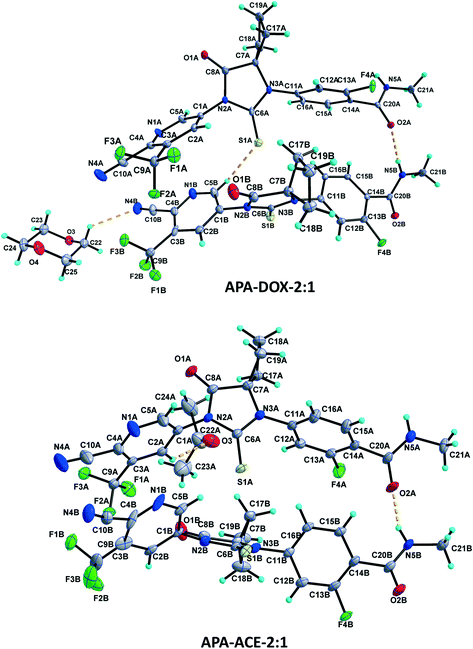 | ||
Fig. 4 Asymmetric units of the APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–ACE-2 1 and APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvates. Displacement ellipsoids are drawn at the 30% probability level. Hydrogen bonds are shown as dashed lines. 1 solvates. Displacement ellipsoids are drawn at the 30% probability level. Hydrogen bonds are shown as dashed lines. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–DMA-1
1 (APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–DMA-1
1).
The APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structure crystallizes in the monoclinic P21/c space group with two molecules each of APA (suffix with labels A and B) and DMA (suffix with labels A and B) in the asymmetric unit (Fig. 3). The APA molecules A and B are interlinked by amide N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B (x, −y + 3/2, z − 1/2) and N5B–H5NB⋯O2A) which aggregate them into an infinite one-dimensional chain along the c-axis. Further, the APA molecules A and B are connected by the C5A–H5A⋯S1B (x, 5/2 − y, −1/2 + z) interaction. These N–H⋯O and C–H⋯S interactions lead to the formation of a two-dimensional hydrogen-bonded network. The APA molecule A connects the DMA solvate A through C2A–H2A⋯O3A while APA molecule B connects the DMA solvate B through C5B–H5B⋯O3B. The DMA solvate B links the symmetry-related APA molecule A through the C23B–H23H⋯N4A (x, 5/2 − y, 1/2 + z) interaction. The combination of N–H⋯O, C–H⋯S, C–H⋯O and C–H⋯N interactions aggregates the molecules into a two-dimensional hydrogen-bonded network. In the crystal, the APA molecules are arranged alternately as a row, and each row is interlinked with the adjacent row through APA⋯APA and APA⋯DMA interactions (Fig. 6b).
1 structure crystallizes in the monoclinic P21/c space group with two molecules each of APA (suffix with labels A and B) and DMA (suffix with labels A and B) in the asymmetric unit (Fig. 3). The APA molecules A and B are interlinked by amide N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B (x, −y + 3/2, z − 1/2) and N5B–H5NB⋯O2A) which aggregate them into an infinite one-dimensional chain along the c-axis. Further, the APA molecules A and B are connected by the C5A–H5A⋯S1B (x, 5/2 − y, −1/2 + z) interaction. These N–H⋯O and C–H⋯S interactions lead to the formation of a two-dimensional hydrogen-bonded network. The APA molecule A connects the DMA solvate A through C2A–H2A⋯O3A while APA molecule B connects the DMA solvate B through C5B–H5B⋯O3B. The DMA solvate B links the symmetry-related APA molecule A through the C23B–H23H⋯N4A (x, 5/2 − y, 1/2 + z) interaction. The combination of N–H⋯O, C–H⋯S, C–H⋯O and C–H⋯N interactions aggregates the molecules into a two-dimensional hydrogen-bonded network. In the crystal, the APA molecules are arranged alternately as a row, and each row is interlinked with the adjacent row through APA⋯APA and APA⋯DMA interactions (Fig. 6b).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–CYH-1
1 (APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–CYH-1
1).
The APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structure crystallizes in the monoclinic P21/c space group with two molecules each of APA (suffix with labels A and B) and cyclohexanone solvates (suffix with labels A and B) in the asymmetric unit (Fig. 3). The amide N–H⋯O hydrogen bonds (N5A–H5N⋯O2B and N5B–H2N⋯O2A (x, −y + 3/2, z + 1/2)) link the APA molecules A and B into an infinite one-dimensional chain along the c-axis. The APA molecule A connects its symmetry-related molecule A (x, 3/2 − y, 1/2 + z) through the C19A–H19A⋯F4A hydrogen bond. The APA molecule B interlinks its symmetry-related APA molecule B via the C21B–H21E⋯S1B (x + 1, y + 1/2, −z + 3/2) hydrogen bond. The APA molecule A links the CYH solvate B via C2A–H2A⋯O3B, while APA molecule B connects the CYH solvate A through C5B–H5B⋯O3A and symmetry-related CYH solvate B by C17B–H17C⋯O3B (x, 3/2 − y, 1/2 + z) hydrogen bonds. The CYH solvate B connects APA molecule A by the C23B–H23C⋯O1A hydrogen bond. In the crystal packing, APA molecules A & B and CYH solvates A & B are arranged alternately as a row. Each row is interlinked with its adjacent rows through APA⋯APA and APA⋯CYH interactions and generates a two-dimensional hydrogen-bonded network (Fig. 6c).
1 structure crystallizes in the monoclinic P21/c space group with two molecules each of APA (suffix with labels A and B) and cyclohexanone solvates (suffix with labels A and B) in the asymmetric unit (Fig. 3). The amide N–H⋯O hydrogen bonds (N5A–H5N⋯O2B and N5B–H2N⋯O2A (x, −y + 3/2, z + 1/2)) link the APA molecules A and B into an infinite one-dimensional chain along the c-axis. The APA molecule A connects its symmetry-related molecule A (x, 3/2 − y, 1/2 + z) through the C19A–H19A⋯F4A hydrogen bond. The APA molecule B interlinks its symmetry-related APA molecule B via the C21B–H21E⋯S1B (x + 1, y + 1/2, −z + 3/2) hydrogen bond. The APA molecule A links the CYH solvate B via C2A–H2A⋯O3B, while APA molecule B connects the CYH solvate A through C5B–H5B⋯O3A and symmetry-related CYH solvate B by C17B–H17C⋯O3B (x, 3/2 − y, 1/2 + z) hydrogen bonds. The CYH solvate B connects APA molecule A by the C23B–H23C⋯O1A hydrogen bond. In the crystal packing, APA molecules A & B and CYH solvates A & B are arranged alternately as a row. Each row is interlinked with its adjacent rows through APA⋯APA and APA⋯CYH interactions and generates a two-dimensional hydrogen-bonded network (Fig. 6c).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–ACN-1
1 (APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–ACN-1
1).
The APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structure crystallized in the orthorhombic Pna21 space group with one molecule of APA and one molecule of the ACN solvate in the asymmetric unit (Fig. 3). The amide N5 atom of APA links the ACN solvate through the N5–H5N⋯N6 hydrogen bond. The APA molecule links its symmetry-related molecule through C2–H2⋯O2 (1 − x, 1 − y, 1/2 + z) and C15–H15⋯O1 (1 − x, 1 − y, −1/2 + z) hydrogen bonds and forms a dimer. The C12–H12⋯S1 (−1/2 + x, 1/2 − y, z) and C18–H18A⋯N4 (1/2 − x, 1/2 + y, −1/2 + z) hydrogen bonds interlink the dimeric units. In the crystal packing, the combination of these interactions aggregates the molecules into a two-dimensional hydrogen-bonded network. It is interesting to note that the amide hydrogen bonding between the APA molecules is absent in the present structure (Fig. 6d).
1 structure crystallized in the orthorhombic Pna21 space group with one molecule of APA and one molecule of the ACN solvate in the asymmetric unit (Fig. 3). The amide N5 atom of APA links the ACN solvate through the N5–H5N⋯N6 hydrogen bond. The APA molecule links its symmetry-related molecule through C2–H2⋯O2 (1 − x, 1 − y, 1/2 + z) and C15–H15⋯O1 (1 − x, 1 − y, −1/2 + z) hydrogen bonds and forms a dimer. The C12–H12⋯S1 (−1/2 + x, 1/2 − y, z) and C18–H18A⋯N4 (1/2 − x, 1/2 + y, −1/2 + z) hydrogen bonds interlink the dimeric units. In the crystal packing, the combination of these interactions aggregates the molecules into a two-dimensional hydrogen-bonded network. It is interesting to note that the amide hydrogen bonding between the APA molecules is absent in the present structure (Fig. 6d).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–ACE-2
1 (APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–ACE-2
1).
The APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structure crystallized in the monoclinic C2/c space group, with two molecules of APA (suffix with labels A and B) and one molecule of the ACE solvate in the asymmetric unit (Fig. 4). Both the APA molecules A and B are interlinked by amide N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B (x, −y + 3, z − 1/2) and N5B–H5NB⋯O2A) forming an infinite chain along the c-axis. The APA molecule A interacts with the two symmetry-related APA molecule B through C5A–H5A⋯S1B (x, −y + 2, z − 1/2) and C21A–H21C⋯S1B (−x + 1/2, −y + 5/2, −z + 1) hydrogen bonds. The APA molecule A further links the ACE solvate through C2A–H2A⋯O3 and in turn the ACE solvate links the APA molecule B via C23–H23B⋯N4B (x, y + 1, z) hydrogen bonds. In the crystal structure, the APA molecules A and B are arranged alternately as rows. Each row is interlinked with the adjacent rows by APA⋯APA and APA⋯ACE interactions and constructs a two-dimensional hydrogen-bonded network (Fig. 7a).
1 structure crystallized in the monoclinic C2/c space group, with two molecules of APA (suffix with labels A and B) and one molecule of the ACE solvate in the asymmetric unit (Fig. 4). Both the APA molecules A and B are interlinked by amide N–H⋯O hydrogen bonds (N5A–H5NA⋯O2B (x, −y + 3, z − 1/2) and N5B–H5NB⋯O2A) forming an infinite chain along the c-axis. The APA molecule A interacts with the two symmetry-related APA molecule B through C5A–H5A⋯S1B (x, −y + 2, z − 1/2) and C21A–H21C⋯S1B (−x + 1/2, −y + 5/2, −z + 1) hydrogen bonds. The APA molecule A further links the ACE solvate through C2A–H2A⋯O3 and in turn the ACE solvate links the APA molecule B via C23–H23B⋯N4B (x, y + 1, z) hydrogen bonds. In the crystal structure, the APA molecules A and B are arranged alternately as rows. Each row is interlinked with the adjacent rows by APA⋯APA and APA⋯ACE interactions and constructs a two-dimensional hydrogen-bonded network (Fig. 7a).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 0.5 (APA–BUT-1
0.5 (APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 0.5).
The APA–BUT structure crystallized in the monoclinic P21/c space group, with one molecule of APA and half a molecule of the BUT solvate in the asymmetric unit (Fig. 3). The 2-butanol solvate is sitting on the two-fold symmetry. The amide N5–H5N⋯O2 (x, −y + 5/2, z + 1/2) links the symmetry-related APA molecule into an infinite one-dimensional chain along the c-axis. The APA chain is further interlinked with its adjacent chain by the BUT solvate through O3–H3O⋯O2, C24–H24A⋯O2 (−x, 2 − y, −z) and C24–H24B⋯F4 (x, y, −1 + z) hydrogen bonds. These hydrogen bonds aggregate the APA and BUT solvate molecules into a two-dimensional hydrogen-bonded network (Fig. 7b).
0.5).
The APA–BUT structure crystallized in the monoclinic P21/c space group, with one molecule of APA and half a molecule of the BUT solvate in the asymmetric unit (Fig. 3). The 2-butanol solvate is sitting on the two-fold symmetry. The amide N5–H5N⋯O2 (x, −y + 5/2, z + 1/2) links the symmetry-related APA molecule into an infinite one-dimensional chain along the c-axis. The APA chain is further interlinked with its adjacent chain by the BUT solvate through O3–H3O⋯O2, C24–H24A⋯O2 (−x, 2 − y, −z) and C24–H24B⋯F4 (x, y, −1 + z) hydrogen bonds. These hydrogen bonds aggregate the APA and BUT solvate molecules into a two-dimensional hydrogen-bonded network (Fig. 7b).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 (APA–EtOH-2
1 (APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The APA–EtOH structure crystallized in the orthorhombic P21212 space group, with two APA molecules (suffix with labels A and B) and two half ethanol molecules (suffix with labels A and B) in the asymmetric unit (Fig. 3). One-half of the ethanol molecule is disordered over two-fold and refined with 0.5 occupancies, while the second half ethanol molecule is four-fold disordered and also refined with 0.5 occupancies. The APA molecules A and B are interlinked by the amide N5A–H5NA⋯O2B hydrogen bond. The APA molecule A is linked to its inversion-related (1 − x, 1 − y, z) molecule through C15A–H15A⋯O2A and form a dimer. Meanwhile APA molecule B forms C19B–H19C⋯F2A (1/2 + x, 1/2 − y, 2 − z) with APA molecule A. Thus APA molecule B bridges the APA A dimer unit with its adjacent unit. The EtOH solvate A links the APA molecule A through C22A–H22A⋯O2A (1 − x, 1 − y, z), while EtOH solvate B does not participate in the hydrogen bonding interaction (Fig. 7c).
1).
The APA–EtOH structure crystallized in the orthorhombic P21212 space group, with two APA molecules (suffix with labels A and B) and two half ethanol molecules (suffix with labels A and B) in the asymmetric unit (Fig. 3). One-half of the ethanol molecule is disordered over two-fold and refined with 0.5 occupancies, while the second half ethanol molecule is four-fold disordered and also refined with 0.5 occupancies. The APA molecules A and B are interlinked by the amide N5A–H5NA⋯O2B hydrogen bond. The APA molecule A is linked to its inversion-related (1 − x, 1 − y, z) molecule through C15A–H15A⋯O2A and form a dimer. Meanwhile APA molecule B forms C19B–H19C⋯F2A (1/2 + x, 1/2 − y, 2 − z) with APA molecule A. Thus APA molecule B bridges the APA A dimer unit with its adjacent unit. The EtOH solvate A links the APA molecule A through C22A–H22A⋯O2A (1 − x, 1 − y, z), while EtOH solvate B does not participate in the hydrogen bonding interaction (Fig. 7c).
APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DMA-1
1, APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–CYH-1
1, APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–ACN-1
1 and APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structures have an equal number of APA and solvate molecules, while in APA–DMF-2
1 structures have an equal number of APA and solvate molecules, while in APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DOX-2
1, APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–ACE-2
1, APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–EtOH-2
1, APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–BUT-1
1 and APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, the numbers of APA molecules are more than those of the solvate molecules in the asymmetric unit. The amide catemer interaction is observed in all the APA–solvate structures except in the APA–ACN structure. In the APA–ACN crystal, the amide N–H atom interacts with the ACN molecule. In all nine solvated structures, APA⋯APA interactions are observed in the crystal packing. In DOX, DMA, CYH, ACE and BUT structures, the solvent molecules play an active role and are involved in various intermolecular interactions with the host molecule, thereby stabilizing the crystal packing. ACN and EtOH molecules are bonded to the APA molecules and did not play any linking role in the crystal packing.
0.5, the numbers of APA molecules are more than those of the solvate molecules in the asymmetric unit. The amide catemer interaction is observed in all the APA–solvate structures except in the APA–ACN structure. In the APA–ACN crystal, the amide N–H atom interacts with the ACN molecule. In all nine solvated structures, APA⋯APA interactions are observed in the crystal packing. In DOX, DMA, CYH, ACE and BUT structures, the solvent molecules play an active role and are involved in various intermolecular interactions with the host molecule, thereby stabilizing the crystal packing. ACN and EtOH molecules are bonded to the APA molecules and did not play any linking role in the crystal packing.
3.2. Conformational analysis
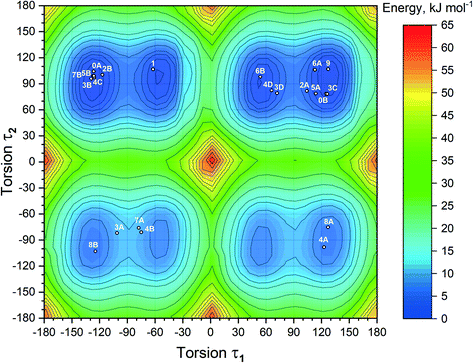
With the inclusion of the solvent molecules into the lattice, the flexible host molecules adopt new conformations, which allow them to maximize the number of intermolecular interactions and result in the formation of a more energetically favorable crystal structure. To better understand the effect of the solvate formation on the conformational preferences of the APA molecules in a crystalline environment, a 2D relaxed conformation scan has been constructed, and the energy barriers of the potential energy surface have been calculated. Two independent torsion angles were considered, corresponding to the relative orientation of phenyl and pyridine rings with respect to the central thioimidazolinone fragment. The angles τ1 (C2–C1–N2–C6) and τ2 (C12–C11–N3–C6) (Fig. 1) varied in the range from 0 to 360 degrees at a step of 10°, resulting in a total of 1332 steps. The resulting molecular structure was relaxed with τ1 and τ2 angles fixed and its total energy determined using Gaussian09 rev. D.01 (ref. 57) in the B3LYP/6-311++(d,p) approximation with the D3 empirical dispersion correction by Grimme et al.48 and the Becke–Johnson damping function.49 The resulting values were plotted on the 2D potential energy map (Fig. 8). Based on the constructed map, the conformations corresponding to local minima were located, and their total energy was determined after a full structure relaxation.The 2D heat map of the conformation energy has four distinct potential energy basins (shown as blue areas) separated by barriers at τ1, τ2 = 0/180°. Such a profile can be explained as follows: the coplanar orientation of rings leads to destabilization of close H–H contacts58 associated with the total energy increase by 22–36 kJ mol−1, with all three rings being coplanar resulting in a conformational penalty up to 65 kJ mol−1. The barrier height between the basins varies within 15–30 kJ mol−1. Within each potential basin, two local minima corresponding to the gauche orientation of the pyridine ring with respect to the central imidazole fragment can be observed. The stabilization of the structures with τ2 close to ±60/±120° can be attributed to intramolecular C–H⋯π contacts59 between the C–H groups of the cyclobutylidene fragment and the π-system of the phenyl ring that is observed during the QTAIMC analysis. The barrier between two local minima within the basin does not exceed 5 kJ mol−1, which is comparable with the thermal energy at RT. Hence, the τ1 value in the isolated APA molecules may vary within ±50°⋯±130°.
The distribution of experimental molecular structures on the heat map is uneven and reflects the depth of a particular potential energy basin. The lowest-energy basin in the upper right part of the graph (τ1 > 0, τ2 > 0) contains 9 individual molecules from the crystal structures of APA and the solvates, while the highest-energy basin (τ1 > 0, τ2 < 0) has only two. Considering the distribution of molecular conformations from the same crystal on the potential energy map, some trends can be deduced. In four out of six crystal structures with two APA molecules in the asymmetric unit, including parent APA, solvates with acetone, ethanol and DMA, the independent molecules have similar τ2 values and opposite signs of τ1. In contrast, two symmetry-independent APA molecules in the solvate with DOX have similar conformations and fall into the same basin. In the APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvate, all four APA molecules in the asymmetric unit belong to different basins, while in APA–DMF-2
1 solvate, all four APA molecules in the asymmetric unit belong to different basins, while in APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, two molecules out of four belong to the lowest-energy basin. APA–ACN-1
1, two molecules out of four belong to the lowest-energy basin. APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is the only crystal where the asymmetric unit contains one independent APA molecule, and no positional disorder was observed. The τ1 value close to −60° in the APA molecule from APA–ACN is uncommon for the molecules of the same basin, which possibly reflects the distinct packing of this solvate. Some of the molecules (3A, 7A and 4B in Fig. 8) are located between the local minima within the basin, indicating the relatively low energy barrier height also in a solid state.
1 is the only crystal where the asymmetric unit contains one independent APA molecule, and no positional disorder was observed. The τ1 value close to −60° in the APA molecule from APA–ACN is uncommon for the molecules of the same basin, which possibly reflects the distinct packing of this solvate. Some of the molecules (3A, 7A and 4B in Fig. 8) are located between the local minima within the basin, indicating the relatively low energy barrier height also in a solid state.
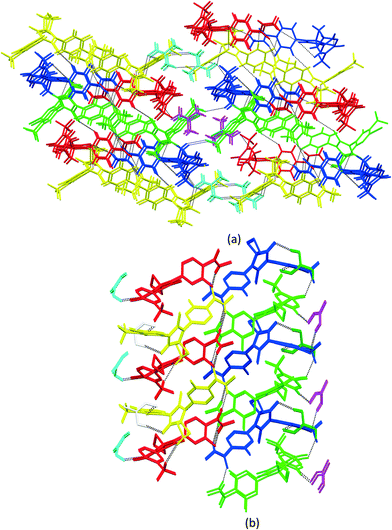
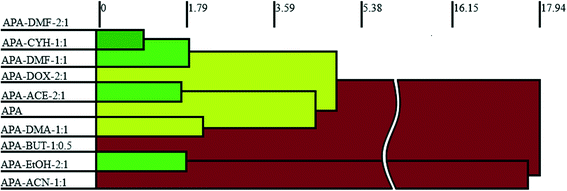
3.3. Crystal packing similarity analysis and void map calculations
Although isostructurality is a commonly observed phenomenon for solvates of organic compounds,10,60–66 APA did not tend to form isostructural solvates with the selected solvents. A comparison of the molecular packing of APA solvates using the CrystalCMP program67 reveals that two distinct groups of related structures are present (Fig. 9). The first and largest group consists of solvates formed by H-bond acceptor type solvents,68i.e. DMF, DOX, DMA, CYH, and ACE solvates, and also includes parent APA. The common structural feature of all these solid forms is the 2D zigzag-like packing arrangement of the APA layers that are separated by domains containing solvent molecules (except for non-solvated APA).Interestingly, the closest similarity in terms of the APA packing was observed for the APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–CYH-1
1, APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DMF-1
1 and APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvates that have different space group systems and API-to-solvent ratios. These three solvates contain the same principal substructure of the APA molecules, which adopt a common arrangement along two crystallographic axes (Fig. S2,† exemplified by APA–CYH-1
1 solvates that have different space group systems and API-to-solvent ratios. These three solvates contain the same principal substructure of the APA molecules, which adopt a common arrangement along two crystallographic axes (Fig. S2,† exemplified by APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The APA–ACE-2
1). The APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DOX-2
1 and APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvates are another pair of structures sharing the same space group (C2/c) and exhibiting a high degree of similarity. In contrast to the DMF and CYH solvates, where crests and troughs of the adjacent zigzag layers of APA are aligned, in APA–ACE-2
1 solvates are another pair of structures sharing the same space group (C2/c) and exhibiting a high degree of similarity. In contrast to the DMF and CYH solvates, where crests and troughs of the adjacent zigzag layers of APA are aligned, in APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DOX-2
1 and APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the neighboring layers of APA are shifted relative to each other by half of the “wavelength”, which results in the formation of large pores, providing a space for solvent molecules (Fig. S3†). A close structural resemblance between parent APA and APA–DMA-1
1, the neighboring layers of APA are shifted relative to each other by half of the “wavelength”, which results in the formation of large pores, providing a space for solvent molecules (Fig. S3†). A close structural resemblance between parent APA and APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was also confirmed by CrystalCMP. Both crystals contain analogous APA layers arranged along the b and c crystallographic axes, while the molecular packing along the a-axis is different due to the presence of a solvent in APA–DMA-1
1 was also confirmed by CrystalCMP. Both crystals contain analogous APA layers arranged along the b and c crystallographic axes, while the molecular packing along the a-axis is different due to the presence of a solvent in APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. S4†). The second group of related structures includes APA solvates with alcohols, i.e. EtOH and BUT, that can be both the donor and acceptor of H-bonds68 (Fig. 9). Although the APA–EtOH-2
1 (Fig. S4†). The second group of related structures includes APA solvates with alcohols, i.e. EtOH and BUT, that can be both the donor and acceptor of H-bonds68 (Fig. 9). Although the APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–BUT-1
1 and APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 structures contain slightly different molecular conformations of APA, the molecules of the drug are packed in a similar manner, forming vivid parallel layers along the a and b axes (Fig. S5†). The APA–ACN-1
0.5 structures contain slightly different molecular conformations of APA, the molecules of the drug are packed in a similar manner, forming vivid parallel layers along the a and b axes (Fig. S5†). The APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvate shows no structural resemblance to other APA solid forms and, presumably, represents the first member of a distinct family of the related solvate structures that are waiting to be discovered. In this structure, piles of the APA molecules are assembled into a rectangular grid network with large voids occupied by solvent (Fig. S6†).
1 solvate shows no structural resemblance to other APA solid forms and, presumably, represents the first member of a distinct family of the related solvate structures that are waiting to be discovered. In this structure, piles of the APA molecules are assembled into a rectangular grid network with large voids occupied by solvent (Fig. S6†).
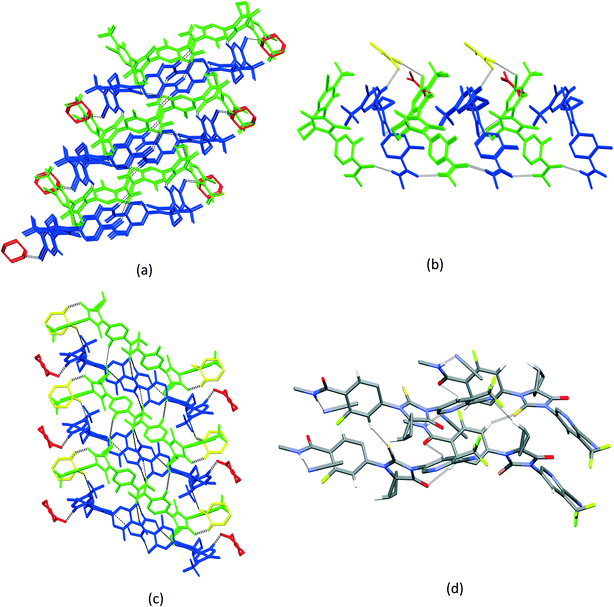
According to void map calculations, the solvates can be characterized by three different types of voids. In APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the continuous voids propagate along the b and c crystallographic axes to form apparent layers (Fig. S2†) that constitute a large part of the cell volume (Table 1). Despite the structural resemblance between APA–CYH-1
1, the continuous voids propagate along the b and c crystallographic axes to form apparent layers (Fig. S2†) that constitute a large part of the cell volume (Table 1). Despite the structural resemblance between APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DMF-1
1, APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DMF-2
1 and APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in terms of APA packing, these solvates show diverse solvent accommodation patterns and void volume. In APA–DMF-1
1 in terms of APA packing, these solvates show diverse solvent accommodation patterns and void volume. In APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, apparent separate channels are seen only along one crystallographic axis (Fig. 10). In the case of APA–DMF-2
1, apparent separate channels are seen only along one crystallographic axis (Fig. 10). In the case of APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, open channels were not observed (Fig. S7†), and the solvent molecules were encapsulated in closed cavities that occupy only 10.9% of the cell volume (Table 1). Although the APA–ACE-2
1, open channels were not observed (Fig. S7†), and the solvent molecules were encapsulated in closed cavities that occupy only 10.9% of the cell volume (Table 1). Although the APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DOX-2
1 and APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvates also contain continuous void channels, these are not connected to each other and extended only along the c-axis (Fig. S3†). A similar void framework is seen in APA–ACN-1
1 solvates also contain continuous void channels, these are not connected to each other and extended only along the c-axis (Fig. S3†). A similar void framework is seen in APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Meanwhile, the APA–EtOH-2
1. Meanwhile, the APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–BUT-1
1 and APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 solid forms belong to the so-called isolated site solvate,69 as the void volume distribution occupied by solvent molecules is clearly discontinuous in void volume maps (Fig. S5†). The described differences in the void structure and solvent accommodation make a considerable impact on the thermal stability of the corresponding solvates, and this aspect is further discussed.
0.5 solid forms belong to the so-called isolated site solvate,69 as the void volume distribution occupied by solvent molecules is clearly discontinuous in void volume maps (Fig. S5†). The described differences in the void structure and solvent accommodation make a considerable impact on the thermal stability of the corresponding solvates, and this aspect is further discussed.
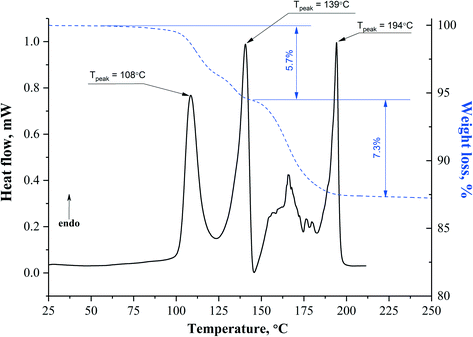
| Solvate | T desolv (HSM), °C | T desolv (DSC, peak), °C | Type of void | T boil, °C | Void space, % |
|---|---|---|---|---|---|
APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
108–128 | 108.0 | Mixed (open and closed) | 153.0 | 18.3 |
| 135–148 | 139.0 | ||||
APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
136–150 | 138.0 | Closed | 153.0 | 10.9 |
APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
97–123 | 110.0 | Open | 56.0 | 11.3 |
APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
110–150 | 112.0 | Open | 101.0 | 12.3 |
APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
100–125 | 122.3 | Open | 155.7 | 25.8 |
APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
100–117 | 109.2 | Open | 165.0 | 26.8 |
APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
110–118 | 112.2 | Open | 82.0 | 11.9 |
APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
115–134 | 123.2 | Closed | 78.0 | 10.2 |
APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5 |
111–130 | 117.4 | Closed | 99.0 | 12.7 |
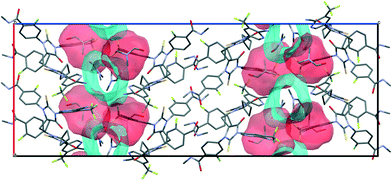 | ||
Fig. 10 Illustration of different types of voids coexisting in the crystal structures of APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | ||
3.4. Thermal analyses
The thermal stability of the APA solvates was investigated using DSC, HSM and TG techniques, and the experimental results are given in Table 1. Although half of the considered here solvates contain channel-like open voids, suggesting an easy “escape route” for the solvent molecules, the common features of the solid forms are the relatively high values of desolvation temperature (above 100 °C). For instance, the desolvation temperature (Tdesolv) of APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is approximately twice as much as the boiling point (Tboil) of neat acetone. For APA–ACN-1
1 is approximately twice as much as the boiling point (Tboil) of neat acetone. For APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the difference between Tdesolv and Tboil equals ca. 30 °C. In addition, no reliable correlation between the solvate desolvation temperature and the boiling point of the corresponding solvents was found. This fact indicates clearly that solvent molecules in these solvates not only act as the void filler, increasing the packing efficiency of the resulting crystals, but also are effectively bound with the host molecules via various intermolecular interactions, providing a notable stabilization effect on the crystal structure (this aspect is discussed below).
1, the difference between Tdesolv and Tboil equals ca. 30 °C. In addition, no reliable correlation between the solvate desolvation temperature and the boiling point of the corresponding solvents was found. This fact indicates clearly that solvent molecules in these solvates not only act as the void filler, increasing the packing efficiency of the resulting crystals, but also are effectively bound with the host molecules via various intermolecular interactions, providing a notable stabilization effect on the crystal structure (this aspect is discussed below).
Particularly interesting thermal behavior is demonstrated by the APA solvates with DMF. The DSC curve of APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 shows multiple well-separated endothermic events and the variable steepness of the TG mass loss (Fig. 11), indicating the stepwise mechanism of the desolvation process, while the existence of the exotherm at ≈145 °C is a clear sign of the solid–solid phase transition. The first sharp endotherm at ≈108 °C seems to be associated with the removal of less tightly bound DMF molecules from the APA–DMF-1
1 shows multiple well-separated endothermic events and the variable steepness of the TG mass loss (Fig. 11), indicating the stepwise mechanism of the desolvation process, while the existence of the exotherm at ≈145 °C is a clear sign of the solid–solid phase transition. The first sharp endotherm at ≈108 °C seems to be associated with the removal of less tightly bound DMF molecules from the APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 crystal structure to form APA–DMF-2
1 crystal structure to form APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
As Fig. 10 shows, in APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, two types of voids coexist within the same framework: two out of four symmetry-independent DMF molecules are located in open channels along the b-axis and expected to escape easily at a lower temperature, whereas the other two symmetry-independent solvent molecules reside in discrete cavities, which hinders their release from the crystal structure. In order to gain additional evidence for such a phase transition, single crystals of APA–DMF-1
1, two types of voids coexist within the same framework: two out of four symmetry-independent DMF molecules are located in open channels along the b-axis and expected to escape easily at a lower temperature, whereas the other two symmetry-independent solvent molecules reside in discrete cavities, which hinders their release from the crystal structure. In order to gain additional evidence for such a phase transition, single crystals of APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were heated up to 130 °C under the control of HSM (Fig. S8†) and further subjected to unit cell determinations, which confirmed the formation of the APA–DMF-2
1 were heated up to 130 °C under the control of HSM (Fig. S8†) and further subjected to unit cell determinations, which confirmed the formation of the APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phase. In addition, the desolvation temperature value for the APA–DMF-2
1 phase. In addition, the desolvation temperature value for the APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 crystal obtained in a separate experiment (Fig. S9 and S18†) was found to be consistent with that of the second endothermic peak in the DSC curve of APA–DMF-1
1 crystal obtained in a separate experiment (Fig. S9 and S18†) was found to be consistent with that of the second endothermic peak in the DSC curve of APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (≈139 °C), indicating that both events correspond to the desolvation process of the APA–DMF-2
1 (≈139 °C), indicating that both events correspond to the desolvation process of the APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phase. According to TG results, however, a cumulative weight loss in the temperature range of 25.0–145.0 °C was recorded to be about 5.7% which corresponds to ca. 0.45 mol of DMF. Further heating of the sample up to 200.0 °C resulted in an additional step mass loss of 7.3%, corresponding to the remaining 0.55 mol of the solvent (Fig. 11). The observed discrepancy in temperatures of endothermic peaks and the sample weight loss is likely because some DMF escaping from APA–DMF-1
1 phase. According to TG results, however, a cumulative weight loss in the temperature range of 25.0–145.0 °C was recorded to be about 5.7% which corresponds to ca. 0.45 mol of DMF. Further heating of the sample up to 200.0 °C resulted in an additional step mass loss of 7.3%, corresponding to the remaining 0.55 mol of the solvent (Fig. 11). The observed discrepancy in temperatures of endothermic peaks and the sample weight loss is likely because some DMF escaping from APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 remained as a liquid at temperatures below the boiling point of the solvent (153 °C) and underwent complete evaporation as the temperature approached the melting point of APA. A similar thermal behaviour has also been reported for the solvates of felodipine and celecoxib with high-boiling point solvents.70,71 It has to be stressed, however, that further investigations via the in situ temperature-dependent PXRD technique are required to rationalize the complex thermal behaviour of this system and to confirm the proposed desolvation pathway.
1 remained as a liquid at temperatures below the boiling point of the solvent (153 °C) and underwent complete evaporation as the temperature approached the melting point of APA. A similar thermal behaviour has also been reported for the solvates of felodipine and celecoxib with high-boiling point solvents.70,71 It has to be stressed, however, that further investigations via the in situ temperature-dependent PXRD technique are required to rationalize the complex thermal behaviour of this system and to confirm the proposed desolvation pathway.
The APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DOX-2
1 and APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvates show a simple one-step desolvation process and a similar evacuation temperature for the corresponding solvent (Fig. S19 and S20†). The similarity in desolvation behavior between these two solvates can be due to the close structural resemblance in terms of the host packing arrangement (Fig. 9) and the structure of voids that solvent molecules accommodate. APA–CYH-1
1 solvates show a simple one-step desolvation process and a similar evacuation temperature for the corresponding solvent (Fig. S19 and S20†). The similarity in desolvation behavior between these two solvates can be due to the close structural resemblance in terms of the host packing arrangement (Fig. 9) and the structure of voids that solvent molecules accommodate. APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DMA-1
1 and APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 contain the largest proportion of open voids among the studied solvates (Table 1) and are expected to liberate the solvent molecules at a low temperature. However, the thermal stability of these solvates is comparable to that of other solvated forms of APA. Although both APA–CYH-1
1 contain the largest proportion of open voids among the studied solvates (Table 1) and are expected to liberate the solvent molecules at a low temperature. However, the thermal stability of these solvates is comparable to that of other solvated forms of APA. Although both APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DMA-1
1 and APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structures are characterized by the presence of interlayer spaces of similar size filled by solvent molecules with comparable values of a van der Waals volume, their desolvation behavior appeared to be slightly different. For APA–DMA-1
1 structures are characterized by the presence of interlayer spaces of similar size filled by solvent molecules with comparable values of a van der Waals volume, their desolvation behavior appeared to be slightly different. For APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the occurrence of two separate endothermic peaks in the DSC curve suggests an apparent two-step desolvation process and indicates that one of the symmetry-independent DMA molecules is accommodated less effectively in the host structure and released at a lower temperature (≈109 °C) (Fig. S21†). In the case of APA–CYH-1
1, the occurrence of two separate endothermic peaks in the DSC curve suggests an apparent two-step desolvation process and indicates that one of the symmetry-independent DMA molecules is accommodated less effectively in the host structure and released at a lower temperature (≈109 °C) (Fig. S21†). In the case of APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, solvent molecules escape the host structure in a cooperative manner seen in the DSC curve as a broad endothermic event with a peak temperature of ca. 122 °C (Fig. S22†). In contrast, APA–EtOH-2
1, solvent molecules escape the host structure in a cooperative manner seen in the DSC curve as a broad endothermic event with a peak temperature of ca. 122 °C (Fig. S22†). In contrast, APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–BUT-1
1 and APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 demonstrate a similar one-step desolvation behavior, liberating the solvent molecules at 123.2 °C and 117.4 °C, respectively (Fig. S23 and S24†). The high thermal stability of these solvates can be attributed to a specific packing feature of the host structure, where the solvent molecules are located in compact closed cavities. Despite the relatively high value of the APA–ACN-1
0.5 demonstrate a similar one-step desolvation behavior, liberating the solvent molecules at 123.2 °C and 117.4 °C, respectively (Fig. S23 and S24†). The high thermal stability of these solvates can be attributed to a specific packing feature of the host structure, where the solvent molecules are located in compact closed cavities. Despite the relatively high value of the APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 desolvation temperature, which is likely due to hydrogen bonding between APA and the solvent in the crystal, the preparation procedure of this solid form exhibited scarce reproducibility, so its thermal analysis was limited to the DSC and HSM studies (Fig. S16 and S25†).
1 desolvation temperature, which is likely due to hydrogen bonding between APA and the solvent in the crystal, the preparation procedure of this solid form exhibited scarce reproducibility, so its thermal analysis was limited to the DSC and HSM studies (Fig. S16 and S25†).
3.5. Structure transformation and desolvation mechanism
As mentioned in the Introduction section, desolvation of solvates is frequently considered as an alternative route to acquire unknown or specific polymorphic forms that are inaccessible otherwise by conventional crystallization techniques.66 Although two unsolvated polymorphs of APA are currently known (form B and form H),34 the PXRD analysis of desolvated products revealed that all the reported here solvates of the drug were transformed into the most thermodynamically stable form B.However, the results of the thermal analysis indicated that there is a clear difference in desolvation pathways and the solid-state thermal evolution between the solvates. The DSC curves of the APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–DOX-2
1, APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–EtOH-2
1, APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–BUT-1
1, APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 solvates show that the endothermic desolvation process is followed by a broad exothermic event that can be attributed to recrystallization of the desolvated residues into the stable crystalline phase of APA. Further PXRD investigations of the intermediate solid phase (using APA–ACN-1
0.5 solvates show that the endothermic desolvation process is followed by a broad exothermic event that can be attributed to recrystallization of the desolvated residues into the stable crystalline phase of APA. Further PXRD investigations of the intermediate solid phase (using APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DOX-2
1 and APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as specimens of this group), obtained by heating the solvates slightly above the corresponding desolvation temperature in a DSC pan, revealed that solvent release leads to a collapse of the parent phase to form a metastable amorphous material which implies that the release of solvent molecules occurs through a destructive process (Fig. S26†). According to the classification scheme proposed by Petit and Coquerel,72 the observed thermal behaviour of this group of solvates corresponds to the two-step mechanism of desolvation defined as class I destructive crystallization (or class I-D.C.).
1 as specimens of this group), obtained by heating the solvates slightly above the corresponding desolvation temperature in a DSC pan, revealed that solvent release leads to a collapse of the parent phase to form a metastable amorphous material which implies that the release of solvent molecules occurs through a destructive process (Fig. S26†). According to the classification scheme proposed by Petit and Coquerel,72 the observed thermal behaviour of this group of solvates corresponds to the two-step mechanism of desolvation defined as class I destructive crystallization (or class I-D.C.).
For the second group of solvates, which includes APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–ACE-2
1, APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, APA–CYH-1
1, APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, DSC analysis displayed no evidence of the exothermic transition signal prior to melting of the sample, indicating that release of solvent molecules is accompanied by a rapid reorganization of the parent packing arrangement so that the dehydration process is likely to follow the class II cooperative reorganization mechanism in terms of Petit and Coquerel's notation. This thermal behaviour is expected for APA–DMA-1
1, DSC analysis displayed no evidence of the exothermic transition signal prior to melting of the sample, indicating that release of solvent molecules is accompanied by a rapid reorganization of the parent packing arrangement so that the dehydration process is likely to follow the class II cooperative reorganization mechanism in terms of Petit and Coquerel's notation. This thermal behaviour is expected for APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as it was found to exhibit packing similarity with unsolvated APA (Fig. 9). It is interesting to note that APA–ACE-2
1 as it was found to exhibit packing similarity with unsolvated APA (Fig. 9). It is interesting to note that APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and APA–DOX-2
1 and APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 appeared in the different groups of solvates despite the observed similarity in desolvation temperature and the close structural resemblance. The difference in desolvation patterns between these two solvates may be explained by considering the set of APA molecular conformations in the crystal structures. As Fig. 8 demonstrates, the APA–ACE-2
1 appeared in the different groups of solvates despite the observed similarity in desolvation temperature and the close structural resemblance. The difference in desolvation patterns between these two solvates may be explained by considering the set of APA molecular conformations in the crystal structures. As Fig. 8 demonstrates, the APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvate contains APA conformations that are similar to these in the bare APA, indicating relatively low energy requirements for conformational adjustment during the reorganization process. According to HSM studies, the crystal lost transparency after solvent removal, but the original crystal integrity was maintained during the desolvation process, suggesting that the pseudomorphosis phenomenon is taking place (Fig. S10†). A similar desolvation behavior was also observed for the APA–CYH-1
1 solvate contains APA conformations that are similar to these in the bare APA, indicating relatively low energy requirements for conformational adjustment during the reorganization process. According to HSM studies, the crystal lost transparency after solvent removal, but the original crystal integrity was maintained during the desolvation process, suggesting that the pseudomorphosis phenomenon is taking place (Fig. S10†). A similar desolvation behavior was also observed for the APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvate (Fig. S13†). In addition, the whole desolvation process for this solvate appeared to be relatively slow, and the parent crystals have enough time to rearrange into the stable solvent-free form of APA. In the case of APA–DOX-2
1 solvate (Fig. S13†). In addition, the whole desolvation process for this solvate appeared to be relatively slow, and the parent crystals have enough time to rearrange into the stable solvent-free form of APA. In the case of APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, however, the direct solid-state phase transformation into APA without losing the long-range order does not seem to be possible due to the high energy barrier associated with conformational changes. A further quantitative study of the desolvation process is currently our priority, and we plan to proceed with a more detailed investigation of the APA solvates' thermal properties, particularly by measuring the kinetics of the desolvation reaction via TG and temperature-dependent PXRD.
1, however, the direct solid-state phase transformation into APA without losing the long-range order does not seem to be possible due to the high energy barrier associated with conformational changes. A further quantitative study of the desolvation process is currently our priority, and we plan to proceed with a more detailed investigation of the APA solvates' thermal properties, particularly by measuring the kinetics of the desolvation reaction via TG and temperature-dependent PXRD.
3.6. Calculation results
To elucidate the forces that govern the crystal packing in the studied solvates, theoretical computations of packing energetics and non-covalent interactions were performed. Our investigation pursued the following goals: 1) to estimate the stability of the crystal structure after solvent removal and to compare it with thermal data; 2) to estimate the binding energy of solvent molecules within the crystal structure of a solvate. To fulfil these tasks, three independent methods were used: DFT-D3, QTAIMC and CrystalExplorer. While DFT-D3 affords reliable and lattice energy estimation, the latter two approaches additionally allow consideration of the contributions of particular non-covalent interactions into Elatt.The lattice energy values, stabilization energies and binding energies of APA solvates are collected in Table 2. While the absolute values of Elatt and its components are different, the results obtained by different methods show common trends that reflect the relative stability of different solvates at zero Kelvin. From the data provided in Table 2, it can be seen that the lattice energy and overall stability of a solvent is a product of two semi-independent factors: i) the relative stability of the APA framework (which is numerically equal to the Estab value – the lattice energy of a crystal with solvent molecules removed) and ii) the binding energy of the solvent molecules Ebind, or the difference between the lattice energies of a solvated and a hypothetical non-solvated crystal (eqn (2)). The ratio of these quantities and absolute Elatt value can be used to rank the solvates from the most energetically favorable to the least.
| Solvate | E latt | E stab | E bind | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DFT-D3 | QTAIMC | CE-B3LYP | DFT-D3 | QTAIMC | CE-B3LYP | DFT-D3 | QTAIMC | CE-B3LYP | |
APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−285.5 | −216.1 | −247.2 | −174.0 | −132.4 | −183.9 | −111.5 | −83.7 | −63.1 |
APA–DMF-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−249.2 | −197.1 | −224.6 | −186.2 | −150.6 | −190.0 | −63.0 | −46.6 | −34.6 |
APA–ACE-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−224.2 | −169.5 | −216.7 | −185.2 | −139.3 | −191.7 | −39.1 | −30.2 | −25.0 |
| −232.7 | −177.1 | −199.3 | −187.8 | −148.0 | −176.4 | −44.9 | −29.1 | −22.9 | |
APA–DOX-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−243.1 | −190.4 | −230.4 | −186.2 | −157.1 | −201.4 | −47.0 | −33.2 | −29.0 |
APA–CYH-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−287.0 | −220.7 | −241.5 | −179.9 | −124.8 | −173.7 | −107.1 | −96.0 | −67.8 |
APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−282.6 | −163.2 | −221.4 | −176.6 | −94.1 | −159.2 | −106.0 | −69.1 | −62.2 |
APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−257.2 | −212.7 | −228.2 | −172.1 | −158.4 | −183.0 | −85.1 | −54.3 | −45.2 |
APA–EtOH-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−151.7 | −190.2 | −189.5 | −177.0 | −120.6 | −181.3 | 25.3 | −93.3 | −8.2 |
| −214.0 | |||||||||
APA–BUT-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5 |
−160.1 | −168.4 | −198.9 | −173.7 | −137.1 | −176.8 | 13.5 | −31.3 | −22.1 |
The way of packing APA molecules in the crystal structures is found to impact the thermal stability of the crystal. For instance, the packing of APA molecules in APA–DMA-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in a manner similar to pure APA is inefficient, resulting in the lowest Estab value of all solvates (−159 kJ mol−1 according to CE-B3LYP). The solvate is stable at low temperatures due to the high fraction of APA–solvent interactions. However, the presence of 2D layers composed entirely of DMA molecules and isostructurality with pure APA prohibits the thermal desolvation with consequent transformation to non-solvated APA. As a result, this crystal is characterized by the lowest desolvation temperature of all considered structures, which is 56 °C lower than the boiling point of the pure solvent. In contrast, the packing of APA molecules in the APA–ACN-1
1 in a manner similar to pure APA is inefficient, resulting in the lowest Estab value of all solvates (−159 kJ mol−1 according to CE-B3LYP). The solvate is stable at low temperatures due to the high fraction of APA–solvent interactions. However, the presence of 2D layers composed entirely of DMA molecules and isostructurality with pure APA prohibits the thermal desolvation with consequent transformation to non-solvated APA. As a result, this crystal is characterized by the lowest desolvation temperature of all considered structures, which is 56 °C lower than the boiling point of the pure solvent. In contrast, the packing of APA molecules in the APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 crystal is rather uncommon, since no H-bond chains between amide fragments are observed in the structure. Instead, the N–H groups form the N–H⋯N bonds with nitrogen atoms of ACN with Eint = 13 kJ mol−1 according to QTAIMC, increasing the Estab value. For this reason, APA–ACN-1
1 crystal is rather uncommon, since no H-bond chains between amide fragments are observed in the structure. Instead, the N–H groups form the N–H⋯N bonds with nitrogen atoms of ACN with Eint = 13 kJ mol−1 according to QTAIMC, increasing the Estab value. For this reason, APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is the only crystal out of the solvates with a 1
1 is the only crystal out of the solvates with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 component ratio with the Tdesolv higher than the Tboil of the pure solvent. Another example of structures with exceptional thermal stability is the pair of solvates with EtOH and BUT, where solvent molecules are trapped within the closed voids of the APA framework. Similar to APA–ACN-1
1 component ratio with the Tdesolv higher than the Tboil of the pure solvent. Another example of structures with exceptional thermal stability is the pair of solvates with EtOH and BUT, where solvent molecules are trapped within the closed voids of the APA framework. Similar to APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, these solvents are characterized by high Estab values and low Ebind values, which is reflected in the desolvation thermogram as Tdesolv > Tboil and the absent exo-effect. For solvates with an open channel structure, a clear correlation exists between the fraction of APA–APA interactions and the desolvation temperature decrease (Fig. S27†). The larger contribution of Ebind leads to destabilization of the APA framework and a decrease in the desolvation temperature.
1, these solvents are characterized by high Estab values and low Ebind values, which is reflected in the desolvation thermogram as Tdesolv > Tboil and the absent exo-effect. For solvates with an open channel structure, a clear correlation exists between the fraction of APA–APA interactions and the desolvation temperature decrease (Fig. S27†). The larger contribution of Ebind leads to destabilization of the APA framework and a decrease in the desolvation temperature.
The combination of open channels and closed voids in the APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 crystal leads to complex desolvation behaviour. Two out of four solvent molecules in the asymmetric unit located in the open pore have a binding energy equal to 19–21 kJ mol−1, while the other two are strongly bound within the framework with Ebind = 36–38 kJ mol−1. The difference in binding energies between symmetry-inequivalent DMF molecules helped to elucidate the two-step desolvation process of APA–DMF-1
1 crystal leads to complex desolvation behaviour. Two out of four solvent molecules in the asymmetric unit located in the open pore have a binding energy equal to 19–21 kJ mol−1, while the other two are strongly bound within the framework with Ebind = 36–38 kJ mol−1. The difference in binding energies between symmetry-inequivalent DMF molecules helped to elucidate the two-step desolvation process of APA–DMF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 observed in the DSC and TG experiments (Fig. 11).
1 observed in the DSC and TG experiments (Fig. 11).
The correlation between the fraction of APA–solvent interactions (which are numerically equal to Ebind) in the Elatt (QTAIMC) and van der Waals volume of the solvent implies that the main contribution to the structure stabilization came from dispersive interactions rather than hydrogen bonds (Fig. S28†). However, the analysis of individual intermolecular contacts reveals the high fraction of C–H⋯O/N/F/S bonds in most studied crystals.
4. Conclusions
In this work, nine solvates of the nonsteroidal androgen inhibitor apalutamide (APA) were obtained and characterized. The crystal structures of the APA solvates were determined for the first time. Single crystal X-ray analysis complemented by the DFT computations revealed that most of the solvates (except APA–ACN-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) contain two or four symmetry-independent APA molecules in the asymmetric unit with close conformation energy. According to the crystal packing similarity analysis, no 3D isostructurality was observed among the studied crystal structure; however, five solvates and the parent APA were found to contain a similar 2D zigzag-like packing arrangement of the APA molecules. The results of the thermal analysis showed that all considered APA solvates decompose at temperatures above 100 °C, despite the presence of a channel-like open void structure found in half of the studied solvates, suggesting an easy “escape route” for the solvent molecules. This fact indicates clearly that solvent molecules in the solvates not only act as the void filler, increasing the packing efficiency of the resulting crystals, but also are effectively bound with the host molecules via various intermolecular interactions, providing a notable stabilization effect on the crystal structure. According to the desolvation patterns, the APA solvates can be separated into two groups: solvates that recrystallize after desolvation via an intermediate amorphous phase with a characteristic exothermal event in the DSC curve, and solvates that rapidly transform to crystalline apalutamide with no exothermal event. The solvates in the second group are characterized by one of the following features: i) packing similarity with pure apalutamide and ii) similarities in conformations of APA molecules in the initial solvate and pure apalutamide. The structure and volume of voids occupied by solvent molecules were found to have an impact on the desolvation temperature of a solvate. As follows from lattice energy calculations and theoretical analysis of non-covalent interactions, the thermal stability of the studied solvates is governed by the fraction of APA–APA and APA–solvent interactions in a crystal. The inefficient packing of apalutamide molecules associated with low stabilization energy leads to lower desolvation temperatures and facilitates the transformation to pure APA, while the structures with a higher fraction of APA–APA interactions in the lattice energy are found to be more stable. The main forces responsible for the binding of solvent molecules in the crystal are weak C–H⋯X hydrogen bonds and van der Waals interactions. In conclusion, the present work provides valuable insights into the interplay between the molecular conformation, packing features and thermal properties of solvated apalutamide crystalline forms.
1) contain two or four symmetry-independent APA molecules in the asymmetric unit with close conformation energy. According to the crystal packing similarity analysis, no 3D isostructurality was observed among the studied crystal structure; however, five solvates and the parent APA were found to contain a similar 2D zigzag-like packing arrangement of the APA molecules. The results of the thermal analysis showed that all considered APA solvates decompose at temperatures above 100 °C, despite the presence of a channel-like open void structure found in half of the studied solvates, suggesting an easy “escape route” for the solvent molecules. This fact indicates clearly that solvent molecules in the solvates not only act as the void filler, increasing the packing efficiency of the resulting crystals, but also are effectively bound with the host molecules via various intermolecular interactions, providing a notable stabilization effect on the crystal structure. According to the desolvation patterns, the APA solvates can be separated into two groups: solvates that recrystallize after desolvation via an intermediate amorphous phase with a characteristic exothermal event in the DSC curve, and solvates that rapidly transform to crystalline apalutamide with no exothermal event. The solvates in the second group are characterized by one of the following features: i) packing similarity with pure apalutamide and ii) similarities in conformations of APA molecules in the initial solvate and pure apalutamide. The structure and volume of voids occupied by solvent molecules were found to have an impact on the desolvation temperature of a solvate. As follows from lattice energy calculations and theoretical analysis of non-covalent interactions, the thermal stability of the studied solvates is governed by the fraction of APA–APA and APA–solvent interactions in a crystal. The inefficient packing of apalutamide molecules associated with low stabilization energy leads to lower desolvation temperatures and facilitates the transformation to pure APA, while the structures with a higher fraction of APA–APA interactions in the lattice energy are found to be more stable. The main forces responsible for the binding of solvent molecules in the crystal are weak C–H⋯X hydrogen bonds and van der Waals interactions. In conclusion, the present work provides valuable insights into the interplay between the molecular conformation, packing features and thermal properties of solvated apalutamide crystalline forms.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr. Virendra M Tiwari, Director, CSIR-IICT, Hyderabad, India, is thanked for his kind encouragement. CSIR-IICT is profusely thanked (Manuscript communication number: IICT/Pubs./2021/167). Dr. Bojja Sreedhar is thanked for the DSC and TGA data. S. B. thanks DST for grant INT/RUS/RFBR/374 and JP acknowledges for his fellowship. This study was supported by RFBR and DST according to the research project N19-53-45002. We thank “the Upper Volga Region Centre of Physicochemical Research” for technical assistance with PXRD and TG experiments. The single-crystal X-ray diffraction studies were performed at the Centre of Shared Equipment of IGIC RAS.References
- Y. Qiu, et al., Developing solid oral dosage forms: pharmaceutical theory and practice, Academic press, 2016 Search PubMed.
- J. M. Miller, et al., Solvent Systems for Crystallization and Polymorph Selection, in Solvent Systems and Their Selection in Pharmaceutics and Biopharmaceutics, ed. P. Augustijns and M. E. Brewster, Springer New York, New York, NY, 2007, pp. 53–109 Search PubMed.
- J. Aaltonen, et al., Solid form screening – A review, Eur. J. Pharm. Biopharm., 2009, 71(1), 23–37 CrossRef CAS PubMed.
- A. Newman, Specialized Solid Form Screening Techniques, Org. Process Res. Dev., 2013, 17(3), 457–471 CrossRef CAS.
- A. Newman, C. Chen and C. Sanrame, Salt and Cocrystal Screening, in Early Drug Development, 2018, pp. 229–270 Search PubMed.
- U. J. Griesser, The Importance of Solvates, in Polymorphism: in the Pharmaceutical Industry, ed. R. Hilfiker, 2006, pp. 211–233 Search PubMed.
- B. Zhu, et al., Solid-State Characterization and Insight into Transformations and Stability of Apatinib Mesylate Solvates, Cryst. Growth Des., 2017, 17(11), 5994–6005 CrossRef CAS.
- H. S. Shah, et al., Molecular Insights into Warfarin Sodium 2-Propanol Solvate Solid Form Changes and Disproportionation Using a Low Volume Two-Stage Dissolution Approach, Mol. Pharmaceutics, 2021, 18(4), 1779–1791 CrossRef CAS PubMed.
- B. Zhu, et al., Study of Crystal Structures, Properties, and Form Transformations among a Polymorph, Hydrates, and Solvates of Apatinib, Cryst. Growth Des., 2019, 19(5), 3060–3069 CrossRef CAS.
- G. Zhang, et al., Hydrates and Solvates of Acotiamide Hydrochloride: Crystallization, Structure, Stability, and Solubility, Cryst. Growth Des., 2019, 19(2), 768–779 CrossRef CAS.
- C. Weiss, et al., Preparation and Characterization of Beclomethasone Dipropionate Solvates, Cryst. Growth Des., 2018, 18(10), 5832–5844 CrossRef CAS.
- P. Klitou, et al., Solid-State Characterization and Role of Solvent Molecules on the Crystal Structure, Packing, and Physiochemical Properties of Different Quercetin Solvates, Cryst. Growth Des., 2020, 20(10), 6573–6584 CrossRef CAS.
- A. Y. Lee, D. Erdemir and A. S. Myerson, Crystal Polymorphism in Chemical Process Development, Annu. Rev. Chem. Biomol. Eng., 2011, 2(1), 259–280 CrossRef CAS PubMed.
- J. Mahieux, M. Sanselme and G. Coquerel, Access to Several Polymorphic Forms of (±)-Modafinil by Using Various Solvation–Desolvation Processes, Cryst. Growth Des., 2016, 16(1), 396–405 CrossRef CAS.
- A. Kons, et al., Polymorphism of R-Encenicline Hydrochloride: Access to the Highest Number of Structurally Characterized Polymorphs Using Desolvation of Various Solvates, Cryst. Growth Des., 2019, 19(8), 4765–4773 CrossRef CAS.
- J. B. de Maere d'Aertrycke, et al., Enabling Cocrystallization of Challenging Systems: Passing through a Stable Cocrystal Solvate as a Pathway to Strenuous Cocrystal Forms, Cryst. Growth Des., 2020, 20(3), 2035–2043 CrossRef.
- S. Gundlapalli, et al., Novel solid forms of insomnia drug suvorexant with improved solubility and dissolution: accessing salts from a salt solvate route, CrystEngComm, 2021, 23(44), 7739–7749 RSC.
- L. Maini, et al., Crystal Forms of Enzalutamide and a Crystal Engineering Route to Drug Purification, Cryst. Growth Des., 2018, 18(7), 3774–3780 CrossRef CAS.
- A. Nangia and G. R. Desiraju, Pseudopolymorphism: occurrences of hydrogen bonding organic solvents in molecular crystals, Chem. Commun., 1999,(7), 605–606 RSC.
- R. J. Davey, et al., Crystallising trimesic acid from DMSO solutions – can crystallography teach us anything about the process of crystal nucleation?, CrystEngComm, 2013, 15(5), 856–859 RSC.
- A. J. Cruz-Cabeza, et al., Can solvated intermediates inform us about nucleation pathways? The case of β-pABA, CrystEngComm, 2020, 22(43), 7447–7459 RSC.
- C. R. Groom, et al., The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- L. Iuzzolino, Survey of Crystallographic Data and Thermodynamic Stabilities of Pharmaceutical Solvates: A Step toward Predicting the Formation of Drug Solvent Adducts, Cryst. Growth Des., 2021, 21(8), 4362–4371 CrossRef CAS.
- J. C. Cole, P. R. Raithby and R. Taylor, Prior Likelihoods and Space-Group Preferences of Solvates, Cryst. Growth Des., 2021, 21(2), 1178–1189 CrossRef CAS.
- J. E. Werner and J. A. Swift, Organic solvates in the Cambridge Structural Database, CrystEngComm, 2021, 23(7), 1555–1565 RSC.
- A. J. Cruz-Cabeza, S. E. Wright and A. Bacchi, On the entropy cost of making solvates, Chem. Commun., 2020, 56(38), 5127–5130 RSC.
- C. P. Price, G. D. Glick and A. J. Matzger, Dissecting the Behavior of a Promiscuous Solvate Former, Angew. Chem., Int. Ed., 2006, 45(13), 2062–2066 CrossRef CAS PubMed.
- A. B
![[e with combining overline]](https://www.rsc.org/images/entities/char_0065_0305.gif) rziņš, D. Zvaniņa and A. Trimdale, Detailed Analysis of Packing Efficiency Allows Rationalization of Solvate Formation Propensity for Selected Structurally Similar Organic Molecules, Cryst. Growth Des., 2018, 18(4), 2040–2045 CrossRef.
rziņš, D. Zvaniņa and A. Trimdale, Detailed Analysis of Packing Efficiency Allows Rationalization of Solvate Formation Propensity for Selected Structurally Similar Organic Molecules, Cryst. Growth Des., 2018, 18(4), 2040–2045 CrossRef. - A. B
![[e with combining overline]](https://www.rsc.org/images/entities/char_0065_0305.gif) rziņš,
et al., On the Rationalization of Formation of Solvates: Experimental and Computational Study of Solid Forms of Several Nitrobenzoic Acid Derivatives, Cryst. Growth Des., 2020, 20(9), 5767–5784 CrossRef.
rziņš,
et al., On the Rationalization of Formation of Solvates: Experimental and Computational Study of Solid Forms of Several Nitrobenzoic Acid Derivatives, Cryst. Growth Des., 2020, 20(9), 5767–5784 CrossRef. - J. El-Amm and J. B. Aragon-Ching, The Current Landscape of Treatment in Non-Metastatic Castration-Resistant Prostate Cancer, Clin. Med. Insights: Oncol., 2019, 13, 1179554919833927 Search PubMed.
- N. J. Clegg, et al., ARN-509: A Novel Antiandrogen for Prostate Cancer Treatment, Cancer Res., 2012, 72(6), 1494–1503 CrossRef CAS PubMed.
- T. V. Volkova, K. V. Drozd and A. O. Surov, Effect of polymers and cyclodextrins on solubility, permeability and distribution of enzalutamide and apalutamide antiandrogens, J. Mol. Liq., 2021, 322, 114937 CrossRef CAS.
- D. L. Hughes, Review of Synthetic Routes and Crystalline Forms of the Antiandrogen Oncology Drugs Enzalutamide, Apalutamide, and Darolutamide, Org. Process Res. Dev., 2020, 24(3), 347–362 CrossRef CAS.
- A. R. Muthusamy, et al., SOLID STATE FORMS OF APALUTAMIDE, Int. Pat., App. WO2018/112001, 2018 Search PubMed.
- A. Dilhas, et al., CRYSTALLINE FORMS OF AN ANDROGEN RECEPTOR MODULATOR, US Pat., App. 2015/0133481 A1, 2015 Search PubMed.
- M. Chen, et al., CRYSTALLINE FORMS OF ARN-509, PREPARATION METHOD AND USE THEREOF, US Pat., App. 2020/0270226 A1, 2020 Search PubMed.
- V. N. Saladi, et al., Novel Pharmaceutical Cocrystal of Apalutamide, a Nonsteroidal Antiandrogen Drug: Synthesis, Crystal Structure, Dissolution, Stress, and Excipient Compatibility, Cryst. Growth Des., 2022, 22(2), 1130–1142 CrossRef CAS.
- G. Sheldrick, SADABS, Program for scaling and correction of area detector data, University of Göttingen, Germany, 1997.
- APEX3, SAINT and SADABS, Bruker AXS Inc., Wisconsin, USA, 2016.
- G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71(1), 3–8 CrossRef PubMed.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71(1), 3–8 Search PubMed.
- G. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64(1), 112–122 CrossRef CAS PubMed.
- K. Brandenburg and H. Putz, DIAMOND, Crystal Impact GbR, Bonn, Germany, 2005.
- C. F. Macrae, et al., Mercury 4.0: from visualization to analysis, design and prediction, J. Appl. Crystallogr., 2020, 53(1), 226–235 CrossRef CAS PubMed.
- R. Dovesi, et al., Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(4), e1360 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96(3), 2155–2160 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37(2), 785–789 CrossRef CAS PubMed.
- S. Grimme, et al., A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed.
- A. V. S. D. Surampudi, et al., Influence of crystal packing on the thermal properties of cocrystals and cocrystal solvates of olanzapine: insights from computations, CrystEngComm, 2020, 22(39), 6536–6558 RSC.
- Q. Tao, et al., Polymorphic Forms of a Molecular Salt of Phenazopyridine with 3,5-Dihydroxybenzoic Acid: Crystal Structures, Theoretical Calculations, Thermodynamic Stability, and Solubility Aspects, Cryst. Growth Des., 2019, 19(10), 5636–5647 CrossRef CAS.
- A. O. Surov, et al., Cocrystals of Fluconazole with Aromatic Carboxylic Acids: Competition between Anhydrous and Hydrated Solid Forms, Cryst. Growth Des., 2020, 20(2), 1218–1228 CrossRef CAS.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19(4), 553–566 CrossRef CAS.
- M. Turner, et al., CrystalExplorer 17.5, The University of Western Australia, Perth, WA, Australia, 2017.
- C. Gatti, V. R. Saunders and C. Roetti, Crystal field effects on the topological properties of the electron density in molecular crystals: The case of urea, J. Chem. Phys., 1994, 101(12), 10686–10696 CrossRef CAS.
- I. Mata, et al., Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields, Chem. Phys. Lett., 2011, 507(1), 185–189 CrossRef CAS.
- M. J. Frisch, et al., Gaussian09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016.
- I. Alkorta, J. Elguero and S. J. Grabowski, How To Determine Whether Intramolecular H⋯H Interactions Can Be Classified as Dihydrogen Bonds, J. Phys. Chem. A, 2008, 112(12), 2721–2727 CrossRef CAS PubMed.
- H. Suezawa, et al., Electronic substituent effect on intramolecular CH/π interaction as evidenced by NOE experiments, J. Chem. Soc., Perkin Trans. 2, 2000, 6, 1243–1249 RSC.
- R. Thakuria and A. Nangia, Olanzapinium Salts, Isostructural Solvates, and Their Physicochemical Properties, Cryst. Growth Des., 2013, 13(8), 3672–3680 CrossRef CAS.
- A. B
![[e with combining overline]](https://www.rsc.org/images/entities/char_0065_0305.gif) rziņš, T. Rekis and A. Actiņš, Comparison and Rationalization of Droperidol Isostructural Solvate Stability: An Experimental and Computational Study, Cryst. Growth Des., 2014, 14(7), 3639–3648 CrossRef.
rziņš, T. Rekis and A. Actiņš, Comparison and Rationalization of Droperidol Isostructural Solvate Stability: An Experimental and Computational Study, Cryst. Growth Des., 2014, 14(7), 3639–3648 CrossRef. - D. E. Braun, T. Gelbrich and U. J. Griesser, Experimental and computational approaches to produce and characterise isostructural solvates, CrystEngComm, 2019, 21(36), 5533–5545 RSC.
- H. Yang, et al., The Phase Transformation and Formation Mechanism of Isostructural Solvates: A Case Study of Azoxystrobin, Cryst. Growth Des., 2019, 19(3), 1550–1558 CrossRef CAS.
- A. D. Bond and C. C. Sun, Intermolecular interactions and disorder in six isostructural celecoxib solvates, Acta Crystallogr., Sect. C: Struct. Chem., 2020, 76(7), 632–638 CrossRef CAS PubMed.
- D. Samohvalov, et al., Isomorphic Channel-Type Pseudopolymorphs of Azathioprine: From Structural Confirmations to a Rational Polymorph Screening Approach, Cryst. Growth Des., 2021, 21(9), 4837–4846 CrossRef CAS.
- M. Nowak, et al., Directing Crystallization Outcomes of Conformationally Flexible Molecules: Polymorphs, Solvates, and Desolvation Pathways of Fluconazole, Mol. Pharmaceutics, 2022, 19(2), 456–471 CrossRef CAS PubMed.
- J. Rohlicek, et al., CrystalCMP: an easy-to-use tool for fast comparison of molecular packing, J. Appl. Crystallogr., 2016, 49(6), 2172–2183 CrossRef CAS.
- C.-H. Gu, et al., Grouping solvents by statistical analysis of solvent property parameters: implication to polymorph screening, Int. J. Pharm., 2004, 283(1), 117–125 CrossRef CAS PubMed.
- H. G. Brittain, Polymorphism in Pharmaceutical Solids, CRC Press, 2016 Search PubMed.
- A. O. Surov, et al., Diversity of felodipine solvates: Structure and physicochemical properties, CrystEngComm, 2015, 17(22), 4089–4097 RSC.
- K. Wang, C. Wang and C. C. Sun, Structural Insights into the Distinct Solid-State Properties and Interconversion of Celecoxib N-Methyl-2-pyrrolidone Solvates, Cryst. Growth Des., 2021, 21(1), 277–286 CrossRef CAS.
- S. Petit and G. Coquerel, Mechanism of Several Solid−Solid Transformations between Dihydrated and Anhydrous Copper(II) 8-Hydroxyquinolinates. Proposition for a Unified Model for the Dehydration of Molecular Crystals, Chem. Mater., 1996, 8(9), 2247–2258 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2151550–2151553 and 2152151–2152157. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00216g |
| This journal is © The Royal Society of Chemistry 2022 |